5

The Mathematization of the World

Philosophy is written in this very great book which always lies open before our eyes (I mean the universe), but one cannot understand it unless one first learns to understand the language and recognize the characters in which it is written. It is written in mathematical language and the characters are triangles, circles and other geometrical figures; without these means it is humanly impossible to understand a word of it; without these there is only clueless scrabbling around in a dark labyrinth.

– Galileo, The Assayer (1623)¹

§ 1

Double-entry bookkeeping goes back at least to the thirteenth century. The principle of double entry is simple: every transaction is entered twice, as a credit and as a debit. So if I buy a bar of gold worth £500, I credit £500 from my current account, and I debit £500 to my list of assets. If I borrow £500, then £500 is a debit to my current account, and a credit to my list of liabilities. In the Renaissance the standard system involved three books. First, a ‘waste book’, in which you recorded everything exactly as it happened, in as much detail as possible: you could refer to this in the event of any future dispute or confusion. Then a register in which you turned your record into a list of transactions. And then the account book proper, with debits and credits on facing pages. If you checked the account book against the register, and the debits against the credits, then you could be confident that the books were accurate; and every time you balanced the books you could establish whether you were making money or losing money. Accounting thus became the basis for rational investment choices and made it possible to decide how to divide up the profits of a partnership.²

Teaching bookkeeping was one of the main ways by which Italian mathematicians earned a living: this is what you learned at the scuola d’abbaco, the school for those going into business, where arithmetic and accountancy were taught. Double entry, like any mathematical technique, depends on abstraction. Bookkeeping turns everything into a notional cash value, even though you do not actually know if you will ever sell it or what you will get for it if you do. When two partners divide up the profits of a business between them they assign a notional book value to the stock in hand.

There would seem to be no connection between bookkeeping and science. But Galileo, who had probably taught bookkeeping himself when he was scrabbling a living together in the years between 1585, when he ceased to be a university student, and 1589, when he obtained his first university appointment, thought there was. When people complained to Galileo that his law of fall did not correspond to the real world, because falling objects do not accelerate continuously since they are retarded by air resistance, he replied that there was no contradiction between the world of theory and the real world, because:

[w]hat happens in the concrete … happens in the same way in the abstract. It would be novel indeed if computations and ratios made in abstract numbers should not thereafter correspond to concrete gold and silver coins and merchandise … Just as the bookkeeper who wants his calculations to deal with sugar, silk, and wool must discount the boxes, bales, and other packings, so the mathematical scientist, when he wants to recognize in the concrete the effects which he has proved in the abstract, must deduct the material hindrances, and if he is able to do so, I assure you that things are in no less agreement than arithmetical computations. The errors, then, lie not in the abstractness or concreteness, not in geometry or physics, but in a calculator who does not know how to make a true accounting.³

Double-entry bookkeeping thus represents an attempt to make the real world, the world of bolts of silk, bales of wool and bags of sugar, mathematically legible. The process of abstraction it teaches is an essential precondition for the new science.

§ 2

Another source of income for mathematicians in Galileo’s day was teaching the geometrical principles of perspective representation.⁴ Galileo’s own mathematics teacher, Ostilio Ricci, taught perspective to painters. Perspective painting was a more recent invention than double-entry bookkeeping. It began sometime between 1401 and 1413 when Filippo Brunelleschi produced a most peculiar work of art.⁵ The object itself no longer survives; we last hear of it in 1494, when it is listed among the effects of Lorenzo the Magnificent, the Medici ruler of Florence, on his death.⁶ Our only half-decent description of it was written in the 1480s, by Antonio Manetti, who was twenty-three years old when Brunelleschi died.⁷ Manetti’s account is puzzling and unsatisfactory, but it is all we have. There have been endless attempts to reconstruct exactly what Brunelleschi did, and why, for contemporaries were clear that this little object represented the birth of perspective painting.⁸ Every attempt at reconstruction runs into difficulties and we have not a single word from Brunelleschi to help us. But we must do the best we can.

The object was a painting on a wooden panel about twelve inches square. It showed the Baptistry in Florence, an octagonal building, and something of the buildings on either side. The top part of the painting, where the sky would have been, was covered in burnished silver. (Brunelleschi had trained as a goldsmith, so producing a flat, silvered surface would have been easy for him.) In this painting, in the centre near the bottom, Brunelleschi made a hole, and the viewer was invited to look through the back of the painting. If they stood in exactly the right place, the place where Brunelleschi intended them to stand when he made the painting, and held up a mirror in front of them while looking through the painting from behind, they would see the image of the painting overlapping with the real Baptistry, and by raising and lowering the mirror they could convince themselves that the painting looked just like the real thing. Because they were looking at both the painting and the real world through one eye, the painting would look more nearly three-dimensional, and the real world more two-dimensional, so the two would become more like each other.⁹ In the burnished silver of the painting the sky was reflected, so that clouds (if there were any) could be seen; reversed on the silver, the clouds would have been reversed again in the mirror so that they, too, would have corresponded to reality. It seems fair to say that Brunelleschi’s image aspires to exemplify what philosophers call a correspondence theory of truth, in which a statement or representation is true if it corresponds to external reality.¹⁰

It is clear that this strange peep-show set-up ensured that the viewer looked at both the painting and the Baptistry with one eye – geometrical perspective depends on a single point of view. But why use a mirror?¹¹ Why not look at the painting directly through a small hole in a board? Evidently, once Brunelleschi had silvered the upper part of his painting, he needed to place it where it could reflect the sky, and then the mirror became necessary if it was to reflect the sky above the Baptistry as it was at that particular moment and at the same time overlap with the real Baptistry. What is not clear is whether this was his original motive or if this was a feature of his peep-show of which he then decided to take advantage.

I want to stress the strangeness of this procedure. If you lowered not the mirror but the painting, what you would see is yourself. Even looking at the painting in the mirror, what you would see when you looked straight at it is the pupil of your own eye, and you would learn that there is a point in the picture which corresponds to or reflects the eye of the painter. This would later be called the centric point, and it is the spot where the vanishing point is placed in a vanishing-point construction. The viewer, in playing their part in the peep-show performance, was constantly reminded of their own role: at one moment they made reality appear and disappear; at another they made themselves the object of their own inspection. Brunelleschi’s ingenious construction serves a double function: it demonstrates that art can successfully imitate nature, so that the two are almost indistinguishable; and it demonstrates that even when art is at its most objective (or rather, especially when art is at its most objective), we make it and we find ourselves in it. It is an exercise, simultaneously, in a new objectivity and a new subjectivity.

After he had produced this image Brunelleschi produced a second one, which we also learn about from Manetti, of the Florentine town hall and the square surrounding it. This time he cut away the board at the skyline, so that a viewer would see the real sky (a neater solution, in many respects, than burnished silver). This time there was no mirror. This object, too, was obviously site specific: you would stand where Brunelleschi stood when he painted it; when raised up the painting would perfectly mask and exactly reproduce the real buildings; when lowered you would see the real buildings. Back and forth you could go, confirming the exact correspondence between reality and image, making and unmaking your own world.

It is evident that both paintings avoided the obvious method of demonstrating depth in a two-dimensional image, which is to show orthogonals, parallel lines running at right angles to the picture plane and converging on a vanishing point. The most straightforward example is a tiled floor.ii Instead, both pictures must have used two-point perspective, where lines which are neither parallel to the picture plane nor at right angles to it converge on distance points to the left and right of the picture plane itself. If Brunelleschi wanted to experiment with depth of field, why not use a vanishing-point perspective, which would have been straightforward, and indeed familiar to him? Ambrogio Lorenzetti’s Annunciation of 1344, for example, uses a tiled floor and converging parallels to create a sense of depth of field.iiii Lorenzetti had not mastered all the complexities of perspective construction – see how the back of Mary’s chair is higher than the front, and how the angel’s left foot is no further back than his right knee. But he did know how to make a tiled floor recede into the distance. If Brunelleschi was simply trying to create an impression of depth, he could have simply shown an interior with a tiled floor.

So what was Brunelleschi up to? A standard view (which can appeal to Vasari’s Lives of the Artists (1550) for support, though Vasari was writing long after the event) is that Brunelleschi was illustrating the geometrical principles of perspective drawing, codified by Alberti more than twenty years later in 1435, in On Painting, a work that founded a long tradition of writing texts on geometrical perspective.¹² We can reasonably assume that Brunelleschi had a fairly sophisticated grasp of geometry. We know he had only a limited education; his father had ensured that he learnt some Latin, probably with a view to his following in his own footsteps as a notary, but Brunelleschi had decided to apprentice as a goldsmith. Then he had turned from jewellery to architecture (he is most famous for having designed the dome of Florence’s cathedral in 1418, a work based on classical models and quite unlike any medieval construction). However, if Brunelleschi had mastered the geometry of perspective as early as 1413 it becomes a little difficult to explain why there are no surviving paintings which embody these principles before 1425. Indeed, it used to be thought that Brunelleschi had produced his demonstration images around 1425 simply because scholars wanted to envisage these images as immediately provoking new art and new theories. Recent documentary evidence, however, strongly implies (as indeed does Manetti’s text) that Brunelleschi’s images were produced earlier. This obliges us to reconsider just exactly what it was that he had accomplished.¹³

It has been argued that both Brunelleschi and Alberti were applying to painting the theories of medieval optics, which ultimately derived from an eleventh-century Arabic author, Ibn al-Haytham, known in the West as Alhazen, whose works were available in both Latin and Italian translations. These works on optics were about ‘perspective’, a term which meant ‘the science of sight’. Alhazen had shown how light travels in straight lines, so that vision depends on a cone of straight lines extending outward from the eye to the object. Depth of field is thus not experienced directly; it is a result of binocular vision and of our capacity to interpret the way in which things closer to us look bigger and things further from us look smaller, so that, to judge distance, we need a reference point – an object whose distance or size is known to us. It is easy to understand why Alhazen had concerned himself only with how we see, not with how we might represent the world in a painting: representational art was forbidden in the Islam of his day. But it is harder to understand why his medieval successors had not developed his theories in order to show how they might be put to work by artists.¹⁴

One claim is that even if the university experts did not discuss painting explicitly, the painters learnt about their theories. Giotto (1266–1337) did his most important work in Franciscan churches, and as it happens the libraries of the friaries attached to those churches contained the crucial texts on perspective. The friars who commissioned his work had, as followers of St Francis, a love of the natural world, and thus a desire for a new realism in art. They would have wanted him to produce a sense of depth because they knew from studying the theory of vision that we make sense of the world by turning a two-dimensional sensation (light rays falling on the eye) into a three-dimensional experience. Giotto’s art, which included using trompe l’oeil to create the illusion of non-existent columns, was, it is suggested, the result of a dialogue with his employers.¹⁵ This is very likely, but there is an important caveat: the medieval theory of vision provided the elements of a theory of what we now call perspective (what came to be called in the Renaissance ‘artificial perspective’), but it did not provide a systematic account of how to create the illusion of three-dimensionality. If it had, Giotto would have completed the perspectival revolution, Brunelleschi’s images would have been unnecessary, and Alberti would have had nothing new to say. It may have seemed to a contemporary that ‘there is nothing which Giotto could not have portrayed in such a manner so as to deceive the sense of sight,’¹⁶ but we may doubt whether Giotto aspired to create images which corresponded throughout to visual reality. Is the angel flying through the wall of the Annunciation of St Anne intended to be an accurate representation of what Mary saw?iiiiii The question is surely misplaced. The reality Giotto wants to convey is not just visual, while in Brunelleschi’s test pieces the whole and sole point is geometrical precision.

We do know that Brunelleschi, in his search for new architectural forms, had made a study of the surviving classical buildings in ancient Rome, a study which involved taking measurements and drawing plans and elevations. He would thus have been familiar with the basic principle that objects appear smaller as they recede into the distance, a principle analysed by Euclid, and familiar in the Middle Ages.¹⁷ This principle makes it possible to work out how big an object is if you know how far away it is and measure the angle, as seen from where you are, between its top and its bottom. Brunelleschi would have had plenty of practice in applying this knowledge when he set out to measure the height of surviving classical buildings in Rome in 1402–4.¹⁸ But there was nothing new about this principle, and the resulting knowledge would have been most obviously useful in drawing standard elevations, rather than perspective images, so it is hard to see why it would suddenly produce a new type of artistic representation.

So we seem to have various elements that might contribute to an answer to the question of what made possible the invention of perspective painting – the application of geometry, medieval optics, the surveying of old buildings – but they do not seem quite sufficient.¹⁹ The crucial missing element, I believe, is provided by the Florentine artist known as Filarete (‘lover of excellence’), who wrote a work on architecture completed around 1461 – this is indeed our earliest source.²⁰ Filarete was twenty-three years older than Manetti, and thus perhaps had a better understanding of Brunelleschi’s world. Filarete was convinced that Brunelleschi had come up with his new method of perspective representation (which he does not describe in any detail) as a result of studying mirrors. The mirror is indeed the obvious source of a correspondence theory of art (and truth). It not only provides the appearance of three dimensions on a two-dimensional surface, it also makes it easy to answer the question ‘How big does the Baptistry look from here?’ Trying to answer that question by measuring angles and distances would be much more complicated than simply holding up a mirror. The mirror works as a scaling device; it is able to do this because it reflects the cone of rays coming from an object as they pass through a plane. This alerts us to a feature of Brunelleschi’s peep-show I have not previously mentioned: he stood, according to Manetti, inside the porch of the cathedral. His view would therefore have been framed by the porch; indeed, his picture may have simply reproduced the view within the frame, as if he were looking through a window.

Some have concluded from Filarete’s comments that Brunelleschi’s board was burnished all over – that he painted on a mirror. But Manetti, who had held the board in his hand, would surely have noticed this. Much more likely is that he had his board and a mirror side by side on an easel. This explains the peculiarly small size of Brunelleschi’s first image: good-quality mirrors were very rare and very expensive at the beginning of the fifteenth century (the revolution associated with Venetian mirrors occurred a century later), and glass mirrors were always small.²¹ Working from a mirror, of course, would produce a reversed image, hence Brunelleschi’s interest in looking at his painting reflected in a mirror – and, happily, he had one to hand. It is true that the Baptistry is a symmetrical building, which means that a reversed image would have been very like a normal view; but Manetti tells us that the square on either side of the Baptistry could be seen, and even a symmetrical building will have markers on it (shadows and moss, for example) which are not symmetrical. Working with a mirror would also have involved Brunelleschi in an endless struggle: he would have wanted to see the Baptistry reflected without distortion in the mirror, but if he placed himself directly in front of the mirror what he would have seen is himself (which is why it is easy to use mirrors for self-portraits). The peculiar feature of his peep-show construction, that the viewer is looking at himself as well as at the painting, simply recapitulates this earlier tension.

It would have been at the point when he looked at his painting in a mirror in order to see it the right way round that Brunelleschi realized he could lay burnished silver on the board to reflect the sky. And it is also at this point that he would have made an unfortunate discovery: looking at his image in a mirror will have had the effect of halving its height. A painting made to correspond exactly in size to the Baptistry when seen from the porch of the cathedral would have ended up one quarter the size because the effect of the mirror would have been to double the apparent distance between the viewer and the Baptistry.²² Of course, Brunelleschi could have foreseen this problem and scaled up his image to allow for it – but we know he did not, because we know he wanted the viewer to stand where the painting had been made, in the porch, and it is easy to show that, standing in that position, an image one foot square would have corresponded to the apparent size of the Baptistry. In order to scale up to allow for the second reflection, Brunelleschi’s board would have needed to have an area of four square feet, not one.

So what had Brunelleschi learnt from his peep-show, apart from the difficulties of working with mirrors? He was demonstrating in this first image that perspective drawing involves establishing a picture plane through which the image is viewed. He took this new understanding forward into his second image, of the town hall. Perhaps this time he worked from an image created in two mirrors (a procedure Filarete recommends). Perhaps he began by looking through translucent parchment and inking an outline directly on to it. Alberti was the first to devise (cuius ego usum nunc primum adinveni; ‘the use of which I found out for the first time just recently’, with primum adinveni often translated as ‘discover’) a method of looking through a grid and using the lines of the grid as reference points – or at least he claimed to have invented this method in the Latin text of On Painting (1435); the claim does not appear in the Italian version.²³ When Alberti says that he does not understand how anyone could ever achieve even moderate success in perspective representation without using his method, one begins to suspect that Brunelleschi may have beaten him to it, and the revision to his text may be taken as confirmation that he had belatedly discovered as much.²⁴ This method later became well known and was illustrated, for example, by Leonardo, Dürer and Vignole (see plate 16).

If this reconstruction is right – that Brunelleschi started by representing what he saw in a mirror – then he was learning to understand that perspective drawing involves establishing a picture plane through which the scene is viewed, and the task of the artist is to construct an image that corresponds to the image as it would appear on a piece of glass placed on that plane. It was this principle that Alberti invoked when he compared a painting to a window that you look through to see the scene beyond, and which led Dürer to claim that the word ‘perspective’ comes from the Latin perspicere in the sense of ‘to see through’, when in fact it comes from its sense of ‘to see clearly’.²⁵ What Brunelleschi had discovered was not the vanishing-point or the distance-point construction; he had not engaged in elaborate measurements or sophisticated geometrical constructions, even if he had the competence to perform them. He had learnt to think of the painted surface as a piece of glass that you look through. He had also learnt something of enormous importance: that for a perspective construction to work, the artist and the viewer must have their eye located in the same place, and to this place there corresponds a point in the picture directly opposite the artist’s eye. A perspective painting appears to be a totally objective representation of reality, yet it depends on having a viewer prepared to look at it in the right way, and when they do this, the viewer can in effect locate themselves in relation to the picture. Brunelleschi’s paintings did not have vanishing points, but they did have situated viewers.

§ 3

Roughly two decades separate Brunelleschi’s first studies and Masaccio’s famous painting of the Trinity (c.1425), the first large-scale painting which fully masters the technique of perspective representation.iviv Masaccio’s painting shows Christ on the cross in front of a chapel with a barrel vault – but of course the chapel does not exist; it is entirely a painted chapel. Here is the difference between Brunelleschi’s studies and Masaccio’s painting: Brunelleschi was representing reality; Masaccio is representing an imaginary space. You can use the various picture-plane techniques to paint reality; but if you want to paint an imaginary world you have to work out how to construct that world so that it appears convincing and aesthetically satisfying.²⁶ You have to decide where you want the vanishing point and/or the distance points to be. You have to sketch out a grid of converging lines. You have to apply the principles of geometry. And we know that this is precisely what Masaccio did: we can see the lines he scored in the plaster on which he painted.²⁷ We know that Brunelleschi discussed perspective with Masaccio,²⁸ and that Alberti was soon to write a textbook on geometrical perspective.

Thus it would seem to be Masaccio who was responsible for the next stage in the development of perspective painting, and it was of course the crucial stage, as most Renaissance art was religious art, and religious art is almost never a direct representation of presently existing reality. Of course painters had models. Masaccio’s patrons, who had paid for his painting, appear on either side, kneeling. Masaccio may well have gone to look at an actual barrel-vaulted chapel and copied actual columns. But to fit these elements on to this wall he had to do sketches, draw converging lines, work out scales and foreshortening. He had to construct a theoretical space which became a painted space.

Perspective painting thus involves the application of theory to particular circumstances. It provides an abstract account of lines in space, travelling from the object, through the picture plane, to the eye, and an account of how these lines appear on the picture plane itself. It trains the eye to think in terms of geometrical shapes. A straightforward example of this is provided by Father Niceron’s Curious Perspective of 1652.²⁹ Niceron explains how to produce anamorphic shapes: shapes like the skull in Holbein’s Ambassadors, which takes form as a skull only if you view it at a sharp angle to the picture’s surface. But first he has to train the reader in understanding and representing shapes.

Take his demonstration of how to draw a chair. First, he shows how to draw a simple rectangular box. Then he adds a back and feet to it. The result looks like a Bauhaus chair for the simple reason that it is a chair made from the simplest of geometrical forms. It looks nothing like a seventeenth-century chair because no seventeenth-century chair would have been entirely devoid of curves and decoration – just look at the curly ribbon which serves as a label to get a sense of the period’s aesthetic. It is an abstract or theoretical chair, a geometer’s chair, not a real chair. Learning to look like this involved learning to isolate mathematical shapes within more complex objects.

Naturally, as soon as they became familiar with the geometrical techniques of perspective representation, artists became fascinated by mathematical shapes and the difficulties of drawing them. Leonardo himself provided the illustrations to Luca Pacioli’s On Divine Proportion (1509). The two were evidently good friends; they were both employed by Ludovico Sforza, Duke of Milan, and they fled Milan together in 1499 when the city fell to the French, ending up in Florence, where for a while they roomed together. In a portrait of Pacioli we see two such shapes: one, a dodecahedron (a regular solid with twelve faces), is sitting on top of a book written by Pacioli; the other, a rhombicuboctahedron (a symmetrical solid with twenty-six faces), is made of glass sheets and has been half filled with water.vv It hangs from the finest thread in empty space, a decorative object, as interesting for the way in which it catches the light as for its geometrical form.³⁰

Pacioli is caught explaining a problem from Euclid to a pupil: Euclid is open on his desk, he is drawing the figure required to understand the problem on a slate, and scattered across the table he has his mathematical drawing instruments and the little tubular case that holds them. Unlike his pupil, Pacioli is not looking at us (he is thinking deep thoughts); but we are looking at him, for his eyes are at the centric point, directly opposite the artist’s and our own (as is emphasized by the stylus he is holding). It is the handsome and aristocratic young man whose eyes are directed at the artist, or at us. Pacioli is a mathematician; the person who painted him was surely also a mathematician, as demonstrated by his understanding of complex mathematical shapes.vivi In portraying a mathematician the artist is thus portraying a version of himself: some even think that the young man in the painting is a self-portrait, in which case the eyes directed at the viewer are a tell-tale indication of a mirror image.viivii

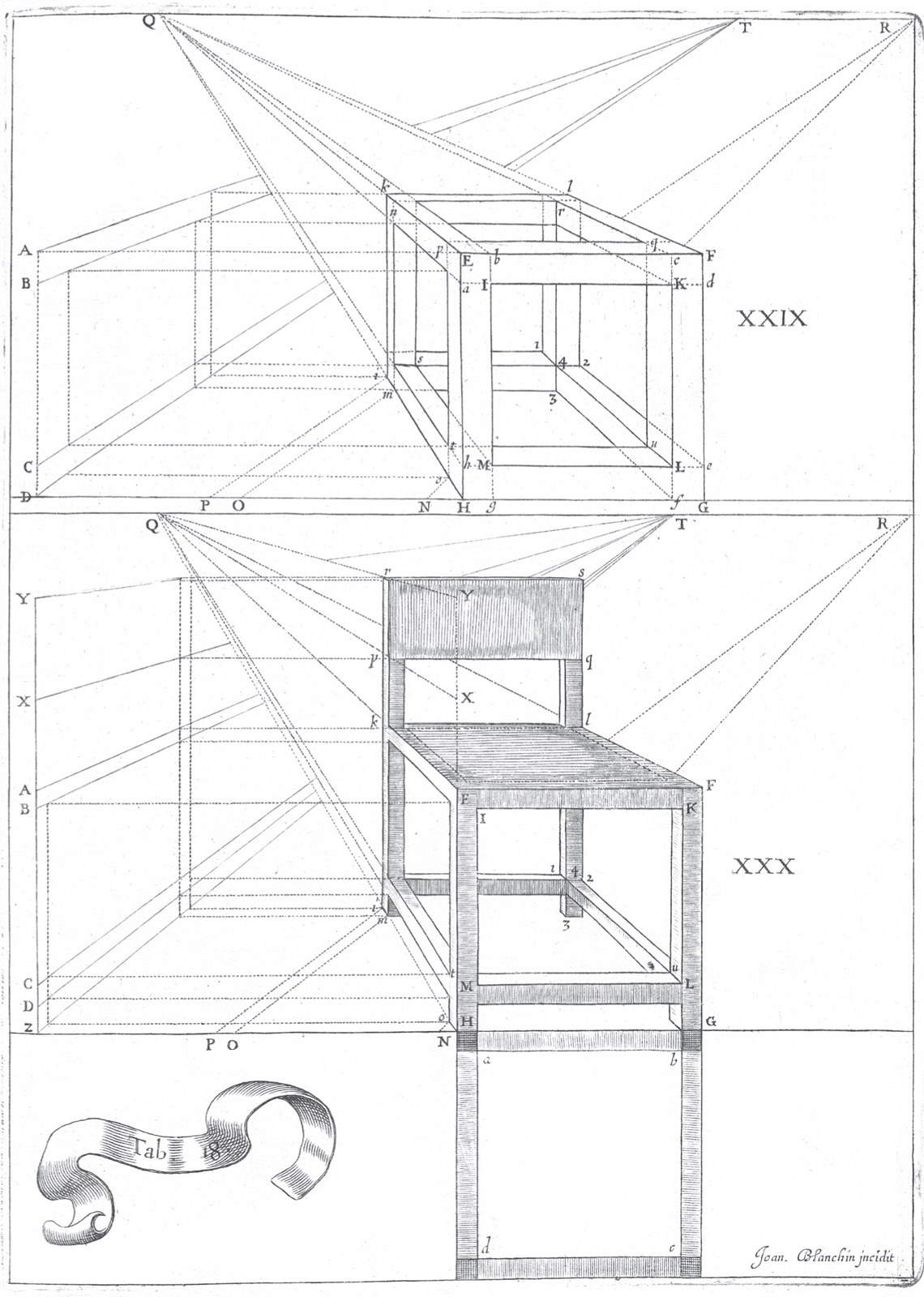
From Niceron’s Curious Perspective (1652): a chair reduced to a problem in geometrical construction.

I doubt both this and the traditional attribution to Jacopo de’ Barbari. On the desk, in front of the young man, is a slip of paper on which a fly is sitting. The paper reads ‘Iaco. Bar. Vigennis. P. 1495’. This has been taken to be a signature, and so the painter has been identified as Jacopo de’ Barbari, although this looks nothing like his work and he was not twenty (vigennis), but a good deal older, in 1495.viiiviii No one seems to have proposed the obvious explanation, that the slip of paper identifies not the artist but the young man (‘P.’ for pictum not pincit), who may well be twenty years old. There are plenty of Italians called Giacomo with last names beginning ‘Bar’ (Bardi, Barozzi, Bartolini, Bartolozzi, and so on). Since the painting originally bore an inscription dedicating it to Guidobaldo da Montefeltro, Duke of Urbino (and a pupil of Pacioli), and it was hung in his dressing room, we can probably assume that Iaco. Bar. was a friend of his, and that it is the prince’s eyes that meet with his. Why record, even in abbreviated fashion, the young man’s name? Again the obvious explanation would seem to be that the painting is some kind of memorial – perhaps he is dead, perhaps he has gone away.

Thus the painting belongs to the court life of Urbino. It was in Guidobaldo’s library that Polydore Vergil wrote On Discovery. Working in this superb room, which not only contained an abundance of books but was embellished with gold and silver, gave Vergil such a distorted view of the world that he claimed that in his day any scholar, no matter how needy, could lay their hands on any book they wanted.³¹ Guidobaldo’s court was later made famous by Castiglione, who set his Courtier (1528) there, notionally locating the imaginary discussions he recorded in 1507. Guidobaldo himself never appears in Castiglione’s book: he lies sick in bed while his wife Elisabetta takes charge.

The portrait of Pacioli illustrates the way in which, once perspective had been discovered, mathematics and art went hand in hand. Piero della Francesca wrote a number of mathematics texts (two survive: The Abacus Treatise and The Short Book on the Five Regular Solids) which deal with practical problems such as how to work out how much grain there is in a conical heap, or how much wine there is in a barrel, as well as a book on perspective, On Perspective for Painting.³² Such problems turn real objects – heaps of grain, barrels of wine – into abstract shapes so that mathematical principles can be applied to them. Pacioli’s publications reproduce material from Piero’s books wholesale. Pacioli was not only a friend of Leonardo but also of Alberti, with whom he stayed for some months as a young man. He was not himself an artist, but On Divine Proportion discusses the golden section, the principles of architecture and the design of typefaces. Pacioli is now known primarily for the fat book on which the dodecahedron sits: A Compendium of Arithmetic, Geometry, Proportions and Proportionality (1494). This was a textbook of applied mathematics, and included within it was the first published account of double-entry bookkeeping – double entry was not new, but printing was, so Pacioli was taking advantage of an obvious opportunity.³³

§ 4

Perspective painting generally involves a peculiar form of abstraction: the construction of a vanishing point. It is worth noting that the term itself is relatively modern: in English it dates to 1715. Alberti calls it the centric point (il punto del centro), and in many early texts it is simply referred to as the horizon.³⁴ But Alberti is perfectly clear that the image in a one-point-perspective painting extends ‘to an almost infinite distance’.³⁵ This, to a Renaissance intellectual, is a deeply puzzling concept. Aristotle’s universe is finite and spherical; moreover, it is not surrounded by infinite space and there is no such thing as empty space. Indeed, Aristotle does not really have a concept of space as distinct from the objects which fill it. So, for Aristotle, all space is finite, all space is place, and the idea of an infinite extension is conceptually contradictory, just like the idea of a vacuum.³⁶

This is not true, of course, in Euclidean geometry, where parallel lines can be extended indefinitely without meeting (nor, it may be added, in the optics of Alhazen). But what you can see when you look across an infinite distance is precisely nothing. It helps, then, if you want to work with a vanishing point, to have a concept of nothing. Euclid lacked the number zero, which was introduced into Western Europe in the early thirteenth century with what we call the Arabic numerals (actually, it is the only one of the ten numerals that is Arabic; the others are Indian). Arabic numerals made possible the paper-based accounting of double-entry bookkeeping. Zeros are wonderfully useful, even if deeply mysterious; perhaps only a culture which had the number zero could have made sense of the idea that a vanishing point could both be a point of non-seeing and the key to the interpretation of a painting.³⁷

As a consequence of the vanishing point, artists found themselves living simultaneously in two incommensurable worlds. On the one hand, they knew the universe to be finite. On the other, perspective geometry required them to think of it as infinite. A good example of this is provided by Cesare Cesariano’s commentary on Vitruvius (1521). Cesariano provides perfectly conventional illustrations of the Aristotelian universe as a series of bounded spheres. But when he introduces the idea of measuring distances he imagines measuring the distance to the sun and the planets and onwards and outwards for ever: he explicitly states that the lines from the spectator through points T and M (picture below) extend to infinity. Perspective thus introduced an anomalous concept of infinity into a finite universe.³⁸

Handling this presented problems for artists. In early perspective paintings the vanishing point is often hidden by a seemingly casually placed foot or a bit of drapery. In religious images, the lurking presence of the infinite could be put to good use. Thus the vanishing point in Masaccio’s Trinity is just above the top of the tomb, in apparently featureless space. But the painting originally had an altar standing in front of it, and the vanishing point would have lain immediately behind the host when the priest elevated it at the dramatic high point of the Mass, the moment when transubstantiation occurs. This is the point to which the viewer’s eyes are drawn. (So successful was Masaccio’s painting in providing a setting for the host that it was soon being copied in the design of tabernacles – wooden boxes constructed to hold the consecrated host.) Similarly, in Masaccio’s Tribute Money the vanishing point lies behind Christ’s head.³⁹

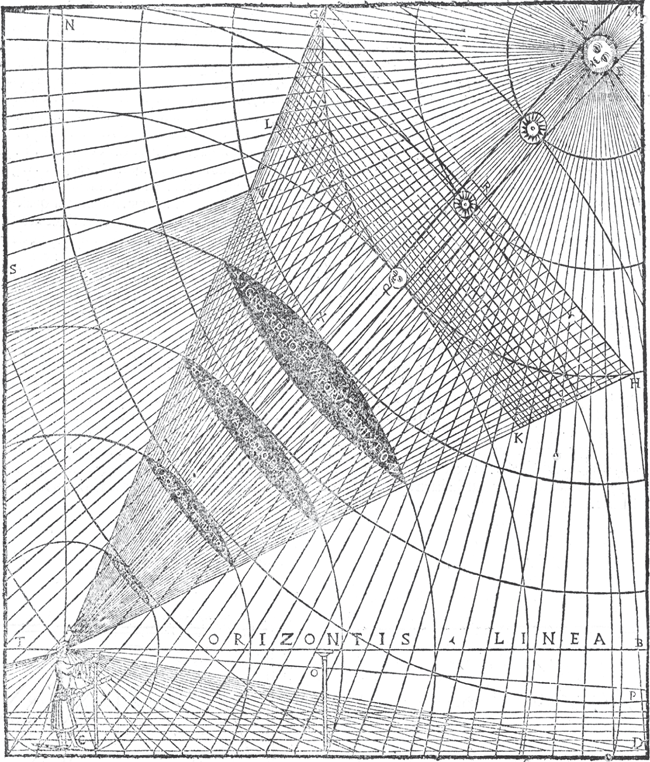
Measuring the universe, from Vitruvius, De architectura (1521), with commentary by Cesare Cesariano.

One particular subject which encouraged artists to explore the vanishing point was the Annunciation. Mary’s womb was compared to a closed garden (‘A garden enclosed is my sister, my spouse; a garden enclosed, a fountain sealed up,’ it says in the Song of Songs), so a closed door leading to a garden was often placed at the vanishing point.⁴⁰ But the incarnation of Christ restores to human beings the possibility of salvation, reopening the gates of Eden, which had been closed against Adam and Eve, and opening to believers the gates of paradise. So an open door leading to a garden could symbolize salvation. And, of course, God is infinite, so the Annunciation represents an encounter between the finite human and the infinite divine: in Piero della Francesa’s Annunciation the vanishing point seems to be used simply to evoke the presence of infinity, and the swirling patterns of marble become a symbolic representation of a God who cannot be seen, or comprehended.ixix

In secular paintings, however, the vanishing point had to be kept under control, for the human world is finite and limited. Thus in a painting of an ideal city, dating to 1480–4 and attributed to Fra Carnevale, the two lines of buildings on either side of a piazza point into the far distance, but that space is blocked by a temple, in which a half-open door suggests that one could explore further, but only within an enclosed space.xx If there is infinity to be found here, it is within a closed religious space. In Uccello’s Hunt by Night there is an alarming multiplication of vanishing points, all of which lead into the darkness. One has a strong sense of how easy it would be to become lost, or for the stag to escape; the painting is a play on the idea of disappearance, for the viewer’s sight disappears into the dark rather than into an infinite distance.

§ 5

By the middle of the fifteenth century artists were experimenting with the idea of infinite, abstract, undifferentiated space. They knew this idea was problematic and anomalous, but they also knew that without it there could be no perspective representation. Art had escaped, or partially escaped, from Aristotle, and it had done so under the guidance of geometry and optics. But perspective also encouraged a new way of looking at the world in three dimensions and of recording what one had seen. This made it possible to see things no one had seen before and to do things no one had done before.

Before perspective drawing, if you wanted to design a piece of machinery, you had to make it, or make a model of it. There was no substitute for working with three-dimensional materials. But once engineers had acquired the capacity to draw three dimensions they could design with a pen or a pencil (the pencil was invented around 1560) in their hand. Leonardo (1452–1519) designed plenty of machines that were never built, many (such as flying machines) that never could be built. Plate 15 shows his design for a ratchet winch. The winch itself is shown in the drawing to the left; on the right, the winch is shown taken apart (or ‘exploded’) to demonstrate its assembly. Each wheel is attached to a ratchet system. If you pull on the lever attached to the right of the winch assembly, one wheel grips and turns the axle, which lifts the weight. If you push, the other wheel grips, but it is geared so that the axle still turns in the same direction and the weight continues to rise. Since you can exert more force pulling and pushing on a lever than you can turning a crank, this is more efficient than a crank mechanism would be at lifting weights. Leonardo’s drawing is clear enough for a model of the machine to have been built and demonstrated to be functional. It is only a step from a drawing such as this to a modern blueprint. Leonardo’s sketch is already implicitly drawn to scale, with a detail of the ratchet mechanism shown at a higher level of magnification.⁴¹

Of course, making a real machine from a drawing is not straightforward. What tools would you require to construct Leonardo’s winch? If you were lifting a heavy weight and pulling hard on the lever, considerable force would be placed on the pegs that drive the mechanism. Out of what sort of wood would you need to make them? Books of drawings produced in the early modern period are mainly intended to advertise an engineer’s skills, not to provide you with the information you would need to do the job yourself. Even the elaborate plates in the great Encyclopaedia (1751–72) of Diderot and d’Alembert seem to be there to help you know what can be done, not to teach you how to do it. Nevertheless, there are examples of the successful transfer of designs through the medium of print. In 1602 Tycho Brahe published his Instruments for the Restoration of Astronomy, which provided elaborate illustrations of the new instruments he had devised for conducting astronomical observations. In Peking, in the 1670s, Ferdinand Verbiest, a Jesuit astronomer, was able to build instruments based on his designs without ever having seen Brahe’s originals.⁴²

Brahe’s design for an equatorial armillary sphere, from his Astronomiae instauratae mechanica (1598).

Apart from being an artist, an architect and an engineer (all professions requiring skills which interlock in their use of geometry and perspective), Leonardo did careful anatomical studies based on the dissection of animals and human beings. But, although he seems to have had plans to publish, he never did. The revolution in anatomy came with the publication of Andreas Vesalius’s On the Fabric of the Human Body (1543). Vesalius (who was teaching at the university of Padua) employed artists from Titian’s workshops in Venice to produce illustrations to the highest possible standard. The illustrations were keyed by letters to textual labels. Leonardo, in his drawing of the winch, was already using letters as labels, and the practice of course has its origins in geometrical diagrams, but Vesalius was the first person to make systematic use of it in anatomy. Vesalius could thus show the reader what he had seen in the body. The engraved plates produced in Venice were then carried over the Alps to Basle, as Vesalius did not trust the Venetian printers to produce work of sufficiently high quality.

The imperial observatory in Peking, from Ferdinand Verbiest, Xinzhi Yixiangtu (‘pictures of newly made instruments’), which was produced from 1668 to 1674, showing instruments built by the Jesuit missionary on the basis of Brahe’s designs.

The whole point of Vesalius’s Fabric is to insist that the evidence of one’s senses must take priority over Galen’s text. Medieval anatomists had frequently lectured by reading Galen aloud and commenting on his text, while assistants opened up the body: the body was intended to illustrate what Galen said, not to correct him when he was wrong. But, even when medieval anatomists had performed their own dissections, what they found (or thought they had found) was what Galen had told them to find. Mondino de Liuzzi (1270–1326), for example, the author of the first medieval textbook on how to perform a dissection, had plenty of hands-on experience, but he still found at the base of the human brain the rete mirabile (miraculous network) of blood vessels that Galen claimed was there, despite the fact that it isn’t there at all – it is only present in ungulates. Leonardo carried out dissections, but he still thought he found a channel linking the male penis to the spinal cord and so to the brain: down it he believed flowed material which became part of the ejaculate and was essential for generation. The first anatomist regularly to disagree with Galen on the basis of direct experience was Jacopo Berengario da Carpi, whose Anatomy was published in 1535, only a few years before Vesalius’s Fabric.⁴³ Only in a culture where the authority of the great classical authors such as Ptolemy and Galen had begun to be undermined could a project like Vesalius’s Fabric be undertaken. In this respect the coincidence in date between the great works of Copernicus and Vesalius points to an underlying correspondence: both lived in a world where respect for antiquity had been fatally weakened, at least among the intellectually adventurous, by the new culture of innovation.

Galen’s text had never been accompanied by illustrations – Galen explicitly said that illustrations were worthless – because in a manuscript culture complex illustrations degrade rapidly each time they are copied.xixi⁴⁴ Thus it was often far from clear exactly what Galen was describing. With Vesalius, on the other hand, it is easy to see what he is talking about. Vesalius claimed to identify scores of errors in Galen and thus undermined his authority, just as Columbus’s discoveries had undermined the authority of Ptolemy. But even more important for later anatomists was the fact that, where anatomical details did not appear in Vesalius’s illustrations, or were incorrectly shown, one could confidently say that he had made a mistake. Sophisticated printed illustrations based on perspective drawings thus turned anatomy into a progressive science, where each generation of anatomists was able to identify mistakes and oversights in the work of their predecessors. In anatomy, discovery does not begin with Vesalius: rather, he provides the base line that allows others to claim to have made discoveries.

The techniques employed by Vesalius in anatomy were at the same time also being employed in botany, where authors faced a similar difficulty to that faced by Vesalius himself: should they portray actual specimens, with all their flaws and faults, and thus accurately reflect reality, or should they provide idealized images of the perfect specimen, as Vesalius had done with his musclemen? Should they show the plant at a moment in time, or show both flower and fruit in a single illustration? Just as Vesalius’s images had made possible the reliable identification of parts of the body and progress in anatomical knowledge, so the new illustrated botanies made possible reliable knowledge of the different species and progress in their naming and identification. But progress involves discrimination: Conrad Gesner, the first compiler of natural historical information in the age of print (Historiae animalium, 1551–8) often supplies illustrations which he labels as false, and even Vesalius at one point illustrates a mistaken claim of Galen’s. The convention that seems basic to us – that illustrations represent reality – was not immediately obvious.⁴⁵

Thus by 1543 two revolutions had come together to make possible a new type of science. On the one hand, there was perspective painting, grounded in geometrical abstraction; on the other, the printing of engraved plates, supplemented by text produced on a printing press. Perspective painting goes back to 1425; engraved prints to at least 1428; the printing press to 1450. The fall of Constantinople, one consequence of which was a flood of Greek manuscripts and Greek-speaking scholars entering the Latin-speaking West from the East (and thus improved knowledge of the Greek originals of Galen’s texts) occurred in 1453.xiixii Why then did it take a further century to complete the transformation brought about by the mechanical reproduction of perspective images? There are two answers to this question. First, the immediate priority of publishers in the years after the invention of printing was to publish the vast body of religious, philosophical and literary texts which had been inherited from the past – first the Latin texts, and then, for a more limited audience, the Greek texts. The first reliable edition of Galen, on which Vesalius had worked, appeared in Basle in 1538; it was there that Vesalius insisted that his Fabric should be printed. Second, a long cultural revolution had to take place, in which book learning came to seem of lesser importance than direct experience. That revolution, as I have argued, began with Columbus.

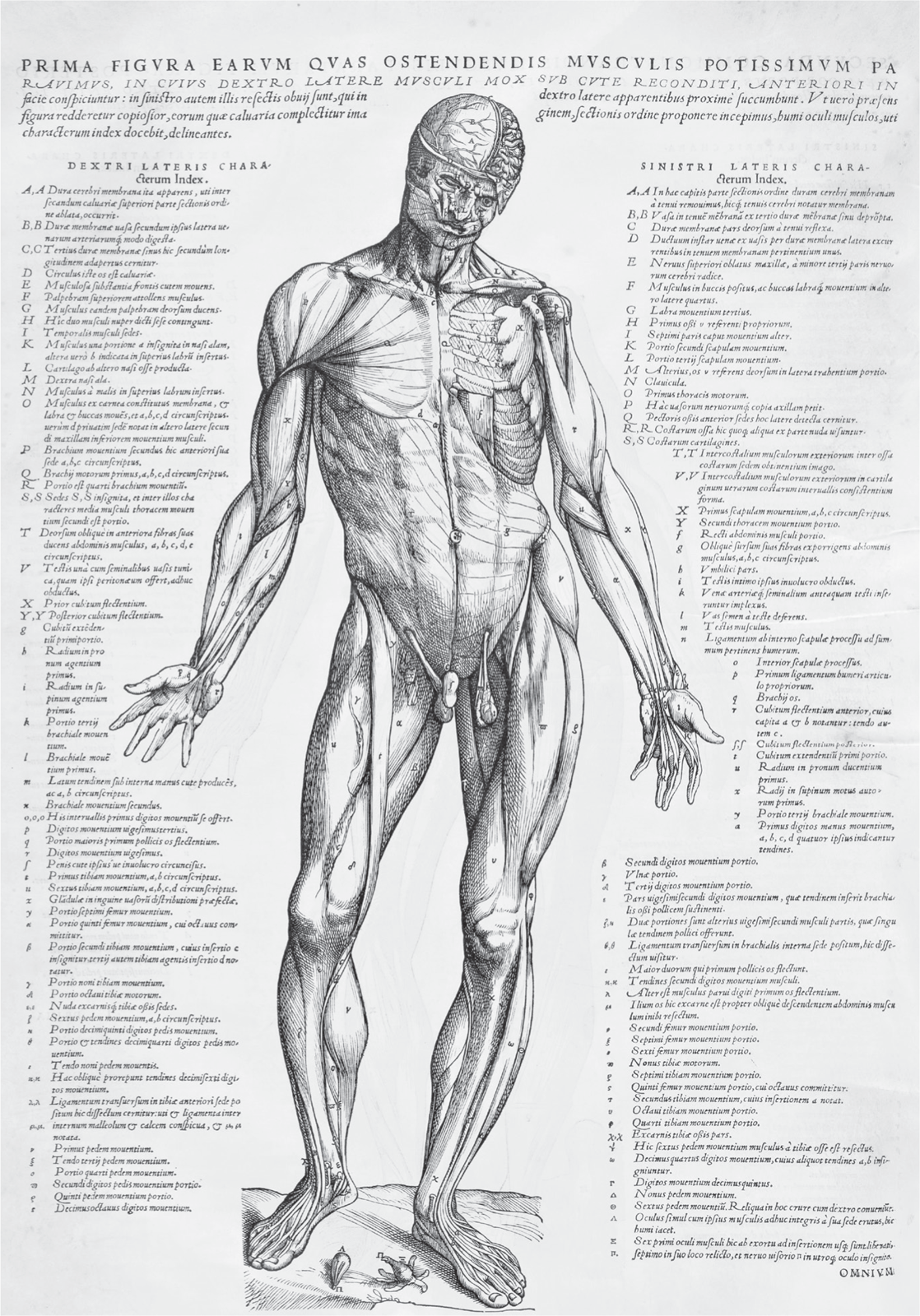
First illustration of the muscles of the body, from Vesalius, On the Fabric of the Human Body (1543).

Alongside the great works of Copernicus and Vesalius we may place On the History of Plants by Leonhart Fuchs, which appeared the year before (1542), and which contained 512 exact images of plants. In his preface Fuchs writes:

Though the pictures have been prepared with great effort and sweat we do not know whether in the future they will be damned as useless and of no importance and whether someone will cite the most insipid authority of Galen to the effect that no one who wants to describe plants would try to make pictures of them. But why take up more time? Who in his right mind would condemn pictures which can communicate information much more clearly than the words of even the most eloquent men? Those things that are presented to the eyes and depicted on panels or paper become fixed more firmly in the mind than those that are described in bare words.⁴⁶

Fuchs’s words represent two distinct revolutions: the demoting of the authority of antiquity (Galen is ‘the most insipid authority’; it is difficult to imagine how shocking these words must once have seemed) and the recognition of the power of images in the new age of mechanical reproduction.⁴⁷ These were both essential preconditions for the Scientific Revolution.

§ 6

In 1464 a German astronomer, Johannes Müller, known as Regiomontanus (Regiomontanus being a Latin version of the place he came from, Königsberg), gave a lecture at the University of Padua.⁴⁸ Regiomontanus had recently completed an exposition and commentary on Ptolemy’s astronomy, begun by his mentor Georg Peuerbach. This was to become the standard textbook in advanced astronomy for the whole of the sixteenth century, and in it Peuerbach and Regiomontanus did not hesitate to criticize Ptolemy for his errors. In 1464 Regiomontanus was writing a pathbreaking guide to plane and spherical trigonometry (On All Sorts of Triangles), which laid out the mathematical foundations of astronomical calculations. He had learnt Greek in Vienna in order to read Ptolemy in the original, and in Italy he had been able to read in Greek Archimedes (who had been translated into Latin in the Middle Ages but was not yet available in print) and Diophantus (who was not yet available in Latin; Diophantus (c.210–c.290) was the originator of algebra).

Regiomontanus was one of the first to benefit from the supply of ancient Greek texts that reached Italy after the fall of Constantinople. At the time of his Paduan lecture, less than a decade after the publication of the Gutenberg Bible, the printing revolution was only just beginning to get under way: Euclid, for example, was first printed in Latin only in 1482, in Greek in 1533, in Italian in 1543 and in English in 1570. Regiomontanus’s lecture thus marks a key moment in the reacquisition of Greek mathematics, and points towards the ambitious programme for the publication of mathematical texts that Regiomontanus developed, though he died before it could be carried out.

Regiomontanus spoke in praise of the mathematical sciences, and he praised them by denigrating the Aristotelian philosophy taught in the universities. Even Aristotle, he said, if he came back to life, would not be able to make sense of what was said by his modern disciples. ‘This [i.e. that the texts are incomprehensible] no one unless mad has dared to assert of our [mathematical] sciences, since neither age nor the customs of men can take anything away from them. The theorems of Euclid have the same certainty today as a thousand years ago. The discoveries of Archimedes will instill no less admiration in men to come after a thousand centuries than the delight instilled by our own reading.’⁴⁹ Regiomontanus’s praise of the mathematical sciences did not, however, imply uncritical admiration for contemporary mathematicians. Only the year before he had written, ‘I cannot [but] wonder at the indolence of the typical astronomers of our age, who, just like credulous women, receive as something divine and immutable whatever they come upon in books … for they believe in writers [such as Ptolemy] and make no effort to find the truth.’⁵⁰ This theme, that one should turn from the study of books to the study of the real world, was to be repeated over and over again by the advocates of the new sciences as they set themselves up in opposition to the old philosophy. It was, for example, one of Galileo’s favourite rhetorical tropes: the suggestion was still as radical in the 1620s as it had been in the 1460s, for the hold over university education of the traditional curriculum had not been diminished. Galileo also shared Regiomontanus’s conviction that Euclid and Archimedes (‘the divine Archimedes’, as he called him) provided the only models for reliable knowledge.⁵¹

In 1471 Regiomontanus worked out a procedure for measuring the parallax of heavenly bodies and so their distance from the Earth.⁵² His procedure presumed use of a cross-staff, an instrument invented by Rabbi Levi ben Gerson (1328).⁵³ The cross-staff is a very simple instrument, a calibrated shaft along which a bar slides. You sight along the shaft and move the bar back and forth until you have lined up its ends with two points, and the angle can then be read off from the scale on the shaft. You can use a cross-staff, for example, to measure the angle between the horizon and the sun at midday. If you know the date and have the right tables, you can then read off your latitude (this, of course, involves squinting at the sun; the backstaff was invented in 1594 to enable you to take this measurement without having to peer at the sun). Alternatively, at night, you could measure latitude directly by measuring the angle between the horizon and the Pole Star. The cross-staff is merely one of a series of instruments, such as the quadrant and the sextant, designed for measuring angles by taking sightings. Before it was invented, the astrolabe (copied in medieval Europe from Islamic models) had provided a sighting device, and also a method of measuring the height of the sun from its shadow. With this device you could establish your latitude if you knew the time of day but, rather more important for most users, you could tell the time of day if you knew your latitude and the date. Specialist forms of all these instruments were developed for surveying, for astronomy and for navigation, but the basic principle that angles could be used to determine distances or times was the same for all of them.xiiixiii⁵⁴

Cross-staff being used for surveying and astronomy – from the title page of Petrus Apianus, Introductio geographica, 1533.

In surveying, if you knew how far away a building was it was now easy to calculate its height. Suppose you wanted to scale the walls of a fortress which was on the other side of a river. You could take two measurements in a straight line with the building and, from the distance between the measurements and the difference between the angles as measured with a cross-staff, you could calculate the height of the walls and make ladders of the right length. The basic principles involved had been described by Euclid and were well understood in the Middle Ages. They are exactly the same principles as are involved in perspective painting. But, where perspective painting takes a three-dimensional world and turns it into a two-dimensional surface, Regiomontanus was now trying to take a two-dimensional image – the night sky – and turn it into a three-dimensional world. To do so you have, in effect, to move from monocular vision to binocular vision.

The principle of parallax enables you to do this. It is a variation of the basic principle that if you know one angle and one side of an equilateral or right-angled triangle, then you can determine the other angles and sides. It thus requires not one measurement but two. Hold up your finger in front of you, close your left eye, and note where your finger appears to be against the background. Then switch eyes. Immediately, your finger will jump to the right. If you know the distance between your eyes and measure the angle that corresponds to the apparent shift in your finger’s position, then you can calculate how far away your finger is – although, of course, no one would bother. In this case the distance between your eyes is a significant proportion of the distance between your eyes and your finger; if you were trying to measure the distance to an object that was very far away, then you would have to set up two observation spots that were far apart – or at least so it would seem.

Regiomontanus grasped that an astronomer does not have to travel in order to get two observation points that are, in effect, far apart.⁵⁵ If the heavens rotate around the centre of the universe, and if that centre is at or near the centre of the Earth, then the observation point of the astronomer, who is on the surface of the Earth, changes in its relationship to the heavens as they move simply because the astronomer is not looking at the heavens from the centre of the universe but from a point distant from that centre.

Imagine you are standing at the dead centre of a merry-go-round on which the horses are arranged in three concentric circles. At the centre there is a stationary, round platform around which the circles of horses, each taking the same time to complete a circuit, revolve. As you look outwards and the horses turn around you, the relative position of the horses will remain the same – a horse which is in line with another horse at one moment will still be in line with it a quarter of a revolution later. But if you take a few steps in any direction, until you reach the edge of the stationary platform, then the relative position of the horses will appear to change all the time. Moreover, if you know the size of the stationary platform and the distance to the outer ring of horses, then you can use changes in the relative position of horses in the other two rings to work out how far away they are. Regiomontanus thus saw that you could measure the parallax of heavenly bodies by taking two observations from the same place but at different times, rather than by taking two observations from different places but at the same time.

According to Aristotle, comets exist in the upper atmosphere. They must, because comets come into existence and disappear, while the heavens continue the same for ever. Comets must therefore be sublunary, not supralunary: below the moon, not above it. Aristotle’s hypothesis was that they represent some sort of exhalation from the earth catching fire. As far as we know, no one had actually tried to measure the parallax of a comet before 1471; it had simply been assumed that the Aristotelian theory was obviously correct.

Although Regiomontanus worked out how to make such a measurement in 1471, the full account of his procedure was not published until 1531. Unfortunately, in 1548 a text, apparently by Regiomontanus, was published which claimed to measure the parallax of the comet which had appeared in 1472, and to confirm that it was close to the Earth because the parallax was a whopping 6 degrees – placing it much closer than the moon, which has a diurnal parallax of about 1 degree. Some cunning detective work has shown that this text is not by Regiomontanus: it must have been found among his papers when he died, and was presumably in his handwriting, so that it was published as being by him, but it does not employ his methods and it had in fact already been published during Regiomontanus’s lifetime by someone else, an anonymous physician of Zurich (tentatively identified as Eberhard Schleusinger). We now know this, but no one in the sixteenth century realized it, and it has caused a great deal of confusion in the historical literature.⁵⁶ Sixteenth-century astronomers accepted in good faith the apparently solid evidence that Regiomontanus had confirmed the traditional account of the distance of comets from the Earth; we now know that there is no reason to think that Regiomontanus had actually applied the system of measurement he had described in 1471; in order to apply it, one would, in any case, first have to work out how to handle the fact that comets are moving, not stationary, objects. In 1532, however, Johannes Vögelin measured the parallax of the comet that appeared in that year and claimed to confirm the erroneous result of pseudo-Regiomontanus.

Then in 1572 Brahe’s nova appeared in the sky. For a time it was the brightest object in the heavens, other than the sun and the moon, brighter even than Venus. Such events occur only once in a thousand years or so. And, unlike a comet, the new star stood still, which made it much easier to measure its parallax. All over Europe astronomers were obsessed with it – and since they now knew Regiomontanus’s real technique for measuring parallax, they naturally tried to apply it. Some found a measurable parallax, but others insisted that there was no parallax to measure. Accurately measuring parallax was far from easy, particularly as it required a more exact measure of time than any sixteenth-century clock could provide, but showing that there was no measurable parallax was much more straightforward. All one had to do was hold up a taut thread as a sighting device and find two stars that were exactly in line with the nova but north and/or south of it; if the same stars were exactly in line with the nova later the same night, then there was no parallax to measure. This simple technique was employed by Michael Maestlin, Kepler’s teacher.⁵⁷ And if there was no parallax, then the comet must be a vast distance away, far further than the moon, whose parallax was quite easy to measure; it must be a supralunary, not a sublunary body.

How to explain the appearance of a new star in the heavens? Since there could be no natural explanation, assuming the star was indeed in the heavens, the event was clearly a miracle, a sign sent by God. The finest astronomers and astrologers – Thomas Digges in England, Francesco Maurolico in Italy, Tadeàš Hàjek in Prague – racked their brains in an attempt to work out what this might portend and hastened to publish their conflicting conclusions.⁵⁸

The new star of 1572 was followed by the comet of 1577, and here again parallax measurement placed the comet beyond the moon. Where a nova could possibly be regarded as a miracle, a comet was too commonplace an occurrence to be handled in this way, so if comets were supralunary phenomena, Aristotle was wrong.⁵⁹ Brahe also worked on a further problem that could be solved by measuring parallax: a crucial difference between the Ptolemaic system on the one hand and the Copernican and Tychonic systems on the other was that under these modern systems Mars must at times approach much closer to the Earth than under the Ptolemaic system. Brahe at first thought that he had obtained a reliable figure for the parallax of Mars which proved the Ptolemaic system was mistaken, although he later realized that there were problems with it. Regiomontanus’s procedure for measuring parallax ideally involved comparing the apparent position of a celestial object soon after dark with its apparent position not long before dawn, thus maximizing the parallax to be measured. Neither the nova of 1572 nor the comet of 1577 set in the night sky as viewed from northern Europe, so the ideal procedure was inapplicable; in the case of Mars, there was no choice but to make measurements when the planet was nearly in line with the sun, and thus it never rose high above the horizon at night. In measuring the location of an object near the horizon, Brahe had to allow for the refraction caused by the greater thickness of atmosphere through which its rays had passed, and eventually he found that he had miscalculated this allowance, thus vitiating what he had hoped would be a key argument against the Ptolemaic system. His long series of measurements of the location of Mars, however, was to prove invaluable to Kepler when it came to calculating Mars’s ‘orbit’ (as he called it; he invented the term as used in astronomy) on Copernican assumptions, and demonstrating that it was best understood as an ellipse.⁶⁰

In 1588 Brahe published Concerning the Recent Phenomena of the Aetherial World, Book II (Book I, on the nova of 1572, was published posthumously in 1602), a definitive study of the comet of 1577, in which he reviewed the extensive literature it had provoked and argued that those observations which found no parallax were the only reliable ones, and that Aristotle was therefore wrong when he claimed that comets were sublunary phenomena.⁶¹ But he went further: in place of the Ptolemaic and Copernican systems, he proposed his own geoheliocentric system, which was geometrically equivalent to Copernicanism but had a moving sun and a stationary Earth. Since his calculations implied that comets moved through the crystalline spheres of the planets, and since his geoheliocentric system required Mars to cut through the sphere of the sun, Brahe abandoned the whole theory of solid spheres, and argued that the sun, moon and planets floated freely in the heavens, like fish in the sea. Brahe’s caution about committing himself to this, the dissolution of the celestial spheres, is probably what had caused the delay in publication.xivxiv It is now generally regarded as a much more important marker of the beginning of modern astronomy than the publication of Copernicus’s On the Revolutions.⁶²

§ 7

This story is a fine example of two fundamental features of the Scientific Revolution. First, path dependency. Once Regiomontanus’s true system for measuring parallax had been published, astronomers embarked on a path that could only lead, sooner or later, to decisive evidence being produced that was at odds with central claims made by Aristotle and Ptolemy (although Regiomontanus would have been astonished to learn this). The fact that there was a long delay does not mean that Regiomontanus’s contribution was not decisive; it means only, first, that there was a delay in the publication of his work and, second, that the nova of 1572 simplified and clarified the issues, producing a classic revolutionary crisis. Certain features of the Ptolemaic system (such as geocentrism) could survive this shock, as Brahe’s geoheliocentric system demonstrated, but key features common to both the Ptolemaic and Copernican systems (unchanging heavens, solid spheres) could not. By 1650 this was universally acknowledged; indeed, no competent astronomer defended the Ptolemaic system as understood (for example) by Regiomontanus after Galileo’s discovery of the phases of Venus had been corroborated in 1611.⁶³

This claim – that new observations were fatal to old theories – is at odds with much recent philosophy of science, which insists that observations and theories are both malleable, and that, consequently, there are always ways in which the phenomena can be saved. A standard approach is to distinguish between data (raw observations, made, for example, with a thermometer in boiling water) and phenomena (interpretations of the data, for example, that the boiling point of water at sea level is 100 degrees Celsius). Theories, it is said, explain phenomena, not data, and it is always possible to open up a gap between data and phenomena as well as between phenomena and theories.⁶⁴ But in the case of the geometrical sciences of the seventeenth century the gaps between data and phenomena, and between phenomena and theories, are intended to be virtually non-existent.

In the case of Brahe’s observations of the nova and the 1577 comet the data was an absence of diurnal parallax, the phenomenon that needed to be explained was that these new bodies were in the supralunary and not the sublunary world, and the immediate theoretical conclusion that resulted was that there was change in the heavens. What tied data, phenomenon and theory together was a geometrical argument (that if there was no observable parallax, the new bodies must be much further away than the moon) which was unbreakable, providing the initial observations were reliable. This was not true in all cases where diurnal parallax was observed; as we have seen, refraction might make it possible to open up a gap between data and phenomena, and even if Brahe’s measurements of Mars’s parallax had been correct, they would not have helped decide between his cosmology and that of Copernicus. But in the cases of the nova of 1572 and the comet of 1577 the data necessitated the phenomenon, and the phenomenon falsified the established theory.

Obviously, if Brahe was to confirm the claim that his argument was unbreakable, he had to provide an explanation for the fact that not everyone had produced observations which showed a complete absence of identifiable parallax. In Recent Phenomena II, consequently, Brahe went carefully through the observations of those whose results differed from his but (conveniently) corresponded to the results that traditional astronomy would have predicted, and identified their errors: one astronomer had measured the distance between the comet and a star but had then confused that star with another when repeating the measurement; another had added when he should have subtracted; a third had made two measurements an hour apart when he should have made them as close together as possible; and a fourth had confused two different systems of heavenly coordinates. Thus Brahe identifies elementary mistakes which neatly explain why their results are different from his; the observations are not, he wants to insist, subjective or personal, but objective and reliable, and once they are granted the rest follows of necessity.

Of course, the mere existence of a diversity of results made it difficult to persuade everyone that Brahe’s arguments were conclusive. Galileo was still going over the measurements of parallax for the nova of 1572 in his Dialogue Concerning the Two Chief World Systems of 1632. There he argued that you could not just pick the measurement that suited your purposes best (as opponents of Brahe continued to do); that the accuracy of instruments would vary and so there would never be uniformity in observations; that outlying results were almost certain to be mistaken; and that results were likely to cluster around the correct measurement. Thus it might be impossible to decide if any particular one of the thirteen measurements he surveyed was correct, but one could identify a range within which the correct measurement almost certainly lay and be confident that all of the outlying measurements were mistaken.⁶⁵ Galileo was here making the distinction (to use the terminology of Bogen and Woodward) between data and phenomena, and using the distinction to develop the first theory of observational error.

Brahe’s observatory: the curved scale is a quadrant for measuring elevations that is built into the wall; inside it is a trompe l’oeil section of Brahe’s observatory, with a giant figure of Brahe himself. The image comes from the 1598 printing of his Astronomiae instauratae mechanica. The painting above the quadrant was done in 1587 by Hans Knieper, Hans van Steenwinckel the Elder and Tobias Gemperle, who were responsible, respectively, for the painting of the landscape at the top, the three pairs of arches representing the three areas of Uraniborg and the portrait of Brahe.

Arguments over the location of novas and comets in the heavens thus continued even after 1610, after which date the traditional Ptolemaic system was abandoned by all competent participants. Within a year or two of Galileo’s telescopic discoveries no one disputed that the moon had mountains, Jupiter had moons, Venus had phases and the sun had spots, and thus Galileo’s observations were conclusive in a way that Brahe’s measurements of diurnal parallax should have been, but weren’t.xvxv

The second fundamental feature of the Scientific Revolution is the impact of the printing press. By the early sixteenth century the printing revolution was well under way. We have seen the impact the publication of Vesalius’s Fabric had on anatomy. It was only printing that ensured that a significant number of astronomers had access to Regiomontanus’s text on parallax after 1531. Printing made it possible for Brahe to survey a wide range of publications (there were over a hundred on the comet of 1577, though many were merely astrological prognostications) and demonstrate that the four best observers had produced results compatible with his own.⁶⁶ It also ensured that Brahe’s new system was quickly known throughout Europe, so that his arguments could be tested against the nova of 1604 and the comets of 1618. Printing created a community of astronomers working on common problems with common methods and reaching agreed solutions. This community had not existed in 1471 (which is another reason why it took so long for Regiomontanus’s method of measurement to have an impact). When did it come into existence? Kepler, reasoning from astrology, dated the moment of transition to 1563: the great planetary conjunction of that year had transformed the world of learning; certainly it had led to a flood of astrological publications.xvixvi My preferred date would be 1564, the very next year, which saw the first published catalogue of the Frankfurt book fair. The Frankfurt catalogues were circulated throughout Europe, setting up for the first time a truly international trade in books.⁶⁷

Before 1572 astronomers measured the positions of the sun, the moon and the planets (the sun and the moon were, technically, planets, too, according to the Ptolemaic system) in the heavens in order to predict their future movements. They had inherited some rough calculations of the size and distance of the sun, the moon and the stars, but distances did not really matter: all they sought to do was predict the angles that defined an object’s position in the heavens at any particular time, and to do so by manipulating the Ptolemaic armament of deferents, epicycles and equants, which together amounted to what was called an hypothesis – a term which meant a mathematical model which produced reliable predictions. But with Tycho Brahe, measurements of distance suddenly became critical. Where before it had always been possible to ‘save the phenomena’, that is, adjust the hypothesis to fit the phenomena (if necessary by adopting two incompatible hypotheses, one to predict movement east and west, and the other movement north and south), Brahe’s observations were simply incompatible with established theories, whether Ptolemaic or Copernican (for Copernicus, it was assumed, had continued to believe in solid spheres carrying the planets through the heavens).⁶⁸ By 1588 astronomy had become concerned with the organization of the heavens in three dimensions, not just in two.

§ 8

Historians of science have often (and rightly) suggested that the key to the Scientific Revolution is ‘the mathematization of nature’.xviixvii⁶⁹ Aristotle and Ptolemy had assumed that the heavens were mathematically legible, and indeed Ptolemy had devised techniques for reading them. One aspect of the Scientific Revolution consists in the extension of mathematical theories to include sublunary phenomena. Where Aristotelian physics was preoccupied with qualities – the four elements (earth, air, fire, water) embody the four qualities (hot and cold, dry and wet) – the new physics was preoccupied with movements and quantities that could be measured, and it quickly led to attempts to measure the speed of falling bodies, the speed of sound and the weight of air. Where Aristotle had assumed that each element behaved differently, the new physics assumed that all heavy objects could be thought of as the same. Where Aristotelian physics had depended on all five of the senses, the new physics relied only on the sense of sight. With Galileo’s discovery of the parabolic path of projectiles (1592) and the law of fall (1604) the sublunary world began to be mathematically legible, and Newton went on to show that the same physical principles were at work in the heavens and on Earth. But long before this the Aristotelian demarcation between superlunary and sublunary had been shattered by Brahe. From 1572 onwards Aristotelian philosophy was facing a crisis from which it could not escape without sacrificing fundamental claims that it had long regarded as unquestionable.

According to Aristotle, the sublunary elements were naturally at rest, while the supralunary spheres rotated in endless circles. Even before he discovered the law of fall, Galileo had been questioning the distinction between the two worlds. In the early manuscript On Motion (pre-1592) he suggested that if you were to slide a stone across a perfectly smooth surface it would continue for ever. He was thinking of circular movement – the stone would circumnavigate the earth – but he was also questioning the idea that rest was more natural than movement, and insisting on the legitimacy of theoretical abstraction, for of course perfectly smooth surfaces exist only in the mind.⁷⁰ His first discovery of a mathematical principle underlying sublunary movement was the identification of the parabola as the path of a projectile such as a cannon ball – of its path, that is, in a theoretical world in which there is no air resistance and in which cannon balls do not spin as they fly. After Galileo’s death practical tests showed that the path of a real cannon ball is very different from Galileo’s theoretical model; his student Torricelli was not in the least put out, any more than he would have been to be told that there are no perfectly smooth surfaces.⁷¹ Galileo, Descartes and Newton constructed a new universe in which matter was inert and its behaviour (at least in theory) mathematically predictable, and in which movement and location were relative rather than absolute.

The traditional historiographical emphasis on the new physics assumes that the mathematization of the world began in the seventeenth century. But perspective painting provided the first glimpse of this new universe. It may be no coincidence that Galileo learnt his mathematics from Ostilio Ricci, who also taught perspective to artists, or that Brahe had a remarkable trompe l’oeil painting on the wall of his observatory (above, p. 196). The mathematization of the sublunary world begins not with Galileo but with Alberti, not in the seventeenth century but in the fifteenth. Alberti’s On Painting starts with a simple exposition of the principles of geometry, in which he defines points, lines and surfaces and continues with a basic exposition of optics, which was traditionally regarded as a branch of mathematics. He also wrote a more sophisticated textbook on geometry for the use of artists, Elements of Painting. From perspective painting, the new mathematical learning spread to cartography. Waldseemüller’s introduction to his world map (1507) begins with elementary geometry for cartographers: they need to understand circles and axes in order to make sense of longitude and latitude, of poles and antipodes. There was nothing particularly new in this: Cicero had thought geography was a branch of geometry.⁷² Sebastiano Serlio’s popularization of Vitruvius (1537) begins with a book expounding the elementary principles of geometry, starting with points and lines, right angles and triangles. But the systematic application of geometry to real-world questions – to architecture, to optics, to cartography, to astronomy, to physics (for Galileo claimed to be able to demonstrate some of his laws of fall through geometrical arguments) – was incompatible, in anything but the short term, with the survival of Aristotelianism.

With geometry came abstraction. This is beautifully illustrated by a diagram Peter Apian drew for his Cosmographic Book (1524). It shows how the measurement of longitude and latitude depends upon reference to an imaginary grid. To simplify things, Apian treats this grid as if it were a flat surface, not a sphere. And he presents it in perspective, with two parallel lines converging towards a vanishing point. It is, in fact, just like the grid used by artists to establish the picture plane, and its representation requires the same techniques as the representation of a tiled floor. The great art historian Erwin Panofsky claimed that the tiled floors in perspective paintings were the first abstract system of coordinates; he was wrong, because Ptolemy had already invented longitude and latitude as a system of coordinates, but he was right to think that perspective painting implies an abstract system of coordinates.⁷³

Peter Apian’s diagram illustrating longitude and latitude, from his Cosmographicus liber (1524).

In the bottom-left-hand corner of Apian’s diagram he has drawn some mountains, suggestive of a real place, perhaps even a reference to the Alps. But these merely serve to conceal the fact that cartography transforms place into space. This seems wrong, because we use maps to get from one place to another: surely maps are about places? But maps function by substituting symbols (here, pins stuck into an imaginary board) for real places and by locating places in abstract space. In Apian’s diagram there is nothing to suggest that Venice is a port but Vienna is not; that Erfurt and Nuremberg are Protestant while Munich and Prague are Catholic; that these cities differ in size or belong to states. Real cities have been replaced by coordinates; real places by theoretical spaces.

Geometry also acquired new importance as a result of the invention of gunpowder: fortifications had now to be built to resist cannon balls, which fly (as seen from a bird’s-eye view) in straight lines. In order to provide raking and flanking fire along every wall, forts needed to be designed on the page, with carefully measured angles and distances. Bastions (called by the French the trace italienne and by the American colonists the ‘star fort’), were being built not just in Europe but in Asia and the New World – wherever cannons were fired – from the late fifteenth century on, so every commanding officer required some knowledge of geometry. The new science of fortification was taught by mathematicians, Galileo among them.⁷⁴ In Shakespeare’s Othello, Iago is furious to find Michael Cassio, ‘a great arithmetician’, whose knowledge of warfare is all book-learning, has been promoted ahead of him.⁷⁵

Fortification plan of Coevorden in the Netherlands, as laid out in the early seventeenth century by Maurice of Nassau, Prince of Orange. Simon Stevin advised Maurice of Nassau on the design of fortifications, and Descartes served in his army.

Alberti had written, ‘Mathematicians measure the shapes and forms of things in the mind alone and divorced entirely from matter.’⁷⁶ But this divorce between mathematics and matter soon turned into a marriage. In Galileo’s famous words, which provide the epigraph to this chapter, the book of the universe is written in geometrical figures. The claim went back to Pythagoras and Plato, but Renaissance Platonists had been interested in number mysticism rather than real mathematics. It is first boldly restated by Tartaglia in his New Science (1537), the new science being ballistics. The frontispiece to that book shows Euclid controlling the gate which leads not only to knowledge of ballistics but to all philosophy.⁷⁷

Tartaglia went on to publish the first translation of Euclid into a modern vernacular language (Italian, 1543) and to devise new instruments and techniques for surveying (Diverse Problems and Inventions, 1546), techniques that could be used to calculate how far away a target was. In 1622, for example, a fleet of Dutch ships tried to seize the Portuguese colony of Maçao. A Jesuit mathematician did the geometry calculations to determine the distance to a stockpile of gunpowder the Dutch had brought ashore and the angle of elevation at which the cannon should be set. A direct hit turned the tide of the battle and ensured that Maçao remained a Portuguese colony.⁷⁸ Thus if we ask how did the Scientific Revolution become mathematized, the answer is through perspective painting, cartography (and the related sciences of navigation and surveying) and ballistics. It was these subjects which gave mathematicians like Tartaglia, Brahe and Galileo (and, as we have seen, Leonardo, too) the confidence that it was they, not the philosophers, who knew how to make sense of the world. Painting, cartography and ballistics do not strike us as cutting-edge sciences but, once, they were.

Frontispiece to Niccolò Tartaglia’s New Science (1537). Euclid controls the gate to the castle of knowledge, where a mortar and a cannon are being fired to illustrate the path of projectiles. Entry to the inner redoubt requires one to pass through the mathematical sciences, with Tartaglia himself standing among them; within is Philosophy, accompanied by Aristotle and Plato.

The different mathematical sciences were interlocked: anyone with the skills to excel in one had the skills to excel in others. Alberti was an architect, a painter and a mathematician; Piero della Francesca was a mathematician and a painter; Pacioli was a mathematician and an architect; Leonardo was a painter and a military engineer; Digges published on surveying and astronomy; the greatest cartographers (Mercator, the Cassinis) were also important astronomers, just as the greatest astronomers (Brahe, Halley) were also cartographers. These were not independent sciences but a family group which held a set of geometrical techniques and measuring instruments in common. According to the standard translation of On the Revolutions, Copernicus wrote, ‘Astronomy is written for astronomers’; but he didn’t. He wrote, ‘mathemata mathematicis scribuntur’ (‘mathematics is written for mathematicians’): Copernicus expected every mathematician to be able to follow his arguments. He, like virtually all the others, worked in more than one field: he published on monetary reform as well as astronomy. As for Kepler, he published not only on optics but also on the mathematical analysis of the volumes of wine barrels (a subject directly related to a problem in his astronomy, that of calculating the area of an ellipse) and on how best to stack cannon balls.xviiixviii

Moreover, it was not only the painters who were concerned with how to represent three dimensions in two: this was also a central problem for the cartographers, who had to project the globe on to a flat surface (some even think that one of Ptolemy’s solutions to this problem influenced Brunelleschi),⁷⁹ and for the sundial makers (always mathematicians; sometimes – Regiomontanus, Benedetti – of the first rank), who had to work out how the sun’s movement through three dimensions would be projected on to a flat dial. One set of images captures this overlapping of interests better than any other. Albrecht Dürer made two trips to Italy (1494–5; 1505–7) to learn the latest artistic techniques. He published on geometry as applied to painting and architecture (Four Books on Measurement, 1525). In 1515 he published, in association with the astronomer and cartographer Johann Stabius, a pair of celestial charts showing the northern and southern hemispheres: these were the first printed star charts, and the first, printed or not printed, to show the heavens with a clearly marked system of coordinates. They were accompanied by the first perspective drawing of the entire Earth as a sphere. Here, geometry, perspective painting and cartography merge into one.

§ 9

The belief that the tools of the mathematician (specifically, the tools provided by geometry) were the correct ones to use to understand the world made possible all sorts of new representations. But did it significantly alter society’s control over the natural world, or the control of one social group over another? Vesalius’s purpose was not only to enhance understanding but also to improve surgery. However, without anaesthetics, antibiotics or reliable methods of controlling blood loss through tourniquets and sutures (let alone transfusions), surgery continued to be painful, risky and often fatal. The knowledge acquired in dissection had few, if any, practical applications.⁸⁰

Dürer’s World Map of 1515. It is part of a set including maps of the northern and southern skies. Dürer’s map illustrates how rapidly the notion of the Earth as a globe established itself after the publication of Waldseemüller’s map in 1507; it also demonstrates Dürer’s complete mastery of perspective representation.

It was very different, of course, with the sciences of cartography and navigation, ballistics and fortification. But it is important to distinguish between the first pair and the second: one deals with space and place; the other with percussive force. Once sailors began to sail for any length of time out of sight of land, they needed new tools (compasses, and devices such as the ship’s astrolabe – a specialized version of the astrolabe for use at sea – or the backstaff for establishing true north by the sun and the stars), new charts and maps, and new supplies (hardtack or ship’s biscuit). There is a tendency in the modern literature to think of maps as technologies for domination, as reflections of imperial culture.⁸¹ This seems to me mistaken, even though John Donne compared mapping the heavens to owning them:

For of Meridians, and Parallels,

Man hath weaved out a net, and this net throwne

Upon the Heavens, and now they are his owne.

Loth to goe up the hill, or labour thus

To goe to heaven, we make heaven come to us.⁸²

European world maps placed Europe at the centre, but when the Chinese were shown a world map by Matteo Ricci and complained that China should be at the centre, he promptly produced a new map which did just that.xixxix Mercator’s projection (1599), when used to produce a world map, shrinks countries close to the equator and makes the northern countries appear much larger than they really are, but this is an entirely accidental consequence of constructing a projection which enables a course plotted on a chart to be used directly for navigational purposes; the Mercator projection, which shows a three-dimensional globe on a flat surface, distorts distances in order to preserve accuracy when it comes to directions. These maps were originally intended as tools for sailors, not assertions of European supremacy; they look like ideological statements only to people who do not use them for navigation.

Moreover, until the eighteenth century, cartographers were mainly interested in producing maps for the purposes of navigation. What generals wanted were not accurate maps but sketch maps that showed the roads along which troops and supplies should move.⁸³ Such maps focused on roads, passes and fords, ignoring everything to left or right of the main route. They did not show abstract space (which is what the open ocean is) but real place. Commanders wanted plans of fortifications, and bird’s-eye views (of a sort pioneered by Leonardo) which enabled them to identify where guns could be brought forward without being exposed to enemy fire, or where an advance could be blocked or ambushed. Thus, visualizing the application of power on land required quite different techniques from at sea, and for a long time cartography enhanced maritime power, not terrestrial power (which is why the Dutch, who were almost exclusively dependent on maritime power, were so preoccupied with cartography).

This brings us back to the harsh truth, that, although, in themselves, maps, compasses, backstaffs and hardtack may be neutral devices, by making it possible for ships to sail the oceans they enabled Europeans to bring gunpowder technology (whether in the form of cannon fired from floating fortresses or landing parties armed with muskets) to bear upon societies which had no comparable means of defending themselves.⁸⁴ Cartography came as a technological package, along with gunpowder weaponry; and gunpowder weaponry really is about power, and nothing else. So while cartography and navigational instruments taken in isolation are neutral devices, in practice they are part of a package of technologies that ensured Western global dominance for five hundred years.

§ 10

My argument so far is that the seventeenth-century mathematization of the world was long in preparation. Perspective painting, ballistics and fortification, cartography and navigation prepared the ground for Galileo, Descartes and Newton. The new metaphysics of the seventeenth century, which treated space as abstract and infinite, and location and movement as relative, was grounded in the new mathematical sciences of the fifteenth and sixteenth centuries, and if we want to trace the beginnings of the Scientific Revolution we will need to go back to the fourteenth and fifteenth centuries, to double-entry bookkeeping, to Alberti and Regiomontanus. The Scientific Revolution was, first and foremost, a revolt by the mathematicians against the authority of the philosophers. The philosophers controlled the university curriculum (as a university teacher, Galileo never taught anything but Ptolemaic astronomy), but the mathematicians had the patronage of princes and merchants, of soldiers and sailors.⁸⁵ They won that patronage because they offered new applications of mathematics to the world. That involved the invention of many new instruments for improved measurements on Earth and in the heavens – cross-staffs, sextants, quadrants – and it was driven by a new obsession with accuracy. Accuracy and certainty: these were the watchwords of the new science.

Regiomontanus may have been one of the first, but he was not the last, to see in the mathematical sciences a new type of reliable knowledge. In 1630 Thomas Hobbes, who had received a conventional humanistic and scholastic education at Oxford, came across a copy of Euclid’s Elements ‘in a gentleman’s library’ in Geneva. It was open at Proposition 47 of Book I (which we now call Pythagoras’s theorem). ‘From that moment on he was in love with geometry.’⁸⁶ He soon aspired to construct a new science of morality and politics on geometrical principles. What Hobbes had realized is that nothing is more certain than the truths of mathematics. Two plus two always equals four; the square on the hypotenuse is always equal to the sum of the squares of the other two sides. These are universal truths: to understand them is to adopt them.xxxx For two centuries or so, from Regiomontanus (d.1476) to Hobbes (d.1679), Euclid and Archimedes provided the crucial examples of how to construct a new sort of knowledge, the sole defence-works against the sort of doubt so eloquently expressed by Sextus Empiricus and Montaigne.⁸⁷ But if the Revolution begun by the mathematicians was to be successful it needed to identify other ways of establishing and communicating universal truths. It is to these that we now turn.