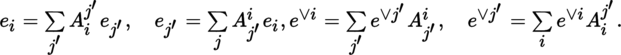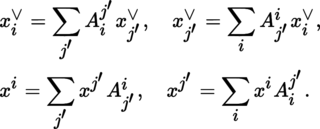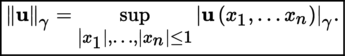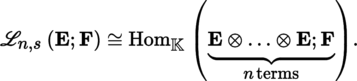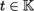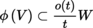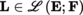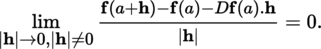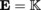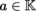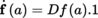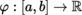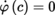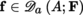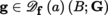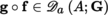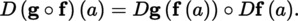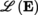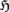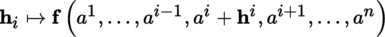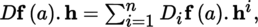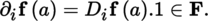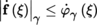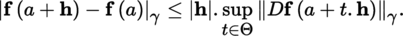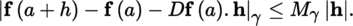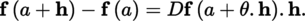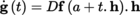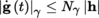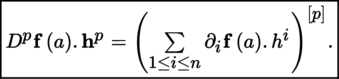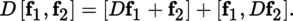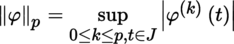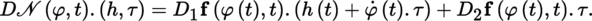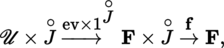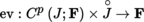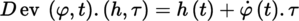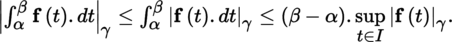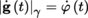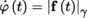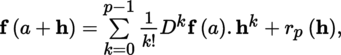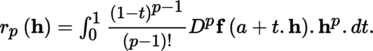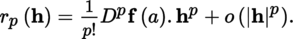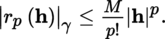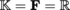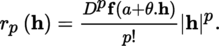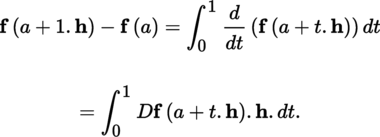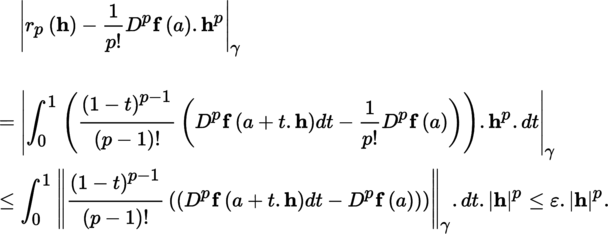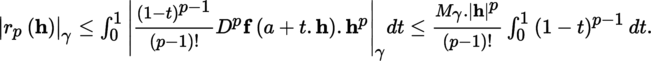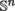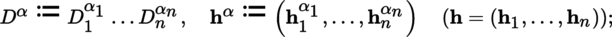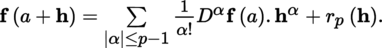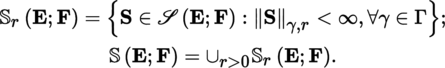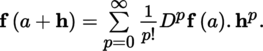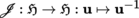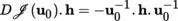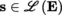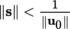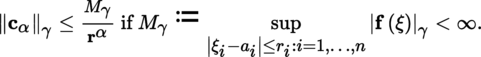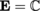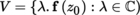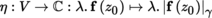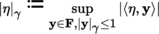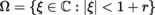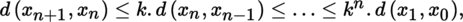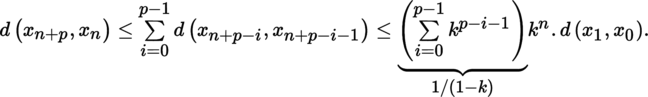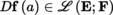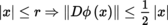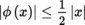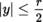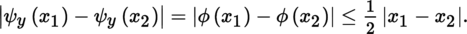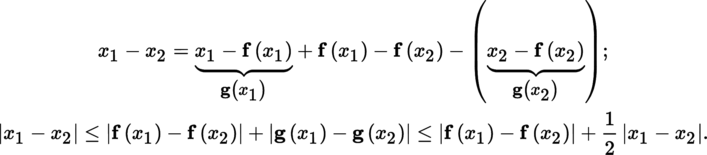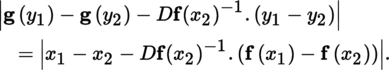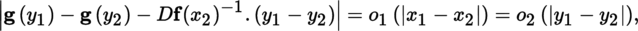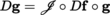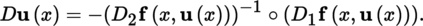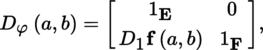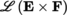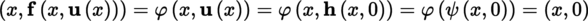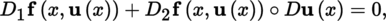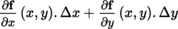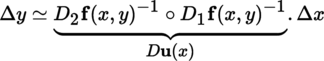Differential Calculus
Abstract
We could cite various forerunners of differential calculus, including Descartes, Fermat and Cavalieri, but Newton and Leibniz should be remembered as the true pioneers of the field. This dual paternity created terrible priority disputes where the only certainty is the complexity of the controversy. Newton’s “fluxions” and Leibniz’s “vanishing quantities” are analogous to our modern concepts of derivative and differential, respectively. The extension of these ideas to functions of several variables was due to Euler (who introduced partial derivatives) and Clairaut. After contributions by many other mathematicians, including Volterra and Hadamard, the concept of a derivative of arbitrary order (Lemma-Definition 1.4) was ultimately introduced by Fréchet between 1909 and 1925. The inverse mapping theorem was proved by Lagrange in 1770, and the simplest case of the implicit function theorem was proved by Cauchy around 1833, followed by the case of vector-valued functions of several variables by Dini in 1877. Gateaux then extended Fréchet’s earlier ideas to develop his concept of differential, which was presented in a posthumous publication in 1919. The “convenient” form of differentials, one of their most recent incarnations, was introduced by Frölicher, Kriegl and Michor in the early 1980s (p. 73). These differentials were intended for mappings taking values in locally convex non-normable spaces, in particular nuclear Fréchet spaces (see, in particular, section 5.3.2 on manifolds of mappings). Wherever possible, this chapter therefore chooses to present differential calculus for mappings which take values in locally convex spaces rather than the normed vector spaces considered by the standard approach (nothing essential changes). Nonetheless, for the inverse mapping theorem and the implicit function theorem (Theorems 1.29 and 1.30), we will restrict attention to the Banach case (for a more general context, which uses yet another concept of differentiability distinct from any of those mentioned above). Both theorems are proved in full detail, including the Banach analytic case, by explicitly filling in the hints from. Together with the Carathéodory theorems mentioned below, these two theorems are the most profound results of this chapter.
Keywords
Calculus of variations; “Convenient” differentials; Differential Calculus; Existence and uniqueness theorems; Fréchet differential calculus; Gateaux differentials; Lagrange variations; Mappings of class Cp; Parameter dependence; Taylor’s formulas
1.1 Introduction
We could cite various forerunners of differential calculus, including Descartes, Fermat and Cavalieri, but Newton and Leibniz should be remembered as the true pioneers of the field. This dual paternity created terrible priority disputes where the only certainty is the complexity of the controversy [HAL 80]. Newton’s “fluxions” and Leibniz’s “vanishing quantities” are analogous to our modern concepts of derivative and differential, respectively. The extension of these ideas to functions of several variables was due to Euler (who introduced partial derivatives) and Clairaut. After contributions by many other mathematicians, including Volterra and Hadamard, the concept of a derivative of arbitrary order (Lemma-Definition 1.4) was ultimately introduced by Fréchet between 1909 and 1925. The inverse mapping theorem was proved by Lagrange in 1770, and the simplest case of the implicit function theorem was proved by Cauchy around 1833, followed by the case of vector-valued functions of several variables by Dini in 1877. Gateaux then extended Fréchet’s earlier ideas to develop his concept of differential, which was presented in a posthumous publication in 1919. The “convenient” form of differentials, one of their most recent incarnations, was introduced by Frölicher, Kriegl and Michor in the early 1980s ([KRI 97], p. 73). These differentials were intended for mappings taking values in locally convex non-normable spaces, in particular nuclear Fréchet spaces (see, in particular, section 5.3.2 on manifolds of mappings). Wherever possible, this chapter therefore chooses to present differential calculus for mappings which take values in locally convex spaces rather than the normed vector spaces considered by the standard approach (nothing essential changes). Nonetheless, for the inverse mapping theorem and the implicit function theorem (Theorems 1.29 and 1.30), we will restrict attention to the Banach case (for a more general context, see [GLÖ 06], which uses yet another concept of differentiability distinct from any of those mentioned above). Both theorems are proved in full detail, including the Banach analytic case, by explicitly filling in the hints from [WHI 65]. Together with the Carathéodory theorems mentioned below, these two theorems are the most profound results of this chapter.
The classical Cauchy–Lipschitz conditions for the existence and uniqueness of solutions of ordinary differential equations were considerably weakened by Carathéodory ([CAR 27], section 576 and following) using measure and integration theory ([P2], section 4.1), which was an extremely recent development at the time. It was judged useful to give a full proof of Carathéodory’s theorems in section 1.5.1, since the available literature seems to expect the reader to reassemble this proof from a scattered collection of isolated results and special cases, at the expense of clarity. The parameter dependence of solutions is studied in section 1.5.3. Again, proofs are given in full, with the exception of one result: the differentiability of solutions with respect to the initial condition when the classical hypothesis (Corollary 1.82) is replaced by Lusin’s condition. This generalization is important (Remark 1.84) and the proof is not uninteresting ([ALE 87], Chapter 2, section 2.5.6); it is omitted from these pages not because it is too difficult but because it is too long.
1.2 Fréchet differential calculus
1.2.1 General conventions
The conventions presented below apply throughout the entire volume. The conventions listed under (II) are motivated by tensor calculus (Chapter 4).
(I)
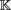 denotes the field of real or complex numbers. Two elements ∞ and ω are adjoined to the set of integers
denotes the field of real or complex numbers. Two elements ∞ and ω are adjoined to the set of integers
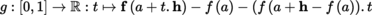 . The usual order relation on
. The usual order relation on
 is extended by the convention n < ∞ < ω for every integer
is extended by the convention n < ∞ < ω for every integer
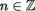 , with ∞ + n = n + ∞ = ∞, ω + n = n + ω = ω. We define
, with ∞ + n = n + ∞ = ∞, ω + n = n + ω = ω. We define
 if
if
 and
and
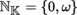 if
if
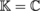 , and
, and
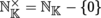 . See also the convention (C) in section 2.2.1
(II)
.
. See also the convention (C) in section 2.2.1
(II)
.
For
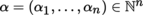 , recall that α! = α
1!…α
n
!. For
, recall that α! = α
1!…α
n
!. For
 , | α | = α
1 + … + α
n
.
, | α | = α
1 + … + α
n
.
The locally convex vector spaces considered below are defined over
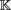 and are always Hausdorff, with the exception of semi-normed spaces. We will use the Landau notation: let X be a topological space, a some point in X, F a locally convex space, and
and are always Hausdorff, with the exception of semi-normed spaces. We will use the Landau notation: let X be a topological space, a some point in X, F a locally convex space, and
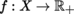 , g : X → F two mappings; suppose that f (x) > 0 in some neighborhood of a. We write g = O (f)(x → a) (respectively g = o (f)(x → a)) and say that g is dominated by f (respectively is negligible with respect to f)in the neighborhood of a if the function g/f is bounded in some neighborhood of a (respectively tends to 0 as the variable x tends to a). If there are several such mappings, we can write O
1 (f), O
2 (f) (respectively o
1 (f), o
2 (f)), etc.
, g : X → F two mappings; suppose that f (x) > 0 in some neighborhood of a. We write g = O (f)(x → a) (respectively g = o (f)(x → a)) and say that g is dominated by f (respectively is negligible with respect to f)in the neighborhood of a if the function g/f is bounded in some neighborhood of a (respectively tends to 0 as the variable x tends to a). If there are several such mappings, we can write O
1 (f), O
2 (f) (respectively o
1 (f), o
2 (f)), etc.
(II) Unless otherwise stated, the dual of a locally convex space E is denoted by E
∨
1
. Let (e
i
) be a basis of the finite-dimensional vector space E, (e
∨ î
) the dual basis, (e′
i
) some other basis of E and (e′∨ i
) its dual basis ([P1], section 3.1.3(VI)). In practice, we can unambiguously write e
i′ for e′
i′, e
∨ i′ for e′∨ i′. Similarly, given a change-of-basis matrix A = (A
i
i′) (where i ranges over the rows and i′ ranges over the columns), we can write
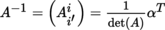 , where α is the matrix of cofactors of A ([P1], section 2.3.11
(V)
); thus, Σ
i′, A
i
i′ A
i′
j
= δ
i
j
2
. Let x = Σ
i
x
i
e
i
∈ E; E is typically a left
, where α is the matrix of cofactors of A ([P1], section 2.3.11
(V)
); thus, Σ
i′, A
i
i′ A
i′
j
= δ
i
j
2
. Let x = Σ
i
x
i
e
i
∈ E; E is typically a left
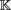 -vector space and so the vector x can be represented by the row (x
i
) with respect to the basis (e
i
) ([P1], section 3.1.3(II)). By contrast, E
∨ is typically a right
-vector space and so the vector x can be represented by the row (x
i
) with respect to the basis (e
i
) ([P1], section 3.1.3(II)). By contrast, E
∨ is typically a right
 -vector space; thus, if x
∨ = Σ
i
x
i
∨
e
∨ i
∈ E
∨, the covector x
∨ can be represented by the column (x
i
∨) with respect to the basis (e
∨ i
) ([P1], section 3.1.3(IV)).
-vector space; thus, if x
∨ = Σ
i
x
i
∨
e
∨ i
∈ E
∨, the covector x
∨ can be represented by the column (x
i
∨) with respect to the basis (e
∨ i
) ([P1], section 3.1.3(IV)).
Memory aid:– Indices such as i, j, k refer to the old basis; primed indices such as i′, j′, k′ refer to the new basis and are written as superscripts for the change-of-basis matrix A or as subscripts for its inverse A − 1. The indices of the components of a vector are usually written as superscripts; the indices of the components of a covector are usually written as subscripts. The indices of a sequence of vectors are always subscripts; the indices of a sequence of covectors are always superscripts. This is motivated by “Einstein’s summation convention” (see Remark 4.2 in section 4.2.1).
If x ∈ E, x ∨ ∈ E ∨, the duality bracket of these two vectors is written as 〈x, x ∨〉. A change of basis in E and E ∨ may therefore be written as:
Let x = Σ i x i e i ∈ E and x∨ = Σ i e ∨ i x i ∨ ∈ E′. Then, x = Σ j′ x j′ e j′ and x ∨ = Σ j′ e ∨ j′ x j′ ∨, where:
Since
 is commutative, we do not need to distinguish between left
is commutative, we do not need to distinguish between left
 -vector spaces and right
-vector spaces and right
 -vector spaces. Therefore, the duality bracket of x ∈ E, x
∨ ∈ E
∨ can also be written as 〈x
∨, x〉. For example, if
-vector spaces. Therefore, the duality bracket of x ∈ E, x
∨ ∈ E
∨ can also be written as 〈x
∨, x〉. For example, if
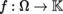 is a differentiable function in some non-empty open subset Ω of E, then, at each point a of Ω, we have Df (a) ∈ E
∨ (see Lemma-Definition 1.4). If h
a
∈ E, it might seem more convenient to write (Df (a), h
a
) instead of (h
a
, Df (a)) for the quantity Df (a).h
a
, but the reverse notation is also perfectly justifiable (section 2.2.4
(IV)
).
is a differentiable function in some non-empty open subset Ω of E, then, at each point a of Ω, we have Df (a) ∈ E
∨ (see Lemma-Definition 1.4). If h
a
∈ E, it might seem more convenient to write (Df (a), h
a
) instead of (h
a
, Df (a)) for the quantity Df (a).h
a
, but the reverse notation is also perfectly justifiable (section 2.2.4
(IV)
).
(III) Recall the following fact ([P2], section 3.9.3(II)): let E
1, …, E
n
be normed vector spaces, each equipped with a norm |.|, and suppose that F is a semi-normed vector space equipped with a semi-norm |.|γ. The space
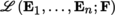 of continuous n-linear mappings from E
1 × … × E
n
into F is a semi-normed vector space when equipped with the semi-norm ||.||γ defined for any mapping
of continuous n-linear mappings from E
1 × … × E
n
into F is a semi-normed vector space when equipped with the semi-norm ||.||γ defined for any mapping
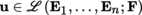 by:
by:
If F is a Hausdorff locally convex space whose topology is induced by the family of semi-norms (|.|γ)γ ∈ Γ ([P2], section 3.3.3), then
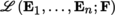 is a Hausdorff locally convex space when equipped with the family of semi-norms (|.|γ)γ ∈ Γ. This space is quasi-complete whenever F is quasi-complete ([P2], section 3.4.2
(II)).
is a Hausdorff locally convex space when equipped with the family of semi-norms (|.|γ)γ ∈ Γ. This space is quasi-complete whenever F is quasi-complete ([P2], section 3.4.2
(II)).
Write
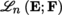 for the space
for the space
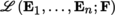 whenever E
i
= E for all i ∈ {1, …, n}. An element u of
whenever E
i
= E for all i ∈ {1, …, n}. An element u of
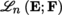 is said to be symmetric if, for all (h
1, …, h
n
) ∈ E
n
and every permutation
is said to be symmetric if, for all (h
1, …, h
n
) ∈ E
n
and every permutation
 ,we have u(h
1, …, h
n
) = u(h
σ(1), …, h
σ(n)). The set of symmetric elements of
,we have u(h
1, …, h
n
) = u(h
σ(1), …, h
σ(n)). The set of symmetric elements of
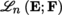 is written as
is written as
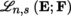 and is a vector subspace of
and is a vector subspace of
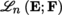 ; this subspace is equipped with the family of semi-norms (||.||γ)γ ∈ Γ. If h ∈ E and
; this subspace is equipped with the family of semi-norms (||.||γ)γ ∈ Γ. If h ∈ E and
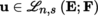 , set:
, set:
If E is finite-dimensional, then we have the following canonical isomorphism:
(IV) See also the conventions (C1) (section 2.2.1 (III) , p. 55), (C2) (section 2.2.2 (III) , p. 58), (C3) (section 6.2.1 (II), p. 253).
1.2.2 Fréchet differential
(I) Let E, F be two locally convex spaces and ϕ a mapping from U into F, where U is some neighborhood of 0 in E.
From this lemma, we immediately deduce the following claim (ii):
The notion of the Fréchet differential is especially fruitful when E is a normed vector space. In this case, if A is an open subset of E, F is a locally convex space, a is a point of A, and f : A → F is a mapping, then f is differentiable at a with differential D f (a) at this point if and only if
The canonical isomorphism
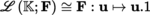 ([P2], section 3.3.8) reintroduces the usual notion of derivative, including the notion of a “complex derivative” when
([P2], section 3.3.8) reintroduces the usual notion of derivative, including the notion of a “complex derivative” when
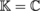 ([P2], section 4.2.1, Theorem-Definition 4.45). Indeed, keeping the same notation as before, we obtain:
([P2], section 4.2.1, Theorem-Definition 4.45). Indeed, keeping the same notation as before, we obtain:
If f is differentiable at the point a, then it is also continuous at this point (exercise). Let A be a non-empty open subset of E and write
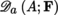 for the set of mappings from A into F that are differentiable at the point a ∈ A. The mapping
for the set of mappings from A into F that are differentiable at the point a ∈ A. The mapping
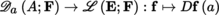 is known as the differentiation operator at the point a and is
is known as the differentiation operator at the point a and is
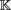 -linear.
-linear.
(II) Let E be a real Hilbert space, A some non-empty open subset of E, and
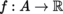 a function that is differentiable at the point a ∈ A. Then, Df (a) ∈ E
∨. By Riesz’s theorem ([P2], section 3.10.2(IV), Theorem 3.15(1)), there exists some uniquely determined element x
* ∈ E such that Df (a) coincides with the linear form h ↦ 〈x
∗| h〉.
a function that is differentiable at the point a ∈ A. Then, Df (a) ∈ E
∨. By Riesz’s theorem ([P2], section 3.10.2(IV), Theorem 3.15(1)), there exists some uniquely determined element x
* ∈ E such that Df (a) coincides with the linear form h ↦ 〈x
∗| h〉.
(III) Some of the classical results of differential calculus ([DIE 93], Volume 1, Chapter 8) are reproduced below. A few are stated in a slightly more general form than the cited reference; however, the reasoning is identical and entirely straightforward in each case.
(IV) Let E 1, …, E n be normed vector spaces. Then, E = E 1 × … × E n can be canonically equipped with the structure of a normed vector space ([P2], section 3.4.1 (I)). Let A be a non-empty open subset of E and suppose that a = (a 1,…,a n ) ∈ A. Suppose further that F is a locally convex space. If f : A → F : (x 1, …, x n ) ↦ f (x 1, …, x n ) is differentiable at the point a, then the mapping
is defined in some open neighborhood of 0 in E
i
and differentiable at 0 for all i ∈ {1, …n} (exercise); its differential at this point is written as D
i
f (a) (or d
i
f (a) or
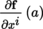 ).
).
Given the conditions stated above, the differential D f (a) can be expressed in terms of the partial differentials D i f (a) as follows:
where h = (h
1, …, h
n
). If
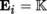 , the element ∂
i
f (a) = D
i
f (a).1 ∈ F is called the i-th partial derivative of f at the point a; writing (e
i
)1 ≤ i ≤ n
for the canonical basis of
, the element ∂
i
f (a) = D
i
f (a).1 ∈ F is called the i-th partial derivative of f at the point a; writing (e
i
)1 ≤ i ≤ n
for the canonical basis of
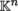 , we have
, we have
If
 , the existence of the partial differentials D
i
f (a)(i = 1, …, n) does not imply the existence of the differential D
f (a) (however, see Theorem 1.16(ii)).
, the existence of the partial differentials D
i
f (a)(i = 1, …, n) does not imply the existence of the differential D
f (a) (however, see Theorem 1.16(ii)).
If
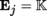 for all j ∈{1, …, n} and
for all j ∈{1, …, n} and
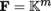 , then the linear mapping D
f (a) can be represented with respect to the canonical bases by the Jacobian matrix [∂
i
f
j
(a)]1 ≤ i ≤ m, 1 ≤ j ≤ n
, where f = (f
1, …, f
n
). If n = m, the determinant of this matrix is called the Jacobian of f at the point a and is written as
, then the linear mapping D
f (a) can be represented with respect to the canonical bases by the Jacobian matrix [∂
i
f
j
(a)]1 ≤ i ≤ m, 1 ≤ j ≤ n
, where f = (f
1, …, f
n
). If n = m, the determinant of this matrix is called the Jacobian of f at the point a and is written as
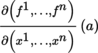 .
.
(V) In the following,
 . Let F be a locally convex space and |.|γ a continuous semi-norm on F.
. Let F be a locally convex space and |.|γ a continuous semi-norm on F.
Let E be a normed vector space with norm |.|. With the notation of [1.3] (with n = 1), we have the following result:
Theorem 1.13 has the following two corollaries:
1.2.3 Mappings of class Cp
In this section,
 .
.
(I) Let E be a normed vector space and suppose that F is a locally convex space. Write
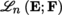 for the space of continuous n-linear mappings from E
n
into F equipped with the family of semi-norms [1.3].
for the space of continuous n-linear mappings from E
n
into F equipped with the family of semi-norms [1.3].
Let A be a non-empty open subset of E and suppose that f : A → F is a mapping. We say that f is of class C
0 if it is continuous in A. We say that it is of class C
1 if it is differentiable in A and its differential
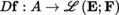 is continuous. We say that f is twice differentiable (respectively is of class C
2 )in A if its differential
D
f is differentiable (respectively is of class C
1) in A. At any given point a ∈ A, the second differential D (D
f)(a), written as D
2
f (a), is an element of
is continuous. We say that f is twice differentiable (respectively is of class C
2 )in A if its differential
D
f is differentiable (respectively is of class C
1) in A. At any given point a ∈ A, the second differential D (D
f)(a), written as D
2
f (a), is an element of
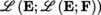 ; this space can be identified with
; this space can be identified with
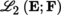 by ([P2], section 3.9.3(II)). Similarly, we may recursively define a p-times differentiable mapping (respectively a mapping of class C
p
)in A for any integer p ≥ l, as well as the p-th order differential
by ([P2], section 3.9.3(II)). Similarly, we may recursively define a p-times differentiable mapping (respectively a mapping of class C
p
)in A for any integer p ≥ l, as well as the p-th order differential
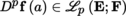 for any point a ∈ A. We say that f is of class C
∞ if f is of class C
p
for every p ≥ l. We write
for any point a ∈ A. We say that f is of class C
∞ if f is of class C
p
for every p ≥ l. We write
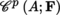 for the
for the
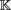 -vector space of mappings of class C
p
from A into F (0 ≤ p ≤ ∞).
-vector space of mappings of class C
p
from A into F (0 ≤ p ≤ ∞).
From ([DIE 93], Volume 1, (8.12.1), (8.16.6)), mutatis mutandis, we have the following result:
By Theorem 1.16(ii), a mapping f from a non-empty open subset Ω of
 into
into
 is of class C
p
if and only if its n
p
partial derivatives exist and are continuous, i.e.
is of class C
p
if and only if its n
p
partial derivatives exist and are continuous, i.e.
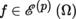 ([P2], section 4.3.1
(I)).
([P2], section 4.3.1
(I)).
(II) In the context of Theorem 1.16(i), when
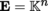 , introducing “symbolic powers” gives us an easy way to express D
p
f (a).h
p
(with the notation of section 1.2.1
(III)) in terms of the partial derivatives of order p:
, introducing “symbolic powers” gives us an easy way to express D
p
f (a).h
p
(with the notation of section 1.2.1
(III)) in terms of the partial derivatives of order p:
where D i denotes the partial differential in the i-th variable. Writing h = (h 1, …, h n ), we have D 2 f (a).h 2 = Σ1 ≤ i,j ≤ n ∂ i ∂ j f (a).h i h j 4 . This can be expressed as (Σ1 ≤ i ≤ n ∂ i f (a).h i )[2] by developing the latter like any other squared parentheses and replacing (∂ i f (a).h i ) (∂ j f (a).h j ) by ∂ i ∂ j f (a).h i h j . With the same conventions, we can continue inductively to obtain the following result:
If
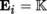 (i = 1, …, n),
(i = 1, …, n),
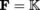 , and
, and
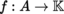 is twice differentiable at some point a of A, then the matrix H f (a) = (∂
i
∂
j
f (a))1 ≤ i,j ≤ n
is called the Hessian matrix
5
of f at the point a. Identifying the vectors of
is twice differentiable at some point a of A, then the matrix H f (a) = (∂
i
∂
j
f (a))1 ≤ i,j ≤ n
is called the Hessian matrix
5
of f at the point a. Identifying the vectors of
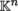 with the columns of this matrix gives D
2
f (a).h
2 = h
T
.H f (a).
h
.
with the columns of this matrix gives D
2
f (a).h
2 = h
T
.H f (a).
h
.
(III) Suppose that l ≤ p ≤ ∞. The following results can be shown by induction (exercise). The composition of two mappings of class C p is also of class C p . If E is a normed vector space, A some non-empty open subset of E, F and G locally convex spaces, u a continuous linear mapping from F into G and f : A → F a mapping of class C p in A, then u ∘ f is of class C p in A and D p (u ∘ f) = u ∘ D p f. With the same hypotheses on E and A, if F 1, F 2, and G are locally convex spaces, [.,.] is a continuous bilinear mapping from F 1 × F 2 into G, and f i is a mapping of class C p from A into F i for i = 1, 2, then [f1, f2] is of class C p from A into G and the so-called Leibniz rule holds:
(IV) Nemytskii Operator
Let F be a Banach space, J a compact interval of
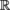 with non-empty interior, and
with non-empty interior, and
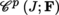 the space of mappings of class C
p
(p ≥ 1) from J into F. Then,
the space of mappings of class C
p
(p ≥ 1) from J into F. Then,
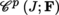 is a Banach space when equipped with the norm
is a Banach space when equipped with the norm
(exercise). Let U be an open neighborhood of 0 in F, f : U × J → F a mapping of class C
p
and
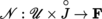 the so-called Nemytskii operator, defined by
the so-called Nemytskii operator, defined by
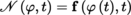 , where
, where
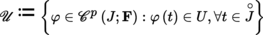 .
.
1.2.4 Taylor’s formulas
Throughout this section,
 , and F denotes a quasi-complete locally convex space. Readers who are only interested in mappings taking values in a Banach space (see Remark 1.1) may skip (I) and (II) below.
, and F denotes a quasi-complete locally convex space. Readers who are only interested in mappings taking values in a Banach space (see Remark 1.1) may skip (I) and (II) below.
(I) Mackey Convergence Let B be a balanced convex subset (also known as an “absolutely convex” subset ([KÖT 79], Volume 1, section 16.1(2))) that is closed and bounded in F, and write F 1 = ∪ n = 1 ∞ nB. The gauge of p B of B in F 1 ([P2], section 3.3.2 (I)) is a norm on F 1 (exercise) and F 1 is a Banach space, written as F B , when equipped with this norm.
Mackey convergence of a sequence of elements of F implies the usual notion of convergence and is equivalent to it whenever F is a Fréchet space or the strong dual of an infrabarreled Schwartz space ([HOG 71], p. 8, Example 3), such as the distribution spaces studied in ([P2], section 4.4.1).
(II) Generalized Riemann integral To state Taylor’s formulas in a general framework, it will be useful to introduce the generalized Riemann integral of a function of a real variable taking values in a quasi-complete locally convex space 6 .
If F is a Banach space, this recovers the classical notion of the integral of a continuous function. The integration operator ∫ a b defined above satisfies the usual properties ([KRI 97], Chapter 1, Corollary 2.6). In particular, we have the following result:
(III) Taylor’s formulas Let E be a normed vector space with norm |.|, A some non-empty open subset of E and F a quasi-complete locally convex space whose topology is defined by a family of semi-norms (|.|γ)γ ∈ Γ. With the conventions of section 1.2.1 and p ≥ l, we have the following result:
(IV) If E = E
1 × … × E
n
, where each E
i
is a normed vector space, let α be the multi-index (α
1, …, α
n
),
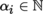 (i ∈ {1, …, n}). Define
(i ∈ {1, …, n}). Define
the operator D
α
is called the partial differential of order α. If each E
i
is equal to
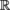 , write ∂
α
for D
α
([P2], section 4.3.1
(I)). Let U be an open neighborhood of a in E and suppose that the function f : U → F is of class C
p
in U. Then, Taylor’s formula can be rewritten as follows:
, write ∂
α
for D
α
([P2], section 4.3.1
(I)). Let U be an open neighborhood of a in E and suppose that the function f : U → F is of class C
p
in U. Then, Taylor’s formula can be rewritten as follows:
1.2.5 Analytic functions
(I) Power series
Let E be a normed vector space with norm |.| and suppose that F is a Hausdorff quasi-complete locally convex space (see Remark 1.1 for the case where F is normable). With the notation of section 1.2.1, let
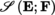 be the
be the
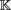 -vector space of formal power series S = ∑
p
S
p
, where S
p
= c
p
.X
p
and
-vector space of formal power series S = ∑
p
S
p
, where S
p
= c
p
.X
p
and
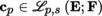 . Let (|.|γ)γ ∈ Γ be a family of semi-norms which induces the topology of F and let r > 0; we write that ‖S‖
γ, r
= ∑
p
r
p
‖c
p
‖
γ
and
. Let (|.|γ)γ ∈ Γ be a family of semi-norms which induces the topology of F and let r > 0; we write that ‖S‖
γ, r
= ∑
p
r
p
‖c
p
‖
γ
and
The set
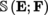 is a
is a
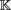 -vector space called the space of convergent power series. If
-vector space called the space of convergent power series. If
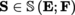 , we say that
, we say that
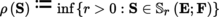 is the radius of convergence of S. Suppose that ρ (S) > 0; if we replace the indeterminate X with an element h ∈ E such that | h | < ρ (S), then the family c
p
.h
p
is summable ([P2], section 3.2.1
(III)), as can be seen by adapting the proof of ([P2], section 3.4.1
(I), Theorem 3.41), and the mapping S : S ↦ S (h) is continuous in the open set | h | < ρ (S).If F is a Banach space and ρ (S) > 0, then the power series S is absolutely convergent in | h | < ρ (S) and normally convergent in | h | ≤ r′ for every r′ such that 0 < r′ < ρ (S) ([P2], section 4.3.2
(I)).
is the radius of convergence of S. Suppose that ρ (S) > 0; if we replace the indeterminate X with an element h ∈ E such that | h | < ρ (S), then the family c
p
.h
p
is summable ([P2], section 3.2.1
(III)), as can be seen by adapting the proof of ([P2], section 3.4.1
(I), Theorem 3.41), and the mapping S : S ↦ S (h) is continuous in the open set | h | < ρ (S).If F is a Banach space and ρ (S) > 0, then the power series S is absolutely convergent in | h | < ρ (S) and normally convergent in | h | ≤ r′ for every r′ such that 0 < r′ < ρ (S) ([P2], section 4.3.2
(I)).
(II) Analytic functions
Let A be a non-empty open subset of E. We say that a function f from A into F is analytic (or is a mapping of class C
ω
) if, for each point a ∈ A, there exists a convergent series
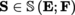 , denoted by f
a
, such that f (a + h) = f
a
(h) for every h ∈ E with sufficiently small norm. This definition generalizes ([P2], section 4.3.2
(I), Definition 4.74). Write
, denoted by f
a
, such that f (a + h) = f
a
(h) for every h ∈ E with sufficiently small norm. This definition generalizes ([P2], section 4.3.2
(I), Definition 4.74). Write
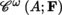 for the
for the
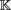 -vector space of analytic functions from A into F. If
-vector space of analytic functions from A into F. If
 and
and
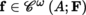 , then f is of class C
∞ in A, and so is each of its differentials D
p
f (p ≥ 1). Every mapping
, then f is of class C
∞ in A, and so is each of its differentials D
p
f (p ≥ 1). Every mapping
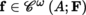 admits the following Taylor series expansion at the point a, which converges in | h | < ρ(f
a
):
admits the following Taylor series expansion at the point a, which converges in | h | < ρ(f
a
):
If | a | < ρ(f a ), then the radius of convergence of the Taylor expansion of f at the point a is greater than or equal to ρ (f a ) − | a |. If A = E and ρ (f a ) = +∞, then the function f is said to be entire.
Let E, F be Banach spaces, G a quasi-complete locally convex space, A an open subset of E, f : A → F an analytic function, B an open subset of F containing f (A) and g : B → G an analytic function. Then, g ∘ f is analytic (exercise); see ([BOU 82a], 3.2.7), ([WHI 65], p. 1079).
The principle of analytic continuation ([P2], section 4.3.2, Theorem 4.76) can be generalized as follows (exercise: see [WHI 65], p. 1080): let E and F be two Banach spaces, Ω a connected open subset of E and f, g two analytic functions from Ω into F. If f and g coincide in any non-empty open subset of Ω, then they must be equal.
(III) Holomorphic functions
Let E be a normed complex vector space with norm |.|, A some non-empty open subset of E, and F a complex quasi-complete locally convex space. Goursat’s theorem ([P2], section 4.2.4, Proposition 4.56) can be generalized as follows ([BOU 82a], 3.1.1): the function f : A → F is analytic if and only if it is holomorphic (i.e. complex-differentiable). If this condition is satisfied for E = E
1 × … × E
n
, let a =(a
1,…, a
n
) ∈ A, r = (r
1, …, r
n
), where r
i
> 0, and
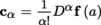 , where α is the multi-index (α
1,…, α
n
). The Cauchy inequalities ([P2], section 4.3.2
(II), Lemma-Definition 4.78(2)) can be generalized as follows (exercise): for r
α
≔ r
1
α
1
…r
n
α
n
,
, where α is the multi-index (α
1,…, α
n
). The Cauchy inequalities ([P2], section 4.3.2
(II), Lemma-Definition 4.78(2)) can be generalized as follows (exercise): for r
α
≔ r
1
α
1
…r
n
α
n
,
Hence ([P2], section 4.3.2 (II), Theorem-Definition 4.81(3)), if f is entire in E and bounded in F, then it must be constant (Liouville’s theorem). The statement of Hartogs’ theorem ([P2], section 4.3.2 (II), Corollary 4.80) also holds, mutatis mutandis, for a function f : A → F, where A is an open subset of E 1 × … × E n , and each E i is a complex normed vector space: any such function is analytic if and only if it is analytic in each of its variables when the others are held fixed.
1.2.6 The implicit function theorem and its consequences
(I) Banach–Caccioppoli fixed point theorem
(II) Inverse mapping and implicit function theorems Below, we assume that 0 < p ≤ ω.
This definition can be localized in the obvious way as we did for homeomorphisms ([P2], section 2.3.4 (III)). Every diffeomorphism (respectively local diffeomorphism) is clearly a homeomorphism (respectively local homeomorphism). A local diffeomorphism of class C p is also known as an étale mapping of class C p (see [P2], section 5.3.2 (II)).
(III) Immersions, submersions, subimmersions, the rank theorem In the following, we assume that 0 < p ≤ ω.