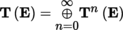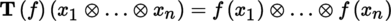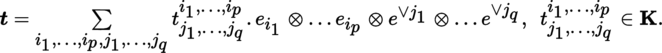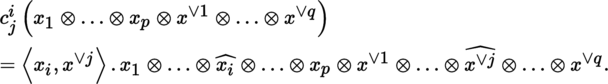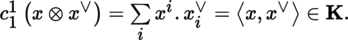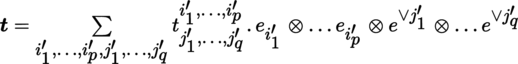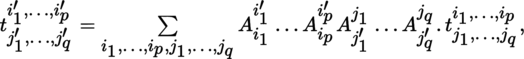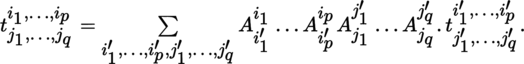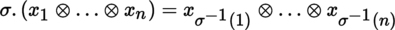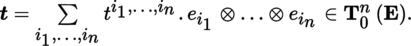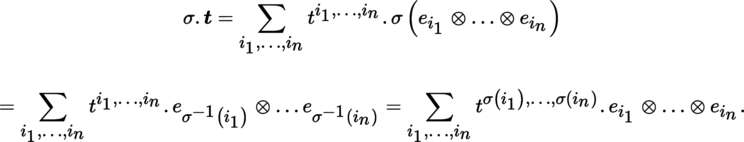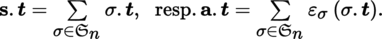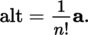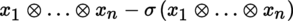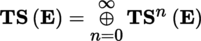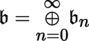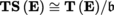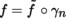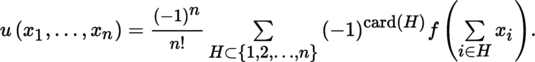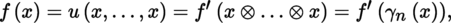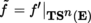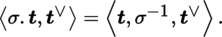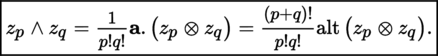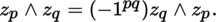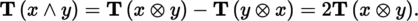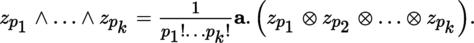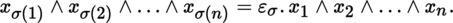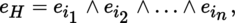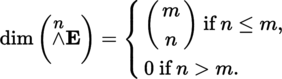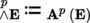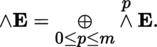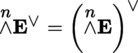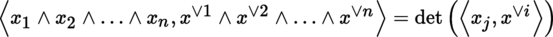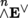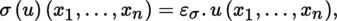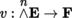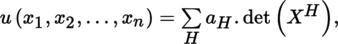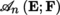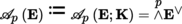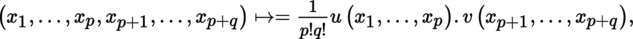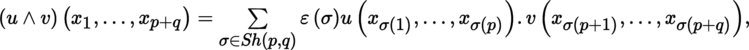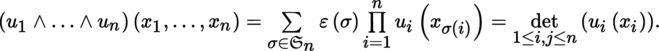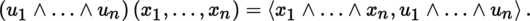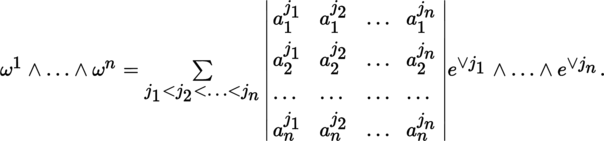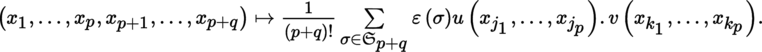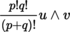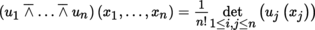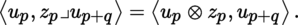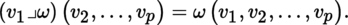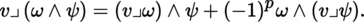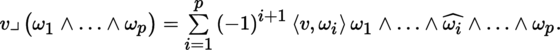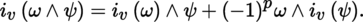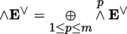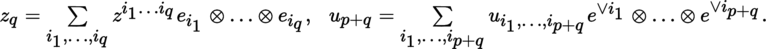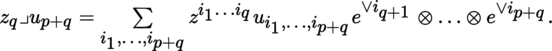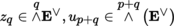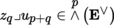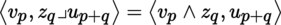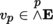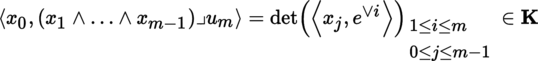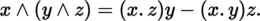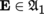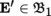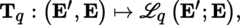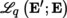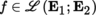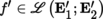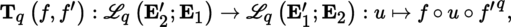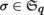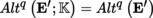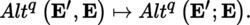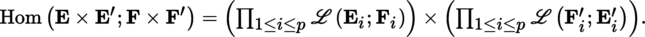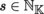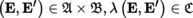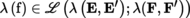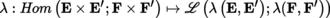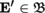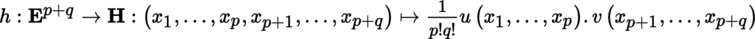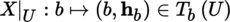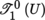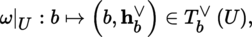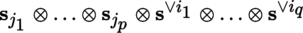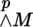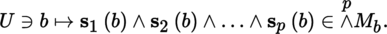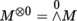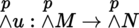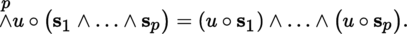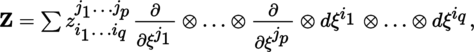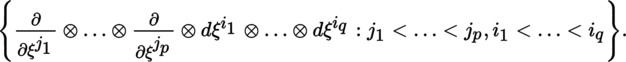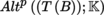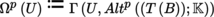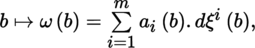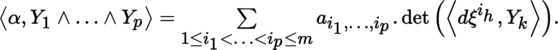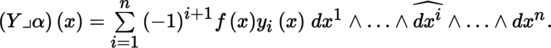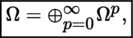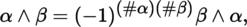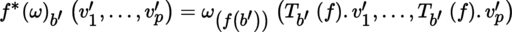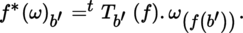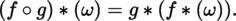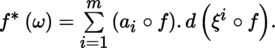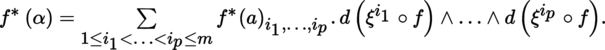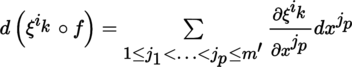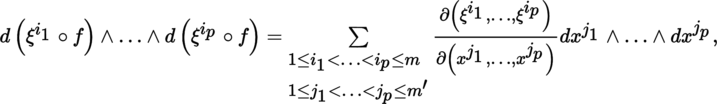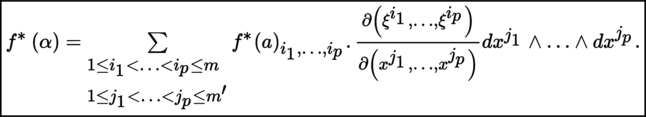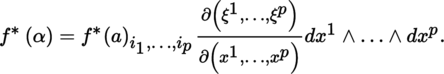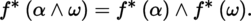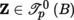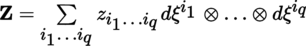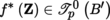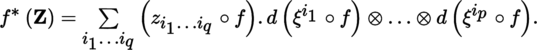Tensor Calculus on Manifolds
Abstract
Tensor calculus was the culmination of pioneering work by B. Christoffel and G. Ricci, in 1869 and 1887–1896, respectively. It reached maturity in a joint publication by Ricci-Curbastro and Levi-Cività in 1900. It is difficult to overstate its importance as a field – general relativity could not exist without it. Tensor calculus plays an essential role in every area of physics; it is also crucial for continuum mechanics and many other engineering sciences, and it, of course, lies at the heart of differential geometry. Section 4.2 of this chapter is purely algebraic (with some algebraic topology in section 4.2.6). The mathematical objects that physicists call tensors are more precisely tensor fields; they are only introduced in section 4.3. Historically, “tensors” were presented to students as exotic mathematical millipedes of the form t j 1, …, j p i 1, …, i p (or more briefly) that behave in a certain way under change of coordinates (see [4.3, 4.4]). This stemmed from the decision to only define the components of the tensor (see [4.2]). As a result, students could complete an entire course of tensor calculus without finding a satisfactory answer to the question: “But what actually is a tensor?” We will, of course, choose a different approach by defining tensor fields before attempting to study them.
Keywords
Banach spaces; Covector field; Differential form over a chain; Exterior algebra; Interior products; Metrics; Pseudo-Riemannian manifolds; Symmetric tensors; Tensor Calculus on Manifolds; Vector fields
4.1 Introduction
Tensor calculus was the culmination of pioneering work by B. Christoffel and G. Ricci, in 1869 and 1887–1896, respectively. It reached maturity in a joint publication by Ricci-Curbastro and Levi-Cività in 1900 [RIC 00]. It is difficult to overstate its importance as a field – general relativity could not exist without it. Tensor calculus plays an essential role in every area of physics; it is also crucial for continuum mechanics and many other engineering sciences, and it, of course, lies at the heart of differential geometry. Section 4.2 of this chapter is purely algebraic (with some algebraic topology in section 4.2.6). The mathematical objects that physicists call tensors are more precisely tensor fields; they are only introduced in section 4.3. Historically, “tensors” were presented to students as exotic mathematical millipedes of the form t j 1, …, j p i 1, …, i p (or more briefly) that behave in a certain way under change of coordinates (see [4.3, 4.4]). This stemmed from the decision to only define the components of the tensor (see [4.2]). As a result, students could complete an entire course of tensor calculus without finding a satisfactory answer to the question: “But what actually is a tensor?” We will, of course, choose a different approach by defining tensor fields before attempting to study them.
The fields of contravariant tensors of order 1 are just the vector fields. The fields of antisymmetric contravariant tensors of order p are called p-vector fields. The fields of covariant tensors of order 1 are the covector fields, or fields of differential forms of degree 1; the fields of antisymmetric covariant tensors of order p are the fields of differential forms of degree p, also called p-forms or p-covectors ([P1], section 3.3.8(VII)). The integral of an m-form over an m-dimensional manifold (line integral if m = 1, surface integral if m = 2, volume integral if m = 3) is a key idea that has various applications in physics (see, for example, section 5.6.4). These forms also allow us to define the orientation of a manifold (section 4.4.4). The differential forms of degree 1 go back to Euler [SAM 01]; higher-order differential forms were introduced by É. Cartan [CAR 99], who made abundant use of them [CAR 22a], whereas the differential forms “of odd type” were developed by G. de Rham [DER 84]. Differential forms are easy to define on
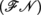 or
or
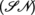 manifolds (Remark 4.33), and their exterior and interior products have properties analogous to those stated in section 4.4.3 ([KRI 97], Chapter VII, section 33).
manifolds (Remark 4.33), and their exterior and interior products have properties analogous to those stated in section 4.4.3 ([KRI 97], Chapter VII, section 33).
The fields of non-degenerate symmetric covariant tensors of order 2, on the other hand, allow us to define pseudo-Riemannian manifolds, which lead to the Riemannian and Lorentz manifolds of general relativity as special cases. The notion of a Riemann space (or Riemannian manifold) is, of course, due to Riemann; they were introduced in his inaugural lecture, mentioned in section 2.1. Pseudo-Riemannian manifolds (and in particular Lorentz manifolds) are the result of a work by Minkowski, Einstein, and Grossmann ([PAU 58], Chapter II, section 7 and Chapter IV, section 50).
4.2 Tensor calculus
As a reminder, we are using the conventions outlined in section 1.2.1, especially those which relate to the representations of vectors and covectors.
4.2.1 Tensors
(I) Notion of a tensor
Let K be a field. Recall that, if E and F are K-vector spaces, the tensor product E ⊗ F is defined as the K-vector space generated by the products x
i
⊗ y
i
(x
i
∈ E, y
i
∈ E), where ⊗ E × F → E ⊗ F is a canonical bilinear mapping that is the solution of a universal problem ([P1], section 3.1.5). In particular, if (e
i
)
i ∈ I
and (f
j
)
j ∈ J
are bases of E and F, respectively, then E ⊗ F consists of the elements of the form ∑
i, j
a
ij
e
i
⊗ f
i
(a
ij
∈ K). If G is a third K-vector space, then
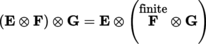 ; thus, this space can be written as E ⊗ F ⊗ G.
; thus, this space can be written as E ⊗ F ⊗ G.
Let E be a finite-dimensional vector space over K, and let E
∨ be its dual.
1
Write T
0
n
(E) = E
⊗ n
for the n-th tensor product of E, namely ⊗
i = 1
n
E
i
, where E
i
= E (i = 1, …, n), with the convention that E
⊗ 0 = K; furthermore, write T
m
0(E) = (E
∨)⊗ m
and T
q
p
(E) = T
q
0(E) ⊗ T
0
p
(E). The elements of the vector space T
q
p
(E) are called p-times contravariant and q-times covariant tensors (or tensors of type
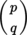 or (p, q))
2
; the order of any such tensor is the integer p + q. Thus, a vector of E is an element of T
0
1(E) and hence a tensor of type (1, 0), i.e. a once contravariant tensor. A linear form on E (also called a covector) is an element of T
1
0(E) and hence a tensor of type (0, 1), i.e. a once covariant tensor. The vector space T
0
n
(E) is also written as T
n
(E).
or (p, q))
2
; the order of any such tensor is the integer p + q. Thus, a vector of E is an element of T
0
1(E) and hence a tensor of type (1, 0), i.e. a once contravariant tensor. A linear form on E (also called a covector) is an element of T
1
0(E) and hence a tensor of type (0, 1), i.e. a once covariant tensor. The vector space T
0
n
(E) is also written as T
n
(E).
If E and F are finite-dimensional K-vector spaces, we know that the space E
∨ ⊗ F can be identified with
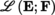 by identifying x
∨ ⊗ y with the K-linear mapping f : x ↦ 〈x, x
∨〉 y ([P1], section 3.1.5(I)). If (e
i
∨)1 ≤ i ≤ n
is a basis of E
∨ and (f
i
)1 ≤ i ≤ m
is a basis of F, the elements of E
∨ can be represented by columns of n elements, the elements of F can be represented by rows of m elements, and so the elements of E
∨ ⊗ F can be represented by n × m matrices, like the elements of
by identifying x
∨ ⊗ y with the K-linear mapping f : x ↦ 〈x, x
∨〉 y ([P1], section 3.1.5(I)). If (e
i
∨)1 ≤ i ≤ n
is a basis of E
∨ and (f
i
)1 ≤ i ≤ m
is a basis of F, the elements of E
∨ can be represented by columns of n elements, the elements of F can be represented by rows of m elements, and so the elements of E
∨ ⊗ F can be represented by n × m matrices, like the elements of
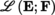 . An element of E
∨ ⊗ F of the form x
∨ ⊗ y can be identified with an n × m matrix of rank 1. Recall that any arbitrary element of E
∨ ⊗ F is a finite sum of terms of this form.
. An element of E
∨ ⊗ F of the form x
∨ ⊗ y can be identified with an n × m matrix of rank 1. Recall that any arbitrary element of E
∨ ⊗ F is a finite sum of terms of this form.
(II) Duality and index contractions The space T q p (E)∨ can be identified with T q p (E) using the relation
An arbitrary element t of T q p (E) can be expressed in the following form with respect to the basis (e i )1 ≤ i ≤ m of E and its dual basis (e ∨ i )1 ≤ i ≤ m :
The t j 1, …, j q i 1, …, i p are the components of the tensor t .
Write c j i for the K-linear index contraction mapping T q p (E) → T q − 1 p − 1(E), i ∈ {i 1, …, i q } and j ∈ {j 1, …, j p }, defined by 3
In particular, if x = ∑ i x i e i and x ∨ = ∑ i x i ∨ e i ∨, then
(III) Change of basis Let A = (A i j ′ ) be a change-of-basis matrix in E. Consider the tensor [4.2]. By [1.1] and [1.2], with the conventions of section 1.2.1 ( II ) and noting that K is commutative,
with
4.2.2 Symmetrie tensors and antisymmetric tensors
(I) Case of contravariant tensors
Let E be an m-dimensional K-vector space. Consider the action of the permutation group
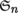 on space of contravariant tensors T
0
n
(E) defined by
on space of contravariant tensors T
0
n
(E) defined by
for
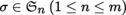 .
.
Given a basis (e i )1 ≤ i ≤ m of E, the e i 1 ⊗ … ⊗ e i n form a basis of the vector space T 0 n (E). Thus, let:
Now, define:
This tensor
t
is said to be symmetric, respectively antisymmetric if σ (
t
) =
t
, respectively σ
t
= ε
σ
t for every
 , where ε
σ
is the signature of the permutation σ.
, where ε
σ
is the signature of the permutation σ.
This is equivalent to saying that its coordinates satisfy:
Let t ∈ T 0 n (E) The symmetrization, respectively antisymmetrization ([P1], section 3.3.8(VII)), of this tensor is defined by
We sometimes write ([SPI 99], Volume 1, Chapter 7):
If t is already symmetric (respectively antisymmetric), then s. t = n! t (respectively a. t = n! t , so alt t = t ). Write TS n (E) ⊂ T 0 n (E) (respectively A n (E) ⊂ T 0 n (E)) for the space of symmetric (respectively antisymmetric) contravariant tensors of order n on E.
Consider the sets H = {i
1, …, i
n
} ⊂ {1, …, m}, i
1 < i
2 < … < i
n
. Then, the elements e
H
= a. (e
i
1
⊗ … ⊗ e
i
n
) form a basis of A
n
(E), and this basis has
 elements.
elements.
The space TS
n (E) can also be defined as a quotient of T
0
n
(E): consider the vector subspace
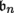 of T
0
n
(E) generated by all the elements of the form
of T
0
n
(E) generated by all the elements of the form
for every x
i
∈ E and
 . Then, TS
n
(E) can be identified with
. Then, TS
n
(E) can be identified with
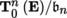 .
.
(II) Case of covariant tensors We saw above that T 0 n (E) can be identified with the dual of T 0 n (E) (section 4.2.1 (II)). By [4.1], it follows that:
Furthermore, T 0 n (E) can be identified with the space of n-multilinear forms on E; thus, the symmetric (respectively antisymmetric) covariant tensors can be identified with the symmetric (respectively alternating) multilinear forms on E.
4.2.3 Exterior algebra
(I) Exterior n -th power Let E be an m-dimensional K-vector space and let z p ∈ A p (E), z q ∈ A q (E) (section 4.2.2(I)). The exterior or wedge product ([P1], section 3.3.8(VII)) z p ∧ z q ∈ A p + q (E) is defined by:
This product is associative and anticommutative, i.e.
In particular, if x, y ∈ E, then x ∧ y = a. (x ⊗ y) = x ⊗ y − y ⊗ x. If T is a twice covariant antisymmetric tensor, then
More generally, if z p i ∈ A p i (E)(i = 1, …, k), then
Applying the above to vectors z p i = x i ∈ E gives
As a result of [4.9], the vector space A
n
(E) is also called the exterior n-th power of E and can be written as
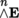 . The basis of this space associated with the basis (e
i
)1 ≤ i ≤ m
consists of the
. The basis of this space associated with the basis (e
i
)1 ≤ i ≤ m
consists of the
 elements:
elements:
where the index sets H are defined as above, so that H = {i 1, …, i n } ⊂ {1, …, m}, i 1 < i 2 < … < i n . Hence,
In particular,
 if n = m and
if n = m and
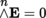 if n > m.
if n > m.
We write that
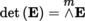 (and so det (E) ≅ K).
(and so det (E) ≅ K).
(II) Calculating an
n
-vector in a given basis
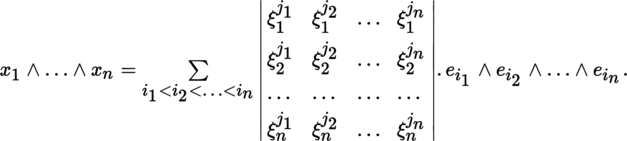
Let
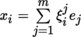 ; explicitly writing out the expression from [P1], section 3.3.8(VII) gives:
; explicitly writing out the expression from [P1], section 3.3.8(VII) gives:
(III) Exterior algebra
Let
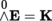 and consider the direct sum
and consider the direct sum
This sum has an associative K-algebra structure (for the exterior product) and is called the exterior algebra of E. The exterior algebra ∧ E is therefore clearly an anticommutative graduated K-algebra ([P1], sections 2.3.10(I) and 2.3.12), and the elements of
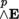 are the homogeneous elements of degree p.
are the homogeneous elements of degree p.
4.2.4 Duality in the exterior algebra
We can repeat the above for covariant tensors and covectors. This gives
with the duality bracket ([P1], section 3.3.8(VII))
and the following result:
If ω i = ∑ j = 1 m a i j e ∨ i (i = 1, …, n), then we have the following relation, similar to [4.11]:
4.2.5 Interior products
Let p, q be integers ≥ 0 and z q a contravariant tensor in T 0 q (E), where E is an m-dimensional K-vector space. The mapping v p ↦ z p ⊗ v p from T 0 q (E) into T 0 p + q (E) is K-linear. Its transpose may therefore be identified with a K-linear mapping from T 0 p + q (E ∨) into T 0 p (E), written as (with u p + q ∈ T 0 p + q (E ∨))
which is said to be the interior product of z q and u p + q . Thus, by definition:
For example, if ω is a p-covector and v 1, …,v p are vectors, then
If ψ is also a n-covector and v is a vector, this gives the “distributivity relation”:
If ω 1,…, ω p are covectors,
4.2.6 Tensors on Banach spaces
(I) Tensors
Let
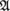 ,
,
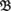 and
and
 be subcategories of the category of Banach
be subcategories of the category of Banach
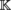 -spaces ([P2], section 3.4.1
(I)) and let
-spaces ([P2], section 3.4.1
(I)) and let
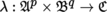 be a functor that is covariant in
be a functor that is covariant in
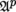 and contravariant in
and contravariant in
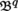 ([P1], sections 1.1.1(I) and 1.2.1).
([P1], sections 1.1.1(I) and 1.2.1).
For every E,
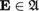 , E′,
, E′,
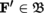 , with E = E
1 × … × E
p
, E′ = E′1 × … × E′
q
, and similarly for F and F′, set
, with E = E
1 × … × E
p
, E′ = E′1 × … × E′
q
, and similarly for F and F′, set
(II) Antisymmetric Continuous Multilinear Mappings
Let E, F be two Banach spaces. The space Alt
q
(E; F) of antisymmetric continuous q-linear mappings from E
q
into F is defined as in Example 4.14(3). Alt
q
(E; F) is a closed subspace of
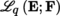 and hence a Banach space.
and hence a Banach space.
Let G, H be two other Banach spaces and Φ: F × G → H a continuous bilinear mapping; for every (y, z) ∈ F × G, write Ф(y, z) = y.z. Let u ∈ Alt p (E; F) and v ∈ Alt q (E; G). Then, the mapping
is continuous and (p + q)-linear. The statement of Lemma-Definition 4.10 remains valid in this more general context (note that the linear and multilinear mappings must be continuous), and u ∧ v ∈ Alt p + q (E; H).
The interior product v 1┘ω of v 1 ∈ E and ω ∈ Alt p (E; F) is defined by [4.14] and belongs to Alt p–1 (E; F). The relations [4.15] and [4.16] still hold, as well as Remark 4.12.
4.3 Tensor fields
Let B be a manifold and U an open subset of B. Write
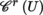 for the
for the
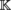 -algebra of mappings of class C
r
from U into
-algebra of mappings of class C
r
from U into
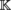 .
.
4.3.1 Vector fields
Let (U, ξ, E) be a chart of B centered on some point a ∈ B, where E is a Banach space. The restriction to U of a vector field
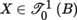 is a mapping X |
U
: U → T (B) such that π ° v = 1
U
, so
is a mapping X |
U
: U → T (B) such that π ° v = 1
U
, so
is a vector field on U. We already know that there exists an isomorphism [3.2]
4.3.2 Covector field
Let (U, ξ, E) be a chart of B centered on a point b ∈ B. The restriction to U of any such covector field ω isa mapping ω | U : U → T ∨ (M) satisfying π ° ω = 1 U , so
is a covector field on U. (For the finite-dimensional case, see Theorem 2.71.)
4.3.3 Tensor fields and scalar fields
(I) Tensor bundle
Let π : M → B be a vector bundle. Write T
q
p
(M) for the vector bundle of class C
r
whose fiber over an arbitrary point b ∈ B is T
q
p
(M
b
) (sections 4.2.1 and 4.2.6). This is called the bundle of p-times contravariant and q-times covariant tensors (or tensors of type (p, q)) on M. If M is of finite rank, then T
q
p
(M) = (M
∨)⊗ q
⊗ (M)⊗ p
. By convention, T
0
1(M) = M, T
1
0(M) = M
∨ (Definition 3.36) and
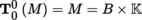 . The following result is clear:
. The following result is clear:
(II) Tensor product, Whitney sum and exterior product The constructions of section 3.4.4 can be extended to the tensor product and Whitney sum of an arbitrary finite number of vector bundles with the same base; in particular, we can define the tensor power M n ⊗ of a vector bundle M with base B and finite rank (section 3.4.1). We can also define the tensor field T 0 n (M) whose fibers are T 0 n (M) b (b ∈ B).
Furthermore, the same construction enables us to define the exterior power
of a vector bundle M of finite rank (with p > 0). For every sequence (s j )1 ≤ j ≤ p of sections of M on an open subset U of B, write s 1 ∧ s 2 ∧ … ∧ s p for the mapping
Consider a morphism of vector bundles u : M → N, where M and N are vector bundles with base B and finite rank. There exists a unique morphism
such that, if s 1,…, s p are arbitrary sections of M over the open set U ⊂ B, then
(III) Tensor fields Let B be a manifold, T (B) its tangent bundle and T ∨ (B) its cotangent bundle. Write T q p (B) for T q p (T(B)) if this is not ambiguous. Thus, T 0 1(B) = T(B) and T 1 0(B) = T ∨(B).
Let (U, ξ, n) be a chart of B. Every tensor field
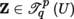 can be uniquely written in the form
can be uniquely written in the form
where the components z
i
1…i
q
j
1…j
p
are of class C
r
. Hence,
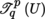 is a free
is a free
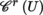 -module with basis
-module with basis
More generally, if U is an arbitrary non-empty open subset of B, then the set
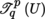 is a
is a
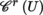 -module that is free whenever T (U) is trivializable, and the mapping
-module that is free whenever T (U) is trivializable, and the mapping
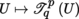 is a sheaf of
is a sheaf of
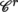 -Modules, where
-Modules, where
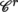 is the sheaf of rings
is the sheaf of rings
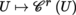 (see Remark 3.34).
(see Remark 3.34).
If B is m-dimensional, a section of class C
r
of the bundle
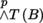 of tangent p-vectors over U (section 4.2.3) is said to be a p-vector field..
of tangent p-vectors over U (section 4.2.3) is said to be a p-vector field..
(IV) Scalar fields
By Remark 4.22,
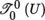 is the set of mappings of class C
r
is the set of mappings of class C
r
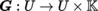 and can be identified with
and can be identified with
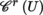 .
.
4.4 Differential forms
4.4.1 Differential forms of degree p
(I) Let B be a manifold. Write
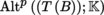 for the vector bundle of class C
r
of alternating continuous p-linear mappings from T (B) into
for the vector bundle of class C
r
of alternating continuous p-linear mappings from T (B) into
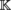 . The fiber of
. The fiber of
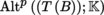 over an arbitrary point b ∈ U is given by
over an arbitrary point b ∈ U is given by
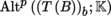 (sections 4.2.1 and 4.2.6).
(sections 4.2.1 and 4.2.6).
The set Ω
p
(U) is a
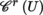 -module. The mapping U → Ω
p
(U), where U is an open subset of B, is a sheaf of
-module. The mapping U → Ω
p
(U), where U is an open subset of B, is a sheaf of
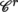 -Modules. The set Ω
p
(U) is in fact just the
-Modules. The set Ω
p
(U) is in fact just the
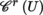 -module of antisymmetric p-times covariant tensor fields of class C
r
on U.
-module of antisymmetric p-times covariant tensor fields of class C
r
on U.
(II) Finite-dimensional case Suppose that the manifold B is locally finite-dimensional and let (U, ξ, m) be a chart of B. By Theorem 2.71, every differential form on U can be written in the form
where the a
i
are m functions
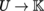 . For ω to be of class C
r
, it is necessary and sufficient for the a
i
to be of class C
r
. Every p-form α ∈ Ω
p
(U) can be uniquely written as
. For ω to be of class C
r
, it is necessary and sufficient for the a
i
to be of class C
r
. Every p-form α ∈ Ω
p
(U) can be uniquely written as
where the a
i
1, …, i
p
are of class C
r
. Hence, the differential p-forms dξ
i
1
∧ … ∧ dξ
i
p
stated above form a basis of the free
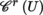 -module Ω
p
(U). The
-module Ω
p
(U). The
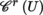 -module Ω
p
(B) is free whenever T (B) is trivializable.
-module Ω
p
(B) is free whenever T (B) is trivializable.
Identifying
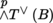 with the dual bundle of
with the dual bundle of
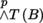 , if Y1,…, Y
p
are p vector fields, then
, if Y1,…, Y
p
are p vector fields, then
The indices h and k range from 1 to p in each determinant by [4.12].
Let
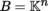 , α (x) = f (x) dx
1 ∧ … ∧ dx
n
, and Y (x) = Σ1 ≤ i ≤ n
y
i
(x) ∂/∂ x
i
. Then, [4.14] implies that:
, α (x) = f (x) dx
1 ∧ … ∧ dx
n
, and Y (x) = Σ1 ≤ i ≤ n
y
i
(x) ∂/∂ x
i
. Then, [4.14] implies that:
(III) De Rham algebra Set
with
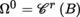 (section 4.3.3
(IV)) and Ω
p
= Ω
p
(B). The notion of exterior algebra introduced in section 4.2.3 allows us to state the following result (see footnote 1(b), p. 132):
(section 4.3.3
(IV)) and Ω
p
= Ω
p
(B). The notion of exterior algebra introduced in section 4.2.3 allows us to state the following result (see footnote 1(b), p. 132):
4.4.2 Preimage of a differential p-form
(I) Let B, B′ be two manifolds, ω ∈ Ω p (B), and f : B′ → B a morphism of manifolds.
In particular, if p = 1, then 〈f ∗(ω) b ′ , v 1 ′〉 = 〈ω (f(b ′)), T b ′ (f). v 1 ′〉 = 〈 t T b ′ (f). ω (f(b ′)), v 1〉, so
If B″ is a manifold and g : B″ → B′ is a morphism, then (exercise)
(II) If B, B′ have dimensions m, m′, respectively, (U, ξ, m) is a chart of B with ξ = (ξ i )1 ≤ i ≤ m , and ω is defined on U by [4.19], then the expression of f ⁎ (ω) on f –1 (U) is given by:
If the p-form α ∈ Ω
p
(B) can be written in the form [4.20] on U, i.e.
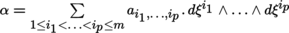 , then f
⁎ (α) ∈ Ω
p
(B′) has the following expression on f
–1 (U), setting f
⁎ (α)= α ° f:
, then f
⁎ (α) ∈ Ω
p
(B′) has the following expression on f
–1 (U), setting f
⁎ (α)= α ° f:
Write ξ = f(x), x = (x 1, …, x m ′ ) Then:
and (exercise)
where
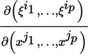 is the Jacobian of (ξ
i
1
, …, ξ
i
p
) relative to (x
j
1
, …, x
j
p
) (section 1.2.2(
IV
)). Hence:
is the Jacobian of (ξ
i
1
, …, ξ
i
p
) relative to (x
j
1
, …, x
j
p
) (section 1.2.2(
IV
)). Hence:
If m = m′ = p, the sum [4.20] has a single term a. dξ 1 ∧ … ∧ dξ p , and [4.23] can be restated as follows:
(III) Let α ∈ Ω p (B), ω ∈ Ω p (B). Then (exercise: see [DIE 93], Volume 3, (16.20.9.5)):