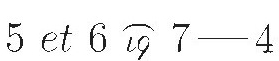
| 2 | Reading and Writing Arithmetic The Basic Symbols |
How would you write the statement "When 7 is subtracted from the sum of 5 and 6, the result is 4" using arithmetic symbols? Would you write (5 + 6) – 7 = 4? Probably. If you did, your expression would have several advantages over the sentence it represents: it's more efficient to write, clearer and less ambiguous to read, and understandable by almost anyone who has studied elementary arithmetic, regardless of the country they're in or the language they speak.
The symbols of arithmetic have become universal. They are far more commonly understood than the letters of any alphabet or the abbreviations of any language. But that hasn't always been the case. The ancient Greeks and their Arab successors didn't use any symbols for arithmetic operations or relations; they wrote out their problems and solutions in words. In fact, arithmetic and algebra statements were written only in words by most people for many, many centuries, right through the Middle Ages.
Arithmetic symbols arose as written shorthand in the early years of the Renaissance, with very little consistency from person to person or from country to country. With the invention of movable-type printing in the 15th century, printed books began to exhibit a little more consistency. Nevertheless, it was a long time before today's symbols became a common part of written arithmetic.
Here are some ways in which (5 + 6) – 7 = 4 would have appeared during the centuries from the Renaissance to now. In most cases the date given is the year that a particular book was published; think of it as an approximation of the time in which that notation was in fairly common use, at least by mathematicians of a particular region.
1470s: Regiomontanus in Germany would have written
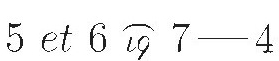
(The word et is "and" in Latin.)
1494: In Luca Pacioli's Summa de Aritmetica, widely used in Italy and other parts of Europe, this would have appeared as
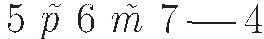
The grouping of the first sum probably would have been ignored, assuming that it obviously was to be done first. This notation for plus and minus became very common throughout much of Europe.
1489: About the same time in Germany, our now-familiar plus and minus signs appeared in print for the first time, in a commercial arithmetic book by Johann Widman. Widman had no symbol for equality, so his version of our statement would likely have been something like
(The German phrase "das ist" means "that is.") But Widman also used + as an abbreviation for "and" in a non-numerical sense and – as a general mark of separation. The idea that these symbols had primary mathematical meanings was not yet clear.
1557: The first use of + and – in an English book occurs in Robert Recorde's algebra text, The Whetstone of Witte. In this book Recorde also introduces = as a symbol for equality. He justifies it by saying, "no two things can be more equal" (than parallel lines of the same length). His other signs are elongated, too. He might have written
Recorde's notation was not immediately popular. Many European writers preferred to use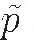 
and 
for plus and minus, particularly in Italy, France, and Spain. His equality sign didn't appear in print again for more than half a century. Meanwhile, the symbol = was being used for other things by some influential writers. For instance, in a 1646 edition of François Viète's collected works, it was used for subtraction between two algebraic quantities when it was not clear which was larger.1
1629: Albert Girard of France would have represented the left side of our equation either as (5 + 6) – 7 or as (5 + 6) ÷ 7; to him they meant the same thing! In fact, ÷ was widely used for subtraction during the 17th and 18th centuries, and even into the 19th century, particularly in Germany.
1631: In England, William Oughtred published a highly influential book, known as Clavis Mathematicae, emphasizing the importance of using mathematical symbols. His use of +, –, and = for addition, subtraction, and equality contributed to the eventual adoption of these symbols as standard notation. However, if Oughtred wanted to emphasize the grouping of the first two terms of our expression, he would have used colons. Thus, he might have written
In this same year, Recorde's long equality symbol appeared in an influential book by Thomas Harriot, along with > and < for "greater than" and "less than," respectively.
1637: René Descartes's La Géométrie, the book that simplified and regularized much of the algebraic notation we use today, was also responsible for delaying universal acceptance of the = sign for equality. In this and some of his later writings, Descartes used a strange symbol for equality.2 In this book Descartes also used a broken dash (a double hyphen) for subtraction, so his version of our equation would have been
Descartes's algebraic notation spread rapidly through the European mathematical community, often carrying with it the strange new symbol for equality. Its use persisted in some places, particularly in France and Holland, into the early 18th century.
Early 1700s: Parentheses gradually replaced other grouping notations, thanks largely to the influential writings of Leibniz, the Bernoullis, and Euler. Thus, by the time the American colonies were preparing to separate from British rule, the most common way to write our simple equation was the one we use today:
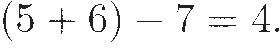
Does it surprise you that there were so many different ways of symbolizing addition, subtraction, and equality? Do you find it strange that people should put up with such ambiguity? It's not really so different from some things we routinely do nowadays. For instance, we still have at least four different notations for multiplication:
•3(4 + 5) means 3 times (4 + 5). Writing multiplication as juxtaposition (just placing the quantities to be multiplied side by side) dates back to Indian manuscripts of the 9th and 10th centuries and to some 15th century European manuscripts.
•The x symbol for multiplication first appears in European texts in the first half of the 17th century, most notably in Oughtred's Clavis Mathematicae. A larger version of this symbol also appears in Géométrie, a famous textbook by Legendre published in 1794.
•In 1698, Leibniz, bothered by the possible confusion between x and x, introduced the raised dot as an alternative sign for multiplication. It came into general use in Europe in the 18th century and is still a common way to symbolize multiplication. Even today, 2 · 6 means 2 times 6.
•Today, calculators and computers use an asterisk for multiplication; 2 times 6 is entered as 2 * 6. This very modern notation was used briefly in Germany in the 17th century;3 then it disappeared from arithmetic until this electronic age.
Signs for division are just as diverse. We write 5 divided by 8 as 5 ÷ 8, or 5/8. or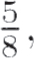 
or even as the ratio 5:8. The use of ÷ for division, rather than subtraction, is primarily due to a 17th century Swiss algebra book, Teutsche Algebra by Johann Rahn. This book was not very popular in continental Europe, but a 1668 English translation of it was well received in England. Some prominent British mathematicians began using its notation for division. In this way, the ÷ symbol became the preferred division notation in Great Britain, in the United States, and in other countries where English was the dominant language, but not in most of Europe. European writers generally followed the lead of Leibniz who (in 1684) adopted the colon for division. This regional difference persisted into the 20th century. In 1923, the Mathematical Association of America recommended that both signs be dropped from mathematical writings in favor of fractional notation, but that recommendation did little to eliminate either one from arithmetic. We still write expressions such as 6 ÷ 2 = 3 and 3 : 4 :: 6 : 8. (For the history of fractional notation, see Sketch 4.)
In this brief sketch we have skipped over many, many symbols that were used from time to time in written or printed arithmetic but are now virtually (and happily) forgotten. Clear, unambiguous notation has long been recognized as a valuable ingredient in the progress of mathematical ideas. In the words of William Oughtred in 1647, the symbolical presentation of mathematics "neither racks the memory with multiplicity of words, nor charges the phantasie [imagination] with comparing and laying things together; but plainly presents to the eye the whole course and process of every operation and argumentation.''4
For a Closer Look: For a readable history of mathematical notation that also reflects on its power and importance, see [123]. The information for this sketch was drawn primarily from [22], which remains a good reference. See also Earliest Uses of Various Mathematical Symbols, a website maintained by Jeff Miller.
1 In other words, it was used for the absolute value of the difference.
2 Cajori ([22], p. 301) is of the opinion that it is the astronomical sign for Taurus rotated a quarter turn to the left.
4 From William Oughtred's The Key of the Mathematicks (London, 1647), as quoted in [22], p. 199, adjusted for modern spelling.