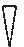for "one" and 
for "ten" which were repeated in combination to stand for any counting number from 1 to 59. For instance, they wrote 72 as| 3 | Nothing Becomes a Number The Story of Zero |
Most people think of zero as "nothing." The fact that it is not nothing lies at the root of at least two (some would say three) important advances in mathematics. The story begins in Mesopotamia, the "cradle of civilization," sometime before 1600 B.C. By then, the Babylonians had a well developed place-value system for writing numbers. It was based on grouping by sixty, much as we count 60 seconds in a minute and 60 minutes (3600 seconds) in an hour. They had two basic wedge-shaped symbols— 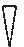for "one" and for "ten" which were repeated in combination to stand for any counting number from 1 to 59. For instance, they wrote 72 as
with a small space separating the 60s place from the 1s place.1
But there was a problem with this system. The number 3612 was written
(one 3600 = 602 and twelve 1s) with a little extra space to show that the 60s place was empty. Since these marks were made quickly by pressing a wedge-shaped tool into soft clay tablets, the spacing wasn't always consistent. Knowing the actual value often depended on understanding the context of what was being described. Sometime around the 4th century B.C., the Babylonians started using their end-of-sentence symbol (we'll use a dot) to show that a place was being skipped, so that 72 and 3612 became
respectively. Thus, zero began its life as "place holder,'' a symbol for something skipped.
Credit for developing the base-ten place value system we now use belongs to the people of India, sometime before 600 A.D. They used a small circle as the place-holder symbol. The Arabs learned this system in the 9th century, and their influence gradually spread it into Europe in the two or three centuries that followed. The symbols for the single digits changed a bit, but the principles remained the same. (The Arabs used the circle symbol to represent "five"; they used a dot for the place holder.) The Indian word for this absence of quantity, sunya, became the Arabic sifr, then the Latin zephirum (along with a barely Latinized cifra), and these words in turn evolved into the English words zero and cipher. Today zero, usually as a circle or an oval, still indicates that a certain power of ten is not being used.
But that's only the beginning of the story. By the 9th century A.D., the Indians had made a conceptual leap that ranks as one of the most important mathematical events of all time. They had begun to recognize sunya, the absence of quantity, as a quantity in its own right! That is, they had begun to treat zero as a number. For instance, the mathematician Mahāvīra wrote that a number multiplied by zero results in zero, and that zero subtracted from a number leaves the number unchanged. He also claimed that a number divided by zero remains unchanged. A couple of centuries later, Bhāskara II declared a number divided by zero to be an infinite quantity.
The main point here is not which Indian mathematician got the right answers when computing with zero, but the fact that they asked such questions in the first place. To compute with zero, you must first recognize it as something, an abstraction on a par with one, two, three, etc. That is, you must move from counting one goat or two cows or three sheep to thinking of 1, 2, and 3 as things that can be manipulated without concern for what kinds of objects are being counted. Then you must take an extra step, to think of 1, 2, 3,..., as ideas that exist even if they aren't counting anything at all. Then, and only then, does it make sense to treat 0 as a number. The ancient Greeks never took that extra step in abstraction; it was fundamentally at odds with their sense of a number as a quantitative property of things.
The Indian recognition of 0 as a number was a key for unlocking the door of algebra. Zero, as symbol and as concept, found its way to the West largely through the writings of the 9th-century Arab scholar Muhammad ibn Musa al-Khwārizmī. He wrote two books, one on arithmetic and the other on solving equations, which were translated into Latin in the 12th century and circulated throughout Europe.
In al-Khwārizmī, zero is not yet thought of as a number; it is just a place holder. In fact, he describes the numeration system as using "nine symbols," meaning 1 through 9. In one of the Latin translations, the role of zero is explained like this:
But when [ten] was put in the place of one and was made in the second place, and its form was the form of one, they needed a form for the tens because of the fact that it was similar to the form of one, so that they might know by means of it that it was [ten]. So they put one space in front of it and put in it a little circle like the letter o, so that by means of this they might know that the place of the units was empty and that no number was in it except the little circle...2
The Latin translations often began with "Dixit Algorizmi," meaning "al-Khwārizmī said." Many Europeans learned about the decimal place system and the essential role of zero from these translations. The popularity of this book as an arithmetic text gradually led its title to be identified with the methods in it, giving us the word ''algorithm."
As the new system spread and people started to compute with the new numbers, it became necessary to explain how to add and multiply when one of the digits was zero. This helped make it seem more like a number. Nevertheless, the Indian idea that one should treat zero as a number in its own right took a long time to get established in Europe. Even some of the most prominent mathematicians of the 16th and 17th centuries were unwilling to accept zero as a root (solution) of equations.
However, two of those mathematicians used zero in a way that transformed the theory of equations. Early in the 17th century, Thomas Harriot, who was also a geographer and the first surveyor of the Virginia colony, proposed a simple but powerful technique for solving algebraic equations:
Move all the terms of the equation to one side of the equal sign, so that the equation takes the form
[some polynomial] = 0.
This procedure, which one author calls Harriot's Principle,3 was popularized by Descartes in his book on analytic geometry and is sometimes credited to him. It is such a common part of elementary algebra today that we take it for granted, but it was a truly revolutionary step forward at the time. Here is a simple example of how it works for us:
To find a number x for which x2 + 2 = 3x is true (a root of the equation), rewrite it as
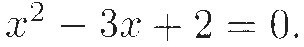
The left side can be factored into (x – 1) · (x – 2). Now, for the product of two numbers to equal 0, at least one of them must equal 0. (This is another special property of zero that makes it unique among numbers.) Therefore, the roots can be found by solving two much easier equations,
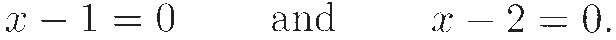
That is, the two roots of the original equation are 1 and 2.
Of course, we chose this example because it factors easily, but a lot was known about factoring polynomials, even in Harriot's time, so this principle was a major advance in the theory of equations.
When linked with the coordinate geometry of Descartes,4 Harriot's Principle becomes even more powerful. We'll use modern terminology to explain why. To solve any equation with real-number variable x, rewrite it as f(x) = 0, where f(x) is some function of x. Now graph f(x). The roots (solutions) of the original equation occur where this graph crosses the x-axis. Thus, even if the equation can't be solved exactly, a good picture of it will give you a good approximation of its solutions.
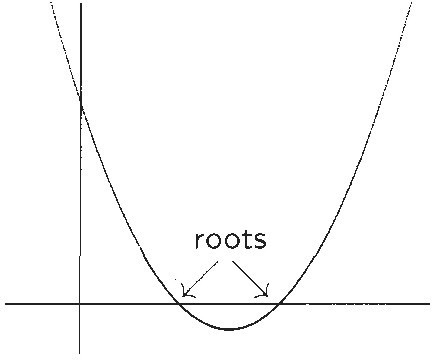
By the 18th century, then, the status of zero had grown from place holder to number to algebraic tool. There is one more step in this number's claim to mathematical prominence. As 19th-century mathematicians generalized the structure of the number systems to form the rings and fields of modern algebra, zero became the prototype for a special element. The facts that 0 plus a number leaves that number unchanged and 0 times a number results in 0 became the defining properties of the "additive identity" element of these abstract systems, often called simply the zero of the ring or field. And the driving force behind Harriot's Principle — if a product of numbers is 0, then one of them must be 0 — characterized a particularly important type of system called an integral domain. Not a bad career for a cipher, don't you think?
For a Closer Look: Many books discuss the history of zero. The material in [35] and in [135] is particularly interesting. Also worth noting is [96], a more literary take on the story.
1 See Sketch 1 for some more details about the Babylonian numeration system.
2 From [33]. The actual text has the Roman numeral "X" for "ten."