| 16 | Shapes by the Numbers Coordinate Geometry |
One of the most powerful ideas in all of mathematics is the understanding of how to represent shapes by equations, a field we now call analytic geometry. Without this bridge between geometry and algebra there would be no calculus for science, no CAT scans for medicine, no automated machine tools for industry, no computer graphics for art and entertainment. Many things we take for granted simply wouldn't exist. Where did this marvelous insight come from? Whose idea was it, and when did it happen?
When you think of analytic geometry, what's the first thing that comes to mind? For most people, it's a pair of coordinate lines, an x-axis and a y-axis at right angles to each other, often called a Cartesian coordinate system. "Cartesian" refers to the 17th century French philosopher/mathematician René Descartes, who is usually credited with the invention of analytic geometry. He did, indeed, formulate most of the key ideas of analytic geometry, but the rectangular coordinate system as we know it today was not one of them.
In a way, the story begins when surveyors in ancient Egypt used a rectangular grid to divide the land into districts, much the same as our modern road maps are divided into squares for indexing purposes. This enabled them to catalog locations by using two numbers, one for a row and the other for a column. That method was also used by Roman surveyors and Greek mapmakers in early times. However, labeling locations by a number grid is only a small step in bridging the gap between geometry and algebra. The much more fundamental question is the connection between algebraic expressions — that is, equations and functions — and shapes in a plane or in space.
A glimmer of this idea is traceable back to ancient Greece. About 350 B.C. Menaechmus related some kinds of curves we now call conic sections (the curves formed by cutting a cone by a plane, discussed in more detail in Sketch 28) to the solution of numerical proportions. This laid the groundwork for the exploration of conic sections by Apollonius a century or so later. Apollonius and other mathematicians of his day were interested in locus1 questions: What points satisfy a given set of conditions, and do they form some kind of line or curve? For instance, the locus of points a fixed distance from a given point is a circle; the locus of points whose distance from a given point equals the perpendicular distance to a given line is a parabola. Apollonius investigated much more complex locus questions and showed that some (but not all) of them resulted in conic sections. Was this analytic geometry? Not exactly. Apollonius was headed in that direction, but his geometric figures were connected with numerical relationships by means of ratios and words. Development of the pattern-rich symbolic language of algebra was still many centuries in the future.

a conic section
The evolution of an efficient algebraic symbolism took a long time. (See Sketch 8.) It was not yet in place in the 14th century when Nicole Oresme described a way of graphing the relationship between an independent variable and a dependent one. Late in the 16th century, François Viète attempted to distill the essence of the ancient Greeks' geometric analysis by representing quantities with letters and relationships with equations. In so doing, he took a giant step toward focusing the power of algebra on the problems of geometry. All that was needed at this point was the right creative insight.
That insight came independently and almost simultaneously from two Frenchmen in the first half of the 17th century. One was Pierre de Fermat, perhaps the world's finest mathematical amateur. Fermat was an unobtrusive lawyer and civil servant who indulged in mathematics of all sorts just for the fun of it. He published very little, preferring to exhibit his extraordinary creativity in correspondence with some of the other leading mathematicians of his day.2 One of those letters tells us shows that Fermat had developed many of the key concepts of analytic geometry by about 1630. Motivated by his interest in the locus problems of Apollonius, Fermat devised a coordinate system of sorts for plotting the relationship between two unknown (positive) quantities, A and E, as follows.
Starting at some convenient point, he drew a horizontal reference line to the right. He marked off one variable, A, from the starting point on the horizontal axis, and at its other end placed a segment at a fixed angle to the first, representing the other variable, E. He envisioned the length of E varying as the length of A varied, according to the equation he was studying, and the position of the E segment moving to the right, always making the same angle with the A segment. Fermat said3 that "It is desirable, in order to aid the concept of an equation, to let the two unknown magnitudes form an angle, which usually we would suppose to be a right angle," but in fact he allowed other angles also.
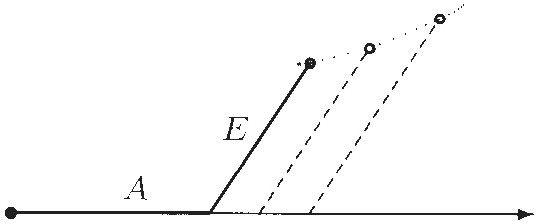
Display 1
Fermat's crucial insight was to see that whenever he could find an equation relating his two variables A and E, he would get a curve that corresponded to this equation. The top endpoint of the E segment would trace out a curve, and it would be the locus associated to the equation. In Fermat's own words:
Whenever two unknown magnitudes appear in a final equation, we have a locus, the extremity of one of the unknown magnitudes describing a straight line or a curve.
(To illustrate the general case, the angle in Display 1 is not a right angle. If it were, this picture would look a lot like the familiar way of graphing E as a function of A.)
Notice, in particular, Fermat's claim that this process will give you a locus for any equation. Since it is easy to write down equations, we suddenly have a huge number of curves available, without having to create them via some sort of geometric construction. In addition, we have a natural question: Given a class of equations, describe the corresponding class of curves. Fermat did this for all quadratic equations, showing, in fact, that the resulting loci are always conic sections.
Fermat's writings on the algebraic approach to geometry were not published until after his death, so much of the credit for inventing analytic geometry was given to someone else. The "someone elsé" is René Descartes, a French nobleman by birth, a student of mathematics in his youth, a soldier by choice in his physical prime, and an eminent, free-thinking philosopher and mathematician in the last twenty years of his life. Many mathematicians regard the development of analytic geometry as one of his crowning achievements, but to Descartes it was just one of three case studies in a much grander scheme. He wrote it as one of three appendices to a philosophical tract commonly known as Discourse on Method. Its full title clearly reveals his intentions: Discourse on the Method of Rightly Conducting Reason and Seeking Truth in the Sciences. His actual goal was to redefine the methodology for seeking truth in all matters; the word "sciences" had a much broader connotation at that time than it does now. In his own words:
The long chains of simple and easy reasonings by means of which geometers are accustomed to reach the conclusions of their most difficult demonstrations, had led me to imagine that all things, to the knowledge of which man is competent, are mutually connected in the same way, and that there is nothing so far removed from us as to be beyond our reach, or so hidden that we cannot discover it, provided only we abstain from accepting the false for the true, and always preserve in our thoughts the order necessary for the deduction of one truth from another.4
Descartes regarded his method as a synthesis of classical logic, algebra, and geometry, in which he discarded their excesses and fixed their limitations. He sets the stage for this blending of ideas by saying,
[A]s for Logic, its syllogisms and the majority of its other precepts are of avail rather in the communication of what we already know... than in the investigation of the unknown. . . . [A]s to the Analysis of the ancients and the Algebra of the moderns, . . . the former is so exclusively restricted to the consideration of figures, that it can exercise the Understanding only on condition of greatly fatiguing the Imagination; and, in the latter, there is so complete a subjection to certain rules and formulas, that there results an art full of confusion and obscurity calculated to embarrass, instead of a science fitted to cultivate the mind.
To illustrate the power of his new way of thinking, Descartes wrote three appendices to the Discourse on Method — on optics, meteorology, and geometry. In the geometry appendix, simply called La Géométrie, were the main ingredients for analytic geometry. His main graphical device was essentially the same as the one devised by Fermat: the independent variable, now called x, marked off along a horizontal reference line, and the dependent variable, now y, represented by a line segment making a fixed angle with the x segment. Descartes, perhaps even more than Fermat, emphasized that the angle choice was a matter of convenience, and need not always be a right angle.
Besides introducing an improved system of algebraic notation in this appendix (see Sketch 8), Descartes explicitly broke with the Greek-inspired view of powers as geometric dimensions by defining a unit of length and then interpreting all quantities in terms of that unit. In particular, just as x was a length relative to that unit, so were x2, x3, and any higher power of any unknown. Since his goal was to match geometry and algebra, he also showed how to construct segments with those lengths. Since any power of the unkown can be represented as a length, we no longer need to connect squaring to squares and higher powers begin to make sense. This conceptual shift, which was only implicit in Fermat's work, let him (and us) consider curves defined by functions containing various powers of an unknown, graphing them without any associated restriction of geometric dimension. Descartes used his new techniques to solve a major locus problem posed by Apollonius but still unsolved by classical Greek methods, thereby claiming to demonstrate the superiority of his "Method of Rightly Conducting Reason and Seeking Truth."
Despite the power of his algebraic approach to geometry, Descartes's La Géométrie did not have an immediate impact on the mathematics of his time. There were several reasons for this. One was the suspicion of some mathematicians that algebra lacked the same level of rigor as classical geometry. Then there was the simple matter of language. Descartes, who was living in Holland at the time, wrote the Discourse on Method and its appendices in his native French. However, the "universal" language of 17th-century European scholarship was Latin. Many scholars couldn't read French at all. Also, Descartes had deliberately omitted the details of many of his proofs, saying to his readers that he did not want to "deprive you of the pleasure of mastering it yourself.'"5 For example, you won't find the equation of a straight line discussed in La Géometrie.
Credit for removing these roadblocks and making the ideas widely available belongs primarily to the Dutch mathematician Frans van Schooten, who translated La Géométrie into Latin and published a greatly expanded version, which included a wealth of detailed commentary. During the years 1649 to 1693, Van Schooten's work was published in four editions and grew to be about eight times as long as the original. It was from these Latin versions that Isaac Newton learned about analytic geometry on his way to developing the fundamental ideas of calculus. By the end of the 17th century, the methods of Cartesian geometry were fairly widely known throughout Europe.
But the coordinate geometry of that time did not yet include one feature that we take for granted today — the ordinate, or vertical axis! For both Descartes and Fermat, the first coordinate of a point was a line segment starting at the origin and extending to the right, and the second coordinate was a segment that started at the end of the x segment and extended upward at a fixed angle to the point. It is true that Fermat usually considered this angle to be a right angle (see the quote above), but neither he nor Descartes ever referred to a second axis. Moreover, since they regarded these "unknown magnitudes" to be (lengths of) line segments, they only considered positive coordinates. John Wallis, an English mathematician writing in the 1650s, extended these ideas to include negative coordinates. Yet, as late as the middle of the 18th century, even such a prominent mathematician as Leonhard Euler did not consistently include a vertical axis in coordinate diagrams. The two-axis rectangular coordinate system that we commonly attribute to Descartes seems instead to have evolved gradually during the century and a half after he published La Géométrie.
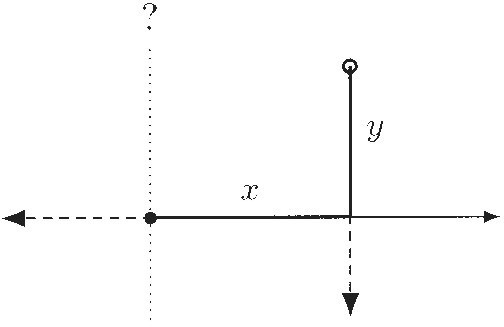
Display 2
Coordinate (or analytic) geometry is a prominent link in the historical chain of big mathematical advances. Just as the development of symbolic algebra paved the way for analytic geometry, so analytic geometry, in turn, paved the way for calculus. Calculus, in its turn, opened the door to modern physics and many other areas of science and technology. In the past several decades this algebraic way of describing shapes has also combined synergistically with the calculating speed of modern computers to produce increasingly astounding visual images for a wide range of uses. All of this rests on the truly simple idea of giving each point in space a numerical address, so that we can describe shapes by the numbers.
For a Closer Look: The birth of coordinate geometry is discussed in all of the standard references. For a more detailed account, see [17]. For the adventurous, there is [42], a bilingual edition of the original La Géométrie.
1 Locus, the root of our English words local and location, means "place" in Latin. Its plural is loci.
2 For more about Fermat, see Sketch 13.
3 This and the following quote are from Fermat's Introduction to Plane and Solid Loci, in [167], pp. 389–396.
4 This and other quotes from the Discourse on Method, are taken from the translation available online at Project Gutenberg.