| 8 |
The Cossic Art Writing Algebra with Symbols |
When you think of algebra, what comes to mind first? Do you think of equations or formulas made up of x's and y's and other letters, strung together with numbers and arithmetic symbols? Many people do. In fact, many people regard algebra simply as a collection of rules for manipulating symbols that have something to do with numbers.
There's some truth in that. But describing algebra solely in terms of its symbols is like describing a car by its paint job and body style. What you see is not all you get. In fact, like a car, most of what makes algebra run is "under the hood'" of its symbolic appearance. Nevertheless, just as an automobile's body styling can affect its performance and value, so does the symbolic representation of algebra affect its power and usefulness.
An algebra problem, regardless of how it's written, is a question about numerical operations and relations in which an unknown quantity must be deduced from known ones. Here's a simple example:
Twice the square of a thing is equal to five more than three times the thing. What is the thing?
Despite the absence of symbols, this is clearly an algebra question. Moreover, the word "thing" was a respectable algebraic term for a very long time. In the 9th century, al-Khwārizmī (whose book title, al-jahr w'al muqābala, is the source of the word "algebra") used the word shai to mean an unknown quantity. When his books were translated into Latin, this word became res, which means "thing"'. For instance, John of Seville's 12th-century elaboration of al-Khwārizmī's arithmetic contains this question, which begins "Quaeritur ergo, quae res...":1
It is asked, therefore, what thing together with 10 of its roots or what is the same, ten times the root obtained from it, yields 39.
In modern notation, this would be written either as 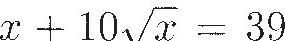 or as x2 + 10x = 39. (An "X" appears in the Latin version of this question, but it's actually the Roman numeral for 10. To avoid such confusions and emphasize more significant variations in notation, we use familiar numerals in all these algebra examples.)
or as x2 + 10x = 39. (An "X" appears in the Latin version of this question, but it's actually the Roman numeral for 10. To avoid such confusions and emphasize more significant variations in notation, we use familiar numerals in all these algebra examples.)
Some Latin texts used causa for Al-Khwārizmī's shai, and, when these books were translated into Italian, causa became cosa. As other mathematicians studied these Latin and Italian texts, the word for the unknown became Coss in German. The English picked up on this and called the study of questions involving unknown numbers "the Cossic Art" (or "Cossike Arte" in the spelling of those days) — literally, "the Art of Things".
Like most of our familiar algebraic symbols, the x and other letters we now use to represent unknown numbers are relative newcomers to the "art." Many early symbols were just abbreviations for frequently used words: p or  or
or 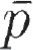 for "plus," m or
for "plus," m or  or
or  for "minus," and so on. They saved writing time and print space, but they did little to promote a deeper understanding of the ideas they expressed. Without consistent and illuminating symbolism, algebra was indeed an art, an often idiosyncratic activity heavily dependent on the skill of its individual practitioners. Just as standardization of parts was a critical step in the mass production of Henry Ford's automobiles, so the standardization of notation was a critical step in the use and progress of algebra.
for "minus," and so on. They saved writing time and print space, but they did little to promote a deeper understanding of the ideas they expressed. Without consistent and illuminating symbolism, algebra was indeed an art, an often idiosyncratic activity heavily dependent on the skill of its individual practitioners. Just as standardization of parts was a critical step in the mass production of Henry Ford's automobiles, so the standardization of notation was a critical step in the use and progress of algebra.
Good mathematical notation is far more than efficient shorthand. Ideally, it should be a universal language that clarifies ideas, reveals patterns, and suggests generalizations. If we invent a really good notation, it sometimes seems to think for us: just manipulating the notation achieves results. As Howard Eves once said, "A formal manipulator in mathematics often experiences the discomforting feeling that his pencil surpasses him in intelligence."2
Our current algebraic notation is close to this ideal, but its development has been long, slow, and sometimes convoluted. For a flavor of that development, we'll look at various ways in which a typical algebraic equation would likely have been written in different times and places during the progress of algebra in Europe. (To highlight the notational development, we use English in place of Latin or other languages when words, rather than symbols, would be used.)
Here is an equation containing some common ingredients of early algebraic investigations:
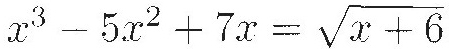
In 1202, Leonardo of Pisa would have written that equation (perhaps rearranged for clarity) entirely in words, something like this:
The cube and seven things less five squares is equal to the root of six more than the thing.
This approach to writing mathematics is usually called rhetorical, in contrast to the symbolic style we use today. In the 13th and 14th centuries, European mathematics was almost entirely rhetorical, with occasional abbreviations here and there. For instance, Leonardo began to use R for "square root" in some of his later writings.
Late in the 15th century, some mathematicians started to use symbolic expressions in their work. Luca Pacioli, whose Summa de Aritmetica of 1494 served as a main source of Europe's introduction to the cossic art, would have written
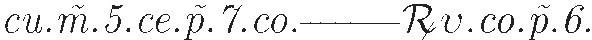
In this notation, co is an abbreviation for "cosa," the unknown quantity. The abbreviations ce and cu are for "censo" and "cubo," words that the Italian mathematicians used for the square and the cube of the unknown, respectively. Notice that we refer to the unknown here. A fundamental weakness of this notation was its inability to represent more than one unknown in an expression. (By way of contrast, Indian mathematicians had been using the names of colors to represent multiple unknowns as early as the 7th century.) Some other interesting features of Pacioli's notation are the dots that separate each item from the next, a long dash for equality, and the symbol 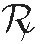 to denote square root. The grouping of terms after the root sign was signaled by υ, an abbreviation for "universale." The notation used in Girolamo Cardano's Ars Magna half a century later in Italy was almost identical to this.
to denote square root. The grouping of terms after the root sign was signaled by υ, an abbreviation for "universale." The notation used in Girolamo Cardano's Ars Magna half a century later in Italy was almost identical to this.
In early 16th-century Germany, some of the symbols we use now began to appear. The + and – signs were adopted from commercial arithmetic and the "surd" symbol, √ for square root evolved, some say from a dot with a "tail," others say from a handwritten r. Equality was noted by abbreviating either the Latin or German word for it, and the grouping of terms (such as the sum after the √ sign) was signaled by dots. Thus, in Christoff Rudolff's Coss of 1525 (which has an impossibly long formal title) or Michael Stifel's Arithmetica Integra of 1544, our equation might have appeared as

As in the earlier Italian notation described above, different powers of the unknown had distinct, unrelated symbols. Its first power was called the root (radix) and represented by 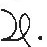 The symbol for its square was
The symbol for its square was  a small script z which was the first letter of its German name, zensus. The third power, cubus, was symbolized by
a small script z which was the first letter of its German name, zensus. The third power, cubus, was symbolized by  . Higher powers of the unknown were written by combining the square and cube symbols multiplicatively, when possible; the fourth power was
. Higher powers of the unknown were written by combining the square and cube symbols multiplicatively, when possible; the fourth power was 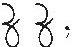 the sixth power was
the sixth power was 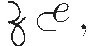 and so on. Higher prime powers were handled by introducing new symbols.
and so on. Higher prime powers were handled by introducing new symbols.
Easier ways to denote powers of the unknown had already begun to emerge in other countries. One of the most creative instances of this appeared in a 1484 manuscript by Nicholas Chuquet, a French physician. Like others of his time, Chuquet confined his attention to powers of a single unknown. However, he denoted the successive powers of the unknown by putting numerical superscripts on the coefficients. For example, to denote 5x4 he would write 54. He did a similar thing for roots, writing 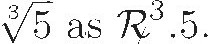 Chuquet was also well ahead of his time in treating zero as a number (particularly as an exponent) and in using an underline for aggregation. If our example equation had appeared in his manuscript, it would have looked like this:
Chuquet was also well ahead of his time in treating zero as a number (particularly as an exponent) and in using an underline for aggregation. If our example equation had appeared in his manuscript, it would have looked like this:

Unfortunately for the development of algebraic notation, Chuquet's work was not published at the time it was written, so his innovative ideas were known only to a few mathematicians by the beginning of the 16th century. This system of denoting powers of the unknown reappeared in 1572 in the work of Rafael Bombelli, who placed the exponents in small cups above the coefficients. Bombelli's work was more widely known than that of Chuquet, but his notation was not immediately adopted by his contemporaries. In the 1580s it was picked up by Simon Stevin of Belgium, a military engineer and inventor, who used circles around the exponents. Stevin's mathematical writing emphasized the convenience of decimal arithmetic. Some of his publications were translated into English early in the 17th century, thereby carrying both his ideas and his notation across the English Channel.
A major breakthrough in notational flexibility and generality was made by François Viète in the last decade of the 16th century. Viète was a lawyer, a mathematician, and an advisor to King Henri IV of France with duties that included deciphering messages written in secret codes. His mathematical writings focused on methods of solving algebraic equations, and to clarify and generalize his work he introduced a revolutionary notational device. In Viète's own words:
In order that this work may be assisted by some art, let the given magnitudes be distinguished from the undetermined unknowns by a constant, everlasting and very clear symbol, as, for instance, by designating the unknown magnitude by means of the letter A or some other vowel... and the given magnitudes by means of the letters B, G, D or other consonants.3
Using letters for both constants and unknowns allowed Viète to write general forms of equations, instead of relying on specific examples in which the particular numbers chosen might improperly affect the solution process. Some earlier writers had experimented with using letters, but Viète was the first to use them as an integral part of algebra. It may well be that the emergence of this powerful notational device was delayed because the Hindu-Arabic numerals were not commonly used until well into the 16th century. Prior to that, Greek and Roman numerals were used for writing numbers, and these systems used letters of the alphabet for specific quantities.
As soon as equations contained more than one unknown, it became clear that the old exponential notation was insufficient. It would not do to write 53 + 72 if one meant 5A3 + 7E2. In the 17th century, several competing notational devices for this appeared almost simultaneously. In the 1620s, Thomas Harriot in England would have written it as 5aaa + 7ee. In 1634, Pierre Hérigone of France wrote unknowns with coefficients before and exponents after, as in 5a3 + 7e2. In 1636, James Hume (a Scotsman living in Paris) published an edition of Viète's algebra with exponents elevated and in small Roman numerals, as in 5aiii + 7eii. In 1637, a similar notation appeared in René Descartes's La Géométrie, but with the exponents written as small Hindu-Arabic numerals, as in 5a3 + 7e2. Of these notations, Harriot's and Hérigone's were the easiest to typeset, but conceptual clarity won out over typographical convenience and Descartes's method eventually became the standard notation used today.
Descartes's influential work is also the source of some other notational devices that have become standard. He used lowercase letters from the end of the alphabet for unknowns and lowercase letters from the beginning of the alphabet for constants. He also used an overline bar from the sign to indicate its scope. However, he introduced the symbol for equality. Thus, Descartes's version of our sample equation would be very much, but not entirely, like our own:

The = sign for equality, proposed in 1557 by Robert Recorde4 and widely used in England, was not yet popular in continental Europe. In the 17th century it was only one of several different ways of symbolizing equality, including ~ and the ∞ sign of Descartes. Moreover, = was being used to denote other ideas at this time, including parallelism, difference, and "plus or minus." Its eventual universal acceptance as the symbol for "equals" is probably due in large part to its adoption by both Isaac Newton and Gottfried Leibniz. Their systems of the calculus dominated the mathematics of the late 17th and early 18th centuries, so their notational choices became widely known. During the 18th century, the superior calculus notation of Leibniz gradually superseded that of Newton. Had Leibniz chosen to use Descartes's symbol instead of Recorde's, we might be using ∞ for equality today.
This sketch has tried to capture the flavor of the long, erratic, sometimes perverse way in which algebraic symbolism has developed. In hindsight, '"good'' notational choices have proved to be powerful stimuli for mathematical progress. Nevertheless, those choices often were made with little awareness of their importance at the time. The evolution of exponential notation is a prime example of this. Powers of an unknown quantity were trapped for centuries by the limited geometric intuition of squares and cubes, and the notation reinforced this confinement. Descartes finally liberated them by treating squares, cubes, and the like as magnitudes independent of geometric dimension, giving a new legitimacy to x4, x5 x6, and so on. From there the notation itself suggested natural extensions — to negative integral exponents (reciprocals), to rational exponents (roots of powers), to irrational exponents (limits of roots of powers), and even to complex exponents. And in the 20th century, this exponential notation was reconnected with the geometric idea of dimension to help lay the foundation of a new field of mathematical investigation: fractal geometry.
For a Closer Look: Joseph Mazur's [123] is a readable account of the evolution of mathematical notation. The standard surveys also discuss the topic. For information on the history of specific mathematical notations, the best reference is still [22], though Earliest Uses of Various Mathematical Symbols, a website maintained by Jeff Miller, is now a serious contender. For more on the history of algebra, see [101].
1 See p. 336 of [22] for both the original Latin and this translation.
2 See [55], entry 251.
3 From Viète's In artem analyticam Isagoge of 1591, as translated by J. Winfree Smith. See [107], p 340.
4 See Sketch 2 for more details about this.
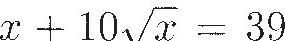 or as x2 + 10x = 39. (An "X" appears in the Latin version of this question, but it's actually the Roman numeral for 10. To avoid such confusions and emphasize more significant variations in notation, we use familiar numerals in all these algebra examples.)
or as x2 + 10x = 39. (An "X" appears in the Latin version of this question, but it's actually the Roman numeral for 10. To avoid such confusions and emphasize more significant variations in notation, we use familiar numerals in all these algebra examples.) or
or 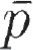 for "plus," m or
for "plus," m or  or
or  for "minus," and so on. They saved writing time and print space, but they did little to promote a deeper understanding of the ideas they expressed. Without consistent and illuminating symbolism, algebra was indeed an art, an often idiosyncratic activity heavily dependent on the skill of its individual practitioners. Just as standardization of parts was a critical step in the mass production of Henry Ford's automobiles, so the standardization of notation was a critical step in the use and progress of algebra.
for "minus," and so on. They saved writing time and print space, but they did little to promote a deeper understanding of the ideas they expressed. Without consistent and illuminating symbolism, algebra was indeed an art, an often idiosyncratic activity heavily dependent on the skill of its individual practitioners. Just as standardization of parts was a critical step in the mass production of Henry Ford's automobiles, so the standardization of notation was a critical step in the use and progress of algebra.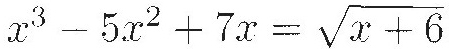
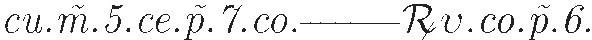
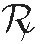 to denote square root. The grouping of terms after the root sign was signaled by υ, an abbreviation for "universale." The notation used in Girolamo Cardano's Ars Magna half a century later in Italy was almost identical to this.
to denote square root. The grouping of terms after the root sign was signaled by υ, an abbreviation for "universale." The notation used in Girolamo Cardano's Ars Magna half a century later in Italy was almost identical to this.
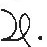 The symbol for its square was
The symbol for its square was  a small script z which was the first letter of its German name, zensus. The third power, cubus, was symbolized by
a small script z which was the first letter of its German name, zensus. The third power, cubus, was symbolized by  . Higher powers
. Higher powers 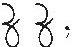 the sixth power was
the sixth power was 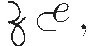 and so on. Higher prime powers were handled by introducing new symbols.
and so on. Higher prime powers were handled by introducing new symbols.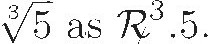 Chuquet was also well ahead of his time in treating zero as a number (particularly as an exponent) and in using an underline for aggregation. If our example equation had appeared in his manuscript, it would have looked like this:
Chuquet was also well ahead of his time in treating zero as a number (particularly as an exponent) and in using an underline for aggregation. If our example equation had appeared in his manuscript, it would have looked like this:
