| 30 | Barely Touching From Tangents to Derivatives |
It's one of the standard problems in any calculus text: find the tangent line to the curve y = f(x) at x = a. One might think that derivatives were invented precisely to solve this problem. But finding tangent lines is something that goes back long before calculus.
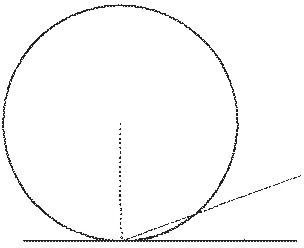
A theorem in Euclid's Elements says that if we take a point on a circle and draw a line through that point perpendicular to the radius, the line will "touch the circle." In Latin, "to touch'' is tangere, so the touching line was "tangente," whence tangent. Euclid went on to say that, if you try to fit another line in between the tangent line and the circle, you will fail, since that other line would actually cut the circle at a second point.
The Greeks studied many other curves besides the circle. In particular, they spent a lot of time studying the conic sections. (See Sketch 28.) In Apollonius's Conics, there are explanations of how to find tangent lines to hyperbolas, ellipses, and parabolas.
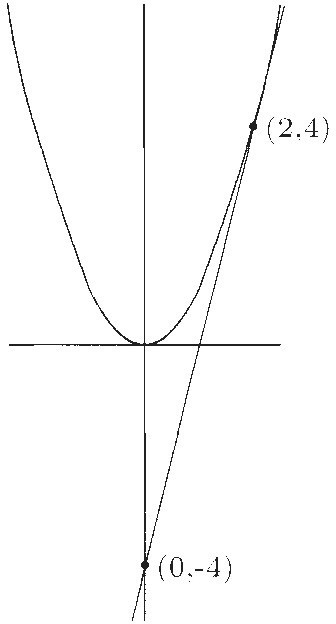
Take the case of the parabola. It is no longer right to say that a line that intersects the curve only once is tangent to it. Any vertical line intersects the parabola y = x2 only once, but it's certainly not a tangent. So the first thing we need is to explain what a tangent line actually is. Apollonius defined it, following Euclid: The line is tangent if it is impossible to fit another line into the angle it makes with the parabola. Of course, Apollonius did not use an equation to describe the parabola, but we can translate his theorem for our standard parabola y = x2. Here's what it says. Take x = a, so that y = a2. Find the point on the y-axis that is on the other side of the vertex and at the same distance, i.e., the point (0, –a2). Draw the line from (a, a2) to (0, –a2); it will be tangent to the parabola. A quick calculation using derivatives checks that this is indeed correct.
The conic sections being done, tangent-finding seemed to become less interesting. To have new problems, one needs new curves. A few were known and studied, but it seems that the problem of their tangents was either not considered or turned out to be too hard. In any case, the question had to wait until new curves became abundant, which happened in the 17th century.
Given their interest in all things Greek, mathematicians of early modern times knew about the conic sections and their tangents. They were also interested in how things move. Thinking about motion led to a new and interesting curve. Suppose a circle is rolling along a straight line. Its center just moves forward, but what curve does a point on the circumference trace out? The question seems to have been asked first by Nicholas of Cusa. Marin Mersenne made a more precise description of the curve, known as the cycloid, and popularized the obvious questions: What is the area under it? What is its length? Can we find tangent lines?
The cycloid apparently fired the imaginations of geometers everywhere, because everyone worked on it. Galileo, Mersenne, Roberval. Wren, Fermat, Pascal, and Wallis all made discoveries and then fought about who had done it first. The real action, however, started after Fermat and Descartes invented coordinate geometry. Their work vastly expanded the range of available curves. Fermat pointed out that any equation in two variables defines a curve. On top of that, if a curve is described algebraically, one naturally wants to find its tangent algebraically, as well. In La Géométrie, Descartes described a complicated algebraic method for finding tangents. He used the parabola as his example, in part because that allowed him to demonstrate that his method found the right answer, i.e., the one discovered by Apollonius.
Fermat had a slightly better method for tangents. Moreover, he realized that there was a connection between the problem of finding a tangent and the problem of finding maximum and minimum values. In both cases, Fermat's key insight was to connect the problem to what we would call "double roots." If you imagine a line cutting a curve in two nearby points and translate that into algebra, you get an equation with two roots close together. As the points converge, the line becomes closer and closer to a tangent. So a tangent occurs when the two roots become equal — i.e., when the equation has a double root. This was useful because there were known criteria to detect a double root.
Fermat soon developed a more effective method for doing the same thing: he wrote the x-coordinates of the two intersection points as a and a + e, so that the corresponding y-coordinates are a2 and a2 + 2ae + e2. The slope of the line connecting them is
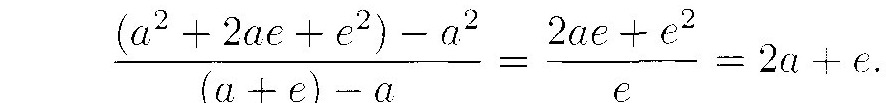
To make the two points coincide, set e = 0 and you get the slope.
All of these mathematicians were essentially "doing calculus," but of course there wasn't any "calculus" yet. We might call this the heroic period of calculus: individual mathematicians solving tangent and maximum problems for individual curves, sometimes with specially created methods. When supposedly general methods were proposed, they tended to work well only for polynomials. The cycloid, which is not a polynomial curve, was interesting for that very reason. To do anything with it required tricks quite different from ones that worked for the parabola. If someone came up with a new curve, one would have to start from scratch, because there was no general method.
It is in this context that we can understand how exciting it would have been to read the title1 of Leibniz's famous first article on calculus, published in 1688: "A new method for maxima and minima and the same for tangents, unhindered by either fractional or irrational powers, and a unique kind of calculus for that." What that title says is that Leibniz has discovered a way to compute tangents and to solve maximum and minimum problems that will work for any equation. Even more, he says he has developed "a calculus"— that is, a straightforward computational way to solve this kind of problem.
Reading Leibniz's paper is a remarkable experience. He says that we should take an arbitrary quantity and call it dx. If there is a formula relating y to x that defines a curve, then dy is defined to be whatever quantity makes dy/dx the slope of the tangent line.2 And then he starts teaching the rules: d(y + z) = dy + dz, d(yz) = y dz + z dy, d(xn) = nxn-1 dx, etc. "Just calculate," we can imagine him saying. "Finding dy lets you find dy/dx, and hence the tangent line. Setting dy = 0 finds maximum values of y. Here's an example." The article reads like a Cliff's Notes version of a calculus book. Leibniz gives only the slightest hint of what all this means and does not explain how he figured out these rules. He just gives the method: No need to think, just calculate this way and the answers will come out. For the parabola, Leibniz's instructions move you at once from y = x2 to dy = 2x dx.
We can think of Leibniz's calculus as the beginning of a new period. It was no longer necessary to go to heroic extremes to solve this kind of problem. There was a method, and it just worked. Now it was a matter of exploring and extending the method. Because the method was fundamentally algebraic, just a bunch of rules for manipulating things, we might call this the algebraic period of the calculus.
Newton and Leibniz are considered joint inventors of the calculus because both of them invented methods to solve the same set of problems, but Newton's approach was more intuitive and more physical. He emphasized the idea of a rate of change, which he called the fluxion of a variable ("flowing") quantity. For Newton, x is a quantity that changes over time, and x is simply its rate of change, which he doesn't really define. Instead, he would say things like "when a moment of time o passes, x becomes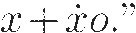 
So a Newtonian computation of the slope of the tangent to the parabola would look sort of like this. The parabola is given by y = x2. When a moment of time o passes, y becomes 
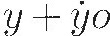and x becomes x + ẋo. So we will have
Subtracting y = x2 and simplifying we get
now "let the augments vanish" to get the "ultimate ratio," ẏ/ẋ = 2x.
Leibniz's version was the more successful one, as we can see from the fact that his reference to "a calculus" has become the name of the whole subject. It quickly emerged that one should understand Leibniz's dx as an "infinitely small" quantity. Jakob and Johann Bernoulli developed and taught this point of view, which was then included in the first calculus textbook, by the Marquis de l'Hospital, published in 1696.
L'Hospital was a competent French mathematician. Moreover, being a Marquis, he had lots of money. Johann Bernoulli needed a job, so l'Hospital hired him as his calculus tutor. It was from Bernoulli's notes that l'Hospital put together his book, whose title translates to "Analysis of the Infinitely Small for the Understanding of Curved Lines." The book treats only the differential calculus, and it is indeed focused on using the calculus to understand curves. Finding tangents is the first and easiest part of this "understanding of curves."
As the title indicates, l'Hospital's book is all about infinitely small quantities such as dx and dy. But how do those work? The idea is roughly like this: if there is a normal (finite nonzero) number around, an infinitely small change does not matter. So, for example, x2 + 2dx is the same as x2 for any such number x. But when there is no finite number around, then infinitely small things do matter: 2dx is not 0. It gets even more complicated when you run into products of infinitely small things: such a product is supposed to be "infinitely smaller"; it doesn't matter in comparison to things that are merely infinitely small. So here's how we prove that Leibniz's rule is correct in the case of y = x2. When x becomes x + dx, y becomes y + dy, so
That last equal sign is the hard one: it is there because (dx)2 is infinitely smaller than 2x dx, so it can be thrown out. At least so says l'Hospital.
This is recognizably the same computation as Newton's, though the underlying ideas are different: In one case, there are rates of change; in the other, everything is static but we use infinitely small increments. Both methods had their strange parts. In Newton's approach, there was this "moment of time" o that was nonzero until we "let it vanish." In Leibniz there were the "infinitely small things don't matter except when they do." This troubled some people, but most mathematicians seemed to learn to accept it. Their fundamental argument was a practical one: it worked. There were criticisms, notably from George Berkeley (see page 47), but they did not have much impact. Mathematicians took the calculus and ran with it. The main contributor in the 18th century was Leonhard Euler. He realized that Newton's laws of motion could be expressed using Leibniz's differentials, so one could do physics using them. The calculus became the key to everything. Physical problems could be reduced to equations involving differentials, and solving these differential equations allowed one to predict what would happen. Geometric questions could be analyzed in a similar way. It all boiled down to using the calculus intelligently, and there has never been a calculator more talented than Euler.
The one time Euler tried to explain what he was doing was when he wrote his own introduction to the differential calculus. The result is very strange: He agrees that a number smaller than any positive number must be zero, so infinitesimals such as dx are zero, so dy/dx really is 0/0. But he argues that not all 0/0 expressions are alike, and that if one considers where the zeros had come from one could assign a value to them. The idea seems to be that 0 is not just a number, it is a number with a memory! So the 0 that appears in the numerator and denominator of (x2 – 4)/(x – 2) when we set x = 2 "remembers" enough information to let us know that in this case 0/0 = 4.
Why worry about foundations when there were so many new problems to solve? The answer turned out to be "in order to explain it better." After the French Revolution, mathematicians were asked to teach the calculus not only to other gifted mathematicians, but also to future engineers and civil servants. That required coming up with clear explanations, which is hard to do if the underlying concepts are not clear in the first place. Hence, beginning with Lagrange and Cauchy and continuing until late in the 19th century, mathematicians worked on laying the foundations for the calculus. They looked for clear definitions that did not depend on physical intuition about moving or flowing things or on philosophical ideas about infinitely small quantities.
Lagrange was the one who invented the "derivative function" and the notation f'(x). His goal was to do Leibniz one better and reduce the whole of calculus to algebra. Here's how he wanted to do it. Given a function f(x), use algebra to find a formula
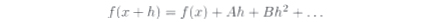
Then we define f'(x) = A. The example of the parabola becomes very simple: Since (x + h)2 = x2 + 2xh + h2, the derivative of f(x) = x2 is f'(x) = 2x. The problem was that the method is much harder to use for more complicated functions, such as the sine.
It was in textbooks written by Cauchy that the notion of a limit was finally introduced and used to give a definition of the derivative:
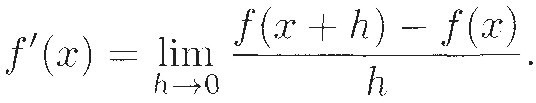
Cauchy's notion of what "limit" meant was still not quite precise, however, and it took a few more decades for everything to get sorted out. Nonetheless, it all did get sorted out. While mathematicians found examples where the easy assumptions of Euler's time would fail, they also discovered precise conditions of validity and showed that those conditions usually held in practical situations. The new definition made things clearer, but did not invalidate any of the earlier work. This is why Judith Grabiner says3 that
The derivative was first used; it was then discovered; it was then explored and developed; and it was finally defined.
Derivatives are still fundamental to the understanding of curved lines, of surfaces, and also of more complicated geometrical objects; this is the subject of differential geometry. They are one of the basic tools used to describe how things change and evolve, mostly via differential equations. And while the foundational issues are resolved, there are still plenty of problems for today's heroes to solve.
For a Closer Look: A famous and readable account of the story of the derivative is [71]. Historians have done a lot of work on the beginnings of calculus. The results are well summarized in standard references such as [99] and [77], and [76],
1 We quote the translation in [169], which includes the paper both in the original Latin and in English.
2 Not in these exact words, but close.