The History of Mathematics in a Large Nutshell

The story of mathematics spans several thousand years. It begins as far back as the invention of the alphabet, and new chapters are still being added today. This overview should be thought of as a brief survey of that huge territory. Its intention is to give you a general feel for the lay of the land and perhaps to help you become familiar with the more significant landmarks.

Much (but by no means all) of the mathematics we now learn in school is actually quite old. It belongs to a tradition that began in the Ancient Near East, then developed and grew in Ancient Greece, India, and the medieval Islamic Empire. Later this tradition found a home in late-Medieval and Renaissance Europe, and eventually became mathematics as it is now understood throughout the world. While we do not entirely ignore other traditions (Chinese, for example), they receive less attention because they have had much less direct influence on the mathematics that we now teach.

Our survey spends far more time on ancient mathematics than it does on recent work. In a way, this is a real imbalance. The last few centuries have been times of great progress in mathematics. Much of this newer work, however, deals with topics far beyond the school mathematics curriculum. We have chosen, rather, to pay most attention to the story of those parts of mathematics that we teach and learn in school. Thus, the survey gets thinner as we come closer to the present. On the other hand, many of the topics we might have mentioned there appear in the sketches that make up the rest of this book.

The study of the history of mathematics, like all historical investigation, is based on sources. These are mostly written documents, but sometimes artifacts are also important. When these sources are abundant, we are reasonably confident about the picture of the period in question. When they are scarce, we are much less sure. In addition, mathematicians have been writing about the story of their subject for many centuries. That has sometimes led to "standard stories" about certain events. These stories are mostly true, but sometimes historical research has changed our view of what happened. And sometimes historians are still arguing about the right story. In order to stay short, this survey ignores many of these subtleties. To make up for this, we provide references where you can find more information. To help you on your way, we have also provided an annotated list of books that might be good points of entry for further study. (See "What to Read Next," starting on page 223.)

As you read through this overview, you may be struck by how few women are mentioned. Before the 20th century, most cultures of Western civilization denied women access to significant formal education, particularly in the sciences. Moreover, even when a woman succeeded in learning enough mathematics to make an original contribution to the field, she often had a very hard time getting recognized. Her work sometimes ended up being published anonymously, or by another (male) mathematician who had access to the standard outlets for mathematical publication. Sometimes it wasn't published at all. Only in recent years have historians begun to uncover the full extent of these obscured mathematical achievements of women.¹

In our times, most of the barriers to women in the sciences have been dissolved. Unfortunately, some of the effects of the old "uneven playing field" still persist. The perception that mathematics is a male domain has been a remarkably resilient self-fulfilling prophecy. But things are changing. The results of careful historical research and the outstanding achievements of many 20th century female mathematicians show that women can be creative mathematicians, have made substantial contributions to mathematics in the past, and will certainly continue to do so in the future.

Beginnings

No one quite knows when and how mathematics began. What we do know is that in every civilization that developed writing we also find evidence for some level of mathematical knowledge. Names for numbers and shapes and the basic ideas about counting and arithmetical operations seem to be part of the common heritage of humanity everywhere. Anthropologists have found many prehistoric artifacts that can, perhaps, be interpreted as mathematical. The oldest such artifacts were found in Africa and date as far back as 37,000 years. They show that men and women have been engaging in mathematical activities for a long time. Modern anthropologists and students of ethnomatheniatics also observe that many cultures around the world show a deep awareness of form and quantity2 and can often do quite sophisticated and difficult things that require some mathematical understanding. These range all the way from laying out a rectangular base for a building to devising intricate patterns and designs in weaving, basketry, and other crafts. These mathematical (or pre-matheinatical) elements of current pre-literate societies may be our best hint at what the earliest human mathematical activity was like.

By about 5000 B.C., when writing was first developing in the Ancient Near East, mathematics began to emerge as a specific activity.³ As societies adopted various forms of centralized government, they needed ways of keeping track of what was produced, how much was owed in taxes, and so on. It became important to know the size of fields, the volume of baskets, the number of workers needed for a particular task. Units of measure, which had sprung up in a haphazard way, created many conversion problems that sometimes involved difficult arithmetic. Inheritance laws also created interesting mathematical problems. Dealing with all of these issues was the specialty of the "scribes." These were usually professional civil servants who could write and solve simple mathematical problems. Mathematics as a subject was born in the scribal traditions and the scribal schools.

Most of the evidence we have for this period in the development of mathematics comes from Mesopotamia, the area between the Tigris and Euphrates rivers in what is now Iraq, and from Egypt, the land in the valley of the Nile, in northeast Africa. It is likely that a similar process was happening at about the same time in India and in China, though we have far less evidence about the specifics.

The ancient Egyptians wrote with ink on papyrus, a material that does not easily survive for thousands of years. In addition, most Egyptian archaeological digs have been near stone temples and tombs, rather than at the sites of the ancient cities where mathematical documents are most likely to have been produced. As a result, we have only a few documents that hint at what ancient Egyptian mathematics was like. Thus, our knowledge is sketchy and scholars are not in complete agreement about the nature and extent of Egyptian mathematics. The situation with respect to the Mesopotamian cultures is quite different. These people wrote by imprinting clay tablets with a wooden stylus. Many of those tablets have survived, and careful study has led to a much more detailed — though still incomplete and controversial — understanding of their mathematics. These two civilizations existed at about the same time and certainly interacted at several levels, from war to commerce. This contact must have led to some communication of mathematical ideas, but it is hard to trace exactly what was shared. In any case, what has come down to us from these cultures is very different in style and content.

The most extensive source of information about Egyptian mathematics is the Rhind Papyrus, named after A. Henry Rhind, the 19th century archaeologist who brought it to England. It dates back to about 1650 B.C. The papyrus contains, on one side, extensive tables that were used as aids to computation (particularly multiplication) and, on the other side, a collection of problems probably used in the training of scribes. The examples cover a wide range of mathematical ideas but stay close to the sorts of techniques that would be needed by the scribe to fulfill his duties. From this source and others, we can deduce some basic features of ancient Egyptian mathematics:

•The Egyptians used two numeration systems (one mostly for writing on stone, the other for writing on papyrus). Both were based on grouping by tens. One system used different symbols for various powers of ten. Multiples of a particular power were shown by repeating the symbol as many times as needed. For instance, | and stood for one and ten, respectively, so 57 was represented by The method is essentially the same as in Roman numerals, except that only powers of ten are used. The other system was more complicated, still based on powers of ten but with many more symbols. (See Sketch 1.)

•Their basic arithmetic operations were adding and doubling. To multiply or divide, they used an ingenious method based on doubling. (The basic idea is still used today in computer algorithms.)

•Rather than working with fractions, they worked only with the idea of "an nth part." They would speak of "the third'' (meaning 1/3) and "the fourth" (meaning 1/4). What we would describe as "other fractions" they would express as sums of such parts. For example, what we call "three fifths" they would call "the half and the tenth." Since doubling was so important in their mathematics, one of the numerical tables in the Rhind Papyrus is a table listing the doubles of the parts. For example, the double of the fifth (i.e., 2/5) is the third and the fifteenth (i.e., 1/3 + 1/15). Scholars are still arguing about exactly how these expressions were computed. (See Sketches 4 and 9.)

•They could solve simple linear equations. (See Sketch 9.)

•They knew how to compute or approximate the areas and volumes of several geometric shapes, including circles, hemispheres, and cylinders. Perhaps the most difficult geometry problem discussed in the known sources (this time not the Rhind Papyrus) is the (correct) computation of the volume of a truncated square pyramid. For some shapes, all they could give were approximations. For example, the area inside a circle was approximated as follows: Take the diameter of the circle, remove "the ninth part" of it, and find the area of the square with the resulting side length. In our terms, this says that the area inside a circle of diameter d is which is actually a pretty good approximation. (See Sketch 7.)

The Rhind Papyrus was used to train young scribes, so it is a bit hazardous to draw conclusions about the whole of Egyptian mathematics from it. Still, we can say that the Egyptian mathematics of 4,000 years ago was already a fairly well-developed body of knowledge with content very similar to some of what we learn about calculation and geometry in elementary and high school today. It was recorded and taught by means of problems that were intended as examples to be imitated. Most of the problems seem to have their roots in the actual work of the scribes. A few, however, seem designed to give young scribes a chance to show their prowess at difficult or complicated computations. It is unclear to what extent the Egyptian mathematicians developed their science beyond what was needed for everyday work, and we also know next to nothing about how their methods were discovered.

The history of ancient Iraq spans thousands of years and a number of cultures, including Sumerian, Babylonian, Assyrian, Persian, and eventually Greek. All of these cultures knew and used mathematics, but there was a lot of variety. Most of our information about the mathematics of Mesopotamia comes from tablets produced between 1900 and 1600 B.C., sometimes called the Old Babylonian period. For this reason, one sometimes refers to the mathematics of this region as Babylonian mathematics. Unlike what happens for Egyptian mathematics, a great many such tablets have been discovered. Once again, most of them seem to be school texts. The abundance of these texts allows us to develop a clearer picture of what Mesopotamian mathematics was like, though of course many mysteries remain.

The mathematical activity of the Babylonian scribes seems to have arisen from the everyday necessities of running a central government. Then, in the context of the scribal schools, people became interested in the subject for its own sake, pushing the problems and techniques beyond what was strictly practical. Like a musician who is not satisfied with playing at weddings and graduations, the well-trained scribe wanted to go beyond everyday problems to something more elaborate and sophisticated. The goal was to be a mathematical virtuoso, able to handle impressive and complex problems. Supporting this was an ideology that saw the scribe as someone who would establish justice and ensure fairness by being able to deal correctly with measurement and quantity. The ability to solve complex problems was a guarantee that the scribe could perform this duty.

Most of the mathematical tablets from this period are either tables to assist in computation or collections of problems for training young scribes. Some of the problem tablets contain answers or full solutions, but there is very little that would explain the discovery process behind the methods being demonstrated. Scholars have developed a good picture of what those methods might have been, but, like all historical reconstructions, the picture involves a large dose of conjecture. Still, there are several things one can say with some certainty:

•In their calculations, the Mesopotamian scribes often represented numbers using a place-value system based on sixty. Repetitions of a ones symbol and a tens symbol were used to denote the numbers 1 through 59. The positions of these groups of symbols relative to each other indicated whether they stood for units or 60s or 60²s, etc. (See Sketch 1.)

•They made use of extensive tables of products, reciprocals, conversion coefficients, and other constants. Fractions were often expressed in "sexagesimal" format. This is analogous to our way of writing fractions as decimals, but it used powers of 60 instead of powers of 10. (See Sketch 4.)

•Like the Egyptians, the Babylonian scribes could handle linear equations. They could also solve a wide range of problems that we would describe as leading to quadratic equations. Many of these problems are quite artificial and may have existed solely as a way for scribes to demonstrate their prowess. The ideas behind the methods for solving quadratic equations were probably based on a "cut-and-paste geometry" in which pieces of rectangles and squares were moved around to discover the solution. The solutions in the tablets, however, are entirely numerical and are meant to drill students in applying the method. (See Sketch 10.)

•Babylonian geometry, like that of the Egyptians, was devoted mainly to measurement. They appear to have known and applied instances of what we now call the Pythagorean Theorem, and they had formulas for computing or approximating areas and volumes of various common shapes.

One interesting aspect of Babylonian mathematics is the occurrence of problems that do not even attempt to be practical, but instead have a recreational flavor. These are fanciful problems that usually reduce to solving a linear or quadratic equation. Here's an example:

A trapezoidal field. I cut off a reed and used it as a measuring reed. While it was unbroken I went 1 three-score steps along the length. Its 6th part broke off for me, I let follow 72 steps on the length. Again 1/3 of the reed and 1/3 cubit broke off for me; in 3 three-score steps I went through the upper width. I extended the reed with that which [in the second instance] broke off for me, and I made the lower width in 36 steps. The surface is 1 bur. What is the original length of the reed?4

Except for the rather strange language and the fact that most of us do not know how many square cubits make up a "bur," this is a problem that could still appear in many a "recreational math" column — and it's still quite hard. Puzzles like this one continue to appear throughout the history of mathematics.

The end of the Old Babylonian period brought many social and political changes. The ideology of justice through fair measurement became less influential, and the organization of scribal schools seems to have changed. It is possible, too, that other kinds of writing material came into use, so fewer records were preserved. The mathematical work that survives seems less exciting and less accomplished. Some tablets mix mathematics with several other subjects. Mathematics loses its separate identity, and most of the enthusiasm and creativity disappear. Only much later, around 300 B.C., do we see a resurgence of interest in mathematics, this time in the service of Babylonian astronomy.

The overall impression is that Babylonian mathematics was driven by methods. Once a method for solving a certain kind of problem was on hand, the scribes seemed to revel in constructing more and more elaborate problems that could be solved by that method. Keep in mind, however, that most of what we have are tablets for training young scribes; we might get a similar impression from our own textbooks!

Babylonian mathematics has several impressive features, in particular the solution of quadratic equations. Their representation of numbers in terms of powers of 60 was also very important, particularly in regard to fractions. The fact that we still divide an hour into 60 minutes and a minute into 60 seconds goes back, via the Greek astronomers, to the Babylonian sexagesimal fractions; almost 4000 years later, we are still influenced by the Babylonian scribes.

Until very recently, we did not know a lot about very early Chinese mathematics. Before the invention of paper, the Chinese wrote on wood or bamboo strips, which were often tied together with string. These materials are highly susceptible to decay, so few mathematical texts from before 100 A.D. survived. These natural difficulties were sometimes compounded by human perversity. Just after the Imperial unification of China, at the beginning of the Qin Dynasty (about 220 B.C.), it appears that the Emperor ordered that all books from earlier periods be burned, except for official records and books on medicine, divination, forestry, and agriculture, which were considered "useful."5

The situation has changed over the last couple of decades, with various older texts being found by archaeologists. In many cases, the bamboo or wooden strips have survived, but not the string that held them together, so scholars find themselves having to figure out which strips go with which and in what order. For example, in 2007 the Yuelu Academy of Hunan University purchased some 1300 bamboo slips from an antiquities dealer, which seem to contain at least six different books. Among them are 231 slips that make up a book on Shu (Numbers), dating back to around 210 B.C.

Many of these newly-discovered texts are still being studied by scholars. They reveal a sophisticated mathematical culture. Besides elementary arithmetic, there are problems involving proportions, some that require the Pythagorean Theorem, and other important ideas. We may expect that there will be further discoveries, and that they will continue to enrich our idea of Chinese mathematics.

The best known mathematical texts from China are the Ten Mathematical Classics, books studied by civil servants who were expected to demonstrate the ability to solve mathematical problems before they could get their jobs. Like the texts from Egypt and Mesopotamia, they contain problems and solutions. In China, however, the solutions are often presented with a general recipe for solving that type of problem.

The earliest of the Mathematical Classics is usually known as The Nine Chapters on the Mathematical Art (in Chinese, Jiuzhang Suanshu). The version that has survived was annotated and supplemented by Liu Hui in 263 A.D. Liu's preface says that the material in the book goes back to the 11th century B.C., but he also says that the actual text was put together around 100 B.C. The later date is almost universally accepted, but scholars differ about the earlier one.

The topics in the Nine Chapters are quite varied. The problems are presented in the context of practical situations, but they have already been formalized. Some have a recreational flavor. Several are also known in Western mathematics, sometimes in identical form. This presumably reflects cultural contact along the "Silk Road" trade route connecting China to the Western world. Proportionality was a central idea for these early Chinese mathematicians, both in geometry (e.g., similar triangles) and in arithmetic (e.g., solving numerical problems by using proportions). Many geometric problems are analyzed by imagining figures being cut up and moved around; because this often involved removing some pieces and putting in others, the Chinese called it the "out-in" method. Most spectacularly, there is a chapter dedicated to solving systems of linear equations by a method that is essentially the same as the one6 rediscovered by Gauss in the 19th century. The original Nine Chapters contains only problems and solutions, but Liu Hui's commentary often gives justifications for the rules used to solve the problems. These are not formal proofs based on axioms, but they are proofs nonetheless. Chinese proofs, from Liu Hui on, usually had this informal character. Together with the other Mathematical Classics, the Nine Chapters played a central role in Chinese mathematics. Many later mathematicians wrote commentaries on it and used it as a jumping-off point for further mathematical work.

The Chinese mathematical tradition that started before 100 B.C. continued to develop and grow for many centuries. The extent of the contact between China and the West is still an open question, but it is clear that at least some ideas migrated along the Silk Road or influenced mathematicians in India. Nevertheless, Chinese mathematics remained quite independent (and different) until European explorers arrived in the 16th century. Because the influence of Chinese ideas on Western mathematics was so indirect, we will not discuss it further in detail.

We know even less about very early Indian mathematics. There is evidence of a workable number system used for astronomical and other calculations and of a practical interest in elementary geometry. The most significant early texts are the Vedas, a large collection of verses that probably achieved its final form around 600 B.C. They come with supplementary texts called the Śulbasūtras, which mostly focus on the rules for building altars. That requires some mathematics; we find a statement of the Pythagorean Theorem (see Sketch 12), methods for approximating the length of the diagonal of a square, and lots of discussion about the surface areas and volumes of solids. Other early sources show an interest in very large numbers and hint at other mathematical developments that almost certainly played a role in later developments in India. The Indian tradition influenced Western mathematics quite directly, so we will come back to it later.

Were there contacts between these civilizations, and did the mathematics of one influence the other(s)? In many cases, there certainly was contact of some form, but it is hard to tell whether mathematical ideas were transmitted. Interest in non-Western mathematics has grown7 in recent years, but a scholarly consensus on the spread and transmission of ideas has not yet developed.

There are good introductory articles on ancient Egyptian, Mesopotamian, Chinese, and Indian mathematics in Part 1 of [75] and in [159]. For a readable, full-length survey, look at [95], which contains both an account of non-Western mathematics and a passionate argument for its influence and importance. Robson's [149] is a detailed account of how mathematics fit into the social structures of Ancient Mesopotamia. Plofker's [142] surveys the whole tradition of mathematics in India, from the earliest stages to the late Medieval period. For extensive information about Chinese mathematics, see [121] or [116]. Papers on the notion of proof in various ancient cultures are collected in [28]. Finally, nothing replaces reading the real thing: Selected, translated, and annotated mathematical texts from non-Western cultures can be found in [98].

Greek Mathematics

Many ancient cultures developed various kinds of mathematics, but the Greek mathematicians were unique in putting logical reasoning and proof at the center of the subject. By doing so, they changed forever what it means to do mathematics.

We do not know exactly when the Greeks began to think about mathematics. Their own histories say that the earliest mathematical arguments go back to 600 B.C. The Greek mathematical tradition remained a living and growing endeavor until about 400 A.D. There was much change and growth during those thousand years, of course, and historians have worked hard to understand the process that led to the particular Greek slant on the subject. This task is made harder by the fact that most of our sources of information are rather late. Apart from some remarks in Plato and Aristotle and some fragments, our earliest witness to Greek mathematics is Euclid's Elements, which dates from around 300 B.C. Much of our information on the history of Greek mathematics is even more recent, coming from the 3rd and 4th centuries A.D. These texts probably preserve earlier material, but it's hard to be sure. A lot of scholarly detective work has gone into reconstructing the overall history, and the issues are still far from settled. Our account here can only scratch the surface of the vast body of scholarship on Greek mathematics.

It is important to stress that when one speaks of "Greek mathematics"' the main reference of the word "Greek" is to the language in which it is written. Greek was one of the common languages of much of the Mediterranean world. It was the language of commerce and culture, spoken by all educated people. Similarly, the Greek mathematical tradition was the dominant form of theoretical mathematics. It is certain that not all "Greek" mathematicians were born in Greece. For example. Archimedes was from Syracuse (in Sicily, now a part of Italy), and Euclid is traditionally located in Alexandria (in Egypt). In most cases, we know nothing about the actual ethnicity, nationality, or creed of these mathematicians. What they had in common was a tradition, a way of thought, a language, and a culture.

Like most Greek philosophers, the mathematicians of the earliest period seem to have been people of independent means who spent their time on scholarly pursuits. Later, some mathematicians made a living as astrologers, a few were supported by the state in one way or the other, and some seem to have done some teaching (usually one-on-one, rather than in schools). On the whole, however, mathematics was a pursuit for those who had the means and the time — and, of course, the talent. The total number of working and creative mathematicians at any given time was probably very small, maybe a dozen or so.8 Mathematicians worked mostly alone and communicated with each other in writing. Despite this, they built an intellectual tradition that continues to impress everyone who comes in contact with it.

The dominant form of Greek mathematics was geometry, though the Greeks also studied the properties of whole numbers, the theory of ratios, astronomy, and mechanics. The latter two were treated very much in geometric and theoretical style. There was no sharp dividing line between "pure" and "applied" mathematics. (In fact, that distinction dates back only to the 19th century.) Most Greek mathematicians had little interest in practical arithmetic or in the problems of actually measuring lengths and areas. These issues only came to the fore relatively late (for example, during the 1st century A.D. in the work of Heron, who may have been influenced by Babylonian mathematics), and they remained to some extent a separate tradition.

According to the ancient Greek historians of geometry, the first Greek mathematicians were Thales, who lived around 600 B.C., and Pythagoras, a century later. When those histories were written, both Thales and Pythagoras were already mythic figures from the distant past. Many stories are told about them, and it is hard to know which, if any, of these stories contain any historical truth. Both men are said to have learned their mathematics in Egypt and in Mesopotamia. Thales is said to have been the first person to attempt to prove some geometrical theorems, including the statements that the sum of the angles in any triangle is equal to two right angles, the sides of similar triangles are proportional, and a circle is bisected by any of its diameters.

Later Greek authors told many stories about Pythagoras. The legends center on a semi-religious society called the Pythagorean Brotherhood (even though women were virtually equal members). The home base of the Pythagoreans was probably Crotona, a city founded by Greek settlers in southern Italy. The Brotherhood was a secret society dedicated to learning of various kinds, mostly religious and philosophical.

Lots of strange stories were passed on about the Brotherhood. Most of them were written down centuries after the fact by "neo-Pythagorean" philosophers. They describe a society some of whose customs would strike us today as strange, others as eminently sensible. The members apparently never ate meat or beans, never hunted, used no wool, dressed in white, and slept in white linen bedding. They had a variety of rituals to strengthen their sense of community, and the pentagram was their symbol. They believed in a sort of reincarnation and developed a kind of number mysticism, a belief that numbers were the secret principle of reality. Each day followed a common, simple regimen designed to strengthen both mind and body. They exercised to keep physically fit, had periods of silent contemplation, and spent a large part of each day discussing and studying mathematike, "that which is learned."

Many of the ideas and achievements of the later Pythagoreans probably were eventually attributed to Pythagoras himself. Most scholars believe that Pythagoras himself was not an active mathematician, though he may have been interested in number mysticism. But at some later point it seems that some Pythagoreans began to construct formal arguments, and hence to do mathematics. Because the Pythagoreans remained influential for some time, we know (or can guess at) some of their mathematical ideas. They seem to have been much concerned with the properties of whole numbers and the study of ratios (which they related to music). In geometry, they are, of course, credited with the Pythagorean Theorem. (See Sketch 12.) It is likely, however, that the most important success often credited to the Pythagoreans is the discovery of incommensurable ratios.

Ratios played a very important role in Greek mathematics, because the Greek geometers did not directly attach numbers to the objects they studied. A line segment was a line segment. There are equal line segments, longer and shorter line segments, and a segment might be equal to two others put together, but at no time did the Greek mathematicians talk about the length of a line segment.⁹ Areas, volumes, and angles were treated as different kinds of quantities, none of which was necessarily connected to any numbers. So how does one compare quantities? What the Greek mathematicians did was to work with ratios of quantities. For example, to find the area of a circle, we use a formula, A = πr², which tells us to take the length of the radius and multiply it by itself and then by a constant we call π. The result will be a number, which we call the area of the circle. The Greeks expressed the same idea by saying:

The ratio between two circles is the same as the ratio between two squares with sides equal to the radii of the circles.

In our language we would say "the areas of two circles" and "the areas of two squares." We would probably also use symbols: If A^₁ and A^₂ are the areas of the two circles and r^₁ and r^₂ are the two radii, then

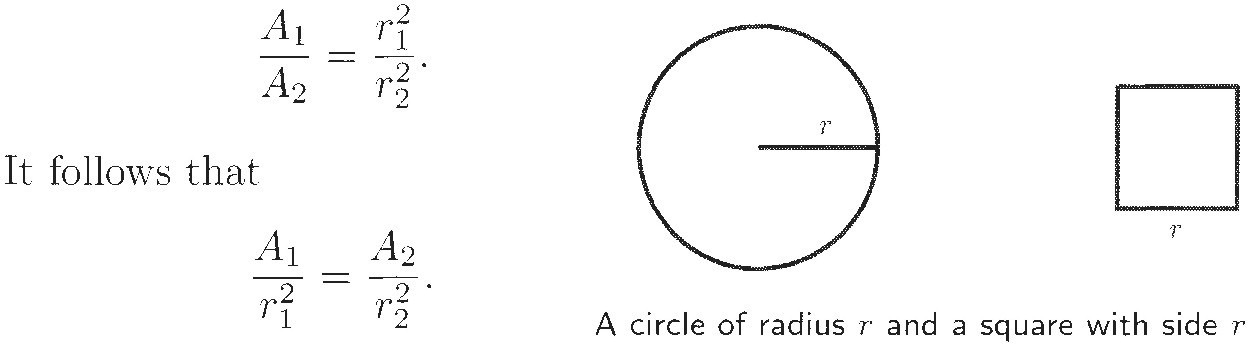
That is, the ratio of a circle to the square whose side is equal to the radius (i.e., A/r²) is always the same, regardless of the size of the circle. We now regard this ratio as a number, which we call π, and we know that it is quite a complicated number. (See Sketches 7 and 29.)

Some ratios are easy to understand because they are equal to the ratios of two whole numbers. If a segment is equal to twice another segment, their ratio is 2 to 1. Similarly, it is easy to understand what is meant by two segments whose ratio is 3 to 2. The great insight of the Pythagoreans was to see that the ratio of two segments will not always be that simple. In fact, they proved that the ratio between the side and the diagonal of a square cannot be a ratio of any two whole numbers. They called segments of this kind incommensurable, and they called the ratios between such segments irrational.10 (See Sketch 29 for more on incommensurability and irrational numbers.)

By the time of the philosophers Plato and Aristotle, knowing about the existence of incommensurable segments was part of every cultured person's education. Both philosophers used it as an example of something that was not evident to the senses but could be discovered by reason. Both also showed great interest in and respect for mathematics. It is said that Plato had a sign at the door of his Academy saying, ''Let no one ignorant of geometry enter here." The story may not be true, since the earliest surviving text that mentions the inscription was written more than 700 years after Plato's time. Nevertheless, such an inscription would be consistent with his attitude towards mathematics. For example, he listed mathematics as a fundamental part of the ideal education in his Republic. He also mentions mathematical results in several of his dialogues. (See Sketch 15 for a description of the "Platonic Solids.")

Aristotle also mentions mathematics frequently in his works. For instance, he uses mathematical examples when discussing correct reasoning. This suggests that by his time mathematicians were already engaged in working out formal proofs of mathematical statements. Around this time, they probably began to understand that in order to prove theorems one must start with a few unproved assumptions. In fact, Aristotle says so explicitly. These basic assumptions, or postulates, were taken for granted and accepted as true. This is the structure of the oldest Greek mathematical work that still survives (mostly) intact, the Elements of Euclid.

Between the time of Plato and Aristotle and the time of Euclid, an important change in Greek culture had occurred. The two philosophers, and probably most of the mathematicians associated with them, lived in Athens, one of the centers of Ancient Greek civilization. In Aristotle's time, however, Alexander the Great had set out to conquer other peoples and create a great empire. In so doing, he spread the Greek language, culture, and learning to many other parts of the world. For several centuries to follow, most educated people living in the countries bordering the Eastern Mediterranean spoke Greek. In effect, Greek became the international language of that region. Greek learning also spread. It flourished in a spectacular way in northern Egypt, in a city called Alexandria (one of many cities named for Alexander the Great), near the mouth of the Nile. The mathematical tradition there was particularly strong. Perhaps it was connected to the famous temple to the Muses (the Museum) and to its equally famous library. By the end of the 4th century B.C., Alexandria was the real center of Greek mathematics.

Beyond the fact that he probably lived in Alexandria around 300 B.C., we know almost nothing about Euclid himself. What we have are his writings, of which the most famous is a book called Elements. It is a collection of the most important mathematical results of the Greek tradition, organized systematically and presented as a formal deductive science. The style is dry and efficient. The book opens with a list of definitions, followed by postulates and "common notions" (which Euclid takes as self-evident). After that comes a sequence of propositions, each followed by a proof. There is no connecting material, no attempt at motivation. Next to each proposition is a diagram, and the proof typically refers to it in a crucial way. (See Sketch 14.) Later, as he moves on to other subjects, Euclid introduces more definitions and postulates. In this way, he covers plane and solid geometry, studies the divisibility properties of whole numbers, works out a sophisticated theory of ratios (twice, in fact; once for magnitudes and once for whole numbers), and develops a complicated classification of quadratic irrational ratios. The Elements brings together in one place the main accomplishments of Greek mathematics up to that time.

The Elements was a massive achievement, and its style and content were enormously influential, not only on Greek mathematics, but also on the Western mathematical tradition. Studying the first portion of the Elements became an intellectual rite of passage in the West, even as recently as the early part of the 20th century. Euclid's book was held up as a model of clear and precise reasoning, and was imitated by others who aspired to rigor and precision.

Greek geometry does not end with the Elements. Euclid himself also wrote books on conic sections, geometric optics, spherical geometry, and solving geometrical problems. Archimedes wrote about areas and volumes of various curved figures, and Apollonius wrote a treatise on conic sections that is still an impressive display of geometric prowess. (See Sketch 28.) Geometry continued to be a central interest of Greek mathematicians for several centuries.

The systematic and ordered presentation of mathematical results that we see in the Elements is only one part of the Greek tradition. Another important component (some claim it's the most important) is the tradition of mathematical problems. In fact, at times one can see such problems "sitting behind" Euclid's text. For example, since the Greeks did not measure areas by assigning numbers to them, they attacked the measurement of areas by trying to construct a rectangle (or square) whose area is the same as the area of a given figure. For figures bounded by straight lines, this is done in the first two sections (known as "books") of Euclid's Elements. From this point of view, the Pythagorean Theorem can be seen as a way to construct a square equal to the sum of two other squares. By the end of Book II, he has shown that he can construct a square equal to any given polygonal figure.

What happens, however, when one tries to do the same for a circle? That is, given a circle, can one construct a square with the same area as the circle? This is called the problem of squaring the circle, and it turns out to be very hard. In fact, it leads quickly to the question of what we mean by "construct." Greek mathematicians knew how to solve the problem of squaring the circle provided they were given a specially defined curve (either a quadratrix or an Archimedean spiral). But is this really a solution to the problem? Some mathematicians objected that constructing these curves was itself problematic, so the problem had not really been solved.

Besides the problem of squaring the circle, two other problems became famous in Greek times. One was trisecting the angle — constructing an angle that is one-third of a given angle. The other was duplicating the cube — constructing a cube whose volume is twice the volume of a given cube. Greek mathematicians eventually solved both problems. Their solutions, however, always involved using some sort of auxiliary device, sometimes a mechanical device, sometimes a mathematical one. (See Sketch 28 for how the problem of duplicating the cube is related to conic sections.) Later mathematicians reinterpreted the problems by adding the requirement that the constructions use only a ruler and a compass, i.e., using only lines and circles. We now know that under this constraint neither construction is possible, but this was not proved until the 19th century. Some Greek mathematicians knew (or suspected) this too, though they could not prove it. For example, Pappus (writing ca. 320 A.D.) criticizes a proposed ruler and compass solution of the problem of duplicating the cube by saying that everyone knew that this problem required other techniques.

These and other problems were among the main motivations behind Greek geometry. Theorems seem often to have been discovered as steps towards solving some problem. In fact, some Greek geometric problems were so difficult that they served as motivation for the development of coordinate geometry by the mathematicians of the 17th century.

While geometry was the central topic in Greek mathematics, many other subjects also show up. There was also a lot of interest in astronomy, and an elaborate spherical geometry (the geometry of the surface of a sphere) was developed to explain and predict the movement of the stars and planets. To be able to locate a planet in the sky one needs to have a way of measuring angles, so numbers and magnitudes cannot be kept completely separate. Greek astronomers borrowed from Babylonian mathematics and started using numbers to measure angles. One can see the Babylonian connection because fractions of angles were written in sexagesimal fashion, as they still are today, in "minutes" and "seconds" of angle. Also in this context we see the beginnings of trigonometry. (See Sketches 18 and 26.)

The most famous Greek astronomer was Claudius Ptolemy, who lived in Alexandria around 120 A.D. He wrote on many subjects, from astronomy and geography to astrology, but his most famous work is the Syntaxis, known today by the nickname given to it by Arabic scholars many centuries later. They called it Almagest, derived from a Greek term meaning "the greatest." Ptolemy's book is an amazing achievement; it provides a workable and accurate description of all visual astronomical phenomena. It was the basis of almost all positional astronomy until the 16th century.

Diophantus, who probably lived a century or so after Ptolemy, was one of the most original of the Greek mathematicians. His Arithmetica contains no geometry and no diagrams, focusing instead on solving numerical problems. The book is simply a list of problems and solutions. In the problems, Diophantus used a notation for the unknown and its powers that hints at the algebraic notation developed a thousand years later in Europe. His problems always asked for numbers, which to him meant rational numbers (common fractions). For example, one problem asks for a way to write a square as the sum of two other squares. In his solutions. Diophantus always used specific numbers and proceeded to explain how to find a solution. When solving the problem of writing a square as the sum of two squares, he started by saying ''suppose the square is 16." Then he went through several steps and ended up with While his solutions use specific numbers, they are intended to be general. The reader is supposed to see that a similar process works for any initial number chosen. One interesting feature of this approach is that, every once in a while, there will be a problem that is solvable for some initial numbers but not for others. In such cases, Diophantus usually worked out the conditions under which his problems are solvable, thereby confirming that he was trying to find general solutions.

Diophantus's work seems to have been lost and rediscovered many times. Eventually, it had a deep influence on the European algebraists of the 16th and 17th centuries. We still refer to equations that are to be solved in whole numbers or rational numbers as Diophantine equations. It's not clear, however, whether it had any impact in his own time.

After about 300 A.D., Greek mathematics lost some of its creative flair. In this period, there begins to be an emphasis on producing editions of and commentaries on older works. These books are actually our best sources for the Greek mathematical tradition, since they collect so much earlier material. At the same time, they create the difficult problem of distinguishing between their additions and comments and the original texts.

Probably the most important of the later Greek mathematicians is Pappus, from the mid-4th century. His Collection is a kind of "collected works'" that includes original work, commentaries on earlier work, and summaries of the works of other mathematicians. Perhaps the most important part of Pappus's work, from a historical point of view, was his discussion of "the method of analysis." Roughly speaking, "analysis" was the method for discovering a proof or a solution, while "synthesis" was the deductive argument that gave the proof or the construction. Euclid's Elements, for example, is all synthesis. Pappus's discussion of analysis is not very specific. This vagueness ended up being important, because the mathematicians of the Renaissance understood him to mean that there was a secret method behind much of Greek mathematics. Their attempts to figure out that method led to many new ideas and discoveries in the 16th and 17th centuries.

After Pappus, most of the significant Greek mathematicians were involved in writing commentaries on earlier work. Theon, who lived in Alexandria in the 4th century, prepared new editions of Euclid's Elements and Ptolemy's Syntaxis. Theon's daughter Hypatia11 wrote commentaries on her father's work, on Apollonius's Conics and on Diophantus's Arithmetica. Hypatia was also famous as a teacher of Platonic philosophy in Alexandria, where Christianity had become the dominant religion. Unfortunately, she became entangled in a power struggle between the Prefect Orestes and the Archbishop Cyril and was brutally murdered by followers of the Archbishop.

Proclus was one of the last important writers in the Greek tradition. He wrote a commentary on parts of Euclid's Elements that is heavily influenced by Neoplatonic philosophy. His commentary includes a history of early Greek mathematics, which most scholars feel incorporates portions of a much earlier work by Eudemus.

The 5th century A.D. marks the end of the Greek mathematical tradition in its classical form. Before leaving that period, however, we should note that this Greek tradition was not the only kind of mathematics going on in Greek, Hellenistic, and Roman culture between 600 B.C. and 400 A.D. Beneath the surface, so to speak, of the "scientific" tradition of the mathematicians there was a "subscientific' tradition. This was the mathematics of everyday life. Regardless of the mathematicians' fascination with geometry and disdain for numbers, merchants had to add and subtract, tax collectors had to measure areas of fields, and architects and engineers had to make sure their buildings and bridges didn't fall down. All of this required mathematical knowledge, which seems to have been passed on almost independently of what the mathematical scholars were doing. In fact, much of it was never written down. (The exception is the work of Heron, who sits somewhere in the middle between the scientific and subscientific traditions and tries to get them talking to each other.) One of the interesting features of the subscientific tradition is the presence, once again, of recreational problems, much like the ones in the Babylonian texts.

A vast amount has been written about Greek mathematics. Because it was so influential, it gets a large chunk of every survey of the history of mathematics, and reading the Greek chapters in such a survey (e.g., [99] or [30]) is a good way to start learning more. There is also a brief summary in [75]. The most accessible and most up-to-date book-length survey of Greek mathematics is [34]. Many of the original Greek texts are available in English translation, largely thanks to Thomas L. Heath and Dover Books; for example, see [49] and [50]. One can often find these texts online. The subscientific tradition is discussed in [92]; for the recreational aspect, see the work of David Singmaster (e.g., [165] and [164]). Finally, there are several recent books that have changed our understanding of Greek mathematics. Typically these are difficult, but they are often exciting to read; three important examples are [109], [64] and [133].

Meanwhile, in India

For the next four hundred years or so, Europe and North Africa saw very little mathematical activity. In Western Europe, North Africa, and the Middle East, barbarian invasions fragmented the Roman Empire. The resulting social conditions did not favor intellectual activity. The Eastern Roman Empire was still strong and very much under the influence of Greek culture, but the scholars of Byzantium were more interested in other things. They preserved copies of the ancient mathematical manuscripts, but only occasionally did anyone show any real interest in their contents. The advent of Islam in the 7th century further unsettled these areas. In the 8th century, Islamic forces attacked and conquered all of North Africa, most of the Middle East, and even parts of Europe. It was only after the Islamic Empire began to settle down politically that the right conditions for mathematical research could be found.

Of course, throughout this period people were still building, buying, selling, taxing, and surveying, so the subscientific tradition certainly persisted in all of these areas. In many cases, we have little textual evidence of how mathematics was understood and passed on. The texts we do have suggest a mathematics that was practical but not deep. The subject still kept its prestige. Western philosophers would say nice things about the importance and significance of geometry, for example. But when they actually explained what geometry they meant, they presented a mixed bag containing some Greek geometry, some traditional material on measuring and surveying, and quite a bit of metaphysical speculation.

During this quiet period in Europe and North Africa, the mathematical tradition of India grew and flourished. As mentioned above, at the time Greek mathematics was beginning to develop, there was already a local mathematical tradition in India. It is likely that this tradition received some influence from earlier astronomers, Babylonian and Greek. Astronomy was, in fact, one of the main reasons for the study of mathematics in India. Many of the problems studied by the Indian mathematicians were inspired by astronomical questions. Having started there, however, the Indians became interested in mathematics for its own sake. Even a playful element comes in.

The earliest surviving mathematical texts from India are written in Sanskrit verse. This required a great many tricky ways of expressing mathematical ideas. Each key term (say, the name of a number or of an operation) could be expressed in several different ways, allowing the poet to choose the one that fit his verse. These texts are therefore very hard to understand! Soon a tradition of writing commentaries explaining older texts was in place, as well.

As in the case of Greek mathematics, there is only a handful of mathematicians whose names we know and whose texts we can study. The earliest of these is Āryabhaṭa, who did his mathematical work early in the 6th century A.D. In the 7th century, the most important mathematicians are Brahmagupta and Bhāskara, who were among the first people to recognize and work with negative quantities. (See Sketch 5.) Probably the most important mathematician of medieval India was another Bhāskara, who lived in the 12th century. (To distinguish the two, most historians talk about Bhāskara I and Bhāskara II.) In almost all cases, the mathematical texts we have are portions of more extended books on astronomy.

The most famous invention of the Indian mathematicians is their decimal numeration system. (See Sketch 1.) From an earlier system, they retained nine symbols for the numbers from 1 to 9. They introduced place value and created a symbol, a dot or a small circle, to denote an empty place. (See Sketch 3.) The result was the numeration system that we still use today. The history of this momentous step is obscure. It seems likely that there was some influence from China, where a decimal counting board was used. In any case, before the year 600 Indian mathematicians were using a place-value system based on powers of ten. They had also developed methods for doing arithmetic with such numbers. All of the mathematicians mentioned above dedicated a portion of their works to explaining the decimal system and giving rules for computation.

The convenience of the new system seems to have been a powerful argument in its favor. It quickly spread to other countries. A manuscript written in Syria in 662 mentions this new method of calculation. There is also evidence that the system was used in Cambodia and in China soon after. By the 9th century, the new numeration system was known in Baghdad, and from there it was transmitted to Europe.

The Indians also made an important contribution to trigonometry. Greek astronomers had invented trigonometry to help them describe the motion of planets and stars. The Indian astronomers probably learned this theory from Hipparchus, a predecessor of Ptolemy. Greek trigonometry revolved around the notion of the chord of an angle. To a central angle β in a circle, one attached the line segment determined by the intersection of the sides of the angle with the circle, as in (a) of the display below. This was called the chord of β. It turns out, however, that in many cases the right segment to consider is not the chord, but rather half the chord. The Indian mathematicians used half the chord of twice the angle as their basic trigonometric segment. They called it a "half-chord." This name was mistranslated into Latin (via the Arabic) as "sinus," giving rise to our modern sine of α. Indeed, (b) of the display shows that

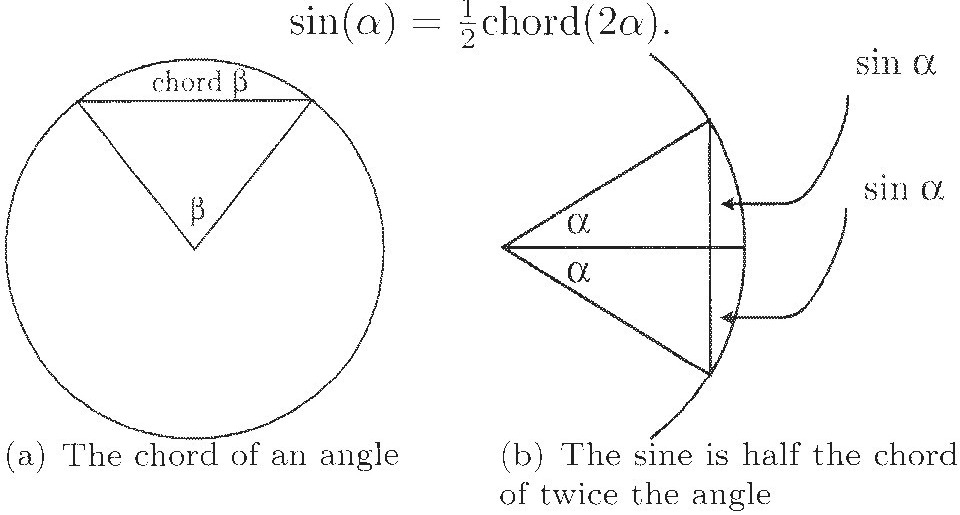
The move from chords to sines made trigonometry much simpler than it had been before. (See Sketch 18 for more details.)

However, the sine was thought of as a line segment in a particular circle, not as an abstract number or ratio. Āryabhaṭa, for example, worked with a circle of radius 3438 to construct a table of sines. (Why 3438? Because he wanted the circumference of the circle to be as close as possible to 21600 = 360 × 60. That would make one unit of length on the circumference correspond to one minute of arc.) For each angle, the table of sines gave the length of the sine of that angle, that is, of a certain line segment related to that circle. Thus, the sine of 90° was given as 3438. To apply the table to a circle with a different radius, one had to use proportionality to adjust the values.

Since it is almost always impossible to determine the sine exactly, constructing a table of sines requires approximation techniques. Ptolemy had already used such techniques to construct his table of chords. The Indian mathematicians took his ideas much further, and approximation methods became an important part of their mathematics. Starting from simple ideas, the mathematicians of India eventually developed quite sophisticated formulas for approximate computation.

Indian mathematicians were also interested in algebra and in some aspects of combinatorics. They had methods for computing square and cube roots. They knew how to compute the sum of an arithmetic progression. They handled quadratic equations using essentially the same formula we use today, except that they expressed it in words, usually in verse. Their examples are often problems posed in a playful manner. Here's an example from Bhāskara II:

The eighth part of a troop of monkeys, squared, was skipping in a grove and delighted with their sport. Twelve remaining monkeys were seen on the hill, amused with chattering to each other. How many were there in all?12

In addition to equations in one variable, the Indian mathematicians studied equations in several variables. Such equations usually have many solutions, so to make the problem interesting one must add some conditions, usually specifying that the solutions be of a particular type. A typical example would be to look for solutions that involved only whole numbers. Āryabhaṭa and Brahmagupta could solve linear equations of the form¹³ ax + by = c, where a, b, and c are whole numbers and the solutions sought are those in which x and y are also whole numbers. Brahmagupta also studied some much harder problems of this kind, such as finding integers x and y for which 92x² + 1 = y². Later, Bhāskara II generalized Brahmagupta's ideas. He described a method that will find a solution of nx² + b = y² in whole numbers whenever such a solution exists. Problems of this type are difficult, and the Indian achievement in this area is quite impressive.

Between the 6th and 12th centuries, Indian mathematicians produced a wide range of interesting mathematics. From our perspective, the main thing that is mostly missing from their texts is any explanation of how their methods and results were found. They did not give proofs or derivations. One cannot simply guess at such results, however, so they must have derived them somehow. One conjecture is that they considered the derivations to be trade secrets and so did not write them down.

The Indian tradition did not stop in the 12th century, of course. For example, the Kerala school made amazing discoveries between the 14th and 16th centuries. The later work, however, does not appear to have influenced European mathematics, so we will not discuss it in detail.

India is very far from Europe. There was little contact between European and Indian scholars until the 16th century, and so Western mathematics did not directly learn from the mathematicians of India. Instead, as we discuss in the next section, many of the results found in India made their way to the West through Baghdad and the Arabic mathematical tradition.

The best survey of the history of mathematics in India is [142], Also interesting is [95], which is particularly interested in the value and influence of non-Western traditions. Both books include a discussion of the later work as well. For shorter surveys, go to [75, Section 1.12]. [159], and [99, Chapter 6]. Translations of some of the main sources can be found in [98]. For the brave, there is [102], which gives an annotated translation of our earliest source, Brahmagupta's commentary on the mathematical work of Āryabhaṭa.

Arabic Mathematics

In 750 A.D., the Islamic Empire stretched all the way from the western edge of India to parts of Spain. The period of expansion was coming to an end. A new dynasty, the Abbasids, had just come into power. One of their first actions was to establish a new imperial capital. This new city, called Baghdad, quickly became the cultural center of the Empire. Its location, on the Tigris River in what is now central Iraq, made it a natural crossroads, the place where East and West could meet.

The first scientific works brought to Baghdad were books on astronomy, probably from India. Early in the 9th century, however, the Abbasid caliphs took a more deliberate approach to the intellectual growth of the empire. They obtained scholarly manuscripts in Greek and Sanskrit and brought to Baghdad scholars who could read, understand, and translate them. Over the following years, many important Greek and Indian mathematical books were translated and studied. As a result, a new era of scientific and mathematical creativity began. One of the first Greek texts to be translated was, of course, Euclid's Elements. It had a huge impact. Once they had learned and absorbed the Euclidean approach, the mathematicians writing in Arabic adopted it wholeheartedly. From then on, many of them formulated theorems precisely and proved them in Euclid's style.

Like the Greek, the Arabic mathematical tradition is marked by the use of a common language. Arabic was the language of scholars in the far-flung empire. Not all of the great mathematicians writing in Arabic were ethnically Arab, and not all of them were Muslim. Their common language allowed them to build on each other's work, creating a new and vital mathematical tradition that was active from the 9th to the 14th centuries.

Muhammad ibn Mūsa al-Khwārizmī was one of the earliest Arabic mathematicians to make an enduring name for himself. His name indicates that he was from Khwārizm, a town (currently called Khiva) south of the Aral Sea in what is now Uzbekistan. Al-Khwārizmī was active in the middle of the 9th century, and he wrote several books that were to be enormously influential. One was an explanation of the decimal place value system for writing numbers and doing arithmetic, which he said came from India. Three hundred years later, after being translated into Latin, this book was the major source for Europeans who wanted to learn the new numeration system. (See Sketch 1.)

Also by al-Khwārizmī was the book of "al-jabr w'al muqābala," which means something like "restoration and compensation.'' This book starts off with a discussion of quadratic equations, then goes on to practical geometry, simple linear equations, and a long discussion of how to apply mathematics to solve inheritance problems. It is the portion on quadratic equations that became famous. (See Sketch 10.) Al-Khwārizmī explains how to solve such equations and justifies the method using a naïve geometric approach reminiscent of Mesopotamian mathematics — which is not surprising, since Baghdad is only some 50 miles away from ancient Babylon. When this book was later translated into Latin, "al-jabr" became "algebra."

In these and other books, al-Khwārizmī seems to have been passing on material he had learned from various sources. He had learned decimal numeration from India. The sources of his algebra book are less clear. There was some influence from India, some from Hebrew mathematics, and probably some from the native Mesopotamian tradition. A good bit of the material may have been part of the subscientific, practical tradition. If so, al-Khwārizmī's work is an instance of scientific mathematics learning from the subscientific tradition.

After al-Khwārizmī, algebra became an important part of Arabic mathematics. Some mathematicians worked on the foundations of the subject, giving Euclidean-style proofs that algebraic methods worked. Others extended the methods. Arabic mathematicians learned to manipulate polynomials, to solve certain algebraic equations, and much more. All of this was done using no symbols at all. Arabic algebra was done entirely in words. For example, to express an equation such as 3x² = 4x + 2, they would say something like "three properties14 are equal to four things plus two dirhems." The solution would similarly be spelled out in words. (See Sketch 10 for more details.)

One of the most famous Arabic mathematicians was 'Umar al-Khāyammī, known in the West as Omar Khayyám. Nowadays mostly known as a poet, in his day he was also famous as a mathematician, scientist, and philosopher.¹⁵ Khayyám also wrote a book on algebra. One of his goals was to find a way to solve equations of degree 3. He was unable to find a numerical solution, but he did find a way to solve all such equations using geometric constructions. (Greek mathematicians had done this for some cubic equations, as we discuss in Sketch 28, but Khayyám does it systematically.) His solution was obtained by going beyond ruler and compass, using parabolas and hyperbolas to determine points. He notes in his book, however, that if one wants to find a number that solves the equation, this geometric solution isn't very helpful. The challenge he laid down with these words was to be taken up by Italian algebraists many centuries later. (See Sketch 11.)

To the Arabic mathematicians, only positive numbers made sense. On the other hand, they were much more willing than the Greeks to consider lengths of various line segments as numbers. In part, this is due to their interest in trigonometry: tables require numbers. Trigonometry also led them to notice that by choosing a fixed segment as the unit one could obtain the lengths of other segments in terms of ratios.

The Arabs did significant work in geometry and trigonometry. They investigated the foundations of geometry, focusing in particular on Euclid's fifth postulate. (See Sketch 19.) They also undertook original geometrical investigations, extending the work of the Greeks. Trigonometry was a major concern, mostly because of its applications to astronomy. The work on trigonometry led inevitably to work on approximate solutions of equations. A particularly notable instance of this is a method for approximating the nth root of a number, developed by al-Kashi in the 14th century.

Combinatorics also shows up in the Arabic tradition. They knew at least the first few rows of what we now call "Pascal's Triangle," and they understood both the connection with (a + b)ⁿ and the combinatorial interpretation of these numbers. Stimulated by their translations of Euclid and Diophantus, they also did work in number theory. There is hardly any part of mathematics on which they did not make their mark.

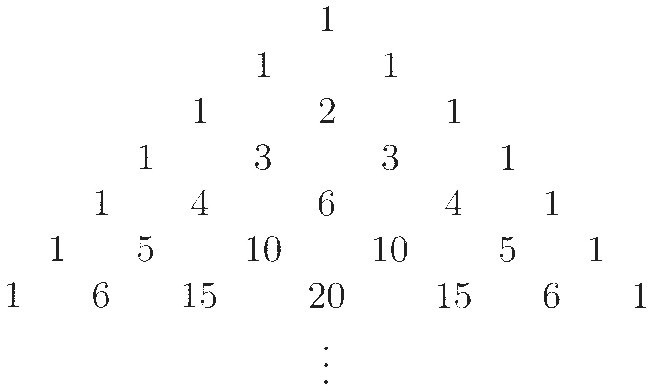
Pascal's Triangle: Each inside number is the sum of the two numbers diagonally above it.

Finally, it is important to mention that practical mathematics was also advancing. One example may be due, at least in part, to the Islamic prohibition against graven images, which included any artistic representation of the human body. As a result, a complex and sophisticated art of ornamentation was developed. Buildings were decorated by repetitions of a simple basic motif. This kind of decoration requires some level of forethought, because not all shapes can be repeated in such a way as to cover a plane surface. Deciding what sorts of shapes can be used in this way is really a mathematical question, linked both to the study of plane tilings and the mathematical theory of symmetry. There is no evidence, however, that Arabic mathematicians even noticed that there was interesting mathematics here. Instead, the patterns were developed by artisans, probably by experimentation. It was only in the 19th and 20th centuries that mathematicians discovered the underlying mathematical concepts.

The Arabic tradition was intensely creative, picking up the best from Greek and Indian mathematics and developing it further. Unfortunately, only a small part of it was transmitted to Europe. As a result, many of these results had to be rediscovered, sometimes many centuries later. It was in the 19th century that European scholars began to investigate the Arabic mathematical texts. Since then, historians have learned a lot about this period. There are still many manuscripts to read and study, and new discoveries are being made all the time. Our picture of the Arabic achievement is still incomplete.

To read more about Arabic mathematics, one could start with [75, Section 1.6], [99, Chapter 7], and [159, pp. 137-165]. Some of the articles in [172. Part V] offer specific examples of the work of Arabic mathematicians. Two useful book-length introductions are [13], which is more mathematical, and [152], which is more interested in astronomy. See also [146. Volume 2].

Medieval Europe

Around the 9th century, political and social life in Western Europe began to be stable enough for people to pay attention to education. In many places "cathedral schools" sprang up, dedicated to the training of future priests and clerics for the local diocese. They concentrated on the ancient tradition of the introductory trivium (grammar, logic, and rhetoric). The more advanced students might go on to the quadrivium (arithmetic, geometry, music, and astronomy). It is likely that very few students actually studied the mathematical topics in the quadrivium, but their presence in the curriculum helped stimulate interest in mathematics.

Once people became interested in mathematics, where could they go to learn more? The obvious thing was to go to places under Islamic control, of which the most accessible was Spain. Gerbert d'Aurillac, later to be Pope Sylvester II, is an example. Gerbert visited Spain to learn mathematics, then reorganized the cathedral school at Rheims, France. He reintroduced the study of arithmetic and geometry, taught students to use the counting board, and even used the Hindu-Arabic numerals (but not, it seems, the full place value system).

In the following centuries, many European scholars spent time in Spain translating Arabic treatises on all sorts of subjects. While few European scholars knew Arabic, many Jewish scholars living in Spain did, so the translations were often done by having a Jewish scholar translate from Arabic to some common language, then translating from that language into Latin. Many of the mathematical and philosophical texts in Arabic were translated. In addition, a wide range of ancient Greek texts, from Aristotle (the most influential) to Euclid, were translated from the Arabic to make their impact in the West.¹⁶

Spain is very far from Baghdad, and it was not really a center of mathematical activity. Only the oldest and easiest mathematical texts were likely to be found in Spanish libraries. This is probably the reason why al-Khwārizmī's works were so prominent. His algebra book was translated by Robert of Chester in 1145. (It was this translation that Latinized "al-jabr" into "algebra.") His book on arithmetic with Hindu-Arabic numerals seems to have been translated or adapted several times. Many of these versions began with the words "dixit Algorismi" ("so says al-Khwārizmī"), and it is because of this expression that the word algorism came to mean the process of computing with Hindu-Arabic numerals. The modern word algorithm, meaning a "recipe" for doing something, is a modern variant of algorism, which was a recipe for doing arithmetic.

The system of cathedral schools eventually led to the establishment, in the 11th and 12th centuries, of the first universities in Bologna. Oxford, Paris, and other European cities. For the most part, the scholars at the universities were not interested in mathematics. Aristotle's work did have a great impact, however. His work on the theory of motion led a few scholars at Oxford and Paris to think about kinematics, the study of moving objects. It is to these scholars that we owe the notions of instantaneous velocity and of uniformly accelerated motion. Perhaps the greatest of them was Nicole Oresme, at the University of Paris. Oresme worked on the theory of ratios and on several aspects of kinematics, but his most famous contribution is a graphical method for representing changing quantities that anticipates the modern idea of graphing a function. In addition, questions of motion led him to consider infinite sums of smaller and smaller terms. He obtained several significant results about such sums, sometimes by using ingenious graphical tricks.

Trade was another source of contact between Europeans and the Islamic Empire. Leonardo of Pisa17 was the son of a trader. Traveling with his father, he learned quite a bit of Arabic mathematics. In his books, Leonardo explained and extended what he had learned. His first book was the Liber Abbaci ("Book of Calculation"), published around 1202 and revised in 1228. It started by explaining Hindu-Arabic numeration and went on to consider a wide array of problems. Some of the problems were practical: currency conversion and computing profits, for example. Others were more like the word problems in today's algebra texts. The book contains a geometric explanation of the rules for solving quadratic equations and a few other theoretical passages, but the focus is on the problems and the methods for solving them.

Leonardo's other works are also important. His Practica Geometriae is a manual of "practical geometry" which seems to have been heavily influenced by the work of Abraham bar Hiyya, who lived in Spain in the 12th century. (Abraham bar Hiyya wrote in Hebrew, but his work was one of many translated into Latin during that century.) Leonardo also wrote the Liber Quadratorum, the "book of squares." Here he reveals himself to be a creative and talented mathematician. The book discusses how to solve various kinds of equations involving squares, under the restriction that the solutions be whole numbers. The problems typically involve more than one variable. The Liber Quadratorum anticipates and points toward the work of Fermat and Euler, 400 or more years down the road.

Leonardo's work may have been one of the sources of what was to become a lively tradition in Italy. As the Italian merchants developed their businesses, they had more and more need of calculation. The Italian "abbacists" tried to meet this need by writing books on arithmetic and algebra. They often wrote in everyday Italian rather than in Latin, which was the language of the scientists. The culmination of this tradition was the work of Luca Pacioli, whose Summa de Aritmetica, Geometria, Proportione e Proportionalita was a huge compendium of practical mathematics, from everyday arithmetic to double-entry bookkeeping. Printing had just been developed in Germany and was flourishing in Italy. Pacioli's Summa was one of the first mathematics books to be printed. This gave it wide circulation, and it became the basis of much later work on algebra. (See Sketches 2 and 8 for details about Pacioli's notation.)

Not much has been written specifically about the history of mathematics in Medieval Europe, though many translations and editions of the main texts are available. There is a good overview of this period in [99, Chapter 8]; part 2 of [75] is a useful complement. Biographies are a good way to get a sense of the times: Gerbert d'Aurillac is the topic of [18], while Leonardo of Pisa is at the center of [46] and [45].

The 15th and 16th Centuries

Around the end of the 14th century, many different cultures around the world were producing interesting mathematics. In Central America, the Maya had developed a base-twenty system for numeration (see Sketch 1) and an elaborate calendar. In China, mathematicians had developed sophisticated methods for solving many kinds of problems. Both Indian and Arabic mathematics had also continued to grow.

These cultures were somewhat insulated from each other and from European culture. There were some contacts, especially in commerce, but little mathematical knowledge seems to have been exchanged at that time. All of that was about to change dramatically. Beginning in the 15th century and intensifying from then on, Europeans began to develop the art of navigation and to travel to distant continents, taking European culture with them. By the late 1500s. Jesuit schools had been established in many places, from South America to China. The Jesuit cultural network eventually extended throughout the world. As a result, European mathematics was taught and studied everywhere and eventually became the dominant form of mathematics worldwide.

As European sailors began to travel to other continents, solving the technical problems of navigation became more and more important. Long-range navigation depends on astronomy and on a good understanding of the geometry of the sphere; this helped propel trigonometry to the center of attention. Astrology was also a very important part of the culture of this period, and making star charts also depends on having a good grip on (spherical) trigonometry. Because of this, trigonometry was one of the major themes in the mathematics of the 15th and 16th centuries.

In parallel with the intense study of navigation, astronomy, and trigonometry, there was also growing interest in arithmetic and algebra. With the rise of the merchant class, more people found that they needed to be able to compute. Since algebra was thought of as a kind of generalized arithmetic, it was natural for scholars to move from arithmetic to algebra as they went deeper into their studies. Algebra remained a central interest of mathematicians well into the 17th century; we discuss it in detail in the next section.

Of course, algebra and trigonometry are related, and they influenced each other. Trigonometry is a kind of algebraized geometry, and both algebra and trigonometry are methods for solving problems. Often the same scholars wrote on both subjects. A leading example was Johannes Müller, also known as Regiomontanus (a Latinized version of "from Königsberg." referring to his birthplace). Besides translating many classical Greek works and studying the stars, he wrote De Triangulis Omnimodis ("On All Sorts of Triangles"), one of the first treatises devoted solely to trigonometry.

A great many new ideas were introduced into trigonometry at this time. The list of trigonometric functions (sine, cosine, tangent, cotangent, secant, cosecant) became standardized. New formulas and new applications were discovered. Given the interest in navigation and astronomy, most of the focus was on spherical triangles, whether on the celestial sphere or on the earth. Throughout all this, sines and cosines continued to be thought of as lengths of particular line segments. No one thought of them as ratios or as lengths on a unit circle. All sine tables were based on a circle of fixed radius, and in applications one had to use proportionality to adapt the information to the radius at hand. (See Sketches 18 and 26 for more about early trigonometry.)

Somewhat related to all this was the discovery of perspective by Italian artists. Figuring out how to draw a picture that gave the impression of three-dimensionality was quite difficult. The rules for how to do it have real mathematical content. Though the artists of the Renaissance did not subject these rules to a complete mathematical analysis, they understood that what they were doing was a form of geometry. Some of them, such as Albrecht Dürer, were quite sophisticated in their understanding of the geometry involved. In fact, Dürer wrote the first printed work dealing with plane curves that went beyond the conics, and his investigation of perspective and proportion is reflected both in his paintings and in the artistic work of his contemporaries. (See Sketch 20.)

There are good surveys of the mathematics of this period in [99, Chapters 9 and 10] and [75, Part 2]. For the non-European aspects, look at [159]. The best account of the early history of trigonometry is [177]. For perspective, look at [61] and [6].

Algebra Comes of Age

As we reach early modern times, mathematics begins to get broader and more diverse. While certain concerns were dominant at certain times, there were always other topics being studied. From this point on, our overview selects and follows a few important threads, rather than attempting to cover everything. In the 16th and early 17th centuries, it is algebra that takes center stage.

It's important to understand what algebra was like at this time. Leonardo's Liber Abbaci, like the Arabic algebra which inspired it, was entirely rhetorical. Equations and operations were expressed in words, written out in full. Between the time of Leonardo and the 16th century, scholars developed abbreviations for many of the words, such as writing p for "plus." But they didn't really change the nature of the enterprise and, in particular, did not introduce any sort of general or standardized notation. One started from the rules of arithmetic and attempted to solve equations. The equations treated were mostly of degree 1 or 2 or were easily reducible to such equations.

The Italian algebraists used the word cosa, meaning "thing," for the unknown quantity in their equations. When scholars from other countries got involved, they used coss. As a result, they were sometimes called the "cossists," and algebra was sometimes known as "the cossic art."18 The English scholar Robert Recorde is a good example of this tradition. In his The Grounde of Artes (1544), he explains basic arithmetic. This book, written in English in dialogue form, was so popular that it went through 29 editions. His next book, The Whetstone of Witte (1557), is a kind of sequel which he describes as dealing with "the cossike arte," that is, algebra. (The title is a pun: cos happens to mean "whetstone" in Latin!) This was typical of the early algebraic tradition: it was viewed as a popular, practical kind of mathematics, a way to sharpen your wit after having laid down the groundwork of arithmetic.

[from Recorde's title page]

Recorde in England is just one example. From Pedro Nunes in Portugal to Michael Stifel in Germany, the cossists were all over Europe. They were particularly good at inventing notations. They had different symbols for the unknown, the square of the unknown, and sc on. Some used special notations for the algebraic operations and for the extraction of roots. Others simply abbreviated the crucial words. They did not use symbols for quantities other than the unknown; these were always numerical. Hence, they could write the equivalent of x² + 10x = 39, but they could not write something like ax² + bx = c. Thus, while they certainly "knew" the quadratic formula, they could not write it down as a formula the way we do. Instead, they would give a verbal recipe and many examples. (See Sketches 2 and 8 for more about the evolution of algebraic symbolism.)

Several algebraists of this period attempted to find a method to solve cubic equations. The crucial breakthrough was made in Italy, first by Scipione del Ferro and then by Tartaglia.19 Both men discovered how to solve certain kinds of cubic equations. They kept their solutions secret, because at this time scholars were mostly supported by rich patrons and had to earn their jobs by defeating other scholars in public competitions. Knowing how to solve cubic equations allowed them to challenge the others with problems that they knew the others could not solve, so people were inclined to keep quiet about their discoveries.

In the case of the cubic, this pattern was broken by Girolamo Cardano. Promising never to reveal it, Cardano convinced Tartaglia to share the secret of the cubic with him. Once he knew Tartaglia's method for solving some cubic equations, Cardano was able to generalize it to a way of solving any cubic equation. Feeling that he had actually made a contribution of his own, Cardano decided that he was no longer bound by his promise of secrecy. He wrote a book called Ars [from Magna ("The Great Art"). This scholarly treatise (written in Latin) gave a complete account, with elaborate geometric proofs, of how to solve cubic equations. It also included a solution for the general equation of degree 4 that had been found by Cardano's student Lodovico Ferrari. Despite the fact that Cardano acknowledged his contribution, Tartaglia was furious at Cardano's breach of promise. He protested publicly, but in the end there was little he could do. In fact, the formula for the solution of a cubic equation is still often called "Cardano's formula." (See Sketch 11 for more about this story of human nature at work.)

[from Cardano's title page]

Cardano's notation was still in the old tradition. He would have written the equation x³ = 15x + 4 something like this:

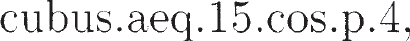
which was read as "a cube is equal to 15 things plus 4." He would then give a procedure for solving the equation that was basically the same as the cubic formula we use today. Since the coefficients of his equations were always numbers, he described the method in words and gave examples of its application.

There was one very serious problem, though. Applying Cardano's method to the equation above yields (in modern notation)

In a quadratic equation, the appearance of the square root of a negative number is a signal that there is no solution. But here it's easy to check that x = 4 is a solution. Cardano's methods solved most cubics, but got him in trouble in cases like this. His solution to this issue was to sweep it under the rug. Equations like this one are barely mentioned in this book, and the few mentions are cryptic and short. (See Sketch 17.) His method worked for every one of the equations he discussed in detail.

The missing step was provided by Rafael Bombelli. In his Algebra, Bombelli extended Cardano's ideas in several different directions. In particular, he developed a method for dealing with cubic equations which led to expressions such as the one above, involving square roots of negative numbers. We might describe Bombelli's method as the beginning of a theory of the complex numbers, though it is unclear whether he really thought of them as "numbers." He described them as "linked cubic radicals of a new type'' and explained how to operate with them in such a way as to obtain the solution. (See Sketch 17 for more about the beginnings of complex numbers.)

Another important idea developed by Bombelli was to link algebra and geometry in a more direct way. Cardano could only conceive of x³ as meaning the volume of a cube of unknown side. Bombelli, on the other hand, was prepared to consider diagrams containing segments whose length was, say, x² and to use these diagrams to explain his equations. By emphasizing the connection to geometry, Bombelli was anticipating the direction algebra would soon take.

Bombelli's Algebra had one other important feature. While he was working on the book, Bombelli learned that Regiomontanus had translated a portion of Diophantus's Arithmetica. He located it and read it, and it is clear that this old Greek book had a huge impact on his thinking. In fact, a large portion of the latter part of Bombelli's work contains problems taken from Diophantus. These problems were usually equations in several variables which had many solutions, but for which one was supposed to find solutions in whole numbers or in fractions. They require a completely different set of algebraic techniques. Bombelli didn't go much beyond what Diophantus had already done, but here, too, he paved the way for future developments.

Algebra began to look more like it does today towards the end of the 16th century, in the hands of François Viète. Among many other things, Viète worked for the French court as a cryptographer, a code-breaker who deciphered intercepted secret messages. This may be what led him to one of his most important innovations: the notion that one could use letters to stand for numbers in equations. Viète used the vowels A, E, I, O, U to indicate unknown quantities and consonants to indicate known numbers. He was thus the first to be able to write an equation like ax² + bx = c, though his version would have looked something like

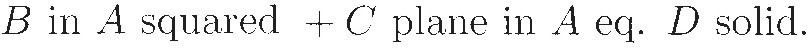
(Remember that the vowel A is an unknown and the consonants B, C, and D stand for numerical parameters).

The form of this equation highlights one of Viète's worries: he always wanted quantities to be equidimensional. Since multiplying B by A² would make a "solid" (i.e., three-dimensional) quantity, he specified that C must be plane, so that CA is also solid, and that D must be solid. Bombelli, as mentioned above, had no such worries. Descartes would later convince everyone that it was best not to worry about dimensionality.

Perhaps the most important thing Viète did, however, was to promote algebra as an important part of mathematics. In algebra, one often starts by assuming that, say, ax² + bx is, in fact, equal to c, and then one deduces what x must be equal to. This reminded Viète of what the 4th century Greek mathematician Pappus called analysis, in which one assumes a problem has been solved and proceeds to deduce things from this assumption. Hence, Viète argued that the Greek analysis was actually algebra, which the Greeks were supposed to have known and kept secret.20 At this time, algebra was often considered less serious and less important than geometry. By giving it a Greek pedigree, Viète made algebra more acceptable to more mathematicians. (See Sketch 8 for more about Viète's contributions to algebra.)

René Descartes completed the process of bringing algebra to a mature state. In his famous book La Géométrie (published as an appendix to Discourse on Method), Descartes proposed essentially the notation we use today. He suggested the use of lowercase letters from the end of the alphabet (such as x, y, and z) for unknown quantities and lowercase letters from the beginning of the alphabet (such as a, b, c) for known quantities. He also came up with the idea of using exponents on a variable to indicate powers of that variable. Finally, he pointed out that once one fixes a unit length, any number can be interpreted geometrically as the length of a line segment. So x² could just mean a line segment whose length is equal to the number x². With this, Descartes did away with Viète's worries about dimensionality. (See Sketch 8 for more about how Descartes influenced algebraic notation.)

Three innovations from this period were to be extremely important. First, the fact that no one could figure out how to solve the general quintic (fifth-degree) equation led algebraists to start asking deeper questions. Slowly, a theory about polynomials and their roots evolved. Second, Descartes and Pierre de Fermat linked algebra and geometry, inventing what we now call "coordinate geometry." They showed that, just as we can interpret algebraic equations geometrically, we can also interpret geometric relations algebraically. (See Sketch 16 for more about coordinate geometry.) Both Fermat and Descartes demonstrated the power of algebra to solve geometric questions by applying it to famous difficult geometric problems that had been discussed by Pappus. Third, Fermat introduced a whole new category of algebraic problems. These were related to the work of the Greek mathematician Diophantus, but went far beyond his work. Specifically, Fermat began asking "questions about numbers," by which he meant whole numbers. For example, can a square be equal to 1 plus a cube? This amounts to the equation y² = x³ + 1, which Fermat wanted to solve under the restriction that x and y should be whole numbers. There is an easy solution, x = 2 and y = 3. But are there any others? Fermat developed methods for answering such questions. He could also use his methods for proving what he called "negative propositions." These were statements that said that certain equations cannot be solved. For example, he proved that the equation x⁴ + y⁴ = z² has no solution in (non-zero) whole numbers.

Unfortunately, for a long time Fermat was alone in finding these questions interesting. Mathematicians of the time felt that good mathematics was about what can be done, so their reaction to Fermat's negative propositions was puzzlement. Why glory in not being able to solve certain problems? Furthermore, Fermat was not a professional mathematician, but a lawyer serving on the court in Toulouse, France. As a result, he never published his proofs. Instead, he wrote letters to friends, explaining his ideas and discoveries, but without the technical details. It was left to other mathematicians, a century later, to rediscover the subject and find the proofs all over again. We'll get back to that when we discuss the work of Euler and others in the 18th and 19th centuries.

The early history of algebra is discussed in Chapters 9 and 11 of [99]. For a more detailed treatment, one might go to [160] or [101].

Calculus and Applied Mathematics

While the mathematicians of the late 16th and early 17th century were developing algebra, another group of people were beginning to use mathematics to try to understand the universe. At that time, they were usually called "natural philosophers." Perhaps the most famous of them was Galileo Galilei, who lived mostly in Florence, Italy. Galileo's studies included astronomy and the physics of moving bodies. He blended observation and experimentation with mathematical analysis. In fact, he insisted that one had to use mathematics in order to have a chance of understanding the world.

He was not alone. Johannes Kepler, in Germany, was using the old Greek geometry of conic sections to describe the solar system. The Greeks had studied the ellipse for its mathematical interest. Kepler discovered that the planets moved around the sun in elliptical orbits and formulated mathematical laws to describe how fast each planet moved. (See Sketch 28.) In France, Father Marin Mersenne²¹ was trying to get many scholars from different areas to come together, talk, and cooperate in order to understand the world. In England, Thomas Harriot was developing algebra and applying mathematics to optics, navigation, and other questions. And René Descartes, who had revolutionized both algebra and geometry by bringing them together, also began trying to understand comets, light, and other phenomena.

All of this work brought some specific mathematical issues to everyone's attention. Studying motion inevitably led to difficult questions related to the infinite divisibility of space and time. When an object is moving in such a way that its velocity is continually changing, how does one even understand what its velocity is? And how does one figure out what distance it covers in a given amount of time?

These questions were not new. They had been studied and discussed by medieval scholars such as Nicole Oresme and by many others since then. But their new relevance made them more urgent. So did the related questions of finding tangents to curves and areas of curved figures. As a result, many mathematicians started to work on them. One such person was Bonaventura Cavalieri, a Jesuat22 former student of Galileo and professor at the University of Bologna. To study the areas and volumes of curved figures. Cavalieri worked with the "principle of indivisibles." This is the idea that a planar region can be considered as an infinite set of parallel line segments and a solid figure can be considered as an infinite set of parallel planar regions. For example, a cylinder would be thought of as a stack of circles, all of the same size, and a sphere would be a stack of circles of varying sizes. Using this idea, Cavalieri could compute many areas and volumes that would previously have been very hard to analyze. Similar work was done by Fermat and Descartes in France and by many other European mathematicians. By 1660 or so, it was clear that problems of this kind could be solved as needed. What was not available, however, was a general method.

In the late 1660s, Isaac Newton and Gottfried Wilhelm Leibniz independently discovered such a method. In fact, they discovered two slightly different methods. Newton's approach emphasized what he called "flowing quantities" and their rates of flow, which he called their "fluxions." Leibniz's approach used the idea of "infinitesimal," or infinitely small, quantities. If a quantity was represented by a variable x. Leibniz defined its "differential" dx to be the amount by which it changed in an infinitesimal amount of time. Both fluxions and differentials are basically what we now call derivatives. (See Sketch 30.)

The most important part of the discovery may well have been the realization that one could develop a kind of recipe for computing these things. It was a method of calculation, "a calculus.'' Leibniz was the one who saw this most clearly. In his very first paper about the subject, he emphasized the importance of being able to solve problems without really having to think about what was going on. One simply applied the rules of the calculus.²³

With such a powerful tool in hand, many people set out to apply it to the world. This became the main theme of 18th century mathematics. Newton himself had prepared the way with his Principia, a mathematical analysis of the laws of motion and the workings of the solar system. Jakob Bernoulli, his brother Johann, and others learned to use the calculus. Johann played an especially important role. Since his brother was professor of mathematics in their home town (Basel, Switzerland), he had to go elsewhere. To earn money, he arranged to teach the new calculus to a French nobleman, the Marquis de l'Hospital. They agreed that Bernoulli would write letters explaining the calculus, and the content of these letters would then belong to l'Hospital. The result was the first calculus textbook, published by l'Hospital in 1696.

Soon there were many such books, and many mathematicians were using the calculus to study the natural world. Among them was Daniel Bernoulli, son of Johann Bernoulli, who studied mechanics and hydrodynamics. In Italy, Maria Gaetana Agnesi became one of the first women to have an impact on modern mathematics when she wrote her own textbook, a unified treatment of algebra, coordinate geometry, and calculus. Agnesi's book was rather old-fashioned, but it proved useful to many people. Agnesi herself became quite well known; she was even named professor at a university, though she did not accept the position.

In France, the spread of the new mathematical ideas of calculus was tied to the spread of the new Newtonian ideas about motion and gravitation. Many scholars were involved in this process. One of the most important was a woman, Emilie de Châtelet. Among other things, she produced a richly annotated translation into French of Newton's Principia. Since Europeans tended to prefer the language and notation used by Leibniz, Châtelet also had to translate the mathematics. In the process she clarified several significant issues and helped convince people that the new physics was correct.

The greatest mathematician of the time, however, was Leonhard Euler. He was born in Switzerland and had private lessons from Johann Bernoulli (who by this time had replaced his older brother on the faculty at Basel). Euler spent most of his life, however, in St. Petersburg (in Russia) and Berlin (then the capital of Prussia). At this time, the universities had little interest in scientific research. Instead, several of the European kings established royal scientific academies where scholars could work and communicate. There was even some competition as to who could catch the best scholars. For almost all of his life, Euler was associated with the St. Petersburg Academy. At one point, he was lured away and spent a few years at the Berlin Academy, but he ended up returning to Russia.

Reading Euler's work gives one the impression of a mind overflowing with ideas. He wrote on every aspect of mathematics and physics and also had much to say about astronomy, engineering, and philosophy. In mathematics, he developed the calculus into a powerful instrument and applied it to all sorts of complicated problems, both in pure mathematics and in physics. He wrote textbooks explaining all this to others. In his "precalculus" textbook, he emphasized the idea of a function. Many of the conventions and notations we still use were introduced in his books.

Euler didn't stop there. He rediscovered Fermat's number theory and put it in order. He found correct proofs of Fermat's statements and established number theory as an important part of mathematics. He investigated algebra and polynomials and came close to proving the Fundamental Theorem of Algebra. He studied the geometry of the triangle, discovered a basic theorem about solid polyhedra, and began to study the geometry of curves and surfaces. He applied mathematics to the design of ships and turbines and to other engineering problems. He even considered lotteries and a puzzle about walking over a set of seven bridges without crossing any of them twice. When the mathematics needed to study something was available, he used it. When it wasn't, he developed it. Euler's works now fill more than 80 printed volumes. Euler didn't wait until he had just the right approach to analyzing something. He just plowed in and got to work. If later he saw a simpler or better way, he'd write another paper. Reading his papers allows one to see why he was interested in each problem and to follow how his ideas developed.

Euler's influence was enormous. He was the first to suggest that it was best to consider the sine and cosine as functions of the angle, and to define them in terms of the unit circle. He was the first to express Newton's law of motion in its modern form. He popularized the use of π for the ratio of the circumference to the diameter of a circle, and he invented e as the name of the number which is the base of the natural logarithm. His textbooks established the style and the notation that were used for a long time. All over mathematics one finds ideas marked with his name.

Perhaps one can see the culmination of 18th century mathematics in the work of two mathematicians. Pierre Simon Laplace and Joseph-Louis Lagrange. Laplace was an applied mathematician through and through. He wrote famous books on celestial mechanics and on probability. They are both huge books, dense with mathematics. They also both come accompanied by more popular versions: The System of the World to explain how the solar system works, and a Philosophical Essay on Probabilities that explained the basic ideas and argued for their broad applicability. (See Sketch 21 for the early history of probability.) Lagrange, for his part, worked in all areas of mathematics, from algebra to the calculus. One of his most important books is a treatise on mechanics, in which he lays out a mathematical theory of how and why things move. This remarkable book is quite important in the history of physics, but it is also famous for having no pictures in it at all! Lagrange felt that his formulas had captured physical reality so well that diagrams were no longer needed.

The 18th century was an optimistic time. Laplace did not hesitate to apply his calculus of probabilities to the activities of judges and juries. Modern readers often find his assumptions very strange.²⁴ Similarly, Lagrange did physics without diagrams. Mathematicians felt they had in their hands the key to reality. And, for the most part, the key did seem to unlock many doors.

Not all was well, however. The most famous sign of trouble was a tract by George Berkeley, Irish philosopher and Anglican Bishop of Cloyne. Berkeley was offended by the public atheism of a mathematician who argued that theology was speculative and uncertain. He responded by showing that the foundations of the calculus, which the mathematicians prized so much, were just as shaky. His scathing essay, The Analyst, showed that both Newton's fluxions and Leibniz's infinitesimals were ill-defined and in some ways contradictory. Fluxions were computed by taking the quotient of two increments. Newton seemed sometimes to say these increments were both zero and sometimes to say that they were not. Berkeley put his finger directly on the contradiction:

And what are these fluxions? The velocities of evanescent increments. And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?

The central point is made early in the essay: ". . . he who can digest a second or third fluxion... need not, methinks, be squeamish about any point in Divinity.''

Berkeley also argued that Newton, for example, would cut corners in his writing, skipping over difficulties or choosing just the right way to say something so that certain issues were obscured. Berkeley's critique showed that the very foundations of the calculus were insecure.

For many mathematicians, the answer was "but it works!" Jean le Rond d'Alembert, a French mathematician and philosopher who was one of the editors of the famous Encyclopédie, is supposed to have said to a student: "Persist, and faith will come." Nevertheless, several mathematicians, including D'Alembert himself, began to look for better foundations. The first results of this search came early in the 19th century, though the task was not completed until much later.

The early history of the calculus has been the subject of much historical investigation. Chapters 12 and 13 of [99] are a good place to start, and the first half of [76] is a good source of further information. Both contain pointers to further reading.

Rigor and Professionalism

The 19th century saw a huge explosion in mathematical activity and significant changes in where and how mathematicians did their work. Progress was made in so many different directions that it is hard to find one main theme which characterizes all this work. We've chosen to emphasize three important aspects of 19th century mathematics. First, there was a deep concern with rigor, especially with regard to calculus. Second, physical problems led to more, and more sophisticated, mathematics. Third, mathematicians became professionals in a new and different way.

The opening years of the 19th century were marked by the aftermath of the French Revolution of 1789. The revolution affected all of Europe. Among the changes the revolutionaries introduced in France was a new emphasis on education. They established schools, such as the École Polytechnique in Paris, whose main mission was to provide a technical education to the middle class. The goal was to create a class of well-trained civil servants to run the new French Republic. One result was that mathematicians were now expected to teach. What's more, their students were expected to learn from their teaching. This put a new value on clarity, precision, and rigor. After all, if the teacher doesn't understand the basis of what is being studied, how can the student understand it? At about the same time, the French Academy of Sciences devised the metric system as a standardized system of measurement for use in science and commerce. After its official adoption by the French government in 1795, this system gradually spread to other countries. By the end of the 19th century, it had become a recognized international standard. (See Sketch 6.)

As the 19th century opened, the dominant mathematical figure was Carl Friedrich Gauss. He was a child prodigy, able to do arithmetic by the time he was three. At age 17, he was already making significant new discoveries, which he recorded in his mathematical diary. His first important book, published in 1801, was called Disquisitiones Arithmeticae (Arithmetical Investigations). It dealt with whole numbers and their properties, and it was marked by what came to be known as the Gaussian style: spare, precise, with almost no motivation or explanation beyond the technical proofs.

Gauss's work spanned all of pure and applied mathematics. In fact, he is just as famous for his work on physics and astronomy as he is for his strictly mathematical work. He also had a way of combining the two. For example, after doing some surveying, he applied ideas he had developed for that task to his study of the geometry of surfaces. This interaction between applications and theory was quite typical of the work of the great 19th century mathematicians.

The other great figure of the early 19th century was Augustin Louis Cauchy. As a very young man, Cauchy was made a professor at the École Polytechnique in Paris. His main job was teaching calculus, which he preferred to call analysts. He clearly was not satisfied with the way the foundations of the subject then stood. The result was one of the most famous textbooks in the history of mathematics. The title, The École Polytechnique Course in Analysis, didn't really indicate how revolutionary the contents were. The first volume²⁵ was called Algebraic Analysis and tried to make precise such ideas as continuity and convergence. In his courses, Cauchy's goal was to "do calculus right." For the first time, there were definitions of the derivative and the integral. For the first time, the Fundamental Theorem of Calculus was highlighted as indeed fundamental. And, much as we do today, Cauchy emphasized the algebraic side of calculus, preferring computations to diagrams and formulas to geometric intuitions.

Cauchy's work ranged far and wide in mathematics and mathematical physics. He wrote about everything. In fact, he was so prolific that at one point the editors of a major French journal imposed a quota on him. In response, he convinced a publisher (who happened to be family) to put out a journal containing nothing but papers by Cauchy! His emphasis on rigor had a great impact on other mathematicians. There is a story that Laplace once listened to him explain the importance of convergence of infinite series. Alarmed. Laplace ran home to check the series in his massive book on celestial mechanics. The influence of the new ideas was deep.

Many mathematicians continued Cauchy's work of making the calculus precise and rigorous. In the process, they found flaws in his work, of course, and tried to improve on it. The most important of these mathematicians was Karl Weierstrass, whose name, even today, is synonymous with rigor and precision. Weierstrass was also a teacher. In fact, he began his career as a high school teacher. Besides mathematics, he also had to teach other subjects, from physics and botany to calligraphy and gymnastics. It was only after publishing several scientific papers that he was recognized as a creative mathematician. He eventually became a professor at the University of Berlin.

Weierstrass's analysis lectures in Berlin were famous. He was not an animated teacher. Health problems forced him to lecture sitting down while a student wrote formulas on the blackboard. But the content of the lectures was inspired, and many of his students became great mathematicians. One achievement of these lectures was a complete transformation of the basis of calculus. His clear, precise definitions removed any trace of mystery or geometric intuition from calculus, putting it all on a logical foundation that depended only on algebra and arithmetic. The new approach wasn't easy, though, as students who have had to learn his "epsilon-delta" approach to limits will still testify.

Having settled the issue of finding rigorous foundations for the calculus, mathematicians considered other parts of mathematics, too. Richard Dedekind and Giuseppe Peano investigated the foundations of arithmetic, and Georg Cantor invented the notion of a set, which allowed him to make fundamental discoveries about infinity. The theory of sets eventually came to be seen as a possible foundation for all of mathematics. (See Sketch 25.)

Algebra and geometry also were changed in fundamental ways in the 19th century. Algebraic formulas for the solution of equations of degrees 3 and 4 had been found in the 16th century, but no one had been able to solve the equation of degree 5. Gradually, mathematicians had begun to turn from the search for a solution to the search for understanding of why the solution was not forthcoming. In the 18th century, Joseph-Louis Lagrange had noticed that one could understand all the existing solutions by analyzing the effect of permuting the roots of an equation on various polynomial expressions. This showed mathematicians how to think more rigorously about what a "formula" for solving an equation actually is. Together with the discovery of the connection between formulas and permutations, this eventually led to the fundamental algebraic discoveries of the 19th century.

The first breakthrough came from Niels Henrik Abel, a Norwegian mathematician whose brilliant career was cut short by an early death. Abel managed to prove in 1822 that in fact there is no general formula for the solution of the equation of degree 5. This was a remarkable development, but the real revolution in algebra came from the work of Évariste Galois. Galois was brilliant and temperamental, passionate about both mathematics and politics. As a young man, he spent a large part of his short life being thrown out of schools and into jails. Despite these frequent embroilments, he devoted much of his time to mathematics, but his writings went unnoticed. In 1832, shortly before his twenty-first birthday, Galois became involved in a duel that cost him his life.

The night before the "affair of honor," he dashed off a hurried letter to a friend, summarizing the discoveries that he had made in several mathematical papers. He concluded the letter by asking his friend to send it to the best mathematicians of the day and expressing the hope that later there would be "some people who will find it to their advantage to decipher all this mess." He was right. "This mess" was the analysis of the solvability of algebraic equations by means of group theory, a subject which has become the cornerstone of modern algebra and geometry.

Galois also introduced a fundamental change of perspective. He argued that it was necessary to move from considering particular transformations of equations to considering all possible transformations at once. This move to a more abstract perspective was picked up by other mathematicians as the century progressed and eventually led to what is now known as "abstract algebra."

In geometry too, it was a time of revolution. For centuries, people had thought about Euclid's parallel postulate and its role in plane geometry. The work of Gauss, János Bolyai, Nicolai Lobachevsky, and Bernhard Riemann finally settled the issue, leading to the discovery of the non-Euclidean geometries. (See Sketch 19.) Once again, the move was toward abstraction and rigor: rather than attempting to figure out what was "the geometry of the real world," these mathematicians showed that there were several alternative ways to do geometry, each consistent within itself, each interesting, each correct. It must have seemed, at the time, to be a useless but beautiful dream, a move away from applicability. But it didn't turn out that way. When Albert Einstein, in the 1910s, was looking for a way to express his insights into gravitation, he found the right language in Riemann's approach to geometry. It turns out that we may live in a non-Euclidean universe!

The connection between mathematics and theoretical physics remained strong. Applied mathematics was a source of interesting and difficult problems. To solve them, important new mathematics had to be created. In order to study how heat spreads through objects, Joseph Fourier invented what are now known as "Fourier series." These proved to be very useful in applied mathematics, to study light, sound, and other periodic wave phenomena. They also turned out to be interesting mathematical objects, and unraveling their properties required the full power of the rigorous approach to calculus that had just been developed. Many other areas of physics were studied, too. Electricity and magnetism posed interesting problems that led to important mathematics. Understanding machines, fluid flow, the motion of the planets, the stability of structures, the tides, the behavior of elastic materials — all this engaged the attention of many mathematicians.

One example is Sophie Germain, a contemporary of Gauss, Cauchy, and Fourier. Despite growing up during the so-called "Enlightenment." Germain faced real resistance to her desire to become a mathematician. Women could not study at the Polytechnique, so Germain had to borrow notes from male students in order to be able to learn advanced mathematics. Overcoming her society's prejudice against female intellectuals, she became one of France's finest mathematical scholars. Besides doing significant work in number theory (see Sketch 13 for more information), Germain obtained important results in the mathematical theory of elastic materials. Many mathematicians built on her work to perfect the theory of elasticity, which was crucial in the construction of the Eiffel Tower later in the century. (Nevertheless, the name of Sophie Germain is not inscribed on the base of the Eiffel Tower among the seventy-two scholars whose work made possible its construction!)

The problem of understanding electromagnetic phenomena fascinated many mathematicians, including Bernhard Riemann. Riemami's genius led him to make fundamental contributions to all the areas in which he worked. From the geometrical discoveries mentioned above to his work in electromagnetism. all he did was inspired. Sometimes he was so inspired that he left out many of the details, leaving the work of completing his proofs to his successors. In his applied work, Riemann was perfectly willing to use arguments from physics when he did not have mathematical proofs. This, too, left interesting questions for his successors to unravel. In one of his papers, he says something like "it is reasonable to believe that... " The assertion that Riemann thought was reasonable is now known as the Riemann Hypothesis, and it is still to be proved.

Near the end of the 19th century, Felix Klein showed that the new non-Euclidean geometries and the new algebraic theories were linked. One could understand the different geometries by analyzing the algebra of the transformations allowed by them. This demonstrated once again that rigor and abstraction were the keys to progress in mathematics. It also showed that this point of view allowed one to unify disparate branches of mathematics. In a discipline that was growing by leaps and bounds, it was very important to find unifying ideas that would allow people to understand wider ranges of mathematics.

The trend toward unification of mathematics was personified by Henri Poincaré. His almost superhuman memory and powers of logical apprehension enabled him to produce valuable contributions to number theory, algebra, geometry, analysis, astronomy, and mathematical physics. He wrote philosophical works on science and mathematics. Among many other things, Poincaré's work led to completely new points of view in dynamics, particularly in the dynamics of the solar system. It was in this context that Poincaré encountered the first examples of what we now call "deterministic chaos."

As the century came to an end, mathematics was becoming more and more a profession. Most mathematicians worked at universities, where they both taught and did research. Research seminars became a normal feature of university life, and the Ph.D. became the standard entry point to an academic career. The lines separating pure mathematics, applied mathematics, and theoretical physics became more distinct. Professional societies and journals were created. Congresses and meetings began to happen regularly. In 1897, the first International Congress of Mathematicians was held in Zürich. The next was in Paris in 1900, and from then on an ICM has been held every four years (with interruptions due to war), bringing together mathematicians from all over the world.

The mathematics of the 19th century is quite technical, and so are most historical studies of the period. The best sources for the overall story are [99] and [77].

Abstraction, Computers, and New Applications

The end of the 19th century was marked by an important event. In 1900, the organizers of the International Congress of Mathematicians invited David Hilbert, then the most prominent German mathematician, to give a lecture. Hilbert's address focused on the role of unsolved problems in driving mathematical research. He outlined 23 such problems that he felt would be important in the new century. For the most part, he guessed right. The investigation of these problems led, directly or indirectly, to many important advances in mathematics. The solution of even part of one of Hilbert's problems carried with it international recognition for the solver.

Even Hilbert, however, could not foresee how mathematics would grow in the 20th century. There were more and more mathematicians, more and more journals, more and more professional societies. The phenomenal growth that had begun in the 1800s continued, with mathematical knowledge doubling every twenty years or so. More original mathematics has been produced after astronauts first walked on the moon than there had been in all previous history. In fact, it is estimated that 95% of the mathematics known today has been produced since 1900. Hundreds of periodicals published all over the world devote a major share of their space to mathematics. Each year the abstracting database MathSciNet publishes many thousand synopses of recent articles containing new results. The 20th century (and this new century so far) is justifiably called the "golden age of mathematics."

Quantity alone, however, is not the key to the unique position the current era occupies in mathematical history. Beneath this astounding proliferation of knowledge, there is a fundamental trend toward unity. The basis for this unity is abstraction. This has led in two directions. On the one hand, new, more abstract subfields of mathematics have emerged to become established areas of research in their own right. On the other, researchers working on truly big classical problems, such as Fermat's Last Theorem or Hilbert's 23 problems, have become increasingly adept at using new techniques from one area of mathematics to answer old questions in another. As a result, the 20th century was a time when many old questions were finally answered and many new questions came to the fore.

The increase in the sheer amount of mathematics and in the level of abstraction has led, inevitably, to a growth in specialization. Most mathematicians today know their research areas well, the surrounding topics less well, and distant parts of the subject very little, if at all. The unifying power of the abstract point of view makes up for this somewhat, but only the very best mathematicians have a full view of the field. Given all that, we can provide no more than a brief and very incomplete description of 20th century mathematics. We have chosen to highlight the debate on the foundations of mathematics, the role of abstraction, the invention of the computer, and the wide range of new applications.

In the first few decades of the 20th century, mathematicians and philosophers investigated the foundations of the subject. What is a number? Is mathematical knowledge certain? Can we prove that it is impossible for mathematics to contradict itself? There was intense debate about these questions. On one side were the "formalists," whose program was to show that philosophical qualms about mathematical ideas could be laid to rest by a study of formal manipulation of symbols. The hope was to be able to justify working with infinite sets and other contested ideas by giving a proof, using nothing but finite methods, that such ideas would never lead to a contradiction. On the other side were the "intuitionists," who argued that many mathematical ideas were in fact not well-founded. They wanted to reform the whole subject by eliminating most appeals to infinite sets and getting rid of the "law of the excluded middle" (the Aristotelian principle that said that if one can prove that not-A is false, then A must be true).

Neither current got very far. The intuitionists' proposals were too radical for most mathematicians. The formalists' ideas were closer to being acceptable, but their program lost much of its attractiveness after the 1930s. What happened was that Kurt Gödel found a way to prove that it was impossible to find a proof that contradictions would not arise. Gödel's work established for the first time that some things could not be proved.

This had a curious effect. For mathematicians working on foundations, it was a real blow, one that had to be absorbed somehow. For other mathematicians, however, it basically meant that the work on foundations would not be able to offer them much help in solving the big problems. So they went on with the work of trying to prove theorems and solve problems.

As the foundational debate happened, the move to abstraction became the dominant theme of mathematics early in the century. It was not just that it was fashionable (though that surely was part of it). It was also that the abstract method was powerful. Using it, old problems were either disposed of or cast in a new light. Soon mathematics was dominated by abstract analysis, topology, measure theory, functional analysis, and other such areas. In essence, these were vast generalizations of material developed in the 19th century, taking an abstract point of view. The new point of view revealed which ideas were important and which were not. As a result, it often led to new discoveries.

Nowhere was the change more visible than in algebra. The subject became far more general than it had ever been before. Galois's insight that one must consider whole classes of algebraic operations in one blow had been developed further by Dedekind in the second half of the 19th century. In the 1920s, these ideas were picked up and extended by Emmy Noether and Emil Artin. In their hands, the structure and language of abstract algebra became a powerful tool.

Late in the 1930s, a group of young French mathematicians came together with the intention of revolutionizing the subject. They felt that the new ideas had not been sufficiently internalized by the mathematical community, especially in France. It was time to bring down the "old guard." Their plan was to do two things. First, they would collectively write a multivolume textbook, a compendium of all of fundamental mathematics. With a nod towards Euclid, they called their work the Elements of Mathematics. Since they were writing it collectively, they adopted a pseudonym: the author of the new Elements was "Nicolas Bourbaki."26

The members of the Bourbaki group had great fun with their collective persona. They created a biography for Nicolas Bourbaki. gave him a university affiliation, and even, at one point, sent out invitations to his daughter's wedding. When the Encyclopaedia Britannica said that Bourbaki was a collective pseudonym and that therefore no such person existed, they received an angry letter from Nicolas Bourbaki "himself" questioning the existence of the author of the encyclopedia entry! The founders of Bourbaki believed that creative mathematics is primarily a young people's sport, so they agreed to retire from the society before the age of fifty and elect younger colleagues to replace them.²⁷ Thus, Nicolas Bourbaki has become a renowned but mysterious international scholar, always at the peak of his professional productivity, supplying the scientific world with a continuing series of modern, clear, accurate expositions in all fields of contemporary mathematics.

There was a second part to the strategy of the Bourbaki group. They decided to hold a regular seminar about what was going on in mathematics; this became known as the "Séminaire Bourbaki." Now held in Paris three times a year, it is still one of the most important seminars on recent advances in the field, in which top scholars discuss important new ideas and theorems to a packed audience of mathematicians from all over the world.

Bourbaki's influence was mostly felt through the Elements. Since these took many years to write, their impact came around mid-century or later. The books take an uncompromisingly abstract point of view. Nevertheless, they give a precise and reliable account of each of the fields they cover. Many have blamed Bourbaki for having led mathematics teachers to adopt a formal and abstract approach. But the truth is that the Elements of Mathematics was never meant to be a model of mathematical pedagogy. Rather, these volumes were meant to bring together, formalize, and make precise large chunks of mathematics, and this they did (mostly) successfully.

By the last decades of the century, Bourbaki seemed to have lost some of "his" original energy. The Séminaire was (and is) still going strong, but the rate of publication of the Elements slowed to a crawl. In part this was due to the success of Bourbaki's program, but it also reflected a change in the mood of mathematicians, a move away from abstraction and towards concrete examples, computer experimentation, and applications.

The second half of the 20th century was marked by the invention and development of computers. (See Sketches 23 and 24.) At the beginning, mathematicians were deeply involved in this process. They analyzed the possibility of the new machines, invented the notion of a "computer program," helped build the first devices, and provided difficult computational problems to test them. Soon, however, computer science went its own way and focused on its own problems.

It is as tools that computers have had the greatest impact on mathematics. Computers have changed mathematics in at least three ways. First, they allowed mathematicians to test conjectures and discover new results. This allows for "experimental mathematics." Suppose one is trying to find out whether there are infinitely many primes of the form n² + 1, a problem that is still unsolved. One can test whether this is likely or not by using a computer to plug in several million values of n and testing the resulting number for primality. If we find many primes, we may be persuaded that in fact there will be infinitely many of them. Notice that this doesn't decide the issue. The hard work of finding a proof remains to be done. But it can offer clues and it can make us more or less confident that what we arc trying to prove is indeed true.

The second change has to do with simulation and visualization. Computers can make pictures of data, pictures that are often far more illuminating than the numerical data by itself. Furthermore, they allow us to use numerical computation to find approximate solutions to equations. Thus we can use them to understand situations whose precise description is too complicated for complete mathematical analysis. This has, of course, revolutionized applied mathematics. Nowadays, approximate solutions to complicated differential equations are a central part of that endeavor. But it has also impacted pure mathematics. A good example of this effect is the discovery of fractals. These highly complex structures had been considered before, early in the 20th century, but at that point they just seemed horrendously complicated and impossible to deal with. Once we learned to use computers to draw their pictures, however, we discovered that fractals can be beautiful, and a whole new field of mathematics was born.

The third change is related to what are known as computer algebra systems. These are computer programs that can "do algebra." They can work with polynomials, trigonometric functions, exponentials, and lots more. They can add, multiply, factor, take derivatives and integrals, and compute series approximations. In other words, they can do much of what used to be the computational content of school and college mathematics. As these systems become more widely available, there is less and less reason to teach students to do elaborate computations by hand. As a result, mathematicians need to rethink what should be taught and how.

The 20th century also saw a great widening in the range of applications of mathematics. In the late 19th century, "applied mathematics" was almost synonymous with "mathematical physics." This quickly changed. Probably the first change was the development of statistics, initially with a view to applications in biology. The value of statistics as a tool for analyzing data was soon evident to scholars everywhere, and other applications quickly followed. (See Sketch 22 for the early history of statistics.)

More and more mathematical ideas were found to be useful. Mathematical physics began to use probability and statistics, Riemannian geometry, Hilbert spaces, and group theory. Chemists discovered that crystallography had a large mathematical component. Topological ideas proved relevant to the study of the shape of molecules. Biologists used differential equations to model the spread of disease and the growth of animal populations.

Beginning in World War I, governments discovered that thinking mathematically about practical problems led to useful results, and "operations research" was born. In World War II, mathematicians had a crucial role in many ways, most famously in developing the science of cryptography and breaking the German Enigma code. Telephone networks and, later, the Internet were studied mathematically. "Linear programming" was developed to deal with finding the "best way" to do things in all sorts of areas, from industry to government to the military. Computer modeling allowed all sorts of new applications to biology, from the dynamics of populations to studies of blood circulation, neurons, and how animals move. Finally, towards the end of the century, mathematics and physics got together again to produce new and sophisticated physical theories.

Perhaps the most interesting account of the transformation of mathematics after the late 19th century is [78], which sees it in the context of "modernism" in the arts. Another way to get a feel for the early twentieth century is to read about the solvers of the Hilbert problems in [180]. For more recent work, see also [4], [3] and [5], which contain interesting profiles of living mathematicians.

Mathematics Today

The last few decades have continued to be a "golden age" for mathematics. Many old problems have been solved and many new ideas have been introduced. Both pure and the applied mathematics have been strikingly successful. In this concluding section we mention a few of these new discoveries.

At the dawn of the 20th century, Hilbert presented a list of problems he deemed important. Those problems were an important motivation for mathematicians in the first half of that century. As the 21st century began, the Clay Mathematics Institute decided to follow his lead. They chose seven mathematical problems and offered a one million dollar prize for the solution of each of them. The seven "millennium problems" cover the full spectrum from the purest of pure mathematics to mathematical issues related to fluid flow, particle physics, and the theory of computation.

One of the millennium problems went back all the way to Poincaré's work in the late 19th century. It concerned the geometry of three-dimensional space. In the 20th century, it was generalized to higher dimensions, and it turned out to be easier to solve in that case. In dimensions five and higher, the conjecture was proved by Stephen Smale in the 1960s. In dimension four, it was proved by Donald Sullivan in the 1980s. But the original three-dimensional problem remained unassailable until 2002, when Grigory Perelman found a proof. Remarkably, he refused to accept the million dollar prize!

One interesting development has to do with an old conjecture due to Kepler concerning how to place the largest number of spheres into the smallest possible space. Imagine you have a bunch of equal-size marbles; what arrangement of the marbles will pack them most tightly? Kepler came up with a guess, but no one was able to prove it until 1998... maybe! Thomas Hales gave a proof, but his proof requires a very large number of cases to be checked by computer. He sent it to the Annals of Mathematics, which asked 12 experts to check the proof. They ended up deciding, in 2003. that they were "99% sure" that it was correct, but that they could not be certain because they had no way to check the computer part. Is 99% certainty enough?

Number theory was another growth area. As we explain in Sketch 13, Fermat's Last Theorem was proved in 1994. But there have been many other impressive results. In 2004, Ben Green and Terry Tao proved that one can find arbitrarily long arithmetic progressions made up entirely of prime numbers, such as 3 + 4k with k = 0, 1, 2. The longest one known starts with the number 43,142,746,595,714,191 and contains 25 other primes, each 5,283,234,035,979,900 more than the previous. A related problem also saw a huge advance: mathematicians have long suspected that there are infinitely many prime numbers that are two units apart, such as 11 and 13 or 29 and 31, but no one knows how to prove that. But in 2013, Yitang Zhang surprised the world by proving that if we allow a bigger fixed gap instead of two, then there are infinitely many such primes. With the work of many others, we now know that there are infinitely many pairs of primes with a gap no larger than 246.

Number theory is often thought of as the purest of pure mathematics, but in the 1970s we learned otherwise. You may have noticed that multiplying is easier than factoring: if someone asks you to compute 463 times 2029, you can do it easily, but if they hand you 939, 427 and ask you to factor it, that's much harder. In the 1970s, Ron Rivest, Adi Shamir, and Leonard Adleman figured out a way to use this to construct a way of sending secret messages without having to meet the other person to exchange a secret key. We all use this idea today: it is what allows us to encrypt information sent over the Internet. The neat thing for mathematics, however, is that suddenly a better way to factor numbers becomes a powerful tool! A lot of effort has gone into that. Some good methods have been found, but none that is good enough to break the new encryption method.

Some of the most exciting developments are those connected to other fields. In mathematical physics, String Theory has brought to light new and deep mathematical questions. Mathematical and computational biology is beginning to offer up significant insights. Probabilistic methods now pervade mathematical modeling and engineers have been using more and more powerful mathematical techniques. The invention of wavelets has had a deep effect on the processing of signals and images.

We see even more diversity if we broaden our view to include those users and producers of mathematics that are outside of the usual academic institutions. Many of the most interesting and potentially useful issues confronting mathematics today are "crossover questions" involving connections between mathematics and science. In the world of finance, mathematics has become so important that some people have looked for mathematical causes underlying the financial crisis of 2008. Technological advances in many areas of business and commerce are increasingly dependent on more sophisticated mathematical ideas. Mathematics lies at or near the heart of innovations in many of today's multimillion-dollar industries. Aircraft design, genetic research, missile defense systems, CD players, epidemic control, GPS satellites and space stations, cellular phone networks, marketing and political surveys, personal computers and calculators, "morphing" and other special visual effects used in movies and video games, computer animation, and the electronic hardware and software tools that handle the everyday affairs of almost every business of any size — all of these things and many, many others depend on mathematical ideas and require mathematical experts to implement.

Mathematics today involves a huge number of people doing many different things. At universities and research institutes, high-powered research continues to push at the boundaries of our knowledge. Outside academia, many people use and develop mathematical techniques every day. While many of these people don't describe themselves as "mathematicians," their activities help push mathematics and its applications forward. And all of these people are supported by a vast network of teachers and educators at all levels.

So much work in so many different areas gives the impression of fragmentation, but mathematics today, as seen "from the inside," is both more diverse and more unified than it has ever been. It is more abstract and yet has a broader applicability to all areas of modern life than ever before. It is true that research mathematicians are usually specialists in one area or another, and their research almost always lies far beyond the reach of interested amateurs, even those with college degrees in mathematics. Any new theorem in today's research journals is likely to be incomprehensible to most mathematicians whose specialty does not include its topic. But despite the diversity, there is underlying unity. Mathematics has always been about big ideas, and these are still at the center of the held, though they may not be apparent at first look.

The view "from the outside" is understandably a bit confusing. On the one hand, mathematics is seen as an esoteric, daunting subject about which even many well-educated people unblushingly admit ignorance. On the other hand, it is seen as an essential part of modern prosperity, security, and comfort, so that the mathematically adept are pursued as valuable human resources. Governments keep trying to get more people to learn mathematics, but the subject remains difficult and inaccessible to far too many students.

This ambivalence has created a dilemma for mathematical educators. Do they allow the internal demands of the subject to dictate ever more rigorous training in the traditional areas of algebra, geometry, calculus, and the like, so that the next generation of experts will have a firm foundation for their research? Or do they let the external needs of society dictate a broader, less intensive education in mathematical ideas that will allow everyone to become mathematically literate citizens who can interact intelligently with the experts? This apparent conflict of goals has created tension and turmoil in mathematics education today, but the hopeful view is that it is creative, constructive turmoil as educators find ways to achieve both. It is critically important that they do so; tomorrow's world will not accept less.

---

1 Good sources of information are [80], [103], [27], [136], [88], [140], and [151].

² Good references for this are [8] and [65]. The second includes many ideas for how to use some of this material in the classroom.

³ For a theory about how this happened, see [155].

⁴ This text is a lightly modernized form of a translation given in [92], page 30.

⁵ There is some doubt as to how thoroughly the decree was actually carried out.

⁶ It is known as "Gaussian elimination" or "row reduction."

⁷ For example, see the proceedings of a conference on "2000 Years of Transmission of Mathematical Ideas" in [47].

⁸ Reviel Netz estimates that the total number of mathematicians during the whole thousand-year period of Greek mathematics was no more than 1,000. Of those, maybe 300 were known by name late in the Greek period; about 150 are mentioned in the surviving texts. See [133, chapter 7].

⁹ Of course, in everyday life lengths were computed and measured in Greece as they were everywhere else. In the Greek tradition there was a real gap between theoretical mathematics and everyday use of mathematical ideas.

¹⁰ Well, they actually used the Greek words alogos and arrhetos, which could also mean "unspeakable" or "inexpressible." But "irrational," meaning "without ratio," is the word that prevailed historically.

¹¹ Hypatia is not the only woman to have been an active mathematician in Greek times. At least one other is known: Pandrosian. a teacher of mathematics to whom the third book of Pappus's Collection is addressed.

¹² From [99]; the translation is by H. T. Colebrooke.

¹³ We give these in modern algebraic form. This is not how they were expressed at the time! See Sketch 8.

¹⁴ Squares were "properties" because they were areas.

¹⁵ A few scholars argue that al-Khāyammī the poet and al-Khāyammī the philosopher/mathematician were actually two different people, but this is a minority position.

¹⁶ The table in [99, p. 291] gives a good overview of this translation enterprise.

¹⁷ Leonardo is often referred to as "Fibonacci." a reference to his father's name. There is no evidence, however, that Leonardo ever used this name for himself.

¹⁸ English spelling was not standardized at that time, so cossic also appears as "cossick" or "cossike" in various places.

¹⁹ Though this mathematician's real name was Niccolò Fontana, everyone knows him by his nickname, Tartaglia, which means ''stammerer.''

²⁰ He was wrong about this, but inventing a Greek origin for algebra was useful at a time when classical learning was greatly valued.

²¹ Marin Mersenne was a Franciscan friar, an important music theorist, and a competent amateur mathematician.

²² Not to be confused with "Jesuit." The Jesuati were a congregation within the Catholic Church from 1366 to 1668.

²³ Those of us who teach calculus today may be forgiven for feeling that Leibniz did the job a bit too well!

²⁴ Is it really reasonable, for example, to think of human decision-making as analogous to drawing a colored ball from an urn?

²⁵ There never was a second.

²⁶ It has been suggested that the name "Bourbaki" was inspired by a statue in Nancy, France, of General Charles D. S. Bourbaki from the Franco-Prussian War. The motivation for "Nicolas" is unclear, but its choice makes the resulting initials, N. B., an attractive bonus.

²⁷ it is rumored that some of the original founders regretted having made this rule when it came time for them to leave.