| 10 | A Square and Things Quadratic Equations |
The word "algebra" comes from a title of a book written in Arabic around the year 825. The author, Muhammad ibn Mūsa al-Khwārizmī, was probably born in what is now Uzbekistan. He lived, however, in Baghdad, which was then the world's most vibrant cultural center. Al-Khwārizmī was an able synthesizer. Starting from the practical tradition and from Indian scholarship, he wrote books on geography, astronomy, and mathematics. But his book on algebra is one of his most famous.
al-Khwārizmī's book starts out with a discussion of quadratic equations. In fact, he considers a specific problem:
One square, and ten roots of the same, are equal to thirty-nine dirhems. That is to say, what must be the square which, when increased by ten of its own roots, amounts to thirty-nine?
If we call the unknown x, we might call the "square" x2. Now, a "root of this square" is x, so "ten roots of the square" is 10x. Using this notation, the problem translates into solving the equation
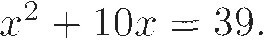
But algebraic symbolism had not been invented yet, so all al-Khwārizmī could do was to say it in words. In the time-honored tradition of algebra teachers everywhere, he follows the problem with a kind of recipe for its solution, again spelled out in words:
The solution is this: you halve the number of the roots, which in the present instance yields five. This you multiply by itself; the product is twenty-five. Add this to thirty-nine; the sum is sixty-four. Now take the root of this, which is eight, and subtract from it half the number of the roots, which is five; the remainder is three. This is the root of the square which you sought for; the square itself is nine.1
Here's the computation in our symbols:

It's not hard to see that this is basically just the quadratic formula as we now know it. To solve x2 + bx = c, al-Khwārizmī uses the rule

The biggest difference between this and the modern formula is that we would consider both the positive and the negative square roots. But taking the negative square root would give a negative value for x. Mathematicians at the time didn't yet believe in negative numbers; the positive root was the only one they cared about. We also put the "–b" part at the beginning. But that would again mean a negative number, so he prefers to put it at the end, as a subtraction. (See Sketch 5.) Finally, he states the equation with the c on the right-hand side, while we would write it as x2 + bx – c = 0.
If we put the "–b" in front, add ± to the root, remember to take into account the sign of his c, and do a little algebra, his formula becomes ours:
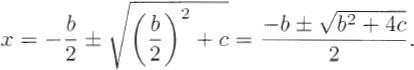
(The coefficient a is missing from this formula because al-Khwārizmī was considering a single square; that is, a = 1.)
But he didn't leave it at that. He felt he should explain why his method worked. Rather than doing this algebraically, as we might today, he did it with a geometric argument. It went like this:
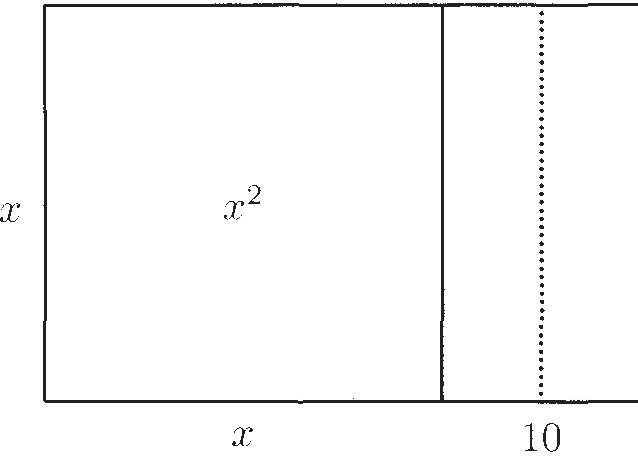
First, we have "a square and ten roots." To picture this, draw a square whose side we don't yet know. If we call the side x, the area of the square is x2. To get 10x, we draw a rectangle with one side equal to x and one side equal to 10, as in Display 1.
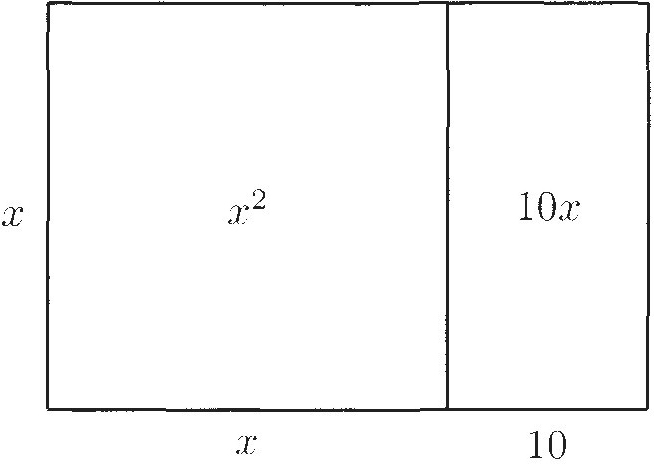
Display 1
The equation tells us that the area of the whole figure is 39. To solve the equation, that is, to determine x. we first cut the number of roots in half. Geometrically, that means we split the rectangle into two halves, each with area 5x, as in Display 2.
Display 2
Now we move one of the half-rectangles to the bottom of the square, making the figure in Display 3. The total area is still 39. But notice that adding in the little square missing in the lower right will make a big square. Since the two rectangles have side 5, the area of the little square must be 25, as shown in Display 4.
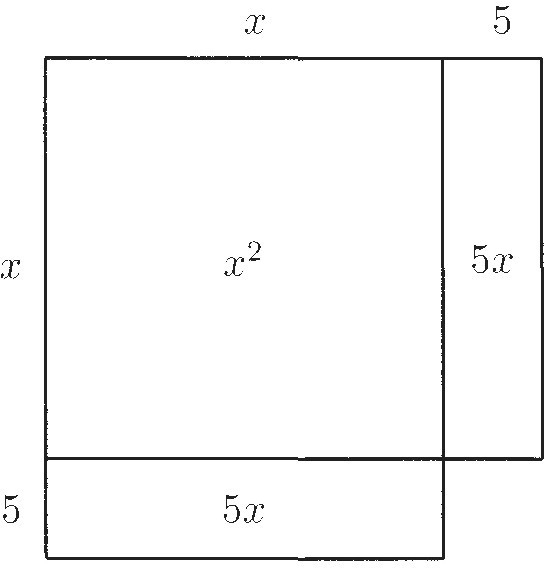
Display 3

Display 4
When we complete the square by adding in the little square, our figure becomes a square whose area is 39 + 25 = 64. But this means that its side is equal to the square root of 64, which is 8. And since the side of the big square is x + 5, we can conclude that x + 5 = 8. So we subtract 5 and get x = 3.
Each step in al-Khwārizmī's rule corresponds to a step in the geometric version. And the geometric version shows us exactly what is going on and why it works! As noted before, this version of the quadratic formula assumes that the leading coefficient is 1. Today, we write the general quadratic equation as ax2 + bx + c = 0, allowing for a different leading coefficient. al-Khwārizmī would have dealt with this simply by dividing through by a and applying his rule.
After al-Khwārizmī's time many other mathematicians wrote about quadratic equations. Their methods and their geometric justifications became more and more sophisticated. But the basic idea never changed. In fact, even the example stayed the same. From the 9th century to the 16th century, books on algebra almost always started their discussion of quadratic equations by considering "a square and ten roots are equal to 39."
Early in the 17th century, mathematicians came up with the idea of using letters to represent numbers. (See Sketch 8.) Descartes suggested the convention we still use: letters from the end of the alphabet would denote unknown numbers, and letters from the beginning of the alphabet would stand for known numbers. Also, by that time resistance to the idea of negative numbers was beginning to fade. (See Sketch 5.) Thomas Harriot and René Descartes noticed that it's much easier to write all equations as something = 0, which we can do as long as we allow some of the coefficients to be negative. The main advantage is that ax2 + bx = c, ax2 + c = bx, and ax2 = bx + c could then be seen as special cases of the general equation

This reduced al-Khwārizmī's three different cases to just one. Moreover, while negative solutions were still regarded with suspicion, it was at least possible to consider them. This meant that there were two square roots to account for, so the general solution could be written as
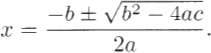
That's what we still do today.
For a Closer Look: There is a lot of information on the history of algebra in both [99] and [77]. Al-Khwārizrnī's text can be found in many sourcebooks, including [59]. For the complete text, see [2], which can easily be found online. On the history of algebra, see [160] for a short account of the story up to the Renaissance and [101] for the full picture.