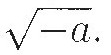| 5 |
Less Than Nothing? Negative Numbers |
Did you know that negative numbers were not generally accepted, even by mathematicians, until a few hundred years ago? It's true. Columbus discovered America more than two centuries before negatives joined the society of numbers. They didn't become first-class citizens until the middle of the 19th century, about the time of the American Civil War.
Numbers arose from counting and measuring things: 5 goats, 37 sheep, 100 coins, 15 inches, 25 square meters, etc. Fractions were just a refined form of counting, using smaller units: 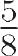 in. is five eighths of an inch,
in. is five eighths of an inch, 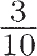 mi. is three tenths of a mile, and so on. And if you're counting or measuring, the smallest possible quantity must be zero, right? After all, how can any quantity be less than nothing? Thus, it is not too surprising that the idea of a negative number — a number less than zero — was a difficult concept.
mi. is three tenths of a mile, and so on. And if you're counting or measuring, the smallest possible quantity must be zero, right? After all, how can any quantity be less than nothing? Thus, it is not too surprising that the idea of a negative number — a number less than zero — was a difficult concept.
"So," you may ask, "where did this strange idea come from? How did anyone think of such numbers?'' The usual answer is that negative numbers first appeared on the mathematical scene when people began to solve problems such as:
"I am 7 years old and my sister is 2. When will I be exactly twice as old as my sister?"
This translates into solving the equation 7 + x = 2(2 + x). where x is the number of years from now that this will happen. As you can see, in this case the answer is 3 (years from now). But the same kind of question can be asked for any ages. That is, we can as easily ask for the solution of 18 + x = 2(11 + x). In this case, however, the solution is negative: x = –4. And this answer even makes sense: if I am now 18 and my sister is 11, I was twice as old as she was four years ago.
In fact, however, negative numbers did not first appear in that context. They appeared as coefficients long before they appeared as answers. For a long time negative answers were just regarded as nonsensical. Later, they were seen as a signal that the question was wrongly posed. In our example, the negative solution would have been understood as revealing that I asked the wrong question; it should have been "how long ago?" (a positive number of years), not "when?".
The scribes of Egypt and Mesopotamia could solve such equations more than three thousand years ago, but they never considered the possibility of negative solutions. Chinese mathematicians, on the other hand, had a method of solution based on manipulating the coefficients of the equations, and they seem to have been able to handle negative numbers as intermediate steps in that process.

Our mathematics, like much of our Western culture, is rooted mainly in the work of ancient Greek scholars. Despite the depth and subtlety of their mathematics and philosophy, the Greeks ignored negative numbers completely. Most Greek mathematicians thought of "numbers" as being positive whole numbers and thought of line segments, areas, and volumes as different kinds of magnitudes (and therefore not numbers). Even Diophantus, who wrote a whole book about solving equations, never considered anything but positive rational numbers. For example, Problem 2 in Book V of his Arithmetica leads him to the equation1 4x + 20 = 4. "This is absurd," he says, "because 4 is smaller than 20." To Diophantus, 4x + 20 meant adding something to 20, and hence could never be equal to 4. On the other hand, Diophantus did know that when we expand (x – 2)(x – 6), "minus times minus makes plus." In other words, he understood how to work with negative coefficients.
A prominent Indian mathematician, Brahmagupta, recognized and worked with negative quantities to some extent as early as the 7th century. He treated positive numbers as possessions and negative numbers as debts, and also stated rules for adding, subtracting, multiplying, and dividing with negative numbers. Later Indian mathematicians continued in this tradition, explaining how to use and operate with negative as well as positive numbers. Nevertheless, they regarded negative quantities with suspicion for a very long time. Five centuries later, Bhāskara II, considered this problem:
A fifth part of a troop of monkeys, minus three, squared, has gone to a cave; one is seen [having] climbed to the branch of a tree. Tell [me], how many are they?2
The equation is  and Bhāskara correctly finds the roots, 50 and 5, But then he says "In this case, the second [answer] is not to be taken due to its inapplicability. For people have no confidence [or "comprehension of"] in a manifest [quantity] becoming negative." The problem is that if x = 5, then
and Bhāskara correctly finds the roots, 50 and 5, But then he says "In this case, the second [answer] is not to be taken due to its inapplicability. For people have no confidence [or "comprehension of"] in a manifest [quantity] becoming negative." The problem is that if x = 5, then  and Bhāskara is nervous about talk of (–2)2 monkeys even though (–2)2 is positive.
and Bhāskara is nervous about talk of (–2)2 monkeys even though (–2)2 is positive.
Early European understanding of negative numbers was not directly influenced by this work. Indian mathematics first came to Europe through the Arabic mathematical tradition. Two books written by Muhammad ibn Mūsa al-Khwārizmī in the 9th-century were especially influential. However, the Arab mathematicians did not use negative numbers. Perhaps this is in part because algebraic symbolism as we know it today did not exist in those times. (See Sketch 8.) Problems that we solve with algebraic equations were solved completely in words, often with geometric interpretations of all the numerical data as line segments or areas. Al-Khwārizrmī, for example, recognized that a quadratic equation can have two roots, but only when both of them are positive. This may have resulted from the fact that his approach to solving such equations depended on interpreting them in terms of areas and side lengths of rectangles, a context in which negative quantities made no sense. (See Sketch 10.)
One thing that the Arabs (and also Diophantus) did understand was how to expand products of the form
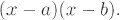
They knew that in this situation negative times negative is positive, and negative times positive is negative. But they expected the answers to any problem to be positive. So, while these "laws of signs" were known, they weren't understood as rules about how to operate with independent things called "negative numbers."
Thus, European mathematicians learned from their predecessors a kind of mathematics that dealt only with positive numbers. Except for the hint about multiplication of negative numbers offered by the distributive law, they were left to deal with negative quantities on their own, and they proceeded much more slowly than their counterparts in India and China.
European mathematics made tremendous leaps after the Renaissance, motivated by astronomy, navigation, physical science, warfare, commerce, and other applications. In spite of that progress, and perhaps because of its utilitarian focus, there was continued resistance to negative numbers. In the 16th century, even such prominent mathematicians as Cardano in Italy, Viète in France, and Stifel in Germany rejected negative numbers, regarding them as "fictitious" or "absurd." When negatives appeared as solutions to equations, they were called "fictitious solutions" or "false roots.'' But by the early 17th century, the tide was beginning to turn. As the usefulness of negative numbers became too obvious to ignore, some European mathematicians began to use negative numbers in their work.
Nevertheless, misunderstanding and skepticism about negative quantities persisted. As methods for solving equations became more sophisticated and algorithmic in the 16th and 17th centuries, a further complication added to the confusion. If negatives are accepted as numbers, then the rules for solving equations can lead directly to square roots of negatives. For instance, the quadratic formula applied to the equation x2 + 2 = 2x yields the solutions  and
and 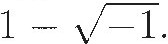 (It was even worse with the formula for cubic equations; see Sketch 11.) But, if negative numbers make sense at all, then the necessary rules of their arithmetic require that squares of negatives be positive. Since squares of positive numbers must also be positive, this means that
(It was even worse with the formula for cubic equations; see Sketch 11.) But, if negative numbers make sense at all, then the necessary rules of their arithmetic require that squares of negatives be positive. Since squares of positive numbers must also be positive, this means that  a number whose square is – 1, can be neither positive nor negative!
a number whose square is – 1, can be neither positive nor negative!
Faced with this apparent absurdity, it was tempting for mathematicians to regard negative numbers as suspicious characters in the world of arithmetic. Early in the 17th century, Descartes called negative solutions (roots) "false" and solutions involving square roots of negatives "imaginary." In Descartes's words, the equation x4 = 1, for example, has one true root (+1), one false root (–1), and two imaginary roots 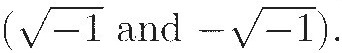 (See Sketch 17 for the story of imaginary and complex numbers.) Moreover, Descartes's use of coordinates for the plane did not use negative numbers in the way that the familiar Cartesian coordinate system (named for him) does now. His constructions and calculations were concerned primarily with positive numbers, particularly with lengths of line segments; the idea of a negative x- or y-axis simply doesn't appear. (See Sketch 16 for more about this.)
(See Sketch 17 for the story of imaginary and complex numbers.) Moreover, Descartes's use of coordinates for the plane did not use negative numbers in the way that the familiar Cartesian coordinate system (named for him) does now. His constructions and calculations were concerned primarily with positive numbers, particularly with lengths of line segments; the idea of a negative x- or y-axis simply doesn't appear. (See Sketch 16 for more about this.)
In fact, even those 17th century mathematicians who accepted negative numbers were unsure of where to put them in relation to the positive numbers. Antoine Arnauld argued that, if –1 is less than 1, then the proportion – 1 : 1 = 1 : – 1, which says that a smaller number is to a larger as the larger number is to the smaller, is absurd. John Wallis claimed that negative numbers were larger than infinity. In his Arithmetica Infinitorum of 1655, he argued that a ratio such as 3/0 is infinite, so when the denominator is changed to a negative (–1, say), the result must be even larger, implying in this case that 3/ – 1, which is –3, must be greater than infinity.
None of these mathematicians had any difficulty with how to operate with negative numbers. They could add, subtract, multiply, and divide with them without problems. Their difficulties were with the concept itself.
Isaac Newton, in his 1707 algebra textbook Universal Arithrnetick, didn't help. He said that "Quantities are either Affirmative, or greater than nothing, or Negative, or less than nothing."3 Because it carried the authority of the great Sir Isaac, this definition was taken very seriously indeed. But how could any quantity be less than nothing?
Despite all this, by the middle of the 18th century, negatives had become accepted as numbers, more or less, in an uneasy alliance with the familiar whole numbers and positive rationals, the much-investigated irrationals, and the highly irregular complex numbers. Even so, many reputable scholars still had misgivings about them. Around the time of the American and French Revolutions, the famous French Encyclopédie ou Dictionnaire Raisonné des Sciences, des Arts, et des Métiers (from which the "Encyclopedists" get their name) said, somewhat grudgingly,

. . . the algebraic rules of operation with negative numbers are generally admitted by everyone and acknowledged as exact, whatever idea we may have about these quantities.4
Leonhard Euler seemed comfortable with negative quantities. In his Elements of Algebra, published in 1770, he says:
Since negative numbers may be considered as debts, because positive numbers represent real possessions, we may say that negative numbers are less than nothing. Thus, when a man has nothing of his own, and owes 50 crowns, it is certain that he has 50 crowns less than nothing; for if any one were to make him a present of 50 crowns to pay his debts, he would still be only at the point nothing, though really richer than before.5
On the other hand, when he has to explain why the product of two negative numbers is positive, he drops the interpretation of negative numbers as debts and argues in a formal way, saying that –a times –b should be the opposite of a times –b.
Nevertheless, half a century later there were still doubters, even in the highest ranks of the mathematical community, particularly in England. In 1831, at the dawning of the age of steam locomotives, the great British logician Augustus De Morgan wrote:
The imaginary expression  and the negative expression –b have this resemblance, that either of them occurring as the solution of a problem indicates some inconsistency or absurdity. As far as real meaning is concerned, both are equally imaginary, since 0 – a is as inconceivable as
and the negative expression –b have this resemblance, that either of them occurring as the solution of a problem indicates some inconsistency or absurdity. As far as real meaning is concerned, both are equally imaginary, since 0 – a is as inconceivable as 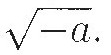 6
6

This represents the last gasp of a fading tradition in the face of the emergence of a much more abstract approach to algebra and the structure of the number system. With the work of Gauss, Galois, Abel, and others in the early 19th century, the study of algebraic equations evolved into a study of algebraic systems — that is, systems with arithmetic-like operations. In this more abstract setting, the "real" meaning of numbers became less important than their operational relationships to each other. In such a setting, negative numbers numbers that were the additive opposites of their positive counterparts — became critically important components of the number system, and doubts about their legitimacy simply disappeared.
Ironically, this move to abstraction paved the way for a true acceptance of the usefulness of negative numbers in a variety of real-world settings. In fact, negative numbers are routinely taught as a fundamental part of elementary school arithmetic. We take them so much for granted that it is sometimes difficult to understand students' struggles with what they are and how to manipulate them. Perhaps a little sympathy is in order; some of the best mathematicians in history shared those same struggles and frustrations.
For a Closer Look: Most full-length histories of mathematics include a discussion of the history of negative numbers. For a book-length discussion of the debate about negative numbers in England between the 16th and 18th centuries, see [145].
1 This wasn't how he wrote it, of course; see Sketch 8.
2 From Bhāskara's Bījagaṇita; translation by Kim Plofker in [98, p. 476].
3 From the 1728 English translation, quoted in [145], p. 192; for the Latin original see [178], volume V. p. 58.
4 Jean le Rond d'Alembert, article on "Negative Numbers," quoted in [108], p. 597
3 [51], pp. 4-5.
6 Quoted in [108], p. 593, from De Morgan's book, On the Study and Difficulties of Mathematics.
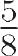 in. is five eighths of an inch,
in. is five eighths of an inch, 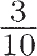 mi. is three tenths of a mile, and so on. And if you're counting or measuring, the smallest possible quantity must be zero, right? After all, how can any quantity be less than nothing? Thus, it is not too surprising that the idea of a negative number — a number less than zero — was a difficult concept.
mi. is three tenths of a mile, and so on. And if you're counting or measuring, the smallest possible quantity must be zero, right? After all, how can any quantity be less than nothing? Thus, it is not too surprising that the idea of a negative number — a number less than zero — was a difficult concept.
 and Bhāskara correctly finds the roots, 50 and 5, But then he says "In this case, the second [answer] is not to be taken due to its inapplicability. For people have no confidence [or "comprehension of"] in a manifest [quantity] becoming negative." The problem is that if x = 5, then
and Bhāskara correctly finds the roots, 50 and 5, But then he says "In this case, the second [answer] is not to be taken due to its inapplicability. For people have no confidence [or "comprehension of"] in a manifest [quantity] becoming negative." The problem is that if x = 5, then  and Bhāskara is nervous about talk of (–2)2 monkeys even though (–2)2 is positive.
and Bhāskara is nervous about talk of (–2)2 monkeys even though (–2)2 is positive.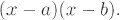

 and
and 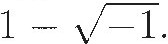 (It was even worse with the formula for cubic equations; see
(It was even worse with the formula for cubic equations; see  a number whose square is – 1, can be neither positive nor negative!
a number whose square is – 1, can be neither positive nor negative!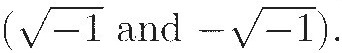 (See
(See 
 and the negative expression –b have this resemblance, that either of them occurring as the solution of a problem indicates some inconsistency or absurdity. As far as real meaning is concerned, both are equally imaginary, since 0 – a is as inconceivable as
and the negative expression –b have this resemblance, that either of them occurring as the solution of a problem indicates some inconsistency or absurdity. As far as real meaning is concerned, both are equally imaginary, since 0 – a is as inconceivable as