25	Beyond Counting Infinity and the Theory of Sets

T he idea of infinity as an unending process has been a useful mathematical tool for many, many centuries. It is the underlying idea of a limit, the foundational concept for calculus. However, dealing with infinite collections of objects is a relatively new mathematical activity. Only two centuries ago, the great European mathematician Carl Friedrich Gauss said:

... I protest above all against the use of an infinite quantity as a completed one, which in mathematics is never allowed. The Infinite is only a manner of speaking... ¹

Gauss"s comments reflected a common understanding going all the way back to Aristotle. But consider this: We recognize a counting number² when we see it, whether it be 5 or 300 or 78,546,291, and we know there is no largest such number because we can always add 1 to any one we have. Now, if we can distinguish the counting numbers from other types of numbers, such as 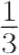or – 17 or doesn't it make sense to consider the collection of all counting numbers as a distinct mathematical object? Georg Cantor thought so.

As the American Civil War ended, Georg Cantor was completing his doctorate under the guidance of German mathematician Karl Weierstrass at the University of Berlin. At this time, European mathematicians were in the final stages of tightening up the logical underpinnings of calculus, a process that had been going on for almost 200 years. As they were doing this, they had come to a much deeper understanding of the real numbers, the numbers that can be used to label all the points on a coordinate axis. The real numbers can be separated into two distinct types — the rational numbers, which can be expressed as ratios of two integers, and the irrational numbers, which cannot. Mathematicians knew that each type was "dense" in the other. That is, they knew that between any two rational points on the number line there are infinitely many irrational points and between any two irrational points there are infinitely many rational points. This had led to a general feeling that the real numbers were evenly divided between rationals and irrationals, more or less.

However, investigations of certain families of functions were beginning to cast doubts on this feeling. Some kinds of functions behaved very differently on these two types of numbers. As Cantor probed these differences, he began to see the importance of considering these various types of numbers as distinct mathematical entities, or "sets." Cantor's concept of set was extremely general — and vague:

By a set we are to understand any collection into a whole of definite and separate objects of our intuition or our thought.3

This means that infinite collections of numbers (and other things) can be considered as distinct mathematical objects, to be compared and manipulated just like finite sets. In particular, it makes sense to ask whether or not two infinite sets are "the same size"; that is, whether or not they can be matched in one-to-one correspondence. These elementary ideas rapidly led Cantor to some of the most revolutionary results in the history of mathematical thought. Here are a few of them:

•Not all infinite sets are the same size! (That is, there are infinite sets that cannot be put into one-to-one correspondence with each other.)

•The set of irrational numbers is larger than the set of rational numbers.

•The set of counting numbers is the same size as the set of rational numbers.

•The set of all subsets of a set is larger than the set itself.

•The set of points within any interval of the number line, no matter how short, is the same size as the set of all points everywhere on the number line!

•The set of all points in a plane, or in 3-dimensional space, or in n-dimensional space, for any natural number n is the same size as the set of points on a single line!

The abstract simplicity of Cantor's starting point made his set theory applicable throughout mathematics. This made it very difficult to ignore his astounding conclusions, which seemed to defy most mathematicians' common-sense understanding of their subject.

His work was well received in many parts of the mathematical community, but acceptance was by no means universal. Cantor's set-theoretic treatment of infinity generated heated opposition from some of his foremost contemporaries, notably Leopold Kronecker, a prominent professor at the University of Berlin. Kronecker based his approach to mathematics on the premise that a mathematical object does not exist unless it is actually constructible in a finite number of steps. From this point of view, infinite sets do not exist because it is clearly impossible to construct infinitely many elements in a finite number of steps. The natural numbers are "infinite'' only in the sense that the finite collection of natural numbers constructed to date may be extended as far as we please; "the set of all natural numbers" is not a legitimate mathematical concept. To Kronecker and those who shared his views, Cantor's work was a dangerous mixture of heresy and alchemy.

To understand what kind of thing Kronecker was worried about, consider the set of all even numbers that can be written as the sum of two odd primes. What numbers are in this set? Well, for any specific even number bigger than four, it's easy (if sometimes tedious) to decide whether or not this number is in the set. For example, 22434 is in the set because 22434 = 12503 + 9931. Is it true that every even number from six on is in the set? We don't know. (That every even number greater than 4 is indeed in this set is a famous conjecture4 which no one — so far — has been able to prove.) But if we can't say what elements belong to our set, how can we talk of our set as a completed whole? Isn't there a danger that such talk would lead us into contradictions?

Kronecker's fears for the safety of mathematical consistency seemed to be justified by the appearance of several paradoxes in set theory. The most famous of these paradoxes was proposed by Bertrand Russell in 1902. Its set-theoretic formulation need not concern us here;⁵ you can get the idea from one of its many popularized versions. Russell himself gave one in 1919:

A barber in a certain village claims that he shaves all those villagers and only those villagers who do not shave themselves. If his claim is true, does the barber shave himself?

In slightly more formal terms, is the clean-shaven barber, himself a villager, a member of the set of all villagers who do not shave themselves, or is he not? If he is, then he does not shave himself, but since he shaves all who do not shave themselves, that means he must shave himself, so he isn't in the set, after all. If he isn't in the set, then he does shave himself, but he only shaves those who don't shave themselves, so he must not shave himself, so he is in the set! There seems to be no way out of this logical loop of contradictions. Dilemmas such as this forced mathematicians of the late 19th and early 20th centuries to undertake a thorough reworking of Cantor's theory of sets in an attempt to free it from the dangers of self-contradiction.

Despite this initial discomfort, Cantor's work has affected mathematics in a decidedly positive way. His basic set theory has provided a simple, unifying approach to many different areas of mathematics, including probability, geometry, and algebra. Moreover, the strange paradoxes encountered in some early extensions of his work encouraged mathematicians to put their logical house in order. Their careful examination of the logical foundations of mathematics has led to many new results and paved the way for even more abstract unifying ideas.

Because much of the opposition to infinite sets was based on philosophical assumptions, Cantor went beyond the usual borders of mathematics to argue for the philosophical acceptability of his ideas. He argued that infinite sets were not just interesting mathematical ideas, but that they really did exist. Because of that, his work received attention not just from mathematicians, but also from philosophers and theologians. The time was especially ripe for this, because in the late nineteenth century, just as Cantor's set theory was emerging into the intellectual daylight, an attempt was being made to formulate a philosophy that accommodated both science and religion.

In 1879, Pope Leo XIII issued the encyclical Aeterni Patris, in which he instructed the Catholic Church to revitalize its study of Scholastic philosophy.6 This type of philosophy is also called Thomism because it is based on the Summa Theologica written by Thomas Aquinas in the 13th century. Aeterni Patris gave rise to neo-Thomism, a school of philosophical thought that viewed religion and science as compatible. It held that modern science need not lead to atheism and materialism. The neo-Thomists felt that their approach led to an understanding of science that avoided any conflicts with religion (in particular, with Catholicism).

When Cantor's work on the mathematics of infinity became known in the 1880s, it generated considerable interest among neo-Thomist philosophers. Historically, the Catholic Church had held that the claim that infinite things actually exist would lead to pantheism, which was considered a heresy. Cantor, a devout Christian, disagreed. He maintained that his mathematics of infinite sets indeed dealt with reality, but these infinite sets were not to be identified with the infinite God. Cantor distinguished the mathematical aspects of his work from the philosophical ones. In mathematics, he claimed, one is free to consider any concept that is not self-contradictory. Whether there is anything in the real world that corresponds to these concepts is not a mathematical question, but a part of metaphysics.

Metaphysics is the branch of philosophy that studies being and reality. Cantor's metaphysical claim was that actually infinite collections of numbers had a real (though not necessarily material) existence. In patient, persistent correspondence with some of the leading Catholic theologians, he distinguished his position from heretical views and gained semiofficial acceptance. Some neo-Thomistic philosophers in Germany even used his theories to assert the existence of actual infinities. For example, they argued that, because the Mind of God is all-knowing, It must know all numbers; hence, not only do all the natural numbers actually exist in the mind of God, but so do all rationals, all infinite decimals, and so forth.

The most important effect of set theory in philosophy goes far beyond the arguments of the neo-Thomists, however. The attempts of Cantor and his successors to rid set theory of contradictions and thereby make it metaphysically sound led to deep investigations into the foundations of mathematics. Those investigations early in the 20th century also led to clarifications of logical forms, methods of proof, and errors of syntax, which, in turn, were used to refine the arguments of philosophy. Modern mathematics has provided philosophy with some explicit, formal guidelines for admissible kinds of reasoning and possible logical constructions. Set theory has also provided philosophy with new questions and new ideas about infinity. The boundaries between religion, philosophy, and science have been brought into sharper focus as a result.

One effect of these efforts was that many people came to view mathematics as a subject removed from the realm of metaphysics! As people began to work on the foundations of mathematics in earnest, it became clear that the philosophical issues involved were extraordinarily deep. Several schools of thought emerged (see page 55), but none of them found answers that were compelling.

For now, what seems to have won the day is the first part of Cantor's point of view. Mathematics can be done without having to first resolve the philosophical issues. Mathematicians can study infinite sets and, provided they can avoid contradictions, the result will be valid mathematics. Much of this mathematics turns out to be useful in the real world, but the connections are often more subtle and surprising than we might think. Meanwhile, the unresolved philosophical questions (such as the question about why mathematics turns out to be applicable) can be left to the philosophers. This might have disappointed Cantor, who cared just as intensely about the metaphysical aspect of his work as he did about the pure mathematics. Most modern mathematicians and philosophers, however, see the recognition of that separation as a giant forward stride in the progress of human thought.

For a Closer Look: Chapter 11 of [48] gives an accessible account of Cantor's work. For a quirky but readable account of ideas of infinity, see [117]. Chapter 2 of [43] is a more general discussion of set theory. Finally, a detailed account of the early history of set theory appears as chapter 5 of [76].

---

¹ Letter to Heinrich Schumacher, July 12, 1831; quoted in [37], p. 120.

² Mathernaticians usually call these numbers natural numbers.

³ From [24], p. 85, modified slightly to reflect modern terminology.

⁴ It's the Goldbach Conjecture, first proposed by Christian Goldbach in a 1742 letter to Leonhard Euler.

⁵ See [43], p. 39, for a more formal, but readable, version of Russell's Paradox.

⁶ An encyclical is a formal letter from the Pope to the bishops which deals with Church doctrine.