Not many outsiders study the Romanian language, so those who are born into it have few opportunities to use it beyond the country’s borders. On the plus side, Romanian is a very special Romance language—a highly preserved form of Latin—and it is very similar to Italian. This, and the fact that the many invaders who have flowed in and out of Romania during the centuries exposed the language to Greek; Slavic; Germanic; and Asiatic, non-Indo-European elements (Hungarian, Tatar, Turkish, in this order), have made it easy for Romanians to understand many modern languages. My French, for example, was good enough that I was able to understand Ilya Prigogine’s speech and his assertion that day in France that the treelike structures that abound in nature are the result of chance.
Had I been reared speaking English, perhaps I would have not understood Prigogine. I am more certain that had I not become an American—and the access to people, places, and ideas that affords—I never would have discovered the constructal law, because I would not have had the opportunity to be present in the room where Prigogine spoke.
I spoke almost no English when I arrived in America in February 1969 to study at MIT. Like most immigrants, I learned English on the fly. Because of my origin, I have always paid particular attention to the history and precise meaning of words. Precision is the foundation of both language and science. The definition of a word, like the boundaries of a thermodynamic system, spells out exactly what it is and what it is not. Science and language are rooted in the past, which means both history and geography. Neither is static or appears out of thin air. Both come from somewhere and evolve in time, building on all that has come before, providing, like the channels of a river basin, better access for the currents that flow through them.
My amateur interest in language took on a more decided purpose sixteen years ago after my discovery in Nancy. Before then, my work as a professor of mechanical engineering involved applying the laws of thermodynamics, mechanics, and heat and fluid flow to practical problems of heat transfer and cooling. If you wanted to build a better computer, refrigerator, or power plant, I was your guy.
When I noticed that the systems I was creating were strikingly similar to those that appear in nature—and that a single principle of physics, the constructal law, accounts for their design—I was thrust into a strange and contentious world. In this scientific Tower of Babel, I learned that the common words I used to describe my discovery—especially “evolution,” “direction,” “purpose,” and “design”—were weighted with history and fraught with controversy. Instead of my computer, I needed a dictionary.
Start with the word “design.” Its meaning seems straightforward. It is the configuration, transformation, or assembly of materials with a specific purpose—taking something today and intentionally changing it so that it will be something else tomorrow. On the one hand, this is one of the most obvious and unchallenged concepts known to humanity. The modern world is built by the simple process of turning raw materials, such as metals and minerals, plants and animals, into useful things. Look around your house. Someone designed everything in it, from the building itself to the pipes that bring water to your sink, to the appliances that sit on your kitchen counter to the money you carry. So, too, were the clothes on your back and the art on your walls. Billions of people earn their livings creating and constructing designs.
Design may be the foundation of the built world, but it is anathema when the conversation turns to nature. Its six letters have become the four-letter word of biology and physics. If you want to send a chill across a lecture hall full of scientists, just mention design in nature. If we claim that rivers, trees, or snowflakes reflect design, the question naturally arises: Designed by whom, for what? For thousands of years, people of varying faiths answered this question with ease. Divine forces created the shapes and patterns in nature. The gods, either one or many depending on the era or belief system, were the Master Builders.
As the Renaissance and the Enlightenment flourished, rational minds searched for evidence of this claim. Creationists and defenders of what we now call intelligent design didn’t produce any ironclad proof. They asserted that natural designs were so intricate and complex, that they exhibited so much order and direction, that they could not have resulted from blind forces. The most famous articulation of this teleological argument—from the Greek telos, meaning “end” or “purpose”—was offered by the British thinker William Paley in his 1802 book, Natural Theology: or, Evidences of the Existence and Attributes of the Deity, where he likened God to a watchmaker:
In crossing a heath, suppose I pitched my foot against a stone, and were asked how the stone came to be there; I might possibly answer, that, for any thing I knew to the contrary, it had lain there for ever: nor would it perhaps be very easy to show the absurdity of this answer. But suppose I had found a watch upon the ground, and it should be inquired how the watch happened to be in that place; I should hardly think of the answer which I had before given, that, for any thing I knew, the watch might have always been there. Yet why should not this answer serve for the watch as well as for the stone? Why is it not as admissable in the second case, as in the first? For this reason, and for no other, viz. that when we come to inspect the watch, we perceive (what we could not discover in the stone) that its several parts are framed and put together for a purpose.… This mechanism being observed … the inference, we think, is inevitable, that the watch must have had a maker: that there must have existed, at some time, and at some place or other, an artificer or artificers who formed it for the purpose which we find it actually to answer; who comprehended its construction, and designed its use.
About a half century later, Charles Darwin seemed to deliver the deathblow to this line of thinking. Confining himself to biology, he argued that the appearance of design we see in complex life-forms does not reflect divine intent. It results instead from the mindless process of evolution by natural selection, the “principle,” he wrote, “by which each slight variation [of a trait], if useful, is preserved.” A bird, for example, is not assembled at once—each part positioned just right in relation to all the others—like a watch. Instead, it has emerged through an evolutionary process with no larger direction or purpose. Small adaptations that provide some advantage make certain species more fit to survive, to reproduce, than others. A finch that lives in an environment where tasty seeds are somewhat hard to reach will do better if it has a longer beak. Those that have longer beaks survive and pass the trait on to their descendants, who continue to evolve.
The finch cannot will itself to have a longer beak. The mechanism by which this occurred remained a mystery until the Austrian monk Gregor Mendel showed through his famous experiments with pea plants how traits are inherited. His work led to the modern science of genetics, so that it is now believed that random genetic mutations create different traits. This process occurs ceaselessly. Sometimes, these changes produce beneficial results, oftentimes not. In general, the theory goes, when helpful variations appear, they tend to stick.
Darwin, Mendel, and others have provided us with tremendous insights that have led to innumerable benefits. More than just a scientific hunch, they have given us a deeply entrenched worldview born out of battles with old ideas. My guess is that most readers of this book have been schooled in its assumptions, embrace its meanings, and speak its language. At best, I was vaguely familiar with their work as I pursued my own. But it was also the furthest thing from my mind as I worked on the constructal law. So when I started speaking of design in nature, of the direction and purpose of evolutionary phenomena, I found myself embroiled in long-simmering controversies. I felt that people wanted me to use old language to describe a new way of understanding. Besides, I had no choice in the matter: Discovery precedes language; it takes time for language to evolve to facilitate the flow of new ideas. This meant that I had to use existing terms to describe my work.
I share this brief history with you because it has defined the terms of the debate I have entered into but want no part of. The constructal law is not a response to these claims but a different way of defining and understanding the concepts it evokes.
It claims no more and no less than this: Everything that moves is a flow system that evolves over time; design generation and evolution are universal phenomena. The changes we witness in animals, plants, rivers, and steaming pots of rice represent a clear improvement over the configuration that had been flowing before. This is the direction of evolution, creating flows that move more easily, better, farther, etc. The design we see in nature—the shape and structure of rivers, animals, cities, etc.—is a manifestation of this tendency in nature to generate shape and structure to facilitate flow access.
This is direction and evolution without intention. Flow systems do not want to move more easily; they do not seek greater access for the currents that flow through them. They do so because they are governed by the principle of physics described by the constructal law. I know this is a hard idea to grasp—design without a designer. It becomes easier when you consider another law, gravity. If you go to the top of a building and drop a rock, it will fall, faster and faster. No one would argue that the rock wants to fall, but it does, it must.
At a basic level, science is the search for such laws—simple, efficient statements of the impersonal and predictable tendencies of nature. Its knowledge turns us into sorcerers and soothsayers, able to tell the future with certainty: If X occurs, Y will happen: Water will boil at a certain temperature; a steel bar will bend if enough pressure is applied to it; I can swim in water but not in the air. Intentionality has nothing to do with any of this. These are the rules of the road that must be obeyed. Imagine if there were no predictability or order in nature. If water had a random rather than a predictable boiling point, it might take a second for you to make tea or an hour or eternity. If steel didn’t have a predictable breaking point, we could never build safe houses or cars. Life as we know it would be impossible if we couldn’t count on the laws of physics.
The constructal law identifies a phenomenon as old as the universe itself but unrecognized until now. Its power and correctness rest on this fact: It enables us not just to describe but to predict the evolution of all flow systems. Before making any observations in nature, we can use the constructal law to imagine what a lung, blood vessel, tree, river, or lightning bolt should look like if it has the freedom to change over time to flow more easily. When we compare our drawings with what we find in the real world, they line up.
The constructal law predicts that for rivers to flow more efficiently, their width should be proportional to their depth; that the circulatory system in our bodies should have a treelike structure of round tubes with a few main channels (arteries and veins) and numerous tributaries (capillaries) in order to deliver water, oxygen, and useful energy to every cell; and that our hearts should have an intermittent beat—lubb-dupp, pause, lubb-dupp, pause—because that is an efficient way to deliver oxygen and other substances to the living body.
To see how, let’s take a closer look at our respiratory system. Its primary function is to draw oxygen from the air by inhaling, oxygenate our blood in the tiny alveoli of the lungs, and then drain carbon dioxide from the blood and then out of our bodies by exhaling. Instead of studying the system we find in nature, we use the constructal law to imagine what a theoretical fluid flow architecture should look like if it is to perform these functions with low mass transfer resistance and low fluid flow resistance, all in a small volume. (This is quite a mouthful! I thought about this when I wrote the constructal law, and I condensed it all into a statement of design and evolution toward greater “access” for all the components in a “finite-size” system.) In this case, we ask: What design would we come up with to promote access to the external air while also bathing the entire volume of the lung with oxygen?
Using pencil, paper, and the constructal law, Professor Heitor Reis and his associates at the University of Évora in Portugal demonstrated that the best oxygen access to the alveolar tissue is provided by a treelike flow structure composed of ducts with twenty-three levels of bifurcation (that is, they continuously double the number of tubes as they split) that ends with alveolar sacs from which oxygen diffuses into the surrounding tissues. Because mice, for instance, are smaller, they should (and do) have nine levels of bifurcation in their lungs.
Among other things (including the dimensions of the alveoli and the total alveolar surface), Reis and his associates determined that good flow access is achieved when the length of each bifurcating airway (the two daughter airways that branch off from each mother airway) is defined by the ratio of the square of the first airway diameter to its length.
When they compared their findings to our actual respiratory system, they found that they had predicted its shape and structure: twenty-three levels of bifurcation with a fixed ratio in the length of mother and daughter airways.
In my own work, I tackled a different aspect of the respiratory system, the rhythm of breathing. I asked: What would be a good rate for inhaling and exhaling to deliver oxygen and remove carbon dioxide? I found that resistance is decreased when there are intervals and that these intervals should be proportional to the mass (M) raised to the power of 0.24. This means that smaller animals should breathe more frequently than larger ones, which is in agreement with voluminous empirical observations.
Physiologists tend to focus on the breathing rhythm, and many have proposed empirical models for summarizing quantitatively the observation that large animals breathe less frequently. By starting with the constructal law, I discovered three other features that are so obvious that nobody had questioned them before:
Of course, most phenomena do not exhibit this splendid predictability of lung structure. Design in nature is not precise to the nth degree—otherwise every tree would be identical. The diversity we find is immense. Phylogeny (the study of the evolutionary relatedness among various groups of organisms) creates genetic architectures that, like boulders in rivers, are slow to erode. Thus, many of the “mistakes” biologists point to in animal design—for example, the long, winding path taken by the recurrent laryngeal nerve in mammals when a shorter path would be more ideal—reflect the move toward better flow within the constraints of evolutionary history. In the inanimate world, ecological variation leads to other anomalies. Multiple factors shape design, just as, for example, constant exposure to a high wind and the input of surrounding sediment would cause a different form of river basin to evolve by processes we ordinarily address without reference to the wind or an exhaustive list of other factors that create idiosyncratic variation.
What the constructal law captures is a central tendency in nature. In the big picture—all the rivers, all the trees, all the animals on Earth—the driving force behind the evolution of everything that flows is the generation of shape and structure to move more easily. This is why we can say that this unintentional tendency has a purpose. All the flow designs on Earth, from air currents, rivers, and trees to fish, people, birds, and technology arise, evolve, and compound themselves to enhance movement. It is because this tendency has a direction, a purpose, that we can predict how things should evolve in the future.
Using the constructal law we can recast organic evolution as a dynamic process that generates better designs. There is a large volume of imperfection involved (genetic drift, selection on linked alleles, extinction, dispersal limitation, environmental heterogeneity in space and time, etc.) as well as idiosyncratic variation. But the central tendency is the selection of characteristics that ease the flow—that allow animals and plants to generate more flow (movement) for their mass with less expenditure of useful energy to achieve this movement. The evolutionary history biologists have charted, the series of adaptations they have detailed, are all expressions of the constructal law. The same tendency governs the evolution of inanimate systems; of all the possible configurations, the ones that persist are those that facilitate flow. Thus, the constructal law shows that animate and inanimate entities develop flow configurations in a manner consistent with the idea of natural selection in biology. The dynamic processes and features of inanimate phenomena, such as river systems, can be united via the constructal law with the dynamic features that inform the evolution of biological organisms including you and me.
One reason that I was able to discover the constructal law is that I was not immersed in the language and history of Darwinism. My field is thermodynamics, and it is from here that my language and insights developed. Through it I identified the principle that generates design in nature.
To have a conversation, we have to speak the same language. Otherwise, we are not communicating. So I turn to thermodynamics to define some basic terms and address some of the deeper questions raised by the constructal law: What is a flow system? Why do things flow? Why do they evolve? How are direction, purpose, and design possible without the guiding hand of God or man?
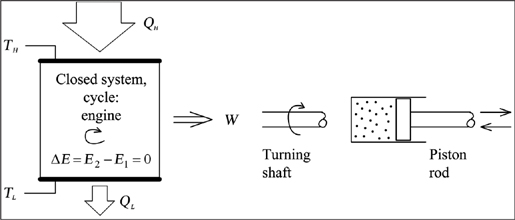
The field of thermodynamics was born because of the Industrial Revolution. It can be said to begin with the great French scientist and inventor Denis Papin (1647–1712), who was fascinated by fire and water. One of his earliest inventions was what he called a “steam digester, or engine for softening bones.” Observing that the pressure inside his cooker could be harnessed for other uses, he devised the first piston and cylinder mechanism, a design that still powers our engines. In his primitive yet practical device, high-pressure steam is created by heating water in a confined space. The steam pushes a piston that resists the pushing, and that means the steam does work on the piston. In modern turbines, such chambers are formed repeatedly between rows of blades rotating against rows of stationary vanes, with steam (or another hot gas) temporarily trapped in these chambers as it expands (Figure 7).

Figure 7. Closed system receiving heat (QH) from a high-temperature reservoir (TH), rejecting heat (QL) into a low-temperature reservoir (TL), and producing work (W). The energy inventory of the system (E) changes from E1 to E2. The first law of thermodynamics states that energy is conserved. The energy that flows in (QH) minus the energy that flows out (W + QL) equals the amount of energy stored inside the system [E2 − E1 = QH − (W + QL)]. If the system executes cycles, then at the end of each cycle, all the system properties return to their original values; for example, E2 = E1. A real engine can always be improved, because its work output (W) is always smaller than its largest theoretical value (Wrev), which occurs in the ideal limit of reversible operation. In this ideal limit imagined by Carnot, all the currents and motions of the engine system occur in the absence of resistances such as friction and heat leaks. Any real engine is completely equivalent to an ideal engine producing maximum work (Wrev) and destroying a portion of this work (Wdiss) into a brake. It is as if the shaft of the ideal engine is resisted by the brake but only partially, because a portion of Wrev (namely W) is eventually delivered to the environment. In the limit where no user exists in the environment to receive the work (W), all the work produced by the engine is dissipated into the brake. This limit represents the design of everything that flows and moves on Earth. (We return to this natural design in Figures 57 and 59.)
In summary, we create work from heat, as in the name “thermodynamics” coined for this science by the nineteenth-century Scottish physicist William Thomson (later Lord Kelvin)—therme (“heat” in Greek) and dynamis (“force”). No animals or slaves are needed to push the body out of the way. Is any idea cleverer than this? Is any idea more humane?
The laws of thermodynamics apply to everything on Earth. All natural designs are engines (of heat, fluid, or mass) driven by useful energy derived from the sun. All things that flow, including people and other biological creatures, acquire evolving designs that allow them to move more current farther per unit of useful energy consumed.
Today thermodynamics encompasses all aspects of energy and energy transformation, including refrigeration (which involves the removal of heat from a system colder than the ambient) as well as the relationships among properties of matter and power production, from the operation of power plants to photosynthesis.
As the study of thermodynamics grew, its practitioners developed a vocabulary that allowed them to know precisely what they were talking about. One of the most basic terms is the word “system,” which means the region in space or the quantity of mass selected by an observer for analysis and discussion. A tree is a system we might study, but so is the forest of which it might be part. How we define the “system” is a personal choice, but it must be placed naked on the table. We define the system by drawing a sharp and precise boundary around the entity in question (Figure 8).
Inside the boundary is the system we have decided to look at—the tree, the forest, the stream, the river basin. Outside the boundary is everything else: the rest of the world. This “other system” in thermodynamics is called the “environment,” or the “ambient.” The water inside Papin’s primitive cylinder was a system for creating steam. A river basin is a system through which water flows; a bird is a system that moves the animal’s mass across the Earth.

Figure 8. The boundary is an imaginary surface with zero thickness that separates the system from the rest of the universe.
The boundary can have special features, which give the system special names. If the boundary is impermeable to the flow of mass, then the system is called “closed” and its mass inventory is fixed even in cases when its state, its “being,” is unsteady. Think of the system represented by the air inside an impermeable balloon. Because there is no leakage of air from the balloon to the environment, the amount of air stored inside the system is fixed.
If mass crosses the boundary, the system is called “open.” Speaking thermodynamically, your body is an open system. Its boundary is an imaginary surface drawn on the outside of your skin—a three-dimensional version of the chalk outline detectives draw at murder scenes. This boundary has inlet ports (the mouth and nose) that introduce substances into the system and outlet ports (including the mouth and nose) as well as skin pores and other organs that leak substances into the environment.
Mass goes in, mass goes out, and the system itself can move in space (e.g., the bird, or vehicle). The key point is that mass is conserved: The difference between input and output is the mass that is being stored (accumulated) inside the system. We have just described a law obeyed by all systems, open or closed: the law of mass conservation: The whole mass must be equal to the sum of its parts. Though this law was discovered by Antoine Lavoisier in the eighteenth century, the ancient Greek philosopher Epicurus hit on this idea when he postulated that “the sum total of things was always such as it is now, and such it will ever remain.”
A similar law applies to energy. It, too, can neither be created nor destroyed. The law of energy conservation is known as the first law of thermodynamics and was articulated (at the same time as the second law, which we will discuss next) by three men from 1851 to ’52—two Scotsmen, William Macquorn Rankine and William Thomson (later Lord Kelvin), and the German Rudolf Clausius. This, much more than the romantic ideal of the lone genius, is usually how science works; an inkling arises that there is a better way to speak of nature, inspiring researchers to try (often in competition with one another) to discover and articulate it. We see this time and again in the history of science in general and the constructal law in particular: Early practitioners observe a phenomenon, but they do not possess the knowledge to predict it. In Darwin’s time, others were working to discover the mechanism of biological evolution; today, many others are examining the phenomenon explored in this book: design in nature.
Building on the visionary ideas of the Frenchman Sadi Carnot (1796–1832), Rankine, Kelvin, and Clausius observed that while a system cannot create energy, it will conserve and can transform it. Our cars transform the useful energy of gasoline into heat that drives our engines; the engines partially convert that heat into the work needed to push our cars on the road. Our bodies convert the energy from food to power ourselves. Power plants transform energy from one type (heat) into another type (work). When we examine any system, we ask: How well is it doing? How efficiently is it using the available useful energy? In thermodynamics the usual way of measuring this progress is by speaking of the “energy-conversion efficiency” of the engine. Better designs are more efficient; they perform more work for less useful energy.
This concept is key when we speak of flow and flow systems. Flow represents the movement of one entity (in the channel) relative to another (the background). To describe a flow we speak of what the flow carries (fluid, heat, mass, information), how much it carries (mass flow rate, heat current, traffic, etc.), and where the stream is located. Flow systems are defined as one or more streams that originate from points and must find easier access to other points.
The constructal law predicts that flow systems should improve over time. This raises the question: Better in terms of what? How do we measure improvement in the system? The answer lies in the fact that flow systems are imperfect thermodynamically because of the resistances their flows must overcome. Resistance is the phenomenon of opposition to movement. It is best known as friction—for example, the horizontal force that a human, animal, or motor must exert on a vehicle in order to make it move horizontally. Fluid friction acts in the same direction: a pump must maintain a high enough pressure at the entrance to a long pipe in order to force the column of water to move along the pipe. Much more subtle is the “friction” encountered and overcome by a heat current, which must be “driven” by a finite-size temperature difference in order to flow. This heat-flow kind of friction is thermodynamically equivalent to the mechanical friction.
Imperfections are unavoidable. In fact, they are necessary. Without imperfections (resistances), flow systems would accelerate continuously, eventually spinning out of control. Thus, imperfection (friction, heat leaks, etc.) acts as a brake on the engines (the designs) that drive flow. I know this firsthand from my own work. Like all engineers, when I set out to design a device or a system, I have to understand the function it will perform and the hurdles that stand in the way. I shape and assemble its parts so that the global system will function in the least imperfect manner possible. My struggle as a designer never ends.
So it is with all natural designs, which encounter various forms of resistance—choke points, bottlenecks, friction, drag, thermal insulation, etc. To cite one common example, imagine that you are on the banks of the River Thames. Don’t forget your jacket, because it’s a typical spring day in England—gray, dank, a bit nippy. Still, the air is filled with excitement because it’s Race Day; the oarsmen of Cambridge are poised for battle against their adversaries from Oxford. As the powerful combatants settle into their boats, they appear to be preparing to compete against each other, but their true foe is the water itself. The legendary Cambridge rower Steve Fairbairn immortalized their mighty motions in “The Oarsman’s Song”:
The willowy sway of the hands away
And the water boiling aft,
The elastic spring, the steely fling
That drives the flying craft.
That has a little more zip than my analysis of the oarsmen’s efforts, but I will try to make up in precision what I lack in grace. Driving the boat requires an expenditure of work (W) from the rower pulling the oars. The work is spent in order to overcome the friction force (F) due to two effects: friction as the boat slides on the water to cover a distance (L) and the need to lift the water, to get it out of the way. This second effect is visible as waves. The work spent is the resistance force times the displacement (W = FL). More friction force requires more work to cover the same distance. This is why the leading boat will move as close as possible to its competitor’s lane. The momentum of the water that the rowers push behind them creates even more resistance for their adversaries to overcome, so that they must do even more work to cover the same distance. It also explains why today’s oarsmen do not use the same boats as their ancestors in that first contest in 1829. Through the years, craftspeople have built ever more hydrodynamic boats to minimize the effects of friction. Better designs lead to greater efficiency, which means easier movement. This is part of the template for all design evolution in nature.
Fish, land animals, birds (that is, all swimmers, runners, and fliers) are flow systems that move mass (themselves) on the globe. The food they take in provides the useful energy that allows them to move across the landscape. To move they must overcome two obstacles—the downward pull of gravity and friction from the water, land, and air. As we will see in chapter 3, their design (which includes everything from the shape and structure of their innards to their total body mass and the rhythmic motion of their tails, legs, or wings) has evolved to allow them to move more easily and efficiently in an environment that resists the movement.
Finally, consider the maple tree. It is not just a source of shade for romantic picnics but is also a flow system for moving water from the ground to the air. While battling gravity and friction to move water up its length, the tree must also stabilize itself against the resistance caused by the wind, which would sever its limbs and topple it over. Through the constructal law we find that every aspect of its design—the shape of its roots, trunk, branches, and leaves—can be predicted when we recognize the two flow systems in the maple: water and stresses. The standing tree is facilitating the movement of water and mass on the globe, as we will see in chapter 5.
This is what we see in every flow system. The road to easier flowing consists of balancing each imperfection against the rest. All the components of the system collaborate, working together to create a whole that is less and less imperfect in time. The distributing and redistributing of imperfection through the complex flow system are accomplished by making changes in the flow architecture. This is true for all animate and inanimate designs, from the placement of branches on a tree to the channels in a river basin to the arrangement of electronics in your laptop.
A prerequisite, then, is for the flow system to be free to morph. The emerging flow architecture is the means by which the flow system achieves its objective under constraints. Freedom is good for design.
Before leaving this discussion of thermodynamics, we have to explore one more crucial point as it relates to flow. Why does anything flow at all? Why does anything move? What is the wellspring of this action? For things people make, there is a simple answer—we provide fuel (i.e., useful energy, exergy) to power the devices and systems we build. But what about everything else? One obvious answer is gravity. It pulls the water from the mountaintop to the plain and sends it barreling down the river. But what puts the water on the mountaintop in the first place?
To find the answer, we return to the work of Carnot. A military engineer felled at a young age by cholera, he was a graduate of the famous École Polytechnique and later spent time at the august institution that features a statue of Papin, the Conservatoire National des Arts et Métiers (CNAM) in Paris. Carnot came to the CNAM in the early nineteenth century to study the steam engines that were transforming Europe. Why were steam engines so popular? Because their effect on people’s lives was very good. It was dramatic. Engines were empowering people. They were facilitating the flow of people and goods across the globe.
As he contemplated this parade of machines, Carnot saw that everything flows in one direction: from high to low. Water flows spontaneously from high pressure to low pressure. Water falls through (and turns) a water wheel by flowing from high to low. He then reasoned that heat flows of its own accord from high temperature to low temperature. Similarly, heat falls through (and turns) the engine by flowing from high temperature to low temperature (the ambient). This “one-way flow” principle is known today as the second law of thermodynamics, irreversibility, dissipation, inefficiency, water under the bridge, etc. By looking at the operation of machines, Carnot discovered a law of nature.
The second law has been stated in several other ways. For example, if the system is isolated (not touched by anything)—and this is a big if—nature tends to efface differences and create uniformity. The simplest example is a glass of ice water left overnight on the kitchen table (the “isolated system” here is the entire room with the glass of water in it). In the morning the water will be at room temperature. In addition, there will be less water in the glass because the drier air has been removing water from the glass in order to reach an equilibrium of vapor pressure.
To see this action on a global scale, let’s take a trip to the warmer latitudes near the Equator. The heating there is more intense because the sun’s rays are almost perpendicular to the Earth’s surface. Think of the rays as a bundle of arrows. Near the poles, they land almost at a slant, and this means very few of them land per unit of ground area. The uneven heating of the Earth sets in motion the ocean currents and global weather patterns. The warmer water and air head toward the poles, to mix and churn with the cold water and air there in order to create uniformity. But the route to this never-reachable uniformity is paved with nonuniformity: sharp currents, rivers, and winds that are distinct from their unmoving surroundings. This nonuniformity facilitates the global flow, and, if the sun were to disappear, accelerates Earth’s system toward uniformity (death).
The sun, however, does not disappear, so the globe is not an isolated system. In the simplest description, our planet is a closed system. The sun heats the Earth and continuously forces the oceanic and atmospheric currents to keep on flowing. It forces the nonuniformity to persist. It uses the currents themselves (what moves is distinct from what does not move), illustrating for all of us that nonuniformity reigns as patterns, configurations, and rhythms. If the system is forced to flow, far from equilibrium, it generates plenty of differences, namely the heterogeneity distributed throughout the volume (or area) as channels and interstices: faster, easier flow through the channels (such as water in a river) and slower, more difficult flow in the interstices (such as the water that seeps from the ground to the river).
Let’s stay in the ocean to find more evidence of spontaneously occurring design and to solve one of the great riddles of fluid mechanics. Scientists have long known that flow regimes change—from a smooth laminar flow to the whirling eddies of turbulent flow, and vice versa. But until the constructal law we didn’t know why.
As the sun beats down, it heats the water on the surface. Warmer water is lighter than colder water. The warm water moves horizontally to climb on the cold water, while the cold moves in the opposite direction to slip under the warm. The upper layer has horizontal momentum (literally movement) and the lower layer does not. The upper layer reaches down, grabs the cold water, and drags it along with it. The fast surface water entrains, or literally pulls along, the slow below-surface water so that the two tend to flow at about the same speed. In physics this entrainment phenomenon is described as a process of transferring motion (momentum) from the fast to the stagnant to achieve a sort of equilibrium. This occurs because the tendency in nature is to equilibrate not only the hot with the cold but also the slow with the fast—equilibrium means uniformity in every respect.
Though the naked eye might see that water is flowing, what’s really going on is the flow of momentum (motion), from fluid packets that move quickly to packets that move slowly. The question of design in nature emerges when we ask how this momentum is transferred. There are two design choices. Laminar flow consists of smooth parallel blades of fluid (one blade rubbing and sliding on its neighbor) as they all move forward. Turbulent flow is characterized by whirling eddies (chaotically) moving forward and perpendicularly (that is, rolling). In both laminar and turbulent flows, the momentum is transmitted vertically downward, that is, perpendicularly to the horizontal movement of the water.
You can observe this same phenomenon by looking at a plume of smoke rising from the smokestack of a power plant; here the fast fluid (the gas) moves vertically as the smoke shoots up in a slender, cone-shaped column. As it transfers its momentum perpendicularly, the plume expands horizontally to encompass more and more air around it. The plume becomes wider as it lifts more and more air with it. The same thing happens when you light a cigarette or a candle. Initially the smoke, which is warmer and lighter than the surrounding air, rises as a slow straight column. As it picks up speed, the flow changes; it starts to create rolling whirls called eddies (or tourbillons in French, from which we derive the words “turbulence” and “turbine”). The cigarette smoke is the upside-down drawing of the airstream entrained downward by the falling toilet paper illustrated in Figure 5.
What the constructal law reveals is that flows choose the design that will better facilitate their movements at any given time. The constructal law also allows us to predict the point at which this transition between laminar and turbulent flow should occur to facilitate the flow of momentum.
We find that all fluids flow in this sheetlike motion, called laminar flow, when this is the better way to spread momentum. This is the flow design when the flow stream is narrow and slow enough. But when the stream is sufficiently thick and fast, the design changes to turbulent flow.
Throughout this book, I refer to flows that are “slow enough” or “fast and thick enough.” This language is necessarily vague because it covers a broad array of phenomena moving in diverse environments. (It is also why I say a particular design is “good” for flow.) Each particular flow is unique. What is fast and thick for one type of flow is slow enough for another. The universal principle is that when the specific threshold is reached in every case, the flow changes (it clicks!) into the better design.
Nevertheless, as I will now show, I have used the constructal law to predict when that transition should occur in an imaginary flow. I have tried to minimize my use of math in this book, but it is important here, and a few other places, to show you the work behind my conclusions. The natural tendency of selecting the flow configuration so that momentum flows more easily across the flow is illustrated in Figure 9.
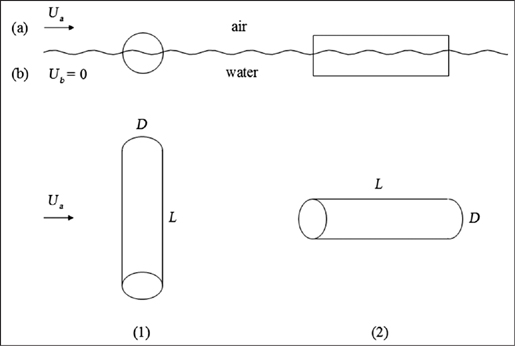
Figure 9. An object (iceberg, tree log) floats on the ocean interface between two fluid masses (a), (b) with relative motion. The atmosphere (a) moves with the wind speed Ua, while the ocean water (b) is stationary. Momentum flows downward from (a) to (b). The constructal law calls for the generation of flow configuration such that momentum flows more easily. The floating object is the mechanism by which the atmosphere (a) transfers momentum to the ocean water (b). The extreme positions of this mechanism are (1) and (2). The forces with which (a) pushes (b) via the object are F1 and, respectively, F2. The selected configuration must be (1), because one can easily show that F1 is greater than F2 when the cylinder’s length (L) is greater than its diameter (D). Momentum flows from (a) to (b) at a higher rate through configuration (1) than through configuration (2). This is why icebergs, waves, and debris orient themselves perpendicularly to the wind direction. This prediction is confirmed by all the forms that drift sideways (perpendicular to the wind) on the ocean: icebergs, debris, water waves, abandoned ships, etc. The emergence of the turbulent eddy is the same design phenomenon as the selection of configuration (1) for the floating object.
Figure 10 shows the shear flow between the fast and slow regions of the same fluid, (a). The threshold or the point at which the flow switches from laminar to turbulent occurs at each flow system’s Reynolds number. When the shear flow is thin and slow such that the Reynolds number is less than 102, the more effective design is viscous shearing (laminar flow). When the shear flow is thick and fast such that the Reynolds number is greater than 102, the more effective design is eddy formation (turbulence).
The Reynolds number 102 marks the birth of the first, smallest eddy. The theoretical leap is that the constructal law demands the occurrence of eddies. In constructal theory, the eddy is predicted, not assumed, not seen and then described, not the aftermath of an assumed disturbance. Every eddy is generated at the intersection of the two curves in the lower part of Figure 10 and expresses the balance between two momentum transport mechanisms. Every eddy is a package of two flow mechanisms: streams (the roll) and viscous diffusion (laminar, inside and outside the roll).
In summary, when the flow is fast enough, the turbulent flow becomes the more effective way to transfer momentum laterally. The key point is that the water (like the smoke from a chimney or a cigarette) has two design options: laminar flow or turbulent flow. When laminar flow entrains more of the surrounding fluid, that is what we observe. That happens when the flow is a trickle, narrow and slow. When the flow is wider and faster, turbulent flow (rolling eddies) rules the momentum transfer process. Like the curls of cigarette smoke, the oceanic eddies are spinning wheels that rearrange the water so that it can transfer momentum more easily and mix the ocean more effectively.
Why do isolated systems evolve toward equilibrium? We don’t know. They just do. This is why the second law of thermodynamics is called a first principle—because it cannot be deduced from other principles. The same is true for the constructal law. Where the second law describes the universal tendency to flow from high to low, the constructal law describes the universal tendency to generate evolving configurations that facilitate that flow. The second law and the constructal law, then, are two different first principles. Together they capture nature much more firmly than the second law alone.

Figure 10. Configuration (1) is the laminar flow. Configuration (2) is the eddy flow, or the wrinkling, rolling, and thickening of the shear layer. The lower part of the figure shows how the shear layer thickness D grows in time, that is, how momentum is being transferred from the fast to the slow. In the laminar configuration (1), momentum is transferred by viscous diffusion, and consequently D increases as t1/2, where t is time. In the eddy configuration (2), D increases in proportion with t, because D scales as U∞t, where U∞ is the speed of the moving fluid. The two D(t) curves intersect when the Reynolds number based on D and U∞ reaches this threshold
![]()
where v is the kinematic viscosity of the fluid. The constructal law calls for the configuration that generates the larger D (more momentum transferred) at any point in time.
To see the constructal law at work, imagine a box filled with a compressible fluid (air), with parts of high pressure and low pressure. The high pressure will move air mass toward the low pressure. When I was a student at MIT, my professors and I never questioned the drawing involved, the path of that movement. I am now amused to see that in my first book, Entropy Generation Through Heat and Fluid Flow (1982), I drew the diagram of a flow system shaped as a blob, as in Figure 8; like everyone else, I took the drawing for granted. On one level, this is akin to my saying “I traveled from Paris to Rome last night” without any consideration about how I got there (bus, train, plane), the route I took, or the time it took. In fact, the journey is everything.
Through the years, doing my best to serve (to protect, to defend, and to save!) the discipline of thermodynamics and apply it correctly, I recognized the necessity and centrality of design. I realized that that black box was not just an abstraction for input-output analysis. It was not filled with scientific abstractions but with drawings that were moving and morphing.
In retrospect it seems surprising that scientists had long ignored this basic phenomenon of design generation and evolution. After all, the concept of flow design was crucial to the work of Carnot and all who have followed him. Nevertheless, they did. As John Steinbeck noted in his wonderful nonfiction book on marine biology, The Log from the Sea of Cortez: “Often a very obvious thing may lie unnoticed.”
Let’s return to the box filled with regions of high and low pressure. If nothing interacts with the box, the second law says that over time the high and low regions will equilibrate themselves. It says nothing about flow, configuration, evolution, and design. In the very beginning the geometry of the flow system is missing—because no flow has occurred. The constructal law accounts for a different phenomenon: the generation of flow configuration in time. This other phenomenon facilitates the access of the high-to-low currents through the box.
Geometric form is generated in natural systems that are internally “alive” with flows and driving gradients (for example, temperature and pressure). Such systems are not in equilibrium internally. They are not dead; they are on the move. In order to get from here to there, everything must create a path. People, then, are only half right when they say things seek the path of least resistance. Instead of finding these already cleared paths, flow systems construct their own flow architectures and body rhythms that enable them to move more easily.
As we look around us we see striking similarities in the architecture and evolution of simple and complex flow systems: lung structure, river basins and deltas, animal movement, respiration, solidification, etc. Consider the blood vessels in your body. Their cross sections are nearly round because, in the abstract, the mathematically circular cross section is the design that offers the least resistance to the mass that flows though it. The cross sections of animal flow channels are never perfectly round because the animal body moves and morphs. Nearly round, however, performs almost as well as the mathematically round (think about it as you press the veins visible on your forearm: you do not faint, that is, you do not feel the effect of having made the cross sections of those blood vessels imperfect). Likewise, moles and earthworms create nearly round tunnels when they burrow through the ground. Same goes for civil engineers whose tunnels and mine shafts are nearly round—for that matter, so, too, do naturally formed tunnels such as the underground caves, the shafts of volcanoes, and those formed by the jets of fluid that pierce water and air. Using the constructal law, we can predict that when one thing goes through another, we will find a rounded cross section.
Coincidences that occur in the billions are a loud hint that a universal phenomenon is at work. It suggests that there is a single principle of physics—not of biology, or geology, or sociology, but of everything—from which the phenomenon of configuration and rhythm can be deduced without any recourse to empiricism.
The movement toward equilibrium—and the pull of gravity—puts things in motion. The constructal law proclaims that nature will generate configurations to facilitate this flow and that there is a direction in time to this phenomenon of configuration generation. Nature is indifferent, impersonal. But it does have a tendency—to mix and to move everything on Earth, more mass, moved farther. This constructal tendency fuels all evolution and design.
Through this discovery, we turn the page on the long-raging debates about direction, purpose, evolution, and design. We begin writing an entirely new chapter in the book of science that shows how the complex forms of shape and structure we see all around us arise from the laws of nature.