Note: It takes a little effort to accurately conceptualize what constitutes a light wave, but when you've done it you understand all electromagnetic radiation, and the subject is rather fascinating. Wavelengths were defined for water in Figure 2.2, but light is a different animal. What I provide here is a relatively simple and accurate classical description that serves much of our discussion and is the basis for our consideration of the quantum nature of light starting in Chapter 2. In particular, following the step-by-step construction in Figure A.1 will require a bit of concentration but will be well worth the effort.
If, however, you'd like a shortcut, a glance at Figure A.1(c) will give you a “picture” of the wave (albeit without full understanding) sufficient to consider the spectrum of electromagnetic wavelengths shown in Figure A.2. That figure has additional information in the rightmost column relevant to Chapter 9.
INTRODUCTION TO FIELDS AND ELECTROMAGNETIC WAVES
In 1865, the Scottish mathematical physicist James Clerk Maxwell developed a theory of electromagnetism suggesting that waves of alternating electric and magnetic fields would propagate through space at the speed of light. He concluded from this that light was itself an electromagnetic wave. This led to the prediction of other electromagnetic waves, among them radio waves.
What Maxwell theorized and what Thomas Young earlier demonstrated (in 1801, as described early in Chapter 2) is that light “looks” and behaves like a wave. It is Maxwell's broader understanding of the nature of light, in this “classical” context, that we present here. Note, however, that light also exhibits quantum, particlelike properties, suggesting that the energy of light is delivered as photons, discrete packages of energy, and a wave-particle duality as described later in Chapter 2. (The photon is described as the purveyor of the electrostatic force, such as the force on the electron as described in Chapter 9, Part IV (C).)
Although we can see light, we can't see the electric (E) and magnetic (B) fields of which light is comprised. Even so, we are all familiar with the magnetic field. It causes magnets to attract or repel each other, latch onto refrigerator doors, and attract the needle of a compass to point toward the North Pole. The electric field is less familiar, but most of us have seen the consequences of a strong electric field: in lightning or in the zapped discharge of the buildup of electrons as we walk across the right type of carpeting.
Note that both E and B are boldface to indicate that they are vectors, that is, they have magnitude but also act or flow in a particular direction. The E field is a measure of how strongly voltage changes across space, how strongly other electric charges push or pull on electrons, and whether the electrostatic discharges described above are likely to occur. Suppose that you have walked across the kind of carpet that lets electrons in some way scrape off and charge you up to some voltage level. And then suppose you step forward to shake hands with a friend who hasn't been on the carpet or isn't wearing the kind of shoes that scrape off electrons. (That is, for this illustration, your friend doesn't carry a charge.) Suppose you are charged to 800 volts, and suppose your hands are one inch apart. Then, ignoring some of the effects of the geometry of your hands and some other factors, there is between the two of you an electric field of E = (800 volts)/(1 inch) = 800 volts per inch. (These are not the usual units for E, but that doesn't matter for our illustration.) Eight hundred volts is not enough to cause a spark through air.
Now suppose your hands come closer, so that they are separated by a tenth of an inch. The voltage changes more rapidly across the much smaller space between your hands. E = (800 volts)/(1/10 inch) = 8,000 volts per inch. Still, nothing happens. Suppose your hands become separated by one hundredth of an inch. Then E = (800 volts)/(1/100 inch) = 80,000 volts per inch, and your friend gets ZAPPED. There is a flash, because electrons leaving your body under the acceleration of the E field break loose electrons from the atoms in the molecules of the air (ionizes them), and then they and those additional electrons are accelerated (in opposite directions under the influence of the E field) and some recombine to form atoms, releasing light in the process. You have finally exceeded the approximately 75,000-volts-per-inch breakdown voltage for air at the pressures found near the earth's surface.
The difference between the carpet-caused zap and lightning is in the number of electrons in the discharge, the size of the gap, and the reduced air pressure high up in the sky, which actually makes the discharge easier. The prominence and shape of objects can also serve to intensify the electric field. Lightning is, of course, a great deal more complicated than is described here, but you have the basic idea.
So, the E field can be a driver of electrons. It exerts a force on them along the direction of the field.
Note that an electron, if it were to travel undisturbed from a place at 800 volts to a place with zero volts, would acquire an energy of 800 electron volts, 800 eV. This compares to the –13.8 eV of the electron in the ground state of the hydrogen atom, as described in Chapter 10. And realize, 13.8 eV is roughly comparable to the ionization energies of most of the elements, as described in Appendix D. So, the electrons released at 800 volts in our thought experiment have much more than enough energy to ionize the atoms of the elements.
THE PLANE-POLARIZED ELECTROMAGNETIC WAVE
We visualize what an idealized light wave might look like through several steps, as shown in Figure A.1. First, in (a) we consider three directions in space, three axes: the x axis, which runs from left to right; the y axis, which runs toward us; and the z axis, which runs vertically upward. The axes cross at a point called the origin. (We define distance along x to have positive values to the right and negative values to the left of the origin; distance along y to have positive values toward us and negative values away from us past the origin; and distance along z to have positive values upward and negative values downward from the origin.)
In (b) we visualize (within short dashed lines) a rectangular block of space roughly centered over and running lengthwise along the x axis. Think of this block as sliced up like a loaf of bread, where the cut surface of each slice is a rectangle that lies in a plane oriented perpendicular to the x axis. (The rectangle defines a limited region within the flat surface of the plane of the cut, but the plane containing the cut surface extends to infinity in the positive and negative of both the y and z directions.)
In (c) we represent an electromagnetic wave. Here's how we construct the concept of it: We start with an identical set of axes to those in (a) and (b), but without the sliced “loaf” that is in (b). At each point where the plane of one of the slices from (b) would cut across the x axis in (c), we indicate by an up or down arrow (vector) the direction and particular strength of the electric field, E, that is present throughout the entire plane of that slice, that is, to infinity in the plus and minus y and z directions.
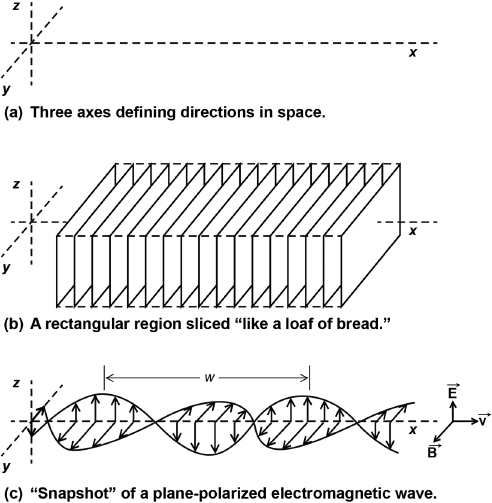
Fig. A.1. Plane-polarized electromagnetic wave. (a) Three axes define directions in space. (b) A rectangular region of space “sliced like a loaf of bread.” (c) A “snapshot” of the wave. Each arrow (i.e., vector) shows the magnitude and direction of the electric field, E, or magnetic field, B, throughout an entire plane in space (beyond the loaf) at the x position where the plane is located. Arrow tips trace out sine waves with crest-to-crest wavelength, w. Each local field (arrow) at each x position alternately increases and then decreases with time, following the rise or fall of the field (arrow) to its left, so that the wave propagates forward in the x direction with velocity v (having a magnitude c = the speed of light). (Image (c) modified from Wikipedia Creative Commons; file: Onde electromagnetique.svg; author: SuperManu. Licensed under CC BY-SA 3.0.)
Consider now the E field in the plane of just one of the slices. The longer the arrow E for that plane, the stronger the E field throughout that plane. Think of the E field in this plane as being represented by an infinite number of arrows of this same length and direction everywhere in that plane. We choose to show only one arrow to represent all of these arrows, and we start this one arrow from the x axis so that we can compare its length with the length of other arrows that similarly represent the E fields that are present throughout other planes.
Now, if we were to cut our loaf into more and more and thinner and thinner slices, the tips of the resulting more closely spaced vectors would trace out an alternating positive to negative (in the z direction) sine wave as shown. The length of the B vector is in direct proportion to the length of the E vector at each point along x, so the B vectors similarly trace out a sine wave, but running positive to negative in the y direction, and the B sine wave is exactly in phase with the E sine wave (both crossing from positive to negative at the same points along the x axis). The peak value of either sine wave is called its amplitude.1 Because our E vectors for this description point only up or down (in the z positive or negative directions) we say that the wave thus produced is polarized in the z direction. And because E for each slice is the same everywhere in the plane of the slice, we say that the wave is plane- polarized.
WAVE PROPAGATION
Now realize that each vector (representing the field throughout its plane) changes with time, at first increasing in length, going to the peak positive level of the sine wave, and then decreasing, going negative, and then increasing again. And each vector is slightly out of phase with respect to its neighbor. The vectors successively reach a peak value, one after the other, before dropping down again. This successive peaking of each vector one after the other propagates the waves forward in the x direction, in analogy to what occurs when sports fans in successive seating sections of a stadium create a human wave (by successively raising then lowering their arms) that propagates the wave around the stadium. Such propagation is also similar to the propagation of waves in water described in Figure 2.2, except that the human wave circles the stadium while the waves in water move left to right until they hit the breakwater. The plane electromagnetic wave that we have described propagates forward in a straight line in the x direction at a velocity v, in this case inducing new E and B vectors in the space just ahead (visualized in new slices and planes). Note: people, molecules of water, or E and B fields in slices rise and fall or move in and out, but do not actually move in the direction of wave propagation.
The vector v shows the propagation of our electromagnetic wave from left to right along the x axis. For all electromagnetic waves, as determined by Maxwell and verified by experiments ever since, v will always have the same magnitude in empty space: the speed of light, approximately c = 300,000,000 meters per second; recall, in scientific notation we write this as 3 × 108 m/sec. (When electromagnetic waves propagate through media, especially for dense media, such as through glass in the case of light, the speed of propagation can be slowed somewhat.)
THE ELECTROMAGNETIC SPECTRUM
As noted earlier, the distance from positive crest to the next positive crest is the same for both the E field and the B field sine waves shown in Figure A.1 and is defined as the wavelength of the electromagnetic wave. I represent this wavelength by the letter w in Figure A.1(c). Were we to count the number of positive crests passing by per second as the wave propagates past us, we would measure the frequency of their passing. We represent this frequency by the letter f.
Note that the frequency, f, and the wavelength, w, are simply related. Because the frequency of the passage of crests times the length between crests is equal to the speed of the propagation c (in a vacuum always c, and very nearly so otherwise), we can write a formula for the relationship between f and w. In scientific shorthand: fw = c. So, if we know the frequency of a wave and wish to know its wavelength, then by dividing both sides of this equation by f we get the formula for w: w = c/f. Similarly, if we know the wavelength of a wave and wish to know its frequency, then by dividing both sides of this equation by w we get the formula for f: f = c/w.
The entire electromagnetic spectrum—from long-wavelength radio waves through microwaves, infrared (IR) light, visible light, ultraviolet (UV) light, x-rays to very-short-wavelength, high-frequency gamma rays—is defined in terms of wavelength as shown along the left side of Figure A.2.
Amplitude modulation, or AM, radios operate at frequencies in the range of one million cycles per second (one megahertz) with wavelengths about the length of a football field. Frequency modulation, or FM, radio waves in the range of 100 megacycles per second (100 megahertz) have wavelengths on the order of one meter. Microwaves have wavelengths an order of magnitude or two shorter, in the range of inches. Light spans a narrow range of wavelength of hundreds of nanometers (where one nanometer equals a billionth of a meter), while x-rays have wavelengths of tenths of nanometers, on the scale of the sizes of atoms. The presence of electromagnetic waves at frequencies in the microwave range and beyond is often referred to as radiation, and this term is even sometimes used to describe the broadcast of radio waves.
LASER LIGHT AND WHITE LIGHT
For any particular quantum of electromagnetic radiation, B vectors are always perpendicular to the E vectors, and both of these vectors are always perpendicular to the axis of wave propagation, in the manner shown in Figure A.1(c). But subject to these requirements, E (and B) can be at any orientation in a plane perpendicular to the axis of propagation. A collection of electromagnetic quanta needn't have a collective alignment or predominant polarization.
Multiple quanta can be produced, however, that all have sine waves of the same wavelength (and corresponding frequency), polarization, and phase (that is, having the crests of their waves all line up “in sync”). This synchronization, called coherence, has been produced in lasers with billions of quanta of light, with powerful and special effects, as described in Chapters 4 and 20.
While light resulting from the transition of electrons from and to specific states in specific elements may produce monochromatic light (of a specific polarization and wavelength and associated color), the light emitted from our sun and from hot bodies in general tends to conform pretty much to a (so-called) blackbody continuous spectrum of randomly polarized light. It was Planck's study of this blackbody radiation that kicked off the quantum revolution, as described at the beginning of Chapter 2.
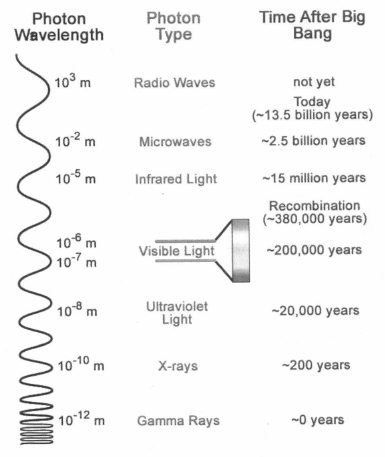
Fig. A.2. Electromagnetic radiation is delivered in quanta of energy called photons. The left column shows photon crest-to-crest wavelengths increasing (from the bottom to the top of the figure) a million million times, from high-energy gamma rays (at a wavelength of 10–12 meters) to the long-wavelength photons of FM radio waves (at a wavelength of about 1 meter). Gamma-ray photons present at the time of the big bang have had their wavelengths stretched by the expansion of space itself (see Chapter 9, Section II) to the point that today, 13.7 billion years after the big bang, we see these photons as a cosmic microwave background radiation with wavelengths in the microwave range, on the order of centimeters or inches. (Figure 12.7 of Big Bang, Black Holes, No Math, by David Toback. Copyright © 2013 by David Toback. Reprinted by permission of Kendall Hunt Publishing Company.)
