This chapter is divided into four sections:

I.Obtaining a Map of the Universe (Basically an Introduction to Understanding the Universe in Which Our Trip Takes Place)

II.Sightseeing (A Quick Tour through the Evolving Universe, from the Big Bang and the Very Small to the Present and the Very Large, with Stops Afterward to Explore Particular Sights, including Those Topics in the Title to This Chapter)

III.Key Aspects of the Big Bang Model

IV.Approaching the Big Bang (Creating the Conditions of the Hot “Quark Soup” just after the Big Bang, to Explore the Fundamental “Building Block” Particles of Nature and the Particles That Convey Nature's Forces)

Section I

Obtaining a Map of the Universe

(Basically an Introduction to Understanding the Universe in Which Our Trip Takes Place)

A. Space, Time, and Relativity

B. Models of the Universe

C. The Big Bang Model

A. SPACE, TIME, AND RELATIVITY

Orientation

We begin now what is probably the most difficult part of our trip: Subsection A of Section I. In this section we are going to briefly leave what most of us conceive of as our universe and enter another one, our actual world, that is forged in the realities of relativity and the quantum. I don't expect you to fully grasp what is presented here, but I need you to just “hang in” and listen, for this is the universe that we live in and what the big bang model describes. (I start with this orientation because I've found that tourists are often otherwise confused. They need this information up front.)

Special Relativity

We'll start slowly by describing some aspects of relativity. First note that observers who are moving relative to each other will get different results when making measurements in space and time. Such differences have actually been observed, as described in the box below.

Objects moving relative to us appear to us to shrink in the direction of their motion, and clocks moving with them are found by us to tick at a slower speed. We normally just don't notice these things, because at the low velocities that we deal with the changes in the objects and the clock are imperceptible. But we do see related effects in high-energy physics accelerators, where particle speeds approach the speed of light. And, with the precise instruments available to us in recent years, we can actually measure these effects even at the much lower speeds of airplanes.

Part of Einstein's genius was to recognize, as described in his theory of special relativity, that physics is the same for every observer and that we can use one frame of reference and relativity theory to correctly predict what observers in the other frames of reference will see. That frame of reference is a four-dimensional combination of space and time called space-time. (Here time is in some sense a fourth dimension along with the three spatial dimensions familiar to us: up and down, forward and back, and sideways). The problem is that we find it very hard to visualize four dimensions, let alone a fourth dimension in time. (Should you wish to get more than this vague sense of space-time, I recommend the very readable book by Barry Parker on Einstein and relativity.1)

General Relativity

Now, realize that the Newtonian classical physics (familiar to us) and Einstein's special relativity are both special cases of Einstein's general theory of relativity (henceforth “general relativity”). Special relativity describes relativity only as an approximation in the limit of small gravitational fields. And Newtonian physics is an approximation of special relativity that is accurate only in the limit of small relative velocities [and small gravitational fields]. But general relatively describes our world for all events whether in large or small gravitational fields and regardless of relative velocities. It predicts, for example, not only that clocks will tick more slowly for an observer when the clock is moving relative to that observer, but also that an observer will see the clock tick more rapidly if the clock is in a gravitational field that is reduced compared to the field at the observer. Here are just a couple of examples of what is observed.

The gravity of the earth diminishes as we move out from the earth's surface. On a hypothetical surrounding sphere twice the earth's diameter, the earth's gravity is 1/4 what it is at the earth's surface. On a sphere three times the earth's diameter, the earth's gravity is 1/9 what it is at the earth's surface, and so on.

Our global positioning system (GPS) works using 31 global positioning satellites that orbit 12,500 miles above our earth (on a hypothetical sphere of about four Earth diameters) and measure the time of flight of signals that they receive from our phones and other devices. From this collection of measurements, this system can normally indicate the position of our devices to within six inches. If corrections were not made for the effect of gravity, an accumulated error in the measurements over the course of a day might total six miles.

And the clock in an airplane, when taken to an altitude of, say, 30,000 feet, will actually tick faster (rather than slower) to an observer on the ground when compared to a clock at the earth's surface. That is because the lower gravity's tendency to make the clock run faster will, at that altitude, be greater than velocity's tendency to make it appear to run slower.

These are interesting effects to illustrate that relativity theory predicts and explains actual observations. Just examples. There is much more to it.

Now Comes the Overarching Concept

As with quantum mechanics, general relativity has successfully described nearly every aspect of our universe in which it has been tested. And general relativity's role in cosmology is profound. Space-time is part of our universe. It is influenced by, and influences, the matter and energy within it.

As the physicist and writer Bojowald describes it: “The form of space-time is determined by the matter it contains. Space-time is not a straight, flat, four-dimensional hypercube extending unchanged all the way to infinity. Like a piece of old rubber, it writhes under its own inner tensions into a curved structure. The inner structure of space-time is the gravitational force.”2 (According to Einstein, gravity is not a force, but it appears like one because of the curvature of space-time.³ This is a really counterintuitive concept, shocking even to physicists when it was first introduced. More on this later. Despite the fact that they now recognize and use curvature as Einstein does in their explanation of gravity, many physicists and cosmologists still tend to refer to gravity as a “force.”)

Later, referring to Einstein's accomplishment, Bojowald writes: “Promoting space-time from a mere stage, serving only to support the change of matter, to a physical object in the theory of relativity is a revolution.” And “the role of space-time, now seen as a physical object, is often compared to a novel in which one of the characters is the book itself.”4 (Pretty heady stuff!)

This then is the relativistic framework of the universe that we explore. Its evolution has been shaped by relativity (and, as you will see, also the quantum), because that's just the way the universe is. “Theory” and “modeling” are only our tools for understanding what we observe.

Einstein assumed that our universe is roughly the same everywhere. This has come to be known as the cosmological principle. He also assumed that there is no center to the universe and that any place in it (on a grand scale) is pretty much comparable to any other. This is known as the Copernican principle.

The latter principle is named with reference to the observation and calculations by Nicolaus Copernicus in 1543 (which he only dared release on his deathbed), that the earth is not the center of the universe. The idea of an earth-centered universe was generally believed at the time and taught specifically by the Catholic Church, since that idea generally supported the biblical text. Galileo, sometimes called “the father of science,” who observed the skies with his own telescopes, spoke and wrote in support of the Copernican idea. He was tried by the Roman inquisition in 1615, was forced to recant his views, and then was placed in house arrest for the remaining nine years of his life.)

Including these assumptions, Einstein found that general relativity predicted either an expanding or a contracting universe, unless he adjusted a “cosmological constant” that would allow him to get the result that he expected at the time—a static universe, neither expanding nor contracting.⁵

But the Russian mathematician and meteorologist Alexander Friedman and the Belgian Jesuit priest Georges Lemaître later used Einstein's equations and concluded that the universe began “as a tiny speck of astounding density…which swelled over the vastness of time to become the observable cosmos.”⁶ According to bestselling author Brian Greene (writing as professor of physics and mathematics at Columbia University), Einstein faulted Lemaître for “blindly following the mathematics and practicing the ‘abominable physics’ of accepting an obviously absurd conclusion.”⁷ It was only a couple of years before observation resolved the issue.

We board the bus to the planetarium. From here on, because it's easier for us to visualize and we'll lose little in meaning, we'll usually talk of our familiar space and time, rather than “space-time.”

B. MODELS OF THE UNIVERSE

At the Planetarium—The Expansion of Our Universe

Here we first look at the stars and the galaxies, as was done historically. Then we'll examine the model of our universe that will guide our tour later on.

Evidence for Expansion of the Universe

Strong evidence lies in the discovery by astronomer Edwin Hubble in 1929 of a Doppler redshifting (see the next paragraphs below) of the wavelength of light arriving from the stars of distant galaxies. This was some five years after Hubble obtained the first clear view of nearby galaxies that had been seen before in earlier, smaller telescopes only as faint, fuzzy nebulae.8 (Hubble used the 100-inch Hooker telescope located on Mount Wilson. Today, using radio telescopes, the Hubble telescope [named after Hubble, but placed in orbit around the earth long after he was gone] and many other types of instruments, we have evidence of some 100 billion galaxies in just that portion of the universe that we can observe. Though they vary greatly, each of these galaxies contains on average over 100 billion stars.)

Doppler shifts occur in waves of various kinds as they are emitted from moving objects. Speeders and baseball fans may know that radar guns use the Doppler effect. And some of us are familiar with the weatherman's observation of the movement of rain, snow, or hail using Doppler radar.

These devices work by sending out electromagnetic microwave pulses and observing the changed wavelength of their reflections. What we see from the stars is light that is emitted rather than reflected. But Doppler shifts for all electromagnetic waves occur in the same way that they occur for sound.

You may have noticed that the engine sound from a race car or the siren of a police car increase in pitch (frequency) when it moves toward you, then suddenly drops to a lower pitch as it passes and moves away. These changes in frequency are referred to as Doppler shifts.

Similarly, light emitted from an object moving toward us has an increased frequency (and decreased corresponding wavelength), while light emitted from an object moving away has a decreased frequency (and increased wavelength). Because red light is at the longer-wavelength end of the optical spectrum, this latter going-away shift is referred to as a redshift.

When Hubble used his telescope to look in any direction at distant galaxies, he found that the wavelength of the light gathered by the telescope is redshifted, indicating that the galaxies are moving away from us. (This would mean, for example, that the spectral lines shown in Figs. 2.8 and 2.9 would be shifted to the right.)

He also found that the more distant the light source (distance revealed by the intensity of light from Cepheid stars of known brightness), the more extreme is the redshift, indicating that those galaxies farthest away are moving away from us at even greater speeds. Though Hubble made his observations on a relatively few galaxies, what he concluded has been supported by all observations since then.

That these observations have been found to hold universally for faraway galaxies is now referred to as Hubble's law. The population of distant galaxies throughout space also looks pretty much the same, as far as we can see in any direction. What emerges from Hubble's observations is a picture of an expanding universe. Friedman and Lemaître were vindicated!

(I have been referring to “distant” galaxies moving away from each other in this expansion. For galaxies that are a sufficient distance apart, continued separation because of expansion dominates. But nearby galaxies can actually be moving toward each other faster than the local expansion of space pulls them apart. And so it is that our nearest-neighbor galaxy, Andromeda, is on a course to collide with our Milky Way in about four billion years.⁹)

Now, so that you have the rest of the overarching background, realize that within the expanding-universe scenario there are a number of mathematically defined, impossible-to-visualize, possible “shapes,” to the space-time of the universe, each having what is defined as “curvature.”10 Based on the shape and curvature, our universe might be viewed in different ways.

In his book Big Bang, Black Holes, No Math and in his course, Toback describes three scenarios, based on the density of matter and energy that can be directly seen in the universe.¹¹ Above a certain critical density, the expansion no longer continues and it contracts back to infinitesimal size in what he calls a “big crunch.” (Matter attracts and causes contraction.) With less than the critical density, it expands forever. With just exactly the critical density, it expands, but at a decreasing, “decelerating” rate. Well, the total of mass and energy that can be directly seen is woefully short of the critical density, so we'd expect continued expansion.

But Toback describes two more components to our universe, “dark matter” and “dark energy” (neither of which are directly seen, both to be described in Section III (B), toward the end of this chapter). As it happens, when these two components are included, the density of all known matter and energy in the universe is exactly 100 percent of the critical density. (Isn't that interesting!) Dark energy, which contributes 72 percent of this density, is inferred from observations in the late 1990s of an accelerated expansion. (As opposed to matter, energy can produce a repulsion, which spurs expansion.) Our best understanding now is that, until about six billion years ago, after a very short initial period of very, very rapid expansion called “inflation,” the expansion was slowly decelerating. But in the last six billion years, because of this dark energy, our universe has been expanding at a faster and faster rate. We call this recent period “acceleration.”

But we're at 100 percent of critical density, and, as described by Greene in his very popular book The Hidden Reality, 100 percent of critical density makes the curvature of the universe “zero.”¹² This zero curvature is referred to as providing a “flat” universe (not flat in any geometrical sense that we can visualize, though). Within this “flat” universe are two possibilities: either the universe is infinite in extent, or it somehow has an “edge,” in analogy to the edge of the screen of a video game. (Think about how Ms. Pac-Man crosses the left edge of the screen and suddenly appears way over on the right edge.¹³) Greene goes on to say that there is nothing that distinguishes between these two possibilities, but that physicists and cosmologists tend to favor the infinite extent (with no sort of edge). He then makes the case that infinite extent implies (as distinct from “many worlds,” which we described in Chapter 6) the existence of a “multiverse” of parallel universes, all identical to the one that we occupy, with identical occupiers and identical events transpiring in each. (This multiverse, and others, are beyond the scope of Quantum Fuzz, but [for those who may wish to explore further] I note that they are part of a set of topics included in Greene's already cited book The Hidden Reality: Parallel Universes and the Deep Laws of the Cosmos, Reference AA.)

Scientists use the following analogy to visualize how the expansion of our infinite universe might occur.

Suppose that we are baking an infinitely large loaf of raisin bread (infinite in extent as defined above, no edges.) We have a very large batter (the space of our universe) populated with an approximately uniform scattering of raisins (galaxies). We are in one of these raisins (the Milky Way galaxy). All that we see in any direction is other raisins, and the distribution of raisins as far as we can see in any direction is about the same. Our sight limitation defines a sphere that we will call our “observed universe.” We believe that someone sitting on another raisin would have pretty much the same set of observations and their own “observed universe.”

The batter (space) is expanding, causing the raisins to (in general) move away from each other. Those raisins already farthest apart move away from each other at the greatest speed, and those galaxies farthest from us move away from us at the greatest speed that we see. (However, raisins may also move slowly through the batter and in different directions. Locally, where the raisins near to us are being carried away by expansion very slowly, those with greater speed of movement through the batter toward us can actually be approaching.)

We postulate the following, based on the information supplied in our orientation earlier and Hubble's findings (with reference to our raisin-bread analogy):

1. The space (actually, space-time) of the universe is uniformly expanding at an accelerating rate, and its contents are (except locally) spreading apart because of that.
2. The universe is infinite in extent—no edges.
3. There is no center or preferred point of observation.
4. We can only know for sure what is within our sight, that is, an observed part of “the universe,” what we will henceforth call “our universe.”

Models of Our Universe

Until 1964, there seemed to be two strongly competing models of our universe that might explain Hubble's observations. There have been many models over time. We describe these two and keep one. Both were structured in conformance with general relativity and the key observations and principles listed and presented above.

As defined by Peter Coles (writing as professor of astrophysics at the University of Nottingham), theories are self-contained with no free parameters, but a model is not complete in this sense.14 To the extent that the model predicts what we actually observe, it may be considered successful.

The “Steady State” Model

This model was steadfastly defended by astronomer Fred Hoyle, among others.¹⁵ It went beyond the cosmological principle to a generalization called the “perfect cosmological principle.” Not only would the universe be without center anywhere in space, it would also be without a center with respect to time. The universe would be constantly expanding but always at the same rate. This process is called “continuous creation.”¹⁶ It would require the introduction of new matter at a steady rate to counteract the dilution caused by steady expansion.¹⁷

The “Big Bang” Model

This model differs from the steady state model in that the nature and rate of expansion of our universe substantially changes with time. However, as Coles points out: “Owing to the uncertain initial stages of the Big Bang, it is difficult to make cast-iron predictions and it is consequently not easy to test.”¹⁸ Nevertheless, for reasons that will be pointed out later, this is the model generally accepted today, and the one that we will use to guide us on our journey. So I describe it in much more detail below. (I understand that the label “big bang” was coined derisively by Hoyle in the heat of the argument over which of these models was correct.)

C. THE BIG BANG MODEL

Expansion and Cooling

We don't know what space-time was like at the beginning, we just speculate about what happened a short time after the beginning. The simplest models of the universe are of the big bang as a singularity (a point at which the mathematics predicts unrealistic infinities).

According to the big bang model, space-time at its beginning was imbued with an exceedingly hot, dense fixed amount of energy and fundamental particulate matter and antimatter (to be described later).19 This universe has expanded and cooled over a stretch of 13.7 billion years from a temperature of trillions of degrees or more at the beginning, at the big bang. The cooling has allowed an “evolution” through a complex of processes to produce additional particles and the constituents of the universe that we see around us today.

As defined by Toback: “the evolution of the universe—is essentially the story of two important facts: (1) as the cosmos expands, the energy of the particles in the universe drop; and (2) the way that the particles interact with each other critically depends on the energy of the particles.”²⁰

The cooling is manifested in expansion of the wavelengths of light (electromagnetic radiation) that occurs along with the expansion of the space of the universe that the light occupies. Longer-wavelength photons are lower in energy and show a cooler universe. They indicate the temperature of the matter with which they interact. (Remember the classical picture of electromagnetic waves and the definition of wavelength provided in Fig. A.1 of Appendix A.) The stretching of wavelength is illustrated schematically in Figure A.2, which shows high-energy, short-wavelength gamma rays at the bottom left (at essentially the same hot time of the big bang listed at the bottom right) stretched to the long-wavelength, low-energy cold microwaves near the top left (that we see today, as indicated at the top right).

Don't be fooled by the seemingly small amount of stretching shown at the far left. This is just schematic. Moving from gamma rays (with a wavelength of 10^–12 m) to microwaves (with a wavelength of 10^–2 m) means the wavelength has expanded ten billion times, which means our universe, correspondingly, has expanded ten billion times as well!)

The results of this stretching can be reported in terms of temperatures, as explained in the indented paragraphs below.

Electromagnetic radiation in the early universe would be constantly interacting with the particulate matter in its presence, being absorbed and reemitted in a constant exchange of energy. The spectrum of radiation in such an energy exchange, such a state of “thermal equilibrium,” has a particular shape indicative of the temperature of the matter with which the radiation is interacting. (It was the derivation of a theory to explain this spectrum of radiation that led Planck to postulate that light would be emitted in “quanta,” as was described in Chapter 2.)

So the temperature of matter in the universe is indicated by the spectrum of radiation at and around a particular wavelength. The wavelengths of electromagnetic waves in thermal equilibrium with particles of matter can thus be used as measures of the temperature of the matter involved.

It is customary in physics to use a Kelvin scale, which measures from the theoretical absolute zero of temperature, the lowest temperature that could ever be achieved. On this scale, the melting and boiling points of water occur, respectively, at 273 Kelvin degrees and 373 Kelvin degrees above absolute zero. Since water freezes at zero degrees Celsius, this means that absolute zero is at –273 degrees Celsius, or at –459 degrees on the Fahrenheit scale more commonly used in the United States. Where not otherwise specified, we'll be using a Celsius scale.

So, high-energy, short wavelength gamma-ray photons released just after the big bang would be characteristic of the trillions of degrees of the hot, dense universe at that time. And the low-energy, long wavelength, cosmic background microwave photons that we see today are indicative of the cool temperatures of deep space now, temperatures in the neighborhood of three degrees Kelvin—that is, three degrees above absolute zero, –270 degrees Celsius, or –453 degrees Fahrenheit. Cold! (We'll see later how these microwaves were found and examined.)

Maps of Expansion and Events

Phases of Expansion

The big bang expansion of our observed universe is depicted qualitatively in the sketch of Figure 9.1. In this figure, the largest observed size of the universe is projected forward and backward in time from what we observe now of its size as it was 0.5 billion years after the big bang21 (the point on the curve to the lower left of the diagram). Half of the 0.16 million-billion-billion-mile diameter²² shown at that point, is what we observe now to be the radius of the universe at that time. That radius is the distance then to the oldest stars and the farthest galaxies that we see now. We also know how fast the universe was expanding then, from a redshifting of the light from the stars in those distant galaxies.

We see these galaxies only now, because it has taken 13.2 billion years for light from those galaxies to reach us. That is why the rest of the curve, which indicates the growing distance of those same galaxies, is only a projection. The light leaving those same galaxies later than 0.5 billion years after the big bang hasn't reached us (and, as you will come to see, will never do so). And so the point at the upper right is only a projection of how that distance and size of the universe observed then will have grown until today.²³

The overall expansion since the big bang is divided into four phases:

1. Near uniformity,
2. (Cosmic) Inflation,
3. Slow Deceleration, and
4. Acceleration.

(Note: The labels for the second and fourth phases are in common use. I have coined the terms to describe the first and third phases. All but the near uniformity phase are visible in Fig. 9.1.)

The acceleration phase, during the last six billion years, is shown in the increasing slope of the curve at the upper right. We can tell that faraway galaxies are moving away from us at an increasing rate. Scientists suggest that this acceleration is driven by a mysterious “dark energy”²⁴ that will be discussed in Section III (B) later.

The slow deceleration phase shows the observed universe expanding at a nearly steady but slightly slowing rate.

The (cosmic) inflation phase is shown as the rapid rise of the curve at the lower left of Figure 9.1. Inflation is described next below and is better shown in Figure 9.2, which spreads out the very early times for better viewing.

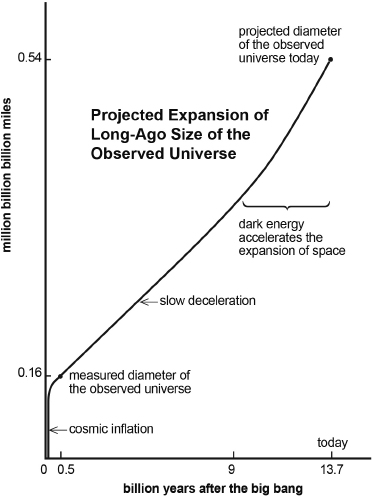
Fig. 9.1. Projected expansion of our observed universe.

The big bang model allows us to project backward from what we observe today of light from 0.5 billion years after the big bang (during the slow deceleration phase) to nearly the time of the big bang itself, suggesting that inflation would start a mind-boggling billion billion billion billionths of a second after the big bang and finish as early as 10,000 billion billion billion billionths of a second later.25 (That's early and that's fast!) Inflation in that short time would bring the projection of our observed part of the universe nearly to the size shown millions of years later at the start of slow deceleration.

The near uniformity phase would appear before inflation. This phase will be described shortly, also in relation to Figure 9.2 (just ahead). But we need to do some homework first.

To easily handle small measurements of time, like 10,000 billion billion billion billionths of a second (that is, 0.000,000,000,000,000,000,000,000,000,000,010 seconds), and to make readable the labeling of the axes of Figure 9.2, we use a scientific notation. With this notation, for example, we write this very, very, very small time much more simply as 10^–32 seconds. Since we will now be considering many more such small numbers in describing objects and events in time and space, and since we will also be considering huge distances and times, it seems appropriate to review again how we use scientific notation to simply describe both very small and very large numbers. And we'll include a review (once again) of a scientific shorthand for expressing physical relationships. Both methods will come in handy to make our reading easy in the pages ahead.

Remember first that the symbol c is used to refer to the speed of light, which we know from Einstein's formula E = Mc², for the energy equivalent of a mass of material. This formula, or equation, is just a scientific shorthand showing how E (energy) is related to M (mass) and c (the speed of light). Recall, c = 299,793,000 meters per second, where 299,793,000 is the number and “meters per second” is the set of units for speed, also written in shorthand as “m/s.” (Remember that a meter, the standard international [SI] unit of length, is just three inches longer than a yard. You may be familiar with the terms yardstick or meterstick for the rulers used to measure length.) The superscript 2 after the c in the equation simply means that c is multiplied by itself: that is, c × c.

To concisely express such large numbers as c, we'll be using scientific notation, in which we: (a) round off to the first few digits expressed in decimal form (2.998, for c) and then (b) multiply times the number ten raised to a superscript (“power”) given by the total number of digits that would follow the decimal point from where we put it in the original number. (This is the same as the number 10 multiplied by itself that many times.) So, in this notation, c = 2.998 × 10⁸ m/s. Rounding off further, we would have the more easily remembered c = 3 × 10⁸ m/s. (Here 10⁸ represents ten multiplied by itself eight times. We say that ten is “raised to the power eight.” Each added multiple of ten is referred to as another “order of magnitude.”)

We can express c in other units, for example c = 5.92 trillion miles per year, the number of miles traveled by light through space in a year's time. Scientists use the light-year, c × one year = 5.92 trillion miles, to describe very long distances. For example, ten light-years is ten times 5.92 trillion miles. It's just easier to use light-years, but miles is a unit that we can relate to, so I use it here.

We will also encounter some very small numbers: for example, as described earlier, the 0.000,000,000,000,000,000,000,000,000,000,010 seconds = 10,000 billion billion billion billionths of a second in which cosmic inflation occurs. (Note the thirty-one zeros before the digit 1, and then one more digit for the 1.) This number is just the number 1 divided thirty-two times by ten, or 1 divided by 10³², more simply written as 1/10³². And this can be even more simply written as 1 × 10^–32, where the minus sign in the exponent means “divided by ten multiplied by itself thirty-two times.” Or the number can be written still more simply as 10^–32, since 1 times any number is just the number itself. And, remember, 10⁰ is just the number 1 (any nonzero value set to the zero power is 1. (Note that 0⁰ is undefined.)

A Map that Expands Small Dimensions and Early Times

Figure 9.2 shows how matter coalesced after the big bang (lower curve, connecting the dots from left to right) against the backdrop of the projection of expansion in the size of the observed universe (upper curve).²⁶

Special Scales

Note that Figure 9.2 is not your ordinary graph. Here we use what is called a logarithmic scale in powers of ten to compress the display of time and distance. This is done so as to show both the smallest and largest measurements of both time and distance reasonably on one page.

To get an idea of the compression, note that the top three divisions along the y-axis (vertical, showing distance) represent first a billion miles, then the hugely larger billion billion miles and finally a million billion billion miles. Similarly, the rightmost two divisions along the x-axis (horizontal, showing time) represent 10⁷ (ten million) years and then the thousand times larger 10¹⁰ (ten billion) years.

The stretching out to show smaller and smaller sizes can be seen in the ten-billion-times (10¹⁰) reduction in meters for each mark along the vertical axis, starting with the 10¹⁰ meters mark just below the division for a billion miles, and proceeding downward beyond 10^–30 meters to include the Planck length of 1.6 × 10^–35 meters, represented by the plus sign at the bottom left of the figure. This is the theoretical minimum increment in the composition of space.

Similarly, the stretching out of the display of shorter and shorter times can be seen in the ten-billion-times (10¹⁰) reduction of seconds for each mark along the horizontal axis, starting with the 10¹⁰ seconds mark located just below the division for 10⁷ years, and proceeding leftward to include the Planck time of 5.4 × 10^–44 seconds, indicated by the same plus sign at the bottom left of the figure. This is the theoretical minimum increment in the composition of time. These tiny, tiny Planck increments in space and time have importance in the study of quantum gravity, string theory, and the earliest, densest and hottest moments after the big bang, as will be discussed later on.

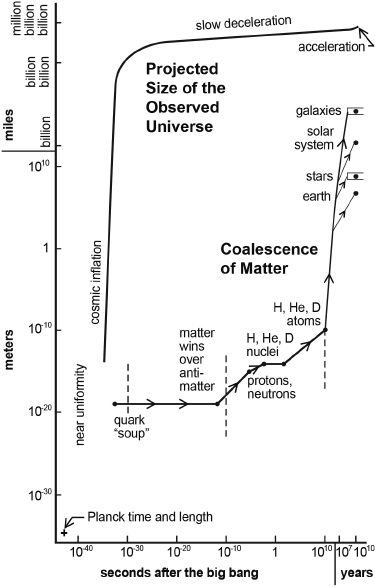
Fig. 9.2. The coalescence of matter in our expanding universe.

Note that the sharp cosmic inflation rise shown at the left of the figure curves over into a greatly decreased and slowly decreasing rate of slow deceleration, which (because of the extreme compression of large distance and expansion of early time in the scaling of this figure) appears as almost flat and unchanging.

To the left of the cosmic inflation shown in Figure 9.2 is the region of the first phase, near uniformity. Here the hot, first, crowded constituents of the universe would interact all with each other and achieve a near uniformity of distribution and a near thermal equilibrium (near uniformity in temperature). In the second phase, inflation would maintain this relative uniformity as it rapidly and substantially expanded the universe and the spacing of its constituents. Were this near uniformity of the first phase not there before inflation, it could never be established afterward, because a redistribution later would require that both particles and light move through space at speeds faster than the speed of light—which is impossible—to keep up with the expansion of space.

These two phases, near uniformity and (cosmic) inflation, together would seem to be necessary to explain the overall broad-brush uniformity in the distribution of mass and energy that we see throughout the universe today. (Remember the raisin-bread model.)

We now conclude Section I. We have our “maps.” It's time to go sightseeing!

Section II

Sightseeing

(A Quick Tour through the Evolving Universe, from the Big Bang and the Very Small to the Present and the Very Large, with Stops afterward to Explore Particular Sights, including Those Topics in the Title to This Chapter)

A.Sightseeing Bus Tour through the Universe

B.Formation of the Galaxies, the Stars, and Our Solar System

C.Black Holes, Their Evaporation, and Gravity Waves

We get on the bus for a quick tour of the universe.

A. SIGHTSEEING BUS TOUR THROUGH THE UNIVERSE (OUR UNIVERSE FROM THE BIG BANG UNTIL NOW)

This is analogous to taking a quick sightseeing bus tour of a city. As often is the case, the bus driver is also the tour guide. He provides a bit of background information as we start out, so that we better understand the sights in the context of the overall layout of the city.

Stages in the Coalescence of Particles

Note the three dashed vertical lines in the bottom third of Figure 9.2. These indicate not only certain events (to be described later) but also three regions of our trip. The fourth region, to the right of the rightmost dashed line, includes the elements, the earth, the stars, the galaxies—stuff pretty much familiar to us—and the atom as described on a deeper level in the first seven chapters of this book and Part Four to follow. Between that line and the middle dashed line is the realm of nuclear and particle physics, revealed to us through experiments first using “atom smashers,” ever larger and more sophisticated particle accelerators that have been built to break apart first the atom and then the nucleus of the atom into their constituent parts.

To the left of the middle dashed line in Figure 9.2 is a realm in which particle accelerators have created collision energies simulating the hotter and hotter conditions of the universe closer and closer to the early moments after the big bang. These experiments, guided by theory and then providing the bases for new theory, have revealed the fundamental particles that we now know. The process has led to the highly successful theoretical Standard Model that includes and describes these particles. (We discuss these particles, these accelerators, and the Standard Model in a later section of this chapter.) To the left of the leftmost dashed line, and particularly beyond the point showing the quark “soup,” we enter a region where what happens gets to be speculative.

Now, the bus driver begins to describe some of the sights as we drive past them.

We trace the coalescence of matter as the universe expands and cools from the near the beginning that is the big bang. We start at the left end of the lower curve with the quark “soup.”

Quark “Soup”

This “soup,” containing nature's building blocks, is expected to have formed nearly uniformly throughout space at about 10^–35 seconds after the big bang.27 It would consist of a very, very high temperature mix of energy, electromagnetic radiation, and fundamental particles of matter and antimatter—the stuff that in stages eventually make atoms and the substances, stars, and galaxies that we see around us. (Most of these particles don't make up things we see today. Included were a lot of second- and third-generation quarks and leptons and probably a lot of neutrinos that are still streaming through space, and perhaps dark matter. We'll stop to take a look at these fundamental particles later on.) According to Turner (to be introduced shortly), it appears that this quark soup was also “the birthplace of dark matter,”²⁸ to be discussed further ahead.

Antimatter

For every particle of matter, there is an antimatter equivalent. And matter and antimatter have a dangerously explosive relationship. When matter combines with its antimatter equivalent, for example, a (negatively charged) electron with a (positively charged) positron, they annihilate each other and leave behind a huge (for those two tiny particles) amount of energy. (Remember, E = Mc², and c is a large number, 3 × 10⁸ m/sec.)

Nobel laureate Richard Feynman, in his Feynman Lectures on Physics presented at Cal Tech over 1961 and 1962, jokingly made an interesting observation. Feynman pointed out that there should also be antiprotons and antineutrons, which together with the positron could, in principle at least, produce anti-atoms. While there might be a certain right-handedness to the direction of spin for the electron in the atom, it would necessarily be opposite, left-handed, in the anti-atom. If one of the anti-atoms should encounter an atom, the two would annihilate each other with the release of an enormous amount of energy (maybe ten thousand times the energy released from the electron-positron annihilation, because of the much greater masses of the atoms being converted to energy).

Feynman went on to reason that if there were anti-atoms, there should also be antisubstances, and antipeople. He wondered what would happen if aliens, perhaps Martians, had been constructed of antimatter: “What would happen when, after much conversation back and forth, we have each taught the other to make space ships [sic] and we meet halfway in empty space? We have instructed each other in our traditions, and so forth, and the two of us come rushing out to shake hands. Well, if he puts out his left hand, watch out!”29

Current theory states that matter and antimatter condensed out of the energy of the big bang in nearly equal proportions, but that matter had a minuscule edge; for normal matter, this would mean one extra quark for every billion antiquarks. (We'll learn about quarks and antiquarks toward the end of this chapter.) So when, at about 10^–11 seconds after the big bang, the universe had cooled sufficiently that matter and antimatter could interact, most of the matter and all of the antimatter annihilated each other into energy. That minuscule greater amount of matter that was left over formed the normal matter of the universe that we see today.

Protons, Neutrons, and Atoms

(Here we follow the narrative of Michael S. Turner, theoretical cosmologist and distinguished professor at the University of Chicago, who coined the term “dark energy.”) As Turner notes in his article titled “Origin of the Universe,”30 at about 10^–6 seconds after the big bang, after the universe had cooled to about a trillion degrees, “up” and “down” quarks formed protons and neutrons. These, during the span of 0.01 to 300 seconds, together formed the nuclei of the lighter elements, including hydrogen (H); helium (He); and the heavy isotope of hydrogen, deuterium (D), consisting of one proton bound to one neutron. Around 350,000 years after the big bang, these nuclei combined with electrons still present from the time of the “soup” to make charge-neutral atoms of the lighter elements. (“Charge-neutral” as distinct from the charged ions formed from atoms that have one or more electrons missing, stripped away, or added.) The combining of nuclei and electrons (a process called recombination) removed the free electrons that had been scattering light radiation, an event marked by the third vertical dashed line from the left, allowing the light throughout the universe to travel freely without scattering from the electrons. Wavelengths then continued to expand with the expansion of space, to produce the cosmic microwave background radiation that we observe throughout the universe today. (I'll describe this radiation and its significance toward the end of this chapter.)

Under the mutual attraction of gravity, the clumping of both dark matter and the atoms of these light elements then led to the formation of the galaxies and the stars within them. There is much to this process, including the formation of the planets, and we examine it more closely just ahead.

Energy and Matter

Realize that we have so far been describing mainly “normal matter,” which constitutes only 4.5 percent of the total of all matter and energy in the universe. Of this, 0.5 percent is found in the stars and the planets, and 4 percent in a more widely distributed gas of molecules.³¹ While normal matter consists overwhelmingly of hydrogen, with some helium, it also includes much smaller amounts of all of the rest of the elements (e.g., carbon, oxygen, nitrogen, iron, gold, etc.) and all of their constituent particles, many of them particles of the Standard Model, which will be described near the end of this chapter. Another 23 percent of the universe is dark matter,32 also described toward the end of this chapter. It forms an unseen “halo” around the core of each of the galaxies. That halo is believed to hold the galaxies together, and by its distribution to be responsible for the peculiarly high speeds of the outer stars in their rotation around the cores of spiral galaxies. The remaining roughly 72 percent of the total of matter and energy is the mysterious “dark energy,” believed to be responsible for an accelerated expansion of the universe displayed toward the top right of Figure 9.1 (as briefly discussed earlier and more fully discussed later in Section III (B)).

The bus driver lets us off now in the first of a series of stops at points of special interest, some of them the topics in the title of this chapter. Local guides take over at each of these places on the tour.

B. FORMATION OF THE GALAXIES, THE STARS, AND OUR SOLAR SYSTEM

The Seeds of Galaxy and Star Formation

Professor David Toback³³ (who wrote our foreword) uses a playful analogy to explain the clumping of atoms toward the formation of the galaxies and the stars that we see today. In his description, gravity is recognized as a distortion of space-time according to Einstein's theory of general relativity, a “dent” in the universe of four-dimensional space-time caused by the presence of a mass of normal matter of any size, even the mass of an atom.³⁴ (Again, for our purposes here, we can just think of a dent in space.)

We visualize the initial collecting of large amounts of matter to form a galaxy by thinking of little kids jumping on a trampoline…. Each child represents some mass (like an atom), and the trampoline represents space-time. As the kids jump, they create dents in the trampoline. If two kids collide, they fall into the trampoline and create an even bigger dent in space-time, making it more likely that other children will fall into that dent. As more kids fall, each dent gets bigger until everyone nearby falls into one of the giant dents.

It is the same way with matter. Essentially, once you get a big dent in space-time, all the nearby matter starts falling into it. These big dents are where galaxies form.

If the universe were perfectly uniform to begin with, star and galaxy formation would have been an exceedingly long process, much longer than the 13.7-billion-year age of our universe.35 But observations suggest that it took only half a billion years for the galaxies and stars to begin to materialize, which is a relatively short time. This would require a small local unevenness in the otherwise- even distribution of energy and particles in the near uniformity first phase of expansion just after the big bang. That unevenness, expanded, would later accelerate the clumping together of atoms and dark matter to make the galaxies and the stars within them. (More on dark matter farther ahead.)

The original unevenness is believed to have resulted from quantum fluctuations (to be explained later on in our discussion of black hole evaporation). But these fluctuations are calculated to occur only over tiny, tiny distances, also suggesting a compact, crowded universe in the initial near uniformity phase. Evidence for these quantum fluctuations is found today in a pervasive slight unevenness in the cosmic microwave background radiation (to be described later in this chapter).

Galaxy and Star Formation

The stars and the galaxies began to form at about the same time. Those expanded regions of space favored by the slightly greater initial energy and presence of mass, through gravitational attraction, would attract more and more matter as time went on, both regular matter (atoms) and dark matter (to be described later) to form clusters of galaxies. Within the clusters, regions favored even further by unevenness on a smaller but still considerable scale would attract atoms to form galaxies and the stars within them. (We'll talk more about the formation of stars and star evolution just a bit further ahead.)

Galaxies

Depending on circumstances, any of a number of types of galaxies may be formed. They all contain stars (which produce light), gas (just atoms) and mostly dark matter.36 We consider here two types as examples: “spiral” galaxies and “elliptical” galaxies.

For spiral galaxies like our Milky Way (shown in Fig. 9.3, which is included in the photo insert), collisions of some of the normal matter in its movement toward the galaxy center would create a relatively dense clumping of a region of stars near the center. Other normal matter would begin to swirl, rotating more or less uniformly about the center while spreading out in a large “equatorial plane.” The spiral arms of the galaxy are just a visual thing. They are places where there is more light, not more stars. The reason that there is more light is because the stars are younger there. The less-interactive dark matter would surround the center sphere in a very much larger unseen “halo.”

The larger elliptical galaxies would more often form from the collisions of smaller galaxies. Stars in these galaxies and in the cores of the spiral galaxies travel in orbits having all manner of shapes and orientations. One such elliptical galaxy is shown in Figure 9.4, in the photo insert.

Stars

Stars were formed through the gathering of more and more atomic material, mainly isotopes of the hydrogen atom, with a heating up as the atoms became compressed more and more under the increasing gravitational attraction of a denser and denser overall mass. At first, the agitation caused by this heating would break loose the electrons from their nuclei, creating a “plasma” of positively charged ions and negatively charged electrons. Then, if the star were massive enough, on reaching a sufficient combination of temperature and pressure, the nuclei at the more compressed and hotter core region would begin to fuse together to produce the nuclei of heavier atoms, at first fusing hydrogen to produce helium. If the star were still more massive, this process would continue, producing additional successive concentric cores emerging at the center to (at various rates) produce the nuclei of heavier and heavier elements, such as lithium, beryllium, boron, carbon, nitrogen oxygen, and so on up to iron (with twenty-six protons and thirty neutrons in its nucleus).37

In each of these “fusion” reactions, the sum of the masses of nuclei that join together is greater than the mass of the nucleus that is produced, and the difference in mass, ΔM, is released as a tremendous amount of energy, as described by Einstein's formula for the equivalence of mass and energy: E = ΔMc². So the star heats up even more than would occur under the heating of compression caused by gravity.

The fusion process ends with iron because, as explained with the quantum mechanics of the nucleus (described briefly later on), it is difficult to add nucleons to iron. In fact, adding nucleons to make heavier elements than iron produces an increase in mass, absorbing rather than producing energy and shutting down the fusion process. Said another way, forming nuclei beyond iron requires the input of energy. Processes in stars of sufficient size provide the needed energy to create the rest of the elements of the periodic table, as we'll discuss further ahead.

As will be described in Chapter 20, efforts have been underway to create fusion reactors, little stars here on Earth, by combining the nuclei of hydrogen isotopes and using the energy released to power turbines and generate electrical power. Though born of the same understanding that produced the (fusion) H-bomb, fusion used this way promises safe nuclear fusion power, using hydrogen isotopes found in either freshwater or seawater as an inexpensive and virtually limitless supply of fuel.

Note that the nuclear reactors that we already have now in our “fission” power plants exploit this process in reverse, by splitting the nuclei of atoms of the heavier elements like uranium into smaller nuclei and particles (a fission process), and using the energy released to produce electrical power.

Pressure produced by the compression of the collapse itself and the added heating due to the release of energy in the fusion process counters the tendency toward collapse of the star under its own gravity. Depending on how this balance sorts itself out for stars of various total masses, and on the stage of consumption of the nuclei undergoing fusion, various stable or unstable types of stars and star remnants are produced. We can follow what happens for three different ranges of star masses, starting with the middle range of stars, stars that behave basically as our sun behaves.

Stars more than 8 percent of and less than eight times the mass of our sun all evolve in a somewhat similar manner.38 They contract under the force of gravity until they heat up in a core region to about ten million degrees, at which point fusion begins. The added heating in the core, due to the fusion of hydrogen to form helium, creates a pressure that slows the collapse. Eventually an equilibrium is achieved at a fusion temperature and star size that depends on the star's mass. For our sun, that temperature is about fifteen million degrees, and the size is about what it is now, 872,000 miles in diameter, about 100 times the diameter of the earth. (The surface temperature of the sun is about 10,000 degrees.)

The star will stay in this equilibrium state until the hydrogen in the core is nearly consumed, at which point there is an initial collapse of the core under its own gravity as the expansive force of the heat of fusion reduces. The relatively quick collapse compresses the helium in the core to the order of a hundred million degrees, where the helium fuses to make beryllium and eventually the more stable carbon (even to make oxygen in stars having more than twice the sun's mass).

According to Gribbin, how this happens is “one of the most important discoveries in astrophysics (arguably, in the whole of science).”³⁹ In his book 13.8: The Quest to Find the True Age of the Universe and the Theory of Everything, Gribbin writes:

The problem is that beryllium-8 is unstable, and quickly splits apart to release two helium-4 nuclei (alpha particles). During the very brief time that a beryllium-8 nucleus (formed from a pair of colliding helium-4 nuclei) exists, it might be hit by another alpha particle; but it is so unstable that this ought to smash the beryllium-8 nucleus apart [not stick to it to make carbon-12]. And yet, if, hypothetically, beryllium-8 were stable, the calculations said that the production of carbon-12 would proceed so rapidly that the star would explode! Seemingly caught between the Devil and the deep blue sea, Hoyle found a way to strike a balance between the options of no carbon and too much carbon, provided that the carbon-12 nucleus has a property called a resonance, with a very specific energy, 7.65 million electron volts [MeV], associated with it….

Hoyle convinced himself that, although there was no experimental evidence for such an excited state of carbon-12, it must exist.40

And he further convinced experimental physicist Willy Fowler and his team at Caltech to check it out, which they did.

This was a sensational discovery whose importance cannot be overestimated. From the fact that carbon exists—indeed, from the fact that we exist—Hoyle had predicted what one of its key properties must be, and opened the way to a complete understanding of how the elements are manufactured inside stars.⁴¹

Fowler would in 1983 receive the Nobel Prize for Physics “for his theoretical and experimental studies of the nuclear reaction of importance in the formation of the chemical elements in the universe.”

The core's sudden further fusion and heating ignites fusion in the surrounding hydrogen shell, heating the rest of the surrounding hydrogen and propelling it outward in an expansion of the star to as much as one hundred times its initial size. The outer hydrogen cools in this expansion, taking on a longer-wavelength, lower-temperature, more red coloring in the light that it emits.⁴² Hence the term red giant for this stage of the star's life, which lasts 0.5 billion to a billion years. When fusion of the helium in the core is complete and all that is left is an “ash” of carbon (and for larger stars also oxygen), the core experiences a second collapse and an intense heating that blows away all of the surrounding hydrogen. This leaves the core alone as a very dense, white hot, but slowly cooling white dwarf,⁴³ at perhaps a hundredth the diameter of the star to begin with, and with more than half of its original mass; such a star would be so dense that a piece of it the size of a sugar cube (½” × ½” × ½”) might weigh several tons. Eventually, the white dwarf star will cool to the point that it will no longer emit any visible light, becoming in the end a black dwarf. But this cooling would take so long that no white dwarfs have ever reached this stage, and no black dwarf stars have been detected anywhere in our universe.

Our sun is 4.5 billion years old, and it is expected to convert to a red giant and then a white dwarf in another five billion years. (So we have a little while to plan for the future.) In general, the larger the mass of a star, the shorter its lifetime.

Stars less than 8 percent of the mass of our sun do not have enough mass to contract to a temperature that would start fusion. These stars are characterized as brown dwarfs, though strictly speaking they aren't stars at all, since their constituents don't undergo fusion.

Stars more than eight times the mass of our sun start out in a manner similar to their less massive brothers, but they have much shorter lifetimes and much more violent transformations at the end of their lives. Because of the much higher temperature created as one of these stars contracts under gravity, a succession of concentric cores form as the helium created from hydrogen is further fused to beryllium and then on to carbon, oxygen, and a succession of elements all the way to iron. Eventually all of the material in the core is converted to iron as the remaining “ash.”44 (The fusion process does not proceed to heavier elements than iron for the reasons described earlier.)

At this point, collapse occurs as it does for smaller stars, but the because of the greater mass of the larger stars, the collapse is not stopped by the mutual repulsion of electrons. The pressures in the cores are so great and the mix of particles so dense that electrons are pressed into combination with protons to produce neutrinos and an entire single core of neutrons. The intense gravity of the neutron core draws outer regions inward with such force that, combined with the energies of the neutrinos, a supernova explosion occurs that blows everything away except the neutron core. In the process, an entire spectrum of heavier elements including gold, platinum, and uranium are created. It is from an accumulation of these elements and everything else that is blown away that the planets of solar systems, such as our Earth, are created.⁴⁵ (Note that the dating of the oldest rocks found on our planet suggests that the earth has been around for about 4.6 billion years, about as long as our sun has been around.)

The light from such a supernova explosion can outshine for weeks or months the light emitted from small galaxies. The super-dense core that remains is called a neutron star.46 Here the density boggles the mind. A sugar-cube piece of this star might weigh as much as the entire Earth. If this remaining neutron star has more than three solar masses, gravity quickly overcomes the mutual repulsion of neutrons and the star collapses into an entity of even higher density, a black hole. If the star is massive enough, it can develop directly from the supernova into a black hole, without the intermediate stage of the neutron star. Toback compares the supernova to a dandelion: “At the end of its life, a dandelion—like a giant star—turns from yellow to white, eventually goes ‘poof!’ and sends its seeds out to create the next generation.”⁴⁷

We make the next stop on our tour.

C. BLACK HOLES, THEIR EVAPORATION, AND GRAVITY WAVES

Black Holes and the Event Horizon

The “discovery” of black holes began with theory. Applying Einstein's general relativity theory to see what would happen to huge masses like stars under the force of their own gravity, the Russian astronomer Karl Schwarzschild in 1916 calculated that a sufficiently large mass would shrink down indefinitely in size to higher and higher densities, eventually reaching a singular point in space-time.⁴⁸ (These mathematically obtained singular points of infinite density and infinitesimal size, for both the big bang and black holes, cannot represent physical realities. The challenge for physicists is then to find what correctly describes what happens here, at these small sizes [where quantum mechanics should work] and these high densities [where relativity should work]. Unfortunately, so far, these theories seem to be incompatible. We discuss, later on, efforts to resolve the issue.) The prediction of black holes is more commonly attributed to Subrahmanyan Chandrasekhar in 1931,⁴⁹ who in 1983 was awarded the Nobel Prize in Physics “for his theoretical studies of the physical processes of importance to the structure and evolution of the stars.”

The term black hole, coined by John Wheeler during a lecture in 1968,50 derives from general relativity's prediction that no things, not even light, can escape from within a given region of such enormous gravity. Hawking describes the black hole as follows:

Thus if light cannot escape, neither can anything else; everything is dragged back by the gravitational field. So one has a set of events, a region of space-time from which it is not possible to escape to reach a distant observer. This region is what we now call a black hole. Its boundary is called the event horizon and it coincides with the path of light rays that just fail to escape from the black hole.⁵¹

With regard to the last sentence, Toback explains the event horizon in a different way: “The event horizon for a black hole is the specific distance from the center where the velocity needed for escape is exactly the speed of light.”⁵²

According to general relativity, the trajectory of light is bent in the presence of a gravitational field. Inside the event horizon, gravity is so strong and the trajectory bent so severely that the light never leaves. And anything impinging from the outside and passing inside of this horizon is sucked into the hole, never to be seen again. Since nothing can escape from this region, particularly no light from the outside, the region inside of the event horizon appears to be black. The size of the event horizon and other characteristics of the hole's formation are all predictable from the mass, rotation, and net charge of the material that would form the hole.

Much is made in science fiction and in the movies of what might happen at the event horizon. Eventually an astronaut passing through the horizon would reach a place where his body would be stretched out and torn apart in a process that has been colorfully called “spaghettification.” We can see that as follows: If, for example, he were to drop toward the center of the hole feet first, the much-greater gravity on his legs would pull on him far more strongly than the lesser gravity at his head. The difference in gravitational attraction would be so strong as to stretch him out and rip his legs from his body.

“Smaller Bangs” in Reverse?

In recent times, the black hole has taken on added importance as an object that can be examined to learn more of the extremely dense and extremely hot conditions that would have been experienced in the early days of our universe after the big bang. One might even think of the black-hole-like collapse of a massive object to a singular point in time and space as being a small model of the big bang in reverse:53 the latter starting from a single, hot, energetic point in time and space and expanding and cooling to produce a coalescence of separate bits of matter as it grew in size.

Black-hole-like objects have been found, but only by inference from the way that they affect their surroundings. Being “black” (i.e., emitting and reflecting no light or matter), the objects simply cannot be seen directly. We classify them by the mass of energy and matter that they contain and the manner in which they affect their surroundings. I give here one example for each of two types of black holes.

“Stellar” black holes, the remnants of star collapse as described above, have been located from what would have been a pair of “binary” stars—except that one of the stars, now a remnant, a black hole, isn't seen. (The two objects rotate around like two dancers locked hand to hand and swinging around a point between them. But gravity, rather than locked hands, holds the two objects together in their rotation about the in-between point. The outward centrifugal force of rotation is countered by the inward attractive force of gravity.) These black holes usually have the order of several solar masses (where the mass of our sun is defined as one solar mass).

“Supermassive” black holes, with hundreds of thousands to billions of solar masses,⁵⁴ appear to provide the attractive force at the cores of spiral galaxies.

Perhaps the most visually striking evidence for a black hole comes from the light that is emitted from material as it is stolen from a nearby star and swallowed up or accreted into orbit around the hole, as shown in Figure 9.5, in the photo insert.

Gravity Waves

The recent detection of gravity waves, apparently from the merger of two black holes, may open the door to a new subfield of astronomy.55 Such waves have been recognized as a theoretical possibility since Einstein's general relativity indicated the elasticity of space. It has been suggested that they may arise from cosmic inflation, supernovae, pairs of neutron stars, and pairs of black holes. A collision and merger of two such black holes might for a time place them in rotation about each other. This could create ripples in space-time at the frequency of their rotation, and these gravity waves would be expected to propagate outward like the ripples of water in a pond.

In September 2015, two very large and extremely sensitive pieces of apparatus located half a continent away from each other were able to detect these ripples, in what became the first direct detection of gravitational waves, and, apparently, the first detection of such binary black holes. Both devices concurrently recorded a nearly identical disturbance at just the frequency of rotation that would have been expected if gravitational waves existed.

The test not only opened up an entirely new mechanism for viewing the cosmos but also confirmed once again general relativity and revealed black hole masses at 29 and 36 times the mass of the sun, larger than the few solar masses typical of stellar black holes.⁵⁶

While this is the first direct detection of gravity waves, there has been indirect evidence of their existence for some time. In 1974 the doctoral student Russell Hulse and his thesis advisor, Joseph Taylor, working at the Arecibo Observatory in Puerto Rico, discovered a rapidly rotating pulsar and a black companion star in a binary system having a loss of energy consistent with the emission of gravity waves. In 1993 they received the Nobel Prize in Physics “for the discovery of a new kind of pulsar, a discovery that has opened up new possibilities for the study of gravitation.”

Black Hole Evaporation

Light can be emitted as a black hole evaporates. In 1973, thirty-one-year-old Stephen Hawking shocked an (at first) incredulous physics community with calculations that showed that quantum fluctuations in the space just outside the event horizon of a black hole would cause the black hole to evaporate. As he describes this in the bestselling book A Brief History of Time, such fluctuations occur all the time in what appears to be empty space.57 Electric or gravitational fields, as described by quantum mechanics, can never really be truly zero, even as one might expect for nominally empty space. (If these fields were zero and unchanging, their rates of change would also be zero, and these certainties would violate the quantum physics embodied in Heisenberg's uncertainty principle.) The quantum nature of our world requires some uncertainty in the combination of the field and its rate of change.

So the fields fluctuate around a zero level. As you will see later on in the section on the forces of nature, fields are manifested in particles. So the presence of fluctuating fields will create short-lived pairs of “virtual particles,” in particular, photons for the electromagnetic field. One particle of the pair would have a small positive energy while the other would have an equally small negative energy, so no net energy is created.⁵⁸ Normally these particles would quickly recombine to leave space pretty much as it was. But when such a pair is created near an event horizon, the particle of negative energy (having insufficient energy to escape, see Chapter 11) may be sucked inside, decreasing the total energy and therefore the total mass of the black hole, while its partner, having positive energy, escapes into space. (Remember that energy is equivalent to mass through Einstein's E = Mc².)

So, in theory, with billions upon billions of these negative-energy particles being captured and the positive-energy particles being released as “Hawking radiation” into the surrounding space, the black hole continually loses mass and shrinks in size at a rate (as Hawking calculated) that increases as the mass of the black hole gets smaller. Hawking suggested that in the end the last remnant of a black hole would disappear “in a final burst of emission equivalent to the explosion of millions of H-bombs.”59 And if the virtual particles were photons, the escaping virtual photons would appear as if they were light escaping from the black hole. But, in fact, they would not have come from inside. Instead they would have come from just outside of the event horizon, thereby in no way violating the theory, which says that light cannot escape from inside the event horizon of a black hole.

Though other theorists have arrived at the same conclusions as Hawking, so the theory is pretty solid, black hole evaporation is very hard to find, and no one has actually observed or detected it yet. That is because black holes of substantial mass, say equivalent to that of our sun, radiate energy characteristic of objects at extremely low temperatures, on the order of 10^–7 Kelvin degrees. The much “hotter” cosmic microwave background, characteristic of a temperature of 2.7 degrees Kelvin, pumps much more energy (equivalent to mass) into such a black hole than Hawking radiation removes. But a small black hole having the mass, for example, of an automobile would shine with luminosity two hundred times that of our sun, but it would evaporate in the order of a nanosecond (10^–9 seconds), so you would have to be looking in the right place at the right moment. The search goes on: NASA's Fermi Gamma-Ray Space Telescope, launched in 2008, continues to search for these flashes, called gamma-ray bursts (GRBs).⁶⁰

Even without experimental confirmation, the theory is so strong that many physicists take black hole evaporation as fact. That led to a serious problem that threatened the fundamentals of quantum theory.

Information Destroyed? Quantum Mechanics Threatened?

As discussed in Chapter 8, all physical things are information. All the contents of the black hole are information. That being the case, black holes appeared to threaten both information theory and quantum mechanics. Here's how.

As Leonard Susskind, professor of theoretical physics at Stanford, describes it in his bestselling The Black Hole War,⁶¹ Hawking at a small meeting in 1981 dropped a “quiet bombshell”⁶² on the physics community by observing that the virtual particles escaping from a black hole would not carry away any of the information stored within the hole. (After all, they come from outside of the hole.) As the black hole evaporates away and disappears, the information within the hole disappears also. It would be lost. This violates a key property and tenet of quantum mechanics (and information theory) called unitarity, which includes that quantum mechanics can move forward and backward in time (the essence of quantum logic) and that information, like energy, is always conserved and never lost.63 (Relativity theory has no such unitarity tenet, and the basic relativistic description of the black hole would be unaffected.) This, more than anything that even Einstein and Schrödinger had put forward years before, might show quantum mechanics to be invalid or incomplete!

Susskind and colleagues eventually, over a period of sixteen years, came up with an answer to this challenge involving concepts well beyond the scope of this book: string theory (which I introduce only briefly later in this chapter), and the holographic principle.⁶⁴ It took another ten years for Hawking to accept that Susskind and company were right. (Hawking is apparently now a strong believer that the information in a black hole can be retained. In 2016 he published two articles in support of the idea, both in collaboration with colleagues Andrew Strominger of Harvard and Malcolm Perry of Cambridge University.⁶⁵)

The last stop on our sightseeing tour is back at the planetarium. There, we examine the big bang model more closely.

Section III

Key Aspects of the Big Bang Model

A.Expansion of Space

B.Dark Matter and Dark Energy

A. EXPANSION OF SPACE

As you are by now well aware, the big bang model is built around the concept of expansion of space. We describe here the prediction and discovery of the cosmic microwave background, the key piece of evidence for that expansion. Peter Coles, then professor of astrophysics at the University of Nottingham and author of Cosmology, A Short Introduction, describes this as the “smoking gun that would decide in favor of the big bang model”66 over the competing steady state model (that is described above in Section I (B)). In Coles's words: “The characteristic black-body spectrum of this radiation demonstrates beyond all reasonable doubt that it was produced in conditions of thermal equilibrium in the very early stages of the primordial fireball.”⁶⁷ The steady state model in no way accommodates such a cooling (change of the universe with time), nor is it supported by many of the other pieces of evidence in Section III. This discovery of the microwave background is not only a critical test but also a fascinating story describing scientists and their instruments and some of the best of physics in an interplay between theory and experiment.

The Theory

The scientists George Gamow and Ralph Alpher (in the 1940s) were finding it difficult to theorize an accounting of the relatively high percentage of helium in the universe compared to what might have been produced by stellar processes alone.⁶⁸ Alpher and Robert Herman in 1948, then at the Applied Physics Laboratory at Johns Hopkins University, considered the idea that radiation at the early time of the formation of nuclei might have an influence on helium production, and that this radiation, expanded as a “cosmic microwave background” (CMB) might be detectable.

A bit of scientist humor has been displayed in the contrived authorship of a paper by Alpher, [Hans] Bethe, and [George] Gamow, in a pun on the Greek letters “alpha,” “beta” and “gamma.” Gamow added Bethe's name (pronounced “beta”) to the paper that he and his student were writing.

Actually, we now know that the light would come not from the formation of helium but from a later time and process called recombination.69

In the very hot early universe, free electrons would scatter electromagnetic radiation. But when the universe cooled from the trillions of degrees just after the big bang to the order of 3,000 degrees 380,000 years later, these electrons would be almost entirely captured in the formation of atoms. Electromagnetic waves, at that temperature light in the visible range of the spectrum, could then exist for reasonable lengths of time and travel freely. If their presence now were simply the result of such travel through space starting then, we would see short-wavelength visible radiation characteristic of the temperature at that time, perhaps redshifted a bit, but not radically. But if the space that these waves occupied were expanding greatly, then the wavelengths of this light would be expanded with it, on the order of several hundred thousand times, until what we find today—the increased wavelengths (reading upward in meters) in the first column of Figure A.2. (Note that time since the big bang [indicated in the last column] and the wavelengths [in the first column] are not spread according to any consistent scales.)

Alpher and Herman predicted that an expansion of space from that time to the present would stretch the wavelength of the radiation emitted at wavelengths typical of 10,000 degrees to a pervasive microwave background radiation characteristic of a temperature of about 5 degrees Kelvin. (Remember, the wavelength of light can indicate the temperature of its surroundings, as described in the section on expansion and cooling, Section I (C).)

How the Evidence Was Found

At the time that they proposed this expansion, the astronomical community was not particularly interested in examining theories of expansion. In fifteen years or so, that attitude changed, and apparatuses began to be constructed to test the theory. Meanwhile, Arno Penzias and Robert Wilson at the Bell Telephone Laboratories in Holmdel, New Jersey, stumbled upon the microwave background.⁷⁰ On May 20, 1964, they made measurements confirming a pervasive radiation corresponding to 4.2 degrees Kelvin (essentially what Alpher and Herman had predicted). Recent, more accurate measurements have pegged this number to be 2.75 degrees Kelvin.

The two men, Penzias and Wilson, had built a sensitive instrument intended for radio astronomy and were testing it. They didn't know that they were looking at CMB at all, thinking it was extraneous electronic noise in their communications system. They also thought it may have resulted from bird droppings in the externalso f the apparatus. They only fully realized what they had measured when they took their findings to Robert Dicke, a noted physicist at Princeton who was actually building an apparatus to look for the CMB. When they published their findings, Penzias and Wilson did so alongside a parallel paper by Dicke on the interpretation of their results.

Fig. 9.6. Robert Wilson (left) and Arno Penzias (right) stand in front of their microwave horn antenna in Crawford Hill, New Jersey, in August 1965. (Image from AIP Emilio Segre Visual Archives, Physics Today Collection.)

Figure 9.6 shows Penzias and Wilson in front of the microwave antenna that they used to scoop-in and analyze the microwaves that they found. Their measurements were the same, regardless of the direction in which they pointed their apparatus. Those early measurements showed what appeared to be a uniformity in all directions of observed space. And because the spectrum of microwaves that were measured resemble what would be expected from radiation of cosmic origin, but with wavelengths stretched into the microwave range, their measurements support the big bang expansion of space as distinct from other expansion theories. In 1978, Penzias and Wilson would share the Nobel Prize in Physics “for their discovery of cosmic microwave background radiation.”

Quantum Fluctuations Accelerate Star and Galaxy Formation

Recent, More Precise Measurements

Recent, more precise measurements of the CMB radiation collected over a period of nine years (until 2012) show a slight unevenness in this background, which is indicative of a very small plus or minus 2 × 10^–4 degrees Kelvin (about 4 × 10^–4 = 0.0004 degrees Fahrenheit) unevenness in temperature. When this unevenness in temperature is converted into a variation in color, we see a “picture” of temperature variation throughout the observed universe like that shown as brighter to darker colors in the “sky map” of Figure 9.7(b), in the photo insert. This sky map has a construction similar to the map of the earth shown in Figure 9.7(a), except that the sky map is made from outward-looking observations and the map of the earth is from inward-looking observations.

Interpretation

This temperature map is evidence of the quantum nature of our world, of quantum fluctuations, even back to the time before cosmic inflation. The lighter and darker areas of this map are also consistent with the unevenness in the web of clusters of galaxies that we see today, in support of the suggestion that that acceleration of the formation of the stars and galaxies was ultimately caused by those quantum fluctuations. What is seen more directly in the CMB is an unevenness in the distribution of energy and particles at the time of recombination when the radiation observed today was released to be expanded in wavelength with the expansion of the universe. That relative unevenness, because of the magnitude and rapidity of inflation, would not have changed significantly from the unevenness that it grew from during the first near uniformity phase of expansion of our universe shown in Figure 9.2. And that unevenness at near uniformity is consistent with what could have been produced in that densely packed, small universe by quantum fluctuations. (Such fluctuations are discussed in Section II (A) in relation to black hole evaporation.)

The Galaxies

The web of galaxy clusters and the time of formation of the earliest stars and galaxies is consistent with the unevenness in the microwave background described above. And their movement away from us is consistent with the expansion of the universe as central to the big bang model.

B. Dark Matter and Dark Energy

As explained in Section I (A), the curvature and expansion of the universe depends on the density of the matter and energy in it compared to a critical density.⁷¹ As Toback describes it, with the use of several methods of measurement, “our best estimate is that about 5% of the critical density is from known particles (with atoms making up most of the 5%), about 23% of the critical density is in dark matter, and 72% of the critical density is in dark energy”⁷² that is believed to be responsible for an accelerated expansion of our universe.

Dark Matter

Dark matter may have formed in the quark “soup” in the early moments after the big bang.⁷³ As described below, its presence would explain the gravitational attraction needed to hold the galaxies together, and it would explain a number of other features of the galaxies. Dark matter isn't visible to us because it emits (and reflects) no radiation by which we can observe it.74

Dark matter, or something like it, seems to be necessary to explain gravitational effects on associated visible material. One of these effects is a strange, unexpectedly rapid motion of the outer stars and molecular clouds in rotation around the cores of spiral galaxies.⁷⁵ This motion indicates a substantial amount of unseen matter distributed widely throughout the region of rotation. Another is in “gravitational lensing,”⁷⁶ an effect predicted by Orest Khvolson in 1924,⁷⁷ and by Frantisek Link and, more famously, Einstein in 1936.⁷⁸ Light passing near a concentration of matter is bent in its trajectory in somewhat the manner that it would be bent in passing through an optical lens. Such a lensing around clusters of galaxies of light from faraway sources indicates the presence of far more matter than the normal matter seen in optical or radio telescopes.

From these and other effects, dark matter would appear to be distributed spherically around the cores of galaxies, with a density that lessens farther out from the core. This invisible spherical “halo” ascribed to dark matter is found to extend far beyond the visible halo of light from normal matter, suggesting different rates and mechanisms for the condensation of the two types of matter in the formation of the galaxies.⁷⁹

Toback mentions that dark matter may be part of a new, more fundamental class of particles suggested by a possible supersymmetry, to be described a bit more in Section IV (C).⁸⁰

Dark Energy and Accelerated Expansion

Dark energy is suggested as the reason for the apparent accelerated rate of expansion of our observed universe over the last six billion years.⁸¹ We call dark energy “dark” simply because we can't see it and “energy” because it is only energy (as opposed to matter) that can be responsible for expansion.⁸²

The acceleration has been calculated from the redshifting of the light from the explosions of distant Type Ia supernova. The measurements were carried out in the years preceding 1998 in what was called the Supernova Cosmology Project.83 Saul Perlmutter, Brian P. Schmidt, and Adam G. Riess, all part of the project, in 2011 were awarded the Nobel Prize in Physics “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae.”

Section IV

Approaching the Big Bang

(Creating the Conditions of the Hot “Quark Soup”⁸⁴ just after the Big Bang, to Explore the Fundamental “Building Block” Particles of Nature and the Particles That Convey Nature's Forces)

A.Introduction

B.The World's Largest Single Machines—Colliders and Their Particle Detectors

C.Particles and Antiparticles of the Standard Model

D.Relativity and Quantum Mechanics Clash

In Section IV we witness the impressive interplay of experimental observation, analysis, and synthesis of mathematically expressed ideas that has given us a very satisfying, self-consistent view of the fundamental nature of our world, the Standard Model. Humans seek this kind of understanding and scientists feel a particular need for it. Here you get a flavor of the depth and breadth of accomplishment of modern physics and the questions that still remain.

A. INTRODUCTION

The possibility of breaking apart atoms and their constituents in search of the most elementary of particles has led for many years to our building various types of more and more powerful atom smashers and accelerators. But the prospect of creating these undiscovered particles out of pure energy in search of what may have existed at the very beginning of our universe after the big bang has in recent times led to the construction of accelerators of ever greater size, complexity, and power.

For example, Barnett et al., in their book The Charm of Strange Quarks, observe, “any pair of matching particle and antiparticle can be produced any time sufficient energy is available to provide the necessary mass-energy.” (I'll describe antiparticles in Subsection C, just ahead.) As evidence they refer, for example, to a bubble-chamber photograph of the tracks of the creation of an electron/positron pair of particles from one high-energy photon. (You'll get a description of a more modern “drift chamber” in Subsection B.)

Remember Einstein's formula for the equivalence of mass and energy: E = Mc². Dividing both sides of this equation by c² still leaves this equation balanced and gives us E/c² = M, which is the same as M = E/c². Here M would be the combined mass of the electron and its antiparticle, the positron.

Colliders create beams of initial particles that are made to move in opposition at speeds approaching the speed of light.⁸⁵ Smashing them together creates new, more exotic particles to be examined. Among these are the fundamental “building block” particles of nature and the particles that convey nature's forces.

In Subsection C I will discuss the particles that have already been discovered, and other particles that may be expected. First, however, in this subsection (Subsection B), we examine how we find these particles, how we use colliders to create the hot, high-energy conditions that existed soon after the big bang. Here, we get a sense of the huge engineering effort that goes into making these massive and sophisticated instruments of particle physics. What we have learned with these machines is truly impressive, and, incidentally, a verification of quantum physics almost to the beginning of time.

Now our bus stops for a tour of an enormous and complex facility. We'll get to see hardware! But first the driver gives us an overview on these types of machines in general.

B. THE WORLD'S LARGEST SINGLE MACHINES—COLLIDERS AND THEIR PARTICLE DETECTORS

Colliders

Colliders have been built to maximize the amount of energy that goes into the creation of new particles. Because nature conserves momentum in any particular interaction, the net momentum of particles in the particle beams must be left in the products of collision. Any momentum left in products this way has its equivalent kinetic energy, and that energy does not contribute to the production of new particles. But if two particles can (ideally) be made to collide head-on with equal but opposite (in direction) momentum, because they are in opposition, there is no net momentum in their collision and no momentum or kinetic energy left afterward.86 In this special case, all of the energy of the colliding particles goes into creating new particles. Few collisions are head-on, but enough collisions are close enough to head-on for a large fraction of the energy of the collision to be available to create new particles.

Negatively charged particles can be accelerated by attracting them toward regions of positive voltage, in somewhat the same way as was crudely done by Thomson in his discovery of the electron, as illustrated in Figure 2.5. (There, the electrons are accelerated from the cathode at negative voltage through the ring at high positive voltage before entering the collimating slits at A and B.) For particles of positive charge, like protons, the electric field would be reversed and they would be attracted toward negative voltages, and they would be accelerated many times through separate successive rings.

But billions of colliding particles are needed. Unlike other types of accelerators that can hit, for example, fixed solid targets where atoms are densely packed, beams-hitting-beams in colliders produce relatively few collisions. The particles are tiny. The chances of their hitting each other are small. (Imagine two fast-moving mists passing through each other vs. a single mist hitting a solid wall.) Typically, the particles in the beams are created and accelerated in “bunches.”⁸⁷

Barnett et al. describe the historical challenge of creating a sufficient number of particles in the quest to find the “W boson” of the “weak force.” (This particle and this force are to be discussed in Section IV (C), to follow). Much of the accomplishment in high-energy physics is in building the accelerators to meet these kinds of needs. To create just ten W bosons would require a billion proton/antiproton collisions.

Carlo Rubbia, particle physicist and inventor, and technical physicist Simon van der Meer, with their team at the European Organization for Nuclear Research (CERN) near Geneva, devised and engineered the Super Proton Synchrotron (SPS) not only to accelerate protons and antiprotons to the energies required to create the bosons but also to provide an ample quantity of W bosons for detection and study. In 1984, they were awarded the Nobel Prize in Physics “for their decisive contributions to the large project, which led to the discovery of the field particles W and Z, communicators of the weak interaction.”

(The SPS is now used as an injector, a preliminary accelerator to get particles partway up to speed, for the much larger and much higher energy Large Hadron Collider, which will be described shortly).

In colliders, the trajectory of particles and particle beams is controlled using a basic property of nature: charged particles are deflected sideways when traveling through a magnetic field. If the area of the field is large enough, the trajectory of the particles can be continuously bent in an arc that closes on itself. So charged particles can be made to move in a circle. Particles of opposite charge (let's say + and –) can be made to move in opposite directions on essentially the same circular path using the same magnets. As particles increase their velocity, particularly into the high-speed relativistic range approaching the speed of light, the magnetic field strength has to be increased to keep them on their circular path. The magnets that bend the trajectory of the beam by providing a vertical magnetic field are called “dipole” magnets. The particles in the beams repel each other electrically, which is why keeping them focused requires an inward magnetic force toward the beam axis. Magnets producing a field configuration that provides that force and keeps the beam narrow and focused are called “quadrupole” magnets. These are placed in a regular fashion in line with the dipole magnets periodically around the accelerator ring.

Let's suppose a group of particles all of the same type and charge are created by some means, injected in localized groups, and accelerated to higher and higher speeds in the presence of the increasing magnetic field, to circle in one direction. Colliders accelerating particles of opposite charge circulate two such beams (each having a fairly localized group of particles of one charge) in opposite directions. Both beams are accelerated with identically increasing speeds, guided on their circular paths by an increasing field strength. Finally, the two beams are brought together so that their high-speed particles collide in opposition at the location of an appropriate detector that records what happens. (The Large Hadron Collider, to be described shortly, creates two beams of like charge accelerated in opposite directions around essentially the same circular track with the trajectory of each beam controlled by its own set of magnets.)

How Colliders Are Constructed

Now here is where the engineering comes in. In practice, the trajectories of the particle beams have come to be circular and miles in diameter. (Strictly speaking, they are not circles but a series of arcs joined by very short linear accelerator sections.) The beams are enclosed in evacuated tubes so that no other particles will interfere with their passage. The tubes, which are permeable to the magnetic field, are enclosed in a chain of very long, powerful electromagnets linked end to end around the entire circle. As these beams of particles are accelerated to higher and higher speeds, these magnets produce an increasing vertical magnetic field to guide the beam essentially all of the way around the circle. For control, to get the peak strength of field required, and to reduce the power needed to drive them to reasonable field levels, all of the magnets are wound using superconducting wire. (You will learn more about superconductors in Chapter 19 and in Chapter 24.) To operate in the superconducting state (that is, with zero electrical resistance) to these field levels, the magnets are maintained at a very low temperature, just a couple of degrees above the absolute zero of temperature, by having them enclosed in what are essentially Thermos bottles filled or otherwise cooled inside with liquid helium.

A cross section through one of the dipole-magnet sections of the Large Hadron Collider (LHC) is shown in Figure 9.8, in the photo insert. (Note that “Hadron” derives from the Greek word hadrόs, meaning “stout” or “thick.” It describes a family of composite particles composed of quarks held together by the “strong” force, as will be discussed farther ahead.)

In Figure 9.8: (1) The two (colored white) “pupils” of what appear to be “eyes” in the figure are the evacuated tubes through which the particle beams travel. (2) The pair of (colored brown) “irises” are the cross sections of the two sides of the dipole magnet's superconducting windings. (To accelerate the protons in the two beams in opposite directions, the magnetic field from one iris is up while the other is down.) The superconductors are actually small, rectangular cables of superconducting wires, each wound inside of one of the many (colored brown) sectors of the “irises,” traveling, say, in a direction that would be seen here as into the paper, the entire length of the forty-five-foot-long magnet in one sector to the right side of one of the tubes and returning in the equivalent sector on the left side, and around that loop again and again in that manner (crossovers at the ends of the magnets are not shown). (3) To keep magnetic forces from spreading the windings apart, they are enclosed in the (colored green) nonmagnetic, electrically insulating collars and “yoked” by (colored yellow) iron plates. (4) That assembly is enclosed in the inner lining of the Thermos-like inner (colored dark blue) structure. (5) The entire assembly is cooled by superfluid liquid helium at 1.9 degrees Kelvin, that is, just 1.9 degrees Celsius [or 3.5 degrees Fahrenheit] above the absolute zero of temperature, which, as noted earlier, is at –273 degrees Celsius, or at –459 degrees Fahrenheit. (Superfluid helium conducts heat without resistance in much the same way that superconductors conduct electrical current without resistance.) (6) The rest of the inner structure consists of a (colored tan) superinsulation (to reflect heat radiating in from the outside) between the inner and outer (colored light blue) cylinders of the Thermos bottle. (The design of cold components is in the realm of cryogenic engineering—liquid helium, liquid hydrogen, and liquid nitrogen, for example, being cryogens.)

Because the beams of charged particles are accelerated forward to increased speed, and accelerated sideways to stay on their circular trajectories, they emit radiation—lots of it. (Such acceleration is illustrated in Fig. 2.6 and discussed in nearby paragraphs. Remember, this acceleration and radiation is why the Bohr model of atom was flawed, as discussed in Chapter 2.) So, as a safety measure to protect both life and equipment during operation of the collider, the entire ring of tubes, magnets, and cryogenic enclosures is assembled and housed in an underground circular tunnel, appropriately enclosed for protection against the elements. Figure 9.9 shows the assembly of Figure 9.8 inside the tunnel. Figure 9.10 sketches the layout of the LHC ring, its experiment stations, and its preaccelerators. (All three figures can be found in the photo insert.)

A Comparison of the Latest and Future Colliders

Five generations of the most powerful recent, presently operating, and planned88 colliders are listed below.⁸⁹ These have already been introduced or will be introduced and/or described at various points in the remaining sections of this chapter. (Not shown in the table is the Superconducting Super Collider, which would have been much larger and more powerful than LHC. Construction was begun in Texas, but the project was canceled during the Reagan administration because it came to be viewed as too expensive.)

(The column labeled “Accelerated” displays colliding beams of: protons and antiprotons, pp [protons and protons], AuAu [gold ions and gold ions], CuCu [copper ions and copper ions], pPb [protons and lead ions], and PbPb [lead ions and lead ions].)

Many of the particles of the Standard Model of particle physics (to be described in the next section) were discovered using the Tevatron and other contemporary or earlier colliders and accelerators (not shown in the table above). The Tevatron, built at Fermilab near Chicago to smash protons and antiprotons together, was the most powerful operating accelerator in the period from 1987 until 2011, producing a maximum single-beam energy of one TeV, that is a million million electron volts. All in all, the construction of the main ring of the Tevatron in 1983 and then its upgrade in 1993 cost over $400 million.

Note that “Tevatron” derives from the collider's operation in the terra-eV (= million million electron volt) range of energy for each colliding beam of particles. Each particle in the beam can be made to achieve that energy before collision. As you will see with further discussion in Chapter 11, eV, the electron volt, is a commonly used measure of energy in atomic and particle physics. The energy of the violet photon emitted in transition of the electron from the n = 5 to the n = 2 state in the hydrogen atom (shown in Fig. 2.9) is approximately 3 eV. Five times that energy, 15 eV, will easily break an electron free of the atom. The Tevatron created particle energies more than 60 billion times larger, going beyond what is needed to split atoms, beyond the energy needed to break the nuclei of the atoms apart, beyond the energy needed to break their constituent protons and neutrons into their constituent quarks, and, finally, to the energy that is needed to create the (heaviest of all) top quark described in Figure 9.11 (in the photo insert), the last fundamental fermion to be discovered. (These particles are described in the following section of this chapter.)

The Large Hadron Collider

The latest particle collider to be built of the list above is the presently operating Large Hadron Collider. In 1998, construction was begun on the LHC at CERN near Geneva; at $4.4 billion, it is the most complex experimental facility ever built, and it is the largest single machine in the world. The LHC started operation in 2010, accelerating beams of protons in an underground tunnel that runs as deep as 574 feet below the surface, crossing under the French–Swiss border and then back through a circular trajectory that is over five miles in diameter. Opposing beams are collided to create and explore the behavior of particles at the energy densities experienced in the beginning fractions of a second of the existence of our universe, just after the big bang.

In all, 1,232 superconducting dipole magnets (each about forty-five feet long and weighing nearly forty tons) are positioned end to end to bend a beam of protons through its 5.3-mile-diameter accelerator ring. It circulates up to 2,800 bunches of protons with 118 billion protons in each bunch at up to 6.5 TeV per proton, for a total collision energy of up to 13 TeV per collision pair. At peak energy, the bunches of protons move at just 7 miles per hour slower than the speed of light92 (which is 3 × 10⁸ m/sec = 3 × 10⁵ km/sec = roughly 2 × 10⁵ miles per second, or 700 million miles per hour.

In 2012, using this facility, physicists found first evidence of a Higgs boson. (By that time, six quadrillion [6 × 10¹⁵] LHC proton-proton collisions had been analyzed. Since that time, additional work has found the Higgs boson to behave in ways predicted by the Standard Model, including that it has a zero spin.

Although one justification for construction of the LHC was to find the Higgs boson, the long-sought predicted particle of the Higgs field that would give particles their masses and complete the Standard Model (all of this will be discussed in Section IV (C)), the maximum design energy of the LHC far exceeds what was thought to be necessary for the Higgs. The extra energy may have provided a cushion on that quest, but it is now also opening the door to new particles and new physics, taking us a big step closer to understanding the big bang.

Particle Detectors

Creating particles is one thing. Detecting them is another. There are many kinds of particle detectors, and these may be chosen according to the types of particles to be detected. Or they may be built specifically for a particular experiment.

In some of these, the high-energy particles produced in the accelerator strip away electrons from atoms in a gas as they pass through it, leaving a trail of charged ions and electrons. The gas is in an enclosure called a “chamber” in a magnetic field that bends the trajectory of any particle with charge. From their trajectories we can determine the particle's momentum and charge.

In the boxed text below, I quote part of a paragraph from the book by Barnett et al., to outline just one example of a commonly used detector.

A drift chamber “contains many anode wires (wires at positive potential [voltage]), each surrounded by a grid of cathode wires (negative potential [voltage] relative to the anode wires). Each anode wire collects ions from the region between itself and the nearest set of cathode wires.”93 “The ‘drift time,’ that is, the time taken for the ion to travel from its point of origination to the wire, is proportional to the minimum distance between the track and the anode wire.”⁹⁴ And so, without going into further detail: from the measurement of this drift time for all of the ions created along the detected particle's path, we can determine where each ion started its drift, and then we can plot the particle's path.

Sometimes the sought particle isn't detectable directly, but it might have a “signature,” for instance, decaying into other particles in a particular way that can be detected. A good description of the sophistication involved in particle detection is provided in the article: “The Higgs at Last.”⁹⁵ (We'll learn about the Higgs in Section IV (C), just below.)

I won't go on. You get the idea—particle physics involves sophisticated experiments that require a lot of engineering and extensive construction (in addition to cadres of scientists, mathematical tools, and computer-automated tools to analyze massive amounts of data). But, what we have learned from these experiments is truly amazing, as you are about to discover.

C. PARTICLES OF THE STANDARD MODEL

In this Section IV (C), we make a very long story very, very short. Humankind has always been on a quest to determine what the substances of the universe are made of. The Greek word atom was used to describe the smallest piece of matter, something that literally could not be cut into smaller pieces. Starting in 1930, a “zoo” of subatomic particles was discovered. Today we know not only that atoms are composed of nuclei consisting of neutrons and protons surrounded by clouds of electrons, we know that the neutrons and protons are formed from different combinations of smaller particles called quarks. So far as we know today (although there is speculation to the contrary), the quarks and electrons are not composed of anything smaller, and so are considered fundamental particles.⁹⁶ There are many other fundamental particles, as will be described shortly. And, by 1970 most of the fundamental particles had been explained by theories that fit into what is called the Standard Model.

Now realize that all particles in our universe are of two general types.

Fermions97 are particles having half-integral units of spin (i.e., plus or minus 1/2, 3/2, 5/2, and so on). In nature, no two fermions are found to occupy the same state. (Remember the electron with spin ½, and the Pauli exclusion principle.) This leads to their being describable by a “Fermi” type of statistics (named after the physicist Enrico Fermi).

Bosons⁹⁸ (named by Paul Dirac after the Bengali physicist Satyendra Bose⁹⁹), are particles of integral spin (i.e., 0 or plus or minus 1, 2, 3, and so on). In nature, any number of bosons may be found to occupy the same state. This leads to them being describable by a “Bose” type of statistics.

Fundamental Particles and the Standard Model

Because of this universal division, the Standard Model includes two sets of “fundamental particles.” “Fundamental fermion” particles comprise the first set. Every one of the twelve fundamental fermions has a spin of ½. All other particles, all matter, is made up of one or more of these fundamental fermions. “Fundamental boson” particles comprise the second set. Four of the five fundamental bosons convey the forces of the fields responsible for the interactions between fermions, otherwise described as “mediating interactions among fermions.”¹⁰⁰ These four are called “gauge” bosons. The fifth fundamental boson is the Higgs boson. (More about the Higgs boson later on.)

The fundamental fermions and bosons have all been discovered in nature or created in the laboratory. They are listed in Figure 9.11, which is included in the photo insert.¹⁰¹ Not included in Figure 9.11 is a possible fifth fundamental gauge boson, the “graviton,” which would convey the force of gravity. But the graviton has not been found, nor has a theory been developed to formally project it. (More on the graviton toward the end of this chapter.)

At present, these fundamental fermions and bosons are all of the known fundamental particles. But it has been suggested that a “supersymmetry” exists that would have every fundamental fermion particle have a related fundamental boson particle. This would change our view of what is “fundamental,” and it should involve the existence of new particles as yet undiscovered but possibly in the range of energies that can be provided by the LHC and its successors. (Perhaps some of these particles are what we call dark matter.) We'll just have to see. New theory may be required. Regardless, I proceed here with what most scientists accept for now as the fundamental particles and the theories of the Standard Model that describe them.

In the pages ahead I am going to present the fundamental fermion particles first and describe some of their properties. Then I'll provide a very short history of how fermions and bosons were discovered. Next, after that, we'll count the number of fundamental particles. And finally, we'll examine the collection of theories making up the Standard Model that explain the fundamental fermions and the bosons responsible for their interactions.

The two sets of fundamental particles (as far as we know) comprise all of the fundamental particles in the universe. Together they make up all of the particles of the Standard Model. The model both incorporates and describes them. There are other fermions and bosons, but they are made up of fundamental particles and are not shown or discussed here. The fundamental particles are listed in their fermion and boson groups in the table for the Standard Model shown in Figure 9.11, in the photo insert.

Note that the electrical charge for all of the fundamental particles is given in Figure 9.11 at the top right of the round icon labeling the particle. And note that the mass of every particle in the figure is given below the round icon for that particle in millions of electron volts, MeV. For now, to get a feel for how massive the various particles are, just realize that the electron mass is about half an MeV.

Fermions are shown in the first three columns of Figure 9.11. Each successive column contains a successively heavier “generation” of fermions. With their antiparticles (to be discussed shortly), fermions comprise all that has been found or created in our universe of what is called “normal matter.”¹⁰² (Dark matter was considered in Section III (C), above.)

Bosons are listed in the last column of the figure. The top four of these bosons convey the forces of nature, as will be described later in this section. The fifth boson, the Higgs boson, is different, as will also be described later.

Fermions

The fermions are listed in two major subgroups: the first subgroup consists of the two families of quarks (both shown in red): those in the first row with +2/3 electrical charge, and those in the second row with –1/3 electrical charge. The second subgroup contains the two families of leptons (both shown in green): those in the third row all have zero electrical charge, and those in the last row all have a –1 electrical charge, including the familiar electron at the bottom left corner of the table.

All normal matter found in nature today is made of quarks or leptons, or matter constructed from them. Protons are composed of two +2/3 charge “up” quarks and one –1/3 charge “down” quark, yielding the net +1 charge that we observe. Neutrons are composed of one +2/3 charge “up” quark and two –1/3 charge “down” quarks, yielding the net zero charge that we observe. Protons and neutrons form the nuclei of atoms, with a net positive charge given by the number of protons. Those nuclei, surrounded by an equal number of –1 charge electrons make up the charge-neutral atoms of the elements. (When electrons are stripped away or added, what results is ions of positive or negative charge that are part of the fascinating chemistry to be described in Part Four of this book.) The properties of each type of atom, of each element, are related in fascinating ways (to be described in Part Four of this book) to the specific number of electrons or equal number of protons that they contain.

Fermions, Fields, Forces, and Bosons in a Historical Context

The Strong Force

How could it be that a nucleus that consists of protons each having electrical charge (and neutrons having no net electrical charge) can stay tightly bound together? After all, like electrical charges repel. The protons should push each other apart. The answer is that the nucleus is bound by a strong nuclear force, which is stronger than the electrical repulsion. This force was proposed by the Japanese physicist Hideki Yukawa in 1935. According to Yukawa, this force would result from neutrons and protons exchanging subatomic particles of a kind that at that time had not yet been detected. In 1949, Yukawa became the first Japanese to be awarded a Nobel Prize in Physics, “for his prediction of the existence of ‘mesons’ on the basis of theoretical work on nuclear forces.” But this was an intermediate result. We now know that the mesons, protons, and neutrons themselves are composed of fundamental particles called quarks, which produce the strong force by exchanging gluons.

Quarks, Gluons, and the Photon

Particularly throughout the 1960s and culminating in 1970, scientists examined the “zoo” of subatomic particles by cataloging them according to their properties. In a manner similar to Mendeleev's finding the pattern of the periodic table that then led to the understanding of electrons and the quantum mechanics of the atom, Murray Gell-Mann explained a threefold symmetry in the properties of the particles by postulating (and then explaining them theoretically) an entire set of fundamental fermions and force-exchange-particle bosons.103 To distinguish them he invented an imaginative new set of labels.

The fermions, he called quarks, borrowing the spelling from a line in Finnegans Wake by the Irish novelist James Joyce, “Three quarks for Muster Mark.”¹⁰⁴ The bosons he called (appropriately, it would seem) gluons. Six quarks occupy the top, leftmost group (in red) of the particles of the Standard Model shown in Figure 9.11. The first three to be discovered were named (strangely) “up,” “down” and “strange.” The gluon is shown as the second boson in the last (blue) column, after the familiar boson associated with electromagnetic radiation, the photon—and, like the photon, it has no mass.

The Electro-Weak Force, the Neutrino and W and Z Bosons

In 1930, Wolfgang Pauli suggested that “beta decay,” the observed transformation of a neutron into a proton and an electron, must be accompanied by the emission of an as-yet-unseen electrically neutral particle of ½ spin and having little or no mass.¹⁰⁵ Fermi in 1933 developed the theory of beta decay, describing the unseen particle as “the little neutral one,” in his native Italian, the neutrino,¹⁰⁶ what we now know to be the first-generation “electron neutrino” lepton type of fermion shown in the table. It wouldn't be until 1956 that neutrinos were actually detected, inside of a nuclear reactor that produced scads of free neutrons that might decay.¹⁰⁷

By 1970, theorists Sheldon Glashow, Abdus Salam, and Steven Weinberg (who would share the Nobel Prize for this), had combined the weak force with electromagnetism to produce the electro-weak theory, which included the W and Z bosons in conveyance of the force and predicted a fourth type of quark that they called charm.108 The W and Z bosons are shown second and third in the last column of bosons in Figure 9.11.

The Higgs Boson

Three groups of theorists working in parallel in 1964 came up with theories that predicted an unusual field, constant almost everywhere, that would allow existing particles to acquire mass. This eventually became known as the “Higgs field,” after one of the investigators, possibly because his theory described not only the field but also the associated particle. Their work was pretty much ignored initially. But as more and more particles began to be discovered during the 1970s, these theories came to be recognized and became one of the theories of the Standard Model.

Though the Higgs boson is not a carrier of force in the same sense as the other bosons, it is nevertheless listed with the gauge bosons of the Standard Model as the last particle in the last (blue) column of Figure 9.11.

Mass

Note again that the mass of every particle in Figure 9.11 is given below the round icon for that particle, as an energy in millions of electron volts, MeV. That is because of the equivalence of mass and energy—remember, E = Mc². (Again, just remember that the mass of the electron is about 0.5, and the numbers tell you how heavy the rest of the particles are compared to the electron.)

This conversion of energy to mass has already been discussed in the box dealing with colliders in Subsection B. It is interesting to note that the 0.511 MeV energy equivalent of the mass of an electron (shown under the icon for the electron at the lower left in Figure 9.11) is about thirty thousand times the roughly 15 eV energy needed to break an electron loose from the hydrogen atom. The latter is the sort of energy involved in chemical reactions. The former is the sort of energy involved in particle physics.

As noted before, any mass can be created out of pure energy. The top quark and the Higgs boson have masses the order of three hundred thousand times the mass of the electron. It takes a lot of energy to create these heavier particles. That is why the top quark was the last quark to be produced and discovered in the Tevatron, and why it has taken until the last couple of years and the LHC to produce the Higgs boson. Part of the energy delivered in collisions can come from the mass of the particles colliding. But most of the energy for the creation of new particles comes from the very high kinetic energy of the colliding particles, the energy of motion. With speeds for the colliding protons of the LHC approaching to within 7 miles per hour of the speed of light, about 700 million miles per hour, enormous energies are available.

“Color Charge”

Protons and neutrons are part of a family of particles called baryons, defined as “a hadron formed of three quarks”109 reflecting the threefold symmetry mentioned above in the discussion of the strong force. And quarks have never been found alone. Murray Gell-Mann postulated and then showed that the quarks would have another property that he called color charge, or simply color (not to be confused with electrical charge or the color of light): either a “red charge,” a “blue charge” or a “green charge” (named after the colors that combine to make the colors we see on our color television sets). The three color-charge quarks combine to produce the (exceedingly strong) strong force. Fred Bortz, physicist, science writer, and critic, describes this force: “Unlike gravity and electromagnetic forces, which decrease as particles move apart, the color force behaved more like a coil spring, pulling quarks together with increasing intensity the farther apart they became. This is the reason that bound quarks are inseparable.”¹¹⁰ Gell-Mann, by his labeling choices, made it so that the only way that quarks bind together is when they form a white composite. (Similarly, in a color TV, blue, green, and red make white.) The hadron may also contain additional quark/antiquark pairs,¹¹¹ which are also tightly bound together. One color charge and its anti–color charge together also produce white. Mesons are composed of one or multiple quark/antiquark pairs.

Antiparticles and the Number of Fundamental Particles

An antiparticle is predicted (and found) to have the same mass as its equivalent particle, but the opposite of all other particle characteristics; in particular, a positive electrical charge would become a negative electrical charge in the antiparticle.¹¹²

For example, each of the fermions has a partner particle (also a fermion) that mirrors its properties (as described in part earlier in the discussion of the evaporation of black holes, and with Feynman's humorous description of the meeting of Martians in space). The first indication that there should be such a mirroring came through the theoretical work of Paul Dirac, when in 1930 he used quantum mechanics and relativity to derive, from just its mass and its unit of minus charge, all of the rest of the properties of the isolated electron. His calculations also showed that there should be an antielectron with opposite (positive) charge.

This particle was found by Carl Anderson one year later in a cloud-chamber photograph of cosmic radiation. Dirac shared the Nobel Prize in Physics in 1933 “for the discovery of new productive forms of atomic theory,” and Anderson was awarded the Prize in 1936 “for his discovery of the positron.” Dirac's analysis, extended to the rest of the particles, would say that they all should have antiparticles, and these have also been observed as products created in particle accelerators.

Every particle of the Standard Model shown in Figure 9.11 has an antiparticle, so the total of fundamental particles is 34.

The Theories of the Standard Model

Whereas the big bang model has at its core general relativity, the fundamental particles of nature (now and as they existed in early times near to the big bang) are described through the quantum description of the fields of nature and their interactions. Each of the four fundamental fields interacts with matter through its associated gauge boson force carrier, those bosons listed first in the last column of Figure 9.11. The Higgs field is different in that its boson is not a purveyor of force and not a gauge boson.

Quantum mechanics applied to each of the fields is described below in order of its historical development. The first application to electromagnetism, is described in a little more detail to provide a sense of the way experimental and theoretical approaches came together.

(Remember: All of the fundamental particles and fields of the Standard Model have been found in nature or in particle accelerators. They behave as quantum entities. It's a quantum world. The theory just explains how that happens.)

Quantum Electrodynamics—Quantum Mechanics Applied to Electromagnetism

Recall that Bohr and Schrödinger developed their models of the hydrogen atom recognizing that a negatively charged electron would be attracted to the positive charge of the proton nucleus. Classical theory would say that the electron was attracted via the electric “field” that extended through space in all directions from the positive charge of the proton. Well, this view of how the forces would act, though useful for Schrödinger and still for most practical purposes, was changed with a further development of quantum mechanics, particularly, during a period of seven years starting in 1942, with an interactive effort including five physicists in the United States.113 One scientist in Japan worked on this alone.

The work started in the United States when twenty-four-year-old Richard Feynman, in graduate school at Princeton—and, independently, another comparably young New Yorker, Julian Schwinger—tackled a longstanding problem. Previous attempts to use quantum mechanics predicted that the energy of a charged particle in its own electric field would become infinite (exhibit a singularity). The work was also spurred when Willis Lamb precisely measured the spectrum of atomic hydrogen and found a tiny shift in results that couldn't be explained by any previous theory (the “Lamb shift”).

Schwinger would avoid the singularity using a mathematical process called normalization. Feynman realized that he could better describe the action of an electric field as resulting from virtual photons. In particular, the force between a proton (positive charge) and an electron (negative charge) would be viewed as a continual emission and absorption of a pair of virtual photons exchanged between the proton and the electron. (The photons are virtual because the sudden appearance of two real particles with mass [each equivalent to energy through E = Mc²] would violate the conservation of energy. What allows the existence of the two virtual particles is that they are an “uncertainty” in energy, ΔE. As long as their lifetime, Δt, is short enough, they can exist as described by Heisenberg's uncertainty principle applied to energy: ΔE × Δt < h [Planck's constant again]).

Both approaches and a third pursued independently by Japanese physicist Sin Itiro Tomonaga avoided the singularity and explained precisely the Lamb shift. In 1965, the three men received the Nobel Prize in Physics “for their fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles.” The resulting zero mass, spin = 1 photon, the gauge boson of the electromagnetic field, is listed as the first force particle in the last (blue) column of bosons listed in Figure 9.11.

In the course of his work, Feynman created simple diagrams to provide a good visual approach for conceptualizing particle interactions, and his summing-over-all-possible-paths method for calculating probable outcomes became standard practice for generations of physicists.114

Because of the insight and precision offered by quantum electrodynamics, Feynman called it “the jewel in the crown of quantum mechanics.”

The Electro-Weak Theory—Quantum Mechanics Applied to the Weak Force

The description of the “weak force” particles W and Z (presented earlier, responsible for one process of the decay of atomic nuclei) was integrated around 1970 with quantum electrodynamics into what became known as the electroweak theory. It is this theory that explains the beta decay mentioned earlier and the bonding together of protons and neutrons in the nucleus of the atom, radioactivity, and why many of the heavier elements are unstable. Sheldon Glahow, Abdus Salam, and Steven Weinberg received the 1979 Nobel Prize in Physics “for their contributions to the theory of the unified weak and electromagnetic interaction between elementary particles, including, inter alia, the prediction of the weak neutral current.” Their work was furthered by Gerrard ‘t Hooft, who would in 1999 share the Nobel Prize in Physics with his thesis advisor Martinus J. G. Veltman “for elucidating the quantum structure of the electroweak interactions.”

Quantum Chromodynamics—Quantum Mechanics Applied to Color Charge and the Strong Force

As described earlier, this theory was developed by Murray Gell-Mann in the 1960s to describe the strong force that binds together quarks to produce the proton and neutron constituents of the atomic nucleus, in this case through the exchange of massless particles called gluons. In recognition of this work, Gell-Mann in 1969 received the Nobel Prize in Physics, “for his contributions and discoveries concerning the classification of elementary particles and their interactions.”

The Higgs Field and Its “Carrier” Boson

While Gell-Mann was pondering the makeup of the neutron and the proton, Peter Higgs pondered where mass came from. As described earlier, in 1964 he and others proposed that the universe was filled with a third type of field, in addition to the fields of electromagnetism and gravitation.115 Most of the particles of the Standard Model would acquire their masses through their interaction with this Higgs field. (As noted earlier, other individuals and groups had similar theories and ideas.)

As noted above, fields of force have associated “carrier particles” labeled as “gauge bosons.”¹¹⁶ In a similar manner, the Higgs field would suggest a new carrier particle or particles, to be called Higgs bosons. The July 2012 finding of a Higgs boson is strong evidence confirming the Higgs field as part of the Standard Model. More studies are needed to further verify that this Higgs boson behaves in accordance with the Standard Model, and maybe that there is more than one type of Higgs boson, as predicted by other theories. However, the Higgs boson was sufficiently established that the development of the theory would be recognized in 2013 through the award of the Nobel Prize in Physics to Peter Higgs and François Englert “for the theoretical discovery of a mechanism that contributes to our understanding of the origin of mass of subatomic particles, and which recently was confirmed through the discovery of the predicted fundamental particle, by the ATLAS and CMS experiments at CERN's collider.” The latter's partner, Robert Brout, had died in the interim, or he too may have shared the prize.

D. THE CLASH OF RELATIVITY AND QUANTUM MECHANICS

In the course of our tour, we've followed the “map” provided by the very successful big bang model. At the core of this model is Einstein's general relativity, which is particularly successful in dealing with gravity, space-time, and the huge masses of the larger constituents of the cosmos. Later, we entered the realm of the Standard Model to explain the fundamental particles of matter and the forces of nature. This model has at its core quantum mechanics, which we know primarily as dealing with the very small. (Though actually it applies broadly.)

Quantum mechanics and relativity come together in two specific areas. First, as noted in the beginning of this chapter, gravity results from the curvature of space-time. But we talk in terms of a “gravitational field.” One might expect then that quantum mechanics could be applied (in the manner described above for the fields and the forces of nature) to predict and describe the existence of a carrier particle called the “graviton” (which has been suggested but not found). And, second, at the big bang and at the center of black holes we have the combination of very high density of mass and a very small size. Relativity applies to the density of mass, and quantum mechanics applies for small size. The logical question then is, might there be some “theory of both”? Would it resolve the mathematical singularities at the point of the big bang and the core of a black hole? Would it describe what actually happens there? Is there, to use Hawking's words, “a theory of everything”? The answer, for now at least, is no, not yet. There seem to be some deep-seated conceptual and mathematical incompatibilities.

Two general approaches seem to be followed in pursuit of a merger of theories toward answers of these sorts of questions. One is called loop quantum gravity; the other, string theory. Both may be considered speculative, though considerable effort has been invested in each. And both are far beyond the expertise of this author and the scope of this book.

So I end this tour now. But I would like to point the way toward your exploration of these topics. For each approach I recommend an interesting book and provide you with an introduction to the subject: In regard to loop quantum gravity, I recommend the book that I cited several times at the beginning of this chapter: Once before Time: A Whole Story of the Universe, by Martin Bojowald (Reference FF). In regard to string theory, I recommend The Little Book of String Theory, by Steven S. Gubser (Reference II).

LOOP QUANTUM GRAVITY

Loop quantum gravity (LQG) applies the ideas of quantum mechanics toward describing the universe, including gravity. Since gravity results from distortions in space-time, LQG is a theory of quantum space-time. It attempts to treat gravity as a field of force in the same sense that quantum mechanics successfully treated electromagnetism in quantum electrodynamics.

In LQG, space takes on a granularity in the graviton in the same sense that photons represent the quantized granularity of electromagnetic fields. (Remember Section IV, earlier.) Space takes on the nature of finite loops, on the scale of the Planck length, 10^–35 meters, woven into a network, or fabric. There is thus a smallest size to the elements of space.

This theory is being pursued in two general directions: spinfoam theory (covariant LQG) and canonical LQG. One consequence of the theory is that the evolution of the universe may be traced back to times before the big bang.

STRING THEORY

String theory has been an approach toward describing physical phenomena dating back at least to the 1960s, when it was used in an attempt to model the strong nuclear force. It was subsequently used to describe only bosons. Later, superstring theory was developed to show a connection between bosons and fermions in what is called supersymmetry (also mentioned in Section IV). In the mid-1990s, five versions of the theory were combined as parts of an eleven-dimension M theory; and in 1997, it was discovered that string theory may relate to quantum field theory.

Instead of particles, the fundamental elements of nature are minuscule, one-dimensional “strings.” Its properties are determined by its vibrational states, which give it charge, mass, and other properties. But the overall theory does not apply universally; it's more that the individual five theories work in an overlapping fashion, each applying perhaps with one neighboring theory to a particular area of physics. String theory also describes a multitude of possible universes. In that regard, I would suggest again that you read Greene's The Hidden Reality—Parallel Universes and the Deep Laws of the Cosmos (Reference AA). K. C. Cole in Quanta Magazine, September 15, 2016, describes how string theory has so far failed to live up to its promise of uniting gravity and quantum mechanics, but also suggests that the theory has produced significant advances in mathematics and other aspects of physics.117

In this book, Quantum Fuzz, we next turn to the practical results of quantum mechanics, for me its greatest gift. I show in Part Four how, based on a few simple concepts, quantum mechanics explains chemistry and the atoms of all of the elements, the building blocks of everything around us. In Part Five I describe the many inventions and practical products that are explained by or have directly resulted from our understanding of this theory, including levitated trains, atomic monolayer materials, MRI diagnostic medical imaging, and potential sources of unlimited power for the future.