Remember, all of our considerable understanding thus far of the electronic structure of the atom is based on our crude construction of tables from aspects of quantum mechanics: (a) the raw spatial-state solutions of Schrödinger's equation for the hydrogen atom (some represented by the “clouds” shown in Fig. 3.8 and Table I); (b) the +½ and –½ electron spin states found by Dirac; (c) exclusion; and (d) an additional consideration for the screening of an electron from the charge of the nucleus by the charges of the other electrons in the many-electron atom.

In this chapter we see how quantum mechanics goes much further than these tables in explaining the fascinating diversity of chemical and physical properties of the elements and their tendency to bond.

I sincerely expect that most of you will emerge from the reading of this chapter with a sense of wonder at the awesome beauty of nature. But I do need to let you know that we are about to discuss the physics of the many-electron atom in part on a conceptual level beyond what is taught in most introductory physics and chemistry courses.

From what you have already learned, you have an excellent background for understanding this material. However, should this chapter turn out to be a bit too “heavy” or detailed for you, I would suggest that you skim a bit to get a sense of what is presented here. If you decide to skim through, I suggest the following: read the unindented paragraphs, but skip Figure 14.1 and the indented paragraphs, and then read the sections titled “Putting It All Together,” and “Introduction to Appendix D” in the concluding paragraphs of this chapter, before you move ahead to Chapter 15.

THE HYDROGENLIKE PHYSICS OF THE MANY-ELECTRON ATOM

Here we deal conceptually with what happens to the states of the electron in the atom as we consider atoms of successively higher and higher atomic number, that is, atoms having more and more electrons (and, of course, by definition of atom, always in each case an equal number of more and more protons). Then we use this conceptual framework to understand the measured physical sizes and the chemical properties of the elements. I mainly describe groups of elements, but I highlight here and there the physics and chemistries of a few of the more interesting elements.

Recall that the electrons in an atom of any element have their own set of possible states somewhat similar to those described for hydrogen in Table I, each set with its own relative sizes somewhat similar to those shown for a few of the states of hydrogen in Figure 3.8. In principle (and, for the atoms of some of the elements, in practice) these states are the solutions (with the aid of computers and numerical approximation) of Schrödinger's equation for the many-electron atom. For these solutions, in addition to taking into account the electrostatic attraction of the negatively charged electrons to the positively charged protons in the nucleus, the equation includes the electrostatic screening (shielding) of this attraction from each electron by the negative charges of the other electrons (to the extent that the other electrons lie between that electron and the nucleus). The effective nuclear charge that the electron then sees is the charge of the protons minus that part of the charge (on average) of all of the other electrons that (for the spatial states that they occupy) lie between our electron and the nucleus.

Remember that in Chapter 13 we developed a generic table of states, Table II, for the many-electron atom, by recognizing in a qualitative way that the degree of penetration of each electron through this screening or shielding (i.e., the fraction of the nuclear charge that our electron still sees despite the screening) is different and shifts the energy levels differently depending on whether the electron is in an s, p, d, or f type of state. In the indented paragraphs below we examine in further detail how this happens, considering the physics of electron states and their energies. I generalize the results in unindented paragraphs that follow afterward.

(A) As we consider first the hydrogen atom and then successively the atoms of higher atomic number, we find that the states for each successively heavier atom are drawn down (compared to those of the preceding atom) to successively lower energies and smaller sizes by the increased attraction of the additional proton in each successive atom's nucleus. To begin to quantify this, we look first at the attraction of just one electron to a nucleus of Z number of protons, without the complicated screening that would result from the presence of the other electrons. (We will bring the effect of these other electrons into the picture later on.) Schrödinger's equation for the energies of the spatial states of the single electron can be solved exactly and gives us the formula

E = (–13.60 eV) × (Z)²/(n)²,

where the multiplier (Z)² shows the greater negative binding energy (with an associated greater attraction) of the larger number of protons. (This is the same expression that we used in Chapter 11 to calculate the energy levels for the Z = 1 hydrogen atom, but there “1” was substituted for Z so that we didn't see Z in the formula. Remember, just as described for the hydrogen atom in Chapter 11, there are 2 × n² combined spatial and spin states at each energy level n.)

In Figure 14.1, I show the results of calculations using this formula for three simple cases, each involving only one electron.

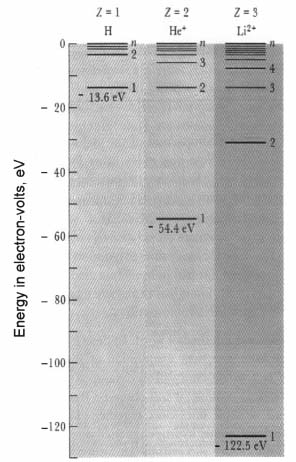
Fig. 14.1 Energy levels for singleelectron atoms and ions: for the Z = 1 hydrogen atom (first column), the singly ionized Z = 2 He⁺ ion (second column), and the doubly ionized Z = 3 Li²⁺ ion (third column). Note the fourand nine- times lower energies at all n = 1, 2, 3, and so on levels for the two ions, respectively. (Figure 14-11 from Fine and Beall, Reference E, with permission from Dr. Leonard W. Fine.)

Case (1) is the Z = 1 hydrogen atom, which of course is one electron around a nucleus of one proton. The negative energy of the n = 1, 1s, lowest energy, most tightly bound state of the one electron is (plugging in 1 for Z and 1 for n in the above formula):

E = (–13.60 eV) × (1)²/(1)² = –13.6 eV,

as shown by the lowest horizontal line in the first column of the figure.

The energies for the first few of the higher-n, higher-energy states for the electron in hydrogen are also shown in this first column. (We also calculated and tabulated these energy levels earlier, in Chapter 11.) Only the n = 1, n = 2, and n = nth of these levels are labeled in Figure 14.1. We show only a few of the infinity of states because the higher-n states become bunched closer and closer together as they approach a zero-energy level, so there is no room to include or label them. The labeling of the nth, topmost, state shown is meant to indicate that there are more and more states, an infinite number, with states eventually getting infinitesimally close to the zero level of energy as n approaches infinity. At zero energy, the electron is free, unbound, and no longer attached to the atom. As n approaches infinity and the energy levels of the states approach zero, the electron in these states is more and more weakly bound, and the probability clouds for these states are larger and larger in size (until the probability cloud for the electron is spread essentially everywhere, and the electron can be almost anywhere, is essentially no longer bound, and breaks free of the atom).

Case (2) is the Z = 2 singly-ionized He + helium ion, that is, the helium atom with one of its electrons removed so that the resulting ion consists of one electron around a nucleus having two protons. (Note that we continue to label an ion with the Z atomic number of the atom from which it is formed. Note also that the unbalanced plus charge [the valence] of the ion is indicated in the superscript following the symbol for the element. In general, the valence indicates the charge imbalance of an ion, plus by the number of electrons shy of matching the number of protons in the nucleus of the ion, minus by the number of electrons exceeding the number of protons in the nucleus.) The energies that are calculated for the electron states for the helium ion are shown in the second (lightly shaded) column of Figure 14.1. Note that the n = 1, 1s, lowest-energy state is

E = (–13.60 eV) × (2)²/(1)² = –54.4 eV,

four times the negative energy of the comparable state for the electron in the hydrogen atom.

Case (3) is the Z = 3 doubly-ionized Li 2+ lithium ion, with two of its electrons removed so that the resulting ion has one electron around a nucleus having three protons. The energies that are calculated for the states available to this electron are shown in the third column of the figure. Note that in this case the energy of the n = 1, 1s, lowest-energy state is at

E = (–13.60 eV) × (3)²/(1)² = –122.4 eV,

nine times the negative energy of the comparable state for the electron in the hydrogen atom.

(B) Comparing the energy levels for each quantum number n, we see in Figure 14.1 that the energy in each successive column is lowered further in proportion to the number of protons in the nucleus squared.

This is most easily seen by comparing the n = 1 energy levels for each of the three cases. A correspondingly greater electrostatic attraction of the electron to the nucleus and consequent tighter and tighter binding of the electron (smaller hydrogenlike probability-cloud size) occurs in each successive case. And this continues for heavier and heavier elements. Electron transitions from higher energy levels to the extremely low energy levels for the inner-electron states in the atoms of copper, Z = 29, and tungsten, Z = 74, is demonstrated dramatically in the production of x-rays (as described in Appendix E).

(C) When the removed electrons are replaced in the helium and lithium ions, so that we address them now as atoms with two and three electrons, respectively, the energy levels shown in the second and third columns of Figure 14.1 will be shifted upward to reflect the effectively smaller charge of the nucleus that is caused by the mutual screening of these added electrons. (By screening we mean that on average the other electrons spend some of their time partly between our electron [at whatever location in its probability cloud it might be on average] and the nucleus, so that our electron sees a net smaller positive charge equal to that of the positively charged protons minus that of the on average interfering fraction of the negative charges of the other electrons.)

(D) Similar proton attraction and screening effects occur for the electrons of the many-electron atoms of higher atomic number, that is, in atoms of the rest of the elements.

PUTTING IT ALL TOGETHER

And so we have an overall picture of what happens as we consider atoms of higher and higher atomic number. Nature always tends to seek an overall lowest-energy situation. For each successively higher-Z atom, electrons occupy successively one more state starting from the lowest and extending to higher and higher (less-negative) energy levels and larger and larger corresponding sizes within each atom's ladder of energy levels. At the same time, the whole ladder of energy levels is drawn down to lower energies and smaller sizes by each added proton in the nucleus. It's not an even process because the screening of the nucleus is uneven as the s, p, d, or f subshells of states are filled. It's as if the additional electron in the atom of each successive element reaches the next unevenly spaced (energy) rung on a ladder, while at the same time the entire ladder of state energy levels is being drawn downward and somewhat stretched because of the additional screened charge of the added proton in its nucleus. So, the topmost electron for one element on its ladder isn't a whole lot higher in energy and larger in size (if higher in energy and larger at all) than the topmost electron from the preceding element on its ladder. This is true even though the atom of the succeeding element has one more electron and this electron is on a higher-numbered rung of its ladder of energy levels.

As you can see, it's complicated. No wonder it has been so difficult to solve Schrödinger's equation for atoms having more than a few electrons, even by approximation methods using powerful modern computers.

INTRODUCTION TO APPENDIX D

Fortunately, as I describe in Appendix D, there is a way of directly measuring the energy levels of the outermost occupied states of the atoms of all of the elements. These measurements explain much of the chemical properties of the elements, the sizes of their atoms and the arrangement of the periodic table. (And with these we also see how the measured sizes of atoms are actually smaller and smaller as we successively consider heavier and heavier elements with more and more electrons within each period of the periodic table. In our periodic tables, each period is the span of a single row of elements.) Appendix D is a fascinating, partly visual, and triumphant conclusion to all that we have learned so far, but it's a bit too detailed to be presented here. Even though I have removed it from the main flow of the book, I nevertheless strongly encourage you to at least scan through to see what is there.

And realize that (from the quantum framework of the present chapter and earlier parts of this book) you already have the deep understanding of why we get these measurements and associated chemical behaviors. Specifically, our reading until now has provided an exceptional view into what electrons are; how the electron states get their sizes, their shapes, and these measured outer energies; and why the energies and associated chemical properties vary periodically as we consider successively atoms of higher and higher atomic number.

We see next how the properties of the outer electrons of the atoms of the elements determine some of the chemical bonds that may form between atoms, using just a few familiar, interesting examples of the metals and compounds that result from such bonding.