In Kapitel 4 haben wir die Korrelation als wichtiges Werkzeug besprochen, um versteckte Risiken (ereignisbedingte Risiken, die nicht aus dem Track Record hervorgehen) zu erkennen und zu beurteilen. Es bestehen allerdings beträchtliche Missverständnisse bezüglich der Frage, was Korrelationen anzeigen und was nicht. In diesem Kapitel nehmen wir die Korrelation und einige häufige Formen ihrer Fehlinterpretation genauer unter die Lupe.
Der Korrelationskoeffizient, der normalerweise durch den Buchstaben r (oder ρ) bezeichnet wird, gibt den Grad einer linearen Beziehung zwischen zwei Variablen an. Der Korrelationskoeffizient liegt zwischen -1,0 und +1,0. Je näher er bei +1,0 liegt, umso enger ist der Zusammenhang zwischen den beiden Variablen. Eine perfekte Korrelation von 1,0 tritt nur in künstlichen Situationen auf. Beispielsweise sind die Körpergrößen einer Gruppe von Menschen, die in Zentimetern gemessen wurde, und die Körpergrößen derselben Gruppe von Menschen, die in Zoll gemessen wurde, perfekt korreliert. Je näher der Korrelationskoeffizient bei -1,0 liegt, umso enger ist die umgekehrte Korrelation zwischen den beiden Variablen. Beispielsweise sind die durchschnittlichen Wintertemperaturen im Nordosten der Vereinigten Staaten und der Heizölverbrauch in dieser Region umgekehrt korrelierte Variablen (Variablen mit negativem Korrelationskoeffizienten). Wenn zwei Variablen einen Korrelationskoeffizienten nahe null haben, zeigt dies an, dass kein signifikanter (linearer) Zusammenhang zwischen den Variablen besteht. Dabei muss einem unbedingt klar sein, dass der Korrelationskoeffizient nur den Grad des Zusammenhangs zwischen zwei Variablen angibt, aber nichts über Ursache und Wirkung aussagt.
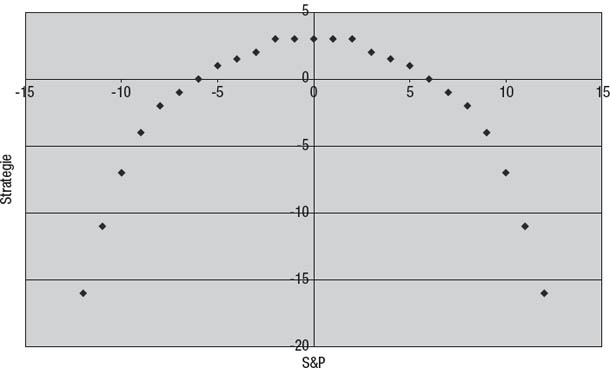
Korrelationen geben nur lineare Zusammenhänge an. Zum Beispiel zeigt Abbildung 9.1 die Renditen einer hypothetischen Strategie des Verkaufs von Aktienindex-Optionen (Verkauf von Calls und Puts, die aus dem Geld sind) im Vergleich zu den Renditen des Standard & Poor’s (S&P) 500. Calls, die unter dem Basispreis verfallen, und Puts, die über dem Basispreis verfallen, bringen dabei als Gewinn die kassierte Prämie ein. Optionen, die weit genug jenseits ihres Basispreises verfallen, ergeben einen Nettoverlust – je größer die Preisbewegung, umso größer der Verlust. Die größte Rendite bringt diese Strategie, wenn der S&P 500 unverändert bleibt. Sie bleibt so lange profitabel, wie sich der S&P 500 nicht wesentlich ändert. In unserem Beispiel (Abbildung 9.1) sind die Renditen der Strategie in dem Bereich zwischen -6 Prozent und +6 Prozent profitabel.1
Abbildung 9.1
Die Renditen der Strategie und des S&P 500 im Vergleich

Wenn die Preisänderungen über +6 Prozent oder -6 Prozent hinausgehen, werden die Renditen immer negativer. Abbildung 9.1 gibt zwar eindeutig eine enge Beziehung zwischen der Strategie und den Renditen des S&P 500 wieder, aber die Korrelation zwischen den beiden beträgt tatsächlich null! Warum? Weil eine Korrelation nur lineare Beziehungen wiedergibt und zwischen diesen beiden Variablen keine lineare Beziehung besteht.
Für das Quadrat des Korrelationskoeffizienten, das man als Determinations-koeffizient beziehungsweise als r2 bezeichnet,* gilt eine ganz spezielle
Interpretation: Er stellt den Anteil der Varianz einer Variable dar, der sich durch die andere erklären lässt. Wenn beispielsweise der Korrelationskoeffizient r eines Fonds zum S&P 500 0,7 beträgt, bedeutet das, dass sich fast die Hälfte der Varianz der Fondsrenditen durch die Renditen des S&P 500 erklären lässt (r2 = 0,49). Bei einem Investmentfonds, der ein sogenannter heimlicher Benchmarker ist – dessen Portfolio sich also kaum vom S&P 500 unterscheidet –, ist r2 sehr groß (zum Beispiel über 0,9). Das heißt, dass bei einem solchen Fonds die Änderungen des S&P 500 fast alle Änderungen des Fonds erklären würden.
Man muss unbedingt begreifen, dass der Korrelationskoeffizient r und der Determinationskoeffizient r2 nichts über Ursache und Wirkung aussagen. Unsere auf Ursache und Wirkung bezogene Auslegung dieser statistischen Zahlen beruht nur auf unserem theoretischen Verständnis des Prozesses, der ihnen zugrunde liegt. Dass eine signifikante Korrelation zwischen dem Stromverbrauch in New York im Juli und den dortigen Temperaturen besteht, liegt auf der Hand, weil sich die Temperatur auf den Stromverbrauch auswirkt und nicht umgekehrt. Aber wenn wir keine Ahnung hätten und feststellen wollten, ob die Sommertemperaturen in New York vom Stromverbrauch der Stadt beeinflusst werden, würde die Korrelationsanalyse auch diese absurde Behauptung scheinbar stützen. Somit gibt der Wert von r2 nur den Grad der Korrelation zwischen zwei Variablen wieder und belegt in keiner Weise eine Ursache-Wirkungs-Beziehung.
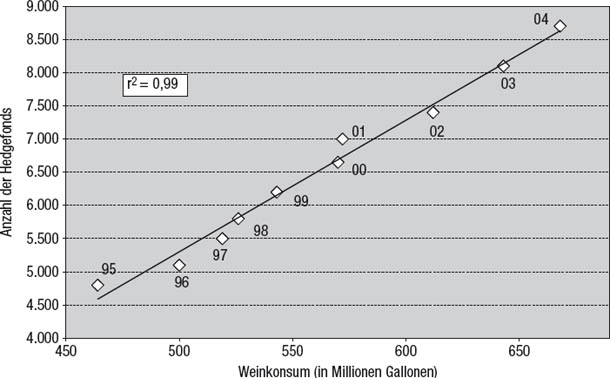
Wie töricht es sein kann, aus r2 eine Ursache-Wirkungs-Beziehung abzuleiten, veranschaulicht Abbildung 9.2. Anscheinend sieht man dort einen augenfälligen Zusammenhang zwischen der Anzahl der Hedgefonds und dem Weinkonsum in den Vereinigten Staaten. Tatsächlich beläuft sich r2 für die Zahl der Hedgefonds und den Weinkonsum in den Vereinigten Staaten auf hohe 0,99! Welche Schlüsse können wir aus diesem Chart ziehen?
Abbildung 9.2
Die Anzahl der Hedgefonds und der Weinkonsum in den Vereinigten Staaten
•Zunehmender Weinkonsum veranlasst die Menschen, in Hedgefonds zu investieren.
•Hedgefonds verleiten die Menschen zum Trinken.
•Die Hedgefonds-Industrie sollte den Weinkonsum durch Werbung fördern.
•Die Winzer sollten Investitionen in Hedgefonds durch Werbung fördern.
•Alle vier Schlussfolgerungen.
•Keine der vier Schlussfolgerungen.
Tatsächlich lässt sich die auffallende Korrelation zwischen Weinkonsum und der Anzahl der Hedgefonds ganz leicht erklären. Beide Variablen wurden im dargestellten Zeitraum von einer gemeinsamen dritten Variable beeinflusst. Daher haben die Anzahl der Hedgefonds und der Weinkonsum in diesem Zeitraum ausgeprägte Wachstumstrends erlebt. Die scheinbare Beziehung rührt daher, dass die Trends gleichzeitig stattfanden. Eine solche zufällige lineare Beziehung bezeichnet man als „unechte“ oder „unsinnige“ Korrelation. Die Korrelation ist ja eigentlich real, nur ihre Auslegung im Sinne von Ursache und Wirkung ist unsinnig.
Das Bisherige soll betonen, dass man bei der Interpretation der Konsequenzen von Korrelationen vorsichtig sein sollte. Die Tatsache, dass ein Fonds signifikant mit einem Index korreliert ist, bedeutet nicht unbedingt, dass die Strategie des Fonds von diesem Index abhängt, sondern nur, dass sie davon abhängen kann. Es ist ja absolut möglich, dass die Korrelation auf einer gemeinsamen dritten Variable oder gar auf Zufall beruht. Je kürzer der Track Record, umso größer die Möglichkeit, dass eine offensichtliche Korrelation vielleicht nicht bedeutsam ist. In ähnlicher Weise bedeutet die Tatsache, dass zwischen zwei Fonds eine signifikante Korrelation besteht, nicht unbedingt, dass sie ähnliche Strategien verwenden oder den gleichen Risiken ausgesetzt sind, sondern vielmehr nur, dass dies der Fall sein könnte. Da viele Fonds nur kurze Track Records haben, ist die Wahrscheinlichkeit, dass man zumindest auf ein paar unechte Korrelationen stößt, ziemlich beträchtlich. Deshalb sollte man Korrelationen eher als ernst zu nehmende Anzeichen für mögliche Risiko-Exposures betrachten anstatt als schlüssige Beweise dafür.
Oft zeigen Korrelationen nicht das, was die Menschen glauben, und es kann sein, dass die Verwendung von Korrelationen beim Filtern von Investments nicht das gewünschte Ergebnis bringt. Die Abbildungen 9.3 und 9.4 zeigen die Renditen zweier hypothetischer Fonds im Vergleich zu den Renditen des S&P 500.2 Welcher Fonds hat demnach eine engere Korrelation zum S&P 500? (Ein Tipp: Fonds A steigt immer dann, wenn der S&P 500 steigt, und er fällt immer, wenn der S&P 500 fällt.) Doch halt: Lesen Sie erst weiter, wenn Sie diese Frage beantwortet haben.
Abbildung 9.3
Fonds A im Vergleich zum S&P 500
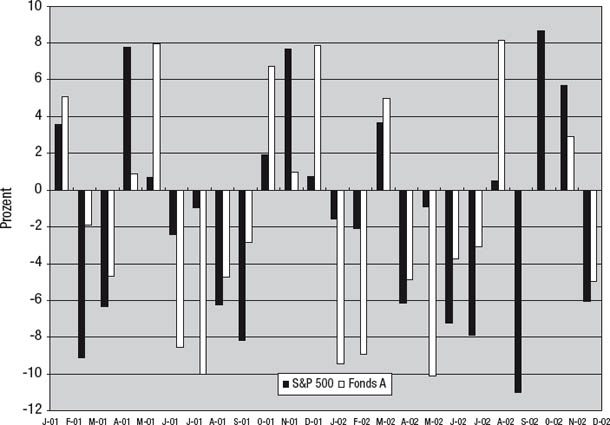
Abbildung 9.4
Fonds B im Vergleich zum S&P 500
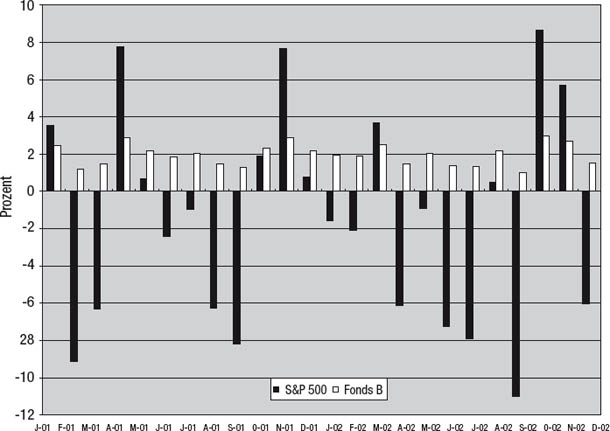
Falls Sie meinen, Fonds A sei mit dem S&P 500 korreliert, haben Sie recht: r = 0,41. Diese Korrelation ist allerdings recht mäßig und liegt wahrscheinlich weit unter dem, was man bei der Betrachtung des Charts annehmen könnte. Die eigentliche Überraschung hat allerdings mit Fonds B zu tun, denn er besitzt eine Korrelation von 1,0 zum S&P 500. Doch wie kann das sein? Wie kann Fonds B perfekt zum S&P 500 korreliert sein, obwohl er nie fällt, wenn der S&P 500 fällt?
Abbildung 9.5 trägt die Renditen von Fonds B und des S&P 500 in aufsteigender Folge der Renditen des S&P 500 gegeneinander ab und daraus geht hervor, was passiert. Man sieht, dass die Renditen von Fonds B steigen, wenn der S&P 500 steigt. Aus diesem Grund ist Fonds B perfekt zum S&P 500 korreliert. Dabei ist jedoch eines festzuhalten: Nicht einmal eine perfekte Korrelation muss bedeuten, dass ein Fonds wahrscheinlich fällt, wenn der S&P 500 fällt. Es ist absolut möglich, dass ein weniger mit dem S&P 500 (oder einem anderen Aktienindex) korrelierter Fonds für Rückgänge des Aktienmarkts anfälliger ist als Fonds mit einer viel engeren Korrelation. Unsere Darstellung anhand von zwei hypothetischen Fonds A und B liefert lediglich ein Extrembeispiel, um diesen Punkt in seiner krassesten Form zu verdeutlichen – nämlich dass sogar ein Fonds, der bei jedem Fall des S&P 500 fällt, weniger mit ihm korreliert sein kann als einer, der jedes Mal steigt, wenn der S&P 500 fällt.
Abbildung 9.5
Die Renditen von Fonds B im Vergleich zu den Renditen des S&P 500
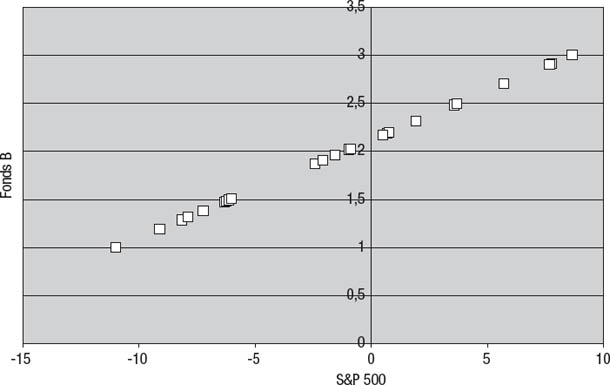
Die Anleger haben zwar bei einem Fonds Bedenken, der schlecht läuft, wenn der S&P 500 fällt, aber das ist gar nicht das, was die Korrelation misst. Sie misst vielmehr die lineare Beziehung der Renditen über alle Monate. Bei einem Fonds, der jedes Mal Gewinne verzeichnet, wenn der S&P 500 steigt, haben die Anleger wohl kaum Bedenken – eigentlich wäre ihnen das sogar lieber –, aber ein solches Muster würde den Wert der Korrelation nur steigern und das sehen die Anleger ironischerweise negativ. Diese Beobachtungen führen uns zu folgender wichtigen Schlussfolgerung bezüglich der Geldanlage:
Investment-Prinzip: Wenn einem Baisse-Monate Sorgen machen, sollte man sich die Baisse-Monate betrachten.
Wenn Anleger aus Gründen, die im vorigen Abschnitt dargelegt wurden, befürchten, ihre Anlagen könnten für Baissen anfällig sein, reicht die Korrelation zu einem Aktienindex als Kennzahl nicht aus. Die nun folgenden Kennzahlen stellen nützliche Ergänzungen zur Korrelation dar, wenn man einschätzen will, wie anfällig eine Anlage für einen Marktindex ist.
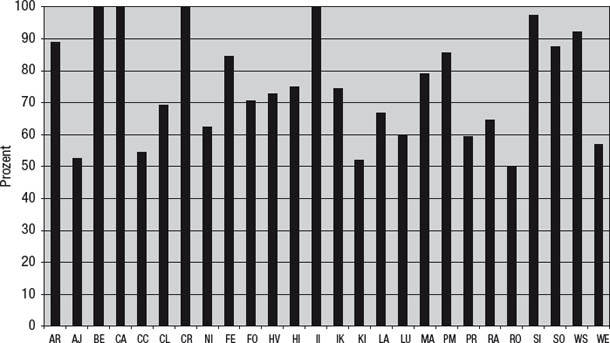
•Der Anteil von Monaten mit Gewinn, wenn der Markt fällt. Diese Kennzahl gibt den Anteil der Monate an, in denen ein Fonds eine positive Rendite liefert, wenn man nur die Monate betrachtet, in denen sich der Index negativ entwickelt hat. Ein hoher Gewinnanteil bei fallendem Markt kann die Bedeutung der Korrelation relativieren. Als Beispiel zeigt Abbildung 9.6 die Korrelationen von Fonds innerhalb eines Hedgefonds-Portfolios zum S&P 500. Dieses Portfolio enthält zwar keine Fonds mit hoher Korrelation zum S&P 500, aber einige mit mäßiger Korrelation. Abbildung 9.7 zeigt den Anteil der Monate mit Gewinn des gleichen Portfolios an den Verlustmonaten des S&P 500. Die Tatsache, dass nur einer der Fonds in mehr als 50 Prozent der Verlustmonate des S&P 500 gestiegen ist, relativiert die mäßige Korrelation, die einige Fonds aufweisen.
Wie bereits erklärt, kann es sogar sein, dass ein Fonds signifikant zum S&P 500 korreliert ist, aber trotzdem in allen Monaten steigt, in denen der S&P 500 fällt. Wenn ein Fonds in den meisten Fällen steigt, in denen der S&P 500 fällt, ist eine mäßige und sogar eine hohe Korrelation bedeutungslos, denn ein Anleger, der Diversifizierung anstrebt, sorgt sich um Verluste, die zur gleichen Zeit auftreten, zu der andere aktienabhängige Investments fallen. Er sorgt sich nicht darum, ob die Renditen zu Zeiten, zu denen der S&P 500 steigt, größer sind als zu Zeiten, zu denen er fällt – und das ist ja eher das, was die Korrelation angibt.
Abbildung 9.6
Korrelationen von Portfoliofonds zum S&P 500
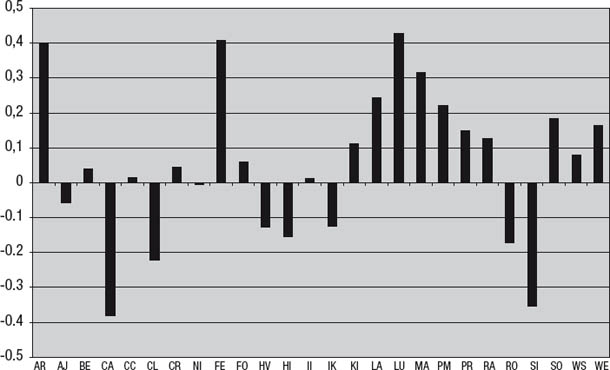
Abbildung 9.7
Portfoliofonds: Anteil der Gewinnmonate an den Verlustmonaten des S&P 500
•Die durchschnittliche Rendite bei fallenden Märkten. In Kombination mit dem Anteil der Gewinnmonate bei fallenden Märkten liefert diese Kennzahl ein umfassendes Bild der Performance eines Fonds in Baisse-Situationen. Außerdem trifft die Kombination dieser beiden Angaben den Kern dessen, worum es den Anlegern geht, viel genauer als die weitaus häufiger verwendete Korrelation. Abbildung 9.8 zeigt die durchschnittliche Rendite der in dem Portfolio aus Abbildung 9.6 enthaltenen Fonds in Monaten, in denen der S&P 500 fällt. Wie man sieht, haben alle Fonds außer einem in den Monaten, in denen der Markt fällt, eine positive Durchschnittsrendite. In diesem Zusammenhang sind die mäßigen Korrelationen zwischen einigen der Fonds und dem S&P 500 von untergeordneter Bedeutung.
Abbildung 9.8
Portfoliofonds: Die durchschnittliche Rendite in Monaten mit negativem S&P 500
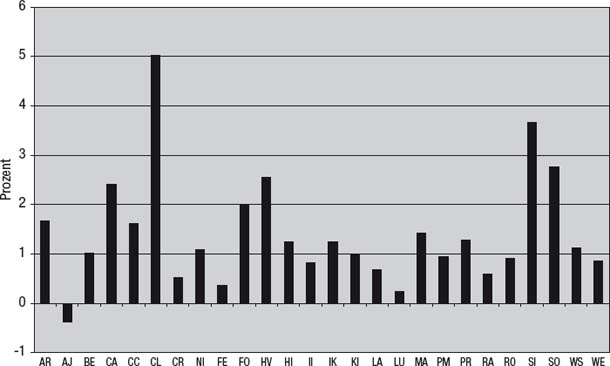
Hier eine weitere Überlegung: Die Korrelation sagt überhaupt nichts über die relative Bedeutung einer Variable für Veränderungen einer anderen Variable aus. Abbildung 9.9 stellt das hypothetische Beispiel eines Fonds dar, der ein Prozent seines Vermögens in den S&P 500 investiert und für die restlichen 99 Prozent eine Strategie einsetzt, die eine konstante Monatsrendite von einem Prozent einbringt.3 Ein solcher Fonds wäre zum S&P 500 perfekt korreliert (r = 1,0), denn alle seine Schwankungen erklären sich durch Änderungen des S&P 500. Doch trotz dieser perfekten Korrelation wirken sich Fluktuationen des S&P 500 sehr schwach auf die Renditen des Fonds aus: Eine Änderung des S&P 500 um ein Prozent bewirkt eine Änderung des Fonds um nur 0,01 Prozent. Die Korrelation gibt nicht die Bedeutung einer Variable (zum Beispiel der Renditen des S&P 500) für Änderungen einer anderen Variable (zum Beispiel der Renditen des Fonds, den man als Anlage in Erwägung zieht) an – aber das Beta tut das.
Abbildung 9.9
Fonds C im Vergleich zum S&P 500
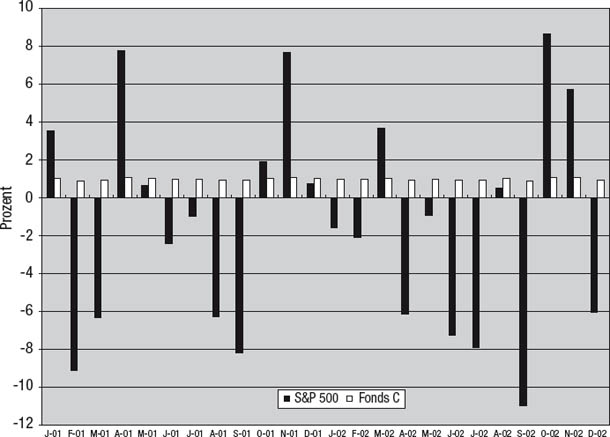
Das Beta gibt die zu erwartende Größe der Veränderung eines Investments bei einer Veränderung der gewählten Benchmark um ein Prozent an. Wenn ein Fonds beispielsweise gegenüber dem S&P 500 ein Beta von 2,0 hat, kann man erwarten, dass jede Veränderung des S&P 500 um ein Prozent eine Veränderung des Fonds in die gleiche Richtung um 2,0 Prozent nach sich zieht. Abbildung 9.9 zeigt als Beispiel einen Fonds mit maximaler Korrelation (r = 1,0), aber sehr niedrigem Beta (Beta = 0,01). Tatsächlich gibt das Beta viel besser als die Korrelation wieder, worum es dem Anleger wirklich geht – um die erwarteten Auswirkungen von Preisänderungen der Benchmark auf den Preis des Investmentkandidaten. Beispielsweise sollte ein Anleger, der Fonds meiden will, die wahrscheinlich für Baisse-Monate anfällig sind, mehr Bedenken gegen ein Investment mit einer Korrelation von 0,6 und einem Beta von 2,0 haben als gegen ein Investment mit einer Korrelation von 0,9 und einem Beta von 0,1. Obwohl die Bewegungen von Ersterem weniger mit den Bewegungen des Aktienmarkts korreliert sind, sind die zu erwartenden Auswirkungen einer Bewegung des Aktienmarkts bei ihm 20-mal so groß wie bei Letzterem.
Das Beta und die Korrelation sind mathematisch miteinander verwandt und sind zwei verschiedene Arten, gleiche Informationen zu untersuchen. Die Korrelation gibt an, in welchem Maße die Preisänderungen zweier Variablen (zum Beispiel eines Investments und eines Benchmark-Index) linear miteinander in Zusammenhang stehen, während das Beta angibt, welche prozentuale Veränderung des Investments bei einer prozentualen Änderung der Benchmark um ein Prozent zu erwarten ist.4
Investment-Missverständnis 29: Eine geringe Korrelation zwischen den Renditen einer Strategie und eines Marktes bedeutet, dass zwischen beiden keine Beziehung besteht.
In Wirklichkeit: Auch wenn dieser Schluss oft zutrifft, kann man lediglich davon ausgehen, dass zwischen der Strategie und dem Markt keine lineare Beziehung besteht. Es lässt sich aber nicht ausschließen, dass die beiden In einem nichtlinearen Zusammenhang stehen (wie etwa bei einer Strategie des Optionsverkaufs).
Investment-Missverständnis 30: Eine hohe Korrelation zwischen zwei Variablen bedeutet, dass zwischen Ihnen eine Ursache-Wirkung-Beziehung besteht.
In Wirklichkeit: Es ist möglich, dass zwei Variablen hochgradig korreliert sind, aber in keinerlei Beziehung zueinander stehen – wenn beide Variablen zu einer dritten Variable korreliert sind, zum Beispiel zu einem zeitbedingten Trend während des Betrachtungszeitraums.
Investment-Missverständnis 31: Bei Investments, die stärker mit dem Markt korreliert sind, ist es wahrscheinlicher, dass sie in Baisse-Monaten fallen.
In Wirklichkeit: Wenn man zwei Investments miteinander vergleicht, kann es durchaus sein, dass dasjenige, das weniger verlustanfällig ist, wenn der Markt fällt, in Monaten enger zu ihm korreliert ist, in denen der Markt steigt – was ja eine positive Eigenschaft ist. Außerdem kann es sein, dass ein Investment eine signifikante Korrelation zum Markt aufweist, da seine Renditen in Monaten, in denen der Markt fällt, geringer sind als in Monaten, in denen er steigt – aber trotzdem sind seine Renditen bei fallendem Markt positiv. Eigentlich geht es den Anlegern nur um die nach unten gerichtete Korrelation: Sie wollen zwar nicht, dass ihr Investment fällt, wenn der Markt fällt, aber sie sind vollkommen glücklich, wenn es bei steigendem Markt steigt. Da die Korrelation nicht zwischen Monaten mit Gewinn oder Verlust unterscheidet, sollte man sie durch Kennzahlen ergänzen, die sich speziell auf die Performance in Monaten konzentrieren, in denen der Markt fällt.
Investment-Missverständnis 32: Je höher die Korrelation zwischen einem Investment und einem Markt, umso stärker wird es von Marktbewegungen beeinflusst.
In Wirklichkeit: Die prozentuale Veränderung eines Investments, die zu erwarten ist, wenn sich ein Markt um ein Prozent ändert (das Beta), ist eine Funktion sowohl der Korrelation als auch der relativen Volatilität des Investments zum Markt. Wenn man zwei Investments miteinander vergleicht, kann man dann damit rechnen, dass das weniger zum Markt korrelierte stärker von ihm beeinflusst wird, wenn seine Volatilität in ausreichendem Maße größer ist als die des Marktes. Wenn man als Anleger die Auswirkungen von Marktpreisen auf ein Investment beurteilen will, sollte man lieber auf das Beta als auf die Korrelation schauen.
Ob ein Investment zu den gleichen Zeiten für Verluste anfällig ist, zu denen Aktienmärkte und andere Positionen fallen, ist ein bedeutender Risikofaktor, den man besonders dann beachten muss, wenn die gewählten Investments eine Diversifizierung zu anderen Portfoliopositionen liefern sollen. Die Korrelation ist eine wichtige Kennzahl, die man als Warnung vor diesem Risiko verwenden kann. Allerdings garantiert eine mäßige bis hohe Korrelation nicht, dass dieses Risiko vorliegt – und eine geringe Korrelation garantiert nicht, dass es nicht vorliegt. Wenn ein Anleger befürchtet, er könnte einen Fonds auswählen, der wahrscheinlich Verluste erleidet, wenn die Aktienmärkte fallen, reicht die Korrelation als Kennzahl nicht aus. Anstatt zu diesem Zweck nur die Korrelation zu verwenden, sollte man sich als Anleger lieber an eine umfassendere und aussagekräftigere Kombination aus folgenden vier Zahlen halten:
1. Korrelation
2. Beta
3. Anteil der Gewinnmonate bei fallendem Markt
4. Durchschnittliche Rendite bei fallendem Markt
* Der Vollständigkeit halber und um dem Widerspruch statistisch versierter Leser zuvorzukommen: Es handelt sich hier nicht um eine Definition des Determinationskoeffizienten, sondern um einen Ausnahmefall. Der normalerweise als R2 oder B bezeichnete Determinationskoeffizient besitzt nur bei linearen Regressionsmodellen die eindeutige Definition als Quadrat des Korrelationskoeffizienten und lässt sich andernfalls unterschiedlich definieren. [Anm. d. Ü.]
1 Abbildung 9.1 ist eine vereinfachte hypothetische Illustration. An einem echten Markt wäre das Muster nicht symmetrisch, weil sinkende Preise wahrscheinlich die implizite Volatilität erhöhen und dadurch die Verluste vergrößern würden, während steigende Preise wahrscheinlich die implizite Volatilität senken und dadurch die Verluste dämpfen würden.
2 Die hypothetischen Beispiele für Fondsrenditen (die Fonds A, B und C) in diesem Kapitel sind erfunden und sollen keine tatsächlichen Fonds darstellen. Die Renditezahlen wurden bewusst so gestaltet, dass sie entscheidende Konzepte im Zusammenhang mit den Eigenschaften von Korrelationen verdeutlichen.
3 Das ist zwar ein erfundenes und unrealistisches Beispiel, aber es veranschaulicht das Konzept, dass eine hohe Korrelation nicht unbedingt starke Auswirkungen auf den Preis nach sich zieht.
4 Mathematisch ist das Beta die Korrelation multipliziert mit dem Quotienten aus der Standardabweichung des Investments und der Standardabweichung der Benchmark. Wenn beispielsweise die Korrelation 0,8 beträgt und die Standardabweichung des Investments halb so groß ist wie die der Benchmark, beträgt das Beta 0,4. Somit wäre zu erwarten, dass das Investment einen Verlust von 0,4 Prozent verzeichnet, wenn die Benchmark um ein Prozent fällt.