Vor vielen Jahren habe ich als Researchdirektor bei einer Brokerfirma gearbeitet und war außerdem der Fachmann der Abteilung für die quantitative Beurteilung von Commodity Trading Advisors (CTAs). Diese Aufgabe veranlasste mich, mir über bessere Methoden für die Zusammenstellung von Multimanager-Fonds Gedanken zu machen. Irgendwann wurde mir klar, dass man dann, wenn alle Manager die gleiche erwartete künftige Performance haben, das Rendite-Risiko-Verhältnis steigern kann, wenn man das gesamte Kapital monatlich neu gewichtet und die anteiligen Allokationen der Manager wieder zurückstellt.1
Die Annahme, dass alle Manager eine gleichwertige künftige Performance haben würden, bedeutete aber nicht, dass dieses Ergebnis buchstäblich zu erwarten war, sondern vielmehr, dass man über die relative Rangfolge der künftigen Performance der Manager keine Vorhersage treffen konnte. (Die bisherige Rangfolge war zwar bekannt, aber ich ging davon aus, dass die frühere Rangfolge ein schlechter Indikator für die künftige Rangfolge ist.)
Da fiel mir folgende Analogie ein: Man kann sich die angenommene gleichwertige Performance als monatliche Ergebnisse vorstellen, die durch eine Reihe von Karten dargestellt werden – für jeden Monat eine Karte –, wobei die Ergebnisse jedes Managers einer anderen Verteilung aus den gleichen Karten entsprechen. Der Annahme zufolge haben alle Manager den gleichen Satz von Monatsergebnissen (also die gleichen Karten in verschiedener Reihenfolge) und aus einer geringeren Schwankungsbreite lässt sich auf eine höhere Rendite schließen (siehe Kapitel 5). Deshalb schien es mir, als müsste das auf dem Durchschnitt aller Karten pro Monat basierende Rendite-Risiko-Verhältnis – das mathematische Äquivalent zu einer monatlichen Neugewichtung – gleich der Rendite eines einzelnen Kartensatzes (also der Performance jedes einzelnen Managers) oder größer sein. Anders ausgedrückt: Wenn es a priori keinen Grund zu der Annahme gab, dass irgendein Manager innerhalb der ausgewählten Gruppe in Zukunft eine bessere Performance bringen würde als die anderen Manager, würde eine monatliche Neugewichtung des Kapitals am Ende die gleiche oder eine höhere Rendite bringen als eine einmalige statische Allokation.
Nehmen wir als ganz einfaches Beispiel, um ein Gefühl für diesen Gedankengang zu bekommen, einen aus zwei Managern bestehenden Fonds mit einer zweimonatigen Performance-Periode an, wobei Manager A im ersten Monat zehn Prozent Gewinn und im zweiten Monat fünf Prozent Verlust macht und Manager B die umgekehrten Monatsergebnisse erzielt. Daraus würden sich folgende Nettoinventarwerte (NAVs) ergeben:
NAV Manager A = 1.000 × 1,10 × 0,95 = 1.045
NAV Manager B = 1.000 × 0,95 × 1,10 = 1.045
Fonds bei Neugewichtung = 1.000 × 1.025 × 1.025 = 1.050,60
Fonds ohne Neugewichtung = (1.045 + 1.045) / 2 = 1.045
In jedem Monat gewinnt der eine Manager zehn Prozent der Hälfte des Kapitals (oder fünf Prozent des gesamten Kapitals) und der andere verliert fünf Prozent der anderen Hälfte (oder 2,5 Prozent des gesamten Kapitals). Deshalb entsteht in jedem Monat ein Nettogewinn von 5% - 2,5% = 2,5%.
An diesem Beispiel sieht man, dass der Fonds mit monatlicher Neugewichtung eine höhere Rendite erzielt als der Fonds, der die Anlagen nicht neu gewichtet.
Um nachzuprüfen, ob die Idee der monatlichen Neugewichtung auch in der wirklichen Welt funktioniert, habe ich ein empirisches Experiment durchgeführt. Ich habe aus der vorhandenen Datenbank 30 Gruppen zu je sechs Managern ausgewählt. Für jede Gruppe habe ich für die beiden folgenden Situationen den NAV über einen Zeitraum von drei Jahren ausgerechnet:
1.Anfängliche gleichmäßige Gewichtung des Kapitals und keine spätere Umverteilung.
2.Monatliche Neugewichtung (zurück zur gleichmäßigen Gewichtung), gesteigert um einen Hebelfaktor von 1,25 (da die monatliche Neugewichtung das Risiko senkt, habe ich einen Teil dieses Nutzens durch Hebeleinsatz auf die Ertragsseite übertragen).
Dabei stellte ich fest, dass der neu gewichtete und gehebelte Fonds fast ausnahmslos eine höhere Performance brachte als der Fonds ohne Neugewichtung. Noch frappierender war allerdings die Beobachtung, dass die Rendite des gehebelten und neu gewichteten Fonds gewöhnlich grob der des besten oder zweitbesten Managers der Gruppe entsprach, während der maximale Drawdown und die Standardabweichung (Risikomaße) ungefähr den niedrigsten oder zweitniedrigsten Werten innerhalb der Gruppe von Managern entsprachen. Anders gesagt war es möglich, sich mithilfe einer Strategie aus monatlicher Neugewichtung und Hebeleinsatz der Rendite der Manager mit den besten Renditen innerhalb der Gruppe sowie dem Risiko der Manager mit dem besten (niedrigsten) Risiko innerhalb der Gruppe anzunähern. Im Endeffekt war die Neugewichtung unter Hebeleinsatz also eine Methode, um die künftige Performance zu erhöhen – denn dadurch wurden Rendite-Risiko-Eigenschaften erzielt, die denjenigen Managern innerhalb einer ausgewählten Gruppe entsprachen, die in Zukunft die beste Performance brachten.
Ich war von meiner Entdeckung sehr begeistert. Dann versuchte ich das Management meines Unternehmens von der Logik und Attraktivität eines Multimanager-Portfolios zu überzeugen, das nach dem Konzept der monatlichen Neugewichtung mit Leverage strukturiert wäre. Es gab ein paar Besprechungen, aber ich merkte, dass aus meiner Idee nichts wurde. Dann versteifte ich mich auf die Idee, meine Strategie der Neugewichtung/Hebelwirkung auf einen hypothetischen Fonds anzuwenden, der aus den fünf Single-Manager-Fonds des Unternehmens bestand. Die meisten von ihnen hatten enttäuschende Track Records und deshalb war das Management von ihnen nicht gerade begeistert. Es zeigte sich, dass der theoretische Multimanager-Fonds, den ich mithilfe meiner Strategie konstruiert hatte, nur wenig schlechter als der beste Manager in der Gruppe und weitaus besser als die vier anderen Manager war. Da man den besten Manager nur im Nachhinein hätte auswählen können, schien der Vorteil meiner Methode zwingend auf der Hand zu liegen.
„Damit müsste die Sache doch niet- und nagelfest sein“, dachte ich mir. Ich erstellte ein paar bunte Charts, um den Performance-Vergleich zu illustrieren, und setzte eine weitere Besprechung mit dem Bereichsleiter an, dessen Zustimmung unerlässlich war. Als ich meinen 15-minütigen Vortrag beendet hatte, lehnte ich mich zurück und wartete darauf, dass der Bereichsleiter die Klugheit meines Vorschlags rühmen würde.
Stattdessen rief er aus: „Sie meinen also, Sie nehmen den Gewinnern etwas weg und schlagen es den Verlieren drauf!“ Und das einem Ton, als hätte ich gerade die Vorzüge des Muttermords angepriesen.
„Nein“, erwiderte ich, „Sie verstehen das falsch. Wir gehen von der Annahme aus, dass alle im Fonds enthaltenen Manager Gewinner sind – das ist ja wohl auch der Grund, aus dem wir sie überhaupt ausgesucht haben. Wir machen Folgendes: Wir nehmen das, was die Gewinner in Zeiten des Gewinns gewinnen, und schlagen es dann auf andere Gewinner drauf, wenn sie einmal Verlust machen.“ Doch alle Logik der Welt konnte nichts ausrichten. Über den „schockierenden“ Charakter meines Vorschlags kam der Bereichsleiter nicht hinweg. Aus meiner Idee wurde nie etwas.
Als ich mir diese Episode für dieses Buch noch einmal vornahm, merkte ich, dass meine ursprüngliche Analyse einen Fehler enthielt. Die Datenbank, aus der ich meine Proben entnommen hatte, enthielt ja nur aktive Manager (also überlebende Manager). Manager, die dichtgemacht hatten – eine Gruppe, die mit höherer Wahrscheinlichkeit eine schlechte Performance aufwies –, konnte ich daher nicht auswählen. Vielleicht hätte ja die monatliche Neugewichtung, also im Endeffekt die Verschiebung von Gewinnern auf Verlierer, nichts gebracht, wenn meine Stichproben auch dahingeschiedene Manager umfasst hätten. Möglicherweise hätte sie sich dann sogar nachteilig ausgewirkt. Kurz gesagt unterlag meine ursprüngliche Analyse dem Survivorship Bias. Ich hatte keine Möglichkeit, festzustellen, ob der scheinbare Vorteil der Neugewichtung, den ich bei meiner ursprünglichen Analyse entdeckt hatte, ausreichte, um diese Verzerrung zu überwinden.
Um das Konzept der Neugewichtung im Rahmen einer neuen Analyse zu überprüfen, die das Survivorship Bias umging, beschaffte ich mir die vollständige CTA-Datenbank von Stark & Company (www.stark-research.com) – diese Daten enthalten sowohl die noch aktiven als auch die nicht mehr aktiven Manager. Aus dieser kompletten Liste wählte ich nach dem Zufallsprinzip zehn Portfolios aus jeweils zehn Managern aus2 und ging von einer gleichmäßigen Gewichtung sowie von dem Anfangsdatum 1. Januar 2005 aus. Dann verglich ich die Portfolio-Ergebnisse des gesamten Zeitraums (2005 bis 2010) ohne spätere Anpassungen der Allokationen mit den Ergebnissen, die ich bei monatlichem Rebalancing der Portfolios auf eine gleichmäßige Gewichtung erhielt.
Für die Behandlung von Managern, die nicht mehr aktiv waren, gab es ganz einfache Regeln:
•Für das Portfolio ohne Neugewichtung: Es wurde angenommen, dass das Restvermögen eines nicht mehr aktiven CTA zum Zeitpunkt der Schließung für den restlichen Testzeitraum in Schatzwechseln angelegt wurde.
•Für das Portfolio mit Neugewichtung: Der nicht mehr aktive CTA wurde durch ein Investment in Schatzwechsel ersetzt, das weiterhin jeden Monat gegenüber den anderen Investments gleichmäßig neu gewichtet wurde (auf eine Allokation von zehn Prozent). Wenn beispielsweise in einem bestimmten Monat drei CTAs ihren Betrieb eingestellt hatten, wurden jeden Monat 30 Prozent der Portfolio-Allokation in Schatzwechseln platziert.
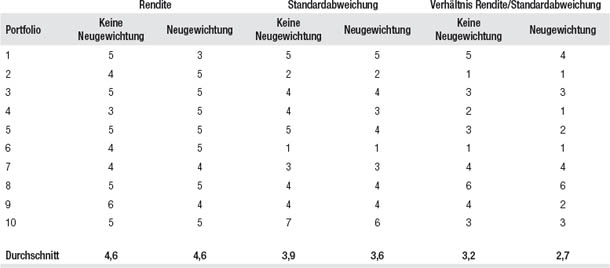
Tabelle 19.1 vergleicht die Platzierung des Portfolios mit der Platzierung der in jedem Portfolio enthaltenen CTAs hinsichtlich der Rendite (durchschnittliche kumulierte Jahresrendite), der Standardabweichung (einem Näherungswert für das Risiko)3 und des Rendite-Risiko-Verhältnisses. Da jedes Mal elf Platzierungen errechnet werden (für das Portfolio und seine zehn Investment-Bestandteile), ist sechs die mediane Platzierung. Der beste Performance-Rang ist „1“ und der schlechteste „11“. Bei der Standardabweichung sind niedrigere Werte als bessere Platzierung definiert (also eine niedrigere Rangziffer). Beide Portfoliogruppen (mit und ohne Neugewichtung) erzielen bezüglich der Rendite, der Standardabweichung und des Rendite-Risiko-Verhältnisses signifikant bessere als mediane Platzierungen – und das demonstriert eindeutig den Nutzen der Diversifizierung. Bezüglich der Rendite landen die Portfolios mit und ohne Neugewichtung im Schnitt auf dem gleichen Rang, allerdings erzielen die Portfolios mit Neugewichtung hinsichtlich des Risikos und des Rendite-Risiko-Verhältnisses bessere Platzierungen.
Tabelle 19.1
Die Platzierung der Portfolios im Verhältnis zu den CTAs in den Portfolios

Tabelle 19.2 vergleicht das Portfolio ohne Neugewichtung und das Portfolio mit Neugewichtung bezüglich des Rendite-Risiko-Verhältnisses – das ist die entscheidende Kennzahl. (Man kann aus einem Portfolio mit einem höheren Rendite-Risiko-Verhältnis bei geringerer Rendite als ein anderes Portfolio durch Hebeleinsatz bei gleichem oder geringerem Risiko eine höhere Rendite erzielen.) In acht von zehn Fällen erzielte das Portfolio mit Neugewichtung ein höheres Rendite-Risiko-Verhältnis und in den beiden Ausnahmefällen war es nur geringfügig niedriger. Im Schnitt war das Rendite-Risiko-Verhältnis der neu gewichteten Portfolios um 18 Prozent höher.
Tabelle 19.2
Rendite-Risiko-Vergleich der Portfolios
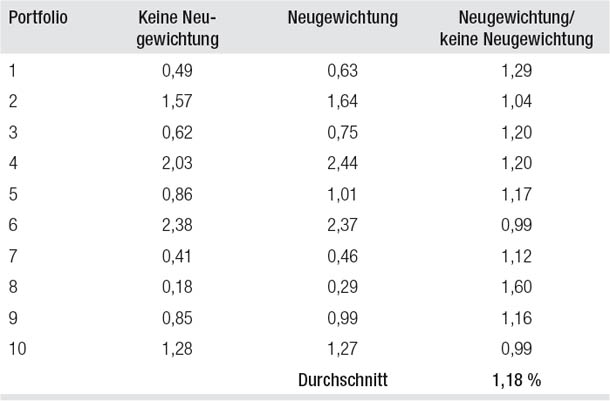
Tabelle 19.3 zeigt den Anteil der Portfolios, bei denen die Neugewichtung zu einer besseren Performance bezüglich aller drei Kennzahlen führte: Rendite, Standardabweichung (Näherung für das Risiko) und das Verhältnis Rendite/Standardabweichung. Das Rebalancing resultierte bei 80 Prozent der Portfolios in einem niedrigeren Risiko und einem höheren Rendite-Risiko-Verhältnis, lieferte aber nur in der Hälfte der Fälle eine höhere Rendite. Da die Neugewichtung bei den meisten Portfolios die Volatilität senkt, zeigt Tabelle 19.3 zum Vergleich auch noch die Angaben für ein Portfolio mit Neugewichtung und einem mäßigen Hebel von zehn Prozent. Diese kleine Modifizierung führt dazu, dass 80 Prozent der Portfolios mit Neugewichtung sowohl hinsichtlich der Rendite und des Rendite-Risiko-Verhältnisses eine bessere Performance bringen als die Portfolios ohne Neugewichtung, wobei 70 Prozent der Portfolios dann immer noch ein geringeres Risiko beinhalten.
Tabelle 19.3
Anteil der Portfolios, deren Performance mit Neugewichtung besser ist als ohne

Die Tabellen 19.2 und 19.3 zeigen, dass in unserem Versuch, der das Survivorship Bias vollständig ausschaltet, das Rebalancing offenbar immer noch eine wesentliche Verbesserung der Performance bewirkt. Diese Ergebnisse liefern zwar einen empirischen Beleg, der die Hypothese stützt, dass die Neugewichtung – also dass regelmäßig „den Gewinnern etwas weggenommen und den Verlieren zugeschlagen wird“ – tendenziell die Performance steigert, aber sie beweisen diese Behauptung keinesfalls. Für einen verlässlicheren Test müsste man das Experiment mit viel mehr als zehn zufällig ausgewählten Portfolios wiederholen – eine Anforderung, die sowohl meine Geduld übersteigt, Rechenschritte in Excel-Tabellen zu wiederholen, als auch meine Fähigkeiten als Programmierer, die gleich null sind. Die Leser können diesen Vergleich zwischen Neugewichtung oder nicht allerdings mit den früheren Renditen ihrer eigenen Portfolios wiederholen. Manche Leser, die dieses Experiment machen, werden zwar merken, dass das Rebalancing geschadet hätte, aber ich glaube, die meisten werden feststellen, dass es vorteilhaft gewesen wäre. Der Vergleich sollte sich nicht auf die Rendite, sondern auf das Rendite-Risiko-Verhältnis beziehen, denn die Neugewichtung senkt eher das Risiko – ein Vorteil, den man auf Wunsch mittels Hebelwirkung in eine höhere Rendite verwandeln kann.
Wenn die in einem Portfolio enthaltenen Manager alle die gleiche Performance hätten (definiert als identische Monatsrenditen in verschiedenen Reihenfolgen), wäre es eine mathematische Gewissheit, dass Rebalancing die Performance steigert. Dieser Punkt wurde am Anfang des Kapitels anhand des Karten-Vergleichs bewiesen, wenn auch nicht streng. Wenn es also keinen guten Grund gibt, zu erwarten, dass einer oder mehrere der Manager, die für das Portfolio ausgewählt wurden, die anderen Manager in Zukunft outperformt, liefert die Neugewichtung einen mathematischen Vorteil.
Die Marktbedingungen begünstigen zu verschiedenen Zeiten verschiedene Strategien. Eine Strategie, die in einem bestimmten Zeitraum besonders gut funktioniert, bringt in einem anderen Zeitraum vielleicht eine sehr schlechte Performance. Beispielsweise laufen Gegentrend-Strategien wahrscheinlich sehr gut, wenn sich die Märkte im Allgemeinen wechselhaft innerhalb von Schwankungsbereichen bewegen, Trendfolge-Methoden fallen aber dem Schaukeleffekt zum Opfer. Wenn sich die Marktbedingungen dahingehend ändern, dass sich viele Trends durchsetzen, sind Trendfolge-Methoden sehr profitabel, aber Gegentrend-Trader erleiden dann Verluste. Das Rebalancing hält die Asset Allocation auf verschiedene Marktstrategien, die von verschiedenen Managern repräsentiert werden, konstant. Ohne Rebalancing würde sich das Vermögen mehr auf die Strategien konzentrieren, die in der Vergangenheit am besten funktioniert haben. Sofern sich nun die Marktbedingungen ändern, entfällt das meiste Vermögen auf die verwundbarsten Strategien. Im Endeffekt dämpft die Neugewichtung die negativen Auswirkungen der unvermeidlichen Verschiebungen der Marktbedingungen, die dazu führen könnten, dass man eine Strategie mit überdurchschnittlicher Performance gerade dann übergewichtet, wenn sie ihren Lauf hinter sich hat, und eine Strategie untergewichtet, die kurz vor einem riesigen Lauf steht.
Weshalb das Rebalancing funktioniert, kann man auch auf eine andere Art verstehen: Im Endeffekt zwingt es einen zu Gewinnmitnahmen, wenn ein Manager einen Ausflug nach oben erlebt, und zur Aufstockung eines Investments, wenn ein Manager einen Drawdown erleidet. Die Investition in einen Manager, der das unvermeidliche Retracement erlebt, das auf einen besonders rentablen Anstieg unvermeidlich folgt, wird dann kleiner, als es ohne Rebalancing wäre. Und wenn im Gegenzug ein Manager nach einem Drawdown einen Rebound erfährt, ist die Investition in diesen Manager dann größer, als sie es ohne Rebalancing wäre.
Zur Vereinfachung der Darstellung sind wir in diesem Kapitel davon ausgegangen, Rebalancing bedeute, jeden Monat zu gleich großen Allokationen zurückzukehren. Allerdings erfordert und bedeutet Rebalancing oder Neugewichtung keine gleichgewichtete Allokation. Oft gibt es gute Gründe, die Manager ungleich zu gewichten. Beispielsweise wäre es vollkommen vernünftig oder gar besser, riskanteren Managern eine kleinere Allokation zuzuweisen. Bei ungleichen Allokationen würde die Neugewichtung bedeuten, jeden Monat die Ziel-Allokationen wieder herzustellen. Wenn beispielsweise ein Portfoliomanager beschließt, dass Manager A wegen seines höheren Risikos nur die Hälfte der Allokation anderer Manager erhalten sollte, würde das Rebalancing die Allokationen so anpassen, dass dieses Verhältnis in den späteren Monaten gewahrt bleibt.
Investment-Missverständnis 48: In einem Multimanager-Portfolio kann man die Performance dadurch verbessern, dass man die Allokation von Managern mit guten Ergebnissen erhöht und die Allokationen derjenigen senkt, die eine geringere Performance bringen.
In Wirklichkeit: Meistens bringt das genaue Gegenteil – dass man das Portfolio regelmäßig neu gewichtet – ein besseres Ergebnis. Natürlich kann ein Portfoliomanager aus zahlreichen Gründen beschließen, von einem Manager Abstand zu nehmen, aber das ist ein anderes Thema. Doch solange ein Manager im Portfolio verbleibt, ist es normalerweise eine bessere Strategie, die Allokationen nach Zeiten der Underperformance zu vergrößern und sie nach Zeiten der Outperformance zu verkleinern.
Theoretische Argumente und empirische Belege lassen den Schluss zu, dass eine monatliche Neugewichtung des Kapitals ein Mittel ist, um das erwartete Rendite-Risiko-Verhältnis von Multimanager-Portfolios zu steigern. Das bedeutet aber nicht, dass die Neugewichtung die Performance (also das Rendite-Risiko-Verhältnis) jedes Multimanager-Fonds steigern würde, sondern nur, dass sie wahrscheinlich die Performance der meisten derartigen Fonds steigert. Das heißt, bei einem Multimanager-Fonds sprechen die Wahrscheinlichkeiten dafür, dass Rebalancing die Performance verbessert. Portfoliomanager und Anleger können das Rebalancing an ihren eigenen Portfolios testen, indem sie die tatsächlichen Ergebnisse mit den Ergebnissen vergleichen, die sie erzielt hätten, wenn sie ihre anteiligen Allokationen jeden Monat auf ihre ursprünglichen Allokationen eingestellt hätten.4
Wenn das Rebalancing so offenkundige Vorteile hat, warum wird diese Methode normalerweise nicht verwendet? Die Antwort auf diese Frage ist einfach: die Natur des Menschen. Die Vorstellung, Vermögen von Tradern, die in einem Portfolio gerade die beste Performance gebracht haben, auf diejenigen umzuschichten, die gerade die schlechteste Performance gebracht haben, läuft den natürlichen menschlichen Instinkten zuwider. Doch wenn man diesen Instinkten folgt, resultiert das gewöhnlich in schlechten Marktentscheidungen. Zu den Voraussetzungen für Erfolg am Markt gehört die Fähigkeit, Entscheidungen anhand von Belegen zu treffen und nicht anhand dessen, was sich gut anfühlt.
1 Wenn die Manager unterschiedliche Risikoniveaus haben, ist es sinnvoller, die gleichmäßige Allokation risikobereinigt zu definieren (anstatt anhand des Dollarbetrags) – dieses Konzept wird in Kapitel 21 besprochen. An den Schlüssen, die in diesem Kapitel gezogen werden, ändert das nichts.
2 Ich benutzte die Excel-Funktion „Zufallsbereich“, um 100 Zufallszahlen zu erzeugen (zehn Portfolios mal zehn Manager) und nahm als obere Grenze die Gesamtzahl aller aktiven und nicht mehr aktiven Manager in der Datenbank.
3 Bei CTAs, die mit sehr liquiden Futures handeln (wie in Kapitel 4 erläutert), sind versteckte Risiken normalerweise kein Problem, sodass die Standardabweichung (ein Maß für die Volatilität) eine brauchbare Näherung für das Risiko liefert.
4 Ein solcher Test würde durch die Aufnahme und Rücknahme von Positionen, die im Laufe der Zeit wahrscheinlich stattfindet, verkompliziert werden. Man kann eine solche Situation vereinfachend so handhaben, dass man monatlich auf diejenigen prozentualen Allokationen neu gewichtet, die im letzten Monat mit einer Portfolio-Änderung galten. Somit würden sich die prozentualen Allokationsziele für die Neugewichtung jedes Mal ändern, wenn eine Position in das Portfolio aufgenommen oder eine herausgenommen wird.