IV
The Continuous Channel
24. The Capacity of a Continuous Channel
In a continuous channel the input or transmitted signals will be continuous functions of time f(t) belonging to a certain set, and the output or received signals will be perturbed versions of these. We will consider only the case where both transmitted and received signals are limited to a certain band W. They can then be specified, for a time T, by 2TW numbers, and their statistical structure by finite dimensional distribution functions. Thus the statistics of the transmitted signal will be determined by
P(x1,…, xn) = P(x)
and those of the noise by the conditional probability distribution
Px1,…, xn(y1,…, yn) = Px(y).
The rate of transmission of information for a continuous channel is defined in a way analogous to that for a discrete channel, namely
R = H(x) — Hy(x)
where H(x) is the entropy of the input and Hy(x) the equivocation. The channel capacity C is defined as the maximum of R when we vary the input over all possible ensembles. This means that in a finite dimensional approximation we must vary P(x) = P (x1,…, xn) and maximize
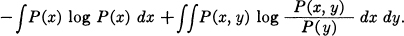
This can be written
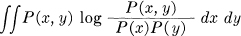
using the fact that ∫∫ P(x, y) log P(x) dx dy = ∫ P(x) log P(x) dx. The channel capacity is thus expressed as follows:
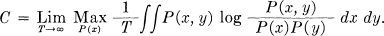
It is obvious in this form that R and C are independent of the coordinate system since the numerator and denominator in log 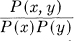 will be multiplied by the same factors when x and y are transformed in any one-to-one way. This integral expression for C is more general than H(x) — Hy(x). Properly interpreted (see Appendix 7) it will always exist while H(x) — Hy(x) may assume an indeterminate form ∞ — ∞ in some cases. This occurs, for example, if x is limited to a surface of fewer dimensions than n in its n dimensional approximation.
will be multiplied by the same factors when x and y are transformed in any one-to-one way. This integral expression for C is more general than H(x) — Hy(x). Properly interpreted (see Appendix 7) it will always exist while H(x) — Hy(x) may assume an indeterminate form ∞ — ∞ in some cases. This occurs, for example, if x is limited to a surface of fewer dimensions than n in its n dimensional approximation.
If the logarithmic base used in computing H(x) and Hy(x) is two then C is the maximum number of binary digits that can be sent per second over the channel with arbitrarily small equivocation, just as in the discrete case. This can be seen physically by dividing the space of signals into a large number of small cells, sufficiently small so that the probability density Px(y) of signal x being perturbed to point y is substantially constant over a cell (either of x or y). If the cells are considered as distinct points the situation is essentially the same as a discrete channel and the proofs used there will apply. But it is clear physically that this quantizing of the volume into individual points cannot in any practical situation alter the final answer significantly, provided the regions are sufficiently small. Thus the capacity will be the limit of the capacities for the discrete subdivisions and this is just the continuous capacity defined above.
On the mathematical side it can be shown first (see Appendix 7) that if u is the message, x is the signal, y is the received signal (perturbed by noise) and v the recovered message then
H(x) — Hy(x) ≥ H(u) — Hv(u)
regardless of what operations are performed on u to obtain x or on y to obtain v. Thus no matter how we encode the binary digits to obtain the signal, or how we decode the received signal to recover the message, the discrete rate for the binary digits does not exceed the channel capacity we have defined. On the other hand, it is possible under very general conditions to find a coding system for transmitting binary digits at the rate C with as small an equivocation or frequency of errors as desired. This is true, for example, if, when we take a finite dimensional approximating space for the signal functions, P(x, y) is continuous in both x and y except at a set of points of probability zero.
An important special case occurs when the noise is added to the signal and is independent of it (in the probability sense). Then Px(y) is a function only of the (vector) difference n = (y — x),
Px(y) = Q(y — x)
and we can assign a definite entropy to the noise (independent of the statistics of the signal), namely the entropy of the distribution Q(n). This entropy will be denoted by H(n).
Theorem 16: If the signal and noise are independent and the received signal is the sum of the transmitted signal and the noise then the rate of transmission is
R = H(y) — H(n),
i.e., the entropy of the received signal less the entropy of the noise. The channel capacity is
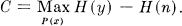
We have, since y = x + n:
H(x, y) = H(x, n).
Expanding the left side and using the fact that x and n are independent
H(y) + Hy(x) = H(x) + H(n).
Hence
R = H(x) — Hy(x) = H(y) — H(n).
Since H(n) is independent of P(x), maximizing R requires maximizing H(y), the entropy of the received signal. If there are certain constraints on the ensemble of transmitted signals, the entropy of the received signal must be maximized subject to these constraints.
25. Channel Capacity with an Average Power Limitation
A simple application of Theorem 16 occurs when the noise is a white thermal noise and the transmitted signals are limited to a certain average power P. Then the received signals have an average power P + N where N is the average noise power. The maximum entropy for the received signals occurs when they also form a white noise ensemble since this is the greatest possible entropy for a power P + N and can be obtained by a suitable choice of the ensemble of transmitted signals, namely if they form a white noise ensemble of power P. The entropy (per second) of the received ensemble is then
H(y) = W log 2πe (P + N),
and the noise entropy is
H(n) = W log 2πeN.
The channel capacity is
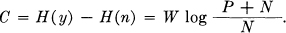
Summarizing we have the following:
Theorem 17: The capacity of a channel of band W perturbed by white thermal noise of power N when the average transmitter power is limited to P is given by
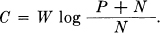
This means that by sufficiently involved encoding systems we can transmit binary digits at the rate W log2 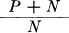 bits per second, with arbitrarily small frequency of errors. It is not possible to transmit at a higher rate by any encoding system without a definite positive frequency of errors.
bits per second, with arbitrarily small frequency of errors. It is not possible to transmit at a higher rate by any encoding system without a definite positive frequency of errors.
To approximate this limiting rate of transmission the transmitted signals must approximate, in statistical properties, a white noise.6 A system which approaches the ideal rate may be described as follows: Let M = 2s samples of white noise be constructed each of duration T. These are assigned binary numbers from 0 to (M — 1). At the transmitter the message sequences are broken up into groups of s and for each group the corresponding noise sample is transmitted as the signal. At the receiver the M samples are known and the actual received signal (perturbed by noise) is compared with each of them. The sample which has the least R.M.S. discrepancy from the received signal is chosen as the transmitted signal and the corresponding binary number reconstructed. This process amounts to choosing the most probable (a posteriori) signal. The number M of noise samples used will depend on the tolerable frequency ∊ of errors, but for almost all selections of samples we have
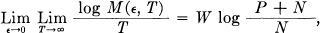
so that no matter how small ∊ is chosen, we can, by taking T sufficiently large, transmit as near as we wish to TW log 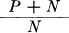 binary digits in the time T.
binary digits in the time T.
Formulas similar to C = W log 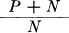 for the white noise case have been developed independently by several other writers, although with somewhat different interpretations. We may mention the work of N. Wiener,7 W. G. Tuller,8 and H. Sullivan in this connection.
for the white noise case have been developed independently by several other writers, although with somewhat different interpretations. We may mention the work of N. Wiener,7 W. G. Tuller,8 and H. Sullivan in this connection.
In the case of an arbitrary perturbing noise (not necessarily white thermal noise) it does not appear that the maximizing problem involved in determining the channel capacity C can be solved explicitly. However, upper and lower bounds can be set for C in terms of the average noise power N and the noise entropy power N1. These bounds are sufficiently close together in most practical cases to furnish a satisfactory solution to the problem.
Theorem 18: The capacity of a channel of band W perturbed by an arbitrary noise is bounded by the inequalities
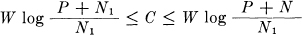
where
P = average transmitter power
N = average noise power
N1 = entropy power of the noise.
Here again the average power of the perturbed signals will be P + N. The maximum entropy for this power would occur if the received signal were white noise and would be W log 2πe(P + N). It may not be possible to achieve this; i.e., there may not be any ensemble of transmitted signals which, added to the perturbing noise, produce a white thermal noise at the receiver, but at least this sets an upper bound to H(y). We have, therefore
C = Max H(y) — H(n)
≤ W log 2πe(P + N) — W log 2πeN1.
This is the upper limit given in the theorem. The lower limit can be obtained by considering the rate if we make the transmitted signal a white noise, of power P. In this case the entropy power of the received signal must be at least as great as that of a white noise of power P + N1 since we have shown in Theorem 15 that the entropy power of the sum of two ensembles is greater than or equal to the sum of the individual entropy powers. Hence
Max H(y) ≥ W log 2πe(P + N1)
and
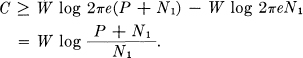
As P increases, the upper and lower bounds in Theorem 18 approach each other, so we have as an asymptotic rate

If the noise is itself white, N = N1 and the result reduces to the formula proved previously :
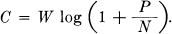
If the noise is Gaussian but with a spectrum which is not necessarily flat, N1 is the geometric mean of the noise power over the various frequencies in the band W. Thus

where N(f) is the noise power at frequency f.
Theorem 19: If we set the capacity for a given transmitter power P equal to
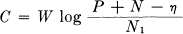
then η is monotonic decreasing as P increases and approaches 0 as a limit.
Suppose that for a given power P1 the channel capacity is
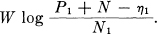
This means that the best signal distribution, say p(x), when added to the noise distribution q(x), gives a received distribution r(y) whose entropy power is (P1 + N — η1). Let us increase the power to P1 + ∆P by adding a white noise of power ∆P to the signal. The entropy of the received signal is now at least
H(y) = W log 2πe(P1 + N — η1 + ΔP)
by application of the theorem on the minimum entropy power of a sum. Hence, since we can attain the H indicated, the entropy of the maximizing distribution must be at least as great and η must be monotonic decreasing. To show that η → 0 as P → ∞ consider a signal which is a white noise with a large P. Whatever the perturbing noise, the received signal will be approximately a white noise, if P is sufficiently large, in the sense of having an entropy power approaching P + N.
26. The Channel Capacity with a Peak Power Limitation
In some applications the transmitter is limited not by the average power output but by the peak instantaneous power. The problem of calculating the channel capacity is then that of maximizing (by variation of the ensemble of transmitted symbols)
H(y) — H(n)
subject to the constraint that all the functions f(t) in the ensemble be less than or equal to 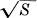 , say, for all t. A constraint of this type does not work out as well mathematically as the average power limitation. The most we have obtained for this case is a lower bound valid for all
, say, for all t. A constraint of this type does not work out as well mathematically as the average power limitation. The most we have obtained for this case is a lower bound valid for all 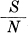 , an “asymptotic” upper bound (valid for large
, an “asymptotic” upper bound (valid for large 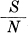 )and an asymptotic value of C for
)and an asymptotic value of C for 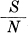 small.
small.
Theorem 20: The channel capacity C for a band W perturbed by white thermal noise of power N is bounded by
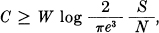
where S is the peak allowed transmitter power. For sufficiently large 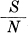
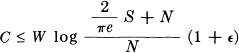
where ∊ is arbitrarily small. As 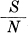 → 0 (and provided the band W starts at 0)
→ 0 (and provided the band W starts at 0)
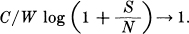
We wish to maximize the entropy of the received signal. If 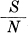 is large this will occur very nearly when we maximize the entropy of the transmitted ensemble.
is large this will occur very nearly when we maximize the entropy of the transmitted ensemble.
The asymptotic upper bound is obtained by relaxing the conditions on the ensemble. Let us suppose that the power is limited to S not at every instant of time, but only at the sample points. The maximum entropy of the transmitted ensemble under these weakened conditions is certainly greater than or equal to that under the original conditions. This altered problem can be solved easily. The maximum entropy occurs if the different samples are independent and have a distribution function which is constant from —  to +
to +  . The entropy can be calculated as
. The entropy can be calculated as
W log 4S.
The received signal will then have an entropy less than
W log (4S + 2πeN)(1 + ∊)
with ∊ → 0 as 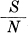 → ∞ and the channel capacity is obtained by subtracting the entropy of the white noise, W log 2πeN :
→ ∞ and the channel capacity is obtained by subtracting the entropy of the white noise, W log 2πeN :
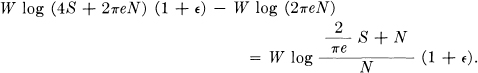
This is the desired upper bound to the channel capacity.
To obtain a lower bound consider the same ensemble of functions. Let these functions be passed through an ideal filter with a triangular transfer characteristic. The gain is to be unity at frequency 0 and decline linearly down to gain 0 at frequency W. We first show that the output functions of the filter have a peak power limitation S at all times (not just the sample points). First we note that a pulse 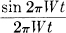 going into the filter produces
going into the filter produces
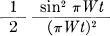
in the output. This function is never negative. The input function (in the general case) can be thought of as the sum of a series of shifted functions
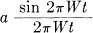
where a, the amplitude of the sample, is not greater than 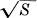 . Hence the output is the sum of shifted functions of the non-negative form above with the same coefficients. These functions being non-negative, the greatest positive value for any t is obtained when all the coefficients a have their maximum positive values, i.e.,
. Hence the output is the sum of shifted functions of the non-negative form above with the same coefficients. These functions being non-negative, the greatest positive value for any t is obtained when all the coefficients a have their maximum positive values, i.e., 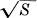 . In this case the input function was a constant of amplitude
. In this case the input function was a constant of amplitude 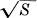 and since the filter has unit gain for D.C., the output is the same. Hence the output ensemble has a peak power S.
and since the filter has unit gain for D.C., the output is the same. Hence the output ensemble has a peak power S.
The entropy of the output ensemble can be calculated from that of the input ensemble by using the theorem dealing with such a situation. The output entropy is equal to the input entropy plus the geometrical mean gain of the filter:
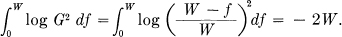
Hence the output entropy is
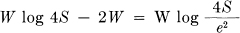
and the channel capacity is greater than
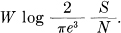
We now wish to show that, for small 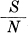 (peak signal power over average white noise power), the channel capacity is approximately
(peak signal power over average white noise power), the channel capacity is approximately
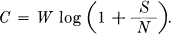
More precisely 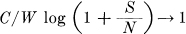 as
as 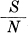 → 0. Since the average signal power P is less than or equal to the peak S, it follows that for all
→ 0. Since the average signal power P is less than or equal to the peak S, it follows that for all 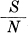
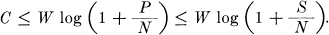
Therefore, if we can find an ensemble of functions such that they correspond to a rate nearly W log (1 + 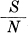 ) and are limited to band W and peak S the result will be proved. Consider the ensemble of functions of the following type. A series of t samples have the same value, either +
) and are limited to band W and peak S the result will be proved. Consider the ensemble of functions of the following type. A series of t samples have the same value, either + 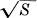 or —
or — 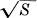 , then the next t samples have the same value, etc. The value for a series is chosen at random, probability
, then the next t samples have the same value, etc. The value for a series is chosen at random, probability 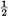 for +
for + 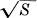 and
and 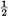 for —
for — 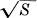 . If this ensemble be passed through a filter with triangular gain characteristic (unit gain at D.C.), the output is peak limited to ± S. Furthermore the average power is nearly S and can be made to approach this by taking t sufficiently large. The entropy of the sum of this and the thermal noise can be found by applying the theorem on the sum of a noise and a small signal. This theorem will apply if
. If this ensemble be passed through a filter with triangular gain characteristic (unit gain at D.C.), the output is peak limited to ± S. Furthermore the average power is nearly S and can be made to approach this by taking t sufficiently large. The entropy of the sum of this and the thermal noise can be found by applying the theorem on the sum of a noise and a small signal. This theorem will apply if

is sufficiently small. This can be ensured by taking 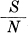 small enough (after t is chosen). The entropy power will be S+N to as close an approximation as desired, and hence the rate of transmission as near as we wish to
small enough (after t is chosen). The entropy power will be S+N to as close an approximation as desired, and hence the rate of transmission as near as we wish to
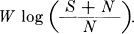
6 This and other properties of the white noise case are discussed from the geometrical point of view in “Communication in the Presence of Noise,” loc. cit.
7 Cybernetics, loc. cit.
8 “Theoretical Limitations on the Rate of Transmission of Information,” Proceedings of the Institute of Radio Engineers, v. 37, No. 5, May, 1949, pp. 468-78.