2 Making Learning Visible Starts With Teacher Clarity

Image 13

Copyright © Erin Null

Early in Will’s second year of teaching middle school, after learning about the importance of routines and procedures, he felt sure that he finally had his classroom running smoothly. His teaching pattern was this: students would come in and get their notebooks, open a textbook from the middle of their tables, and do the warm-up on the assigned page. When they finished the warm-up, they would be introduced to the daily objective—a “students will be able to” or SWBAT—and then Will would explain the math before students got started on the problem set from the textbook that usually consisted of practice exercises on that skill. When two thirds or so of the students had finished (some with Will’s individualized help), the class would go over the questions together and students would have the opportunity to change their answers to the correct ones. Then he’d assign homework, and the bell would ring. Although Will’s students were relatively well behaved and seemed busy, they weren’t learning as much as they deserved to. Like many novice teachers, Will valued compliance over learning. Here are five reasons why true learning was limited:

  • Will’s students didn’t know what they were supposed to learn, or why they were supposed to learn it. So, they were less likely to learn it, or even to want to learn it.
  • Even if Will’s students did decide to memorize his objective from the SWBAT on the board, and even if they understood what it meant, at the end of the lesson they wouldn’t know whether or not they had learned it.
  • Will’s students didn’t really benefit from Will’s expertise.
  • Will’s students didn’t have a sense of where this learning would lead, or how it connected to what they had already learned.
  • Will’s students never learned how to manage their own learning.

As we begin this journey of visible learning, let’s think about the importance of teacher clarity. Teacher clarity involves the instructional moves a teacher makes that begin with carefully planning a lesson and making the learning intentions for that lesson or unit clear to herself and her students. It extends to consistently evaluating where students are in the learning process and describing the success criteria on which students can assess their own progress and on which the teacher bases her evaluation of a student’s progress with a mathematical idea or concept. What was lacking in Will’s early teaching experiences was clarity!

Will went on to drastically improve his teaching when he read about and applied some key ideas, and his early struggles made him more effective in coaching and leading other teachers to success in their classrooms later on. A major step in this journey was when he examined the way he planned his lessons.

A starting place for lesson planning is the learning intention, or the statement of what students are expected to learn from the lesson. The learning intention for a given lesson, and the ability to communicate it clearly to students such that they can use it to gauge their progress, is foundational in the learning sciences. Stated simply, when one knows what the target is, there is an increased likelihood that the target will be achieved. Knowing one’s learning destination is crucial for mathematics students.

If learning intentions serve as one bookend for learning, the other bookend consists of the criteria used to measure success. How do you know whether your students are successful at learning what you wanted them to? How do they know whether they’re successful? How can they know whether or not they’ve met the intended learning intentions, or whether they’re making progress toward doing so? With success criteria. Success criteria are statements that describe what success looks like when the learning goal is reached. They are specific, concrete, and measurable. In this chapter, we will focus on the importance of knowing and communicating learning intentions and success criteria to students. When success criteria are communicated clearly, and teachers and students are actively looking for evidence of learning, learners understand the importance of the lesson. Even better, strategic use of learning intentions and success criteria promote student self-reflection and metacognition—that is, thinking about their own thinking. These are two essential yet often overlooked lesson outcomes. For students, this means knowing what they are expected to learn (learning intentions) and what the learning goal looks like when they have learned it (success criteria), having an idea of the route or strategies that will help them get there, and knowing what to do when they don’t know what to do (Bransford, Brown, & Cocking, 2000).

As we noted in the previous chapter, Hattie (2009) underwent the enormous task of studying and consolidating more research on quality teaching and learning than had ever been amassed before. After completing this monumental feat, John realized that the single most important thing teachers can do is to know their impact on student learning. Teachers need to be aware of the effect they have on their students (Hattie, 2009). Thus, teachers have to assess students’ understanding. To determine if learning occurred, teachers first use preassessments to identify baselines in understanding and performance.

Taken together, learning intentions, success criteria, preassessments, and checking for understanding contribute to teacher clarity. Fendick (1990) defined teacher clarity as “a measure of the clarity of communication between teachers and students—in both directions” (p. 10) and further described it across four dimensions:

  1. Clarity of organization such that structured lessons include links to the objectives and outcomes of learning.
  2. Clarity of explanation such that explanations are accurate and comprehensible to students.
  3. Clarity of examples and guided practice such that the examples are illustrative and illuminating, and students gradually move to independence, making “quick and accurate progress without help” (p. 10). Guided practice refers to the guidance teachers provide as they make strategic decisions about the right type of practice for each student throughout instruction.
  4. Clarity of assessment of student learning such that the teacher is regularly seeking out and acting upon the feedback he or she receives from students, especially through their verbal and written responses.

Learning Intentions for Mathematics

Effective teachers know where their students are in the learning cycle and design their instruction to foster learning. As we mentioned in Chapter 1, learning intentions can include a combination of surface, deep, and/or transfer learning, with the exact combination dependent on what kinds of choices a teacher makes based on where her learners are and where she wants them to go. A teacher who fails to identify where her students are in their mathematical learning is likely to undershoot or overshoot expectations for them. In mathematics and science, it is more often the latter, and there’s a term for it: the expert blind spot (Nathan & Petrosino, 2003). This is the condition created when a teacher knows the content well, but fails to recognize the fits and starts of students as they attempt to learn new concepts. This can often happen in mathematics when students have learned a procedure but do not know the meaning of the calculation they’ve done. Our algebra example in Chapter 1 included a discussion on the meaning of slope as an example of deep learning. A teacher with an expert blind spot might mistake the fact that students can identify or calculate the slope without understanding of what it means and how to interpret its value. “But I taught it! Why don’t they get it?” is the lament of anyone who has possessed an expert blind spot. That’s why it is essential to align the right instructional practices at the right time in the learning cycle. Kolb (1984) defines the learning cycle as having four elements: concrete experience, reflective observation of that experience, abstract conceptualization (based on the experience and reflection), and active experimentation (applying the new learning to daily life). Different strategies support learning at each phase in this cycle. The first three elements of the learning cycle will incorporate surface and deep learning, while the active experimentation phase is about transfer. The daily learning intentions that are communicated by the teacher are an end product of her careful planning, as she determines the type of expected learning (surface, deep, or transfer) and how to implement instruction for that type of learning. The success criteria provide a means for students and the teacher to gauge progress toward learning, thereby making learning visible.

Video 2.1 Learning Intentions in the Elementary Classroom

Figure 10

http://resources.corwin.com/VL-mathematics

Learning intentions (which some people call objectives, learning goals, targets, or purpose statements) are where teacher planning begins. Learning intentions are different from standards. Standards are statements for teachers that identify what students should know and be able to do at a given point in time. Standards are tough for yet-to-be- educated students to understand, and they are too broad for students to master in a single lesson. Effective teachers start with a standard, break the learning that standard requires into lesson-sized chunks, and then phrase these chunks so that students will be able to understand them. Each one of these chunked phrases—a daily statement of what a student is expected to learn in a given lesson—is a learning intention. Learning intentions can focus on knowledge, skills, or concepts, and should be aligned to the mathematics standards and to the learning intentions of related lessons. As mathematics researchers and educators Margaret Smith and Mary Kay Stein (2011) remind us, “The key is to specify a goal that clearly identifies what students are to know and understand about mathematics as a result of their engagement in a particular lesson” (p. 13). Following are some examples of learning intentions that we have seen in mathematics classrooms.

Video 2.2 Learning Intentions in the Secondary Classroom

Figure 11

http://resources.corwin.com/VL-mathematics

  • Know that a ten is really just a group of ten ones.
  • Recognize that area is a specific kind of array (built from unit squares) that measures two-dimensional space, and understand why we find area by multiplying the length times the width of a rectangle.
  • Learn to add two fractions with like denominators by modeling on a number line.
  • Understand how to divide a decimal number by a decimal number by considering place value.
  • Examine a given data set to determine if the function that it describes is linear or exponential by assessing the way the function changes over equal intervals and relating this change to students’ knowledge of a given context.

Some mathematics teachers might be concerned that statements such as these can rob students of a period of investigation and inquiry. Learning intentions don’t have to be used at the outset of the lesson and may be revisited over time. Teachers can withhold their learning intentions until after an exploration has occurred. And teachers can invite students to explain what they learned from the lesson and compare that with the initial learning intention for the lesson. Interesting class discussions about the alignment (or lack of alignment) can provide a great deal of insight on student understanding.

Learning intentions are themselves evidence of a scaffolded process that unfolds over many lessons. A key to planning a lesson is in knowing where your students currently are in their learning. It would be tough to teach students that a ten is really just a group of ten ones if they don’t understand the value of one, just as it would be difficult for students to determine growth patterns in functions if they don’t really understand what functions are or why they’re useful. However, learning intentions can (and often should) have an inherent recursive element in that they build connections between previously learned content and new knowledge. Savvy teachers embed previous content in the new content. The teacher is not only creating a need and a purpose for students to hone learned skills, but also providing opportunities for students to experience those “aha” moments that relate concepts to a previous lesson’s content. In this way, students are continually connecting and deepening their mathematical knowledge.

There are a few other hallmarks of good learning intentions that Clarke, Timperley, and Hattie (2003) have identified:

  • Learning intentions should be shared with students, so that students understand them and what success looks like. Recognize that not all students in the class will be working at the same rate or starting from the same place, so it’s important to adapt the plan relating to the intentions to make it clear to all students.
  • Learning does not happen in a neat, linear sequence; therefore, the cascade from the curriculum aim (the standard) through the achievement objective (unit goals) to the learning intention (for a specific lesson) is sometimes complex.
  • Learning intentions and activities can be grouped if one activity can contribute to more than one learning intention, or one learning intention may need several activities for students to understand it fully.
  • Learning intentions are what we intend students to learn, but it is important to realize students may learn other things not planned for, so teachers need to be aware of unintended consequences.

Student Ownership of Learning Intentions

Doug travels the world talking about quality instruction for all learners. He speaks to teachers and administrators, and he used to tell them that teachers should communicate their learning intentions because doing so has been shown by extensive research to boost student learning and achievement (Hattie, 2012). Furthermore, it is consistent with the first of NCTM’s (2014) effective mathematics teaching practices: to establish mathematical goals to focus learning. But he found that people actually took this advice more seriously when he framed learning intentions as a students’ rights issue. Students have a right to know what they’re supposed to learn, and why they’re supposed to learn it. After all, teachers are going to evaluate student performance and mark report cards and transcripts that last a lifetime. These records open doors to colleges and careers, or close them. It’s only fair that students understand what they’re expected to learn if teachers are going to evaluate that learning.

Students can write or verbally share what they already know about the concept or skill they’ll be learning, pose questions about it, or write about concepts they need to understand before they can tackle the day’s learning. They can solve problems that are related to the day’s learning (Sidney & Alibali, 2015; Sloyer, 2004). The point is to get learners ready to learn the new content by giving their brains something to which to connect their new skill or understanding.

After the opening exercise, some teachers have students turn to their groups and share what they’ve written or explain their reasoning in arriving at their answers. This gives students the chance to construct mathematical arguments and critique the reasoning of others, which is mathematical practice 3 (see Appendix B for a complete list of mathematical practices). An outcome of this may be to solidify their individual understanding of a mathematical concept or address any misconceptions remaining from previous experiences. This is important—connecting new learning to incorrect prior knowledge can hurt understanding (van Loon, de Bruin, van Gog, & van Merriernboer, 2013). The opportunity for students to speak also helps them firm up their understanding and learn from each other’s expertise. This use of an opening routine is just one of many ways to activate students’ prior knowledge, and the important thing is that it’s activated. Once prior knowledge is activated, students can make connections between their knowledge and the lesson’s learning intentions.

Make Learning Intentions Inviting and Engaging

The ways in which teachers talk about learning intentions make a difference. William Purkey (1992) described four patterns with which students perceived lessons: intentionally disinviting, unintentionally disinviting, unintentionally inviting, and intentionally inviting.

Teachers who were intentionally disinviting were easily recognizable because of their dismissive and harsh tone. Most of us would, thankfully, not be in that category. However, teachers who were unintentionally disinviting were negative and pessimistic about their students’ capabilities, and their low expectations were apparent to the learners (and they were often successful in having low impact on student learning!). For example, consider this introduction to a lesson on adding fractions with unlike denominators. The teacher starts by saying, “Today we are going to work on adding fractions with different denominators. This is a really difficult concept, and I know that most of you are going to struggle with being able to add fractions, so you are going to have to pay close attention.” Little does the teacher realize that he has just told the students that they will not be successful in this lesson. In addition to being disinviting, using this type of introduction encourages a fixed mindset in students who are thinking, “This is going to be hard and I probably won’t be able to do it!”

On the other hand, there is a group of teachers Purkey categorizes as unintentionally inviting. The teachers are energetic and enthusiastic, but they lack a plan for their journey. Students like being with them, but don’t benefit as fully as they could from instruction because it is inconsistent and naive. An unintentionally inviting teacher might begin the same fraction lesson by saying, “Good morning, scholars. Today we are going to learn more about fractions! I know you will find this interesting work, and I cannot wait to get started!” This is unintentionally inviting because the teacher is all about getting students excited and interested in the lesson, but notice how the statement doesn’t talk about exactly what students are going to learn or why it is important. It may not take long before the students realize that despite their enthusiasm, they have no idea of what is going on.

The final category—intentionally inviting—consists of teachers who are consistently positive and are sensitive to the needs of students. They take action and promote a growth mindset. Most of all, they are purposeful and effectively transmit a sense of instructional urgency. As teachers set the learning intentions, they also set the tone for their classroom. Let’s take a look at an intentionally inviting learning intention on adding fractions with unlike denominators in Mrs. Schmidt’s fifth grade.

“Good morning, scholars. You may recall that last year you worked with adding fractions with common denominators. This year we will move on to adding fractions with unlike denominators. Let’s start by solving this problem.

Joey ate 2 5 Equation 1 of the pumpkin pie. His sister ate 1 5 Equation 2 of the pie. How much pie did they eat? How much pie is left?

I would like you to start by representing this problem in any way that you would like.”

(After giving students the opportunity to write their ideas, the teacher gives them time to explain their work with partners or small groups while she circulates to observe and listen to discussions, noting students that may need additional support or review and those who are successful in solving the problem.)

Mrs. Schmidt now has enough information to know if students are ready for adding fractions with unlike denominators, or if some time needs to be spent reviewing and filling in the gaps from last year’s work. She continues by inviting students to identify situations in which addition of fractions is important so that students understand the need for representing, understanding, and applying this concept.

Algebra teacher Jeff Turnbull has a consistent place where he posts daily learning intentions prominently on the board. In a unit on solving systems of equations, Mr. Turnbull referred back to the day’s learning intention: “Use graphing to figure out x and y when you have two equations that intersect, and you don’t know x or y at that point.” Mr. Turnbull then said,

“This skill is used in many different jobs. You can use this skill to figure out which cell phone plan is the best deal for you or to decide if you want to buy a monthly subway pass or pay for each ride. These are important skills, and the most important part, to me, is that it makes you a better thinker. It lets you have conversations about math at a higher level, so that you can communicate better. You see, solving for two different variables, like we’re doing today, builds on the solving equations and graphing work we’ve done, but the cool thing is that it opens up into more advanced algebra and even physics. It’s like a gateway for you. Besides, graphs give us so much more information than substitution or elimination.”

While some students know that Jeff’s enthusiasm is a bit contrived, they prefer him to their previous teacher, who would tell them that they “have to learn” something, or that they will “get through” some content, as though it were a chore for which the teacher was apologizing. These unintentionally disinviting statements have a negative effect on student learning. After all, Jeff figures, how can students be expected to be engaged and excited about something if their teacher isn’t engaged and excited about it?

Figure 2.1 contains a few sample learning intentions that were initially less than effective, and how teachers revised them.

Learning intentions are more than just statements to convey to students what the learning is composed of; they are a means for building positive relationships with students. While much of this book is about instructional practices, teacher-student and student-student relationships are foundational to learning. Learning intentions that are intentionally inviting, are aligned to current student learning, are designed to advance students from surface to deeper learning, and set high expectation targets deliver positive results that accelerate learning (Hattie, 2012). Taken together, these practices make learning visible to students who understand they are under the guidance of a caring and knowledgeable teacher who is invested in their success.

Language Learning Intentions and Mathematical Practices

We have seen some of the best teachers set several learning intentions in a given lesson. These teachers communicate learning intentions in terms of content, but they also have language goals for their students and specific learning intentions related to these language goals. The language demands of mathematics are extensive, as students are expected to attend to precision, construct viable arguments, express their reasoning, and critique the reasoning of others. For students identified as English Learners, the stakes are even higher, as they do “double work” of learning mathematics while also learning the academic and disciplinary language needed (Short & Fitzsimmons, 2007). It is unfortunate that instruction of mathematical language is often overlooked, further disadvantaging those who do not possess a strong foundation of background knowledge. As well, technical mathematical terms are rarely encountered in daily life.

Language learning intentions can be related to the vocabulary words that students will need to know in order to master the lesson’s content. For example, fifth-grade teacher Katie McKenna keeps her language goals on the wall, right under her content learning intentions. For a lesson in a unit on adding and subtracting fractions, she posted the words numerator and denominator. Many students were familiar with these words, but their understanding was limited to the numerator as the “top number in a fraction” and the denominator as the “bottom number.” To make matters even worse, students had been given the “hint” that numerator contains the letter u which reminds them of up and denominator begins with the letter d so denominator is down. Granted, these are challenging words for students in Grades 3 through 5, and the need to develop deeper understanding of the meanings of the numerator and denominator in a fraction is even more complex. However, intentionally introducing these words in a context and expanding the meaning of each term across the grades have a much greater impact on the development of deep understanding of what a numerator or denominator actually means in a given situation.

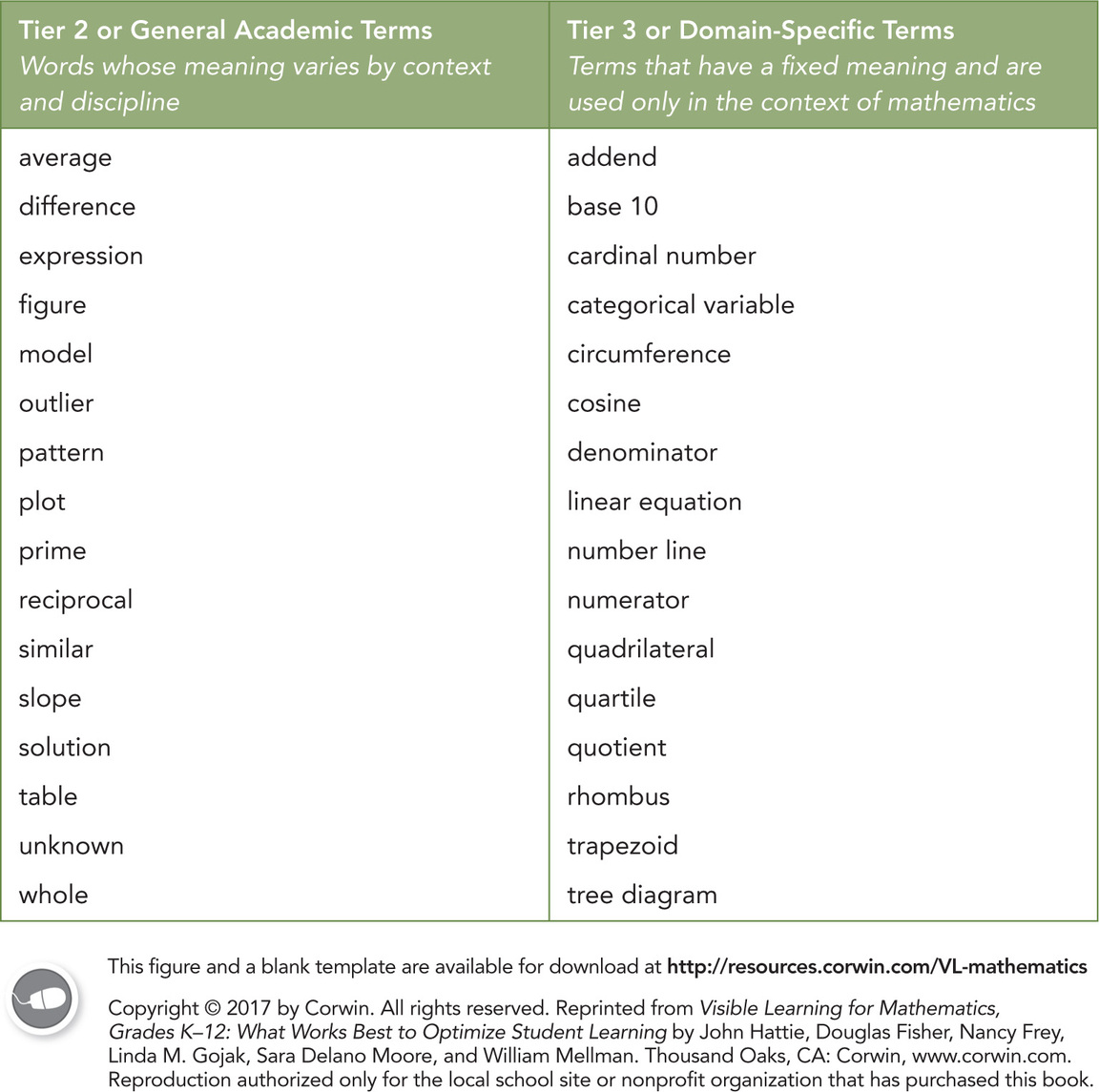
Language learning intentions can be constructed to highlight the use of what educational researchers call Tier 2 or general academic words (Beck, McKeown, & Kucan, 2013). Tier 2 words are words that all students should know by the time they graduate, and they extend beyond math class. These are words like analyze, synthesize, and extrapolate. Other Tier 2 words have specific meanings in mathematics, such as set, prime, similar, and area, that differ from the way these words are used outside of mathematics. These multiple-meaning words are especially vexing, as students often possess a limited set of definitions for words like these. For instance, they may understand that area refers to a space, but they do not know that finding the area of a figure requires a level of precision. Students are more likely to remember words when they are learning them for a reason, so it makes sense to set the expectation that students will use these words and phrases when they talk about their math work. Tier 1 words are everyday words like small and size and are not usually the focus of math teachers. Tier 3, or domain-specific, words are terms that are used specifically for mathematics such as absolute value, angle bisector, or numerator. Typically, general academic and domain-specific words are the focus of language learning in a mathematics classroom. Additional examples of these types of words can be found in Figure 2.2. The best teachers remind students why they’re learning these words.

In addition to vocabulary, teachers can focus on the function that language serves. In mathematics, we typically describe, explain, convince, solve, question, sequence, inform, justify, evaluate, and the like. When students understand these terms, teachers should expect them to engage in these actions as they work collaboratively with their peers. For example, mathematics teacher Melissa Juarez’s middle school students have been multiplying and dividing fractions. She had planned a lesson with their health and nutrition teacher, Chuck Branson, in which students would have to produce rewritten recipes with the correct calculations based on the number of people assigned. She explained that in order to do so, they would need to correctly use terms such as conversion, portions, and scaling in their written explanations. “I don’t just want to read your procedure. Convince me why your answer is correct. To do so, you’ll need to identify any patterns you used to help solve the problem.” She listed these terms on the whiteboard as she spoke. As she explained,

“Some recipes are written for larger groups of people, like 14 to 20. You want to prepare it for yourself and a couple of friends. So, we’ll work on the mathematical thinking here, and then you’ll be able to make these recipes in Mr. Branson’s class. It’s not just about the calculations, but explaining how you came up with the answers. I’m interested in having you solve these problems in your expert group, inform the others in your home group, and justify your answers in writing.”

During this time, Ms. Juarez accomplished several important instructional goals. The first is that she made her learning intentions clear to students, giving attention to language as well as content. In addition, the task was designed to facilitate their learning as they transitioned from surface learning of conversions to deeper learning in applying knowledge to new situations. Third, the lesson supported several of NCTM’s (2014) effective mathematics teaching practices, including “implement tasks that promote reasoning and problem solving” and “use and connect mathematical representations.” Finally, the task incorporates many of the standards for mathematical practice in order for students to continue to develop important mathematical habits of mind.

Social Learning Intentions and Mathematical Practices

Since high-quality math lessons involve a good deal of collaboration (as we’ll discuss in the next chapter), it makes sense for teachers to set social learning intentions as well. Social learning intentions are those that focus on the social skills that foster effective collaboration and communication. Will has seen one frustrated teacher post the social goal “Be quiet when the teacher is talking!” This is not the type of social goal that we mean here, even though respect for a teacher talking is important. However, a social goal of “be quiet and listen when others are talking” is a valued skill in small and large group work. It makes sense to attend to the social skills of mathematics students. After all, Vygotsky (1962) and others have certainly shown us that all learning is a social endeavor. The ways in which peers interact and work with one another, and with their teacher, are an engine in the classroom.

Social learning intentions can include things like “Ask your teammates for help,” “Listen to really understand what your group members are saying,” “Explain your reasoning,” or “Give helpful feedback to others.” These and other communication skills contribute to a sense of classroom cohesion, which Hattie (2009) describes as “the sense that all (teachers and students) are working toward positive learning gains” (p. 103). As with content and language learning intentions, social intentions should be based on what teachers learn from their students as they watch them work and review individual and group products. Listening to and observing the interactions of students in small and large group settings is essential for making such decisions.

Shortly into the school year, Mr. Milam asks his students to create a list of class norms they will agree to as they work on doing mathematics together throughout the school year. The students come up with an excellent list, and because it is their list, they work hard to follow these norms and politely remind each other of their agreed-upon ideas when they slip! Here is a list that a group of sixth graders developed.

  1. We will listen when others are speaking. That means

    • Looking at the speaker
    • Not playing with pencils or other distractions
    • Not interrupting or talking with a neighbor

  2. We will work to support each other in our math groups. That means

    • Answering a teammate’s question
    • Sharing our work without copying or telling others how to do it
    • Asking good questions of one another

  3. We will come to class prepared to work hard to learn important mathematics. That means

    • We will be ready to start when the bell rings.
    • We will have the correct supplies (paper, pencil, notebook, textbook).
    • We will complete the practice and come with questions about parts we did not understand.

As the year progressed, students added other norms to this list. Mr. Milam did not have to spend time preaching to students about their behavior or being prepared for class. These norms had been decided and agreed upon by the entire class, and by giving students ownership, Mr. Milam thus increased the likelihood that students would take responsibility for their behavior and their work.

Sometimes social learning intentions support the mathematical practices (MPs) we alluded to in the preface. These practices are often described as habits of mind students must develop to be proficient in doing mathematics, and there is agreement that these are general practices that students must develop. The language in these practices differs based on specific states, provinces, or countries. As an example, let’s consider the practices (Standards for Mathematical Practice) recommended in the Common Core State Standards (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010):

  1. Make sense of problems and persevere in solving them.
  2. Reason abstractly and quantitatively.
  3. Construct viable arguments and critique the reasoning of others.
  4. Model with mathematics.
  5. Use appropriate tools strategically.
  6. Attend to precision.
  7. Look for and make use of structure.
  8. Look for and express regularity in repeated reasoning.

In setting learning intentions, a teacher might identify a mathematical practice, such as “Construct viable arguments and critique the reasoning of others” (MP 3), and turn it into more student-friendly language, such as “Justify your thinking so that you can convince a partner you’re correct.” Integrated Math III teacher Brian Stone posts the mathematical practice he wants his high school mathematicians to focus on, sometimes even more prominently than the learning intention. When his students were learning about logarithms, he had “Look for and make use of structure” (MP 7) posted to remind students what to look for as they completed the tasks. Another day, when students were working on a particularly challenging task, he had posted “Make sense of problems and persevere in solving them” (MP 1). Before delving into the task, he led his students in a discussion about perseverance, and together they identified what this would sound like and look like, including items such as asking for help, asking for clarification, and tracking the speaker.

This example is from the practice standards from the Common Core, and nearly all state and national standards have a version of these higher order thinking skills. For example, in Texas, the processes are described as the following (Texas Essential Knowledge and Skills for Mathematics, 2012):

  1. Apply mathematics to problems arising in everyday life, society, and the workplace.
  2. Use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution.
  3. Select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate.
  4. Communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate.
  5. Create and use representations to organize, record, and communicate mathematical ideas.
  6. Analyze mathematical relationships to connect and communicate mathematical ideas.
  7. Display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.

Australia’s Mathematics Curriculum Key Ideas (Foundation–Year 10 Australian Curriculum, 2015) include the following:

  • Understanding
  • Fluency
  • Problem solving
  • Reasoning

You can find a nonexhaustive list of practice standards around the world in Appendix C.

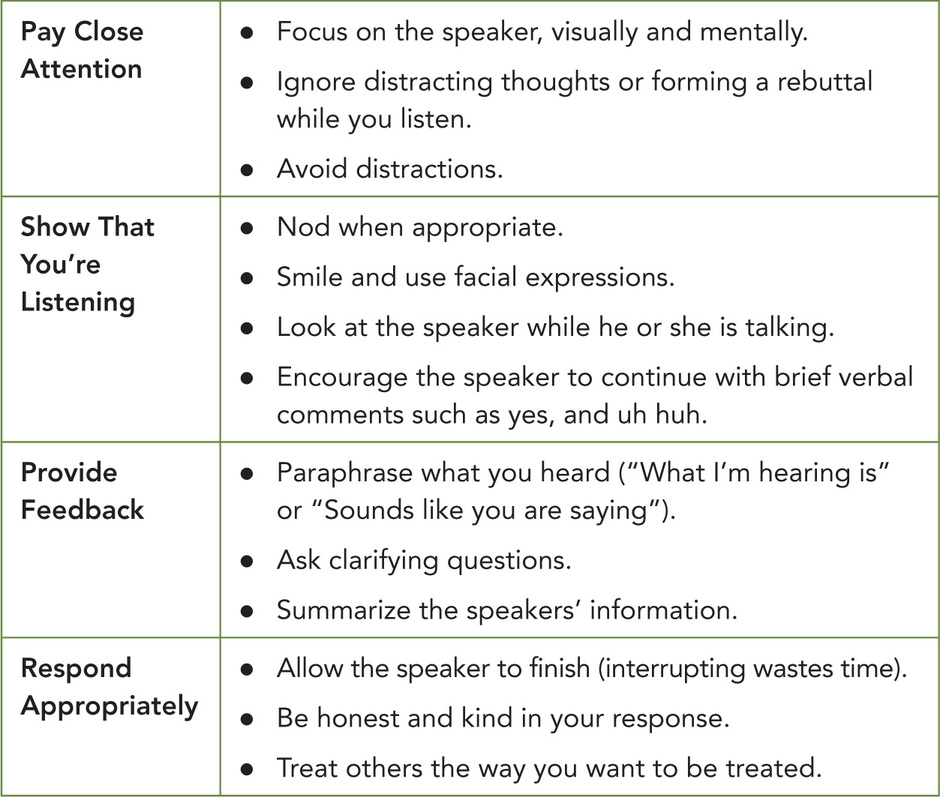
Fourth-grade teacher Andrea Villanova reminded her students to “take turns as you work to solve the problems. Remember, your group should work together to solve the problem using pictures, words, and numbers. You’ll only be able to hear the reasoning of your group members if you take turns and if you listen with intention.” The poster in Ms. Villanova’s room outlined what it meant to listen with intention, and students had practiced each of these skills at the outset of the school year. A copy of her poster can be found in Figure 2.3.

As with academic learning intentions, savvy teachers return to social learning intentions before releasing students to work collaboratively, and ask students to self-assess whether they thought they met these goals once they’re finished. Even young children can rate their skill at taking turns, sharing ideas, or disagreeing respectfully during a discussion.

Success Criteria for Mathematics

Effective math teachers establish not only the learning intentions but also the success criteria. In addition to knowing what they’re supposed to learn, students should know how they will know they’ve learned it, and how they can assess themselves along the way.

Success Criteria Are Crucial for Motivation

As mathematics teachers move away from the futile practice of relying on repetitious problem sets and toward mathematically rich tasks, the question of success criteria becomes more complicated than “You’ll know you’re successful if you get sixteen out of twenty of today’s problems right.” Besides, calculating the right answer isn’t the only point of a task. Mathematics is more than getting correct answers. Mathematics is thinking about problems flexibly and working to solve them logically. As students are increasingly called upon to justify and explain their reasoning, connect multiple solutions to a problem, analyze worked examples, and address real-world problems using the tools of mathematics, teachers must offer more nuanced assessments of student learning. The great news about learning intentions and success criteria is that they have been shown to increase students’ internal motivation. And a very convincing case could be made that internal motivation to succeed in mathematics is one of the most important things your students can learn.

Video 2.3 Achieving Teacher Clarity With Success Criteria

Figure 15

http://resources.corwin.com/VL-mathematics

Success criteria work because they tap into principles of human motivation (Bandura, 1997; Elliot & Harackiewicz, 1994). People tend to compare their current performance or ability with a goal that they set, or have a caring teacher help set with them. When there is a gap between where they are and where they want to be, it creates cognitive dissonance. Students are motivated to close the gap and get rid of the dissonance by working and learning. The more explicitly and precisely they can see the goal, the more motivated they will be.

It may seem obvious that teachers should know whether or not their students are learning what they’re supposed to. But students need to know whether they’re on the right track, too. Self-reported grades reflect the extent to which students have accurate understandings of and abilities to predict their achievement. It matters that students can describe their current performance accurately, whether that performance is high or low (Hattie, 2012). When we think about it, though, it’s hard for learners to know whether they are learning something without having some criteria against which they can measure themselves. Teachers should have success criteria in mind for the lesson. As mentioned earlier, success criteria describe what success looks like when the learning goal is reached. It is specific, concrete, and measurable.

Suppose that a teacher establishes a learning intention that students should use their knowledge of area of rectangles to solve real-world problems. How would a student know whether he or she can do this? Would solving one problem involving area be enough? Some area problems are more difficult than others, involving combinations of rectangles and related shapes. Should students solve these problems independently or as part of a team? Will they need to solve three out of four correctly? Eight out of ten? Will the lengths of the sides be round numbers or numbers with decimals, or fractions of units? What if their methods are correct, but they forget a decimal place or mess up their conversions? Each of these questions guides teachers in determining what success looks like for their students. In mathematics, success criteria are measures of success demonstrated by more than simple “answer getting.” Teachers who focus only on the correctness of a student’s answer do so at the peril of misunderstanding the student’s conceptual understanding and problem-solving process.

Without clearly defined criteria, teachers and students are not sure what type of learning has occurred, if any. As we noted earlier, some learning intentions focus on surface learning, and thus the success criteria should be aligned with that level of learning. Other times, the learning intention focuses on deep or transfer levels of learning, and the success criteria need to align with those levels.

Students are much more motivated to work toward success criteria if those criteria are specific (Locke & Latham, 1990). Criteria such as “Do your best” and “Try hard” are not very clear or actionable (they have the lowest of effect sizes and probably should never be used). “I can” statements such as “I can add fractions” may be actionable but are not very specific. Criteria such as “I will be able to clearly explain my reasoning as I factor a polynomial” or “I can solve problems that involve addition or subtraction of mixed numbers and explain my thinking” are more likely to produce results. The more specific your learning intentions and the criteria for reaching those intentions, the more likely it is that your students will achieve them. Learning intentions, which are synonymous with learning goals, should also be proximal (Bandura, 1997). In other words, they shouldn’t be too distant in the future. This is important to keep in mind when assigning long projects—it really is worth establishing daily success criteria that your students can keep in mind as they work on long-term projects, especially at younger ages. Even better might be to teach students how to break larger goals down into smaller ones themselves.

At the beginning of a unit on number theory, Mrs. Martinez assigned her fifth graders a “Special Number Project” that incorporated all of the important mathematical ideas of the unit. This would be the final assessment in lieu of a written test. Students would be working on their projects throughout the unit and checking in regularly with Mrs. Martinez to show their progress. At the beginning of the unit, the project was explained, and by the third day, each student was to choose a special number between 1 and 100. Mrs. Martinez prepared a letter to parents so they were aware of what their children were doing. As the week progressed, Mrs. Martinez shared some examples of former students’ projects (without giving too much information so that students would work to develop original ideas). By the end of the week, students had to turn in a brief description of their special number projects. While they were permitted to change their ideas after a conversation with the teacher, this helped them to commit to an idea rather than flounder throughout the unit. As the unit vocabulary developed, a classroom word wall was built to help students focus on the important mathematical concepts and the new vocabulary. One of the success criteria was that all of the vocabulary had to be meaningfully incorporated into the project. Students discussed what was meaningful and what was not using the project examples the teacher had shared. Mrs. Martinez met with students regularly or collected written updates on their progress throughout the unit so no one was left hanging until the last minute. The best part was that on “Project Day,” students proudly carried their math projects (ranging from posters to board games to stories) into class eager to share their work with others. The project was clear, the learning intention was clear, and the success criteria were clear. Most of the students successfully demonstrated mastery of this important mathematics content and had fun doing it! (And Mrs. Martinez still has many of those projects in her files!)

Hilda Amador uses “I can” statements with her first-grade students throughout the day. She posts the statements on a language chart and leads the class in reading them aloud together. “I can find all of the two-addend combinations to make a given number,” they read. Ms. Amador continues, “Here is a problem for you to solve.”

My mom went to the market and bought some apples and some pears. She bought 10 pieces of fruit altogether. How many apples and how many pears could she have bought?

Using the color tiles, you will work with your partner to model all of the different combinations of apples and pears you can find. Then you will write an equation for each combination you have found.

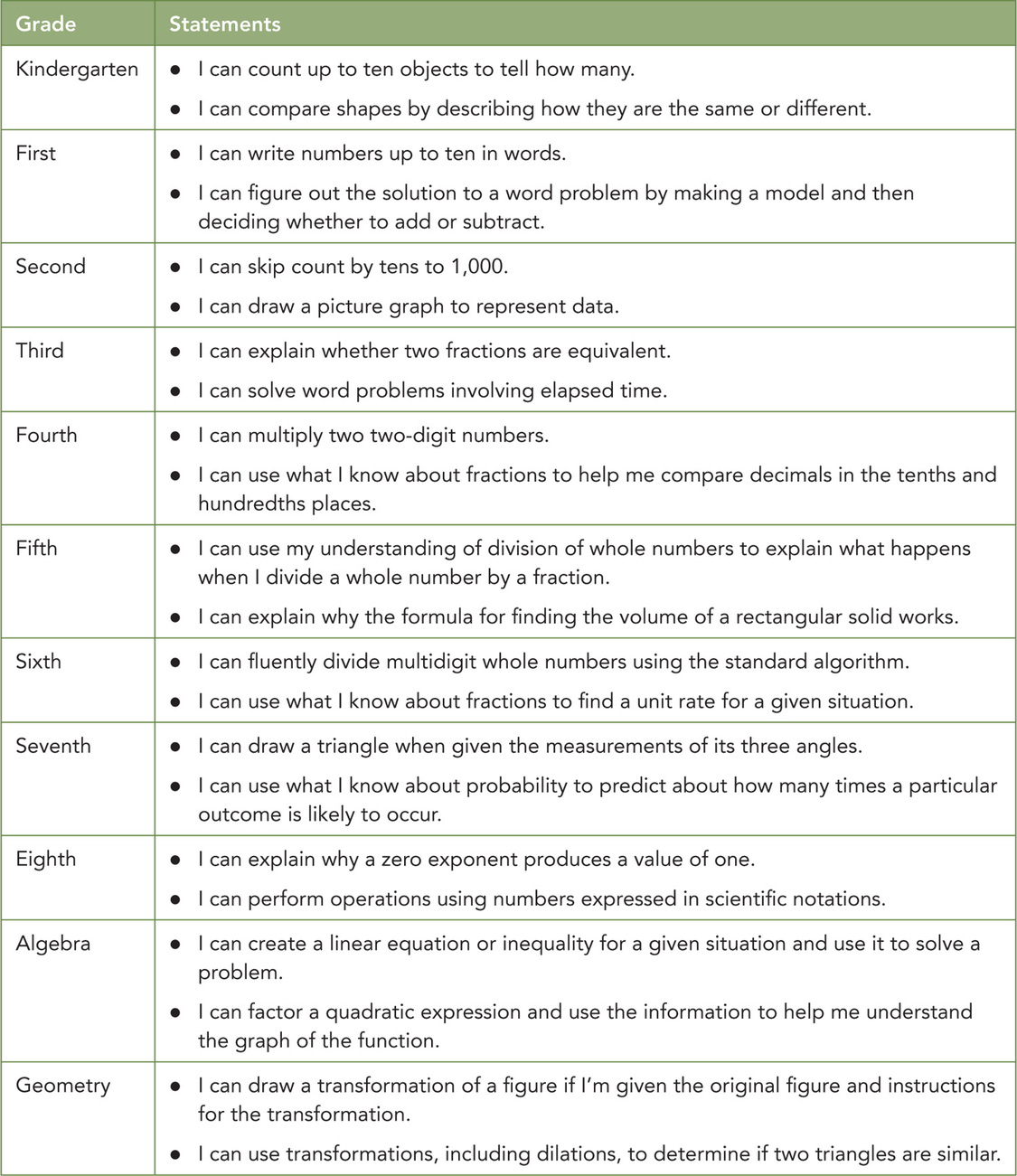
One caution here is to be sure that “I can” statements are specific and tied to the learning intention. General “I can” statements, while well intentioned, are not very helpful to the students or the teacher. Sample “I can” statements in mathematics can be found in Figure 2.4.

In some lessons, especially after students have explored a task to make sense of it themselves, the teacher leads a discussion to have students think aloud and to help clarify their thinking through posing purposeful (carefully constructed) questions. In the case of Ms. Amador’s first grade, she might tell students they will need to convince her they have found all of the combinations. This reminds them of the learning intention and success criteria for the lesson before they head off to work further with their partners. “Let’s review our ‘I can’ statement so we can keep our goal in mind.” As students work together to model and write equations to represent a given sum, Ms. Amador is providing guided learning by asking purposeful questions to student groups that are struggling with the task, as well as pointing out where they are meeting success. At the end of the lesson, she returns once more to the “I can” statement. “We’ll use our traffic light so you can tell me how you’re doing with this.” Her young learners place their magnetized name card on either the red light (“I don’t know this yet”), the yellow light (“I’m almost there”), or the green light (“I can help someone else tomorrow!”). The teacher later said, “They’re not always accurate in their self-assessments, but it’s building a habit of noticing their own learning. I still need to formatively assess and check for understanding, but their self-assessments give me a head start on how I’ll group them tomorrow.”

Getting Buy-In for Success Criteria

Student goal setting, or having students determine their own criteria for success in mathematics, has been shown to boost achievement (Schunk, 1996; Senko & Hulleman, 2013). Interestingly, these benefits have also been evidenced when students have a teacher set goals for them, if students accept the goals as legitimate. Success criteria developed by the teacher allow students to understand their learning goals in measurable terms. An effective way to create this acceptance is to have students collaborate with you to determine the success criteria. Their input on what constitutes success provides the teacher with feedback about how students are viewing their progress and what they believe they will need to get there. For example, when presenting a rubric to students, it is worthwhile to discuss and collaborate on the contents of the rubric with students, to allow them to weigh in on the draft success criteria. This doesn’t mean that you have to let a group of teenagers lower the bar so that they have an easier time. The teacher is still responsible for maintaining high expectations. In our experience, though, students’ desire to slack off is rarely a serious problem when they have input into what determines success with a particular concept, practice, or problem.

Once his students have seen the rubric, Mr. Stone provides students time to discuss, in groups of three or four, and generate recommendations for the rubric. They can process their thoughts with each other and test their ideas on a small and relatively unthreatening audience. Remember that students, like the rest of us, are social creatures who learn and remember best when they’re interacting with others. After the students chat with each other for a couple of minutes, Mr. Stone holds a quick class discussion. He calls on representatives from each group to share their feedback. Sometimes the student feedback is trivial and fun—“We should call the category on the right ‘Nobel Prize’ because that’s the thinking of real experts.” And sometimes it’s substantive—“We could have a fourth column in between good and excellent, in case somebody’s work is in between. That way they get a score that’s more fair.”

For shorter assignments with less complicated success criteria, it may not be necessary to spend this much class time making sure students know all the details of what’s being asked of them. As a rule of thumb, the longer and more complex the assignment, the more class time teachers should devote to making sure that students understand the success criteria.

Mr. Stone also uses a rubric for the rich mathematical tasks he develops (see Figure 2.6). “I use a consistent rubric for the tasks because the criteria are the same, regardless of the content we’re working on,” he explained. “I used to make a different rubric for each task, but realized after a while that what I really wanted them to do was grasp the concepts being taught, furnish an explanation that included a rationale, and use accurate notation and terminology,” he said. The justification element has been especially challenging. “Their tendency is just to explain, without furnishing the mathematical reasoning to support it,” said Mr. Stone. “So no matter what we’re studying, this is a continual teaching point. That’s why I want to use a rubric that keeps this front and center.” Mr. Stone also uses anonymous samples of student work with the class to demonstrate what successful and unsuccessful work looks like for each category. This gives students the opportunity to ask questions or to better understand the expectations through examples of completed work.

Whatever your success criteria, it is both fair and motivating for students to know what quality learning looks like before they begin a task. Just like making sure that students know learning intentions, ensuring that students know the success criteria has been shown by research to dramatically increase their learning (Black & Wiliam, 1998; Hattie, 2009). This makes intuitive sense, but it is lost in many classrooms.

Using exit tickets can be a means for teachers to gauge progress toward the established success criteria. Typically, exit tickets allow students to summarize or synthesize their thinking about some aspect of their learning. This task makes learning more visible to students and their teachers. As some of our students have noted, “I didn’t know what I understood until I wrote it down.” Middle school math teacher Andrea Martin uses exit slips each day to determine if her students have met the success criteria for that day. She changes the prompt each day. Her general prompts have included the following:

  • How does your model demonstrate your thinking?
  • Convince me your method and answer are correct.
  • Describe any patterns you found to help you solve the problem.
  • How can you solve the problem another way?

As students leave Ms. Martin’s classroom, they deposit their exit slips into one of three buckets indicating their level of understanding. One of the buckets says, “I totally understand and could teach this to someone else.” Another says, “I understand it, but my thinking is still a bit shaky.” And the third says, “I am not sure I understand and would appreciate some support.” This self-assessment helps guide Ms. Martin’s work the following day. When Leo placed his paper in the bucket indicating his lack of success, he said to his teacher, “I can’t figure out how to show my thinking. Maybe you could pair me up with someone so I could talk about it and then maybe I could do it.” Students don’t always need support from the teacher; peer support also works.

Available for download at http://resources.corwin.com/VL-mathematics

Copyright © 2017 by Corwin. All rights reserved. Reprinted from Visible Learning for Mathematics, Grades K–12: What Works Best to Optimize Student Learning by John Hattie, Douglas Fisher, Nancy Frey, Linda M. Gojak, Sara Delano Moore, and William Mellman. Thousand Oaks, CA: Corwin, www.corwin.com. Reproduction authorized only for the local school site or nonprofit organization that has purchased this book.

Preassessments

Another factor that influences teacher clarity involves the precision of the lessons to meet the needs of students and not just to cover content. Teachers need to determine the gap between students’ current level of performance or understanding and the expected level of mastery (as indicated in standards documents, for example). It’s not hard to imagine that there are students who have already mastered the content that’s about to be taught to them. What a waste of precious instructional time! It’s also not hard to imagine that there are students who need instructional time focused on a specific aspect of a concept. The only way that a teacher can know this, and increase his or her precision in determining learning outcomes and thus clarity, is through the use of preassessments. Preassessments, or diagnostic testing as it is sometimes called, allow teachers to establish a baseline level of student knowledge before they begin teaching. It will also give teachers information to plan differentiated instruction that fills gaps and scaffolds instruction into smaller pieces for struggling students, plan tasks that move students prepared to learn the concept, and extend tasks for students who are ready to move on. Preassessments also enable teachers to determine what learning has occurred over the time of lesson(s) or units. When teachers use only postassessments, such as end-of-unit tests or projects, they will know who has demonstrated the expected level of achievement (and who has not), but they won’t know who has learned what because learning is a measure of change over time.

Video 2.4 Continual Assessment for Daily Planning

Figure 19

http://resources.corwin.com/VL-mathematics

Will remembers a colleague being delighted when her students showed mastery after her unit on the collection, display, and interpretation of data. Her students could calculate mean and median. They could use that information to visually represent data. They understood a variety of plots and graphs. She had great hopes for them for the coming year. After all, they had mastered this first unit so quickly! However, the teacher soon grew frustrated when her students didn’t learn much quite so easily in the next unit. It turned out that her students had previously learned to analyze simple data the year before arriving in her classroom. In other words, what she thought had been new material in that first unit was really a review. When confronted with new concepts in subsequent units, their learning stalled, in part because she was pacing her instruction based on their early, and somewhat deceptive, success. Will’s colleague would have known this in advance if she had given a preassessment before beginning the unit, thus allowing her to make adjustments to her pacing based on their existing knowledge and gaps. The ideal preassessment mirrors the postassessment in rigor and in the content it assesses, even though the questions may be different.

Another value in giving preassessments is for the teacher to establish appropriate success criteria. Will’s colleague could have asked her students to design their own data collection tools, analyze more challenging data sets, or learn in some other way—or she could have moved more quickly to the next unit instead of wasting valuable instructional time. Many researchers argue that the bigger value in giving preassessments is in knowing your individual students’ understandings going into a lesson (Stiggins, 2001). Armed with data from preassessments, teachers can effectively differentiate instruction and meet more students’ instructional needs (Ainsworth & Viegut, 2006). You will read more about differentiating instruction later in this book. Preassessment data will also be a tremendous help as you connect your lessons to students’ prior knowledge. You will know what you can connect your lesson to and what you can’t. We will discuss assessment more in Chapter 7.

Conclusion

We have taken the position that students deserve to know what they are expected to learn. To our thinking, this is more than writing the standard on the dry-erase board. It’s more than complying with a teacher evaluation tool that requires objectives to be written. Part of the joy of teaching and learning mathematics comes when learners know what they are expected to learn and why. In sum, teachers should establish learning intentions that

In addition, teachers should make the learning intentions explicit at some point in the lesson and reference them to mark progress toward them. When the learning intentions are well developed, the teacher is able to increase his or her clarity mindfully, and mathematics can be enjoyed for its own sake.

Just as important are the success criteria that are used to motivate students and allow them to develop the habit of self-assessing. But keep in mind that your students will not become motivated and reflective learners overnight. Expert teachers know that student motivation levels can increase over time, but that it happens gradually. Those moments in which previously underperforming students “see the light” and suddenly understand the importance of mathematics may initially be short-lived. But over time, these instances become more frequent and sustained, and shift a student’s personal view of mathematics. After all, nothing is more motivating than a sense of competence. Daily success criteria give students a chance to experience competence more frequently, not just when they receive a grade on the unit test. The key is to remain encouraging, but also to remain patient with the process. Remember to encourage students’ growth, effort, and perseverance, rather than praising their intelligence or innate math ability, or their grades. The way you encourage students will help to shape their mathematical mindsets toward becoming more growth-centered and motivated (Dweck, 2006). Show students that you believe in them, but do it thoughtfully, persistently, and warmly.

Reflection and Discussion Questions

  1. Learning intentions can help students make connections between current learning and previously learned content. Identify the learning intention for a lesson you have recently taught. What previously learned content is connected to this learning intention? Did your students see the connection? If so, how did this impact their engagement in the learning? If not, how might you modify the learning intention and experience to bring more attention to this connection?
  2. Learning intentions should be intentionally inviting to students. Look back over your learning intentions from recent lessons and rewrite them to be more inviting to students. Use the examples in Figure 2.1 for guidance.
  3. A lesson can have mathematical content and/or practice learning intentions, language learning intentions, and/or social learning intentions. Consider again your recent lessons and learning intentions, keeping in mind that not every lesson will incorporate every type of learning intention. Which relevant types of learning intentions did you make known to students? What other types of learning intentions might you consider? How can you determine where you want to focus your lessons?
  4. Review the list of Tier 2 words in Figure 2.2. Download the blank template and make a list of the specific general academic (Tier 2) words that are important in your mathematics course(s) along with any Tier 3 (domain-specific) words your students must master. What are your strategies for helping students find success with this vocabulary?
  5. Look at Mr. Stone’s general math rubric in Figure 2.6 and consider one of your learning intentions with its success criteria. Make notes about the specific things you would expect to see from your students in each of the three areas of the rubric, Conceptual Understanding, Explanation and Justification, and Math Terms and Notations.