CHAPTER 6
How to Use a Black Hole to Test General Relativity
The black hole is probably the most bizarre, exotic and fascinating prediction of Einstein’s general relativity. This object, composed purely of warped spacetime, endowed with the ability to trap anything, from light rays to Marvel superheroes, that crosses its famous “event horizon,” has lodged itself in the public imagination like no other aspect of physics. Ask the average person on the street to name the four fundamental forces of nature or the basic particles that make up the atom, and more often than not you will get a blank stare. But ask that person to say something about black holes, and you may well get a fairly coherent summary of their basic properties. You will almost certainly hear the name Stephen Hawking, the person universally attached to the black hole idea, and you may also get a list of movies that have featured black holes.
But even more bizarre is that we know, almost as certainly as one knows anything in science, that black holes exist. In Chapters 7 and 8 we will learn about the spectacular evidence for merging black holes gleaned from the gravitational waves they emitted. But long before those detections, the evidence for black holes obtained by astronomers using light, ranging from gamma rays to radio waves, was so solid that there was very little doubt that these things are really out there. Our goal here is to describe black holes and the evidence (apart from gravitational waves) for them. More importantly, we will explain to you how we may be able to carry out some remarkable new tests of general relativity using black holes.
We have already seen in Chapter 3 how John Michell and Pierre Simon Laplace in the late 1700s speculated on the possibility of a body so dense that it could prevent light from escaping its surface and reaching great distances. While it is tempting to say that they “predicted” black holes, the fact is that the physics they used—Newtonian gravity and the corpuscular theory of light—was not correct in the end. We now know that gravity is governed by general relativity (at least all the evidence supports that so far), and that light is governed by Maxwell’s equations, even if you choose to describe it using the quantum concept of the photon. Nevertheless, it is amusing to learn about the ideas that these great Enlightenment thinkers came up with using their imaginations and the accepted physics of their day.
The modern, relativistic story of black holes began on the battlefields of World War I, with a soldier-scientist named Karl Schwarzschild. He was born in Frankfurt, Germany, on 9 October 1873, the son of a banker. The family traced its roots to medieval Frankfurt, when Jews were confined to a ghetto, but under the protection of the king, or “Kaiser.” Even then, the Schwarzschild family was well-to-do. The family name evidently originates in a tradition of that period of identifying a family by a plaque (“schild” in German) that it would affix to the front of its house. For Karl’s ancestral family the plaque was black (“schwarz”), hence the name. One of their neighbors in the ghetto had a plaque that was red (“rot”). The descendants of that family would become the famous Rothschild family of financiers. By 1811 the Frankfurt ghetto was abolished and some measure of civil rights was granted to Jews.
Schwarzschild showed an early interest in science, and by the age of 23 had received a Ph.D. from the Ludwig Maximillian University in Munich. His career advanced rapidly, with posts in Vienna and Göttingen, culminating in 1909 in the directorship of the Astrophysical Observatory in Postdam, one of the premier observatories of Europe at the time. He contributed seminal work to a wide range of topics, including solar physics, the statistics of stellar motions, the optics of astronomical lenses, the determination of the orbits of comets and asteroids, and the classification of stars by their spectra. He even traveled to Algiers to study the solar eclipse of 1905. This was long before the bending of light was an issue, of course; in those days eclipses were used mainly to study the corona of the Sun, and to search for the hypothetical planet Vulcan between the Sun and Mercury.
When World War I broke out in August 1914 he was 41 years old, and therefore not subject to the draft, nor required to enlist. But, like many Jews in Germany at the time he volunteered, desiring to demonstrate the loyalty of the Jewish community to Germany (other Jewish scientists who served this way included Fritz Haber, James Franck and Gustav Hertz). He never fought on the front lines, but because of his technical background he was assigned to head a meteorological station at Namur, Belgium, and then was attached to the artillery staff in France and later on the Eastern front. He even wrote a paper in 1915 on the effects of air resistance on the path of a projectile, but publication was held up for security reasons.
But in late 1915, at the Russian front, he contracted a rare and painful autoimmune skin disease called pemphigus, that even today is difficult to treat. While undergoing treatment he received copies of the papers that Einstein had delivered a few weeks earlier at the Prussian Academy of Sciences, describing his new theory of general relativity. Schwarzschild recognized that the theory was very complicated mathematically, but he set out to see if, by making some simplifying assumptions, he could find a solution to the Einstein equations of general relativity.
For his first attempt, he assumed that the sought-after solution would be static, or unchanging in time. He then assumed that the solution would be spherically symmetric, or the same no matter how you rotated the system about a central point. He imagined that the solution might apply to a perfectly spherical body, such as a star, sitting at rest, and isolated or far away from any other perturbing bodies. For his first attempt at a solution, he further assumed that the body was so small in size that you could ignore its extent or its internal structure. He called it a “Massenpunkt,” or point mass, an object whose mass was entirely concentrated at a point. This kind of assumption is routinely used in physics because it allows you to get an idea of what the solution outside the body looks like, without having to worry about the messy details of the body’s internal structure. To his surprise, Schwarzschild found a simple exact solution to Einstein’s complex equations.
For his second attempt, he assumed that the body had a finite size, but that its interior density (the amount of mass per unit volume) was constant throughout the body. This is not a totally realistic assumption, because we know that bodies bound by their own gravity, such as the Earth or the Sun, are more dense at the center than at the surface. But once again, such an assumption might give useful insights without having to sweat a lot of messy details such as whether the body is solid, liquid or gas (or a combination), or whether it is hot or cold. Here again, he found an exact solution to the Einstein equations.
He wrote up his solutions in two papers and sent them to Einstein, who communicated the Massenpunkt paper to the Prussian Academy of Sciences on 13 January 1916, and the finite-body paper on 24 February. Einstein was amazed that Schwarzschild had managed to obtain these exact solutions, and pronounced himself very pleased with the second paper. The Massenpunkt paper, not so much.
The Massenpunkt paper had a feature that troubled Einstein greatly. Schwarzschild’s solutions gave formulae for the warped geometry of spacetime that varied as a function of the distance from the center. Very far from the body, the geometry became that of ordinary flat space and time, as you would expect when the gravity of the body becomes negligible at great distances. As you approach the body, the geometry becomes more and more warped, again as expected when gravity gets stronger. But in the Massenpunkt solution, when the distance from the center reaches a value given by twice the mass of the point (multiplied by Newton’s constant of gravitation and divided by the square of the speed of light), things got crazy. One function became infinite (one divided by zero), while another became zero. This behavior is what physicists call a “singularity,” and for years afterward this was called the “Schwarzschild singularity.” Since it occurs wherever the distance from the center has this special value, it is actually a spherical surface surrounding the point mass. It’s not a surface made of matter that you could bounce off or crash into, but is rather an imaginary surface or boundary that we define mathematically because odd mathematical things happen to the solution on that surface. The question was, what?
Einstein believed that such singularities were unacceptable (we will learn in Chapter 7 that he thought he had disproved gravitational waves in 1938 because of the apparent existence of singularities in the solution), and that such a Massenpunkt would therefore not occur in nature. On the other hand, Schwarzschild’s second solution for an extended body was completely acceptable. The geometry of spacetime became more warped as one approached the body (in fact, for the same mass, the external solution was identical to the solution for the point mass), but once inside the body, the solution changed and was perfectly finite all the way to the center. Einstein and others who examined Schwarzschild’s two solutions believed that there must be something in the laws of physics to prevent a body from ever being so small in relation to its mass that it would reside completely inside this special “Schwarzschild” radius. To get a sense of scale, for an object with the mass of the Earth, the Schwarzschild radius is about a centimeter, roughly the size of the tip of your baby finger. For an object with the mass of the Sun, it is about three kilometers. For what we today would call a fifty million solar mass black hole, it is the radius of the Earth’s orbit around the Sun. A body would have to be compressed to an incredibly small size and an enormous density to fit inside its Schwarzschild radius. To Einstein and his contemporaries, the world seemed safe from Schwarzschild’s horrible singularity.
Unfortunately, nothing could save Schwarzschild from the ravages of pemphigus; he died on 16 May 1916. Even though he was German, he was such a famous astronomer that The Observatory in England published an obituary that August. It described his many contributions to astronomy and astrophysics, but made no mention of his solution to the Einstein equations of general relativity. Einstein’s theory was still too new and obscure.
And that pretty much was it for black hole research for the next forty years. A few papers related to Schwarzschild’s solution were published here and there, but they were largely ignored. Ironically, a young student named Johannes Droste, working under the tutelage of the great Dutch physicist Hendrik Lorentz, found the Massenpunkt solution in the spring of 1916, totally independently of Schwarzschild. But his paper was published in the relatively obscure Proceedings of the Royal Netherlands Academy of Sciences (in Dutch), and wasn’t “discovered” until many decades later. During the 1920s and 1930s, a few researchers, including Eddington and Howard P. Robertson, tried to explore what was really going on at the Schwarzschild singularity. Was this a place where bizarre physics occurred, or was the singular behavior merely an artifact of the coordinates that Schwarzschild used, in the same way that the coordinates of latitude and longitude on Earth are singular at the north and south poles where all the lines of longitude meet at one point. Some of these papers, seen in retrospect, held important clues, but they were barely noticed.
In 1939, the American theoretical physicist J. Robert Oppenheimer and his student Hartland Snyder published a remarkable paper entitled “On continued gravitational contraction.” In it they showed that a massive enough star that runs out of thermonuclear sources of energy will no longer be able to support itself against the crushing force of its own gravity, and will contract. Using Einstein’s equations, they showed that the decreasing radius of the star would reach the Schwarzschild radius, but the star would continue to shrink. An observer riding on the surface of the star as it collapses inward would not observe any “singular” or bizarre behavior during the contraction, while observers at great distances would observe light emitted from the star’s surface becoming progressively redder (the gravitational redshift effect) and fainter until, after a long time, the star’s light would be essentially undetectable. For all practical purposes it would be “black,” and the final object would be described by Schwarzschild’s Massenpunkt solution. Eighty years later, this paper reads like a modern paper on black hole physics, with many of the insights into the nature of these objects that we have come to understand. But at the time, it also had almost no impact. Oppenheimer never followed up on the paper, and within three years would turn all of his attention to leading the Manhattan Project to develop an atomic bomb.
We must remember that this was a period when general relativity was considered a backwater of physics. Very few people worked in the field. The noted general relativity theorist Peter Bergmann, who had been an assistant of Einstein during the late 1930s, once joked that if he ever needed to find out everything that was going on in general relativity, he only needed to call up his five best friends. Physicists were much more concerned with quantum mechanics, atomic and nuclear physics, field theory and elementary particles, and, after World War II, with developing the new technologies that had emerged from wartime research, such as radar, nuclear power, transistors, semiconductors, masers and lasers.
In 1956, Martin Kruskal, a mathematical physicist working in the plasma physics laboratory at Princeton University, realized that he could find a new system of coordinates in which Schwarzschild’s “singularity” would disappear. He described his discovery to his Princeton colleague John Wheeler, who had begun to take an interest in general relativity. Wheeler thought it was nice, but otherwise paid little attention to it. But by 1959, Wheeler suddenly realized the significance of the discovery and wrote a paper with Kruskal’s name as the author and submitted it to Physical Review. He somehow neglected to tell Kruskal what he was up to. A few months later, while on sabbatical in Germany, Kruskal received out of the blue the galley proofs of a paper that he didn’t know he had written. But he recognized the figures in the paper as being in a style typical of his friend Wheeler, and he urged him to be a co-author. Wheeler declined, and Kruskal’s paper became one of the foundations of a new understanding of the nature of black holes.
At the same time, George Szekeres, a Hungarian mathematician working at the University of Adelaide, Australia, and David Finkelstein, an American physicist at the Stevens Institute of Technology in New Jersey, were also working on similar approaches to resolving Schwarzschild’s singularity.
These researchers showed conclusively that nothing “singular” or infinite happens at the Schwarzschild radius. A light ray, an atom or a graduate student can head toward the object and cross the Schwarzschild radius without experiencing anything infinite. To be sure, there will be the inevitable stretching and squeezing of a body as it approaches the object. This is nothing more than the same kind of tidal effects that the Moon induces upon the Earth, for example, stretching it along the line directed toward the Moon, and squeezing it in the perpendicular directions. These forces can be large enough to squeeze and stretch the poor graduate student into a long thin noodle, but no matter what, the forces remain finite as the student crosses the “magic” radius.
The true significance of the Schwarzschild radius turned out to be rather different, and quite astonishing. The sphere defined by this special radius turns out to be the boundary between two realms. Outside the sphere is the normal external universe, where people can travel freely, subject to the speed of light limitation, and can communicate with each other using light signals. You can even safely go into orbit around the object.
Once you cross the Schwarzschild radius, however, your fate is very different. Escape is impossible. You can fire up the most powerful rocket imaginable, subject only to the normal laws of physics, but you will be unable to get out. You are pulled inexorably toward a point at the center of the object, there to be squashed to zero volume and infinite density. In desperation you send a light signal outwards, pleading for help, and indeed you witness the signal moving away from you at the speed of light. But, unbeknownst to you, that signal is actually following you inward, later to join you and everything else that ever crossed that fatal sphere in a crushing finality.
It may seem contradictory to imagine sending a light signal outward, yet to have that signal actually follow you inward. One analogy that explains how this might work is to imagine a swimmer who always swims at a fixed speed within water, never faster, never slower. The swimmer is in the Niagara river, just above the famous waterfalls (Figure 6.1). Because her speed is higher than that of the current, she can freely swim up the river, down the river or across the river. Compared to a person treading water and following the current, she is always swimming at the same speed. But if she allows herself to go over the falls, her fate is different. She can try to swim upwards, and indeed relative to the person floating freely with the descending water, she is moving upward at her normal speed. Yet both swimmers are moving downward, to be dashed on the rocks below. Like all the analogies used in this book, this one is not perfect, but it gives a sense of how light can never escape from the Schwarzschild object. Yet contrary to what John Michell thought (see page 29), light never actually comes to rest according to anybody who measures its speed.
Figure 6.1 A waterfall as an event horizon. Above the waterfall a person floats with the current, while a swimmer swims away from him at her fixed speed, and slowly makes her way upstream. Below the waterfall the person still flows with the current, and the swimmer still moves away from him at her standard speed, but now both are falling to the rocks below, and the swimmer will never reach the top.
Because the Schwarzschild radius is the boundary between what can and cannot communicate with the outside world, it came to be called the “event horizon.” Just as you cannot receive light from the Sun after it falls below the Earth’s horizon, you cannot receive any signal from any event that occurs inside the Schwarzschild radius.
By the early to mid 1960s, these kinds of results convinced many general relativists that Schwarzschild’s Massenpunkt solution was something to take seriously. John Wheeler was one of them, and in fact the term “black hole” is often credited to him. He had been ruminating on an appropriate term for these objects, and during a 1967 lecture he was giving at the Goddard Center for Space Studies in New York, he wondered aloud about a suitable name. Somebody in the audience shouted “black hole,” and Wheeler immediately adopted and promoted it.
But to most physicists and almost all astronomers, black holes were curiosities of Einstein’s theory, but so what? That attitude began to change with the discovery of quasars.
In the fall of 1960, Caltech astronomers Thomas Matthews and Allan Sandage prepared to use the 200 inch telescope at Mount Palomar in California to make some observations of a radio source denoted 3C48 (the forty-eighth entry in the third “Cambridge catalogue” of radio sources). They were interested in what kind of visible light this source might be emitting, so on the night of 26 September 1960 they took a photographic plate of the area of sky around 3C48. Conventional wisdom at the time told them that they would find a cluster of galaxies at the location of the radio source, but this was nothing like what they saw. Instead, as far as anyone could tell by looking at the photographic plate, the object was a star. Yet it was like no other star seen up to then, for subsequent observations during October and November of that year and periodically throughout 1961 showed that its spectrum of colors was highly unusual, and that its brightness or luminosity varied widely and rapidly, sometimes over periods as brief as 15 minutes. This was a new addition to the astronomical family, and it needed a special name. It was a powerful radio source, yet it looked “stellar” or starlike (ordinary stars are not strong radio sources); on the other hand, because of its spectrum and variability it was not quite a star, it was only “quasi” stellar. Hence the name quasistellar radio source or “quasar” was soon applied to this object and to others like it.
The discovery of quasars brought general relativity to the attention of astronomers. The reason was an energy crisis of truly cosmic proportions. Within a few years after the discovery of 3C48, it was found that it and other quasars like it were among the most distant objects in the universe. What the astronomers thought were unusual spectra were actually rather ordinary spectra in which all the features were shifted uniformly to the red end of the frequency spectrum. This meant that the quasars must be moving away from us at high speeds, 30 percent of the speed of light in the case of 3C48. The shift in wavelength to the red is a consequence of the expansion of the universe. For 3C48, for instance, the recession velocity corresponded to a distance of about six billion light years. Because the quasars were so distant, one would have expected them to be faint, yet they were very bright sources, both in visible light and in radio waves. Therefore, their intrinsic brightness or luminosity must be enormous. For 3C48, the numbers translated into a hundred times the brightness of our own galaxy.
This was the energy crisis: What could possibly be the source of such power? On cosmic scales the strongest force known is gravity, so it was suggested that the energy of super-strong gravitational fields could provide the answer. Furthermore, the source of this power had to be very compact, for the simple reason that for the source to vary in brightness coherently over a period of, say, one hour, it couldn’t be much larger than the distance light can travel in one hour, in order for one side of the source to know what the other side is doing and thus to behave in unison.
Thus, one solution to the quasar energy crisis involved strong gravitational fields, meaning perhaps a huge concentration of mass, maybe millions of times the mass of the Sun, confined to a region of space smaller than a light hour, or about the diameter of the orbit of Jupiter. This represented a new collapsed state of matter that could only be described by the general theory of relativity.
But relativists and astronomers knew almost nothing about each other, worked on entirely different problems, were housed in entirely different departments within universities, and spoke different scientific languages. To remedy this, in June 1963 a small group of relativity researchers based in Texas sent invitations to astronomers and general relativists around the world to attend a conference on a proposed new discipline, to be called relativistic astrophysics. The First Texas Symposium on Relativistic Astrophysics was held in Dallas on 16–18 December 1963 (page 5). The atmosphere was a mixture of excitement, because of the potential for solving an important problem by bringing these communities together, and grief, because of the assassination of President John Kennedy in that city just three and a half weeks earlier. Indeed, Texas Governor John Connelly, his arm still in a sling from having taken one of the assassin’s bullets, opened the conference and welcomed the participants. There were 300 attendees, of whom roughly 240 were astronomers or astrophysicists, and 60 were relativity researchers. The latter number represented almost all of the world’s general relativists at the time. The only ones missing were relativists from Eastern Europe and the Soviet Union, this being the middle of the Cold War.
The problem of quasars took center stage, and the leading models to resolve the energy crisis involved the collapse of great masses to the Schwarzschild “singularity.” But what was collapsing? William Fowler of Caltech and Fred Hoyle of Cambridge University proposed the collapse of a supermassive star, perhaps millions of times the mass of the Sun. Cornell astronomer Thomas Gold suggested the collapse of an enormous and dense cluster of stars. John Wheeler and his post-docs and students presented papers on the collapse of compact objects such as neutron stars. It is interesting in retrospect to notice that all the models discussed were about the collapse process, while the final Schwarzschild singularity, as it was still called, played no essential role. The concept of the black hole as a standalone object was still poorly understood in 1963, and it would be several decades before supermassive black holes would be identified as the “central engine” for the power of quasars.
There were very few papers devoted purely to general relativity and its consequences. One, given by a young Ph.D. student of Wheeler named Kip Thorne, was on a toroidal, or donut-shaped, configuration of pure electromagnetic fields held together by gravity, a rather esoteric topic. The other was a mathematical paper by a physicist from New Zealand named Roy P. Kerr, who was working at the University of Texas at Austin. He had been using a variety of sophisticated mathematical techniques that exploited symmetry principles to look for new exact solutions of Einstein’s equations. The solution he obtained was expressed in a fairly obscure system of mathematical variables, and so when he gave his talk he must have seemed like a visitor from another planet to the astronomers, who had not yet learned how to comprehend relativistic jargon. But during the question period after his talk, the Greek relativist Achilles Papapetrou admonished the audience to pay attention to this young man’s solution, because he had a feeling it would one day prove to be important.
Indeed, Kerr’s solution was soon identified as the exact solution for a rotating black hole and became the basis for all of modern black hole physics. Schwarzschild’s solution was for the special case of a non-rotating black hole, but, since almost everything in the universe—planets, stars, galaxies—rotates, the Kerr solution would prove to be more physically relevant.
The fact that astronomers and general relativists were being brought together to work together on these kinds of questions was exciting, although at first it had its amusing side. Several participants at that first Texas symposium tell of a general relativity theorist interrupting a lecture by an astronomer to ask what he meant by the “magnitude” of a star (magnitude is the astronomer’s measure of the brightness of a star, an elementary concept taught in every freshman astronomy class), or of the astronomer asking the general relativist what the “Riemann tensor” was (the Riemann tensor is a measure of the curvature of spacetime, to the relativist an equally elementary concept). There were skeptics of this attempt to get the two fields to play together nicely. The MIT astrophysicist Philip Morrison proclaimed himself “interested but unpersuaded” that new physics would come out of collapse to the Schwarzschild radius, while Peter Bergmann admitted that he was “not very optimistic” that the play date between the two communities would amount to much any time soon.
But Tommy Gold had the last laugh during his banquet speech, declaring:
It was … [Fred] Hoyle’s genius which produced the extremely attractive idea that … the relativists, with their sophisticated work, were not only magnificent cultural ornaments, but might actually be useful to science! Everyone is pleased: the relativists, who feel they are being appreciated, who are suddenly experts in a field they hardly knew existed; the astrophysicists, for having enlarged their domain, their empire, by the annexation of another subject, general relativity. It is all very pleasing, so let us all hope that it is right. What a shame it would be if we had to go and dismiss all the relativists again!
Soon, however, the practitioners of this new interdisciplinary field learned how to communicate with each other, so that by later Texas Symposia (the twenty-ninth was held in Cape Town, South Africa in 2017), it was not uncommon to find relativistic astrophysicists who were as knowledgable about the intricacies of curved spacetime as they were about the structure and evolution of stars or about the capabilities and limitations of X-ray telescopes.
From 1963 to 1974, many of the key physical and mathematical properties of black holes were established during a period of intense research by a score of theorists. They learned that, to an observer outside the horizon, the only feature of the black hole itself that is detectable is its gravitational field. All information about what went across the horizon either during the formation of the black hole or during its later life is lost. Any matter or radiation that remains outside the horizon, of course, is detectable. Far away from the black hole, this gravitational field is indistinguishable from the gravitational field of any object of the same mass and angular momentum, such as a star. However, to an observer close to the horizon, things can be very unusual. The deflection of light can be so large that light can be deflected by large angles, not just a few arcseconds. A light ray can even move on a circular orbit just outside the horizon, at 1.5 times the Schwarzschild radius, for a non-rotating black hole. For the Kerr solution, the rotation of the black hole produces the same effects of the dragging of inertial frames as those induced by the rotating Earth. These are the effects confirmed by Gravity Probe-B and the LAGEOS measurements (Chapter 4). But if the observer goes close enough to the horizon, near the equator, the dragging of spacetime becomes so strong that the observer will be dragged around bodily with the rotation of the hole, no matter how hard he blasts his rockets to try to avoid whirling around the body.
But instead of dwelling on the many unusual and remarkable properties of black holes, we will turn to the observational search for black holes, looking particularly for examples where tests of general relativity might be feasible.
While the discovery of quasars spurred interest in the role of general relativity in astrophysics, it would be several decades before the central role of black holes in the quasar phenomenon would be appreciated. Instead, the first serious candidate for an actual black hole in nature came in 1971, from the new field of X-ray astronomy.
The first astronomical X-rays from sources other than the Sun were discovered beginning in 1962, including a source called Cygnus X-1, the name denoting the first X-ray source found in the constellation Cygnus. By 1967 about thirty such sources were known, all detected using instruments placed on sounding rockets or balloons launched far above the Earth’s absorbing atmosphere. However, X-ray astronomy made a giant leap into the mainstream of astronomy with the launch of the Uhuru orbiting X-ray satellite in December 1970. The name Uhuru, meaning “freedom” in Swahili, was given to the satellite because it was launched from a facility in Kenya on that country’s independence day (NASA’s official name was the typically boring “X-ray Explorer Satellite SAS-A”). During its three-year lifetime, Uhuru charted more than three hundred X-ray sources. Later orbiting X-ray satellites found many more sources, including ordinary stars, white dwarfs, neutron stars, galaxies and quasars, as well as a diffuse background of X-rays, reaching us from all directions.
Uhuru’s examination of the X-rays from Cygnus X-1 gave two crucial pieces of information that led to the conclusion that a black hole was present. The first was the observation that the X-rays were variable in time in an irregular fashion, but on timescales as short as a third of a second. This meant that the region from which the X-rays originated had to be of the order of a third of a light second, or around 100,000 kilometers in size. This, in turn, implied that the object at the center of the X-ray emitting region had to be a very compact object, such as a white dwarf, a neutron star or a black hole, because a normal star, like our Sun, would have a diameter ten times too large. The second piece of information provided by Uhuru was an accurate enough position for the source in the sky to make it possible to locate a star, known as HDE 226868, at the same location. Examination of the spectrum of light from this star showed that it was in orbit about a companion. This was determined by looking at the Doppler shifts in its spectral lines, just as the orbits of binary pulsars are determined by looking at the Doppler shifts of their pulse periods (see Chapter 5), or as exoplanets are found using Doppler shifts of the spectra of their parent stars. The companion had to be the X-ray source.
You may be wondering exactly how a black hole meets up with a star in order to perform this dance, since after all, space is a very large and empty place. The standard scenario begins before the black hole was a black hole, back when it was a star orbiting a companion star. Even though our Sun is the only star in the solar system, as many as half the stars in our galaxy are in binary systems, orbiting around each other just as Earth orbits the Sun. After a long enough period of time one of these stars will run out of fuel to burn via thermonuclear reactions, and if it is massive enough it will collapse with an accompanying supernova explosion of its outer layers. For a relatively low-mass initial star, the explosion and collapse frequently produces a neutron star. This is the pathway that can lead to pulsars in binary systems, as we discussed in Chapter 5 (page 80). But if the initial star has a higher mass, the implosion of the core does not halt at the neutron star stage but proceeds all the way to a black hole. What is left then is a black hole and a star in a binary system. Subsequently, if the stellar companion itself is massive enough, it may also eventually undergo a supernova explosion and a core implosion, leading to a black hole companion. Such binary black hole systems will be lead characters in our story of gravitational wave detection in the next three chapters.
But back during the black hole–star phase, if the black hole is close enough to its companion star, its strong tidal gravitational force can distort the star into a shape somewhat like a teardrop (Figure 6.2). At the tip of the teardrop the force of attraction toward the black hole is stronger than that toward the star, and so gas migrates from the star toward the black hole. But the gas does not head right into the black hole, because the hole’s orbital motion has carried it sideways a bit. So just as two ice skaters passing by each other quickly lock arms and begin a rapid spin around each other, the streaming gas is grabbed by the black hole’s gravity and swirls around it in a gaseous disk. Because a ring of gas at a given distance from the black hole moves a little faster than a ring just outside it and a little slower than a ring just inside it, there is friction between adjacent rings of gas. This friction has two important consequences. It heats the gas to such high temperatures that the gas emits light all the way into the X-ray band. The friction also slows down the rings of gas, causing them to spiral inward to the black hole. When the gas reaches a distance from the hole around three times the radius of the horizon, it can no longer maintain a steady circular orbit and it plunges toward the hole, crossing the event horizon and adding a bit to the mass of the hole. This inner edge of the disk is represented by the white region in Figure 6.2. A disk like this is called an “accretion disk” because the gas eventually is accreted by the black hole.

Figure 6.2 Accretion of gas from a companion star onto a black hole. The black hole is represented by the black dot, surrounded by an accretion disk of hot gas that can emit light in the X-ray band. Inside the inner edge of the disk (white region), gas can no longer be in a steady circular orbit but instead plunges directly into the black hole.
This model accounts for the main features of the X-ray source Cygnus X-1, and for many such X-ray sources discovered subsequently. In some cases, in addition to the gas torn from the stellar surface, the massive stellar companion may emit a strong stellar wind, much like the solar wind, but on a much more massive scale. Some of that gas can also find its way to the accretion disk around the black hole. This is thought to be true of HDE 226868, the companion star in Cygnus X-1.
But what makes us think that Cygnus X-1 involves a black hole? Could it not be a neutron star or a white dwarf? It is here that we combine general relativity with information on the orbital motion of the companion star to identify the compact object. From studying the spectrum of HDE 226868, astronomers concluded that it is of a type of star that typically has a mass between 20 and 40 solar masses. In order to induce the observed orbital motion of the star, the mass of the compact object must therefore be at least 10 solar masses. It cannot be a white dwarf, because, as we remarked in Chapter 5 (page 94), the maximum possible mass for a white dwarf is about 1.4 solar masses, the Chandrasekhar mass. This conclusion does not depend on general relativity, because white dwarfs are not very relativistic. What about a neutron star? General relativity plays an important role in the structure of neutron stars; nevertheless, relativists have determined a maximum possible mass for them as well, in this case about 3 solar masses, and by no means as large as 10 (the maximum observed mass of a neutron star is about 2.2 solar masses). Therefore, it is not a neutron star. The only object left that can be massive enough to induce the orbital wobble of the companion, yet is small enough in size to allow the short-term X-ray fluctuations, is a black hole. Even though this argument is somewhat indirect, it has stood up to further observations of the system, as well as to attempts to propose alternate models that do not invoke black holes. Still, to be safe, scientists customarily call these black hole candidates.
Many other black hole candidates have been discovered in X-ray binary systems. Interestingly, as we will learn in Chapters 7 and 8, none of them is as massive as the 20 to 50 solar mass black holes detected using gravitational waves by LIGO and Virgo, and this has challenged astrophysicists to come up with scenarios that could produce such heavyweights. There are also numerous X-ray binaries containing neutron stars. In these systems the mass of the compact object is always smaller than the 3 solar mass limit imposed by general relativity, and in many cases the X-rays are pulsed, indicating that the infalling gas is interacting with the strong, rotating magnetic field of the underlying neutron star.
In addition, there is an intriguing subset of X-ray binaries that shed additional light on the difference between neutron stars and black holes. These are systems in which the rate of accretion of gas from the companion is very low, so that the gas in the disk is thin and friction is much weaker. As a result, the X-ray emission is very faint, but still detectable. However, when one looks at those systems in which the mass of the compact object is less than 3 solar masses, there is an additional X-ray flux superimposed on the disk flux, while for every system where the compact object’s mass is greater than 3 solar masses, there is only the feeble disk flux. Ramesh Narayan and his colleagues at Harvard University have suggested that in the high-mass systems, the gas reaches the inner edge of the disk and plunges into the black hole, emitting no additional radiation. But in the low-mass systems, the gas crashes onto the surface of the neutron star, heats up and emits the additional flux of X-rays. They have suggested that this is the first concrete evidence of general relativity’s prediction of the existence of an event horizon. If this result holds up, it will be a test of a central prediction of Einstein’s theory.
Other researchers are asking whether one can test general relativity by examining the details of the emission from such accretion disks, particularly variations with time and unique features in the spectra. After all, near the inner edge of the disk, the gas is orbiting in an extremely warped region of spacetime compared to that in the vicinity of the Sun. For a 10 solar mass black hole, the orbital period just before plunge is about 5 milliseconds and the gas is moving at half the speed of light. The radiation that the gas emits experiences strong Doppler shifts, extreme gravitational redshifts and strong deflections, with some rays encircling the hole a few times before heading out toward the observer. If the black hole is rotating, the dragging of inertial frames will induce a number of observable effects. The hope is to test whether the spacetime geometry around the compact object really is that of either the Schwarzschild solution or the Kerr solution. Unfortunately this is a very complex problem. One must somehow cleanly separate those phenomena arising from spacetime warpage from those arising from the complicated physics associated with the gas and radiation, sometimes called “dirty gastrophysics.” This is currently an extremely active area of research, and may soon provide some remarkable new tests of general relativity.
The next place you might think to test general relativity using black holes is in quasars. There is widespread agreement that the large redshifts in the spectra of quasars indicate that they are moving away from us at large velocities, and that, according to the picture of the expanding universe, they are therefore at very great distances. The powerhouse of the quasar is believed to be the active and violent central nucleus of a galaxy. The idea that this nucleus involves a relativistic collapsed object has changed little since the first Texas symposium, but now a rotating, supermassive black hole itself is the central engine. The black hole may weigh 100 million solar masses; as large as this is, it may still be only a tenth of a percent of the total mass of the galaxy. The black hole is gobbling up stars and gas at a ferocious rate, perhaps as much as one solar mass of material per year. As the material approaches the hole, friction from collisions with other material heats it up to temperatures high enough to make it radiate the enormous power we see on Earth. The narrow jets of matter that can be seen shooting out at nearly the speed of light on opposite sides of many quasars are believed to be the product of an interaction between magnetic fields embedded in the accreting matter and the strong dragging of inertial frames by the rotating black hole (page 58). There is evidence that quasars were much more prevalent in the early universe than they are at present; as we look farther out in distance, we are also looking farther back in time because the light from the quasar takes a finite time to reach us. It has been found that the number of quasars peaks at a time corresponding to an age of the universe about one-third of its present age. This may be the result of the finite time needed to grow such massive black holes (a problem that is still not fully solved) and the fact that once the black hole has swept up the stars and gas from the core of the galaxy, the quasar phenomenon shuts off.
Although around 200,000 quasars have been found, the current view is that they are a small and temporary subset of a larger population, derived from the observation that essentially all massive galaxies contain massive black holes, and the fact that there are hundreds of billions of galaxies in the observable universe, far more than the number of quasars. These black hole masses range from 100,000 solar masses to the current world (or should we say, universe) record of 20 billion solar masses in the galaxy NGC 4889. It is still unclear exactly how these supermassive black holes form. One hypothesis is that these monsters form when many smaller black holes merge over the aeons of time. If enough small black holes form early enough in the universe, then they will be gravitationally attracted to each other and will merge. This scenario is aided by astrophysical mechanisms that guarantee that heavy objects tend to sink toward the center of galaxies, thus increasing the chances of mergers, as well as by the fact that mergers of galaxies themselves were rather common in the early universe.
With all these massive black holes around, you might expect a plethora of tests of general relativity. But just as with black holes in binary systems, the complications of gastrophysics make the problem hard, although this is also an area of current research. It turns out, however, that there is one supermassive black hole that may be the perfect laboratory for testing Einstein’s theory. All you have to do is to … look up in the (southern) sky! It’s close! It’s clean! It’s Sagittarius A*!
We will devote the rest of this chapter to the story of this remarkable, massive black hole, sitting smack dab in the center of our own Milky Way. The story begins with Karl Jansky (1905–1950), the pioneer of radio astronomy, whom we met briefly in Chapter 3.
Jansky was born in the Territory of Oklahoma to parents of Czech and French–English descent. He finished his undergraduate physics degree at the University of Wisconsin in 1927 and then moved to New Jersey to work for Bell Telephone Laboratory. At the time, the company wanted to investigate the use of electromagnetic waves with a short wavelength (of about 10 meters) in trans-Atlantic telephone services. In 1931 Jansky was tasked with studying what else could produce such waves on Earth and interfere with communication signals. To do this, he built a radio antenna designed to detect waves with a wavelength of about 15 meters (with a corresponding frequency of 20 megahertz), and mounted it on a large turntable. Jansky’s “carousel” was about 30 meters wide and stood about 6 meters tall, allowing him to rotate the antenna and pinpoint the direction of any signals he detected.
Over several months, he collected data. The main sources of radio static were thunderstorms, but in addition to weather effects, roughly once per day his antenna also detected a faint but steady radio “hiss” of unknown origin. Whenever a scientist detects a signal that repeats once per day the usual suspect is the Sun, and Jansky at first reasoned that he was recording radio waves from the Sun.
Upon further study, however, Jansky realized that the signal repeated once every 23 hours and 56 minutes and not every 24 hours. The latter is the time it takes the Earth to complete a full rotation so that the Sun appears in the same position in the sky. This period is called the solar day. But 23 hours and 56 minutes is the time it takes the Earth to complete a full rotation so that the stars appear in the same position in the night sky. This is called the sidereal day. The roughly 4 minute difference is due to Earth’s motion around the Sun, which of course affects when the Sun rises but has no effect on when the stars appear in the night sky. If the signal Jansky had detected had something to do with the Sun, then it should have repeated with the solar day and not the sidereal day. The data indicated an origin far outside the solar system.
By carefully rotating his antenna and taking many more months of data, Jansky was able to show that the signal was strongest in the direction of the center of the Milky Way galaxy. This coincides with the direction of the Sagittarius constellation, near a feature denoted Sagittarius A by astronomers. He published a paper on his discovery in the Proceedings of the Institute of Radio Engineers in 1933.
A New York Times article entitled “New Radio Waves Traced to Centre of the Milky Way” catapulted Jansky to brief public stardom. But despite this, he could not convince other astronomers that there was important science in this “star noise” he had detected. It did not help either that the United States was going through the Great Depression in the early 1930s, followed by World War II. The field of astronomy would eventually recognize Jansky as the father of radio astronomy and name a unit of radio flux, the jansky, after him, but only after his death in 1950 from a heart condition.
For decades, Jansky’s mysterious radio source in the Sagittarius constellation remained mostly unexplored, until in 1974 astronomers Bruce Balick and Robert Brown used radio interferometry to explore the region. Recall from Chapter 3 (page 39) that combining pairs or groups of radio telescopes can enable pinpointing the direction of a radio source with very high precision. In addition, this technique can resolve the size and shape of such sources with good resolution. Working at the National Radio Astronomy Observatory, Balick and Brown tried to resolve the patch of the sky from which Jansky had earlier detected radio waves. To their surprise, they found that most of the emission was confined to a very small area in the sky that was coincident with the Galactic Center. The size was about a tenth of an arcsecond as seen from Earth, or about 800 astronomical units at the source (later observations would narrow the size down to 50 microarcseconds, or about half an astronomical unit).
Balick invented the name Sagittarius A* for the radio source in 1982, arguing that in quantum mechanics the excited states of atoms are sometimes denoted with an asterisk, and this radio source was indeed very “exciting.” Other names were later proposed for Sagittarius A*, but none of them stuck, and a standard abbreviation Sgr A* (pronounced “saj-ay-star”) was soon adopted.
The fact that the radio emission was coming from such a compact region was a hint that a black hole might be there, but confirmation was difficult to come by. It was impossible to observe the region using optical telescopes, because of enormous bands of dust that lie between the solar system and the center of the galaxy, which absorb light in the visible band. However, in a band of wavelengths just beyond the red end of the visible spectrum, called the near infrared, light passes right through the dust, making the Galactic Center “visible” (albeit not by eye, but using special infrared sensors that had been developed to enable this branch of astronomy). Numerous astronomers trained their infrared telescopes on the Galactic Center to try to see what was going on there.
Two teams in particular took advantage of the latest advances in telescope technology. These included the ability to do interferometry at infrared wavelengths, extending a method that had been routine at radio wavelengths (see Chapter 3). Another advancement was a technique called “adaptive optics,” whereby information about disturbances in the Earth’s atmosphere is used to alter the shape of the mirrors of the telescopes in order to achieve the sharpest images. They also had the advantage of working at dry, high-altitude sites. Being high and dry is important because water vapor absorbs near-infrared light. One group, based at the Max Planck Institute for Extraterrestrial Physics in Garching, Germany, headed by Reinhard Genzel, used the Very Large Telescope Interferometer. This is an array of four instruments located on a mountaintop in Chile at about 8,600 feet above sea level, some 1,200 kilometers north of Santiago. The other group, led by Andrea Ghez of the University of California, Los Angeles, used the two telescopes of the 13,000 foot altitude Keck Observatory near the peak of the extinct Mauna Kea volcano in Hawaii.
But when they looked near the location of Sgr A* they saw something astounding. Stars! You might think that this should not be a big deal, since stars are what astronomers are usually paid to see. But these were neither foreground stars, between us and the Galactic Center, nor background stars, on the far side of the central region. Such stars are easy to identify and account for. These stars seemed to be in the close neighborhood of the Sgr A* object itself. The spectra of the light they emitted showed them to be of a class of massive, cool, young stars known as S-stars, around ten times more massive than our Sun. Accordingly, they gave the stars the highly original names S1, S2, S3, and so on (the UCLA group called them SO-1, SO-2, and so on; in 20 years the two groups have sadly been unable to agree on a common set of names). Ghez called this the “paradox of youth,” because these stars could not possibly have formed there from the usual collapse of a large cloud of gas and dust, the way most stars such as our Sun formed. This is because the gravitational field of the central object would have disrupted the cloud before the star could form. So where did they come from and how did they get so close to the central object?
Even more interesting was that within a few years of observing the S-stars, the astronomers could see them move! The Munich group reported the first detections of motion in 1996 and the UCLA group followed two years later. There is a reason why ancient astronomers referred to the “fixed stars.” They are so far away that it’s nearly impossible to see them move. Even in the modern era, it takes careful long-term monitoring of stars with the utmost precision to detect their transverse motion, and even then it works only for stars in our immediate solar neighborhood (detecting their motion along the line of sight using the Doppler shift is much easier, of course). To see a star change its sky position at the Galactic Center after only a few years implied that the star was moving extraordinarily fast. Very soon it was realized that these motions were not random, they were orbital. These stars were in orbit around the spot that had been established for Sgr A*.
The star S2 was particularly important, because it had a relatively short orbital period of around 16 years, and was in a highly elliptical orbit (see Figure 6.3). By 2002, S2 had reached its pericenter, or point of closest approach to Sgr A*, and there was data covering more than half of its orbit.1 With this information, the teams were able to use Newton’s theory of gravity to determine that the point about which S2 was orbiting, whatever it might be, had to be several million times more massive than the Sun. Einstein’s theory is not needed here because the closest approach of S2 to Sgr A* is still distant enough that relativistic effects are unimportant for this calculation. A material object with such a mass, such as a hypothetical supermassive star or a dense cluster of stars, would have been visible in multiple bands. As we have seen, radio measurements had confined Sgr A* to a region several hundred astronomical units in radius. A tremendously massive object confined to such a very small region of space, that emits almost no light, has to be a black hole. Genzel’s team announced this conclusion in Nature in October 2002, and Ghez’s team made a similar announcement in early 2003. Improved measurements indicate that what is now called “the black hole Sgr A*” has the mass of 4.3 million suns.
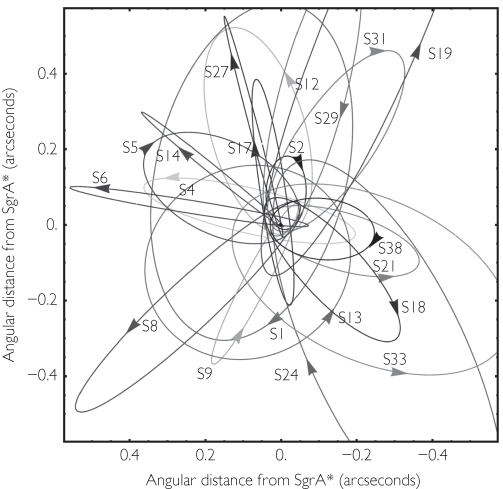
Figure 6.3 Orbits of selected S-stars around the Galactic Center black hole Sgr A*. The black hole is located at the exact center of the graph, with a diameter about 10,000 times smaller than the distance between tick marks at 0 and 0.2 on the graph.
Figure 6.3 shows the orbits of twenty S-stars that have been inferred from the data (over a hundred stars are currently being monitored). The location of Sgr A* is at the very center of the graph, where the lines corresponding to zero angle cross (you may be able to spot the dot just inside the very elongated orbit of S14). A black hole of its mass would be roughly 25 million kilometers in diameter, about 18 times the size of the Sun. The Galactic Center is approximately 26,000 light years away from us, which translates to about one and a half billion times the distance from the Earth to the Sun. At that distance, Sgr A* is about 20 microarcseconds, or 0.00002 arcseconds, in angular diameter. For comparison, this is the size of two American quarters on the Moon as seen from Earth. On Figure 6.3, Sgr A* would be a dot with a width about 10,000 times smaller than the distance between the tick marks at zero and 0.2 arcseconds at the bottom of the figure, much, much smaller than the dot shown.
Sgr A* is a hot playground for testing general relativity. Many of the tests we described earlier in this book can be repeated with careful observations of the stars in its vicinity. A prime example is the recent measurements of the gravitational redshift with S2, which we mentioned at the end of Chapter 2. Because it revolves around the black hole on a highly elliptical orbit, it reaches a mere 120 astronomical units at its pericenter, with a velocity of roughly 7,650 kilometers per second. Therefore, the light that S2 emits there is redshifted relative to the light it emits later in the orbit, because of both the special relativistic time dilation and the gravitational redshift effects. This redshift was measured in 2018 by Genzel’s team and confirmed by Ghez’s team in 2019, thus verifying general relativity’s prediction one more time, but this time close to a black hole.
If this test of Einstein’s theory sounds familiar, it is because we already encountered a similar test back on page 17, when we described the experiments conducted by Pound and Rebka at Harvard University in 1960. In those experiments, Pound and Rebka had control over the light source emitted (gamma rays with a narrow wavelength produced in the decay of an unstable isotope of iron), as well as over the height (74 feet for the Jefferson tower) between the emitter and receiver. What they did not have control over was gravity, which for Earth is so weak that the predicted shift in the frequency of light was a mere two parts in a thousand trillion. For S2, on the other hand, the predicted shift is about six parts in ten thousand, a much larger effect because of the much greater warpage of time near Sgr A*.
We began this book with a test of general relativity using Sgr A*, one of the events of “that very good summer” of 2017. Using orbital data from S2 and S38, a star with an orbital period of 19 years, Ghez’s team searched for a specific deviation from the normal inverse square law that Newtonian gravity predicts for the gravitational force between bodies. General relativity also predicts the same law as a good approximation when the bodies are not too close to each other, which is the case here. But in some alternative theories to general relativity there could be an additional force, which could be attractive or repulsive, depending on the theory, and which falls off more rapidly with increasing distance than the inverse of the square of the distance. Since both S2 and S38 are on very elliptical orbits, they sample gravity over a wide range of distances, from the distance at the pericenter to almost ten times that distance. Thus their orbits were especially sensitive to any change in the force with distance. No such anomaly was found. This was the first test of general relativity involving orbits around a black hole.
The elliptical nature of S2’s orbit also allows for another classical test of general relativity with Sgr A*. As we saw in Chapter 5 when discussing the orbits of binary pulsars, curved spacetime induces a precession of elliptical orbits, leading to the famous perihelion advance of Mercury and the periastron advances of binary pulsars. The close proximity of S2 to Sgr A* at pericenter and the black hole’s large mass lead to a precession of S2’s orbit at a rate of 0.2 degrees per orbit, or about three-quarters of a minute of arc per year. On 19 May 2018, S2 passed through another pericenter, and many measurements of the orbit were made during that critical period when the effects of general relativity are the strongest. These observations should soon resolve this effect, and we expect a test of general relativity by roughly 2020.
But other tests of Einstein’s theory with Sgr A* are possible if we find stars inside the orbit of S2. So far, no other stars have been detected closer to Sgr A*, both because of limitations of the telescopes and also because S2 is so bright and so close to the black hole that it makes it difficult to detect fainter companions between the two. If a companion were observed with the same orbital eccentricity as S2 but about twenty times closer to Sgr A*, it would be possible to measure the precession of the orbit due to the dragging of inertial frames. This frame dragging or Lense–Thirring precession is the same effect that we discussed in Chapter 4, when describing the measurements of the precessions of the orbits of the LAGEOS satellites. This would make it possible to measure the rate of rotation, or “spin,” of the black hole.
Such a measurement is very important, for two reasons. The first is that the spin of a black hole of a given mass can range from zero for a non-rotating black hole, corresponding to the Schwarzschild solution, to a maximum value, corresponding to an extreme limit of the Kerr solution. The spin cannot exceed that maximum value, for if it did, the body would not be a black hole, but instead would be something called a “naked singularity,” a bizarre object that physicists find so horrifying that they are sure that nature would never let them exist. The second reason is that a spin measurement would give hints as to how the black hole formed and grew to its large mass. If it was by the merger of two pre-existing smaller black holes, it would likely have a rather large spin, just as two ice dancers who pull together in a hug at the end of a dance are rotating quite fast. But if it was by the steady accretion of stars and gas falling across the event horizon from random directions, then its final spin might be rather low, since the matter absorbed would spin the hole up as many times as it would spin it down.
If stars even closer to Sgr A* were to be detected and tracked, then it might be possible to perform a test of the underlying assumptions of what is called the “no-hair” theorems of black holes. As theorists began to understand the full implications of the Kerr solution during the 1960s and 70s, they came to a startling realization. This solution was the only possible solution in Einstein’s theory for a quiescent black hole sitting in otherwise empty space, with the Schwarzschild solution being the limiting case of no rotation. And all the details of the external gravitational field of a black hole depend on only two quantities: its mass and spin. If you have two black holes of the same mass and rotation rate, and one was formed from the collapse of gas while the other was formed from the collapse of a huge cloud of Toyota pickup trucks, the external gravity will be identical. This is very different from, say, the Earth, whose external gravity field depends on the rotation of its molten core, the rigidity of its crust, the peaks of mountains and the depths of valleys. Recall from Chapter 4 that the Earth’s field has been measured in exquisite detail by orbiting satellites like GRACE.
Pondering this remarkable property of black holes, John Wheeler coined the phrase “black holes have no hair.” He imagined that if you found yourself in a room full of completely bald men, it might be hard to tell one man from another, in contrast to being in a room of men with full heads of hair. Wheeler’s aphorism has been encoded into mathematical statements about the precise nature of the field around any rotating black hole. Therefore we can contemplate using a number of stars orbiting close to the black hole (they need to be close so that the relativistic effects on their orbits are detectable) to map out the gravitational field of the hole, the way GRACE satellites map the field of the Earth. But if these maps don’t agree with the prediction of general relativity, then either the theory fails in the strong gravity regime of black holes, or Sgr A* is a heretofore unknown object, nothing like a black hole. Are there stars orbiting close enough? We don’t know, but the teams of astronomers peering at the Galactic Center are on the hunt. The next few years should be very exciting, as S2 moves toward apocenter, the farthest point in its orbit from Sgr A*, perhaps revealing the presence of stars even closer to the black hole.
Seeing stars move around Sgr A* is not the same thing as seeing the black hole directly. Needless to say, we cannot see any signal that originates inside the black hole. Fortunately, we now know that the black hole is surrounded by a disk of gas that is accreting into the hole, and is radiating light. Some of this radiation is in the radio band, producing the waves detected by Balick and Brown. Follow-up observations have confirmed the presence of an accretion disk. But unlike the strong X-ray emitting accretion disks associated with black holes like Cygnus X-1, and unlike the incredibly luminous disks associated with quasars, the accretion disk around Sgr A* is a total wimp. Apparently, there just isn’t enough gas migrating into the Galactic Center, either from ambient gas or from disrupted or exploded stars, to feed a luminous disk. Is it possible that Sgr A* was once a bright quasar, now reduced to a faint ember from a lack of fuel? This is an open question at the moment. But as faint as this emission is, the Max Planck team reported in 2018 that they had detected variations in the emission from the accretion disk that are consistent with motions around the black hole of hot spots within the gas. These hot blobs of gas are moving so fast, about 40 percent of the speed of light, that they must be orbiting right at the innermost edge of the disk, close to plunging into the black hole (see Figure 6.2). These blobs are moving in an extremely warped region of spacetime!
But what if we could take an actual “picture” of Sgr A*? What would we expect to see? The answer is complicated because the black hole can bend light in dramatic ways. Taking a picture of somebody with your smartphone is straightforward because the light rays move on straight lines from the subject to the lens of the phone’s camera. Photographing things near a black hole is more like snapping a photo of yourself in front of the warped mirrors that you find in carnivals or fun houses. Depending on where you stand, you could have a fat head (or even two heads) and a slim waist, or you could have a pea-sized head and an enormously fat waist.
Recalling our discussion of gravitational lensing (Chapter 3), a black hole acts like an extremely strong lens, warping and distending what you see, in the same manner as do fun-house mirrors. So if a black hole suddenly appeared in the night sky you would see a number of strange things. First, stars would appear to be pushed away from the black hole, as we illustrated in Figure 3.2. Because of gravitational lensing you might see multiple images of the same constellations, for example two Orion’s belts, or two Big Dippers, as illustrated in Figure 3.10. You might also see stars or constellations that are not normally seen in that part of the sky, but that are actually behind you. In this case, some light rays from the star can pass by you from behind, swing around the black hole and then enter your camera, producing an image of a star that is not actually there (Figure 6.4). There will be a circular black disk in the center, which we would observe to be about 2.6 times the diameter of the black hole itself. This is not the actual black hole, but is about as close to it as you can see.
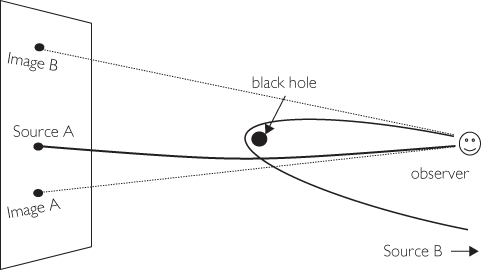
Figure 6.4 Strong lensing by a black hole. Not only can the black hole displace the image of a source (A), but it can also bend light from a source (B) behind the observer, producing an image (B) of a star that is normally not in that part of the sky.
You may recall that earlier in the chapter we mentioned that light can actually orbit the black hole in a circular path at 1.5 times the Schwarzschild radius. This is called the “light ring” (Figure 6.5). The collection of all these rings is a sphere one and a half times the radius of the black hole horizon. Any light ray that enters this “light sphere” will spiral toward the event horizon and be lost (the light ring is not a horizon because the light ray could scatter off a passing atom and be deflected back out of the sphere). Any light ray that passes the black hole just outside the light sphere (path “c” in Figure 6.5) will reach your camera. But even after leaving the light sphere, the ray’s path will still be bent quite a bit until it gets far from the hole. As a result, the black hole appears to a far-away observer as if it were casting a “shadow” about 2.6 times its diameter. In addition, you will see the black shadow outlined by a thin ring of faint light, coming from all the rays of light from all the stars and galaxies anywhere in the sky that just skim the light sphere, orbiting the black hole a number of times and then leaving the hole heading for your smartphone.
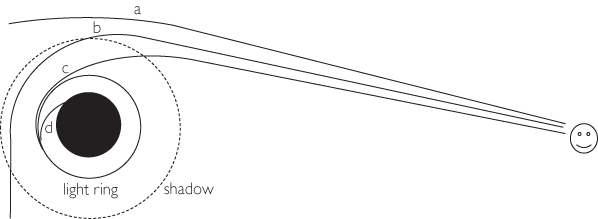
Figure 6.5 Black hole shadow. The black disk represents the black hole itself, and the solid circle is the “light ring,” with a diameter about 1.5 times that of the black hole, where light rays can revolve around the hole on circular orbits. An observer detects a sequence of rays from the vicinity of a black hole, each ray passing closer than the previous. Ray “a” is deflected mildly; ray “b” passes closer and is deflected by around 90 degrees; ray “c” comes from just outside the light ring and is also strongly deflected before reaching the observer; ray “d” originates just inside the light ring, and has to cross the event horizon. Thus the observer cannot see any light rays from inside the dashed circle. This is the black hole’s shadow, with an apparent diameter about 2.6 times that of the black hole’s event horizon.
Similar distortions will occur if you photograph an accretion disk near a black hole. If you are looking at the disk from directly above (see the left panel of Figure 6.6), the image will look more or less like a disk, with an inner edge, where the gas plunges quickly toward the black hole with very little emission of light. The black center shown in the figure is the shadow of the black hole. If you are looking at the disk from an angle of, say, 45 degrees, then you will see the disk in front of the black hole’s shadow, pretty much as expected, and part of the disk heading behind the shadow. But you will also see what looks like a bulge of the disk on the far side of the shadow (middle panel of Figure 6.6). This is not a physical bulge of the disk, but comes from light emitted upward from the top face of the disk that is bent by the black hole’s gravity in a direction toward us. If you are looking at the disk almost perfectly edge on, you see a truly “fun-house” image (right panel of Figure 6.6). You will see the disk in front of the black hole shadow, but you will also see what looks like another disk circling the black hole. In the top part you are seeing the upper face of the disk behind the black hole, whose light starts out going upwards, but then is deflected by 90 degrees, heading toward you. In the bottom part you are seeing the underside of the disk behind the black hole. So in one picture you can simultaneously see both faces of the disk behind the black hole.

Figure 6.6 Schematic image of an accretion disk around a non-rotating black hole. Left: The disk seen face-on with the black hole shadow in the center. Middle: The disk is tilted relative to the line of sight. Some light rays from the top surface of the disk on the far side of the black hole are emitted vertically, then deflected by a large angle toward us in the warped spacetime of the black hole. The back side of the disk appears to be bent upward. Right: The disk is seen edge on. Some rays can be bent by very large angles by the black hole, so that we can simultaneously see both the top surface and the bottom surface of the disk behind the black hole.
By discussing the non-rotating, or Schwarzschild, black hole, we have grossly oversimplified things to bring out the main points. In real life, we expect most black holes to be rotating, possibly at a substantial rate. If that is the case, then the dragging of inertial frames changes the shadow and distorts the images dramatically. The size of the light ring depends on the rotation rate of the black hole and on whether the light is going around the hole in the same direction as its rotation or in the opposite direction. And if the light is on an orbit that is tilted relative to the black hole’s equator, then its motion can be very complicated indeed. For example, in the right panel of Figure 6.6, if the black hole is spinning with its rotation axis perpendicular to the accretion disk, then the bulges will be much more pronounced on the left side than on the right side of the hole. And the black hole’s shadow will no longer be circular. Many of the calculations that lead to these pictures were done in the 1970s by James Bardeen, then at Yale University, and Jean-Pierre Luminet of the Observatory of Paris, during the period of intensive theoretical research into the properties of black holes.
In the movie Interstellar the image of Gargantua’s accretion disk is a more detailed and correct representation of what we have shown very crudely in the right panel of Figure 6.6. The calculations done by Kip Thorne to generate that image took into account all of the gory details. However, some details had to be left on the cutting room floor. An example is various relativistic effects that make the light coming from the part of the disk that is approaching the observer much more intense than that coming from the receding part of the disk. Had these effects been included, the intense light would have completely saturated the image, leaving nothing but a bright spot. While astronomers and physicists love to observe and analyze such details, the film’s director Christopher Nolan wanted a more pleasing image for his audience, so he asked Thorne to suppress those effects.
We are going to need a really good camera to take a picture of the disk around Sgr A*. After all, we already explained how Sgr A* subtends a tiny angle in the sky, a mere 20 microarcseconds, as viewed from Earth. Enter Very Long Baseline Interferometry (VLBI). In Chapter 3 we saw how connecting radio telescopes can lead to very precise measurements of directions of sources such as quasars (page 39). Combining the data from such telescopes in a specific way can also produce images of the source, given enough resolution.
The interferometer used by Balick and Brown only allowed them to limit the size of the region where Sgr A* is located, but not to resolve the source itself. To do better, you need longer baselines. In the late 1990s, astrophysicists Heino Falcke, Fulvio Melia and Eric Agol pointed out that if the baseline between telescopes is about the diameter of the Earth and the observing wavelength is about a millimeter, then the angular resolution at the Galactic Center would be around 20 microarcseconds, smaller than the diameter of the shadow of Sgr A* as seen from Earth. It was later realized that, with the same resolution, it would be possible to detect the shadow of the supermassive black hole in the center of the galaxy, Messier 87, generally called M87. Although, at a distance of 53 million light years, the galaxy is two thousand times farther away than Sgr A*, the black hole is 1,500 times more massive than Sgr A*, and therefore, as seen from Earth, its shadow is about the same size. Sgr A* and M87 seem to be the only two massive black holes so far that have just the right “Cinderella” combination of mass and distance to make this possible.
This inspired Sheperd Doeleman of MIT’s Haystack Radio Observatory and Harvard’s Center for Astrophysics to try to forge a collaboration of radio astronomers working at telescopes around the world to create an array with Earth-sized baselines. This would not be a simple task. The telescopes were operated by different agencies in different countries and had competing scientific priorities. Since each telescope would independently but simultaneously observe the Galactic Center, it was important that the instrumentation at each telescope be either identical or sufficiently similar that the data quality was the same. Each location had to have excellent atomic clocks so that the data could be time stamped accurately enough to permit merging the various data sets properly. The data from each observing session (thousands of terabytes worth of data) would be shipped to a central location for processing into images. It was also essential that the weather be excellent simultaneously at many different locations around the globe. Good luck with that!
As a proof of principle, Doeleman and colleagues managed in 2007 to use a triangle of short-wavelength radio telescopes in Hawaii, California and Arizona to detect something at the Galactic Center at a scale of the order of Sgr A*’s event horizon. This was the breakthrough needed to push ahead.
In 2012, Doeleman and colleagues formally kicked off the project, now called the Event Horizon Telescope. Currently, the array of telescopes in the collaboration numbers ten: two in the mainland USA, three in Chile, two in Hawaii, one in Spain, one in Mexico and one at the South Pole (see Figure 6.7). There are plans to add telescopes in Greenland, France and the USA. The initial full observation run occurred over ten days in April 2017, with eight observatories taking part. One obstacle to analyzing all the data was logistical: by the end of the run in April, winter had set in at the South Pole, and so the data files had to be placed in (literal) cold storage until December 2017, when they could be flown out. The data were copied and sent to four teams who analyzed them independently of each other, and with strict secrecy to guard against mistakes and to enable later checks and counter checks. Finally, on 10 April 2019, they announced that they had obtained an image of the shadow of M87, and that its size was consistent with the prediction of Einstein’s theory. The data on Sgr A* is still being analysed; obtaining an image is more difficult, in part because the accretion rate of gas is on the low side, so it is not very bright, but also because the accretion is highly variable. More observations may be needed before they will be able to see Sgr A*’s shadow.
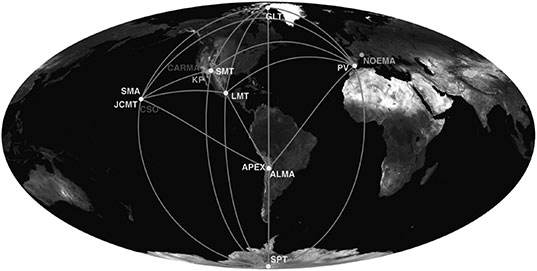
Figure 6.7 The Event Horizon Telescope. The radio telescopes of the project and the baselines joining them. Credit: Event Horizon Telescope Collaboration.
We all delighted in the breathtaking beauty of the pictures they produced; you would be hard pressed to find a newspaper anywhere in the world that did not have the image on its front page. But this is not the only (or even the main) reason for this major undertaking. The accretion disk around both black holes is not static, but changes with time as hot blobs of matter within the disk circle the black hole, thus changing the light emitted. As we already mentioned, such hot spots have already been detected around Sgr A* by the Galactic Center group at the Max Planck Institute. By combining a sequence of joint pictures, EHT hopes to produce a movie of how the accretion disk behaves as its inner edge is swallowed by the black hole. This, in turn, will provide a detailed window into the physics and the dynamics of accretion disks, allowing astrophysicists to compare their models and predictions to actual data.
We may also be able to test general relativity with EHT. The idea is to test the black hole no-hair theorems much closer to the black hole than we could do using stars. In general relativity, the shadow cast by the black hole is a circle for the non-rotating hole, but is off center and somewhat flattened on one side if the black hole is rotating. Once you know the mass and angular momentum of the black hole, this shape is predicted precisely by general relativity, given a particular gastrophysical accretion disk model. But if rotating black holes are not described by the Kerr solution of general relativity, then this shadow will be different, perhaps more flattened or less flattened, perhaps shifted in a different way relative to the Kerr expectation. A precise enough observation of the shadow could therefore test general relativity.
Similarly, because the external gravitational field of the black hole is completely fixed by its mass and angular momentum, the response of an accretion disk and the behavior of the light it emits are predictable and fixed. The black hole no-hair theorems of general relativity leave no wiggle room. Of course, the light that EHT will observe will depend on the nitty-gritty details of the disk itself, such as its density, temperature and composition. But because, unlike its cousins in X-ray binaries and quasars, this disk around Sgr A* appears to be a relative weakling, there is reason to hope that there won’t be too much dirty gastrophysics to complicate the interpretation of the observations. The same tests can be done with follow-up observations of M87.
We have come a long way from a time when Einstein and his contemporaries were sure that Schwarzschild’s Massenpunkt solution would never happen in nature because of its strange singularity. Today we know that black holes exist, and they may soon provide remarkable new tests of Einstein’s theory. But the black holes we have described in this chapter pretty much sit there being, well, black holes. What if we could detect two black holes colliding with each other?