Beauty is the first test; there is no permanent place in the world for ugly mathematics.—G. H. Hardy
A Boston matron was asked where she got her hats. “We don’t get our hats,” she answered haughtily, “we have them.” Replace “hats” by “talents” and that’s the myth we have just exploded. Where, then, are we supposed to get the many different hats a mathematician has to wear? We build up the skills for doing math out of traits common to us all. Let’s look at three of those skills—holding on, taking apart, and putting together—with what will be a running warning that timing is all: what helps at one stage in doing math hinders at another. Keep in mind too that these capacities develop at different times and in different ways, now abetting, now interfering with, their neighbors.
Some parts of math are slippery, some are sheer. We have to learn the mountaineer’s skill of clinging on here while stretching out to there. The ingredients are already in our human nature: stubbornness and its cousin, orneriness; a threshold of frustration that can be raised, a span of attention that can be lengthened, and holding on turned inside out: putting on hold.
You have only to look at the Wright brothers’ faces to know why they overcame the thousand obstacles between Dayton and Kitty Hawk: the mosquitoes, misleading tables, rain, wind, shattered spars. They hunkered down and inched forward again over much old and a little new ground.
In math it is often a case of the data piling up with no system to it, or a system emerging only to crumble at the next example. You come to a crossroads, and nothing in your intuition or in the landscape inclines you to follow one way rather than the other; if you try to follow both, your attention and energy drain away. In most other human callings, the terrain where you find yourself helps your moving through it, and general experience strengthens intuition—but it takes a lot of coming to know the invisible substance of math before you can make its alien-seeming abstraction a locale in your thought, and feel comfortable enough to stroll through it and begin to see that the streets have a plan and the buildings a code.
This sort of grasping is especially difficult because the frustrations in math are so definitive. They strike deep and happen often. It may be worse for novice chess players, who lose match after match before they begin to win—but at least they profit from each loss by seeing vividly that you need to look more than two (or three, or four …) moves ahead, or that certain tactics, good in themselves, suit ill with a particular strategy. You may have to lose the first fifty times you play Go before an inkling dawns of where the sinks and sources of power are on the board. In math, however, you’re beaten not by a human master but by the uncommunicative subject itself. Say you’re attempting to detect a pattern among Pythagorean triples (those integers x, y, and z such that x2 + y2 = z2). One failed attempt may follow another with you being none, or ever so little, the wiser. Just when a pattern seems to settle in (two of the three must be consecutive integers, like 3, 4, 5; 7, 24, 25; or 20, 21, 29), a counterexample spoils it (28, 45, 53). You hear the problem saying that you are too stupid to find the pattern—or that of course there is none, and you were a fool to think there was. Ghosts of pattern spread out and disperse like spume on the restless sea.
How do you develop the kind of doggedness to get through these dark moments? A good teacher can certainly help, by setting a sequence of problems that build up confidence through increasing the resistance gradually. Fellow students help too: working conversationally with others shares out the frustrations and so lessens self-doubt. Both can make the play count for more than the winning or losing. Good, we’ve found one Pythagorean triple (say 3, 4, 5); and another: 6, 8, 10; ah—any multiple of a triple that works will work too—that’s a real gain. And there are triples that aren’t multiples of the one we found (20, 21, 29 isn’t a multiple of 3, 4, 5): so something has come to light and there’s no danger of being bored; more revelations must lie in wait. Dig a level deeper.
The kind of tenacious oblivion needed now has a negative and a positive source. Negatively, you cast yourself in the heroic mode of opposition, invoking your favorite figure of resistance. Dancers and athletes have a well-earned sense that you can still fail despite all your totally dedicated work—and that you then rub your bruises and begin again. Positively, you focus on the particulars of the handful of dirt you’ve just scooped up as you tunnel doggedly forward: this pebble in it, that fragment of china. So (3, 4, 5), (20, 21, 29), (7, 24, 25) and (28, 45, 53) are Pythagorean triples—well, an odd and an even to start with, then an odd. Nothing helpful here, perhaps, but bear it in mind.
Stubbornness roots you in the terrain. We were holding a Math Circle class at Microsoft, in Seattle, for the eight- to twelve-year-old children of some researchers there. The format was a casual lunch with sandwiches. “Has anyone heard of the Pythagorean Theorem?” we asked, while munching. Many had. “OK, would someone go up and draw a right triangle on the whiteboard … oh, and make its legs the same length.” A confident twelve-year-old boy drew a large red right triangle.
“Swell. Let’s say each of its legs is a unit long.” He put a “1” by each of its legs. “So how long is the hypotenuse?” A pair of twins called out, almost together: “The square root of two!”
“Right. And what is the square root of two—I mean, what number does it turn out to be?”
Fortunately there wasn’t a hand calculator in sight, so they were forced to reason it out. An eight-year-old girl said 1 was too small, since 12 was 1, and a ten-year-old said that 2 was too large, since 22 was 4. The likely candidate 3/2 proved to be just too big, giving 9/4 when squared. We had in mind luring them into a proof, after a few frustrations, that 
couldn’t be any fraction whatever—but that wasn’t the direction thought was taking this blustery March afternoon. They were going to pin down the fraction hiding behind the mask of , and they were going to do it before lunch was over.
The twins went to the board with blue markers in their hands and, at the suggestion of the oldest girl there, patiently multiplied 14/10 by itself: 196/100, so we were definitely just about finished. While ideas raced around the table about products of two negatives and why not try decimals and whether the final answer’s numerator would be even or odd, the twins quietly calculated (142/100)2 and then (141/100)2, with results elating or depressing, depending on your point of view. They were very fond of multiplying, and as we started to bet what size fraction would finally do it, numbers appeared out of the blue on the white sky. They actually calculated
(1414/1000)2 = 1999396/1000000,
and—while we held our breaths—
(1415/1000)2 = 2002225/1000000.
Now that the hunt was all but over, others joined in the calculating frenzy, often darkening the waters with conflicting results.
We asked, in a pause which owed more to catching a second wind than to fatigue, what number the numerator would have to end with so that, when squaring the fraction, the result would be all zeros after the 2.
A voice in the wilderness: “Five in one, six in the other?”
“But they have to be the same!”
“Then it can only end in zero.”
“And before the zero?”
“Before the zero—another zero—”
It wasn’t so much that lights went on as that the light went off.
“There’s nothing that works … ”
“We’ve multiplied wrong … ”
The boy who, so long ago, had drawn the triangle on the board, went silently up and erased its hypotenuse.
“You mean … ” we began.
“This triangle has no hypotenuse,” he said—and with that the class ended. (We had exactly the same experience with a group of Scottish children at the other end of the economic scale, showing that mathematics is universal even in its entrées to error: we are all novices when it comes to thinking of numbers not as objects but as sequences.)
Did the class end in failure, do you think? It seems to us rather that their stubbornness gave them an ineradicable sense of the terrain. The next time that hypotenuse once again sits there gleaming evilly at them—a day from now for some, a month, a year for others—they’ll have a vivid context in which to approach it, and the lay of the land they traveled over together may push thought toward a next stratum down in the search for how a line can have a length that isn’t rational. Imagination is born from the vivid conviction that what can’t be, must be.
Isn’t orneriness just another name for stubbornness? Not really. There’s many a mule who won’t let go of a carrot, and many a lawyer who won’t let go of a line of questioning, without a touch of the prickly independence that makes a critter ornery. Their stubbornness amounts to refusing to be moved. Orneriness won the West because it does move in the direction it chooses, whatever the neighbors or the Best Authorities say.
It isn’t that authority means nothing to an ornery soul. It means less than nothing: it is a negative. It stands for persuading by something other than reason, because the reasons probably aren’t very good. We misread the ornery as cantankerous because of its Missourian insistence on proof.
When the third brother goes off to fight the dragon that killed the older two, he goes with fairy-tale confidence—and this, no less than convention, helps him to victory. A strong democratic sense of your being the world’s equal lets you take what you will from the endless advice it offers, and then set blithely out. Someone driven by stubbornness alone pits his will against the world’s, and says that he’ll fight it out along this line, and this line alone, precisely because it is unpromising. Stubbornness tempered by orneriness looks for ways over, under, around, and takes what is eventually the new path as enthusiastically as the old. The chorus of people calling you a fool is so much birdsong.
Martin Hellman, one of the inventors of public key cryptography, wrote of his fellow inventor, Ralph Merkle:
Ralph, like us, was willing to be a fool. And the way to get to the top of the heap in terms of developing original research is to be a fool, because only fools keep trying. You have idea number 1, you get excited, and it flops. Then you have idea number 2, you get excited, and it flops. Then you have idea number 99, you get excited, and it flops. Only a fool would be excited by the 100th idea, but it might take 100 ideas before one really pays off. Unless you’re foolish enough to be continually excited, you won’t have the motivation, you won’t have the energy to carry it through. God rewards fools.
Here’s an example of orneriness in action. You have an 8 × 8 square and cut it into two right-angle triangles and two trapezoids, as here:
Move these four parts around and put them together again in this second configuration, whose height is 5 units and base is 13.
So 64 = 8 × 8 = 5 × 13 = 65.
Someone sufficiently ornery might have thoughts like these: “Maybe it’s true that numbers I took to be different turn out to be the same. After all, it’s happened before: eiπ and –1 are identical. But that’s really a matter of a single value turning out to have two different expressions. Were there a glitch at just one point in the integers—a fold, so that 64 and 65 turned out to be the same—then in fact 1 would equal 0 and all numbers would be identical. While this is possible, it would be too uninteresting, so let’s discard it on aesthetic grounds.
“Perhaps moving shapes around on the plane changes their area … why might area not slosh back and forth like water, and sometimes spill out? How do I know that rotation, translation, and reflection—all used here—preserve area? It’s not something I’ve ever given much thought to. It might be interesting to imagine a geometry in which something like area—‘content,’ in some sense—did alter with certain motions. Keep this in mind.
“Maybe cutting affects area—it certainly does in reality. Look at those shavings falling to the floor. There’s the old joke test of whether or not you’re a mathematician: picture a wooden cube, its top and bottom painted yellow, one pair of opposite sides painted blue, the other pair red. Now saw this cube three times, along each of its three axes. Question: did you see sawdust? If so, you’re no mathematician. What a peculiar idea of how mathematicians think. Why shouldn’t they, like the rest of us, be allowed to enliven conjecture by embodying it?
“Or—like sawing—maybe the thickness of the internal lines in this picture has somehow used up a square of area in the first diagram, which shows up in the second. I remember there were people in the 1920s who fitted whatever shape they wanted—Parthenon or the Mona Lisa—into rectangles that were supposed to be of the most pleasing—‘Golden Mean’—proportions (like 3 × 5, 5 × 8, 8 × 13, each new number the sum of the previous two), just by drawing their enclosing rectangles with sufficiently thick pens.
“Try it conceptually, then: well, conceptually we have two congruent triangles, each with area (3 × 8)/2 = 12 square units, and two trapezoids, each with bases of 3 and 5 and height 5, so each having an area of 5(3 + 5)/2 = 20, and indeed 40 + 24 = 64, so the first diagram is all right, and thickness of lines didn’t matter. So where did the extra square unit come from in the rectangle? Gaining a 64th of the whole area seems pretty drastic (but maybe not, if distributed over the motions of four figures, with 1/256th due to each …)
“Well then, can you in fact dissect an 8 × 8 square into these two congruent triangles and two congruent trapezoids? Evidently you can. The mysterious bit comes in rearranging them, and I know there’s a theorem with a longish proof about reshaping one polygon into another with the same area. So really there’s something of interest here. Is this indeed a polygon we’ve ended with? Evidently it is. Is it a 5 × 13 rectangle? Is it a rectangle? It looks like one.
“Let’s test that. Since AEFC is a straight line, ΔADC is similar to ΔEHC, and so AD/EH = DC/HC. Are these ratios the same? Well, AD/EH = 5/3 = 1.6666 …, and DC/HC = 13/8 = 1.625! The triangles look similar but aren’t, so AEFC wasn’t a straight line after all! ‘Thickness of line’ wasn’t all that far off the mark: the diagonal of the ‘rectangle’ hid a long, narrow parallelogram.”
Some lessons to be learned from this. Resolve more superficial doubts before attacking profounder ones (which of course still lurk). A difference in area of a 64th is enough to fool the eye: be wary of visual proofs. The crucial proportions were 5/3 and 13/8—ratios that are indeed in the sequence that leads to the Golden Mean! Listen more closely to your intuition next time (and think more fully about why the Golden Mean should be involved in this nice deception).
It occasionally happens, especially in younger Math Circle classes, that after working on a problem for a while one of the kids will say: “Come on, you know the answer—just tell us.” There was in fact one Russian seven-year-old who never took part in the discussions but sat with his pencil poised over his pad. When we finally asked, “Andrei, what do you think?” he answered: “I’m just waiting for you to tell us, then I’ll write it down.”
Where does this momentary or habitual checking at the jump come from? Why have those who just now were delighting in the chase turned into Monty Python’s Mr. Gumbies, crying out: “My brain hurts!” It’s as if thinking had suddenly fallen off a cliff, and panic, or despair, replaced the intricate probing of alternative approaches.
There are only so many pathways you can sketch out in your branching tactical diagram, and only so many dead ends you can come up against in the labyrinth of your thought, before everything blurs and foreshortens, your arguments go around in hopeless spirals, and the sense of self you’d lost in pursuing the problem returns with a stature stunted to suit this dreary perspective. You forget why you’d thought the question was worth answering, or why you had arrogantly assumed you could answer it. Knowing becomes nothing more than being told; it shrinks the world to a mere rattle of facts rather than layer on layer of structure, and the truth that shall make you free to an impersonal code of laws.
Dürer gave us the portrait of frustration in his engraving of Melancolia, and the English poet James Thomson put that portrait into words, concluding that the gigantic figure’s eyes stared, only
To sense that every struggle brings defeat
Because Fate holds no prize to crown success;
That all the oracles are dumb or cheat
Because they have no secret to express;
That none can pierce the vast black veil uncertain
Because there is no light beyond the curtain;
That all is vanity and nothingness.
Adolescent? Yes, but many of our students are adolescent, and there is a melancholy adolescent in each of us, moaning to come out.
How can you raise the threshold of frustration so as to stick with a problem for more than twenty minutes—and perhaps for the years it may take to follow its twistings and turnings and to corner it at last? Just as blood vessels proliferate around exercised muscles, so will channels of thought in neighborhoods of inquiry. The more we explore, the more ramified our explorings will become, and the more that external network and the inner network of our personality will merge. Like the characters in Ray Bradbury’s science-fiction classic, Fahrenheit 451, who became the books they had memorized, experiment and experimenter, question and questioner, fuse.
A good example of this is an innocent-seeming question that leads into—and beyond—one of our Math Circle courses. Can you tile a rectangle with squares all of different sizes? What is especially interesting here is that intuition seems to nod neither toward affirmation nor toward denial, so that your thought very quickly tires from getting no nudges toward one possibility or the other. But you reach for a pencil and start drawing. Strategies grow and are put on hold; they influence one another, evolve into subtler approaches, and generate broader and narrower questions—until each of the participants is wholly submerged in the enterprise and one another’s point of view. This means that when the inevitable moments of frustration arise, there is a broad and intricate net of ideas, emotions, and language for them to fall into and rebound from.
Perhaps Heraclitus was right, that nature loves to hide itself, and what better disguise than skewed layers of translucent structure? But mind equally loves to uncover and is, after all, part of the nature it probes.
The father of a seventh-grader in The Math Circle called one night to say he was worried. His son had become too engrossed in the problem we were working on. It wasn’t like him, and it probably wasn’t healthy for a boy that age to be so wrapped up in a math problem.
You could make an argument for the value of disordered, deficient attention (quickened responses to stimuli, a quarterback’s agility in spotting momentary openings, unwillingness to follow paths walked on before), but the odds of winning the argument when applied to math are vanishingly small: math always seems to frisk about the edges of our understanding, and needs whatever lassos and bridles we can find for holding on to it. The standards MTV has set for attention aren’t ones we can measure math, or any of the arts, against.
We want to understand what Newton meant by saying: “If others would think as hard as I did, they would get similar results.” One of the outstanding computer scientists of the last century, Richard Hamming, put it this way:
I worked for ten years with John Tukey at Bell Labs. He had tremendous drive. One day about three or four years after I joined, I discovered that John Tukey was slightly younger than I was. John was a genius and I clearly was not. But Hendrik Bode disagreed: “You would be surprised, Hamming, how much you would know if you worked as hard as he did that many years.”
The more you know, the more you learn; the more you learn, the more you can do; the more you can do, the more the opportunity—it is very much like compound interest.
Is it pure athleticism, then? Will sheer plod make plow-down sillion shine? If it did, hitting a problem with the same blunt instrument for eight hours would crack it. Hamming continues:
The idea is that solid work, steadily applied, gets you surprisingly far. The steady application of effort with a little bit more work, intelligently applied, is what does it. That’s the trouble; drive, misapplied, doesn’t get you anywhere. Just hard work is not enough—it must be applied sensibly.
Well and good, but what does it mean to apply your hard work sensibly? This involves capacities under the headings of Taking Apart and Putting Together. Here the question is how to lengthen your span of attention without snapping or weakening it, so that it will support the strains of whatever those analytic and synthetic capacities turn out to be. Attention holds them in position as tautly as a trampoline’s frame.
There are certainly exercises for lengthening your attention’s span. Following someone else’s reasoning step by step through a proof can be very helpful—especially if you have to make clear to yourself, along the way, what the tactical measures are and how the strategy has been planned. In a long proof the earlier parts may blur in your mind by the time you come to the later ones, and thinking or reconstructing builds them into your thought. The final test is always to run over the outlines of the proof in your mind. Could you explain it to your eight-year-old niece or your eighty-year-old grandmother? Will it hold their attention as it now fills yours? The drawback is that passively following another’s reasoning may ill prepare you for hacking your way through the uncharted jungle of yours.
Two different sorts of factors, it seems to us, go into the lengthening of attention’s span: a Rousseauvian eye and a Jeffersonian hand. That eye is full of the fire of commitment: you want to plunge into the problem and lose yourself in it. Heedless of others, reckless of your future—nothing else matters, so fully does it obsess you. This isn’t an attitude you can fake, at least not to yourself. It is like falling in love. Time disappears in your engagement with this morsel of mathematics. (Time is in fact absent from mathematics as a whole, where we off-handedly invoke an infinity of ever-present instances with our “all,” and by asserting “there exists” mean that something forever is.)
Simply swinging your attention around to the problem, immersing yourself in it without hesitation, will make causes appear within causes, and structures behind structures, as if you were following corridors in the pattern, invisible to the casual eye. You may joke with friends, take in a film, go on walking tours in the Cevennes, but the problem and its context is always with you, like the background hum of the universe. What in fact leads to your crossing the line that divides observer from actor? Something as remote from the problem itself as the personality of the person presenting it, or the excitement of those around you, may face you in the right direction. A question you ask, a suggestion you tentatively make, subtly alters your stance; then the endorphins kick in, and what was a pleasant annex of the day becomes its atrium. As in jogging, you have to go past the reading and talking and dreaming about it, the buying of shoes and clothes, and actually jog. And the second day may be harder than the first, because muscles ache not only in anticipation, but in reality. As in mastering a computer language, intimidation gives way all at once to an enormous feeling of intimate power. As in reading Shakespeare, the barriers of a vast, strange vocabulary and involved sentences are crossed again and again by lines that haunt you. Confidence and competence grow, feeding on one another. But whether intrigued or enticed, in the end it is your will that makes you a participant in the play rather than a spectator. This is never as simple as it sounds, since will has its own array of causes—and half the time, mathematics asks you to watch the behavior of its structures without imposing your will on them.
Altogether different, but as important, is the Jeffersonian hand. How manage your life, let alone this consuming struggle, without some sort of least governing? You know the answer from driving: how can you make the continual, minute adjustments to a car’s steering wheel while clutching and shifting and braking and checking the side and rearview mirrors, not to mention the odometer, speedometer, fuel and temperature gauges and retuning the radio, all the while effortlessly maneuvering your way through the grammar of a sentence spoken to your companion, in which you decide in midstream to hold back this information, phrase that juicy tidbit discreetly, and finish with an ironical flourish, saying one thing but meaning another? At the same time, of course, you’re squirming into a more comfortable position and readjusting the seat belt, while trying to remember if you’d put ketchup on the shopping list, and stray memories and half-acknowledged thoughts flicker and flow in the stream of your consciousness.
You bring off this paragon of complex and lengthy attention by having long since delegated its parts to routines that are now subliminal. While your spinal cord’s lieutenants sort these matters out, the captain in your brain orders the thoughts that count—articulately enough for logic to clear the way, but with sufficient flexibility to respond to suggestive analogies. If it is a wilderness you are looking at, it is from the well-proportioned windows of an inner Monticello.
Best of all, this light governance of our thinking’s network lets us become true travelers in it: lost at times, but never at a loss, because we have an underlying sense of our resources, if not of the geography. Fantastic visions may lead us around, but not astray; gratification, so long delayed, is replaced by the delight of small details. Your attention spans the problem and what you bring to it, as its personality becomes indistinguishable from yours.
One of the charms of reading or listening to German is that a sentence may march positively along only to be brought up short by a “nicht” at the end. You need to reverse the signs of all your suppositions and pull up your expectations by the root. It’s like one of those puzzle pictures that exchange figure and ground. It does teach you, however, to put in brackets larger and larger chunks of your thought, so you’ll be prepared to see them from different angles or in altered contexts.
This willing suspension, not of belief but of commitment, is vital for mathematical expeditions. Think of the times your curiosity has been caught by something to do with numbers (Do they really go on forever, although the universe may not? How does my calculator do its magic? What’s the answer to this Sudoku puzzle?) You worry at it for a while, then let it go; it returns from time to time with diminished intensity, then fades away, to join the background mystery of things. To take the problem seriously would probably mean leaving the familiar world behind for months. You would need to practice thinking conditionally, which means intensely following premises through long and tortuous steps to an ultimate conclusion, but then recalling that they were, after all, only premises—and may not hold. If A then B, and so C and D … : it was the “if” that drove Mr. Ramsay to distraction in Virginia Woolf’s To the Lighthouse, and many a Mr. Ramsay before and since. If the Riemann Hypothesis is true, then look what follows: a looking that takes all your effort. But if we haven’t yet proven the Riemann Hypothesis, you’ll need all the effort you can collect in order to follow along, when you have only a promissory note in your pocket.
Perhaps learning this sort of committed reticence is the most unnatural call mathematics makes on our psychology. You find it at its most vivid in proofs by contradiction: let’s see what follows if we take it that A is so (knowing all along that our effort is to show that A is not so). Now a novel’s worth of consequences may follow before we discover that the end undoes our beginning. This isn’t very different, is it, from the Hindu tale of the youth who encounters a god unawares and is asked to fetch him a bowl of water from the nearby river—and on the river’s bank sees a beautiful girl and falls headlong in love with her, and they run off together, and marry, and have children, and live in a house by the river … until one night a flood sweeps the house and the children and his wife away, and nothing is left save the god, laughing beside him: “Where is my bowl of water? All is Maya!”
A mathematician reading a proof may catch less than half of its drift and less than that of its intricate argument. He isn’t wasting his time, however, but getting a feel for where it fits in, and what it points toward. This keeps the details from blurring his vision—as scientists in their experiments hold all of the variables fixed save the one they wish to follow, and lawyers stipulate so as not to speculate. Of course, they keep auxiliary arguments stored up, and mathematicians, too, have neat packages of techniques and conclusions at hand, to take out and brush off when needed.
It is from the inner Monticello, once more, that we take control of our ifs and thens, and keep our minds clear to focus on the unfolding chain of consequences by storing alternative possibilities neatly away—ready, along with analogies and trusted techniques—to use when the time is right. We look out on chaos from our well-made window, and this keeps us from fretting: this landscape too we shall one day tame, and see beyond it the next frontier.
You’ve plunged in and are thrashing about. As French mathematicians say, “Ici on nage dans un bordel”: literally, we’re swimming in a bordello. Too much data, too few connections, questions swamping answers, every conjecture starting a dozen more with no direction of inquiry looking more likely than another. Even the terminology is losing its sharpness: the words have come to mean anything but what we wanted them to, both more and less (and you suspect that some may now mean nothing at all).
Take, for example, the question we mentioned on page 32: can you tile a rectangle with incongruent squares? There we are, caught on a cusp between yes and no. In Math Circle classes that have struggled with this problem, the first, failed flurry of suggestions often led to the strategic retreat of making more precise what the question was—and this is surely the beginning of taking apart.
“Put in the largest square you can—you know, with a side the length of the rectangle’s shorter side,” an eight-year-old in an otherwise adult London audience suggested.
“Then do the same with the part that’s left, and so on—”
“But what if the part that’s left is longer than what you filled up?” someone else asked.
“Are you going to allow an infinite number of squares?” asked a third. We intentionally pose our problems vaguely, since a large part of doing math consists in making the initial question sharp enough to answer (while avoiding questions you don’t know how to sharpen).
“What would you like?” we said.
“Well, it looks as if you might be able to do it with an infinite number of noncongruent squares, with side-lengths x, x/2, x/4, x/8, …”
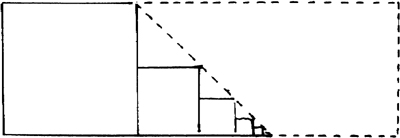
“Really?” said someone else. “Wouldn’t that only fill up half of it—under the diagonal—and you’d have to do something different above, as well as filling in all those little gussets of triangles.”
And another: “Even so, that would work only in 1 x 2 rectangles.”
“You could always spiral around.”
“But even then, would that always work? Did you say it should be for ‘any’ or ‘some’ or ‘all’ rectangles?”4
“And what do you mean by ‘tiling’? Can the tiles overlap?”
“Or have grout between them?”
“Or can some be put in vertically?”
“Or some have a negative area?”
The question and the questioners exert mutual overt and covert pressures, and each deforms to fit the other: we refine our questions until we decide we’ve sufficiently well defined what they’re about, and then—as we begin to answer them—refine and redefine more.
Here are some capacities that help in taking a problem apart to see what makes it tick.
You need only look at the chaos of a child’s room and hear his parents’ nagging about it to see that being methodical is learned. The pleasures of a place for everything and everything in its place compete for dominance with less systematic delights. Necessity often mothers a reluctant sense of method in adulthood, when you find that just muddling through often ends without the “through.” Sorting out the appropriate tools for attacking a problem goes some of the way toward solving it. So cooks let their creative tantrums loose on a carefully assembled mise en place.
But are there really “methods,” like the ones promised by Get Rich Quick and Get Thin Fast plans? “Method” sounds to us like a form, independent of what it is stamped on—but in mathematics, at least, it helps to let the problem’s topography guide you to the most direct or appealing ways into it, or to those that will make best use of your own strengths and viewpoints. Commonsensical advice, like “first decide what the question is,” turns out to be more useful than such nostrums as “when in doubt, factor.” Proverbial methods also have the problem of being applied indiscriminately, like the boy in the tale who, having dragged back a ham from the market and been told he should have carried it on his head, brought back the butter that way on the next hot afternoon. This is why in The Math Circle we tend to use words with less rigid associations than “method,” such as “approach.”
Say you want to prove the Pythagorean Theorem. You could look at this as an exercise in cutting up and moving polygonal shapes around, and some dissections and foldings or rotations of the pieces will come more readily to one person’s mind than to another’s. Or if your inclination is algebraic, you might translate some of these configurations into quadratics, or see the problem as centering on proportions. If you think like President Garfield, you fetch a trapezoid from afar to assist in your proof; if like Leonardo, you add two copies of the original triangle to the whole; if you are Einstein, you look at the area ratio of similar triangles. You might deduce the proof from the properties of chords intersecting in a circle, or from secant and tangent lines. You might apply the so-called method of analysis and synthesis, reasoning backward from the conclusion to true premises, then following in reverse the route you made. You might even prove this theorem about a very small part of the plane by appealing to a limiting argument that involves the plane in its entirety. Why should we try to fit human ingenuity, bred of its bearer’s personality, into the Procrustean bed of some sort of impersonal method?
Approaches, then: gloves that fit your hand as well as the problem’s contours, the better to let you grasp it: a way of keeping tabs on what you’ve done and where it led, so that you can at least catalog the kinds of obstructions you came up against. Do they sketch out a pattern whose reflex shape might be a solution? A catalog too of analogies that flickered between this problem and others you’ve solved—or between parts of the problem and structures you understand. What often turns out to lead to a dazzling solution is generalizing the problem in one way or another, then looking at what sense it makes in that larger setting: keeping track, therefore, of the problem’s evolution, and yours, and the evolution of their interplay, so that stepping back from time to time, you may see revealing shapes.
Something as unimposing as cataloging may be the kind of thing Alfred North Whitehead had in mind when he recommended letting the infantry of your thought do most of the fighting, so that you can save the cavalry for the important charges. And as long as you don’t take its categories too seriously, a list of what’s worked in the past can help in the present: a tool chest that has deduction and induction in it, along with proof by contradiction, and by analysis/synthesis, and by turning your attention to your problem’s contrapositive. Whenever someone devises a new approach to a problem, other people are quick to detach it from that problem and put it, oiled and wrapped, into this chest. More strength to your arm—so long as mind rather than habit or hope directs it, and mind and arm keep in touch with the singular structure they probe.
“Taking apart,” you might argue, is just demotic for “analysis,” and analysis, when you come right down to it, is nothing more than coming right down to it: breaking your problem up into its simplest parts and then dealing systematically with them, or reducing what you don’t know to what you do—dissection rather than destruction. Those exploded drawings of engines and electronic equipment that used to be the favorites of mechanically minded teenagers, and now puzzle them as parents in directions for unclogging the washer are exemplars of this sense of analysis, as are organizational flowcharts and stochastic diagrams. But is it always no more than a mindless matter of laying out the parts and then slipping tab A into slot B? Any problem worthy of the name always seems to have at least one stage that demands ingenuity. Were coming-to-know algorithmic, computers would be able to distinguish acquaintances from friends.
The invention of the quadratic formula is a good example. Everybody had to memorize
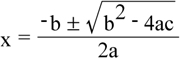
in algebra class, but you might have wondered how that magic answer was derived from the original question: what is x, if ax2 + bx + c = 0?
You want to free x from its encumbrances in
ax2 + bx + c = 0.
Easy enough to ship the constant across the river of equality,
ax2 + bx = –c,
and to rid x2 of its coefficient:
x2 + (b/a)x = –c/a.
But now what? It took medieval time and Middle Eastern cleverness to come up with what we now blithely call “completing the square”: adding (b/2a)2 to both sides of this equation:
x2 + (b/a)x + (b/2a)2 = –c/a + (b/2a)2.
That’s the invention, which reducing called for but couldn’t unthinkingly supply. And now it is all technique again—which is to say, reduction once more to routines you had long since mastered:
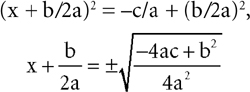
and so to
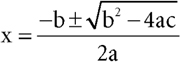
Reduction may, however, deceive you into thinking a proof will run on just the combustion you set going, without any further oversight or insight. Thus many a geometric proof begins by breaking a compound structure up into its constituent triangles—but then what? In his brilliant Proofs and Refutations, Imre Lakatos looked closely at Cauchy’s proof that for a polyhedron with V vertices, E edges, and F faces,
V – E + F = 2.
Consider a cube, says Cauchy (in Lakatos’s retelling), and remove the back:
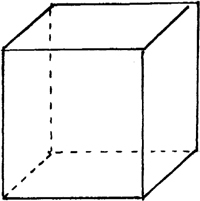
If our formula (the “Euler Characteristic”) holds, then with one face gone, our new figure will have
V – E + F = 1.
And so we need only show this is true: the first appearance of reduction. Squash the open box (let the side pieces stretch, so no V, E, or F will be lost in so doing),
split each face into two triangles (reduction again, though of a different sort)—and notice that you have added an edge and a face to each of our original faces; but since E and F have different signs, there will be no change in V – E + F:
Then begin to remove these triangles (reduction’s third appearance) in, say, this order:
In removing each of triangles 1, 2, 3, and 4, a face and an edge disappear: again no change in V – E + F. In removing each of triangles 5, 6, 7, 8, and 9, the two edges that are taken away are made up for by the removed vertex and face. This leaves us (the last reduction) with one triangle, for which obviously
V – E + F = 1.
Add the original removed face back on, and
V – E + F = 2.
So, says Cauchy, the theorem is true for the cube, and the technique would generalize for a polyhedron with any number of sides.
Notice two quite different points. First, the tactic of reduction, applied again and again, was in the service of a strategy that arose from an idea that reduction alone wouldn’t have come up with: Cauchy—or someone—had to hit on this ingenious analysis. Second, however, how do you know (ask the protagonists in Lakatos’s dialogue) that you can do this remove-and-squash maneuver with anything other than a cube? How do you know that a different order of removing the faces of a cube will leave V – E + F unchanged? How do you know that—in some other polyhedron—you can always find a removal sequence which would leave V – E + F unchanged? Maybe, even if you were able to flatten out another polyhedron, you might create virtual edges, faces, or vertices, or obscure some of those that were there? And since we already know by simple counting that in a cube,
V – E + F = 2,
we didn’t need this elaborate atomizing for the cube itself; it was meant only to exemplify a general procedure—but in fact it seems to exemplify no such thing. Although Cauchy’s method may work each time you try it, he hasn’t proved that it always works.
And what does Lakatos’s analysis itself exemplify? Among other things, that simplifying may simplify the subtleties or the metamorphoses of a problem away; that atomizing, in the sense of breaking down, is a wonderful source of clarification, but must be used cautiously lest its light be blinding instead. Let your infantry indeed reduce the enemy’s fortifications, but always under the direction of a distant commander, and always with your cavalry at the ready.
You can atomize the object of your thought into its constituents, or you can atomize your thoughts as well: reduce the problem to a simpler one (the first reduction in the previous example), or to one you already know (as with what’s left of the quadratic, after completing the square). Mathematicians are notorious for this kind of reduction, as in what passes for a joke about the physicist and the mathematician who each want a cup of coffee. They go into the kitchen, the physicist fills a kettle, puts it on the stove, turns on the burner, and when the water has boiled, pours some into a cup with instant coffee. The mathematician then knows what to do: he empties out the kettle, thus reducing the problem to the previous case, and proceeds as before.
The point is that this kind of reductive thought, set about with so many advantages and perils, comes with the territory of being human: we all profit by and suffer from it. You need only think of how readily we reduce people and events into clichés to see how widespread the habit is. This is a case, then, not of developing an unnatural trait but of channeling one that is all too natural—the sort of laziness that always seeks out the path of least resistance. But don’t dismiss laziness out of hand: efficiency experts look for a company’s laziest employee, to see how he manages to do just enough to hold on to his job.
An outstanding contemporary mathematician, who believes as little as we do in any sort of talent, tells us that of all those he has met in the mathematical community, the one who most seems to have an inborn skill isn’t in fact particularly imaginative, but has an uncanny willingness to break a question down into its tiniest details and then solve each one. This may come, he thinks, from this person having no native language other than mathematics.
You could therefore think of atomizing as a fundamental skill, itself atomic, which amounts to letting your thought, like water, follow the contours of what it flows over, seeking out the gradient, finding the fissures, and splitting the terrain apart along its natural fault lines. But doesn’t atomizing itself really atomize into two skills: a diamond-cutter’s sensitivity to those fault lines in a problem, so that a little tap will cleave it; and what we might call “accessible experience”—that repertoire of instances and approaches we spoke of, scanned now and again for something to fit the new configuration. So atomizing consists in breaking a problem, and how you approach problems, into their fundamental units; then laying one like a transparency over the other, and shifting them, until (with the click of revelation) form fits form.
Here’s an example. Draw any closed shape you like on the plane—as simple as a pancake, or as rococo as this:
Is there a straight-line cut that will divide its area in half? Let’s say that somehow or other you come up with this idea: a line lying wholly to the figure’s left has all of the figure’s area to its right. Likewise, a line parallel to the first, wholly to the figure’s right, has all of its area on its left.
So were the left-hand line to be moved continuously toward the right-hand one, it must at some point divide the figure’s area precisely in half.
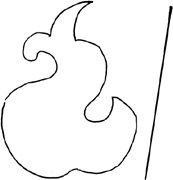
This answers in the affirmative the question of whether there is such a line—although it doesn’t begin to tell you where. A peculiar and somewhat disconcerting solution.
Now let’s say that this “nonconstructive” answer not only sticks in your craw but in your memory, and years later you run across this problem: through a point P inside a convex shape on the plane (“convex” just means that the shape has no indentations—a line between any two points in it or on its border lies wholly inside it too), a line between two points, A and B, on the border is such that AP > PB.
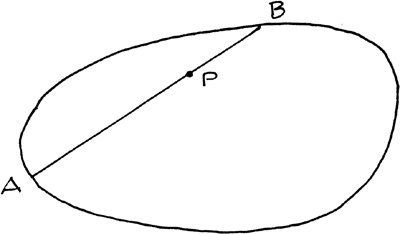
Is there any straight line through P, out to the figure’s border at some A and B, such that AP = PB?
The ghost of that previous problem comes to mind and you think: we began with AP > PB, but if we rotated the line through P until the positions of A and B were interchanged, we’d have AP < PB, so there must be some intermediate position where AP = PB.
This is a solution no more (and no less) satisfactory than that of its tutelary spirit: a style of proof, a kind of thinking, that once encountered, can generate answers to questions that have in common only the way they are posed.
A quality we so much admire in athletes (the archer on a Greek pediment or the quarterback turning, faking, sliding out of the pocket, spotting his receiver in a chaos of oncoming aggression and hitting him with a perfectly threaded pass) is keeping a cool head when all about are losing theirs: poised potential, where readiness is all. This graceful harnessing of power lies at the base of taking apart, since it alone lets you analyze without becoming flustered by discordant data or discouraged by the shutting down of one path of inquiry after another.
Attention without tension sets you not so much in or above or around the problem as at it; it lets you understand by fitting your mind to the shape of what it contemplates: “unassuming, like a piece of wood not yet carved”; as a Zen master put it, “vacant, like a valley.”
Say someone gives you this koan: in a large heap of coins, 877 are heads up, the rest are tails. Can you blindfolded divide the whole heap into two piles with the same number of heads in each? The easiest answer is “no.” Yet if you turn your attention to it without letting your blood pressure rise, this and that begin to make themselves felt—as if indeed you were blindfolded and discovering the question’s character by patting its contours. Two heaps with the same number of heads in each—hence an even number of heads; but 877 is odd. If the problem was correctly stated and there is a solution, it must somehow get around that difficulty.
When we posed this problem to a class of young Math Circle students, a thirteen-year-old suggested that you take all of the coins and, blindfolded, put them on edge—making in effect a roll of coins—then divide that roll into two parts however you like. Each will have the same number of heads showing: namely, none. This is a brilliant solution, arrived at by a combination of self-confidence, humor, and dwelling on the way the problem was stated: paying confident attention to each of its words and just laying out the range of their possible meanings. That “same number” could be … none.
Another student, thinking about it and “turning it this way and that in his powerful mind,” as Homer describes Odysseus doing when baffled, decided that 877 was a red herring; there was nothing special about this number except that it was odd (and prime, which might turn out to play a role). Very well, simplify by restating the problem with an odd number that would be easier to deal with and visualize. Say the heap contained a single head and the rest tails. Now what? We must have two heads before we can even begin to do the separation. Notice the role that calm attention plays here: there will be another problem—the problem of separating the coins, blindfolded, into the required heaps—but that’s for later. Simply put it on hold for now without worrying about it, and first, somehow, get two heads.
Ah … no one said we couldn’t flip a coin; so that would give us two heads—unless, by ill fortune, it was the single heads-up coin we ended up flipping. But then we’d have no heads, and so could now divide the pile up in any way, and each part would have the same number of heads: namely, none.
So it comes down to this: if it was some tails-up coin we’d flipped, we’d now have two heads: how guarantee they would end up in different piles? Confidence, bred of the “flipping” insight, propels relaxed attention along to the next insight: why not first move a single coin away from the heap, and then flip it! If it was a tails it is now heads, and so there is one head in each pile; but if it had been the single heads that was flipped, all are now tails, and each heap (the original pile, less one, and the “heap” of that single coin) has the same number of heads: again, none.
Will this approach work if we are told the heap contains two heads and the rest tails? Well, separate two coins from the heap, then flip each. If neither was heads, there are two heads in the pile, and now two heads in this two-coin heap, as desired. If both were heads, then after flipping, both heaps have no heads. If one was heads, one tails, there is one heads left in the pile, and flipping these two will reverse their faces, so one will be tails, one heads, as desired. Aha! 877 being odd played no role, since it works for two!
Does the reasoning change with three heads in the original pile? No, it just breaks down into four cases, each one of which works in the same way, because the same principle is at work: separate from the pile as many coins as there are heads in the pile; flip each of these separated coins—and this “change of parity” works like a charm.
Wonderful! And notice that attention without tension pervaded the thinking. For after the “flipping” insight it would have been very easy to become too excited to think calmly through the next stages—distracted by one’s cleverness or, more selflessly, by the possibilities and questions opening up everywhere. A focus just narrow enough, then, not to be perturbed, yet sufficiently broad to let in the light that reveals the problem’s texture: the restraints that weren’t there, the latitude for inventing that the terms allowed.
This receptive attention must also hold its focal object steady under the stresses applied to it by all sorts and degrees of ambiguity. In our problem, for example, it seemed that a number had to be both even and odd; and in any problem worthy of the name there will always be at least one of what the Japanese poets call kiriji: a word, a phrase, an idea that bears two senses liable to carry you off in different directions, like an open switch on a railway line—if it doesn’t derail you altogether.
Ambiguity in mathematics? Many people summarize their objections to math by saying that it has none of the ambiguity that gives life and art their roundness and richness: the single possible answer glowers at us, insulting our deep love of freedom and taking from us the summer dream beneath the tamarind tree. In fact, mathematics seethes with ambiguity, which is among the reasons why, when you try to get to the bottom of any problem, you find it is bottomless. It is also why the great Georg Cantor proclaimed in the nineteenth century: “Mathematics is freedom!”
Our first, rough acquaintance with a problem inevitably leads to little ambiguities cropping up in how we understand it—or more insidiously, in our ignoring hidden constraints or seeing constraints where there were none (who said you couldn’t flip a coin?). As we come to know it better, ambiguities signal our changing point of view. Picasso profiles emerge as the problem slowly rotates, and the longer we remain stymied, the profounder these ambiguities become: should our approach to it have been algebraic rather than geometric? Are we stuck in too conservative a two-valued logic, should we move from thinking of it linguistically to structurally? Should we be inventing rather than pretending to discover? Ambiguity segues into doubt, and the current shakiness in the foundations of mathematics undermines our thinking—can we gain insight without proof? Can we ultimately prove anything at all? Will it suffice to convince others—will we be able even to convince ourselves? The legacy of proofs that stood for so long, only to tumble eventually on closer scrutiny, hovers over our tentative work. And there’s the puzzling self-referential quality of any piece of mathematics: where exactly are we and our little problem in the whole? Does the notion of a whole even make sense in this peculiar, infolded enterprise, or is it essentially ambiguous?
Certainly mathematics is pervaded by ambiguity, as the presence of equations everywhere in it shows. For what is an equation but the confronting of two different points of view? To say that the square on the hypotenuse is also the sum of the squares on a right triangle’s two legs is the beginning, not the end, of a deep insight; to say that –1 is another name for eiπ, or that when thinking about polyhedra, the sum V – E + F is also known as 2—is to glimpse startling unities behind the flicker of appearances. With appropriate ambiguity, the ambiguity that began by distracting us promises to be our guide.
Attention without tension amounts to walking steadily on through an inviting landscape, taking in its foggy valleys and cloudy peaks, pausing for views that seem to unify and views where everything falls or rises away. Like good explorers, we’re willing to put up with a bit of uncertainty in our situation for the adventure of it all, and for the suggestiveness with which it frames our arriving.
Richard Hamming, from whom we’ve already heard, sees this question about ambiguity and attention from a window slightly canted to ours:
There’s another trait on the side which I want to talk about; that trait is ambiguity. It took me a while to discover its importance. Most people like to believe something is or is not true. Great scientists tolerate ambiguity very well. They believe the theory enough to go ahead; they doubt it enough to notice the errors and faults so they can step forward and create the new replacement theory. If you believe too much you’ll never notice the flaws; if you doubt too much you won’t get started. It requires a lovely balance.
When you find apparent flaws you’ve got to be sensitive and keep track of those things, and keep an eye out for how they can be explained or how the theory can be changed to fit them. Those are often the great contributions. Great contributions are rarely done by adding another decimal place.
Only a little out of true is false. This can be very discouraging in daily life; it can be paralyzing in mathematics. Apprentice carpenters are wisely told to measure twice and saw once—but measure twice, then take out a magnifying glass and measure again, and then use your micrometer? Truths grow in evasiveness with their growing profundity precisely because we haven’t quite got their measure: because we see more or less what we need to see exactly. It is as if ever finer details of structure demanded matching refinements in our thinking. Safecrackers, they say, sandpaper their fingertips the better to feel the delicate fall of the tumblers. But mathematics goes past the niggling precision of third and fourth decimal places characteristic of the engineering it sprang from, to the glorious absurdity of infinite precision: each number taken to all its decimal places, each geometrical object honed to the ideal accuracy of thought.
A notorious example is that curse of first-year calculus students, the “ε–δ method.” You want to say that as the inputs to your function f(x) approach a certain number, a, the outputs approach a certain value, l. Well, why not just say as much, and go on? Because the multiple ambiguities here aren’t fruitful but pernicious, and the devil is hiding in these details to damn you. The beautiful understanding of change and motion that calculus seeks to achieve depends not on what happens at a, but near it—and this in turn requires us to make very precise sense of what “near” means: a sense that won’t stumble over and into all sorts of unforeseen pitfalls. (What if, for example, the function isn’t even defined at a? We still want to be able to say that its limit exists, and is l. Moscow is still there, even though the three sisters never get to it.)
A great many people worked hard, over a considerable span of time, to refine their intuition and ours into an impersonal way of speaking about and dealing with this idea of “limit.” What they settled on is very clever, because it brings the free will and the personality of the explorer into this formal definition. If the function’s outputs really do approach l as the inputs approach a (from either direction), then they will do so no matter how coarse or fine the degree of tolerance that you wish to measure by. If you ask only that the outputs be within an inch of l, then you will find inputs within a corresponding distance from a; if you ask for a tolerance of a hundredth of an inch, again the inputs will lie within a band around a that corresponds to this new restriction. In fact, for any positive distance ε you choose on either side of l, there will be a corresponding positive distance away from a—call it δ—that the inputs will fall within.
Now watch how this just regard for precision, joined with an inclination to abbreviate, yields a piece of language that will scare not only horses: “For any positive distance ε you choose”—that is, for all ε; or if we use the symbol ∀ to mean “for all,” this opening volley of our definition of “limit” becomes “∀ε”. Remember, though, that we wanted to say “for all positive distances away from l” (a subtle qualification: we’re saying we don’t care what happens exactly at l). So we should write instead “∀ε > 0”.
What happens then? “There will be a corresponding positive distance, δ”: so if we symbolize “there will be” or “there exists” by “∃”, this turns into “∃δ > 0”. What we have so far in our definition of “limit” is this:
Definition: “The function f(x) approaches the limit l as x approaches a” means: “∀ε > 0, ∃δ > 0 … ”
And now what? We want to say that as long as the input, x, is within δ of a, then f(x) is within ε of l. Well, “within”—i.e., no more than δ away from a, on either side of it—is nicely caught by the absolute value notation, which expresses distance: so “the input, x, is within δ of a” turns into “The distance between x and a is less than δ”, or:
|x – a| < δ.
Likewise, “f(x) is within ε of l” becomes
|f(x) – l| < ε.
Now we can put all these very fine bits of crocheting together to arrive at our perfected definition of limit:
Definition: “The function f(x) approaches the limit l as x approaches a” means: “∀ε > 0, ∃δ > 0 such that if |x – a| < δ, then |f(x) – l| < ε.”
If, in the full frenzy of abbreviating, you decide to ditch the mere English words “If … then … ” and replace them by the symbol 
, and scrap the phrase “such that” and put “∃” in its stead, then you can reduce the sense of our definition to a runic:
Definition: “∀ε > 0, ∃δ > 0 ∋ |x – a| < δ 
|f(x) – l| < ε.
We have agonized with you over this condensation of so much watch-maker’s tinkering in order to savor the spirit that hovers over it—the caution and its rewards. A precise grasp of what the notion “limit” entails is mirrored in the notation, which reflects its standards of accuracy back into the way we henceforth think about this notion. Once having stepped onto the beam, you have to go on keeping your balance; a little mistake will bring everything down (you can’t, for example, reverse the order of “∀ε > 0” and “∃δ > 0”: if you thought that the definition of limit began “∃δ > 0 such that ∀ε > 0”, you would be talking about something significantly different). You might get away in conversation with saying “They all didn’t do it” when what you meant was that they didn’t all do it, but the bones of mathematics are as delicate and as linked as those of a bird: twist one and the whole lithe being falls to earth.
This doesn’t mean that in order to take a mystery apart you need to turn into a Dickensian bookkeeper, grown gray in the service of parched accuracy. Any craftsman will tell you that this kind of care, this attention to the meshing of barely visible gears, isn’t only exhilarating in itself (and a sort of haven in the midst of the world’s clamor), but the frame within which invention prospers. Think of the years spent coordinating eye and arm that let a great pitcher shave the slenderest edges off the strike zone.
Precision allows conception to become reality. In the nineteenth century, Charles Babbage designed the first machine that could solve simultaneous equations in several variables: his Analytical Engine. The best craftsmen of his day were unable to build it from his drawings, and people then and after concluded that it was conceptually flawed. A century later, working to far finer tolerances, technicians at the Science Museum in London built a model that whirred and hummed out its solutions: as satisfying in its brass workings as our image of what H. G. Wells’s Time Machine should have been like.
If you look from a train window at a passing orchard, the trees are just a jumble until the one instant when they all line up in neat rows—before the train moves on and all’s chaos again. This is the moment you look for in mathematics, when turning a structure around suddenly reveals the hidden symmetries in it. Taking apart can amount to no more than changing the relation between you and your problem.
Richard Hamming knew that Bell Labs couldn’t hire enough assistants for him to program computing machines in absolute binary, but rather than go to a less interesting place that could, he said to himself, “Hamming, you think the machines can do practically everything. Why can’t you make them write programs?” And so, he says, he turned a defect into an asset, and observes that scientists, unable to solve a problem, begin to study why it might be impossible to solve—and get an important result.
Here is a representative case, from a Math Circle course called “Interesting Points in Triangles” (its format is described in chapter 9). The students first struggle to prove that the perpendicular bisectors of the sides of a triangle are concurrent—that all three meet at one point.
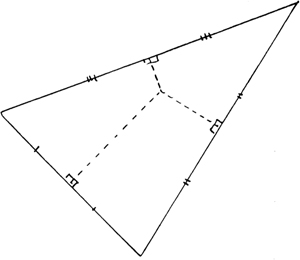
Then they are led to look at the concurrency of angle bisectors,
and then of medians, which run from a vertex to the middle of the opposite side.
Inventing the different sorts of proof each of these require will have left the proof for perpendicular bisectors—and even the fact of their concurrency—buried in a communal subconscious. When they are led to ask about the concurrency of the altitudes—another set of perpendiculars, after all, though this time dropped from a vertex to the opposite side—might they wonder if one triangle’s altitudes could be the perpendicular bisectors of another? Turning the problem around—or inside out—they take the triangle ABC, whose altitudes they wish to show concurrent, and draw through each vertex a line parallel to the opposite base and twice its length, with that vertex as midpoint. Then a new triangle, DEF, takes shape, whose perpendicular bisectors are indeed ABC’s altitudes. Since the former concur, so must the latter.
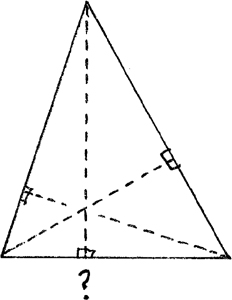
As with everything it touches, mathematics takes even its approaches, such as this, and turns them into its content too. “Seeing from another standpoint” becomes “duality”: that peculiar yet characteristic undertaking where opposites exchange roles. You see this most vividly in projective geometry, where what were points become lines and vice versa; and in the equations that describe them, variables and constants reverse. This outrageous act of the imagination sheds light over the whole projective plane—and over the mind as well that contemplates it.
Rotating a diamond-hard problem around is an antecedent to ingenuity. It allows you to shine the full light of your intelligence, and to bring to bear all your stored-up experience and powers of analogy, on facets previously hidden. We may puzzle over the physicist’s aphorism that in quantum mechanics, the experiment and the experimenter affect one another; but we can’t doubt that in math it is almost impossible to distinguish the subject from the object of thought: for the rotated problem likewise rotates our way of thinking, as if the two were geared to each other. And isn’t the structure that mathematics contemplates the structure of thought?
Why should “Breaking Apart” be a subheading of “Taking Apart”? Because of the violence involved. It’s one thing to lay out your shoes each evening with the obsessive neatness of the little girl who was to become Queen Elizabeth II, and quite another to make candies fly from a piñata by hitting it as hard as you can with a bat. Taxonomy lets us understand a complex landscape by imposing order on it, if none springs naturally to view: no Darwin without a prior Linnaeus. But a stifling order (the regularity of unquestioned conventions) leaves you with nothing but dead certainties. That’s the time for boisterous iconoclasm.
Everyone knows Euclid’s parallel postulate (in the nineteenth-century form of Playfair’s Axiom): through any point not on a given line, there is one and only one line parallel to the given line—
and thinks it is called a “postulate” for some arcane reason, since it is obviously true that there can be only one line parallel to another through a point not on that line. And yet those bold enough to discard this postulate and replace it with an opposite (many lines through the point parallel to the given line; or none at all) founded beautiful geometries—as consistent, as true, as Euclid’s.
Everyone knows that it makes no difference in what order you multiply two numbers: ab = ba. Yet Hamilton came up with his astonishing quaternions when he was willing to break this law. Cayley abandoned the even more fundamental associative law (that a(bc) = (ab)c) in devising the numbers that bear his name.
Anyone but a crank knows that a proposition is either true or false. “A shade, they say, divides the false and true”—but what is this shade that Omar Khayyam says divides them? You’d have to be really iconoclastic to begin thickening a shade. And yet there are those who experiment with three- and, in fact, multiple-valued logic; the constructivists rightly question the status of existence proofs founded on contradictions—and what about the ever-increasing number of propositions proven to be undecidable?
We’re speaking not of the foolish iconoclasm that questions everything for the sake of sounding clever (“What if it were the other way?”) but of the often anguished refusal to accept what just doesn’t make sense to you. The Russian mathematician Nikolai Nikolaievich Luzin, unable as a student to swallow the notion of “limit” as it was served up by his university professors, wrote of “intense intellectual suffering and pain,” adding: “and the more intense the suffering, the better, for suffering is the source of creativity.” Perhaps—but breaking open the box to discover how the locking mechanism works will leave you for a long time with a broken box.
Luzin tried to explain his ideas to his professor, who ended up storming at him: “Always the same! I am talking to you for half an hour about limits and not about your actually infinitely small which doesn’t exist in reality. I prove this in my course. Attend it—although for the time being I don’t advise you to do so—and you will be convinced of this. … Is there anything else you want to tell me?” Rather than saying that this was no way to treat a student, Luzin just walked away. That he persisted on his own in rethinking infinitesimals through the next two years, and indeed, throughout his whole adult life of mathematical research, epitomizes the stubbornness we spoke of earlier. It should come as no surprise that our categories aren’t disjoint, and that holding on and tugging apart are only different incarnations of Beau Geste, firing off cannons from here and there along the parapets of Fort Zinderneuf.
A healthy iconoclasm not only frees you from too timid a relation to authority (“The systems are rot,” said T. E. Lawrence) but supports the buoyant experimentalism whose motto is Nietzsche’s: “Let’s try it!” The limit toward which these complementary processes converge is the Themisto-clean spirit: with the Persians about to invade Athens by sea, the walls to the port of Piraeus had to be strengthened—and where was the stone to come from? Throw in the statues from the Acropolis, said Themistocles. Destroy our greatest works of art? It’s that or lose to the Persians—and if we win, we will carve yet more glorious ones.
If you object that “iconoclasm” overstates the case, that it is as important to attend receptively to a problem as it is to peel away the hardened layers of unexamined assumption that obscure it, we agree. The qualities we have been looking at in isolation not only overlap but need to be titrated with one another: and (in the self-referential style of mathematics) this titrating is itself a quality, which we shall soon look at. Here let’s compromise by saying that doing mathematics subtly changes your attitude toward permission. In his wonderful book, Imagining Numbers (Particularly the Square Root of Minus Fifteen), Barry Mazur tells the story of Gabriel García Márquez first reading Kafka’s Metamorphosis as a teenager and falling off his couch, “astonished by the revelation that you were allowed to write like that!” You’re allowed to invent a number whose square is –1? You’re allowed to pretend that an angled path is straight? Versuchen wir’s! Try it and see what happens.
Of all our inborn analytical tools, the one we most enjoy is deduction, that pursuit of the possible as it scurries simultaneously down divergent branching pathways. We like it so much that we read detective stories in our spare time and elevate to the upper echelons of society those whose work centers on the deductive—doctors, lawyers, and engineers.
Astonishingly few statements in mathematics assert that something is (“There is a number, 0”; “There is a number, 1, and 1 ≠ 0”). The vast majority much more modestly claim that if such and such is the case, then something else must follow. This vast hypothetical structure rests, like St. Mark’s in Venice, on the slenderest pilings, shallowly anchored in Being.
A dog with a long stick in its mouth comes to a narrow opening in a fence, stands back, stares, tilts its head sideways and trots through. A squirrel in winter, eager for the seeds in the capped bird feeder, hangs upside down and unhooks the wire holding the cap on. We’re not alone: animal life and deduction seem made for one another. Then why does it take so much trained effort to follow, and so much more to produce, the deductions in mathematics? The slenderness of those spiles is largely to blame: we’re often so far from familiar ground that we feel none of the solidity that intuition, or just belief, supplies: deduction, for all its authority, seems not quite able to authenticate itself. Why else do we speak of being “forced” to a conclusion? Why is our science fiction populated by coldly rational aliens and inimical thinking machines?
Since mathematics, music, and mountains are, as we remarked before, often enjoyed by the same people, let’s look at the latter two for some help in better understanding the effort needed here. A kind of backward inevitability suffuses great music. When you begin to listen to a new piece, the only sense you have of where it is going is the confidence you have on hearing a spoken sentence: confidence that the enveloping grammar will carry it safely, through however many adventures, to a conclusion whose shape will grow progressively clearer to you. Once heard, however, the continuous fit and flow of part to part makes you feel it couldn’t have been constructed in any other way. So it is with following an intricate proof: why is this here and that there? Which implication will we be following at this juncture, and where will it take us? Only long afterward do we see the design of the whole and recognize the intricate inevitability of the reasoning. Holding on to a strand of melody, a cadential sequence, is at a premium in these inner toils.
Holding on: those skills we spoke of before come sharply into play when you’re struggling up the mountain of someone else’s exposition. The preliminary demonstrations, the lemmas, are pitons driven into the rock face—and at a height where it is hard to catch a reflective breath. Although vast views surround you, you must keep your attention fixed on the minutiae of saving crevices.
Since deduction is meant to display, cogently, from premises to conclusion, the design of what we seek to understand, and since our minds are tuned to just this sort of display, why should there ever be any difficulty? Because our imagination frisks ahead of us at every turning and suggests different directions we might have headed off in; because we have to keep so many “ifs” in mind as we clamber from one “then” to another; because the techniques of deduction may change along the way (an inductive argument, a little contrapositive, an episode of proof by contradiction, in the midst of the on-linking network); because you must keep up the pretense that the exposition is impersonal, when in fact all the little leanings of the author’s personality led to seeing an opening here, and chose the direction of ascent there; because chasms will open up that you must get across—technical passages in an unfamiliar technique—and you take the leap on faith now, but must promise yourself to build a bridge later.
These are just the problems of climbing established routes, laid out by others! What happens when it comes to taking a problem apart yourself, with deduction’s aid? You have to be careful, at each of your argument’s links, that the reasoning is sound. For while deduction as a strategy is straightforward, the growing sophistication of its tactics means that unobtrusive errors can creep in. Even with Aristotelian syllogisms you had to beware of an undistributed middle (people are either rational or irrational; real numbers are either rational or irrational; so real numbers are people). All those scrambling quantifiers have to stay roped together and, with negation, have to arrange themselves as their leader directs, lest they tumble out of control. Worse—it is all too easy for unwarranted assumptions to slip covertly in, under the camouflage of implication. The remit of a word or a concept may grow subliminally, making the transition from premise to conclusion deceptively smooth.
The real problem, however, is that so much follows from so little. We only pretend that deductive thinking is linear; such a wide splay of conclusions opens out of any premise that we often don’t know which path to take or even where we might be taking it to, so that reasoning begins to circle about and can end at a standstill (“Mind,” by Richard Wilbur):
Mind in its purest play is like some bat
That beats about in caverns all alone,
Contriving by a kind of senseless wit
Not to conclude against a wall of stone.
You can even come to believe (as Bertrand Russell did, late in life) that all mathematical thinking is tautological, giving an illusion of insight but in fact only saying the same thing in different ways. This conclusion follows from too great a belief in deduction itself. But deduction is only a means toward taking apart: to see, by putting together, takes those kinds of imaginative play for which holding on and taking apart have set the stage.
The famous Banach-Tarski Paradox of set theory shows that you can cut a pea into a finite number of pieces and put it together again to be larger than the sun. How the mind fits its scattered rubble of questions, its ordered shards of insight, into the whole of a meaningful answer is almost as surprising. What began so recently as serious doubt becomes playful guessing, rearranging the parts that didn’t fit together so that they will: even if this means impudently deforming them—or the rules. Must you really play the hand you’ve been dealt?
Here is an example so beautiful and so telling that it’s worth the effort it may occasionally cost to follow (at least this will make you sympathize with the audience at a math lecture).
Working on a problem rather like that of finding Pythagorean triples, the Swiss mathematician Leonhard Euler needed to know which natural numbers x and y satisfied y3 = x2 + 2. None, perhaps—or a single pair, or a few, or many—perhaps infinitely many. How could anyone possibly tell?
Reduce what you can’t manage to what you can. In the classic technique of first-year algebra, factor: reduce the quadratic on the right hand side to its linear factors. The only difficulty is that the right-hand side has no factors, since factoring, by definition, requires integers: your only possibilities would be (x + 2), (x – 2), (x + 1) or (x – 1)—none of which work. (x + 2) times (x + 1), for example, gives you x2 +3x +2, and every other pair you choose will also produce an unwanted middle term. Nice customs curtsey to great kings, says Shakespeare’s Henry V, and common definitions must likewise curtsey to stubborn mathematicians. Euler wanted this expression factored, so he factored it into
for all that 
isn’t an integer. “I didn’t know you were allowed to do that!” we might exclaim, leaning over the eighteenth century from our perch in the twenty-first.
Having gone so far, Euler saw nothing wrong in going farther. He decided that these two factors themselves had no common factor (which seemed to him a very reasonable decision: for what could possibly divide both?). Yet their product was, as we already knew, a cube:
Since the two terms have no common factors, we can’t combine, say, a couple of 2s from one with a 2 from the other to make a 23. Each factor must, therefore, be itself a perfect cube. Now a perfect cube in the realm of complex numbers is simply some complex number, cubed. This means that 
, for example, must be some 
, where a and b are integers. Likewise, 
would be some 
.
Pause for a moment to catch your breath: to find all real—in fact, integral—solutions of y3 = x2 + 2, Euler has audaciously rewritten his equation with complex factors, each of which must be a perfect cube.
Let’s take one of them—say —and actually expand it fully:
that is:
And since he’d defined 
When you have an equation with complex numbers, such as this one, with real and imaginary terms that don’t combine, the real part on one side must equal the real part on the other, and the imaginary parts will likewise be equal. Here this means that
x = a3 – 6ab2,
and
Dividing both sides by gives us
1 = 3a2b – 2b3,
1 = b(3a2 – 2b2).
Step back and look at what this says (and notice that this stepping back is as creative a move as all those that preceded it): Euler had factored 1 into the product
1 = b(3a2 – 2b2).
Now we begin to return to the natural numbers from our long excursion into the complex, and go back to our familiar definition of factors as integers, which multiply together to produce the desired product. The only integral factors of 1 are 1 and –1. If we let b = 1, then 3a2 – 2 = 1. 3a2 = 3, a2 = 1, so a is either 1 or –1.5 We’re almost there. Remember that
x = a3 – 6ab2,
so if a and b are both 1, then x = 1 – 6 = –5.
But if a = –1 and b = 1, then x = –1 + 6 = 5.
Since –5 isn’t a natural number, the only natural number value for x is 5. Replacing x by 5 in y3 = x2 + 2, we find that
y3 = 25 + 2 = 27,
that is: y = 3. Trial and error would have shown that 5 and 3 do work; but by the most daring and playful series of maneuvers—and some assumptions only justified by much later work—Euler concluded that the only solution to y3 = x2 + 2, in all the infinity of natural numbers, is x = 5 and y = 3!
What Euler cooked up here, in his creative enthusiasm, probably took more holding on than we had to endure in following him, and a long taking apart of the notions “factor” and “complex number,” until he understood each with the easy familiarity that let him risk and invent as he chose. The distance that time has interposed, and the even greater distance between lines of life, make what he did seem to have come up as things do in play—just playfully.
It was stubbornness that let you hold on long enough to reach this creative height, where now flexibility rather than rigidity matters. But is some stubbornness yet needed—stubbornness suited to these changed circumstances?
“I will not let thee go except thou bless me,” said Jacob to the angel as they wrestled all night. Wrestling with a problem for what may be much more than a night will take coming to grips with it in one cunning hold after another, until the problem blesses you at last with an answer. Mere holding on has evolved into shaping yourself to the problem’s nature, so that you know it well enough to anticipate how it will next try to evade you—and you are there, waiting. Knowing what doesn’t work edges you toward what might.
An earlier generation of mathematicians, comfortable in a language that took for granted a sharp distinction between the conscious and unconscious mind, thought of this long struggle as consciously constructing various combinations of ideas—which were then somehow reformed in the unconscious, to emerge into the light of day as a solution, aided by chance in those depths and by choice in our waking. Perhaps; or perhaps these two phases of mind are so fractally interpenetrated as not to be two phases at all, but a virtual continuum. The “combinations of ideas” flicker in and out of focus, like wrestling grips smoothly and suddenly transforming from one into another; and judgment all along appraises what hasn’t yet—what still might—succeed; until the many parts of mind, and of the problem, grow unified. Or we acknowledge it to be a body too slippery for our grappling.
This aspect of putting together, then, is a negative one: building up a picture of what the problem’s nature is by sketching out what it isn’t. (“By indirections,” Polonius tells Laertes, “find directions out.”) Remember that problem about the heap of coins with 877 heads in it? The problem wasn’t about 877; it wasn’t about prime numbers or odd numbers. Remove all this extraneous matter, and the idea of changing the states of some coins may glimmer through. In order to get this far with a stubborn problem—and any problem you haven’t solved is stubborn—you need to fall in love with working on it, and this is obsessive love that doesn’t hesitate to stalk, to pry, to probe. Even more psychologically extreme, you need—as we said before—to throw the whole of your personality into it, at the risk of becoming enthralled.
What happens once the problem is solved, the insight gained, the theorem proved, the theory understood? Different people react differently, as they do in affairs of the heart. With an English taste for depressive irony, the number theorist J. E. Littlewood wrote: “When one has finished a substantial paper there is commonly a mood in which it seems that there is really nothing in it. Do not worry. Later on you will be thinking ‘At least I could do something good then.’” They think of these things differently on the continent: an Italian mathematician built for himself a triumphal arch in his Rome apartment and walked slowly through it, garlanded, whenever he proved a theorem. But the French mathematician André Weil said that “one achieves knowledge and indifference at the same time.”
Some small mammals, like the pygmy shrew, have to keep eating for dear life; they can hardly take off the time to scramble from one source of food to another. When you get wrapped up in a mathematics problem you often feel the same way—don’t stop me to ask where I’m going, it’s taking all my concentration just to go there! One conjecture has led to another, which needs a lemma to support it, and that entails a calculation, which in its turn requires a digression to justify it, while the insight you were after recedes into the distance.
A key part of putting together consists in stepping back at judicious moments to take in more than the next turning. Such pauses not only calm the panic brought on by deduction’s superfluity of consequences, which hide the shortest path to your goal, but also counteract the ever-present infantile hope that plowing on blindly will somehow lead you to the solution.
You saw an example of this stepping back when, with Euler, we looked to see what it meant that 1 = b(3a2 – 2b2): it meant that each of those factors must be 1 or –1, and that insight (or far sight) led swiftly to what he sought.
Since that stepping back was a small part of Euler’s overwhelmingly playful daring, we could do with an example that features stepping back as a major force for insight in its own right. Let’s prove that is irrational by assuming it to be rational and hoping for a contradiction. We assume, that is, that 
, where p and q are whole numbers with no common factor (otherwise we could reduce the fraction before going on). The proof will now flow in deductive style, guided only by the desire to simplify as much as possible.
We assume that . The most complicated part of that equation is the ungainly square root, so we do away with it by squaring both sides:
2 = p2/q2.
What’s most complicated now is the fraction, so we continue to simplify by multiplying both sides by q2. This gives us
2q2 = p2.
There’s not much to simplify now, so instead of hunting around for another deduction, this is the time to step back and ask what we’ve learned. Well, for what it’s worth, we see that p2 must be even: it is 2 times some integer. A small aperçu, but the whole way forward will turn on it.
We now follow our noses again: p2 is even, so p must also be even (for an odd squared is odd—pause for a moment to prove that—or glance at the footnote.)6 Let’s say p = 2a, for some integer a. Of the many paths we might have taken, the desire to simplify, and a small observation made on stepping back, have led us to this. We continue to follow our noses by substituting 2a for p back in the equation 2q2 = p2. This gives us:
2q2 = (2a)2.
Simplify again (stepping back for a methodological moment, you might consider how far the desire just to neaten up has taken us):
2q2 = 4a2.
And of course, keep simplifying:
q2 = 2a2.
We are at the same kind of junction as before, with nothing much of a simplifying sort to do, except to step back: q2 is even, so q must be even too. But wait: p was even, and now q is, so they must have the factor 2 in common, contradicting our assumption that p/q was in lowest terms! Hence can be rational only if a fraction can both be and not be in lowest terms.
It takes a while for the full weight of what we’ve proved to hit you: there are perfectly ordinary square roots that aren’t rational! It may take even longer to be struck by the beauty and elegance of the proof, with its plunging ahead and recoiling to contemplate where we were: a little fuguetta on how the mind synthesizes.
We can step even farther back from stepping back to see what a central role it plays in mathematical thinking. Time and again the way toward understanding a proposition, and proving it, consists in first seeing it as particular, then turning to the general context it belongs to, and doing your proving there. The irrationality of square roots provides a good example.
To prove that 
is irrational we could proceed much as with , but now argue not in terms of odd and even but of the three possible forms that an integer may take: it may be a multiple of 3, like 3a, or such a multiple plus one (3a + 1), or plus two (3a + 2). 3a + 3 is back to being a multiple of 3. The assumption that is rational would then involve this threefold distinction in the same sort of maneuvers we saw for . And the irrationality of 
? Now we would reason similarly, but with the five possibilities: 5a, 5a + 1, 5a + 2, 5a + 3, and 5a + 4. So it would go for the square roots of all primes, though extra work and some different turns of thought would be needed in order to show that 
, for example, was irrational. No wonder that Plato’s tutor, Theodorus the Pythagorean, was renowned for having shown (by a separate proof for each) that , , … up to 
were irrational!
Must we really go through such contortions again and again? What weariness would proving the irrationality of 
involve us in? Step back. Let’s prove at a stroke that 
is irrational if n isn’t a perfect square. We won’t rummage about in the many different forms that numbers may have, but think on a more general level.
We need to know (and this takes a bit of proving) that if a prime number divides the product of two numbers, then it divides at least one of those two: if 1848 can be divided by 2 (and it can, because it’s even) and if 1848 = 7 × 264 (and it does), then either 7 can be divided by 2 or 264 can be (which is true, because it’s even). This points you toward the fact that any natural number can be uniquely decomposed into a product of primes. 1848, for example, ends up as 23×3×7×11, whether you begin with 2×924 or 3×616 or even 11×168.
With this knowledge in hand, assume that 
(again, with p and q having no common factor), and as before, square both sides:
n = p2/q2.
We now have an integer, n, equal to a fraction, p squared over q squared. p/q was in lowest terms, i.e., p and q had no common factors. What about p squared and q squared? They have exactly the same factors as p and q had, except double copies of each; so if p/q was in lowest terms, then p squared over q squared must also be. Wait a minute: if the integer n is equal to a fraction in lowest terms, that can only be a fraction whose denominator is 1; so n = p squared, and so is a perfect square. But that contradicts our hypothesis. We have thus proven that if its square root is rational, then n is a perfect square, so if n isn’t a perfect square, its square root is irrational.
There is something rather awesome in this capacity of mathematics to sweep through whole continents of instance in a single glance, retreating from the particulars while preserving what matters about them. Awesome too is the way taking one step back always seems to invite another. Shall we prove that the cube roots of non-perfect cubes are irrational, and the fourth roots of non-perfect fourths too, and in fact, that the mth root of any number which isn’t a perfect mth power must be irrational? It will be the work of a moment.
For assume that 
(again, with p and q having no common factor). We take the same first steps as before, raising both sides to the mth power:
n = pm/qm
We now repeat, word for word, our previous argument, but applied to the exponent m rather than 2: p to the m and q to the m have nothing other than m copies each of the factors of p and q. But since p and q have no common factor, this is impossible unless q = 1. But if q = 1, we have n = pm, i.e., n is a perfect mth power, which contradicts our hypothesis. We have thus proven that if n isn’t a perfect mth power, its mth root is irrational. We could step even farther back. …
Putting together is almost indistinguishable from stepping back, so that learning how and when to do it (without falling off the narrow ledge you’ve climbed to) is central to doing mathematics. A mathematician turns out to be more like a contemplative gibbon than a tree shrew.
“Analogy is the greatest of my teachers,” said Kepler. The best teachers, however, do no more than point; it is then up to their students to find the way forward. An analogy nudges us toward an insight when close enough to conform to our problem and distant enough to transform it.
Descartes institutionalized one very broad sort of analogy when he invented coordinate geometry, which lets us translate back and forth between an algebraic and a geometric language; and this sort of mapping from one point of view to another is a deep part of modern mathematics, enshrined in category theory. But analogy often works less mechanically, reinforcing our old superstitions about inspiration, divine intervention, or the Familiar perched on your shoulder. We had an example of it before, where a way of proceeding in the problem of bisecting a pancake suggested the same sort of nonconstructive approach to a structurally similar but materially very different situation.
Let’s look at an example where the unpredictable peculiarity, as well as intricacy, of analogy’s working stands out. You want to know what the chances are of getting three heads when you toss a fair coin six times. The mind may dart at once from that three and six to “one chance in two”—an analogy reinforced by the argument that you’d expect heads half the time from random flips, and a second argument that you’ll either get three heads or you won’t, so again the odds would be one in two. The trouble with analogies is that they wobble: we can’t be sure, at first, whether the way they fall short of identity will help or hinder.
Hold off analogizing further, and just look and calculate. The first coin you flip may come up heads or tails (H or T)—let’s say H, and take care of the T case later. The second one again will be H or T—so we have two paths of a branching diagram,
Now we see the way forward: from each of these two branches two further twigs will sprout, and then two from each of them, and so on, making six ramifications in all: And let’s not forget, the first flip might have been T, so exactly the same diagram follows from that. After six flips, you arrive at 64 possible H or T destinations, by 64 pathways (64, by the way, = 26, where the base tells you the number of possibilities at each juncture, and the exponent how many junctures there are). Now check out the pathways, and you’ll find that of the 64, exactly 20 pathways contain 3 Hs. The chances, then, are 20/64, or 5/16: somewhat less than the innocent expectation of 1/2.
This result may be faintly surprising, but the method was sure, if tedious. It leaned, ever so little, on an analogy from events in time to paths in space: not a radical enough change in vision to strike us as due to a private muse.
But one can make a slightly more far-fetched analogy, which though less visually self-evident than the branching tree leads to a numerical formulation of what is going on—one which generalizes more easily to more coins and more flips than you could or would draw trees for. What if someone now said that you could have avoided all that work, and saved some paper as well, by rethinking the coin-tossing problem in terms of choosing three heads-up coins from among six coins laid out in a row under a piece of cloth. Why? How would it help to replace the darkness of future time by literal darkness? And talk about the wobbliness of analogies: we’re supposed to picture the coins as having already been flipped, with three heads among them, yet at the same time as not exactly already flipped, since those heads could be anywhere in the row of six hidden from view.
Let’s follow cautiously on. We’re asked to reach under the cloth and choose three heads from the row of six coins, which (a further minute analogy from number to position) we’ll think of as lying in six numbered slots.
The first H we draw out might have been in any one of those six slots, so six possibilities for it. Having drawn that first H, the next H may lie in any one of the five remaining slots, and after it, the third H in any of the four slots left. That makes 6×5×4 = 120 possibilities in all for where the three Hs might have been. Notice, for what it’s worth, a notational convenience: n! (“n factorial”) is defined as n times all the counting numbers smaller than n. So 6! = 6×5×4×3×2×1; since 3! = 3×2×1, 6!/3! = 6×5×4.
All well and good, except we already know from the tree diagram that the answer should have been 20, not 120 (and anyway, 120 is far more than the 64 possibilities altogether). What went wrong? Ah; we allowed time to enter our imagining of space, and the problems of picturing time came with it. We chose a first H, then a second, then the third: say they had been in slots 1, 2, and 3. The result would have been the same had we first chosen the H in slot 2, then the one in slot 3, last the H in slot 1; or any of the six possible sequences (1×2×3 = 6, or 3!) of choosing the heads in three slots. Because the order of choosing doesn’t matter to our result, we have to divide the 120 possible outcomes by 3!, giving us (6!/3!)/3!, or more simply, 6!/3!×3!, which gives us 20, as desired.
Remember that the first of those 3! came from rewriting 6×5×4 as 6!/3! Had we been trying to choose three heads from among seven coins, we would have had 7×6×5 possible arrangements to choose from, i.e., 7!/4!, or 7!/(7 – 3)!, and once again, we would have to divide by the 6 possible sequences: by 3!
In general, if you want to choose k things (in our case, heads) from among n objects (coins), there will be 
ways to do so. Statisticians tend to call this “n choose k”, and write it nCk, or, more cryptically, 
.
Thanks to an analogy that makes sense retrospectively, we now understand that the chances of getting three heads when flipping a coin six times is the same as the number of ways of choosing three heads from among six coins. Similarly, the number of ways of choosing five heads from nine coins, say, is 
, so the odds of getting five heads in nine tosses would be 126/29, i.e., 126/512. After putting in the conceptual work, the calculation is far easier than making a diagram with 512 branches and launching our counting program.
Could it have been made easier still? What if the Angel of Analogy now whispers in your ear that the answers you seek already lie neatly laid out in Pascal’s Triangle? How can this be—what have these numbers to do with choice or chance? You may recall that the nth row of Pascal’s Triangle gives the coefficients in the expansion of (a + b)n, if the first row is n = 0:
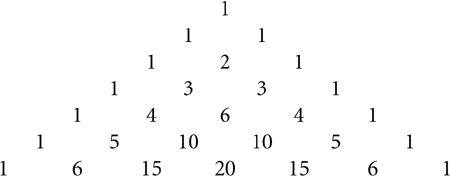
and so on. It also helps to call the first entry in each row the zero-th entry. And look: there in the sixth row, the third entry is 20: 6C3 (you might check that the fifth entry in row nine is indeed 126).
It isn’t enough to see that this is—or might be—so; we need to understand why. We need to see the analogy. Whoever first saw it (or each of us, on rediscovering it), might have reasoned this way:
If you flip a coin you will get a head or a tail: 1H or 1T. Flip two coins and the only possible outcomes are HH, HT, TH, TT. Since HT and TH are the same kind of outcome as far as we’re concerned (one of each), we could rethink this as 1HH, 2 mixed, 1TT. Just for convenience, choose HT as the way of writing “mixed,” and signal HH by H2, TT by T2; the exponent simply plays the role it should: as in a×a = a2, it is simply saying how many of them appear. So we have 1H2 2HT 1T2. This is enough like the second row of Pascal’s Triangle to tempt us to insert a ‘+’ between each pair of terms. We’re encouraged to do so by thinking that the H and T we began with make up the whole world of coin flipping: 1H + 1T add up to the total number of possible outcomes. Two coins flipped (or one flipped twice) yield four possible outcomes, made up of 1 + 2 + 1 kinds.
So with three coins there is only one way of getting all heads—1H3—and one way of getting all tails—1T3—but three ways of having two heads and a tail (HHT, HTH or THH), so 3H2T, and likewise 3HT2. And there you are: 1H3 + 3H2T + 3HT2 + 1T3, or 1 3 3 1 for the eight possible combinations. The chances of getting two heads and a tail, for example, when flipping three coins (or one coin three times) are 3/8.
And is it sheer chance that the binomial coefficients, and the ways of choosing, and of calculating these odds, are all the same? Clearly not. Pascal’s Triangle displays all the ways that two ancestors (call them a and b) can produce combinations of themselves when mated again and again: these are their offspring after successive generations—or, as we say, their products.
So if you ask how many ways there are to choose three of one kind (for instance, a) from among all the offspring, unto the sixth generation of the two parents (a and b), you are asking about 6C3.
If you ask how many offspring (products) there are of a and b, in the sixth generation, which have three parts of a in their makeup, you’re asking for the coefficient of a3b3.
And if you ask what the chances are of coming up with three Hs in six flips of a two-sided coin (H and T), you’re asking again about the sixth generation, and those in it with three heads—so 6C3, or 20—out of all the progeny, or products, thus far: namely, 26 = 64. That makes 20/64, or 5/16.
Production, progeny, product lie behind these various appearances, showing themselves differently in each. This is what really is. Well, on reflection, this is a metaphor too, which has produced each of the others. What really is—what is being borne across into each of its avatars—must be something invisibly structural, not metaphorical at all, receding from each of its offspring. From our standpoint, analogy drops away like scaffolding once its work is done—which is why we take its products as real. Only when we too step back, from time to time, do we recall that the world we understand is inseparable from the world we make.
We seem constitutionally incapable of looking around us without trying to make sense of what we see, and the grander the scheme, the better. Give children any sequence of numbers and they will find pattern after pattern in it, even if those patterns aren’t there. We can’t but make hypotheses; the trouble comes in trying to shake ourselves loose from their grasp (think how hard it is to talk readers of the daily astrology column out of their belief, especially when the predictions are—like enticing analogies—just vague enough to fit both our current and wished-for circumstances).
What a mathematician needs to develop, then, is the right sort of attitude toward his tentative convictions. That “if” with which they begin should act as an open parenthesis, closing only with a proof (and then—again like analogies—the parentheses can drop away and the insight become part of your outlook). Fencing masters since the Renaissance have advised their students to hold the foil as if it were a bird: tightly enough so that it won’t get away, not so tightly as to crush it.
Here is a nice example of the grip we and hypotheses can have on each other. Put two points anywhere on a circle’s circumference and draw the chord connecting them. Into how many regions has the circle’s interior been divided? Clearly two.
And with three points? Obviously four.
Four points give eight regions, when we draw all possible chords,
and five yield sixteen:
Anyone who hasn’t conjectured by now that n points yield 2n–1 regions has been reading too quickly. Just to make assurance doubly sure, go back to the n = 1 case: does one point on the circumference produce 21–1 = 1 region? Yes.
Having seen five examples, the time is past to test—but ripe to prove. Oddly enough, this isn’t as easy as it should be: why the number of regions should double with each successive point on the boundary isn’t clear. Eventually you doodle your way to another example, for want of anything better to try. Perhaps when n = 6 the cause behind the doubling will become clear. For n = 6 we get thirty-one regions—which must simply be an error in our drawing—too many lines in too small a space; Wittgenstein was probably right when Bertrand Russell asked him why his Tractatus had no examples. “What,” he is supposed to have answered, “dirty it up with examples?”
When we posed this problem to a Math Circle class of college students, one even came up with just thirty regions, because she had drawn a regular hexagon to start with, and its regularity caused a region to shrink to an internal crossing point.
This must be the answer then (“Save the hypothesis!”). The question should really have been put this way: what is the maximum number of regions that all possible chords among n boundary points create in a circle’s interior? Our thirty-one regions must have come from the six points not having been distributed maximally enough. As a friend of ours once remarked, nothing in mathematics is as difficult as counting.
For some reason or other, however, none of us were able to come up with the desired thirty-two, no matter how we arranged our six points. Two students got hold of a large piece of drawing paper and decided to see what would happen with seven points on their circle’s boundary, while the rest—scornful of such pedestrian checking of the obvious—framed sub-hypotheses about interior points as disguising minute regions (think back to the line in the figure on page 31 that hid an area), or what a “really random” arrangement of boundary points would mean. Meanwhile, the students with their seven points could come up with no more than fifty-seven regions instead of the predicted sixty-four.
Facts dented our hypothesis but failed to break it. Our belief in order is too important for our physical and mental survival. Remember how long the Ptolemaic astronomers added epicycles onto epicycles, to keep some sort of fit between data and theory.
The students regretfully gave up their beloved powers of two and began to look at how boundary points, and the chords among them, create regions. Forced back and back, they had eventually to ask what a chord was and how it arose—and this clearing of vision proved to be decisive. Any two points on the boundary produce a chord; or differently put, a chord is, in effect, a pair of points. How many chords will n points therefore produce? One for every two points, so n points taken two at a time—oh!—nC2.
That doesn’t give all the regions, however, since many new ones are created where two chords intersect. And what does that mean? A new region for every pair of chords—in other words, one for every four points (two per chord): nC4. The total number of regions made by n boundary points should therefore be nC2 + nC4.
Try it. For n = 3, for example, 3C2 + 3C4 = 3 (since 3C2 = 3!/2!, and 3C4 doesn’t mean anything, so adds no regions), but this is one less than the needed 4. We need a last bit of fine tuning: there was, after all, the one region of the circle we began with, prior to drawing chords—so the number of regions made by all chords drawn among n boundary points should be
1 + nC2 + nC4.
For n = 5 this does indeed give us 16 regions, and for n = 6, 31. A plausible argument and six confirmatory examples. But is this proof enough? We are so delighted by our success that we are sure our new formulation is right: can the hypothesis, having been released, now soar? When Jim Tanton presented this problem to a group of eight- to ten-year-olds in The Math Circle, in 2001, “They decided,” he writes, “to count everything: the number of circles C (always 1!), the number of dots along the boundary, the number of paths drawn L (lines), the number of intersections I, and the number of regions P (pieces). It soon appeared that C + L + I = P and ‘CLIP Theory’, as they called it, was born. They noted that the theory was true for very simple diagrams and seemed to remain true if an extra path were added to a diagram. They reasoned as follows—as soon as this line intersects a pre-existing path, two things occur: the count of intersections increases by one, and a region is split in two, increasing the count of pieces by one. The formula C + L + I = P remains balanced. This equation also remains valid when the path eventually returns to the circumference of the circle: the path is completed, thereby increasing the number of lines by one, which is balanced by the fact that a final region is split in two.”
Mathematics isn’t experimental in the way laboratory sciences are. Its conclusions aren’t ever more fully confirmed by repeated trials under controlled conditions but are assured, once and for all, by a single unbroken (if baroque) chain of inferences from assumptions. Something very like experiment, however, appears—as you have just seen—in the formulation of what we want to prove. Just as mathematics precedes experiment, in providing the structure within which science operates, experiment precedes mathematics in our ferreting out, hypothesizing, and constructing.
In these thought experiments, many of the qualities we’ve already spoken of combine: the confident sort of courage expressed in “Versuchen wir’s!”; the precision that holds all else carefully still while allowing only one idea at a time to vary; the varying itself, which we described as rotating the diamond; the ingenuity, which is always applied analogy. But there are other aspects of the data, and of the mathematician’s relation to it, that combine with these to give a special cast to experimental fervor here.
As for the data, you need only have seen one triangle in your life to know triangularity—and to know at the same time that in fact you have never seen and never will see a triangle at all, which is only badly approximated by steel gable-ends or mechanical drawings. What a peculiar science this is, then, with no single instance of the structures it studies! The instances, the variety of triangles, for example, are instances of form, and the fact that we then operate on them formally gives another odd cast to experiments in mathematics: in them you can no more distinguish the means from the material than you can the investigator’s mind from what it studies. These mirrored involvements add to the recursive character of mathematics, which so many have remarked on.
“The One remains, the many change and pass”—yet what mathematical insight feeds on is, in a deep sense, plural. David Mumford pointed out, in “The Dawning of the Age of Stochasticity,” that computers make available for our scrutiny huge collections of data we had never before been able to collect, so that we may now hope to see unifying patterns in their variety.
Mathematicians develop the traits that experimentalists everywhere have, but they speciate to fit their remote Galápagos. They tinker, and come up with elegant devices (the generalization, for example, of exponential notation to rationals, reals, and complex numbers). They cultivate a quiet yet alert eye, which especially focuses on the peculiar, so that their seeing stretches from the singular to the single. They sometimes won’t admit to, but nevertheless relish, the art of embodying: making miniature models as aids to the imagination. These models are no more real, of course, than what they model: not balsa and tissue-paper flyers, but each is a conceptual apparatus for thought experiments. So to picture where a triangle’s centroid must be, you might think of a metal triangle, with the metal then made molten and drawn off equally to the three vertices, and the edges between them reduced to weightless wires. Now the laws of the balance beam will come to your aid (and all the while, your eyes are closed).
You catch the whiff of this abstract experimentalism best when mathematicians run into each other. “What are you working on?” A single diagram is sketched out, and a flurry of symbols adjusted, erased, expanded. “Have you seen this nifty idea—” and people who may have in common only the language of their craft, follow, with reckoned abandon, the trains of one another’s thoughts on a crowded blackboard.
The desire to build ourselves into the world—to make a safe haven in it—must be among the deepest we have. Birds make nests from linear fragments of non-linear nature, shaping them so as to accommodate their lives to new locales: the crotch of a tree that supports, the leaves that disguise, this fairing of a little world into the large. Yurt and skyscraper equally serve the need to blend structure to structure coherently.
As with all desires, this one grows more rarefied as it intensifies, until structure itself, no matter what embodies it (images, sounds, language), becomes the material we would build with. Mathematics is the natural limit of this desire; its statements are ambiguously about the mind and the world, its proofs intermediate between the two, with immense plasticity, variety of design, and inventiveness. Their artifice builds inner to outer nature.
It is this architectural instinct that drives mathematical thought, seeking to contrive sound foundations and then to rear elegant structures on them, so that we will be at home in the meaningful world. The passion for order, the delight in symmetrical balance and asymmetrical tension, the sense that the whole, which is greater than all its parts, is the whole of those parts—all these are expressions of this instinct.
If it is so deep, if it derives from the yet deeper nest-building urge, then why are we not all mathematicians from birth, unfazed by the many vicissitudes this instinct undergoes as we bear it about with us? Love and fear are the answers. Love of the irreducible particularity of things, which sees a focus on structure as diminishing the value of substance; and fear of the abyss of abstraction, toward which ever more structural thought seems to lure us.
What turns someone into a mathematician—and you can see this in every Math Circle class—is that structures come to acquire the quirky individuality, the breath, of things. Just as a particular cast of light will call up urgent stirrings in an artist, or an interval, struck just so, in a composer, so a configuration—as small as a vanishing point, as immense as the whole of projective geometry—prodded at, poured over, puzzled about, will become a vivid companion. To pick out an example of this architectural instinct at work is perverse, because everything in mathematics exemplifies it. Still, here is one.
In our course on the Pythagorean Theorem, students know almost at once that the first instance they see is—just an instance: this drawing stands for any right triangle with legs of three and four units, and hypotenuse of five, no matter what those units may be and how the triangle is oriented on the board. Then they discover that the relation works as well for a triangle with lengths 5, 12, and 13, and all others of that ilk (since 52 + 122 = 132, (5k)2 + (12k)2 = (13k)2). The awesome generality of this is made up for by an awakening sense of what this statement, of what any statement, is about: not the accidents of here and now, but how things hold.
They come up with a proof, and the same edged excitement pulses again: so it wasn’t just true for triangles with sides proportioned to 3, 4, and 5, or 5, 12, and 13, but for all right triangles: in Borneo, on the dark side of the moon, or in spiral nebulae we haven’t even names for, rotating and aging out at the edge of imagination.
Their proof follows inevitably from what it set out to prove—until they see or devise another, very different one. This must mean that the Pythagorean Theorem is true, independent of them, yet how they know it to be true depends on their contrivings. The architectural instinct is for the world but from the mind. It delights in growing the connective tissue between them.
Those infinite numbers of 3-4-5 right triangles have long since become particulars for them, in this immensely general context. And this general context? They now learn that not just squares but any similar shapes on the three sides of a right triangle obey the Pythagorean principle: however bizarre those shapes may be, the areas of those on the legs add up to the area of that on the hypotenuse.
Our students are busy unpacking one of those Russian babushka dolls from the inside: each is contained in a yet greater replica. Then they unpack this latest one. In the three-dimensional analogue of a right triangle—a right tetrahedron, where three of the faces are right triangles (the right angles all at a common vertex)—the squares
of the areas of those three faces turn out to add up to the square of the area of the fourth, “hypotenuse” face. They push further: this relation holds in the four-dimensional analogue too, and in the fifth, and sixth—in fact, in the n-dimensional “multi-orthogonal polytope,” for any n, world without end (none of which can be drawn). And these are only some of the ways that the architectural instinct leads them from the universal theorem that Pythagoras came up with, 2,500 human years ago.
How could we possibly expect anyone—much less everyone—to have or develop the qualities we have been describing? Quite simply, because they are general human qualities, which can be adapted to the ecology of mathematics. None of us has them all, at an equal pitch, at any one time. They fade and flourish with the calls made on them, as do all our capacities.
The calls aren’t separate, of course. We’re not asked to be ornery and then, in a blink, fervently experimental. With the changing global and local character of the mathematical landscape we find ourselves in, these qualities (and doubtless many others) are linked up in coordinated sequences. By what? It would be most elegant not to have to invoke a detached Overseer—to let the calling and the ecology define the responsive structures in our minds. Think of this explanation, then, as a makeshift, an artifice devised by the architectural instinct to hold this aspect of inner and outer together.
Our orchestra of qualities has a conductor who brings out now this instrument, now that, in accordance with the interpreted score, that is, with a general strategy for coming to grips with the problem. Such a meta-quality may be an amalgam of all the others (like any conductor, who has to know the capacities of each instrument and player). Akin to the untensed attention we spoke of, the conductor looks beyond the immediate dispositions; he is concerned with matters of tact and timing.
What is curious, in the history of the doing and teaching of mathematics, is how often just this unifying quality is missing; a quality so likely sprung from common sense that you would expect it to be the most common. A decade ago two mathematicians even suggested that the practitioners of their craft be divided into those who speculate and those who prove, rather along the lines of experimental and theoretical physicists. While this view was vigorously attacked as “sanitized,” condemning mathematics to “an arthritic old age” (“We now have high standards of proof to aim at,” wrote Michael Atiyah, “but we must be prepared to act in more buccaneering style”), you will still find the stresses in mathematical thinking too often asymmetrically placed. Rigor is so late in development, and so essential for real mathematical thought, that in many a classroom it is taken to be mathematics, and spreads from its rightful place after invention to paralyze thought altogether. It would be just as distorting to let playful freedom, which devises conjectures, hang on to undermine their proofs, but we seem to err less frequently in that direction.
These aren’t the only extremes that need mediating. When do you stop rotating the diamond or following a deductive scent to step back and look? When should you be as hard as ice, when yielding as water? We always need a regulator of our mental temperature. Would that the orchestra could perform by itself, as the Vienna Philharmonic once famously did; would that the music directed its own performance, even while—especially while—improvising. Perhaps this conductor is, at its best, the totality of the parts made into a presence among them: their modeled whole.
