The Man Who Changed Everything

The Maxwells rented a house in the smart new residential district of Kensington ¹. This gave James a vigorous 4 mile walk to work on fine days, with the alternative of a horse-drawn bus ride. Nearby was the great green space of Kensington Gardens and Hyde Park—a fine place to stroll and to ride. Katherine’s pony, Charlie, also made the long railway journey down from Glenlair and, once he was settled into stables from which James could hire a horse, they rode most afternoons. At the top of the house was a big attic, just the place for James’ experimental paraphernalia. Neighbours across the way were alarmed at first to see the two of them spending hours in this room, peering into what looked like a coffin, but it turned out to be James’ new and bigger colour box, about 8 feet long, which they had put near the window to get the best light.

King’s College is in The Strand by the north bank of the river Thames. It had been founded in 1828 as an Anglican alternative to the non-sectarian University College, a mile to the north, which was itself intended as an alternative to the strictly Church of England universities of Oxford and Cambridge. King’s was a modern university. From the outset it strove to give young people an education to fit them for working life in a rapidly developing world. Unlike the traditional fare provided by Cambridge and Aberdeen, its courses were much like those given at today’s universities. It gave classes in new subjects like chemistry, physics, botany, economics and geography, and ran purpose-built courses in law, medicine and engineering.

There was, of course, an inaugural lecture to be given. At the age of 29, James was already becoming an old hand at these. As he had done at Aberdeen, he stressed that he wanted above all to help people learn to think for themselves:

In this class, I hope you will learn not merely results, or formulae applicable to cases that may possibly occur in our practice afterwards, but the principles on which those formulae depend, and without which the formulae are mere mental rubbish.

I know the tendency of the human mind is to do anything rather than think. But mental labour is not thought, and those who have with labour acquired the habit of application, often find it much easier to get up a formula than to master a principle.

He finished the lecture with what turned out to be an extraordinarily prophetic statement:

Last of all we have the Electrical and Magnetic sciences, which treat of certain phenomena of attraction, heat, light and chemical action, depending on conditions of matter, of which we have as yet only a partial and provisional knowledge. An immense mass of facts has been collected and these have been reduced to order, and expressed as the results of a number of experimental laws, but the form under which these laws are ultimately to appear as deduced from central principles is as yet uncertain. The present generation has no right to complain of the great discoveries already made, as if they left no room for further enterprise. They have only given science a wider boundary, and we have not only to reduce to order the regions already conquered, but to keep up constant operations on a continually increasing scale.

James was attacking the widespread misconception that there was little left to do in science beyond measuring nature’s characteristics to more places of decimals. Just the kind of rhetoric one might expect from a keen new professor. But within 4 years he was to turn rhetoric into accomplishment by creating a theory which masterfully brought everything together and, at the same time, extended the boundaries of science into undreamt-of regions.

As at Aberdeen, the post was a demanding one for someone who was also engaged in top-level research. The lecturing load was a little lighter than at Aberdeen but the terms took up 8 months of the year rather than 6. There were also weekly evening talks to artisans—at King’s these were part of the professor’s official duties. The course James took over was well designed but he improved it further by increasing the practical work and introducing the latest discoveries, which were often his own. The pattern served King’s well—100 years later it was still considered a very good course. He tried to make examination questions more interesting by couching them in terms of everyday experiences, and insisted that the question papers should be printed rather than lithographed, to make sure all copies were legible.

Among James’ professorial colleagues was Charles Wheatstone, who is familiar to physics students as the supposed inventor of the Wheatstone bridge—a type of circuit used to measure electrical resistance. Curiously, Wheatstone did not invent this bridge, even though he was a prolific inventor who created the English concertina and, like William Thomson, earned a fortune from patents on telegraph devices. Whatever spurious kudos Wheatstone gained from the bridge is balanced by the genuine credit he lost when one of his outstanding inventions became well known under someone else’s name, the Playfair cipher². He and James clearly had interests in common and it seems odd that they had little, if any, contact. The oddity seems to lie mainly in Wheatstone’s relationship with the university. He had been in post 26 years but for the last 25 of those had spent his time on research and inventions and given no lectures. He played little part in College life and by the time James arrived was not even drawing a salary.

Living in London gave James the chance to attend lectures and discussions at the Royal Society and, more particularly, the Royal Institution, where Faraday had built on Davy’s foundation by establishing a celebrated tradition of popular lectures. He and James had built up a scholarly comradeship by letter but it was a delight for James to meet the scientist he admired above all others. Faraday still attended some lectures but now rarely gave them. He was in his 70s and suffering from failing memory, but he and James took pleasure in one another’s company and it is pleasing for us to picture them together—two modest and genial men from different backgrounds but sharing a passionate interest, whose combined endeavours brought about a metamorphosis in science and technology.

James was invited to give a lecture at the Royal Institution on his work on colour vision in May 1861. Rather than just talk about the principles, he wanted to give the audience a visual demonstration that any colour could be made by mixing the three primaries. The colour box was no good for this purpose because only one person could use it at a time, and the colour top was too small for people in the back seats to see clearly.

But there was another possibility. The basic techniques of black and white photography were known and it was possible to project a photograph on to a screen. Could he make a colour photograph? He would simply need to take three photographs of the same object, through red, green and blue filters in turn, and then project them simultaneously on to the screen using the same filters. There was a problem: photographic plates of the time were sensitive to light at the blue end of the spectrum but hardly, if at all, sensitive to light at the red end. Still, it was worth a try. Thomas Sutton, a colleague at King’s, was an expert photographer and keen to help. They took three pictures of a tartan ribbon, developed the plates, and it worked beautifully. The Royal Institution audience saw the world’s first colour photograph.

The experiment should never have worked because the plates that Maxwell and Sutton used were, in fact, completely insensitive to red light. There had been a bizarre chain of favourable coincidences. The red dye in the ribbon happened to reflect some ultra-violet light as well as the red, and the solution used by Sutton as a red filter happened to have a pass-band in the same ultra-violet region. Moreover, although the emulsion used on the plates was not at all sensitive to red, it happened to be sensitive to ultra-violet. So the parts of the picture which appeared red had actually been obtained with ultra-violet light, well beyond the range of the human eye! Lucky Maxwell. But perhaps he made his own luck. It was a rule with him never to dissuade a man from trying an experiment, no matter how slim the prospect of success, because he might find something entirely unexpected.

Three weeks after his colour show, and one week before his 30th birthday, James was elected to the Royal Society, in recognition of his work on Saturn’s rings and colour vision. It must have given him some gratification to be welcomed formally into the top rank of British physicists—although he was nowhere near as well known as Thomson or Stokes—but the event seems to have barely registered in the Maxwell household. Perhaps he had the private wistful thought that his father would have enjoyed it.

At the time he joined King’s College James had published only one paper on electricity and magnetism, and that had been 5 years before. But the subject was never far from his mind and ideas had been steadily brewing. He believed strongly in the power of subconscious thought to generate insights. As a student he had expressed this theory in a poem:

There are powers and thoughts within us, that we know not till they rise

Through the stream of conscious action from where Self in secret lies.

But where will and sense are silent, by the thoughts that come and go

We may trace the rocks and eddies in the hidden depths below.³

In his Cambridge paper On Faraday’s Lines of Force he had found a way of representing the lines of force mathematically as continuous fields, and had made a start towards forming a set of equations governing the way electrical and magnetic fields interact with one another. This was unfinished business and he now felt ready to make a serious attempt to settle it. He had made progress so far by using the analogy of a swirling body of incompressible fluid—the pressure in the fluid corresponded to electric or magnetic potential and the direction and speed of flow represented the direction and strength of either an electric or a magnetic field. By extending the imagery, so that, for example, sources and sinks of fluid represented electrically charged surfaces, he had been able to derive all the important formulae for static electricity and magnetism. He had also managed to bring steady electric currents and their effects into the scheme by using the fluid analogy in a different role to represent the flow of electricity.

The analogy had served well but could take him no further because it worked only when electrical and magnetic fields were static and electric currents steady. As soon as anything changed, the fields acted in a way that was nothing like the smooth flow of a fluid; in fact their behaviour was completely different from that of any known physical process. So to go further he had to find a new approach.

Two courses seemed to be open. One was to desert Faraday and fields, and assume that all effects result from action at a distance between magnetic poles and electrical charges or currents. This was the approach taken by Siméon-Denis Poisson and André-Marie Ampère, who had derived the original formulae for static fields and steady currents which James had re-derived by the field approach. It was also the basis of an attempt at a complete theory by Wilhelm Weber, which was mathematically elegant and offered an explanation for most of the known effects. But Weber had made a critical assumption—that the force between two electrical charges depends not only on their distance apart but also on their relative velocity and acceleration along the straight line joining them. James respected Weber’s work but his intuition bridled at this assumption and, more generally, at the whole action at a distance concept.

As we have seen, all the known experimental results in electricity and magnetism could be attributed to four types of effect; to gain the day, James’ model would have to account for all of them:

1. Forces between electrical charges: unlike charges attract; like charges repel, both with a force inversely proportional to the square of the distance between the charges.

2. Forces between magnetic poles: unlike poles attract; like poles repel, both with a force inversely proportional to the square of the distance between them; poles always occur in north/south pairs⁵.

3. A current in a wire creates a circular magnetic field around the wire, its direction depending on that of the current.

4. A changing total magnetic field, or flux, through a loop of wire induces a current in the wire, its direction depending on whether the flux is increasing or decreasing.

James began with effect 2, magnetic forces. For his model he needed to envisage a medium filling all space which would account for magnetic attraction and repulsion. To do this, it would need to develop tension along magnetic lines of force and exert pressure at right angles to them—the stronger the field, the greater the tension and the pressure. And to serve its purpose as a model the imaginary medium would have to be built from components which bore some resemblance to everyday objects.

It seemed an impossible task, but James’ idea was amazingly simple. Suppose all space were filled by tiny close-packed spherical cells of very low but finite density, and that these cells could rotate. When a cell rotated, centrifugal force would make it tend to expand around the middle and contract along the spin axis, just as the earth’s rotation causes it to expand at the equator and flatten at the poles. Each spinning cell would try to expand around the middle but its neighbours would press back, resisting the expansion. If all the cells in a neighbourhood spun in the same direction, each would push outwards against the others; they would collectively exert a pressure at right angles to their axes of spin.

Along the axes of spin the opposite would happen. The cells would be trying to contract in this direction and there would be a tension. So if the spin axes were aligned along lines in space, these lines would behave like Faraday’s lines of force, exerting an attraction along their length and a repulsion sideways. The faster the cells spun, the greater would be the attractive force along the lines and the repulsive force at right angles to them—in other words, the stronger the magnetic field.

So the field would act along the spin axes of the cells. But which way? Magnetic force is conventionally defined as acting from north pole to south pole. James built an extra convention into his scheme: the sense of the field would depend on which way the cells were spinning—it would be in the direction a right-handed screw would move if it rotated the same way; if the cells reversed their spin, the field would reverse too.

But if the cells occupied all space, why were they not apparent? And how could they exist in the same space as ordinary matter? James was not put off by such awkward questions. It was, after all, only a model. The cells’ mass density could be so low as to offer no perceptible obstruction to ordinary matter. As long as they had some mass and rotated fast enough they would generate the necessary forces.

The scheme did not yet explain how different materials could have different magnetic characteristics. For example, iron and nickel had a high magnetic susceptibility—they could be readily magnetised—whereas other substances, like wood, seemed to be even less receptive to magnetism than empty space. James solved this problem with his customary sureness of touch. Where cells occupied the same space as an ordinary substance their behaviour would be modified according to the magnetic susceptibility of the substance. The modification was equivalent, in mechanical terms, to a change in the mass density of the cells. In iron, for example, they would become much more dense than in air or empty space, thereby increasing the centrifugal forces, and hence the magnetic flux density, for a given rate of spin.

So far so good. But there were two problems. First, what set the cells in motion? And second, the cells along one line would be spinning in the same direction as those in neighbouring lines, so that where two surfaces made contact they would be moving in opposite directions, rubbing awkwardly against one another. Amazingly, James solved both problems with a single stroke.

To avoid the cells rubbing against one another, he tried putting even smaller spherical particles between the cells. They would act like ball bearings, or like the ‘idle wheels’ engineers put between two gear wheels which need to rotate in the same direction. The idea seemed crazy but James persevered and suddenly things began to fall into place. Suppose the little idle wheels were particles of electricity. In the presence of an electromotive force they would tend to move along the channels between the cells, constituting an electric current, and it would be this movement that set the cells spinning.

But everyone knew that currents could flow only in substances which were conductors, like metals. In insulators like glass or mica, or in empty space, there could be no currents. So James proposed a second way in which the behaviour of the cells would be modified according to the type of substance which shared their space. In an insulator the cells, or perhaps local groups of cells, would hold on to their little particles so that they could rotate but not move bodily. But in a good conductor like a copper wire the particles could move bodily with very little restriction and a current would flow. In general, the lower the electrical resistance of the substance, the more freely the particles could move.

An essential feature of James’ little particles was that they had rolling contact with the cells—there was no sliding. Where the magnetic field was uniform the particles would just rotate, along with the cells. But if the particles in a conductor moved bodily without rotating, they would cause the cells on either side of the current to spin in opposite directions, exactly the condition to create a circular magnetic field around a current-carrying wire—effect 3. If the particles rotated and moved, the circular magnetic field due to their movement would be superimposed on the linear one due to their rotation.

So, by this extraordinary assemblage of tiny spinning cells interspersed with even smaller ‘idle wheel’ particles, James had succeeded in explaining two of the four main properties of electricity and magnetism. A highly satisfactory start, but there was much more to do. The next task was to explain effect 4: a changing magnetic flux through a loop of wire induces a current in the wire. James chose to explain an equivalent effect—that

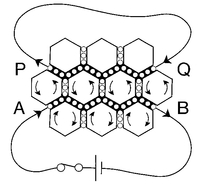
• All cells and idle wheels stationary

• No currents

Figure 2a. Switch open

• No magnetic fields

Figure 2b. Switch first closed

• AB current flows from left to right

• PQ current flows from right to left

• Cells below AB rotate clockwise, causing a magnetic field pointing away from the viewer

• Cells between AB and PQ rotate anticlockwise, causing a magnetic field pointing towards the viewer (in three dimensions, a circular field envelopes AB)

• Cells above PQ still stationary

Figure 2c. Shortly after switch closed

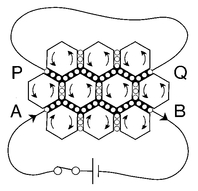
• PQ current slows, then stops

• Cells above PQ start to rotate anticlockwise, and by the time the current stops are rotating at the same rate as those in the row below PQ

Figure 2d. Switch opened again

• AB current stops

• Cells in rows above and below AB stop rotating

• PQ current flows from left to right

• The current will slow, then stop; the situation will then be as in Figure 2a

when a current is switched on in one circuit, it induces a pulse of current in a nearby but separate circuit by creating a magnetic field that links the two. He drew a diagram to illustrate his argument, giving the spherical cells a hexagonal cross-section ‘purely for artistic reasons’. We can see it, slightly adapted for our purpose, in Figures 2a 2b 2c-d.

The diagram shows a cross-section of a small region of space. The idle wheel particles along AB are in a wire which is part of a circuit with a battery and a switch, initially open. Those along PQ are in another wire which is part of a separate circuit having no battery or switch. The idle wheels along AB and PQ are free to move because they are in conductors, but others in the neighbourhood are in a non-conducting material and can only rotate in their fixed positions. AB and PQ are, of course, impossibly thin wires and impossibly close together, but this is to just keep the diagram compact; the argument James produced would apply equally well to normal-sized and normally spaced wires containing many rows of idle wheels and cells. The argument runs like this.

Suppose the magnetic field is zero at first, and the switch open, so that all the cells and idle wheels are stationary (Figure 2a). When the battery is brought into the circuit by closing the switch, the idle wheels along AB move bodily from left to right without rotating. This causes the rows of cells on either side of AB to rotate in opposite directions, thus creating a circular magnetic field around the wire. The idle wheels in PQ are now pinched between rotating cells on the AB side and stationary ones on the other, so they start to rotate (clockwise) and also to move from right to left, the opposite direction from those in AB (Figure 2b).

But the circuit containing the wire along PQ has some resistance (all circuits do), so the idle wheels there, after their initial surge, will slow down, causing the cells above PQ to begin rotating anticlockwise. Soon, the sideways movement of the idle wheels will stop, although they will continue to rotate. By this time the cells above PQ will be rotating at the same rate as those in the row below PQ (Figure 2c).

When the switch is opened again, disconnecting the battery, the idle wheels along AB stop moving and the rows of cells on either side of AB stop rotating. The idle wheels in PQ are now pinched between stationary cells on the AB side and rotating ones on the other, so they start to move from left to right, the same direction as the original AB current (Figure 2d).

Thus, switching on a steady current in AB induces a pulse of current in PQ in the opposite direction and switching the current off induces another pulse in PQ, this time in the same direction as the original current. More generally, any change of current in the AB circuit induces a current in the separate PQ circuit through the changing magnetic field that links them. Equivalently, any change in the amount of magnetic flux passing through a loop of wire induces a current in the loop—effect 4 is explained. If the battery in the AB circuit were replaced by an a.c. generator, the alternating AB current would induce an alternating current in PQ. This is exactly the way transformers work in our electrical power supply systems.

And here, at last, was a mechanical analogy for Faraday’s electrotonic state. It was the effect at any point in the field of the angular momentum of the spinning cells. Like a flywheel, the cells would act as a store of energy, reacting with a counterforce to resist any change in their rotation; this took the form of an electromotive force which would drive a current if a conductor was present.

James had now explained three of the four effects. He had not yet found a way of using the model to account for effect 1, forces between electric charges, commonly called electrostatic forces. But he wrote up the results with full mathematical rigour in a paper called On Physical Lines of Force, which was published in the Philosophical Magazine in monthly instalments: Part 1 appeared in March 1861 and Part 2 was spread over April and May. Not wanting to be misunderstood, he was at pains to point out that his bizarre arrangement of whirling cells and idle wheels was merely a model:

The conception of a particle having its motion connected with that of a vortex^g by perfect rolling contact may appear somewhat awkward. I do not bring it forward as a mode of connexion existing in nature, or even as that which I would willingly assent to as an electrical hypothesis. It is, however, a mode of connexion which is mechanically conceivable, and easily investigated, and it serves to bring out the actual mechanical connexions between the known electromagnetic phenomena; so that I venture to say that any one who understands the provisional and temporary nature of this hypothesis, will find himself rather helped than hindered by it in his search after the true interpretation of the phenomena.

He had failed to achieve a full theory and it was with a feeling of disappointment that he and Katherine left London to spend the summer vacation at Glenlair. But it was good to get back to the easy rhythm of country life, with its concerns over crops, plantations and farm animals, and to the fresh Galloway air. He had not planned to do any serious work on electricity and magnetism during the summer and took no reference books. But his thoughts ran on and an idea began to crystallise.

It seemed a small idea at first. The material making up his little cells had to transmit the twisting forces internally so that each cell would rotate as a body. To do this without dissipating energy the material needed to have a degree of springiness, or elasticity. The idea grew. Could this elasticity be the source of the forces between electric charges which he had so far been unable to explain?

In conductors currents could flow because the electrical particles, the idle wheels, were free to move bodily in response to an electromotive force. Continuous currents could not flow in insulators because the particles were bound to their neighbouring cells. But elastic cells would distort, allowing the particles to move a short distance. The distortion in the cells would cause a restoring force, like a spring. The particles would move until the spring-back force balanced the electromotive force.

So, for example, if a battery were connected by metal wires across two metal plates separated by an insulating material, there would be a small displacement of the electrical particles in the insulator away from one plate and towards the other. This small movement was, in effect, a brief electric current. The movement of electricity would be the same all round the circuit so that in the wires, where particles were not bound to cells, the same brief current would flow. This would result in a surplus of particles on the surface of one plate and a shortage on the surface of the other, so one plate would become positively charged and the other negatively. The distorted cells in the insulating material between the charged metal plates would act like a wound-up spring, exerting a mechanical force of attraction between them. So the elasticity of the cells explained the force between the charged plates.

Following his earlier thinking, James proposed that the elasticity, or spring-stiffness, of the cells would be modified if they were sharing their space with ordinary matter, and that the degree of modification would depend on the type of matter. The higher the electrical susceptibility of the substance, the softer the spring and the greater the electrical displacement for a given electromotive force. For example, filling the space between the metal plates with mica rather than air would soften the spring and increase the amount of charge on the plates for a given voltage across them.

He wrote up the mathematics and everything fitted together. James had shown how the electrical and magnetic forces which we experience could have their seat not in physical objects like magnets and wires but in energy stored in the space between and around the bodies. Electrostatic energy was potential energy, like that of a spring; magnetic energy was rotational, like that in a flywheel, and both could exist in empty space. And these two forms of energy were immutably linked: a change in one was always accompanied by a change in the other. The model demonstrated how they acted together to produce all known electromagnetic phenomena.

One was that there could be electric currents anywhere, even in perfect insulators or in empty space. According to the model, as we have seen, there would be a little twitch of current whenever an electromotive force was first applied to an insulator, because the electrical idle wheels would move slightly before being halted by the spring-back force of their parent cells. In the model all space is filled with cells, so these twitches of current would occur even in empty space.

This new type of current would arise whenever the electric field changed. Its value, at any point, would depend on the rate of change of the electric field at that point. In fact, it was simply the rate of displacement of electricity due to the small movement of the particles. James asserted that it was in every way equivalent to an ordinary current. He gave it the name ‘displacement current’.

The equations governing electrical and magnetic effects had hitherto just dealt with the ordinary conduction current. In James’ new theory, the displacement current had to be added in. When this was done the system of equations was transformed from a motley collection into a beautifully coherent set. This was not immediately evident, however, even to James; he had seen something even more interesting.

All materials that have elasticity transmit waves. James’ all-pervading collection of cells was elastic, so it must be capable of carrying waves. In an insulating material, or in empty space, a twitch in one row of idle wheels would be transmitted via their parent cells to the surrounding rows of idle wheels, then to the rows surrounding them, and so on. Because the cells have inertia they would not transmit the motion instantly but only after a short delay—the twitch would spread out as a ripple. So any change in the electric field would send a wave through all space.

What is more, any twitch in a row of idle wheels would make the neighbouring cells turn a bit and so generate a twitch in the magnetic field along the cells’ axes of spin. All changes in the electric field would therefore be accompanied by corresponding changes in the magnetic field, and vice versa. The waves would transmit changes in both fields; they were electromagnetic waves.

What kind of waves were they? Waves in the sea or along a rope are called ‘transverse’ because the individual particles of sea or rope move at right angles to the direction of the wave. Waves like sound are called ‘longitudinal’ or ‘compression’ waves because the particles move back and forth along the same line as the wave. James’ electromagnetic waves were clearly transverse because the changing electric and magnetic fields were both at right angles to the direction of the wave.

James felt he was on the verge of a great discovery. Light waves were known to be transverse. Could light consist of waves of the kind his model predicted? The speed of light was known with reasonable accuracy from experiments and astronomical observations. It was also well known that the speed of waves in any elastic medium is given by the square root of the ratio of the medium’s elasticity to its density. In the model, the elasticity of the cells controlled the electrostatic (spring-back) forces and their density the magnetic (centrifugal) forces. James’ calculations showed that the spring stiffness of his cells in empty space was not completely determined: it could vary over a factor of three⁶. But if he set it at the lowest value in this range—equivalent to assuming that the cell material was a hypothetically perfect solid—a remarkable result would follow. The wave speed in empty space, or in air, would then be exactly equal to the ratio of the electromagnetic and electrostatic units of electric charge^h. It seemed impossible that such a simple and natural result could be wrong, so James confidently set the elasticity of his cells to fit it.

He now had a very simple formula for the speed of his waves. To check their speed against that of light he first needed to look up the result of an experiment by Wilhelm Weber and his colleague Rudolf Kohlrausch. They had measured the ratio of the electrodynamic and electrostatic units of charge; electrodynamic units are closely related to electromagnetic ones, so James would easily be able to convert their result to give the value for the ratio he needed. He also needed to look up the exact values for the experimentally measured speed of light. But he had brought no reference books; this would have to wait until he got back to London in October. The summer passed in a glow of anticipation.

He had left for Glenlair disappointed at having failed to produce a complete theory of electromagnetism. He returned to London not only with a complete theory but with two entirely new predictions, displacement current and waves. Moreover, the waves might turn out to include light. He eagerly looked up Weber and Kohlrausch’s experimental result and from it worked the speed of his predicted waves. In empty space or air they would travel at 310,740 kilometres per second. Armand-Hippolyte-Louis Fizeau had measured the speed of light in air as 314,850 kilometres per second.

The correspondence seemed too close for coincidence, even allowing for a possible error of a few percent in each of the experimental results. Light must consist of electromagnetic waves. Some of the greatest leaps in science have come when two sets of apparently different phenomena are explained by a single new theory. This was one such leap: at a stroke, he had united the old science of optics with the much newer one of electromagnetism.

James had not expected to extend his paper On Physical Lines of Force beyond Parts 1 and 2 but now he set about writing Part 3, which covered electrostatics, displacement current and waves, and Part 4, which used his model to explain why polarised light waves change their plane of vibration when they pass through a strong magnetic field—an effect discovered experimentally by Faraday. Even for one with the calmest of temperaments it must have been an exhilarating time. The two further parts of the paper were published early in 1862. In Part 3, James announced:

We can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electrical and magnetic phenomena.

The idea of a medium, an ‘aether’ pervading all space, was far from new. Physicists of the day believed an aether of some kind was necessary to transmit light waves, so one might have expected ready acceptance of James’ application of the principle to electricity and magnetism. But there were misgivings; the reaction of his friend Cecil Monro was typical:

The coincidence between the observed velocity of light and your calculated velocity of a transverse vibration in your medium seems a brilliant result. But I must say I think a few such results are needed before you can get people to think that every time an electric current is produced a little file of particles is squeezed along between two rows of wheels.

The difficulty lay deep in the scientific thinking of the time. People believed that all physical phenomena resulted from mechanical action and that all would be clear to us if, and only if, we could discover the true mechanisms. With a century and a half of hindsight we can see the spinning cell model as a crucial bridge between old and new ideas—built from old materials but paving the way for a completely new type of theory, one which admits that we may never understand the detailed workings of nature. One cannot blame James’ contemporaries for seeing things differently. To many of them the model was simply an ingenious but flawed attempt to portray the true mechanism, for which the search would continue.

James himself was not entirely content with the model, but for different reasons. He wanted to free the theory if possible from all speculative assumptions about the actual mechanism by which electromagnetism works. He was to achieve this wish 2 years later by taking an entirely new approach. Scientific historians now look upon his spinning cells paper as one of the most remarkable ever written but hold the one that followed to be greater still.