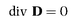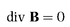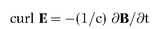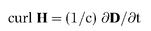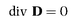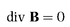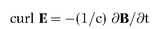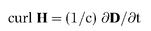NOTES
In the main narrative I have tried as far as possible to tell a simple story. This has meant leaving out much that might be useful or interesting to some readers. The Notes are a second port of call for people who need information on sources or want a little more historical or technical detail on particular points. They also shed some interesting sidelights and I hope that all readers will enjoy browsing through these pages. Anyone who wants to go deeper will find some excellent texts in the bibliography.
Books and articles in the bibliography are generally referred to here only by the name of the author or authors but I have given a fuller description where it seems helpful to do so. Dates of the Maxwell publications described in the main narrative are given here where relevant to the context but readers requiring a full list will find it in the Chronology.
Introduction
The Feynman quotation comes from the book by Feynman, Leighton and Sands listed in the biography.
Chapter 1 A country boy
1 Maxwell was born in Edinburgh on 13 June 1831 in his father’s house at 14 India Street.
2 At the time of Maxwell’s birth, his father’s estate was still referred to as Middlebie. Glenlair was the name his parents gave to their new house and it seems gradually to have come to represent the whole estate. For simplicity I have used the name Glenlair from the start.
3 The title of the ‘Under the sea’ poem is
The Song of the Atlantic Telegraph Company. I have given the second of its four verses; it can be found in full in Campbell and Garnett. The poem is set to the tune of a popular song of the time and it came to Maxwell while on his way by train to Glasgow—perhaps its rhythm was evoked by the clickety-click of train wheels passing over joints in the rails.
4 Much of the information about the Clerk and Kay families comes from David Forfar’s article,
Generations of Genius. Both families were economical with male Christian names: most of the male Clerks were John, James or George and most of the Cays were John or Robert.
5 The Edinburgh Academy was a young school. It was founded in 1824 and had quickly established a fine reputation under its first Rector, the Welshman John Williams, who was still serving during Maxwell’s time at the school.
Chapter 2 Pins and string
1 Aunt Isabella lived at 31 Heriot Row, which adjoins India Street. To the family, the house was always known as ‘Old 31’.
2 Colour plates of many examples of Jemima Blackburn’s work, including several watercolours painted at Glenlair, can be found in
Jemima (Ed. Rob Finley).
3 Maxwell’s school friend P. G. Tait was 1 year behind Maxwell at the Edinburgh Academy, even though they were the same age. Maxwell would, in the normal way, have joined Tait’s class but its teacher, James Cumming, had such a strong reputation that the class was full. Hence, as reported in the narrative, Maxwell had to enrol in the class above, where Lewis Campbell was one of his classmates. Maxwell and Tait both left the Academy in 1847 for Edinburgh University.
4 Both Maxwell and Tait’s classes were taught mathematics by James Gloag, who apparently wielded the tawse even more fiercely than the other masters, but was passionate in championing mathematics within the school and a highly effective teacher. As Forfar and Pritchard report in their article,
The Remarkable Story of Maxwell and Tait, Gloag was ‘beside himself’ when first Tait then Maxwell did so well at Cambridge, and ‘considered the credit entirely his own’!
5 Maxwell’s oval curves paper was given the accurate but unwieldy title
Observations on Circumscribed Figures having a Plurality of Foci, and Radii of Various Proportions. 6 Aunt Jane lived at 6 Great Stuart Street, a few minutes walk from Heriot Row.
7 The title of Maxwell’s poem marking his farewell to school is
Song of the Edinburgh Academician.
Chapter 3 Philosophy
1 As Martin Goldman reports in
The Demon in the Aether, Professors Hamilton and Forbes were implacable enemies. It could hardly be otherwise given Hamilton’s mistrust of all mathematics but geometry. They clashed head on in 1838 over the choice of a new mathematics lecturer; Forbes won this one when his candidate Kelland, a Cambridge expert in algebra and the calculus, got the post.
2 Maxwell’s remark ‘I never try to discourage a man from trying an experiment ... ’ was reported by Arthur Schuster, one of his students at the Cavendish Laboratory.
3 Forbes was also a keen mountaineer and spent a lot of time in the Alps, which is probably where his interest in glaciers began.
4 The quotation ‘If a child has any latent talent for the study of nature ... ’ is from a book review Maxwell wrote for
Nature in 1879. The subject was
Practical Physics, Molecular Physics and Sound by Frederick Guthrie. This is also the review that prompted the poem beginning ‘Worry through duties academic ... ’, which is given Chapter 10.
5 Professor John Wilson, whose classes on moral philosophy Maxwell regarded with disdain, was also known under his pen-name, Christopher North.
6 The type of polarised light Maxwell was experimenting with is plane polarised light. There is another kind—circularly polarised light—in which the wave motion resembles a corkscrew.
General note
The two papers published at this time were On the Theory of Rolling Curves (1848) and On the Equilibrium of Elastic Solids (1850).
Chapter 4 Learning to juggle
1 Maxwell’s views on ‘the dark sciences’ were expressed in a letter to his friend R. B. Litchfield.
2 I have abridged the poem about John Alexander Frere, giving the first and the last two verses of seven. The full version can be found in Campbell and Garnett.
3 Charles Babbage’s main collaborators in bringing Cambridge University mathematics up to date in the early 1800s were George Peacock, Edward Bromhead and John Herschel, son of the renowned astronomer William Herschel. The breakthrough came in 1817 when Peacock, aged 25, was appointed examiner for the Mathematical Tripos. He set questions using the continental notation for the calculus, which was much more versatile than the traditional Newtonian notation and quickly became the standard form.
4 William Hopkins was the most successful Cambridge tutor of the time. In a period of about 20 years he coached over 200 wranglers, 17 of whom were senior wranglers. And he managed to drill his students without stifling their creativity. Among their number were George Gabriel Stokes, William Thomson, P. G. Tait, E. J. Routh and Arthur Cayley, who invented the theory of matrices and the geometry of n dimensions. Hugh Blackburn, who married Maxwell’s artist cousin Jemima, was also a pupil of Hopkins.
5 The friend whose family Maxwell was visiting when he fell ill was G. W. H. Tayler, afterwards Vicar of Holy Trinity, Carlisle. The quotation ‘Let each member of the family be allowed ... ’ comes from a letter to R. B. Litchfield.
Chapter 5 Blue and yellow make pink
1 Helmholtz was ennobled and added the ‘von’ to his name in 1882. As this is after the time of our story, he appears throughout the narrative as plain Hermann.
2 In describing the colour-mixing experiments of Forbes and Maxwell, I have for simplicity omitted the point that white and grey are, technically speaking, the same colour; they differ only in brightness. White may be thought of as a very bright grey. Progressively reducing the brightness gives light grey, dark grey and, ultimately, black. To show that a particular combination of colours on the outer part of the disc gave white, one needed to match them against a mixture of black and white on the inner part, so that the whole disc appeared the same shade of grey.
3 Thomas Young suggested a triangle for representing colour vision about 50 years before Maxwell. But the idea was neglected or rejected by many experts before Maxwell took it up. Forbes had tried using a triangle but could not get it to work because he persisted with red, blue and yellow as primaries. It was Maxwell who demonstrated the validity of the colour triangle and gave it proper mathematical expression.
4 Maxwell’s colour triangle is shown here in the form which I think will be clearest to non-specialist readers. An alternative way is to represent a colour as the weighted sum of three vectors formed by joining any point outside the triangle to each vertex, the weights being the proportional amounts of each primary which make up the colour. The position of the tip of the resultant vector gives the composition of the colour. In this method, the triangle need not be equilateral.
5 The paper on colour vision which Maxwell sent to the Royal Society of Edinburgh in 1855 was
Experiments on Colour, as Perceived by the Eye.
6 Helmholtz and Maxwell independently discovered the fact that mixing lights is additive, whereas mixing pigments is subtractive. Helmholtz was first to publish but at this stage he had not accepted the three-colour theory; in fact, he explicitly rejects it in his paper. Everitt, in
Maxwell’s Scientific Papers, Applied Optics, Vol. 6, No. 4 (1967), gives the opinion that ‘Maxwell and Forbes deserve more credit, and Helmholtz and Grassmann less credit, than is usually given them for the revival of Young’s three-component theory of colour vision’.
7 Strictly speaking, there are no such things as magnetic poles, only states of polarisation at individual points. Some physics texts avoid poles altogether. But we are so accustomed to thinking of the earth’s north and south poles that it would seem perverse to take the purist’s line here, especially as today’s electrical engineers use poles all the time as a convenient device for thinking and calculation. The idea of using (fictitious) poles in this way was first proposed by the British astronomer John Michell in 1750. It has the advantage of making the equations laws of static magnetism identical to those of electrostatics.
8 Newton’s letter, ‘That gravity should be innate, inherent, and essential to matter ... ’, was written to Richard Bentley. The widespread distortion of Newton’s views seems to have come from two sources. The first was his own famous statement, ‘Hypotheses non fingo’—‘I do not frame hypotheses’, which was open to misunderstanding. The second was his disciple and evangelist Roger Cotes, who wrote in a preface to Newton’s
Principia that ‘action at a distance is one of the primary properties of matter’.
9 The quotation ‘Faraday ... shows us his unsuccessful as well as his successful experiments ... ’ is from Maxwell’s
Treatise on Electricity and Magnetism.
10 Maxwell’s tubes of electric flux differ in one way from those of magnetic flux. The tubes of electric flux always terminate at each end in a charged body. An iron magnet produces tubes of magnetic flux which appear to terminate at its north and south external surfaces but the tubes actually extend into the body of the magnet and join up, forming continuous loops. The difference arises because positive and negative electrical charges can exist separately, whereas magnetic poles come only in north-south pairs, like the heads and tails sides of a coin. An iron magnet can be thought of as many tiny magnets joined end to end; in fact the micro-magnets are the atoms themselves and their magnetism is generated by the orbital motion and spin of their electrons. This explanation that magnetism in permanent magnets is due to tiny circulating electric charges was a brilliant conjecture by Ampère in 1823, which Maxwell and others adopted as a working hypothesis and was borne out by twentieth century findings on atomic structure.
11 The geometrical derivation of the inverse square law of electrical and magnetic forces from Maxwell’s analogy can be visualised by imagining fluid flowing uniformly in all directions from a point source. As the fluid is incompressible, the amount of it emerging per unit time from any sphere centred on the point will be the same, whatever the size of the sphere. It follows that the fluid moves outwards at a rate inversely proportional to the square of its distance from the source, and, by analogy, that electrical and magnetic forces follow the same law.
12 George Green probably died from a lung condition brought on by years of inhaling flour dust in his mill, although the cause was recorded as influenza. Less is known about Green than about any other great British mathematician or scientist, but enthusiasts have recently had his mill in Nottingham restored as a working museum and a biography by Mary Cannell was published in 1993. It is listed in the bibliography.
13 George Green’s now famous
Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism made no impact when published by Green at his own expense in Nottingham in 1828. William Thomson arranged for it to be re-published in the Berlin-based
Journal für die Reine und Angewandte Mathematik, commonly called
Crelle’s Journal, after its editor. Crelle published it, in English, in three parts in 1850, 1852 and 1854.
14 Stokes’ theorem, a companion to Green’s theorem in current texts on vector analysis, was set by Stokes as a Smith’s Prize problem in Maxwell’s year but he may not be its originator. When Maxwell wanted to include it, with proper billing, in his
Treatise years later, neither Stokes nor anyone else could remember who had thought of it first. Historians subsequently found it in a letter dated 1850 from Thomson to Stokes, so perhaps it should rightfully be called Thomson’s, or Kelvin’s, theorem.
15 The quantity which Maxwell defined mathematically and identified with Faraday’s electrotonic state is now usually called by the name he later gave it, the ‘vector potential’. Its rate of spatial variation at a point in space (in mathematical terms, its ‘curl’) gives the magnetic flux density at the point and any change in it with time gives rise to an electromotive force. The latter characteristic gave Maxwell a starting point for his thoughts on how to deal with changing fields.
16 Maxwell published
On Faraday’s Lines of Force in two parts. The first dealt with separate static electrical and magnetic fields. The second, which was more mathematical, dealt with the way steady electric currents and magnetism were related, and included the expression for Faraday’s electrotonic state.
17 Faraday’s letter to Maxwell was dated 25 March 1857. The full text can be found in Martin Goldman’s biography of Maxwell,
The Demon in the Aether.
18 After a Ray Club meeting, at which his friend Pomeroy had given a talk on the position of the British nation in India, Maxwell wrote to his father. The letter contains one of Maxwell’s very few recorded comments on a political subject:
... We seem to be in the position of having undertaken the management of India at the most critical period, when all the old institutions and religions must break up, and yet it is by no means plain how new civilisation and self-government among people so different from us is to be introduced. One thing is clear, that if we neglect them, or turn them adrift again, or simply make money of them, then we must look to Spain and the Americans for our examples of wicked management and consequent ruin.
Maxwell felt sure that his friend was exactly the type of man to help bring enlightened government to India. Pomeroy joined the British Civil Service there the following year but, as reported in Chapter 6, died bravely in tragic circumstances during the Indian Mutiny.
19 We can get some idea of the nature and intensity of the emotional attachment between Lizzie and Maxwell from an episode that Lizzie’s daughter described to Francis Everitt. Apparently, Lizzie fell into a depression when Maxwell died and her husband was so furious that he seized and burned about 60 letters which Maxwell had written to her long ago, full of discussions of his philosophical opinions. Everitt has drawn my attention to a wry remark by Sydney Smith that takes on an unusual poignancy here: ‘In Scotland they even make love metaphysically’.
20 The letter containing the quoted passage, ‘At present I confine myself to lucky Nightingale’s line of business ... ’ was to Cecil Monro. Campbell and Garnett give a fuller version.
21 The rival candidate for the Aberdeen post who asked for, and got, a reference from Maxwell was William Swan, later Professor of Natural Philosophy at St Andrews.
General notes
The history of the discovery of the principles of colour vision, from Newton to Maxwell and his contemporaries, is interesting but rather confusing. Helpful accounts which assess Maxwell’s work in this context are given by Everitt (both entries in the bibliography) and by Harman.
Maxwell designed a number of useful devices which I have not described in this book, for fear of producing a catalogue rather than a story. One was the platometer referred to in his letter to Monro. Another was a general purpose educational aid on optical instruments; a third was a stereoscope which produced a real image and was easier to use than the more usual virtual image type.
Chapter 6 Saturn and statistics
1 The passage ‘It is in personal union with my friends ... ’ comes from a long letter to R. B. Litchfield. Campbell and Garnett give the full text.
2 Maxwell’s Saturn paper was called
On the Stability of the Motion of Saturn’s Rings. 3 I have quoted the last four of eight verses of To K. M. D. and the first and last of four verses of Will you come along with me? Campbell and Garnett give the poems in full.
4 James’ and Katherine’s observations to determine the proportions in which primary colours have to be mixed to match pure spectral colours were reported in
On the Theory of Compound Colours, and the Relations of the Colours of the Spectrum, which he sent to the Royal Society in 1860. They were using the second version of the colour box. The one used later in London and at Glenlair was the third and final version.
5 The quotation ‘If you travel at 17 miles per minute ... ’ is from a letter to P. G. Tait. The letter is in the Cambridge University Archive.
6 For simplicity, I have expressed the second statement in Maxwell’s derivation of the distribution of molecular velocities as though the velocity components x, y and z and speed s took discrete values. As they can, in fact, vary continuously, a formal version of the statement would refer not to numbers of molecules with particular values of x, y, z and s, but to numbers with values within the infinitesimal ranges x to x + dx, y to y + dy, z to z + dz and s to s + ds.
7 The account of Adolphe Quetelet’s work, which Maxwell recalled having read about 9 years earlier, was by John Herschel. It had been published in the
Edinburgh Review in 1850. We are greatly in the debt of Francis Everitt, who established the important connection with Herschel and Quetelet and reported it in James
Clerk Maxwell, Physicist and Natural Philosopher, although Everitt has told me that credit is also due to Charles Gillispie, Stephen Brush and Ted Porter. The method of least squares was originally derived, independently, by Karl Friedrich Gauss and Adrien-Marie Legendre.
8 Maxwell’s 1860 paper on gas theory was called
Illustrations of the Dynamical Theory of Gases.
General note
Much of the information about Maxwell’s time in Aberdeen comes from the articles by R. V. Jones and John S. Reid. I am particularly grateful to John Reid for the information about Maxwell’s work in Marischal College and to R. V. Jones for the story about the Music Hall dividends.
Chapter 7 Spinning cells
1 The Maxwells lived at 8 Palace Gardens, now number 16, a newly built four storey house rented from the Church Commissioners. It is close to Kensington Gardens, which adjoin Hyde Park.
2 The Playfair cipher was invented by Charles Wheatstone but named after Lyon Playfair, the chemistry professor who took up politics and was made a baron. Playfair promoted the British government’s use of Wheatstone’s coding system in the mid-nineteenth century. It was easy to use but more secure than earlier systems because the letters in the message to be sent were coded in pairs. When code-breakers became more expert it had to be replaced by more complex ciphers.
3 The lines beginning ‘There are powers and thoughts within us ...’ are from
Recollections of Dreamland, written in 1856 at Cambridge. The full poem can be found in Campbell and Garnett.
4 The quotation ‘I believe there is a department of the mind conducted independently of consciousness ... ’ is from a letter to R. B. Litchfield, written in 1857.
5 See Note 7, Chapter 5, about magnetic poles.
6 Maxwell’s calculations of the spring stiffness of the cells involved two types of elasticity: resistance to twisting and resistance to compression. It was the ratio between the two which could vary over a factor of 3.
General notes
For simplicity, the main narrative does not describe fully the way that the characteristics of Maxwell’s spinning cell model developed in the course of the work. He tried to keep the model as general as possible, introducing specific features at each stage as needed. In Part 1 of On Physical Lines of Force he described the rotating elements in his model as ‘molecular vortices’ in a fluid medium. By Part 3 they had become quasi-solid ‘cells’ with elastic properties and had taken on spherical form. His mathematical analysis was extraordinarily imaginative, even by Maxwell standards. To investigate the stresses in the medium he used portions which were large enough for the action of the tiny cells within to be treated in aggregate but small enough to be themselves treated as infinitesimal elements in the setting up of differential equations.
Despite the novelty of its ideas, the general thrust of On Physical Lines of Force was clear, thanks largely to Maxwell’s consummate prose. But some details were harder to interpret. In Part 3, for example, he seemed to make an error in sign in one equation and then to correct for it in another by changing the meaning of one of his symbols from the force exerted by the particles on the cells to the equal and opposite force exerted by the cells on the particles. The matter is still debated by scholars. Daniel M. Siegel makes an illuminating contribution in his book Innovation in Maxwell’s Electromagnetic Theory.
Chapter 8 The beautiful equations
1 Maxwell reported the results of his home experiment on gas viscosity in
On the Viscosity or Internal Friction of Air and Other Gases, published in 1866.
2 Faraday was not quite the first to discover that electricity is generated by changing the amount of magnetic flux passing through a conducting loop. Joseph Henry, then a teacher in Albany, New York State, doing research in his spare time, made the same discovery a few months earlier but did not publish until after hearing of Faraday’s results. As the main narrative reports, Henry made the world’s first powerful electromagnet and invented the electromagnetic relay. He could have made a fortune from patents on such devices but, like Faraday, had strong religious convictions and spurned wealth. During 32 years as the first Director of the Smithsonian Institution he refused any increase in salary.
3 The results of the experiment to produce a standard of resistance were included in a report to the British Association for the Advancement of Science’s Committee on Electrical Standards in 1863. Maxwell’s and Jenkin’s paper recommending a complete system of units, in which Maxwell introduced the dimensional notation, also appeared in this report, and was reprinted, with revisions, in the
Philosphical Magazine in 1865.
4 Einstein’s use of the tensor calculus, without which he could not have formulated the general theory of relativity, came about through his friend Marcel Grossmann. Grossmann, who was a pure mathematician, spotted the relevance of the earlier work of Levi-Civita and Ricci, and introduced Einstein to it. Levi-Civita and Ricci had developed their methods from the work of Riemann and Christoffel, who, in turn, had built on the ideas of Karl Friedrich Gauss.
5 As the narrative reports, Maxwell made use of Lagrange’s method of setting up equations for dynamical systems in his paper
A Dynamical Theory of the Electromagnetic Field. An alternative formulation of Lagrange’s method had been proposed by the Irish mathematician William Rowan Hamilton. Maxwell later used both forms but came to prefer Hamilton’s because it more clearly demonstrated the relationship between the two basic quantities of a dynamical system—its energy and momentum. As usual, his intuition was right; it is the Hamiltonian form that has become standard in many branches of modern physics.
6 When the equations are written in general form, rather than for the special case of empty space, they include extra terms for charge density and current density and for the electrical and magnetic characteristics of the material present. Even so, they are astonishingly simple.
7 For compactness, the equations of the electromagnetic field are shown in modern vector notation. This substitution is legitimate because Maxwell himself later began the process of modernisation. Even in modern guise the equations vary slightly according to the system of units used. I have chosen so-called Gaussian units, because they best illustrate the role of the constant c (the speed of light) as a kind of gear ratio between the electric and magnetic fields. In the Gaussian system, E is expressed in electrostatic units and H in electromagnetic units, so that c, or 1/c, serves as a conversion rate between the two. When, as is more usual, electromagnetic units are used throughout, 1/c disappears from
equation (3), and 1/c
2 replaces 1/c in
equation (4). The Gaussian system of units was the first internationally accepted system of electrical units, adopted in 1881 at the Paris meeting of the Electrical Congress. As reported in the main narrative, Maxwell, not Gauss, was the chief contributor to this system of units.
To avoid burdening the non-specialist reader with technicalities, I have used as few symbols as possible. It is usual to include extra vectors B and D. The equations then become:
(1)
(2)
D is the density of the electric flux produced by the electric field intensity E. B is the density of the magnetic flux produced by the magnetic field intensity H. But in Gaussian units, in the special case of empty space, D = E and B = H, allowing the equations to be written using E and H only.
8 E and H are, strictly speaking, not forces but rather the
intensities of the electric and magnetic fields at our arbitrary point. They may, however, be thought of as forces waiting to act—specifically, the forces which
would be exerted on, respectively, a unit charge or a unit magnetic pole if either were situated at the point.
9 In the
Dynamical Theory paper, Maxwell expressed his results in rather more expansive form than that used here. It was more important to try to help people understand the new ideas than to put everything in a compact package. He gave eight equations of the electric and magnetic field, remarking that they might readily be condensed but that ‘to eliminate a quantity which expresses a useful idea would be a loss rather than a gain at this stage of our enquiry’. One of the ideas thus expressed was Faraday’s electrotonic state, which in Maxwell’s scheme became the electromagnetic momentum of the field. He did condense the results in some later presentations.
The paper contains an inconsistency in algebraic signs which has been much discussed by scholars. It is similar to the one in his Physical Lines paper and arises in the same context. Maxwell was wrestling with a chicken-and-egg question—does the electric charge cause the electric field or does the field cause the charge?—and seems to have taken different standpoints in different parts of the paper. Thomas K. Simpson gives a fuller account in his guided study, Maxwell on the Electromagnetic Field. Maxwell generally favoured primacy of the field, as Faraday had done, but some followers preferred to regard charge as the fundamental entity and their case was strengthened when the electron was discovered in 1897. Eventually the two viewpoints were reconciled in the formulation which is commonly taught today, a hybrid version which accords fundamental status to both field and charge; Daniel M. Siegel describes this process in Innovation in Maxwell’s Electromagnetic Theory.
There is an interesting short note in the Dynamical Theory paper about gravitation. It was natural for Maxwell to see whether his idea that energy existed in empty space could somehow explain the gravitational field that caused attraction between bodies. He soon found that it could not, and presumably included the note to save others a trip down a blind alley. Maxwell, who loved to take a geometrical approach to problems wherever possible, would surely have delighted in Einstein’s explanation that gravity is simply a manifestation of the geometry of space-time.
General note
Many years after Maxwell left King’s College, a rumour got about that he had been asked to go because he could not keep order in his classes. It came from an apparently authoritative source, the 1928 centenary history of the College, but was later shown by Professor Cyril Domb and colleagues to have no foundation whatever. Astonishingly, the writer of the ‘history’ had reported and elaborated a reminiscence of 60 years before by someone who never knew Maxwell but thought he remembered hearing the story from someone else, who, it turned out, never knew Maxwell either and was never at King’s College. Domb and his colleagues, who included the College archivist, found that almost every ‘fact’ reported was wrong. It seems that the writer had not even looked up the College’s own records to check his sources. Domb gives a detailed account in his article listed in the bibliography.
Chapter 9 The Laird at home
1 The quotations beginning ‘A man of middle height ... ’ and ‘He had a strong sense of humour ... ’ are extracted from longer quotations in Campbell and Garnett. The author of the remarks is not named.
2 Maxwell reported the results of his experiment to measure the ratio of the electromagnetic and electrostatic units of charge in
Method of Making a Direct Comparison of Electrostatic with Electromagnetic Force with a Note on the Electromagnetic Theory of Light, published in 1868. As the title implies, this included the note on his electromagnetic theory, in which he criticised the rival theories of Weber and Riemann. Later, in his
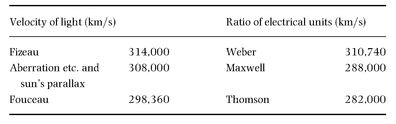
Treatise on Electricity and Magnetism, Maxwell compared his own and others’ experimental results for the ratio of electrical units with the best direct measurements which had been made of the velocity of light in air or through space. His table reads:
Today’s accepted value of the speed of light in a vacuum is 299,792.5 km/s.
3 The Theory of Heat, published in 1871, presented Maxwell’s demon to the public, but the idea had already been talked and written about privately by Maxwell, Tait and Thomson. Maxwell’s first recorded description of the demon is in a letter of 1867 to Tait.
4 Maxwell’s demon facilitated a perpetual motion machine of the
second kind. Whereas a machine of the first kind uses no energy, one of the second kind draws energy from neighbouring matter and will go on working until the temperature of that matter falls to absolute zero (—273° Celsius).
5 The letter in which Maxwell explains that most people’s eyes have the yellow spot was to Cecil Monro. Campbell and Garnett give the full text of the letter.
6 The letter saying ‘I have paid so little attention to the political sympathies of scientific men ... ’ was to W. R. Grove, who was vice-President of the Royal Institution. So far as he was political at all, Maxwell was a Conservative. The Conservatives lost the 1868 election and, as the narrative reports, by the time the Principalship of St Andrews was awarded, Gladstone’s Liberal Party was in power.
7 The story of St Andrews turning down Joule is reported by R. V. Jones.
Chapter 10 The Cavendish
1 The quotation ‘The human mind is seldom satisfied, and is certainly never exercising its highest functions, when it is doing the work of a calculating machine ... ’ is from Maxwell’s presidential address to Section A of the British Association for the Advancement of Science in 1870.
2 Isaac Todhunter’s reaction to being invited to witness conical refraction is reported by Arthur Schuster, one of Maxwell’s students, in
The Progress of Physics.
3 The author of the comment comparing Henry Cavendish’s frequency of speech with that of Trappist monks was Henry Brougham, afterwards Lord Brougham, who, among other accomplishments, was instrumental in establishing University College, London.
4 The American visitor who took umbrage at being invited to use his body as a current meter was Samuel Pierpoint Langley, who invented the bolometer, a device for measuring radiant energy. C. G. Knott reports the incident in
The Life and Scientific Work of Peter Guthrie Tait.
5 Maxwell’s edition of Henry Cavendish’s work was published in 1879 under the title
Electrical Writings of the Hon. Henry Cavendish.
6 Maxwell’s critical review of Guthrie’s book
Practical Physics, Molecular Physics and Sound was published by
Nature in 1879. This review contained the passage ‘If a child has any latent talent for the study of nature ... ’, which is quoted in Chapter 3 in connection with James Forbes. The poem which begins ‘Worry through duties academic ... ’ has not, as far as I know, been included in any collection of Maxwell’s poems. Naturally so, as he never acknowledged authorship—to have done so would, of course, have destroyed the joke. I am much indebted to Martin Goldman, who included the poem in his biography of Maxwell,
The Demon in the Aether.
7 The quotation ‘When the state of things is such that an infinitely small variation of the present state will alter ... ’ is from an essay Maxwell wrote in 1873 for his essay group at Cambridge. The title is
Does the progress of Physical Science tend to give any advantage to the opinion of Necessity (or Determinism) over that of the contingency of events and the Freedom of the Will? No doubt he would have shortened this for a wider audience, perhaps to
Science and Free Will.
8 I have given the first and last of four verses of the poem
To the Committee of the Cayley Portrait Fund. The full version can be found in Campbell and Garnett.
9 Maxwell’s
Treatise on Electricity and Magnetism has inspired many creative physicists and engineers. One of its most dedicated apostles was Oliver Heaviside, the maverick English virtuoso, who transformed telecommunications in 1887 by showing mathematically how to make a distortion-free telephone cable, and made other important innovations we now take for granted. Paul Nahin’s biography is a treasure-house of information about Heaviside and his contemporaries and, concomitantly, about Maxwell’s influence on their work.
10 For a while it was thought that Maxwell’s radiation pressure was the main cause of comets’ tails pointing away from the sun. But in 1958, the American physicist Eugene Norman Parker demonstrated the existence of a ‘solar wind’ of particles thrown out by the sun and this is now believed to be the main influence on the behaviour of comets’ tails. Nevertheless, radiation pressure plays a part.
11 The formula which Maxwell, Boltzmann and others used for the ratio of the specific heat of a gas at constant pressure to that at constant volume was:
where γ is the ratio of the specific heats and n is the number of independent modes of motion of the molecules into which energy can be transferred from molecule to molecule by jostling. The formula is based on the equipartition principle, by which kinetic energy becomes evenly spread over all the n modes of motion. The 2 on the top of the fraction represents the extra energy required for expansion when a gas is heated at constant pressure. (The value 2 derives from the work of the German physicist J. R. Mayer.) In his first paper on gas theory, Maxwell had assumed that molecules behaved like rough-surfaced billiard balls. When they collided they could transfer linear energy in three independent (x, y, z) directions and, being rough-surfaced, could also transfer their rotational energy, again in three independent directions. So Maxwell’s first value for γ was (6 + 2)/6 = 4/3 = 1.333, whereas experiments gave 1.408. When n was later increased to take into account vibrational modes of molecular motion the theoretical value of γ, already too low, decreased and the discrepancy grew. Things got even worse when further results from spectroscopy suggested that a gas could have many different modes of vibrational motion.
12 The paucity of information about Katherine and about the domestic life she shared with James is a source of much frustration for anyone with an interest in Maxwell. He wrote to her every day when they were apart and it is a pity that Lewis Campbell did not include more of the letters in his biography. He gave us a few letters, some matter-of-fact, some pious, but held back a much larger number of light-hearted ones, which were since lost. To compound our frustration, he tells us what we are missing:
... letters full of ‘enfantillages’, as in his boyish endeavours to amuse his father, telling her of everything, however minute, which, if she had seen it, would have detained her eye, small social phenomena, grotesque or graceful (including the dress of lady friends), together with the lighter aspects of the examinations; College customs, such as the ‘grace-cup’; his dealings with his co-examiners, and marks of honour to himself which he knew would please her, though they were indifferent to him.
How much better informed we might have been. But it would be churlish to complain: thanks to Campbell we have a substantial, if not quite complete, picture of Maxwell the man. As for Katherine, there is little to go on beyond what appears in the main narrative. Maxwell’s female relations seem, on the whole, to have disliked her, as do his colleagues and their wives, but some of their comments can, as we have seen, be taken with more than a pinch of salt.
General note
When Maxwell died, the University once again invited William Thomson to accept the Cavendish professorship, and again he decided to stay in Glasgow. The post went to Lord Rayleigh, a 37 year-old Essex gentleman who had built a laboratory next to his manor house. A fine and underrated physicist, he is now remembered chiefly for explaining the scattering of light that makes the sky blue and for discovering argon, jointly with William Ramsay. Nine years earlier, as plain J. W. Strutt, he had been foremost among the young Cambridge dons who entreated Maxwell to return to Cambridge. Rayleigh consolidated the Cavendish’s good start before retiring to his country laboratory in 1884. As proprietor of Lord Rayleigh’s dairies he had developed an acute business acumen which he brought to bear by setting the Cavendish’s finances on a more secure base, starting an apparatus fund to which he contributed generously himself. He also introduced systematic training in laboratory techniques, moving on from Maxwell’s laisser faire approach. The next two professors between them ran the Cavendish until 1939. They were J. J. Thomson, who discovered the electron, and Ernest Rutherford, who discovered the basic structure of the atom.
Chapter 11 Last days
1 William Garnett, Maxwell’s demonstrator at the Cavendish, who visited him at Glenlair in September 1879, collaborated with Lewis Campbell to write
The Life of James Clerk Maxwell. While Campbell wrote the main biographical narrative, Garnett acted as researcher and compiler of material and wrote a 110 page section on Maxwell’s contributions to science. Garnett’s report is, not surprisingly, hopelessly inadequate from our perspective—nobody at the time had a proper grasp of the immense significance of Maxwell’s work. The juxtaposition of extracts from Maxwell’s papers with Garnett’s own prose provides an interesting contrast: Maxwell dances where Garnett plods. But Garnett’s admiration, and indeed love, for the great man shine through and the account has charm as well as historical interest.
2 The full text of Dr Butler’s address at Maxwell’s memorial service is given in Campbell and Garnett. Butler later became Master of Trinity College, where he and Maxwell had met as students.
Chapter 12 Maxwell’s legacy
1 Some readers may welcome a little more background to Maxwell’s part in the genesis of Einstein’s
Special Theory of Relativity.
Michelson and Morley carried out their famous experiment in Cleveland, Ohio, in 1887. They wanted to detect and measure the ‘aether drift’—the motion of the earth through the substance called the aether which was thought to permeate all space and to be the medium by which light waves were transmitted. Maxwell himself had worked out the great accuracy required to do this and doubted whether it could be achieved in any laboratory. He had set out his reasons in a letter to David Peck Todd at the Nautical Almanac Office in Washington, together with a suggestion for an alternative method using observations on Jupiter’s moons. When Maxwell died a few months later Todd had the letter published. Nothing much came of the Jupiter scheme but when Michelson saw Maxwell’s letter he took the great man’s doubts about earthbound methods as a challenge and over the next 8 years developed his interferometer—an instrument which used the tiny wavelengths of light itself as measurement units and so made possible a degree of precision formerly unthought of. With the help of his colleague Morley, Michelson then set out to measure the difference in the speed of the two parts of a light beam split at right angles. This difference would determine the aether drift.
The instrument was amply accurate for its purpose but, to the experimenters’ consternation, the speed of light in both directions was identical. Repeated attempts gave the same result. This was a great disappointment and at first the experiment was seen by the scientific community as no more than another failed attempt to detect the aether drift. Michelson himself seldom mentioned his result and never recognised its immense significance. But others began to see that here was some new and important evidence and put forward ideas to account for it. The Irishman George Francis Fitzgerald proposed that all objects moving through the aether contract along the direction of movement just sufficiently to make the aether drift undetectable, and produced a formula for the contraction. His formula implied that any object which approached the speed of light would appear to be squashed flat. Fitzgerald’s associates thought he had gone mad, but, in Holland, Hendrik Antoon Lorentz independently came up with the same formula and a complementary one, by which movement through the aether makes clocks slow down. Astonishingly, these modifications to space and time seemed to be intrinsic to Maxwell’s equations of the electromagnetic field: they worked perfectly under Lorentz’s transformation. But Newton’s laws of motion, which had been the bedrock of all calculations on moving bodies, did not.
Here was a crisis; leading theorists searched for an explanation. Some, including Lorentz and the great French mathematician Henri Poincaré, came close but it was Albert Einstein who solved the puzzle with a masterly shaft of insight. Despite what our senses tell us, there are no absolute measures of space or time; all are relative. The only absolute quantity is the speed of light, which is the same for all observers in unaccelerated motion, no matter how fast or in what direction they are moving. And the speed of light is completely determined by Maxwell’s theory: his equations are the very core of special relativity, providing the link between space and time.
What of the aether? At first, Einstein, like everyone else, had thought that an aether of some kind was necessary for the transmission of light; but it would need to operate in absolute space and time, and when he demolished those there was no longer a home, or need, for the aether; in their new guise, space and time had themselves taken on the role.
Michelson and Morley’s experiment is now recognised as one of the most important in the history of physics. It handsomely bears out Maxwell’s philosophy: ‘I never try to dissuade a man from trying an experiment; if he does not find what he wants he may find out something else’.
2 The prediction from (classical) theory that matter should radiate away all its kinetic energy came to be known as ‘the ultraviolet catastrophe’, as the problem lay at the highfrequency end of the radiation spectrum, where the ‘classical’ formula for the energy of radiation diverged. Readers with mathematical training will find a fascinating account of the genesis of quantum theory, and much more, in Malcolm Longair’s superb book
Theoretical Concepts in Physics.
3 Lewis Campbell paints a moving pen-picture of his lifelong friend in the closing chapter of Campbell and Garnett. It is here that he writes: ‘The leading note of Maxwell’s character is a grand simplicity’.