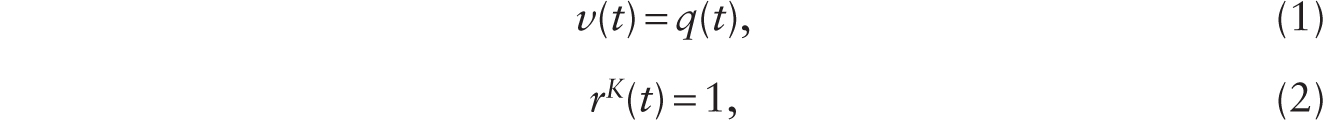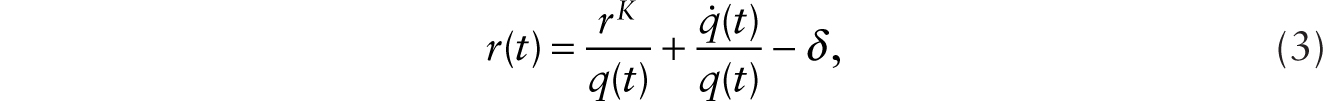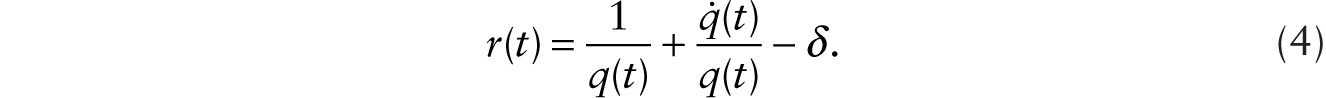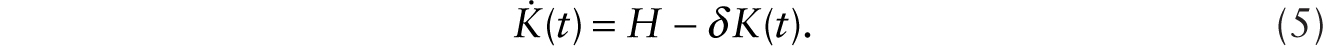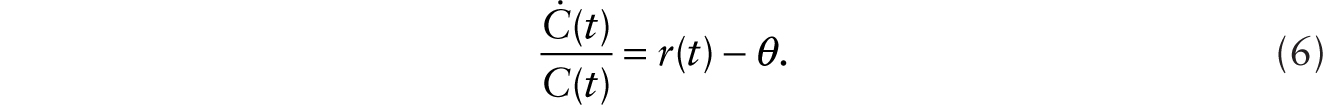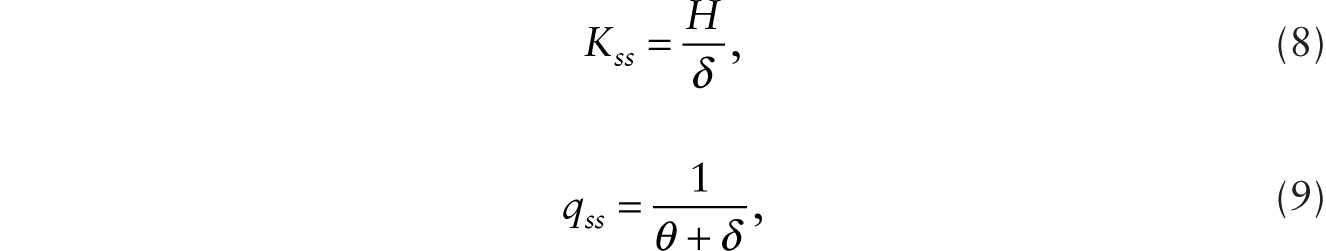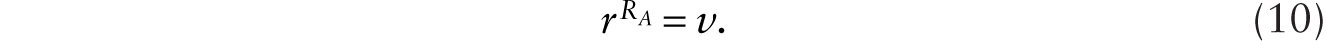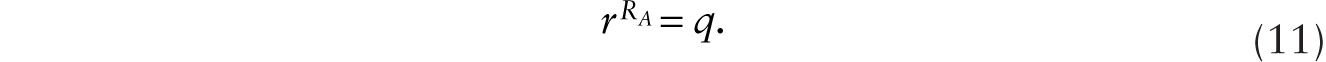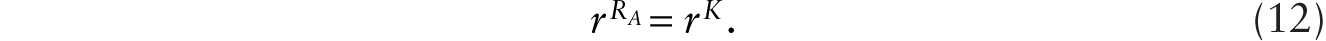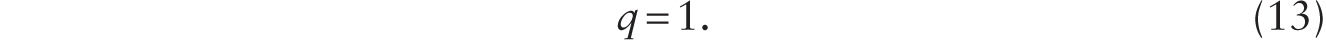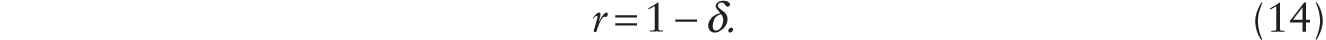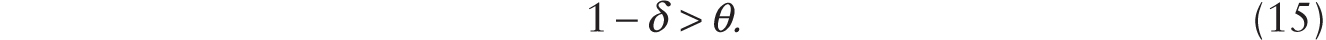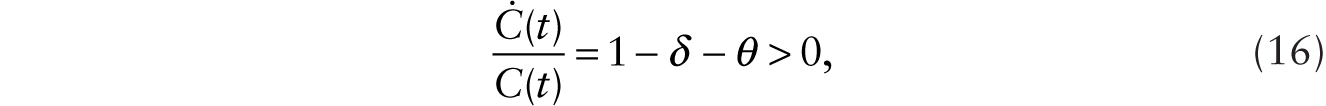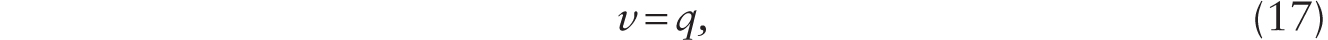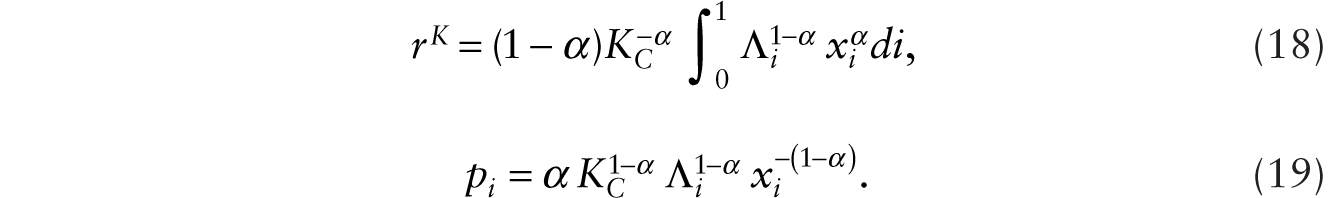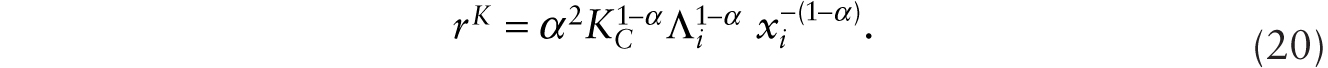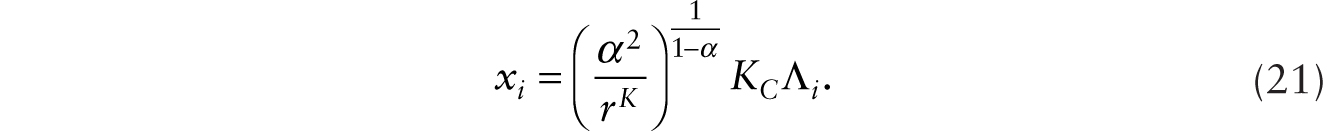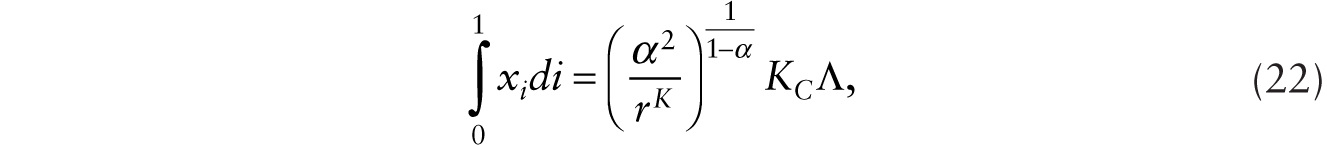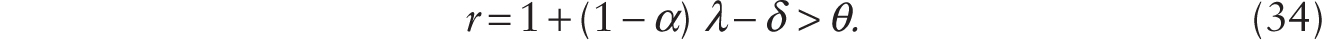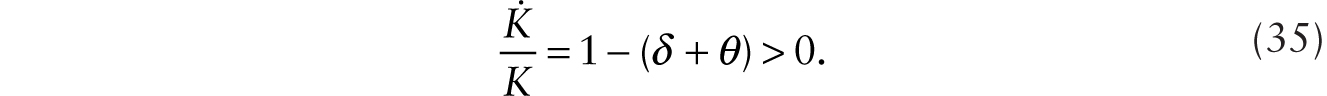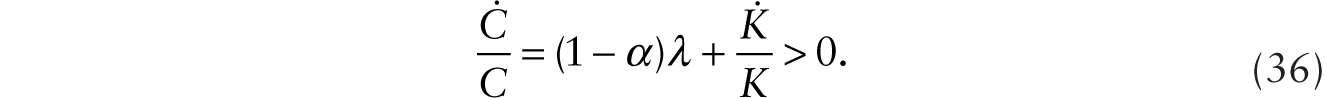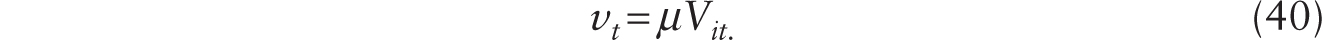10

Additive Robots, Relative Prices, and Indigenous Innovation

Hian Teck Hoon

ABSTRACT    We formalize the idea in a two-sector model that when an influx of additive robots in the capital goods sector causes the relative price of the capital good to fall, economic incentives are created to make indigenous innovation in the consumption goods sector more profitable. This causes some workers in the economy to shift from participating in production to participating in innovative activity. Consequently, the new wage path must ultimately be rising, as long as innovation in the consumption goods sector continues undiminished, exerting its upward pull on wage rates.

Introduction

In this chapter, we study a channel through which the adoption of additive robots leads to wage growth by stimulating innovation in the consumption goods sector as the adoption of additive robots in the capital goods sector reduces the relative price of the capital good. First, we set up a two-sector model where there is no innovation and zero technological progress. The model has the characteristic that there is a sector that uses only human labor to produce a capital good before the arrival of robots. The capital good is used to produce a pure consumption good. With zero technological progress and no innovation, the model exhibits a stationary equilibrium where the wage rate, consumption per capita, relative price of the capital good, and stock of conventional machines are all constant. With the arrival of additive robots, we obtain the result that capital accumulation is stimulated, consumption per capita grows, and the real wage declines to a permanently lower level as the relative price of the capital good permanently declines to a lower level.

Next, we study a two-sector model where there is indigenous innovation, which occurs endogenously within the model. We model innovation by quality improvement of intermediate inputs used in the production of the consumption good. The model has the feature that the consumption goods sector produces a product using conventional machines and a continuum of intermediate inputs supplied by imperfectly competitive firms, which also use conventional machines as primary inputs. In reduced form, such a model is identical to the first model except for the fact that the rate of innovation is now endogenously determined. We derive two main results: (1) a drop in the relative price of the capital good stimulates indigenous innovation, which acts to boost real wages; and (2) the arrival of additive robots spurs investment in conventional machines, which also stimulates indigenous innovation. Thus, once we depart from the first two-sector model to allow for indigenous innovation that raises the productivity of the consumption goods sector, the arrival of additive robots is good for wage growth.

The chapter is organized as follows. In Section 1, we set up the two-sector model with zero technological progress and no innovation to study the effects of introducing additive robots. In Section 2, we develop the two-sector model with indigenous innovation and study the effects of introducing additive robots. Section 3 concludes.

1. The Two-Sector Model with Zero Technological Progress and No Innovation

Consider an economy initially without any robots. There is no technological progress or innovation. Production of the capital good requires only human labor. Capital, in turn, is used to produce a pure consumption good. With suitable normalization, output of the capital good is given by YI = H, and the output of the pure consumption good is given by YC = K. Let q be the relative price of the capital good measured in units of the pure consumption good. Under perfect competition, the following conditions hold:

where v is the real wage and rK is the capital rental rate. The asset pricing relationship is given by

which, using (2), can be written as,

The capital accumulation equation is given by

Household intertemporal optimization, assuming the log utility function, gives the familiar Euler equation

With clearing of the pure consumption goods market, C(t) = YC(t), and using (5) and (6) in (4), we obtain

Equations (5) and (7) give a pair of dynamic equations in K(t) and q(t) that exhibit saddle-path stability given an initial capital stock, K(0). In a steady state,

with rss = θ.

Now, consider the arrival of additive robots. In order for it to be profitable to adopt additive robots, the rate of return to holding robots in the saver’s portfolio must be at least as great as rss = θ. We note that if additive robots are adopted, then the production of the capital good is now given by YI = H + RA. Letting be the rental rate on a unit of the additive robot, we require that

Given (1), this is equivalent to

Moreover, the equality of the rate of return principle requires that

Using (2), equations (11) and (12) imply that if it is profitable to adopt additive robots, then

Using (13) in (4), the rate of return to holding additive robots in the saver’s portfolio is given by

Therefore, if additive robots are profitable to adopt, the following condition must hold:

With the pure consumption-goods market clearing so C = K, it follows from (6), (14), and (15) that

even in the absence of steady technological progress. Using (1), (9), (13), and (15), we see that when additive robots are adopted, the real wage declines from v = (θ + δ)−1 to v = 1. Hence, we rediscover the result obtained in Chapter 8: the adoption of additive robots leads to a one-time permanent drop in the real wage even as the per capita consumption, which was stagnant before the adoption of robots, begins a trend growth without steady technological progress.

2. The Case of Indigenous Innovation Responding to Price Incentives

Before the adoption of robots, the output of the capital goods sector is given simply by YI = HI with suitable normalization. Here, YI is the output of the capital good, and HI is the number of human workers employed in production in the capital goods sector. The output of the consumption good is given by . Here, YC is output of the consumption good, KC is the capital stock employed directly in the consumption goods sector, and xi is the quantity of intermediate good i with quality denoted by Λi. Both the final goods are produced under conditions of perfect competition. However, each intermediate good i is produced under monopolistic competition as in Grossman and Helpman (1991) and Aghion and Howitt (1992).1

Let q denote the relative price of output in the capital goods sector, letting the consumption good serve as the numeraire. Profit maximization by competitive firms in the capital goods sector gives

where v is the real wage. Competitive firms engaged in the production of the consumption good solve the following profit-maximization problem:

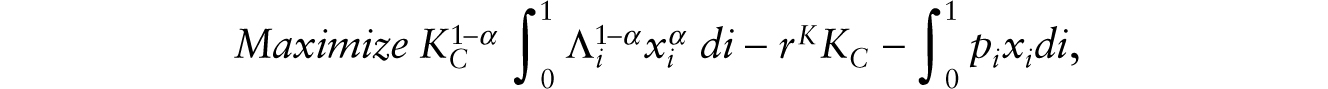
where rK is the rental rate of capital and pi is the relative price of intermediate good i. Solving this optimization problem gives rise to

Turning to monopolistically competitive firm i, the following maximization problem is solved under the assumption that producing one unit of xi requires one unit of conventional machine:

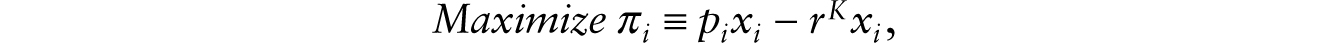
subject to (19). Solving this optimization problem, we obtain

We can reexpress (20) as

Integrating across i in (21), we obtain

where . Using (21) in (22), we obtain, after further simplification,

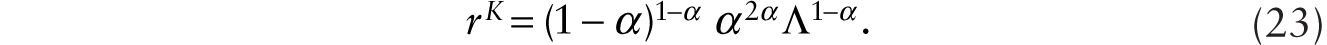
The condition that the total demand for capital is equal to the total supply of capital gives

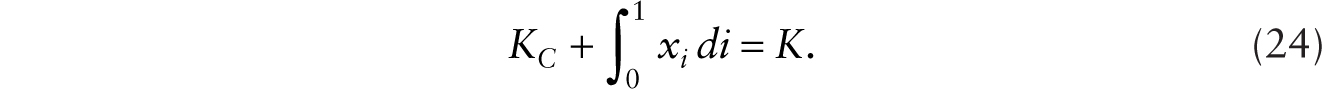
Using (22), (23), and (24), we obtain

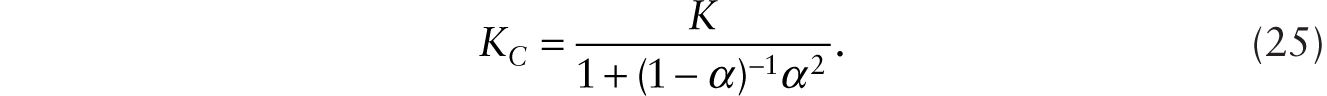
Then, using (22) and (25) with the production function for the consumption good, we obtain an expression for the output of the consumption good:

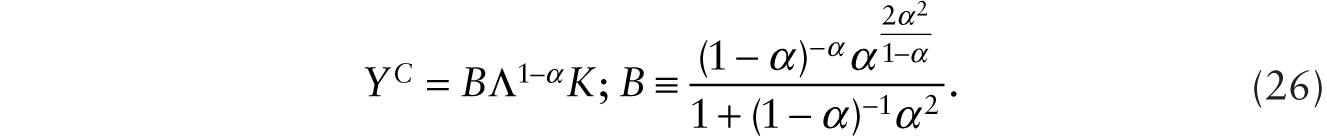
Let the growth rate of technology be expressed as The general equilibrium dynamics of the economy can be summarized as follows. After setting aggregate consumption equal to output of the consumption good and taking note of (3), (6), (23), and (26), we have

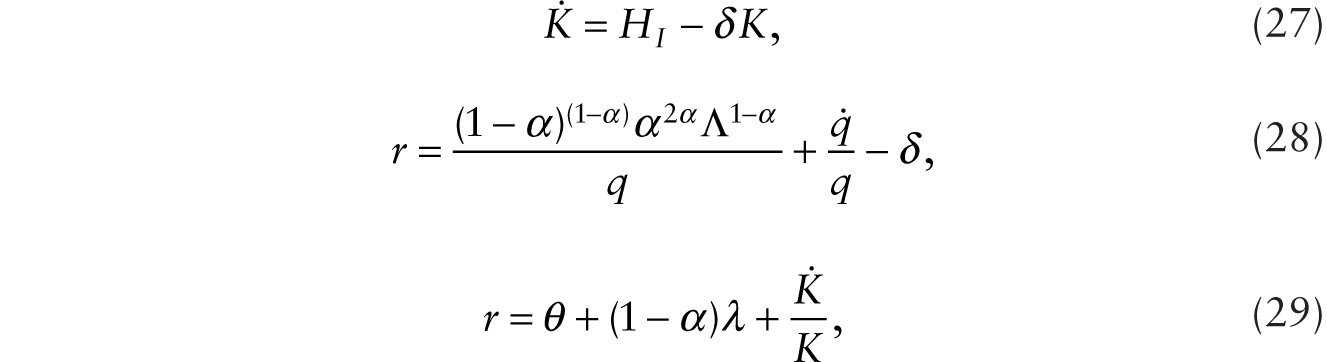
where r is the instantaneous real interest rate and θ is the subjective rate of time preference. Using (27) and (29) in (28), and defining , we obtain

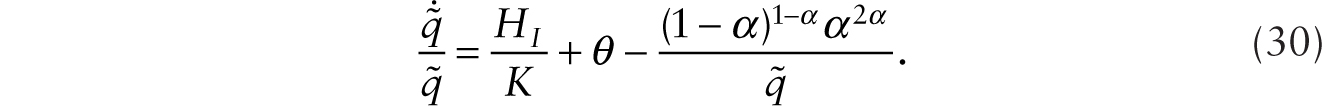
If HI is treated as exogenous, (27) and (30) can be characterized in a diagram with in the vertical axis and K on the horizontal axis. The stationary-K locus is a vertical line and the stationary locus is positively sloped in this diagram. Saddle-path stability is exhibited with a positively sloped saddle path that is less steep than the stationary locus.

To better understand the effects of introducing robots when the rate of technological progress is endogenously determined by the number of innovators, it would be helpful to conduct a preliminary analysis assuming that HI is given exogenously so that, from (37), given later, λ is also given exogenously. In a steady state before the introduction of additive robots, we have

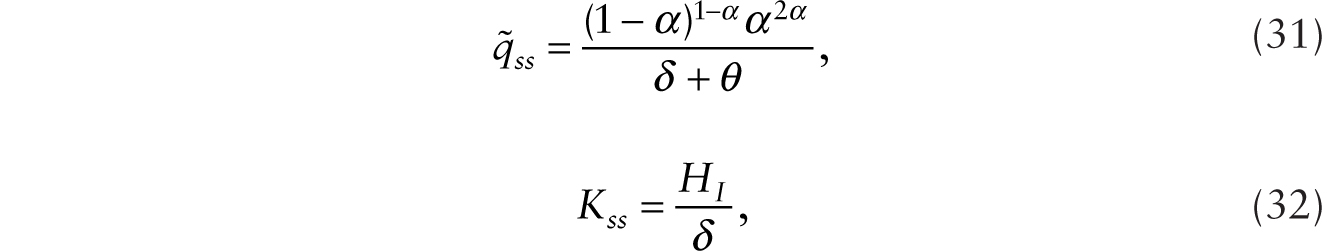
with rss = θ. With the adoption of additive robots, , so using (17) and (23), we obtain

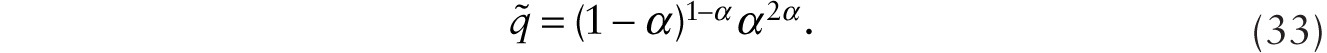
Using (23) and (33) in (3), the rate of return to holding additive robots in the saver’s portfolio is given by

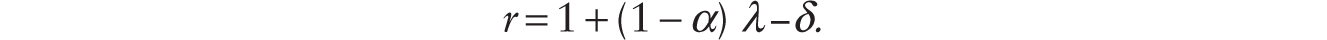
For it to be profitable to adopt additive robots, we require that the following condition holds:

Assume that δ + θ < 1 so (34) is satisfied.2 Comparing (31), (33), and (34), we see that with the adoption of additive robots, real wage experiences an immediate decline. After the immediate impact, the real wage continues on its trend growth at the rate of (1 − α)λ. The growth rate of per capita consumption also increases. This is so because using (34) in (29), we have

Since consumption goods market clearing means that C = YC, we have, using (26), (34), and (35), that

In this preliminary analysis, we have held HI exogenously fixed. We will now show that when HI is endogenously determined, the adoption of additive robots causes an instantaneous drop of the real wage as the relative price of the capital good, q, drops. However, the cheaper capital good stimulates innovation in the consumption goods sector so that λ increases. As a result, although the adoption of additive robots leads to an instantaneous drop of the real wage, the subsequent path of the real wage corresponds to a higher trend growth rate.

To determine the equilibrium allocation of human workers between production and innovation, we let λ be endogenously determined with

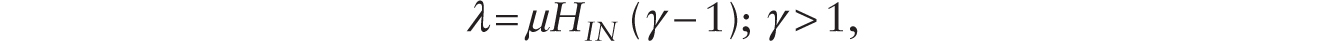
where HIN is human labor doing innovation and μ is the constant probability (in a Poisson process) of a successful innovation. Labor-market clearing requires

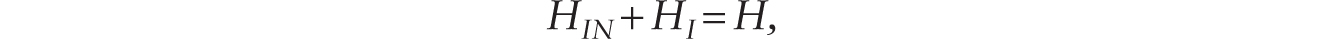
so we can also write,

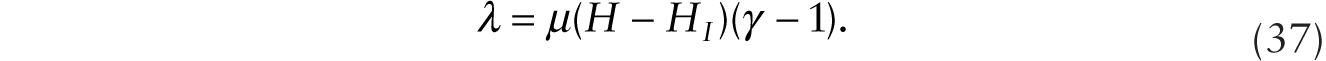
The flow of profit from successful innovation for intermediate good firm i is given by

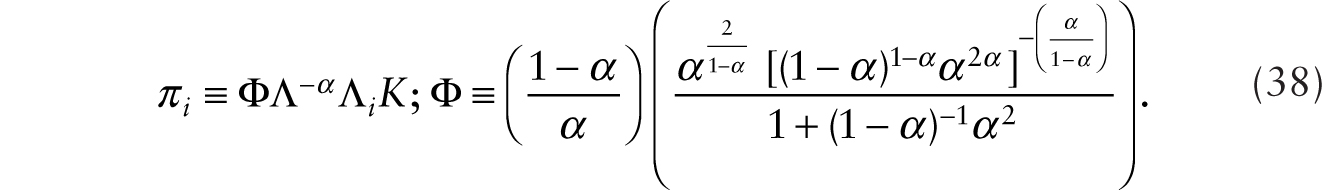
The asset pricing relationship is given by

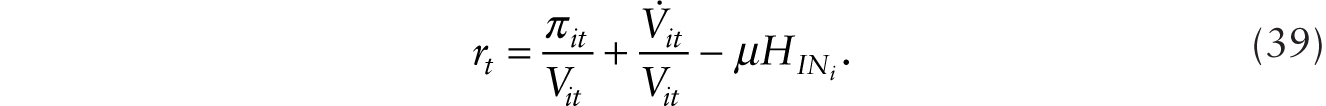
Free entry into innovating is given by

Using (1), (38), (39), and (40), we obtain

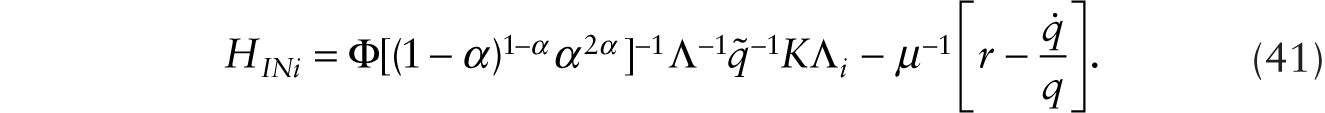
Using (28) in (41), we obtain

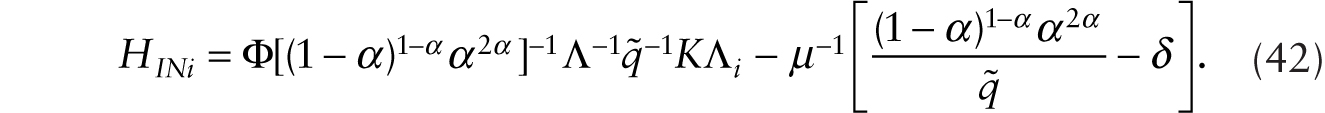
Integrating over i in (42), and using , we have

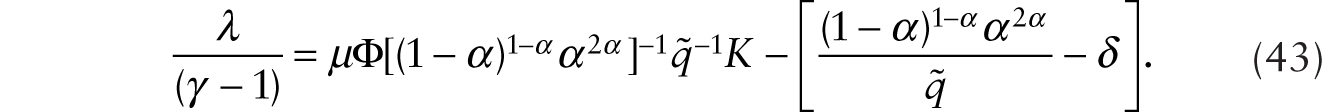
From (43), we obtain the following partial derivatives:

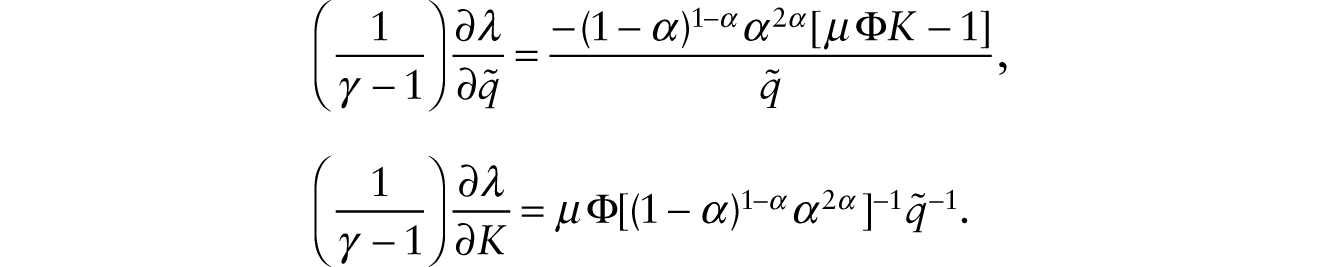
A crucial result from (43) is that, ceteris paribus, a drop in leads to an increase in the number of human workers innovating for sufficiently high probability of successful innovation, μ, which boosts the rate of technological progress, λ. In particular, the sufficient condition is μ > 1/(ΦK). How do we explain this result? There are two channels through which a fall in the relative price of the capital good affects the equilibrium allocation of human labor engaged in the innovative activity. First, a fall in the relative price of the capital good reduces the demand for workers employed in the production of the capital good. This releases workers to be employed in the innovative activity, which increases the rate of technological progress. Second, a fall in the relative price of the capital good, holding other things constant, leads to a fall in the shadow value of a new innovation (Vi).3 This second channel acts to reduce the demand for innovators. Overall, if the probability of success in innovation (μ) is sufficiently high, the first channel dominates so a fall in the relative price of the capital good leads to more workers being employed in the innovative activity and thus increases the rate of technological progress.

Another important result is that, ceteris paribus, an increase in K leads to an increase in the number of human workers innovating. Suppose that the technology to develop additive robots becomes available and that capital is malleable, so a unit of capital can be retrofitted to become an additive robot that perfectly substitutes for one human worker. Suppose that it is profitable to employ an additive robot. Then, the rental price of an additive robot cannot be higher than the current real wage. In equilibrium, with adoption of additive robots, the following condition must hold:

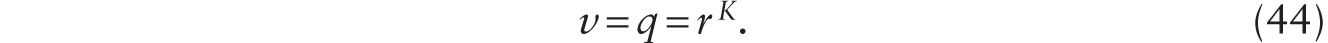
This implies that (33) holds when additive robots are adopted even when the rate of innovation is endogenously determined. For it to be profitable to adopt additive robots, the condition expressed in (34) must hold, where λ is itself determined by (43). Real wage experiences an immediate decline if δ + θ < 1 and drops on impact. From (43), if μ > 1/(ΦK) holds when additive robots are first adopted, this implies that the rate of technical progress, λ, is increased. Since (35) holds, we find that the capital stock is steadily increased. Equation (43) implies that this expansion of the capital stock stimulates the pace of innovation. This would imply that as K steadily increases, HIN steadily increases so λ is also steadily increasing. In recent work, Bloom et al. (2018) show that in many sectors of the economy, it takes many more researchers to achieve a given level of success in innovation.4 This suggests that, according to (43), even though μ, the probability of a successful innovation, is initially high when additive robots are first adopted, there is an exogenous steady decline in μ over time. Turning to (37), a decline in μ leads to a decline in λ both directly and by leading to a fall in HNI, the number of people doing research.

3. Conclusion

In this chapter, we showed that with the arrival of additive robots, capital accumulation is stimulated, and consumption per capita grows at a faster pace. When there is indigenous innovation, we find that while the real wage drops on impact, the decline in relative price of capital stimulates the pace of innovation so that the initial decline in the real wage is compensated with a higher trend growth if the probability of a successful innovation is sufficiently high. Summarizing our analysis, we showed that there are at least three channels that deliver more positive results on wage growth as a consequence of adopting robots. The first channel, examined in Chapter 8, is that the introduction of multiplicative robots that augment the productivity of human labor leads to positive wage growth. The second channel, examined in Chapter 9, is that the adoption even of additive robots has a positive asset price effect that stimulates investment in slow-adjusting, nonmalleable capital (such as factory buildings and physical structures) that complements total human and robotic labor. The third channel, examined in this chapter, works by stimulating innovation in the consumption goods sector as the adoption of additive robots in the capital goods sector reduces the relative price of the capital good.