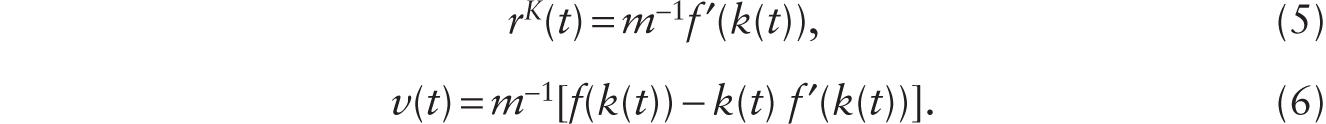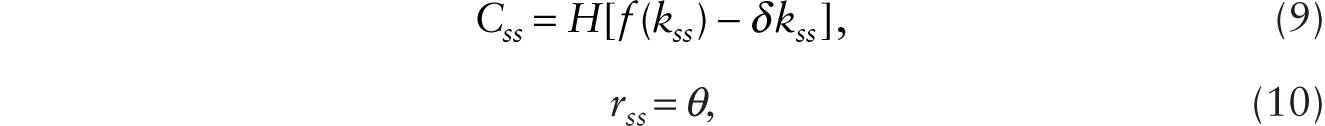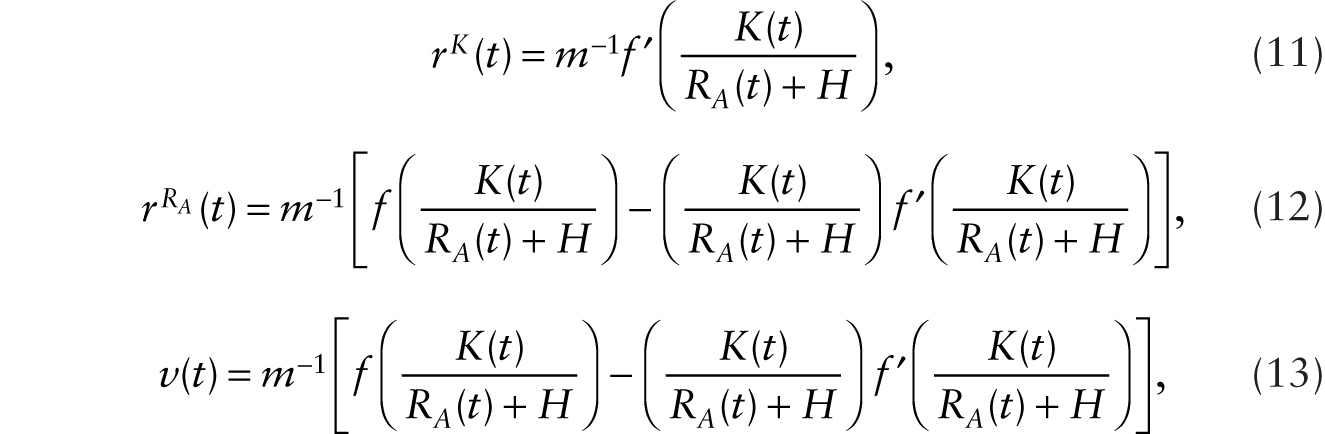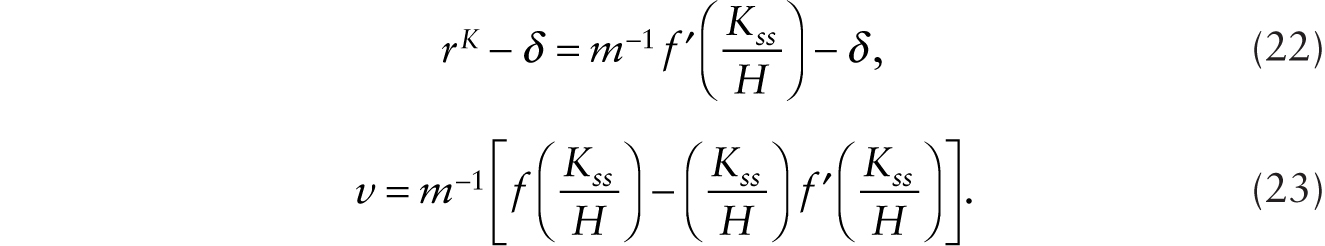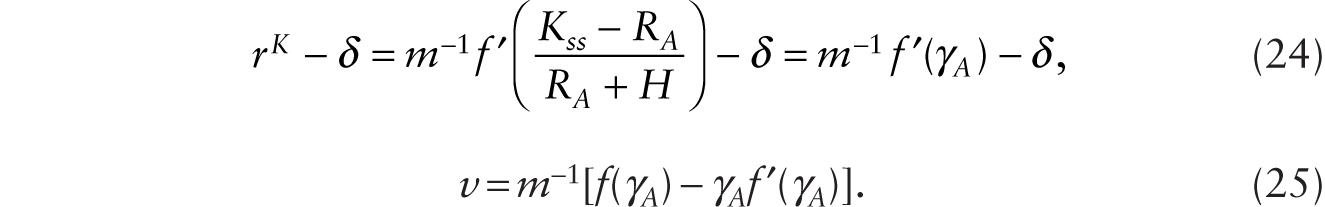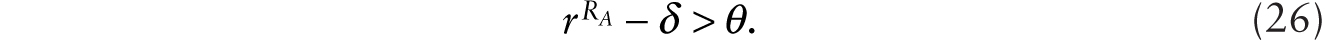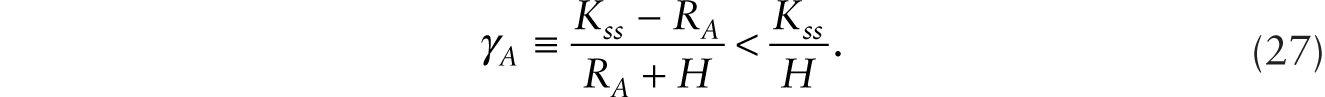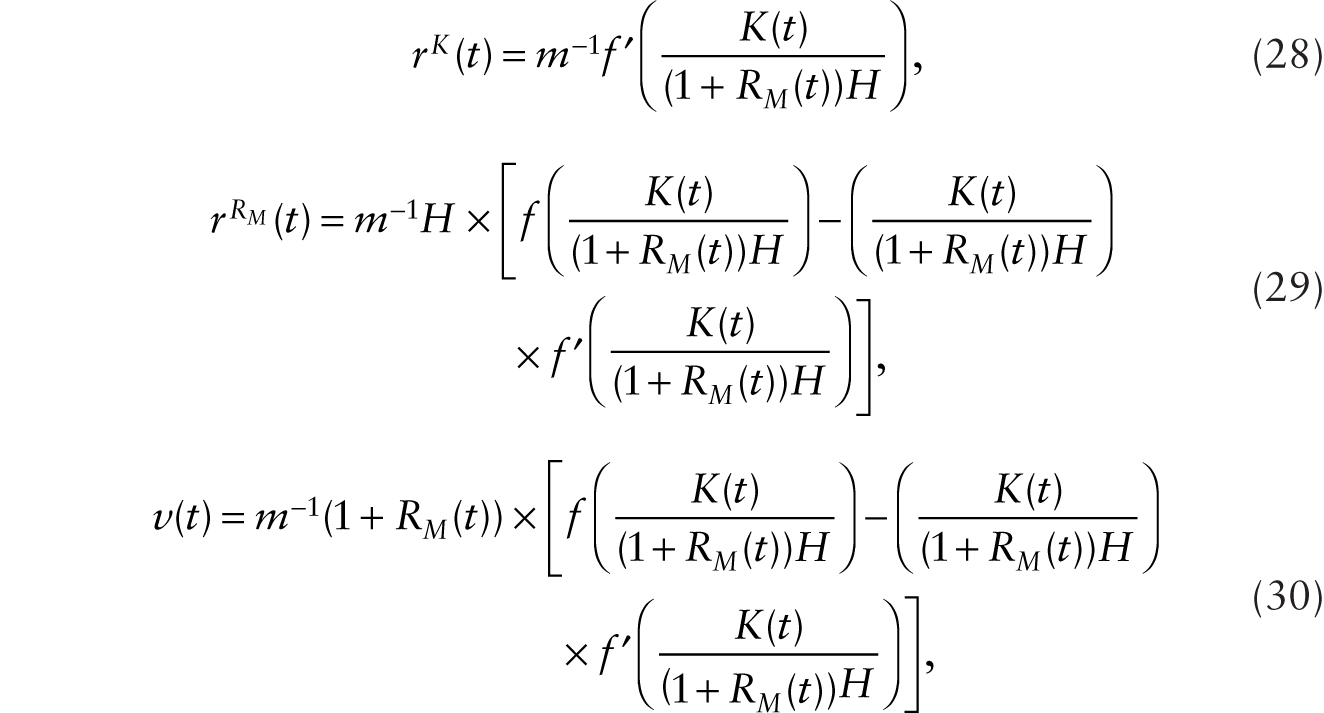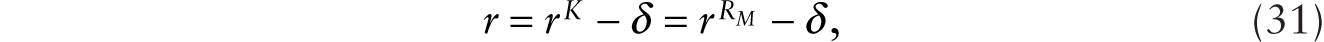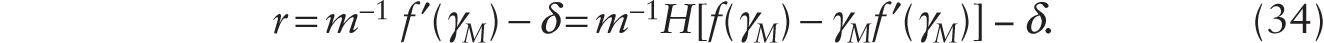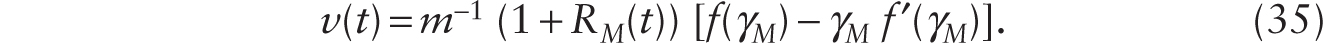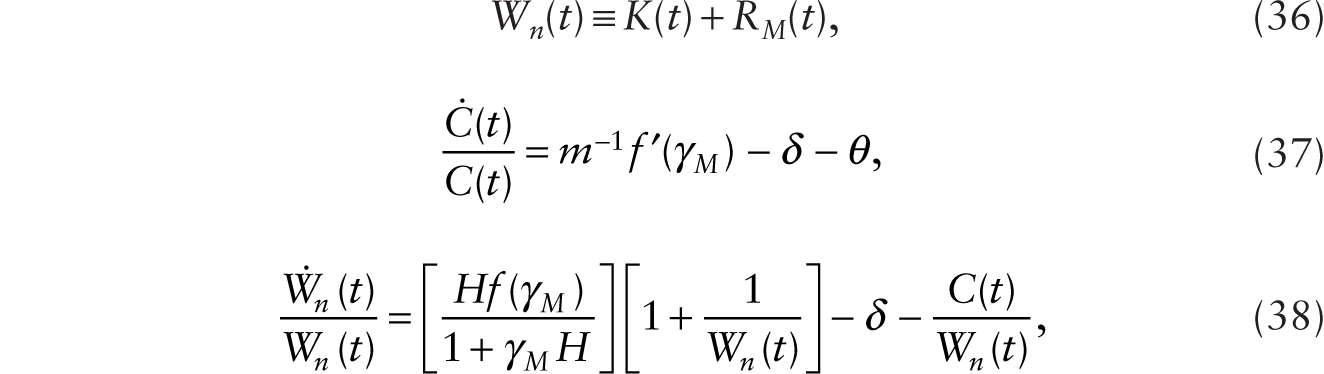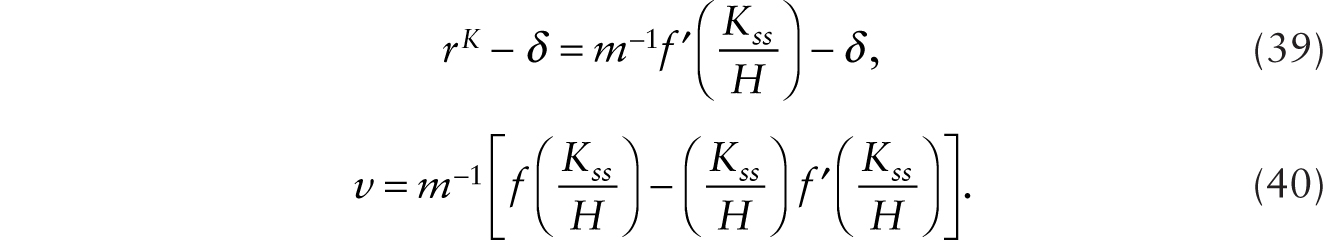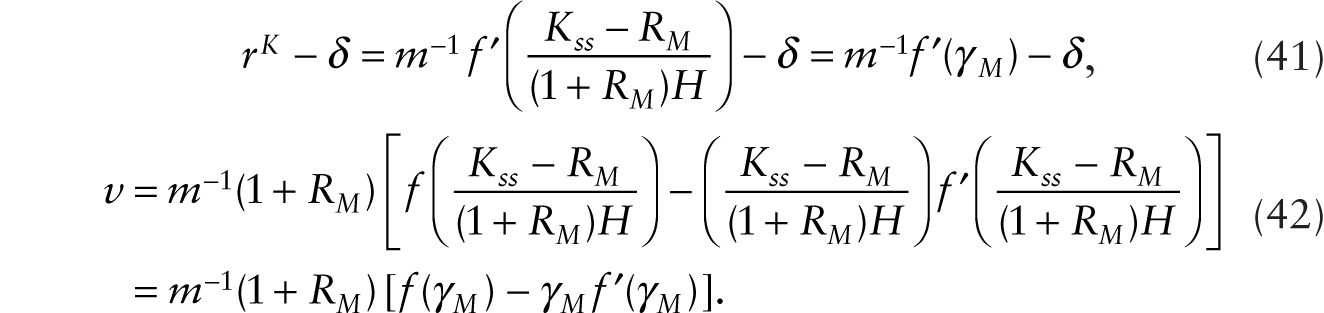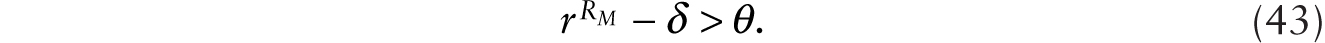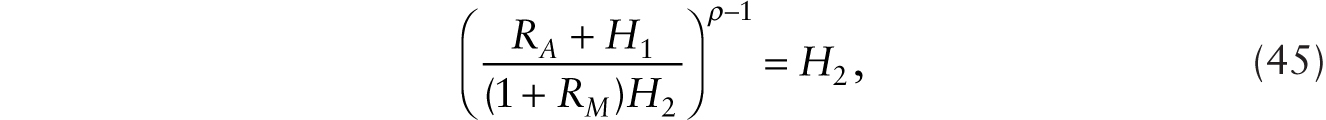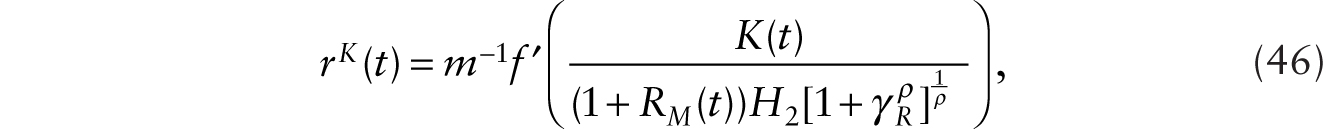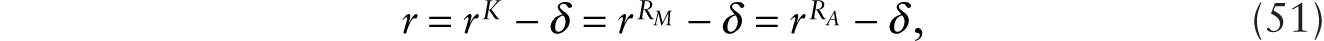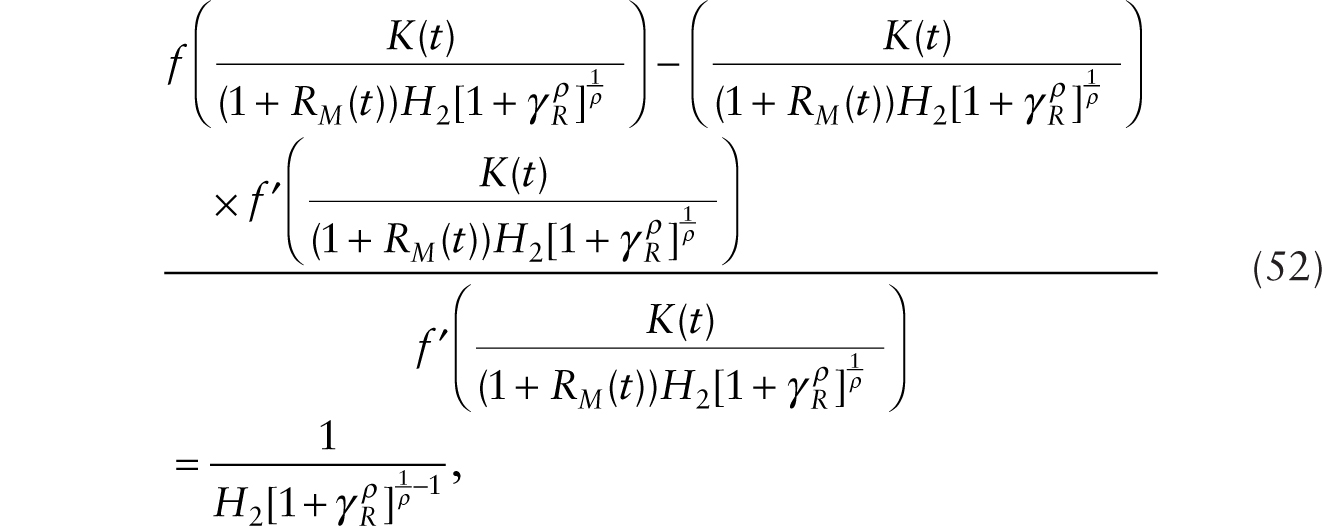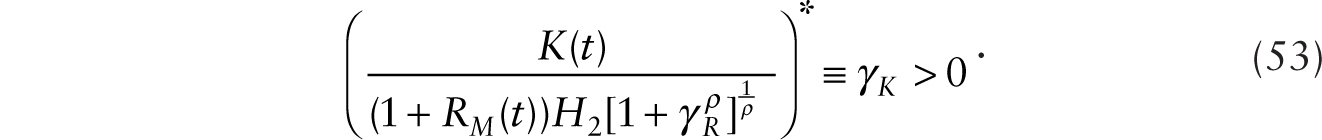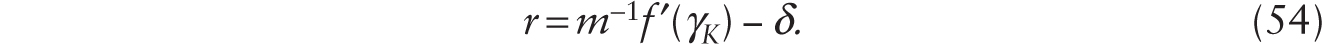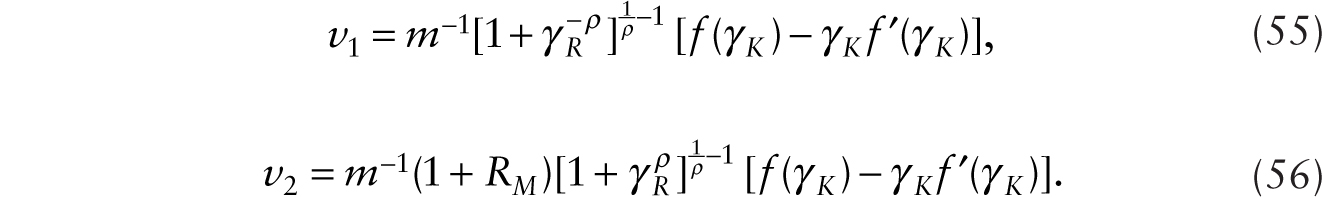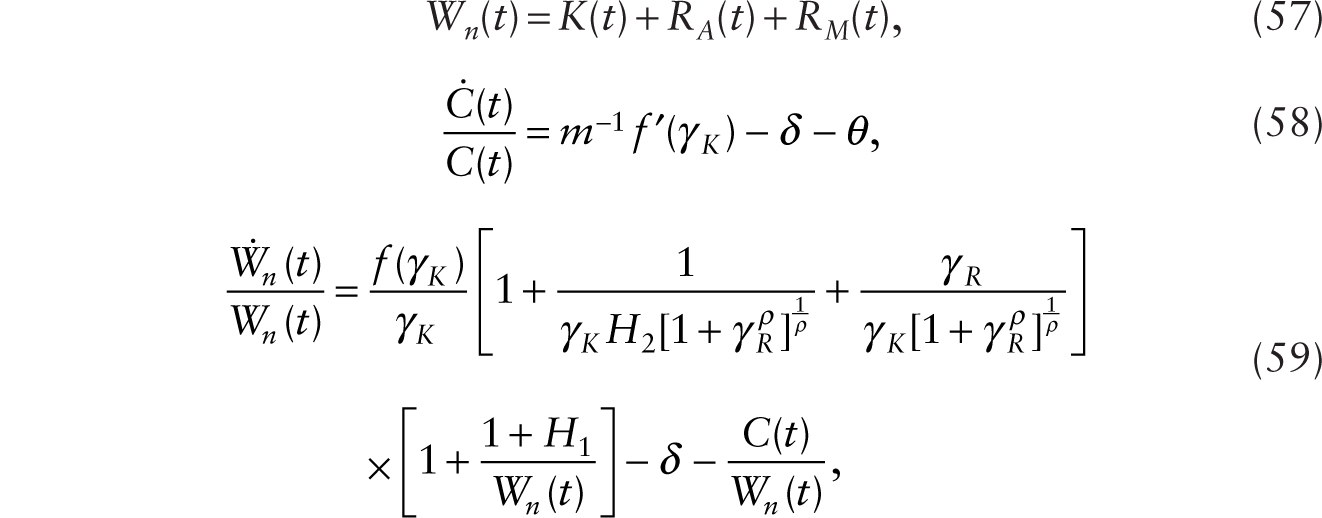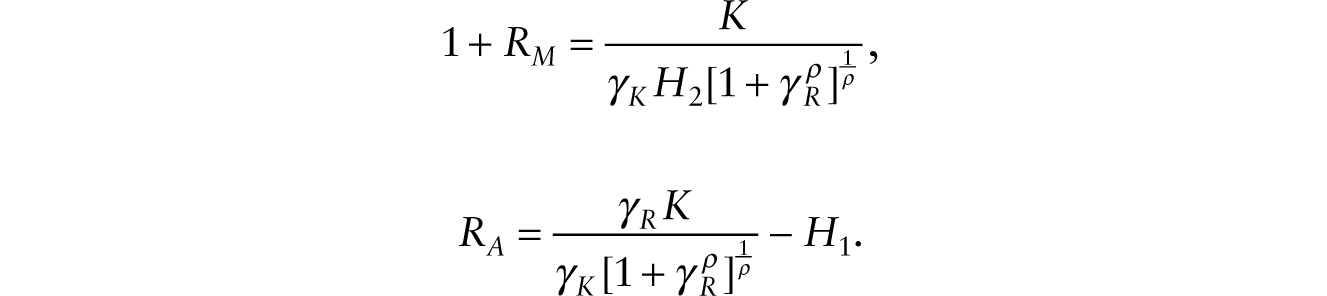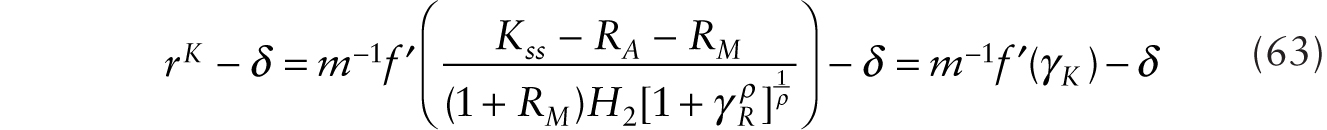8

Growth Effects of Additive and Multiplicative Robots alongside Conventional Machines

Hian Teck Hoon

ABSTRACT    We study the effects of introducing two different types of robots (additive and multiplicative) in an infinitely lived one-sector aggregative model with malleable capital on wages. The wage effects of these two polar cases are dramatically different. Given malleable capital that can be retrofitted for use either as conventional machines or as robots, we show that when it is profitable for firms to adopt additive robots in the production process, the real wage drops on impact and remains permanently at the lower level even as total malleable capital accumulates. However, when multiplicative robots are adopted, we show that while the immediate impact on the real wage is ambiguous, the real wage enjoys a positive trend growth even in the absence of steady technological progress.

Introduction

The introductory chapter quoted Alfred Marshall, who notes that workers with an enterprising attitude to the workplace had shifted more and more from work that was routine or dull to work that engaged the mind. Nevertheless, in chapter 3 of his Elements of Economics of Industry, titled “The Scope of Economics,” he notes that “the steadiest motive to business work is the desire for the pay which is the material reward of work.”¹

In this chapter and Chapters 9 and 10, we take up the question of how the arrival of robots, enabled by artificial intelligence (AI) and machine learning, affects the pay of workers in standard growth models. We start by deriving a stark result in this chapter (with malleable capital), that the adoption of additive robots leads to a permanent decline of real wages and a diminishing labor share of national income. This stark case where a robot is a perfect substitute for a worker is also considered in Samuelson (1988) but in the context of a classical model with circulating capital, where he states, “Now let there be invention of a robot machine that lasts one period and can do exactly the work of one man.”2 Our further analysis (in this chapter and Chapters 9 and 10) using a standard growth model, however, shows that there are at least three other channels that deliver more positive results on wage growth as a consequence of adopting robots. The first channel, examined in this chapter, is via the introduction of multiplicative robots that augment the productivity of human labor. We show that the adoption of multiplicative robots imparts a positive trend to wage growth even in the absence of technological progress. The second channel, examined in Chapter 9, is via the stimulation of investment in slow-adjusting, nonmalleable capital (such as factory buildings and physical structures) that complements total human and robotic labor. Such complementary investment, we show, exerts an upward pull on wage levels. The third channel, examined in Chapter 10, is via stimulation of innovation in the consumption goods sector as the adoption of additive robots in the capital goods sector reduces the relative price of the capital good. We show that by causing some workers in the economy to shift from participating in production to participating in innovative activity, the new wage path must be ultimately rising.

According to forecasts in 2016 by the International Federation of Robotics, more than 1.4 million new industrial robots will be installed in factories around the world by 2019.³ This is the result of a projected 290,000-unit increase in the number of newly installed industrial robots by the end of 2016 and average annual growth of at least 13 percent from 2017 to 2019.⁴ Given these forecasts, what is the likely impact of the widespread adoption of robotics on real wages and what are its effects in the long run?

The wave of research on economic growth beginning with Solow (1956) and Swan (1956) in the 1950s, and continuing into the 1960s with work by Phelps on the Golden Rules of economic growth (1966) and on two-sector growth models by Uzawa (1964), brought forth workhorse models to understand the growth of national income and wages well before the so-called Second Machine Age (see Brynjolfsson and McAfee, 2014).⁵ Thus, that earlier research left unanswered a key question: What happens to the growth of income, productivity, and wages if robots are acquired and deployed that effectively add their “labor” or “work” to the labor of the employed?

Existing research on the impact of automation, robotics, and AI on jobs and wages has mainly aimed at empirically determining whether the net impact has been positive or negative from a task-based perspective. This task-based framework is fully developed in Acemoglu and Restrepo (2018).6 The empirical results are mixed. Graetz and Michaels (2015; updated 2017) analyze panel data on robot adoption within industries in 17 countries from 1993 to 2007.⁷ They find that increased robot use contributed approximately 0.37 percentage points to annual labor productivity growth while at the same time raising total factor productivity and wages. Acemoglu and Restrepo (2017) study the impact of the increase in industrial robot usage between 1990 and 2007 on US local labor markets.⁸ They estimate that one more robot per 1,000 workers reduces the employment-to-population ratio by about 0.18–0.34 percentage points and wages by 0.25–0.5 percent.

The mixed empirical results suggest that opposing effects are at work, and our theoretical investigations seek to clarify the different channels through which robotization has effects within the workhorse models of economic growth. While existing research on the impact of automation and robotics has adopted a task-based approach, and we agree that this approach yields useful insights, such as shedding light on the job polarization highlighted by Goos, Manning, and Salomons (2014), we believe that it is necessary also to conduct the analysis in the standard, and more familiar, one-sector aggregative growth model.⁹ Our confidence in understanding how robotization affects wages will be bolstered by such a thorough analysis.

The invention of the steam engine, electricity, and the microprocessor produced growth opportunities through their pervasive use across vast swaths of the economy. The development of robotics—the design, construction, and operation of robots enabled by AI—holds the promise of spurring growth even as it appears to cause wage declines. Since the First Industrial Revolution, fixed capital has played a central role in the production of output. In the formal neoclassical one-sector model of Solow (1956) and Swan (1956), fixed capital is modeled as conventional machines that appear along with technology and labor to generate physical output.¹⁰ Expressed as Y = F(K, AL), aggregate output (Y) is a homogeneous function of degree one in conventional machine (K) and “augmented labor” (AL). With this specification, the marginal physical productivity of labor is increasing in the ratio capital per augmented worker (K/(AL)). An issue that arises is how to model the arrival of robots in the context of the neoclassical growth model. How are AI-enabled robots different from conventional machines? Once introduced, what are their economic effects, particularly on growth, consumption, and wages?

Our approach in this chapter is to model capital as malleable and flexible in its use either as conventional machines—that is, as traditional capital—or as robots. Given its malleability, the current stock of machines can be retrofitted to function as robots once the robotic technology is available. Implicitly, the “technology” behind the construction of robots is treated as exogenously given. It is the result of technical advances made by research scientists in the AI and robotics community that we do not model explicitly. (Later, in Chapter 10, we do model endogenous innovation undertaken by the labor force to improve the quality of intermediate inputs that is driven by economic incentives.) In this chapter, we model two types of robots: additive and multiplicative. Additive robots can perform the same functions as a human worker and thus are perfectly substitutable for a human worker. This is, perhaps, the type of robot that most closely represents the layman’s image of the arrival of robots in the economy. Denoting the quantity of additive robots by RA and human labor by H, the total labor force (both robotic and human) is equal to RA + H. The development of AI and machine learning has also produced a second kind of robot, which we call multiplicative, that can be described as augmenting labor power. These are robots that can plow through huge databases to provide information within minutes, helping medical personnel to do their jobs more effectively, and robots that enable older workers to carry heavy objects with little effort exerted by the human workers. Such AI-enabled robots, or “multiplicative robots,” are denoted by RM. With the introduction of multiplicative robots, total (robotic and human) labor is given by (1 + RM)H.

If robots are additive, we write the production function as Y = F(K, RA + H) with degree of homogeneity equal to one in the two arguments in the production function. If robots are multiplicative, the production function is written as Y = F(K, (1 + RM)H) with degree of homogeneity equal to one in the two arguments in the production function. We also analyze the wage effects of introducing both types of robots when there are two types of jobs that human workers perform: routine jobs (H1) that additive robots can also perform and nonroutine jobs (H2) whose productivity multiplicative robots augment.¹¹ We assume that routine jobs performed by human and robotic labor, RA + H1, substitute imperfectly for nonroutine jobs enabled by multiplicative robots, (1 + RM)H2, with a constant-elasticity-of-substitution subproduction function: ¹²

With a linear homogeneous aggregate production function in its two arguments, we write , where K represents the stock of conventional machines.

To analyze the economic effects of introducing AI-enabled robots, it is convenient to suppose that before the arrival of robots, the economy is in a stationary equilibrium with a zero rate of technological progress and zero population growth. In a convenient Ramsey infinitely lived economy, the production function, with suitable normalization, is given by Y = F(K, H). The real interest rate is equal to the rate of time preference, the real wage is constant, and per capita consumption is also constant in such an economy.

A key assumption we make in this chapter is that capital is malleable, so that when the technology to produce additive robots becomes available, a piece of conventional machine can be instantaneously retrofitted to function as a robot and vice versa. (In Chapter 9, we will deviate from this assumption to take account of the fact that some types of fixed capital, such as factory buildings and physical structures, are not malleable and take time to install. So there is a high adjustment cost to install such capital.) With malleable capital that can be used to construct robots or conventional machines, a crucial economic principle that must hold is that the rate of return to owning a piece of conventional machine is equal to the rate of return to owning a robot—an equality of rate of return principle.¹³ With the introduction of additive robots, the total nonhuman wealth (Wn) is now equal to K + RA. While Wn evolves gradually over time, the division between RA and K is endogenously determined to satisfy the equality of rate of return principle at each point in time. We note also that, given Wn, the ratio K / (RA + H) adjusts instantaneously with changes in the division between RA and K to satisfy the equality of rate of return principle.

What are some key results of the introduction of additive robots? We show that with the arrival of additive robots, if it is profitable for firms to immediately retrofit some of the existing conventional machines to be used as robots, there is an immediate drop of the real wage. However, the real rate of interest, which is initially equal to the subjective rate of time preference, immediately jumps up to a permanently higher level. The rate of growth of consumption, which is initially equal to zero, also jumps up to a positive number. Along this path, the consumption per capita is growing, fueled by a more rapid pace of capital accumulation that is more than sufficient to cover physical capital depreciation. Along a balanced-growth path, total nonhuman wealth is growing at the same rate as consumption per capita, with constant shares in the form of conventional machines and additive robots. The real wage, which drops on impact when additive robots arrive, remains at a depressed level despite growth in nonhuman wealth. The reason for this is that while nonhuman wealth increases, the ratio K / (RA + H) remains invariant as capital is malleable, so the division of nonhuman wealth between K and RA is adjusted instantaneously to satisfy the equality of rate of return principle.

What happens if the robots introduced are multiplicative in nature? We show that with the arrival of multiplicative robots, while the immediate impact is to cause the stock of conventional machines to fall when it is profitable to adopt robots (tending, by itself, to depress wages), the real wage need not fall because of an offsetting labor-augmenting effect coming from the multiplicative nature of the robot. As in the case of additive robots, the real rate of interest, which is initially equal to the subjective rate of time preference, immediately jumps up to a permanently higher level. The rate of growth of consumption, which is initially equal to zero, also jumps up to a positive number. Along this path, the consumption per capita is growing, fueled by a more rapid pace of capital accumulation that is more than sufficient to cover physical capital depreciation. The real wage, even if it drops initially (though it may actually increase, as just noted), continues to steadily increase along a balanced-growth path as nonhuman wealth grows even in the absence of steady technological progress.

The wage effects of introducing both types of robots are analytically similar to the polar case of introducing only multiplicative robots. More specifically, while the real wage for workers whose productivity is augmented by multiplicative robots might drop on impact, it enjoys a positive trend growth as in the pure multiplicative case. The real wage for workers in routine jobs that additive robots can also perform enjoys a productivity boost from the joint adoption of multiplicative robots if there are relatively abundant routine jobs performed by human workers compared with the number of nonroutine jobs in the economy and the elasticity of substitution between routine and nonroutine jobs is greater than one.

The rest of the chapter is organized as follows. We study the effects of introducing only additive robots in Section 1, and the effects of introducing only multiplicative robots in Section 2. The case in which both additive and multiplicative robots are adopted is examined in Section 3. Section 4 concludes.

1. Robots Perfectly Substitute for Human Labor: Case of Additive Robots, H + RA

The size of the population, which is made up of many identical families and set equal to total human labor force, is constant and normalized to one. The number of hours worked per human worker is fixed at , so total human labor is equal to , which is allocated between overhead labor (Hf) and variable labor (H). Agents derive utility from consumption with a subjective rate of time preference, have infinite lives, face an instantaneous real interest rate r(t), and receive an hourly real wage v(t). Let c(t) denote consumption at time t, wn(t) nonhuman wealth, and wh(t) human wealth.

The agent maximizes

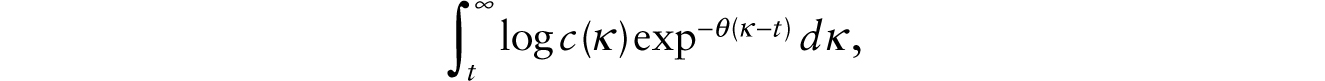
subject to

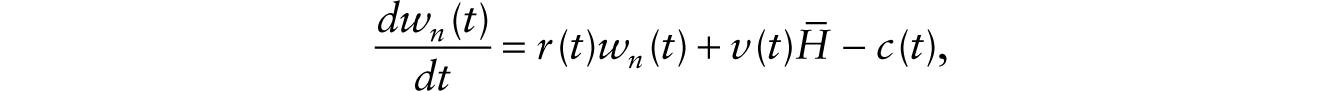
and a transversality condition that prevents agents from going indefinitely into debt. The solution to the agent’s problem is given by

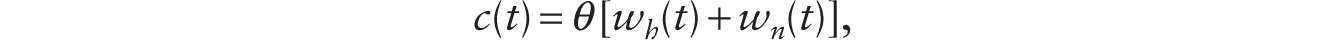
where human wealth is given by

Denoting per capita aggregate variables by capital letters, we obtain

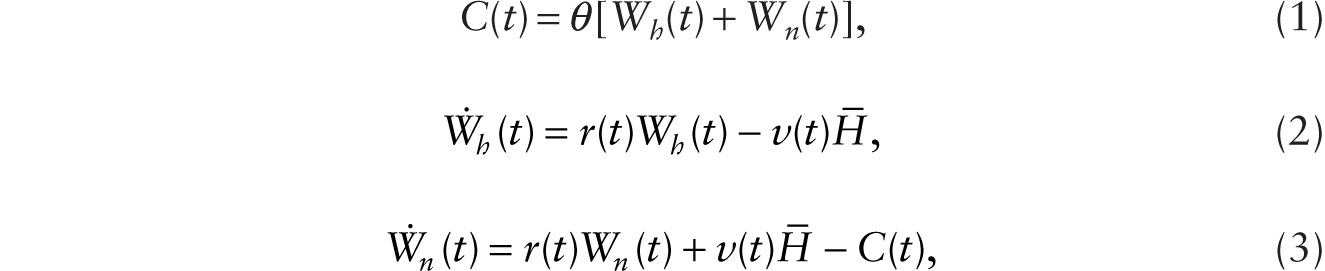
where a dot over a variable denotes its time derivative. Taking the time derivative of (1), and using (2) and (3), we obtain, after rearrangement of terms,

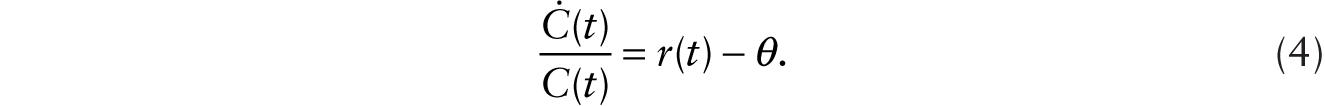
Turning to the production side of the model, we first consider a situation before robots are introduced. With firms having to incur overhead labor costs before actual production (leading to declining average cost), imperfectly competitive firms produce and sell a single good with a markup of price over marginal cost denoted by m > 1, pay wages for human labor input, and make rental payments for capital inputs, which consist entirely of conventional machines. Before the introduction of robots, each firm has access to the following production technology:

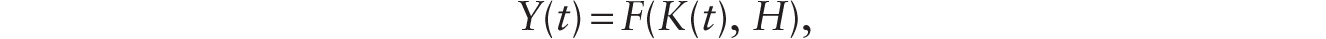
where Y is the flow of output, K is the stock of conventional machines, and H is human variable labor input. The function F(K, H) exhibits constant returns to scale, and, for positive quantities of K and H, it exhibits positive and diminishing marginal products with respect to each input; it also satisfies the Inada conditions. We can write

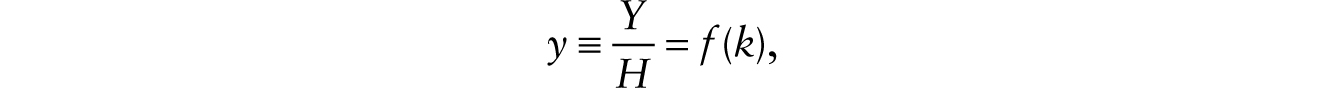
where k ≡ K / H. Capital depreciates at the rate δ. So, when letting rK(t) denote the rental rate on machines, the net rate of return to an agent who owns a unit of machine is rK(t) − δ. With machines and loans as perfect substitutes, we have r(t) = rK(t) − δ. Maximizing profits under imperfect competition leads to

Noting that Wn(t) ≡ K(t) and , we can use (5) and (6) together with (3) and (4) to obtain

With free entry and exit of firms, the condition that total revenue covers total cost pins down the markup of price over marginal cost, m. Equations (7) and (8) give a system of two dynamic equations in C and k with familiar properties given an initial value of capital stock per variable hour worked, k. In a steady state, the consumption level (Css) and the steady-state real interest rate (rss) are determined by the following pair of equations:

where rss = m−1 f ′(kss) − δ.

Consider now the effects of introducing additive robots that perfectly substitute for human labor into this familiar framework. For simplicity, we measure units of robots such that one robot can now perfectly substitute for one unit of human labor input. With the adoption of robots, the production function is now given by

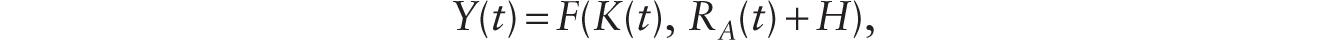
where RA(t) is the number of additive robots. In intensive form, we can write

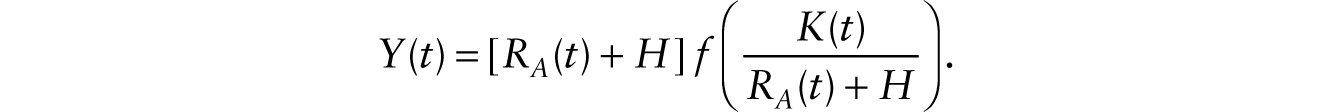
Profit maximization under imperfect competition gives the following first-order conditions:

where rK(t) is the rental rate on a unit of conventional machine and is the rental rate on an additive robot.

If capital is malleable and perfectly mobile across its two functions, we require

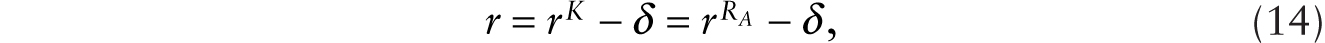
assuming the same rate of depreciation when capital is employed as a piece of conventional machine or as a robot that perfectly substitutes for human labor. Consequently, the “effective capital intensity” is a constant that satisfies

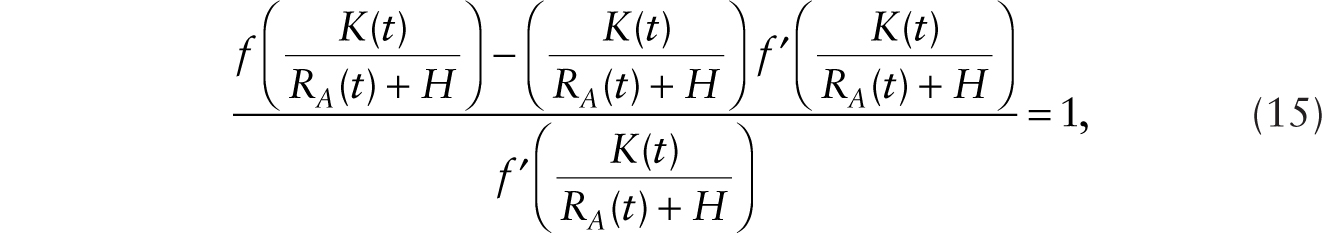
which we write as

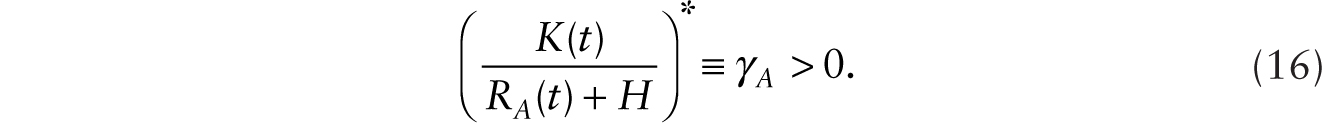
Notice that this makes the instantaneous real rate of interest a constant:

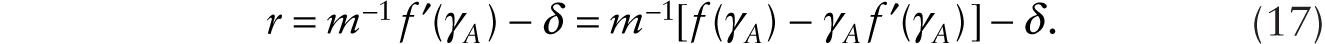
Notice also that the real wage is given by

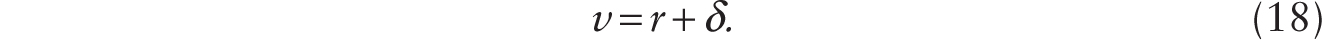
To complete the model, we note that, with the introduction of additive robots,

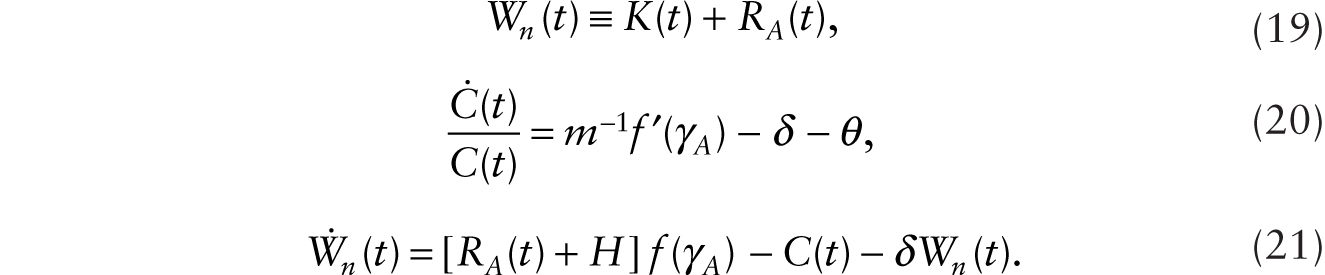
Starting from an initial steady state characterized by (9) and (10), where there are no robots, we study the conditions under which it is profitable to adopt robots that perfectly substitute for workers using the system of four equations given by (16), (19), (20), and (21) and four variables: C, Wn, K, and RA. With some manipulation, we can show that

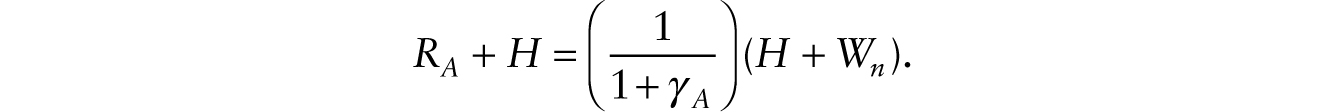
Using this equation in (21), the general-equilibrium system can be summarized in terms of C and Wn as

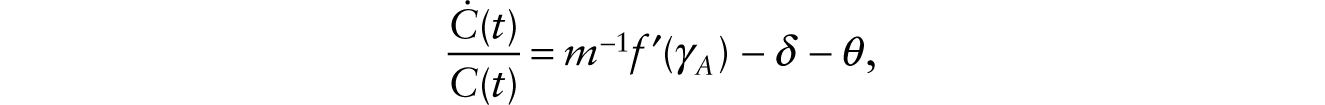
Before the introduction of robots, we have

At the moment that robots are introduced and adopted, we have Wn ≡ Kss, so we can write

Since the rate of return to capital before the introduction of robots is equal to the subjective rate of time preference given by (10), the condition for it to be profitable to invest in robots is

If (26) is satisfied, then some of the initial capital stock in the form of conventional machines will be instantaneously retrofitted to become additive robots, so

This implies that when robots are first introduced, say at time 0, it is unambiguous that

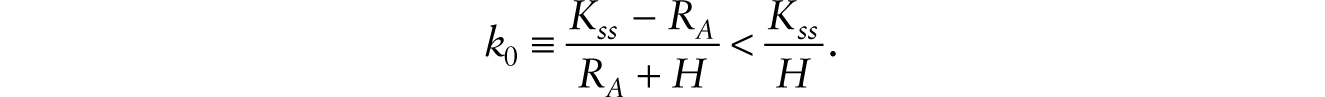
This decline in , taken alone, causes the real wage to fall on impact and remain permanently lower (since k remains equal to γA). In the long run, the general-equilibrium system is given by

with

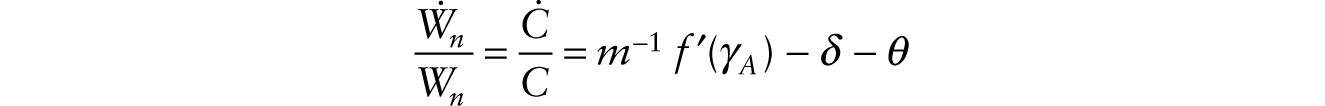
and

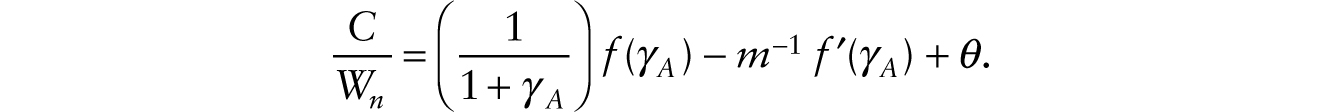
The analysis follows that of the AK model of endogenous growth.14

After the adoption of additive robots, total (human and robotic) labor share of national income tends toward a long-run constant given by

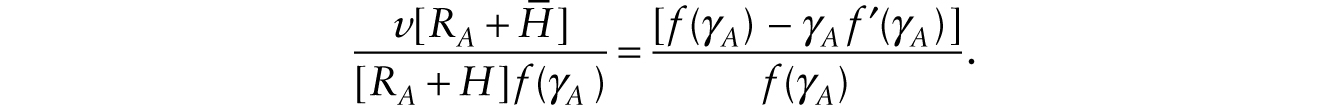
However, the (human) labor share of national income is given at each moment by

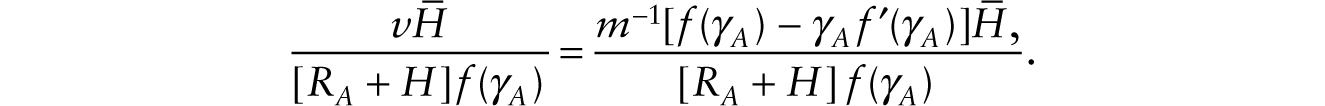
As the stock of additive robots continues to grow, with a fixed human labor force size, we find that the (human) labor share of national income tends toward zero in the long run.

2. Robots Augment Human Labor: Case of Multiplicative Robots, (1 + RM)H

Equations (1) to (10) continue to hold in this economy before the introduction of robots. Suppose that advances in AI and robotics science make it possible to adopt robots that augment human labor. We now have conventional machines (denoted K) and multiplicative robots that augment human labor (denoted RM).

The production function is now given by

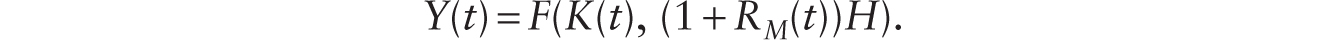
In intensive form, we can write,

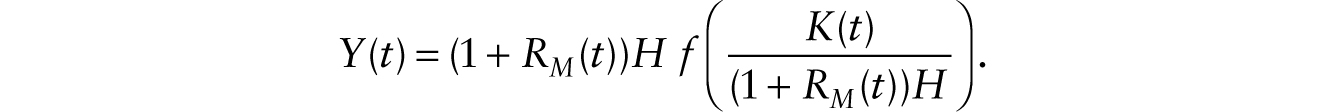
Profit maximization under imperfect competition gives the following first-order conditions:

where rK(t) is the rental rate on a unit of conventional machine, and is the rental rate on a multiplicative robot that augments human labor.

If capital is malleable and perfectly mobile across its two functions, we require

assuming the same rate of capital depreciation across the two functions. The effective capital intensity is given by

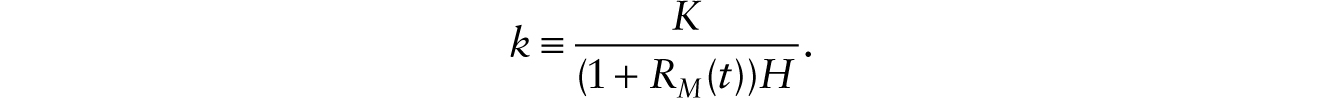
The effective capital intensity is a constant that satisfies

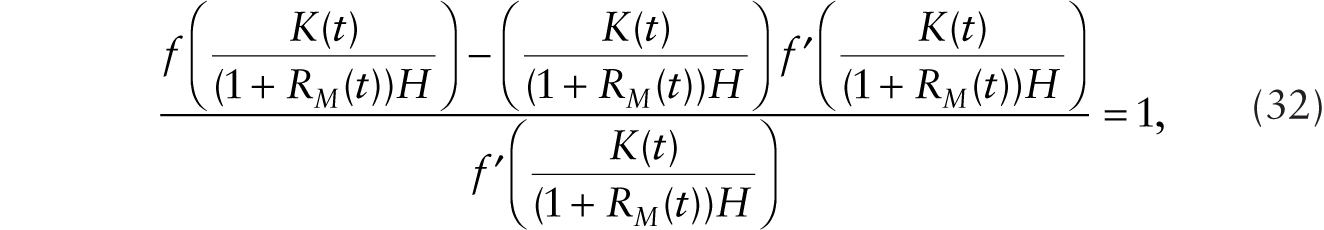
which we write as

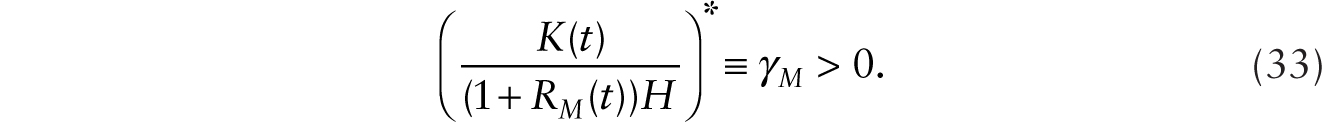
Notice that this makes the instantaneous real rate of interest a constant:

Notice also that the real wage is given by

To complete the model, we note that

where we have used the relationship

Before the introduction of robots, we have

At the moment that robots are introduced and adopted, we have Wn ≡ Kss, so we can write,

We note that, given m,

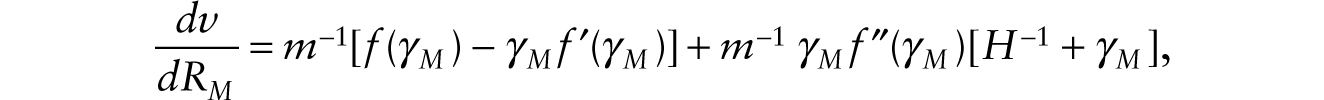
so the real wage can fall or increase on impact.

The condition for it to be profitable to invest in robots is

If (43) is satisfied, then some of the initial capital stock in the form of conventional machines will be instantaneously retrofitted to become multiplicative robots, so

This implies that when robots are first introduced, say at time 0, it is unambiguous that

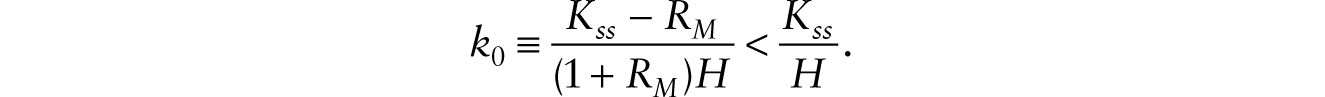
This decline in , taken alone, causes the real wage to fall on impact. However, the real wage rises on account of the term (1 + RM) that multiplies [f(γM) − γM f ′(γM)] in (42). While the immediate impact on the real wage is ambiguous, an examination of (37) and (38) shows that the real wage now grows at a positive trend growth rate. This is because as nonhuman wealth grows and tends toward zero, (38) can be written as

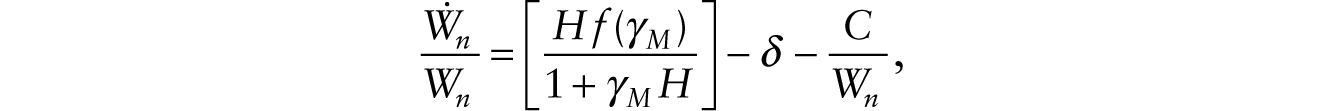
so Wn grows in the long run at the rate m−1 f ′(γM) − δ − θ, maintaining a constant ratio of nonhuman wealth to consumption. Equation (42) shows that the real wage grows steadily as RM steadily grows. We note also that after the adoption of multiplicative robots, the (human) labor share of national income is given by

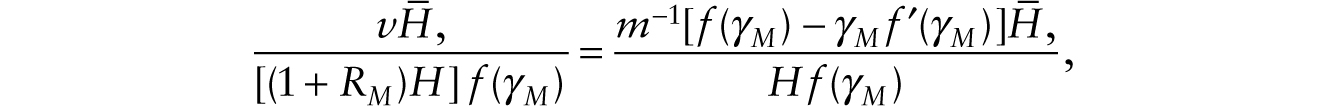
which is a constant in steady state.

3. Both Types of Robots: Case of Imperfect Substitutes

Next, we analyze the wage effects of introducing both types of robots when there are two types of jobs that human workers perform: routine jobs that additive robots can also perform and nonroutine jobs whose productivity multiplicative robots augment. Routine jobs performed by human and robotic labor, RA + H1, substitute imperfectly for nonroutine jobs enabled by multiplicative robots, (1 + RM)H2, with a constant-elasticity-of-substitution subproduction function: . (Note that the elasticity of substitution is given by (1 − ρ)−1.) A fixed fraction of the population performs routine jobs that additive robots can substitute and supply H1 number of hours, while the remaining fraction of the population performs nonroutine jobs that multiplicative robots augment and supply number of hours. We assume that overhead labor (Hf) is supplied only by workers performing nonroutine jobs, so With a linear homogeneous aggregate production function in its two arguments, we write,

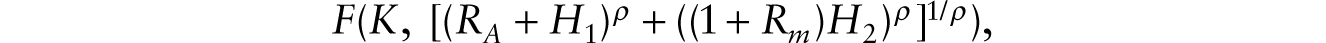
where K represents the stock of conventional machines. The analysis can proceed in two steps. In the first step, we note that the equality of the rate of return principle applied to additive and multiplicative robots implies that the following condition holds:

so we can write,

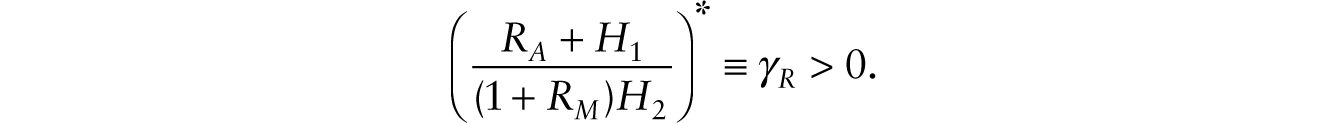
Using this result, we can write the aggregate production function as,

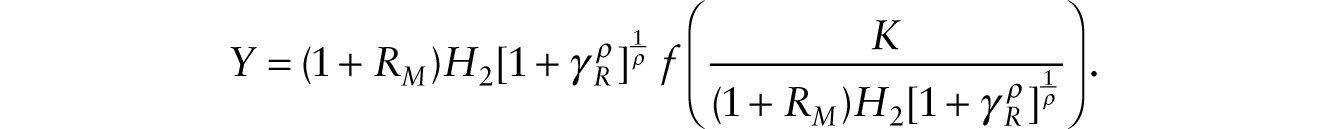
Profit maximization under imperfect competition gives the following first-order conditions:

where rK(t) is the rental rate on a unit of conventional machine, is the rental rate on a multiplicative robot that augments human labor, is the rental rate on an additive robot, v1(t) is the real wage of a worker whose job an additive robot is a perfect substitute for, and v2(t) is the real wage of a worker whose job a multiplicative robot augments.

If capital is malleable and perfectly mobile across its three functions, we require

assuming the same rate of capital depreciation across the three functions. The effective capital intensity is given by

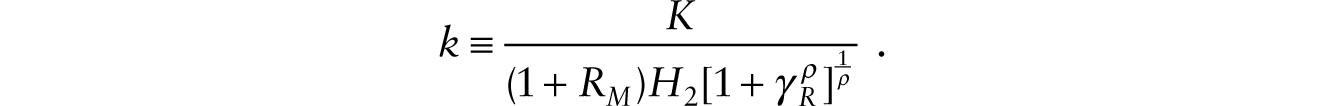
The effective capital intensity is a constant that satisfies

which we write as,

Notice that this makes the instantaneous real rate of interest a constant:

Notice also that the real wages are given by

To complete the model, we note that

where we have used the following relationships:

Before the introduction of robots, we have

At the moment that robots are introduced and adopted, we have Wn ≡ Kss, so we can write,

with per capita consumption now growing.

While the real wage for workers whose productivity is augmented by multiplicative robots might drop on impact, it enjoys a trend growth as in the pure multiplicative case. Comparing (61), which gives the real wage of workers performing routine jobs before the adoption of robots, and (55), which gives the corresponding real wage after the adoption of robots, we see that the effective capital intensity declines with the adoption of robots:

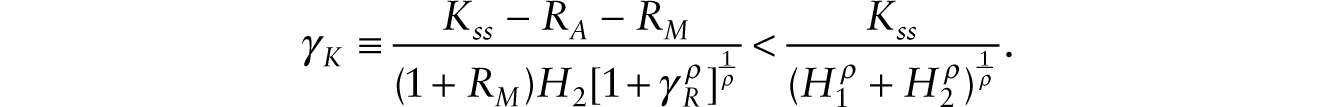
Through this channel, the adoption of robots depresses the real wage of workers doing routine jobs.15 However, the real wage for workers whose jobs are substitutable by additive robots enjoys a productivity boost from the joint adoption of multiplicative robots if the elasticity of substitution between routine and nonroutine jobs is greater than one and the following condition holds:

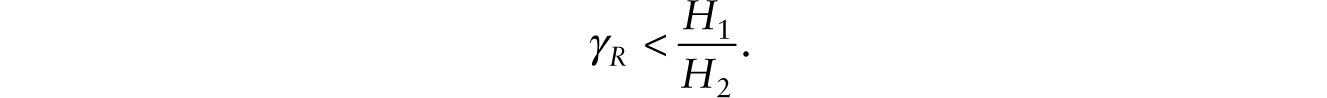
If this channel is sufficiently strong, the real wage of workers doing routine jobs can rise with the adoption of both types of robots.¹⁶

After the adoption of additive and multiplicative robots, the (human) labor share of national income is given by

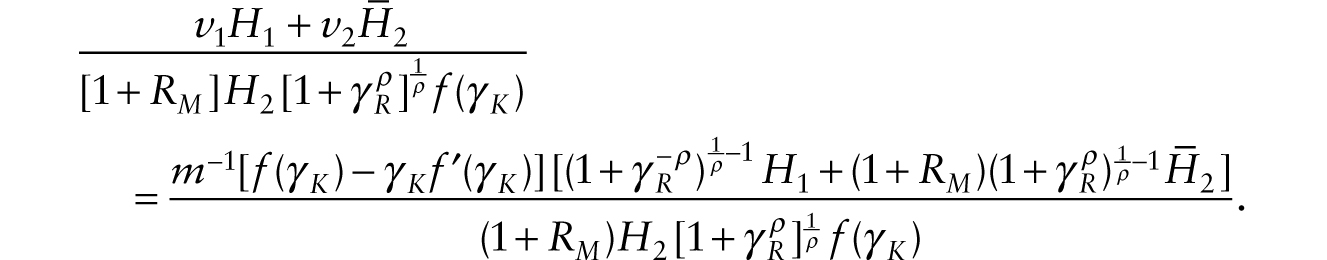
With fixed labor force sizes, the steady growth of multiplicative robots means that in the long run, the labor share of national income is given by

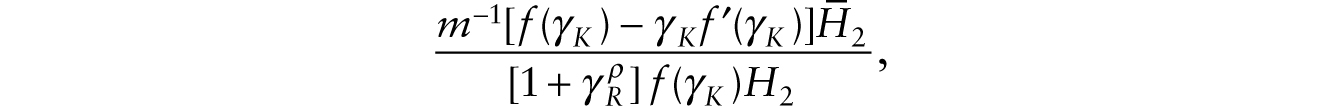
which is a constant.

4. Conclusion

In standard neoclassical growth theory, following Solow and Swan, net investment is equal to zero in the absence of population growth and technological progress. We find that with additive robots, the growth rate of consumption, which is initially equal to zero, also jumps up to a positive number. Along this path, the consumption per capita is growing, fueled by a more rapid pace of capital accumulation that is more than sufficient to cover physical capital depreciation. Along a balanced-growth path, total nonhuman wealth is growing at the same rate as consumption per capita, with constant shares in the form of conventional machines and additive robots. However, we obtain the stark result that real wages are permanently depressed and the (human) labor share of national income asymptotically tends toward zero although total (human and robotic) labor share of national income tends toward a long-run positive constant.

We find that with the arrival of multiplicative robots, while the immediate impact is to cause the stock of conventional machines to fall when it is profitable to adopt robots, the real wage need not fall because of an offsetting labor-augmenting effect coming from the multiplicative nature of the robot. As in the case of additive robots, the real rate of interest, which is initially equal to the subjective rate of time preference, immediately jumps up to a permanently higher level. The rate of growth of consumption, which is initially equal to zero, also jumps up to a positive number. Along this path, the consumption per capita is growing, fueled by a more rapid pace of capital accumulation that is more than sufficient to cover physical capital depreciation. The real wage, even if it drops initially, continues to steadily increase along a balanced-growth path as nonhuman wealth grows even in the absence of steady technological progress. The (human) labor share in national income tends toward a long-run positive constant.

We show that the wage effects of introducing both types of robots are analytically similar to the polar case of introducing only multiplicative robots. While the real wage for workers whose productivity is augmented by multiplicative robots might drop on impact, it enjoys a positive trend growth as in the pure multiplicative case. The real wage for workers in routine jobs that additive robots substitute enjoys a productivity boost from the joint adoption of multiplicative robots if there are relatively abundant routine jobs performed by human workers compared with the number of nonroutine jobs in the economy and the elasticity of substitution between routine and nonroutine jobs is greater than one. In this case, the (human) labor share in national income is a positive constant in the long run.