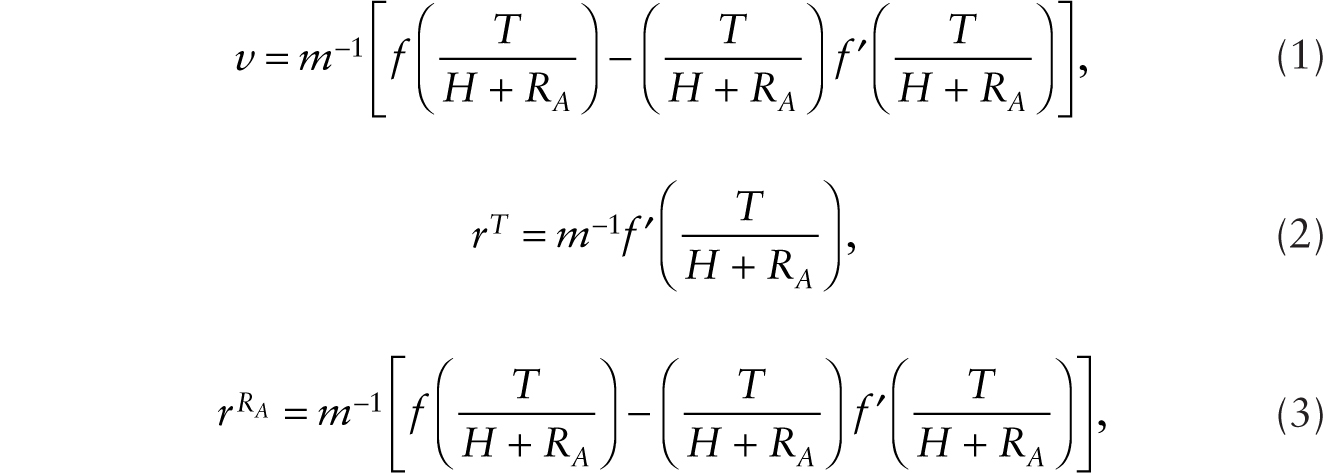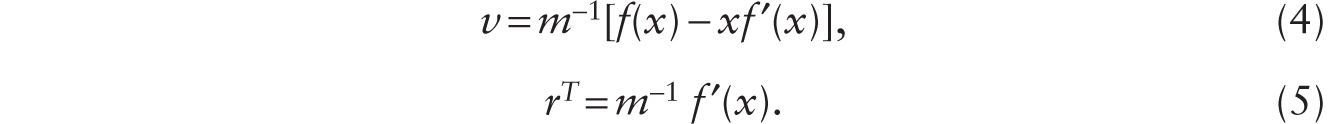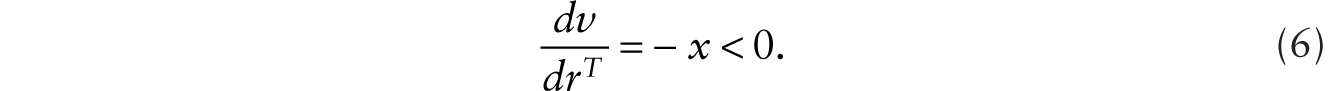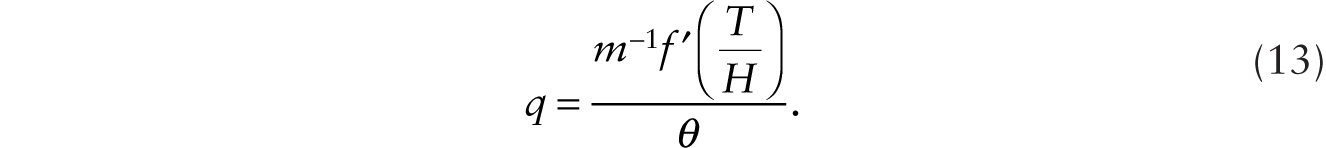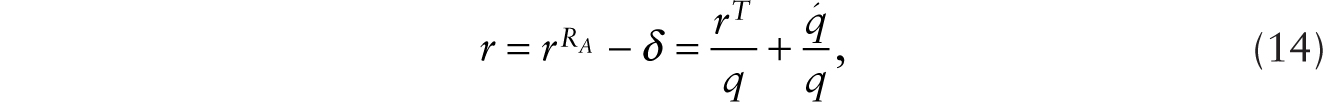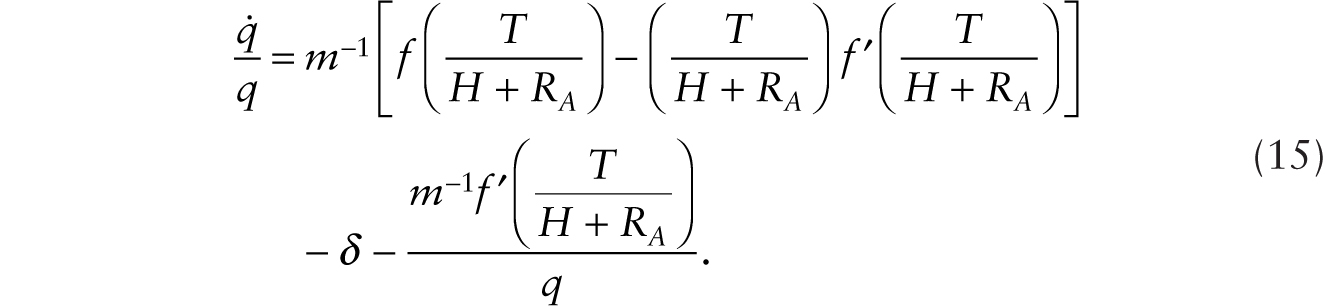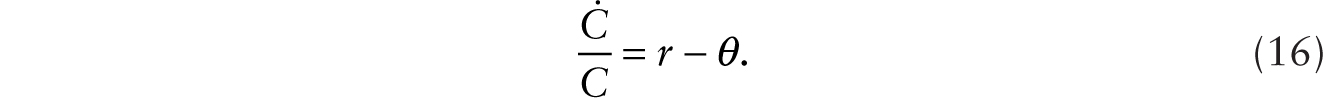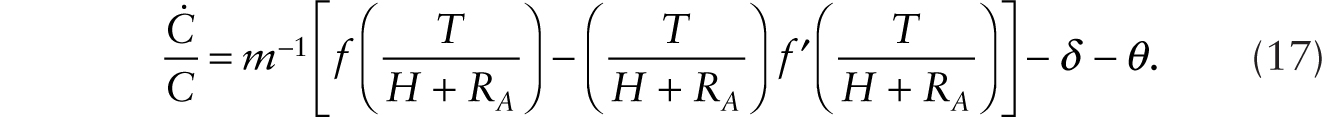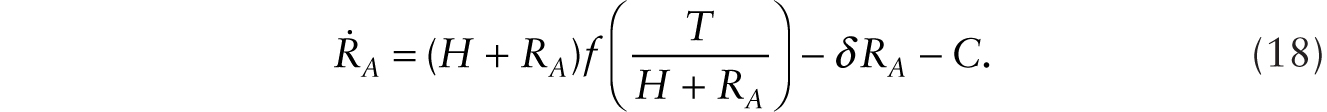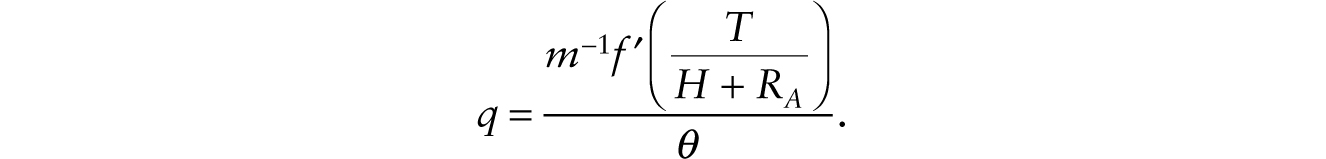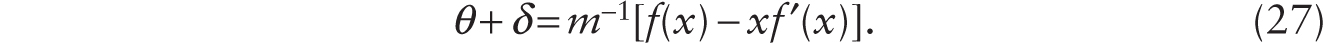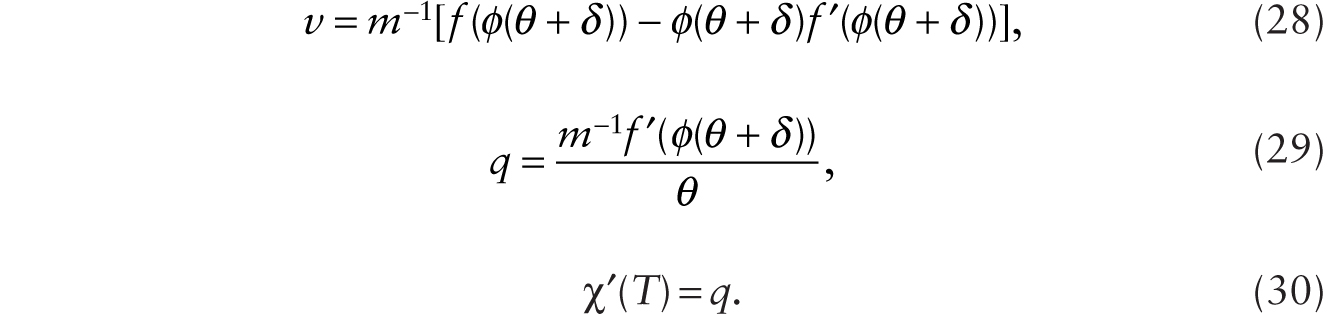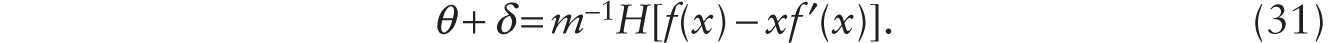9
Wage Effects of Additive and Multiplicative Robots alongside Factory Buildings and Physical Structures
Hian Teck Hoon
ABSTRACT We study the effects of robots, additive and multiplicative, on wages in an aggregative growth model in both the short and long run. There are three factors of production in the model economy: human labor, robots, and a complementary asset that groups together factory buildings and physical structures. We identify three effects from adopting robots: a factor-intensity effect, a labor-augmenting effect, and an asset price effect. When only additive robots are introduced, the real wage gradually declines to reach a permanently lower level as a result of the factor-intensity effect—more “human and robotic labor” working on a constant stock of buildings and physical structures. However, the price of buildings and physical structures unambiguously jumps up—a positive asset price effect from adopting robots. In the long run, the higher price of the complementary asset leads to the development of more factory buildings and physical structures, which attenuates the factor-intensity effect and restores real wages in the case of additive robots and raises real wages in the case of multiplicative robots.
Introduction
In contrast to the assumption of Chapter 8 that conventional machines (being malleable) can be instantaneously retrofitted to function as additive or multiplicative robots, this chapter assumes that the co-operating factor is a slow-adjusting asset like factory buildings and physical structures, which take time to build. The adjustment cost of such investments is large. With this assumption, we write the production function as Y = F(T, RA + H) with additive robots (T representing the stock of factory buildings and structures) and Y = F(T, (1 + RM)H) with multiplicative robots.
Here is a summary of the key analytical results obtained in this chapter. We introduce two different types of robots—additive robots and multiplicative robots—into an aggregative model with human workers and a co-operating asset that groups together factory buildings and physical structures in order to study the effects on wages. The price of physical structures is endogenously determined; a surge in physical structure prices enriches the owners of nonhuman wealth. An additive robot (RA) performs a job that a human worker (H) does, so total human and robotic labor is given by H + RA with suitable normalization. On the other hand, a multiplicative robot (RM) augments human labor, so total effective labor is given by (1 + RM)H. Robots that perfectly substitute for human labor, which are additive to human labor, correspond most closely to the process we commonly refer to as automation. More recently, with “deep learning” algorithms developed by scientists within the artificial intelligence (AI) community, machines are enabled to learn to a certain extent without human supervision. Workers in medical research can take advantage of deep learning to sift through and analyze large volumes of medical data. For example, an application called Face2Gene uses facial analysis and AI to analyze the relevant features of a patient and compare them with a database to provide clinicians with a list of possible rare diseases within a short time. Similar techniques can help scientists sift through experimental data for new discoveries. For example, a French company named CybeleTech uses AI to determine which seeds work best in particular environments.1 Such advances in AI would more nearly correspond to the multiplicative case we study.
The wage effects of these two polar cases are dramatically different in the short run with a constant stock of factory buildings and physical structures. As in Chapter 8, we assume that labor supply is infinitely inelastic, so we abstract from any employment effect. (We leave to the appendix to this chapter to show that we can readily extend the analysis to incorporate endogenous labor supply and thus also study the employment effects of introducing additive and multiplicative robots.) When additive robots are introduced, we show that when it is profitable for firms to adopt the robots in the production process, the real wage gradually declines to reach a permanently lower level even as the price of physical structures jumps up and gradually increases to reach a permanently higher level. Thus, this polar case of additive robots confirms the fear people have that the introduction of robots hurts workers’ wage earnings and enriches the owners of nonhuman wealth. In the long run, however, the stock of factory buildings and physical structures increases, thus restoring the real wage.
When multiplicative robots are introduced in the other polar case, we show that there are two offsetting effects with a constant stock of factory buildings and physical structures: a factor-intensity effect (with more effective labor working on a fixed supply of physical structures in the short run), which tends to reduce wages, and a labor-augmenting effect (with multiplicative robots making each worker more effective), which raises hourly pay. We establish the result that, given the price-marginal cost markup, if the share of factory buildings and physical structures is less than the elasticity of substitution between physical structures and effective labor, then introducing robots must raise the whole path of real wages. This condition is satisfied, for example, in the familiar case of a Cobb-Douglas production function. In the long run, the growth of real wages is further propelled by the accumulation of capital taking the form of factory buildings and physical structures.
In Section 1, we use the concept of the factor-price frontier to illustrate how an introduction of robots affects real wages through the factor-intensity effect and labor-augmenting effect. In Section 2, we introduce an asset price effect of adopting robots by conducting the full dynamic general-equilibrium analysis for the two polar cases: only additive robots, RA, introduced; and only multiplicative robots, RM, introduced. In Section 3, we study the long-run effects of introducing robots when the supply of factory buildings and physical structures has adjusted in response to the changes in asset prices. Section 4 concludes.
1. Robotics and Factor-Price Frontier
Consider first the case of additive robots, RA. The aggregate production function is given by Y = F(T, H + RA), which is assumed to be homogeneous of degree one in its two arguments, T and H + RA, respectively, where Y is output, T is a constant stock of factory buildings and physical structures, H is variable labor supply after overhead labor Hf has been employed with ![]() , and RA is the stock of additive robots. With a linear homogeneous production function, we write Y = (H + RA)f(T/(H + RA)) with f ′(T/(H + RA)) > 0 and f ″(T/(H + RA)) < 0. Firm optimization under conditions of imperfect competition leads to
, and RA is the stock of additive robots. With a linear homogeneous production function, we write Y = (H + RA)f(T/(H + RA)) with f ′(T/(H + RA)) > 0 and f ″(T/(H + RA)) < 0. Firm optimization under conditions of imperfect competition leads to
where v is the real hourly wage, rT is rental rate on factory buildings, ![]() is the rental rate on an additive robot, and m is the markup of price over marginal cost. With free entry and exit of firms, the condition that total revenue covers total cost pins down m.
is the rental rate on an additive robot, and m is the markup of price over marginal cost. With free entry and exit of firms, the condition that total revenue covers total cost pins down m.
Equations (1) and (2) allow us to derive the factor-price frontier. Let x ≡ T / (H + RA). Using x in (1) and (2), we have
From (5), we obtain ![]() . Using this in (4), we obtain
. Using this in (4), we obtain
We also have
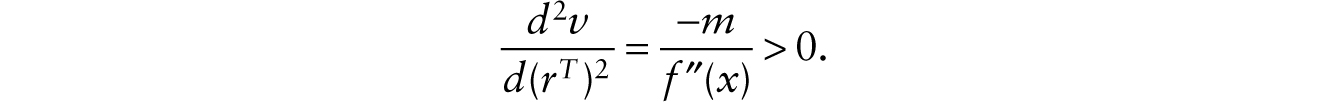
The factor-price frontier is illustrated in Figure 9.1a, given m (see the appendix for all figures). Note that in the additive robot case, ![]() . The effect of introducing an additive robot is to decrease x. As shown in Figure 9.1b, this has the effect of reducing the real wage (from v1 to v2). We call this the factor-intensity effect of introducing robots. Essentially, with more total human and robotic labor working on a constant stock of factory buildings, the marginal revenue productivity of labor falls, and lowers the wage.
. The effect of introducing an additive robot is to decrease x. As shown in Figure 9.1b, this has the effect of reducing the real wage (from v1 to v2). We call this the factor-intensity effect of introducing robots. Essentially, with more total human and robotic labor working on a constant stock of factory buildings, the marginal revenue productivity of labor falls, and lowers the wage.
Next consider the case of multiplicative robots, RM. The aggregate production function is given by Y = F(T, (1 + RM)H), which is assumed to be homogeneous of degree one in its two arguments, T and (1 + RM)H, respectively, where RM is the stock of multiplicative robots. With a linear homogeneous production function, we write Y = (1 + RM)Hf(T / (1 + RM)H). Firm optimization under conditions of imperfect competition leads to
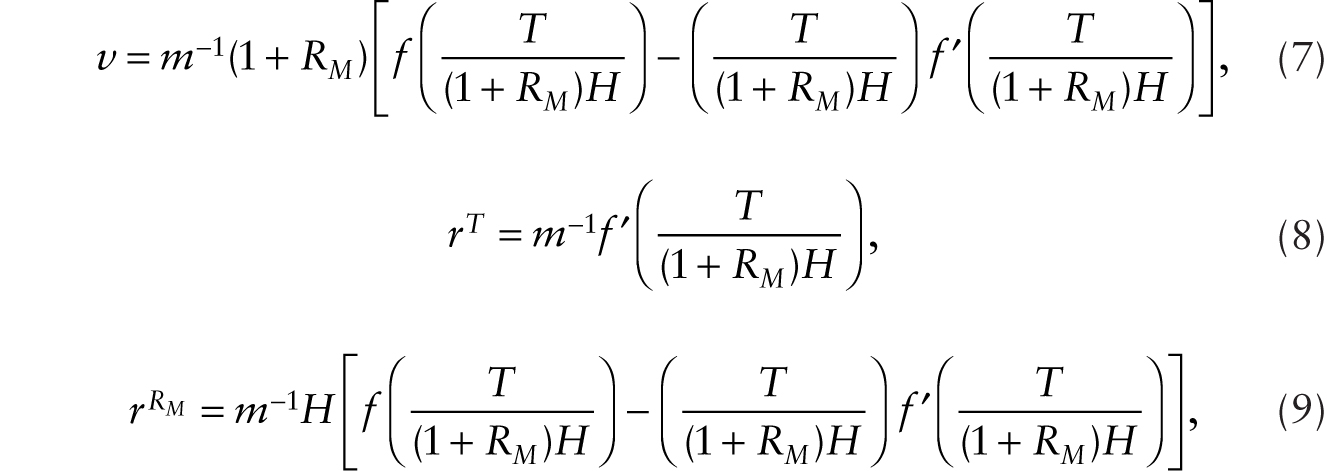
where ![]() is the rental rate on a multiplicative robot.
is the rental rate on a multiplicative robot.
In the multiplicative case, we write x ≡ T/((1 + RM)H). Using x in (7) and (8), and defining ![]() , we have
, we have
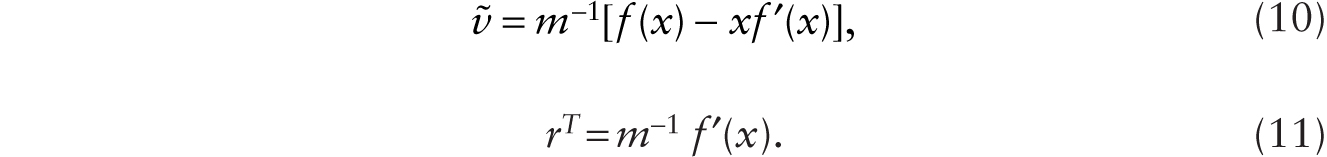
From (11), we obtain dx/drT = m[f ″(x)]−1. Using this in (10), we obtain
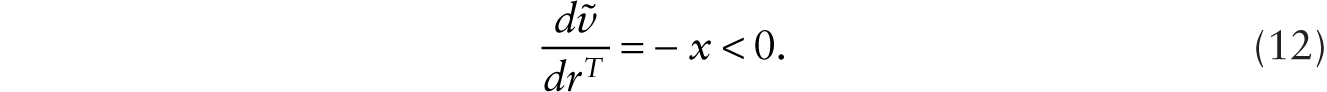
We also have
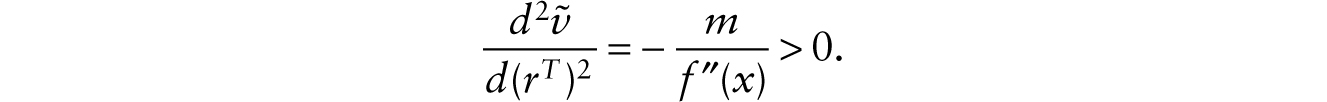
The factor-price frontier can once again be illustrated in Figure 9.1a, given m, noting that ![]() The effect of introducing a multiplicative robot is to decrease x as in the additive robot case. As shown in Figure 9.1b, this has the effect of reducing the adjusted real wage (from
The effect of introducing a multiplicative robot is to decrease x as in the additive robot case. As shown in Figure 9.1b, this has the effect of reducing the adjusted real wage (from ![]() to
to ![]() ). We call this the factor-intensity effect of introducing robots. The effect on the unadjusted real wage—that is, v—however, is represented by
). We call this the factor-intensity effect of introducing robots. The effect on the unadjusted real wage—that is, v—however, is represented by ![]() . Before the introduction of the multiplicative robot, the real wage is given by v = m−1 [f(T/H) − (T/H) f ′(T/H)]. With the introduction of robots, although x decreases (the factor-intensity effect), which results in a fall of
. Before the introduction of the multiplicative robot, the real wage is given by v = m−1 [f(T/H) − (T/H) f ′(T/H)]. With the introduction of robots, although x decreases (the factor-intensity effect), which results in a fall of ![]() , this is offset by the term (1 + RM), which multiplies
, this is offset by the term (1 + RM), which multiplies ![]() . We call this the labor-augmenting effect of introducing robots. In this case, while more “effective” labor working on a constant stock of factory buildings (taken by itself) reduces the marginal productivity of labor, there is an offsetting effect as each human worker’s effective labor input is boosted by the adoption of the multiplicative robot.
. We call this the labor-augmenting effect of introducing robots. In this case, while more “effective” labor working on a constant stock of factory buildings (taken by itself) reduces the marginal productivity of labor, there is an offsetting effect as each human worker’s effective labor input is boosted by the adoption of the multiplicative robot.
2. Dynamic General-Equilibrium Analysis
Consider an economy initially without any robots. There is no technological progress. The only nonhuman asset is the stock of factory buildings and physical structures. The representative household supplies inelastically ![]() units of labor and lives infinitely with a subjective rate of time preference given by θ. Output is given by Y = Hf (T/H). The real wage is given by
units of labor and lives infinitely with a subjective rate of time preference given by θ. Output is given by Y = Hf (T/H). The real wage is given by ![]() and the factory rental rate is given by rT = m−1 f ′(T/H). In the closed economy, consumption, C, is equal to output so C = Y. The real rate of interest is given by θ and the price of factory buildings and physical structures, q, is given by
and the factory rental rate is given by rT = m−1 f ′(T/H). In the closed economy, consumption, C, is equal to output so C = Y. The real rate of interest is given by θ and the price of factory buildings and physical structures, q, is given by
2.1. Case of Additive Robots
With the introduction of additive robots, the aggregate production function is given by Y = F(T, H + RA). Firm optimization under imperfect competition gives rise to (1) to (3). Savers can now invest in factory buildings as well as in additive robots, so equality of rate of return gives us
where r is the instantaneous real rate of interest. Using (2) and (3) in (14), we obtain
Household intertemporal optimization, assuming the log utility function, gives the familiar Euler equation
Using the expression for r, we obtain
The time rate of change in the stock of additive robots is given by
Equations (17) and (18) give a system of two dynamic equations in the variables C, a control variable, and RA, a stock variable. It is readily checked that the system exhibits saddle-path stability, which we illustrate in Figure 9.2a. Note that when RA = 0, consumption is given by Hf(T/H), which is denoted Point I in Figure 9.2a. Upon the introduction of robots, there is an immediate drop of consumption (to Point II), prompting a gradual buildup of the stock of additive robots. The economy travels along a positively sloped saddle path, where ![]() Along the adjustment path, (1) indicates that the real wage is gradually declining as the factor intensity, x = T / (H + RA), gradually decreases to reach a permanently lower level. In the new steady state, the factor intensity is pinned down by
Along the adjustment path, (1) indicates that the real wage is gradually declining as the factor intensity, x = T / (H + RA), gradually decreases to reach a permanently lower level. In the new steady state, the factor intensity is pinned down by
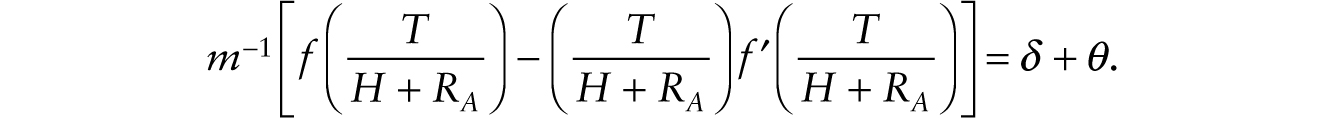
Substituting the relationship between C and RA along the saddle path, C = Φ(RA), into (18), we obtain
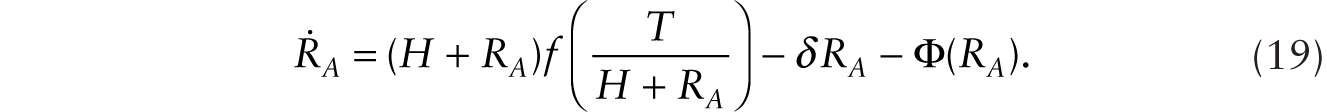
Equations (15) and (19) form another system of two dynamic equations in the variables q, a jumpy variable, and RA, a stock variable. It is readily checked that the system exhibits saddle-path stability, which we illustrate in Figure 9.2b. Note that when RA = 0, the price of factory buildings and physical structures is given by (13), which is denoted Point I in Figure 9.2b. Upon the introduction of robots, there is an immediate upward jump of factory building price, a positive asset price effect, followed by a steady rise until it reaches the new steady state. In the new steady state, the price of factory building is given by
Thus, we see that the case of introducing additive robots leads to an immiserization of real wages but an appreciation of factory building prices. With a representative household, while consumption drops initially, the introduction of the additive robot leads to a rising path of per household consumption. In the new steady state, household consumption is unambiguously higher.
2.2. Case of Multiplicative Robots
With the introduction of multiplicative robots, the aggregate production function is given by Y = F(T, (1 + RM)H). Firm optimization under imperfect competition gives rise to (7) to (9). Savers can now invest in factory buildings and physical structures as well as in multiplicative robots, so equality of rate of return gives us
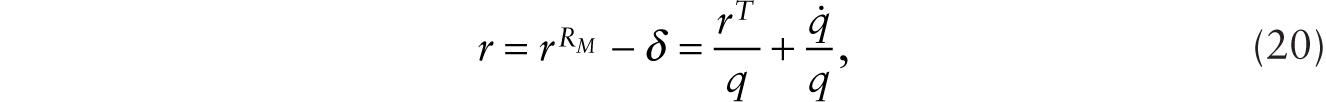
where r is the instantaneous real rate of interest. Using (8) and (9) in (20), we obtain
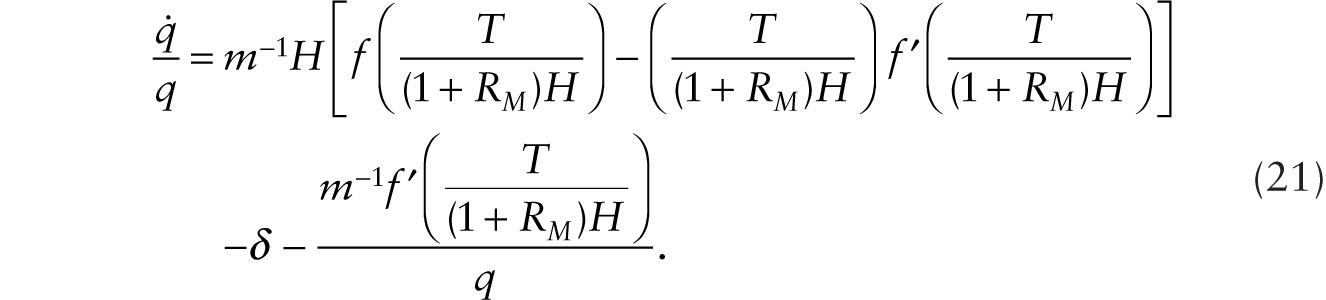
Household intertemporal optimization gives the familiar Euler equation
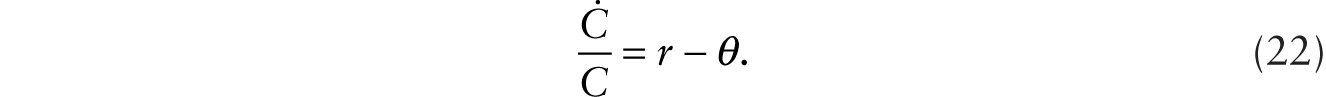
Using the expression for r, we obtain
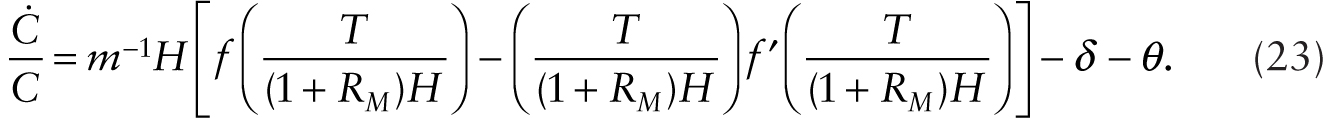
The time rate of change of multiplicative robots is given by
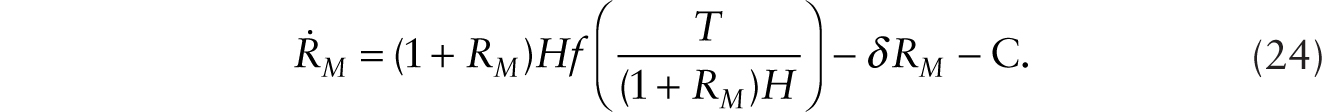
Equations (23) and (24) give a system of two dynamic equations in the variables C, a control variable, and RM, a stock variable. It is readily checked that the system exhibits saddle-path stability and can be illustrated in a diagram similar to Figure 9.2a (not shown). Upon introducing robots, there is a drop in consumption followed by a gradual buildup of robots. Substituting the relationship between C and RM along the saddle path, C = Ψ(RM), into (24), we obtain
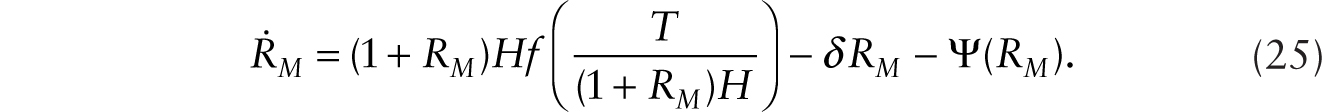
Equations (21) and (25) form another system of two dynamic equations in the variables q, a jumpy variable, and RM, a stock variable. It is readily checked that the system exhibits saddle-path stability, which we can illustrate in a diagram similar to Figure 9.2b (not shown). Upon the introduction of robots, there is an immediate upward jump of factory building price, followed by a steady rise until it reaches the new steady state.
We pointed out in the last section that with multiplicative robots, there are two effects on wages: a factor-intensity effect, which depresses wages, and a labor-augmenting effect, which boosts wages. We now examine the condition under which, given m, the labor-augmenting effect dominates so that, overall, the introduction of multiplicative robots raises the whole path of real wages. Taking the derivative of the real wage, v, in (7) with respect to the stock of multiplicative robots, RM, we obtain
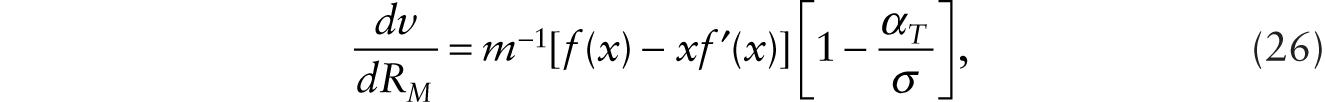
where x ≡ T / [(1 + RM)H], αT ≡ xf ′(x) / f(x) is the share of factory buildings and physical structures in national income, and σ ≡ −{f ′(x)[f(x) − xf ′(x)] / [xf ″(x)f(x)]} is the elasticity of substitution between factory buildings, T, and effective labor, (1 + RM)H. A necessary and sufficient condition for the introduction of multiplicative robots to boost wages is σ > αT. This condition is satisfied with a conventional Cobb-Douglas production function, where the elasticity of substitution is one.2
3. Long-Run Equilibrium with Endogenous Supply of Factory Buildings and Physical Structures
Suppose that the number of factory buildings and physical structures that human and robotic labor work with to produce the final output is endogenously determined. We model this by supposing that resources (measured in units of output) have to be used up in order to add to the stock of factory buildings and physical structures. Let the amount of resources used be given by the function ![]()
In the long-run equilibrium case of additive robots, with x ≡ T / (H + RA), r = θ, so
From (27), we write x = ϕ (θ + δ). Using this in (1) and (14) with ![]() , we have
, we have
We showed earlier that with a constant stock of factory buildings and physical structures, the introduction of additive robots leads to a gradual decline of the real wage. However, the adoption of additive robots boosts the shadow price of factory buildings and physical structures, thus spurring investment. In the long run, the increased stock of factory buildings and physical structures restores the real wage initially depressed by the adoption of additive robots.
In the long-run equilibrium case of multiplicative robots, with x ≡ T / [(1 + RM)H], r = θ, so
We write x = ψ ((θ + δ)/H). The real wage is given by
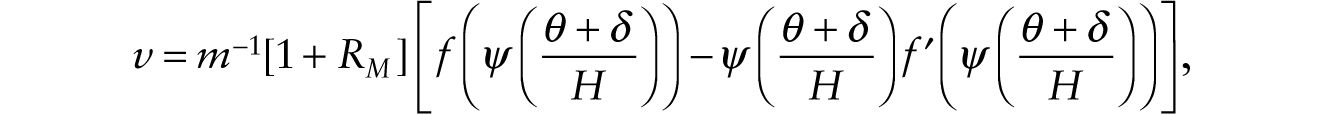
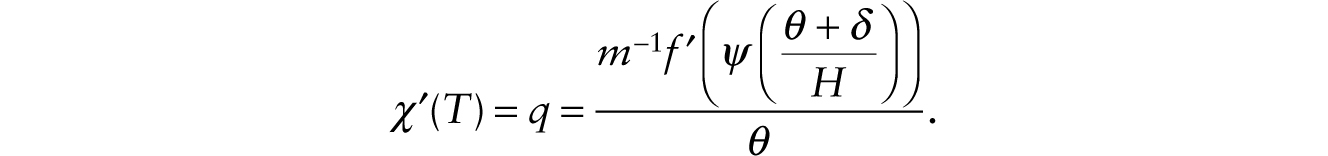
The factor-intensity effect that tends to pull down wages when robots are introduced is absent in the long run when the stock of factory buildings and physical structures adjusts endogenously. Hence, only the labor-augmenting effect of multiplicative robots is at work.
4. Conclusion
In this chapter we first studied the case of introducing only additive robots. We showed that when it is profitable for firms to adopt the robots in the production process, the real wage gradually declines to reach a permanently lower level. Essentially, with more total human and robotic labor working on a constant stock of factory buildings and physical structures, the marginal revenue product of labor falls and thus lowers the wage. This is the factor-intensity effect.
Then, we studied the case of introducing only multiplicative robots. We showed that there are two offsetting effects: a factor-intensity effect (with more effective labor working on a constant stock of factory buildings), which tends to reduce wages, and a labor-augmenting effect (with multiplicative robots making each worker more effective), which raises hourly pay. We establish the result that, given the price-marginal cost markup, if the share of factory buildings and physical structures in national income is less than the elasticity of substitution between physical structures and effective labor, then introducing robots must raise the whole path of real wages. In this case, while having more “effective” labor working on a constant stock of factory buildings and physical structures (taken by itself) reduces the marginal revenue productivity of labor, there is an offsetting effect as each human worker’s effective labor input is boosted by the adoption of the multiplicative robot.
In both cases we studied, the introduction of robots results in an upward shift in the path of the shadow value of factory buildings and physical structures, a positive asset price effect. In our model, we first assumed that the stock of factory buildings and physical structures is constant. More generally, if the stock of factory buildings and physical structures is endogenously determined at a rising marginal cost, the boost in the shadow value of factory buildings and physical structures can be expected to lead to a gradual increase in the stock of factory buildings and physical structures being used in cooperation with workers and robots. The endogenous increase in the supply of these co-operating assets can then act to offset the factor-intensity effect, which is what lies behind the wage-depressing effect of robots. In the long run, with only additive robots, the increased stock of factory buildings and physical structures restores the real wage initially depressed by the adoption of additive robots. With only multiplicative robots, the factor-intensity effect that tends to pull down wages is absent in the long run when the stock of factory buildings adjusts endogenously. Hence, only the labor-augmenting effect of multiplicative robots is at work in the long run.
The basic analysis in this chapter, which uses an aggregative model, suggests that as the stock of robots grows large, even if robots are harmless or even helpful in the long run, nations may at some point encounter resistance from workers to further introduction of robots into the economy, although it will not always be straightforward to classify machinery into additive-robot and multiplicative-robot categories. That development might not only deprive society of some of its future wage growth (and economic growth more broadly) but also stir opposition to most or all innovation, thus depriving society of the satisfactions that come with engagement in the innovation process. If robotization proceeds at a fast pace, and the outcome is these mounting tensions, social and political, these preliminary analyses would be successful.
APPENDIX
In this appendix, we introduce endogenous labor supply so that we can analyze the effects of introducing additive and multiplicative robots both on wages and on employment. To keep the analysis simple, we perform a thought experiment: What happens to the economy’s wages and employment when there is a helicopter drop of additive and multiplicative robots?
Population size is normalized to one. We assume that households are identical as before but now suppose that an individual’s current utility is given by log C + log(![]() ), where the total time endowment is normalized to one, C is aggregate consumption, and
), where the total time endowment is normalized to one, C is aggregate consumption, and ![]() is aggregate employment.3 With this representation of individual preferences, it is readily shown that aggregate employment is given by
is aggregate employment.3 With this representation of individual preferences, it is readily shown that aggregate employment is given by
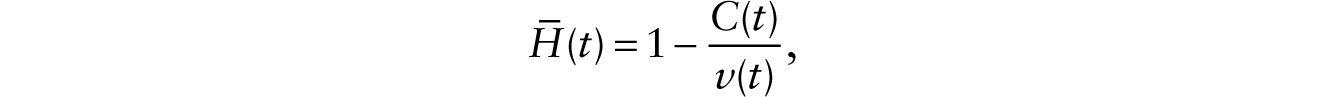
so that aggregate employment (![]() ) is negatively related to the consumption-wage ratio (C/v).
) is negatively related to the consumption-wage ratio (C/v).
In the closed economy that we are studying, assuming for simplicity that the depreciation rate (δ) is equal to zero, market clearing requires that aggregate consumption (C) equals output (F(T, H + RA) in the case of additive robots and F(T, (1 + RM)H) in the case of multiplicative robots). With additive robots, we can then write,
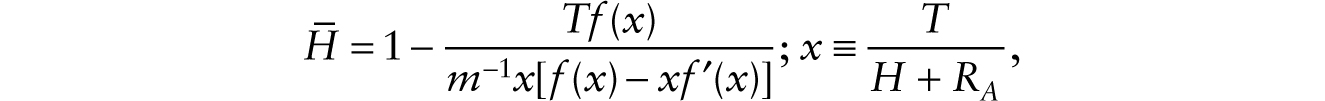
after noting v = m−1[f(x) − xf ′(x)]. We get from here a reduced-form function of aggregate employment:
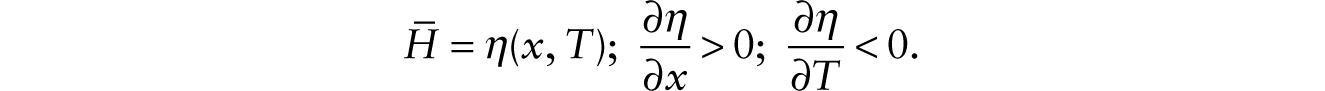
It is now evident that, given T and m, a helicopter drop of additive robots, in reducing x, leads not only to a fall in real wages but also to a decrease in aggregate employment. The real wage does not fall by as much as in the case of infinitely inelastic labor supply, so that part of the downward pressure on wages brought about by the helicopter drop of additive robots is alleviated by a contraction in aggregate employment.
Now consider a helicopter drop of multiplicative robots. With multiplicative robots, we can then write,
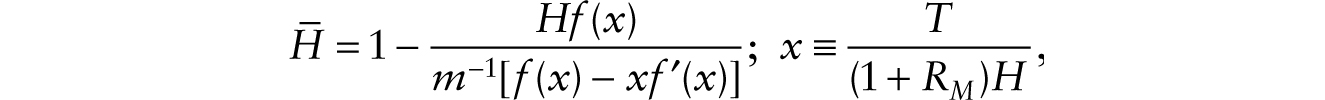
after noting v = m−1(1 + RM)[f(x) − xf ′(x)]. We get from here a reduced-form function of aggregate employment:
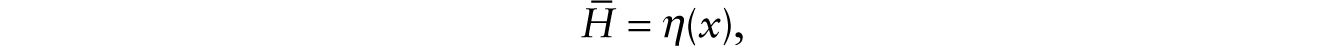
where
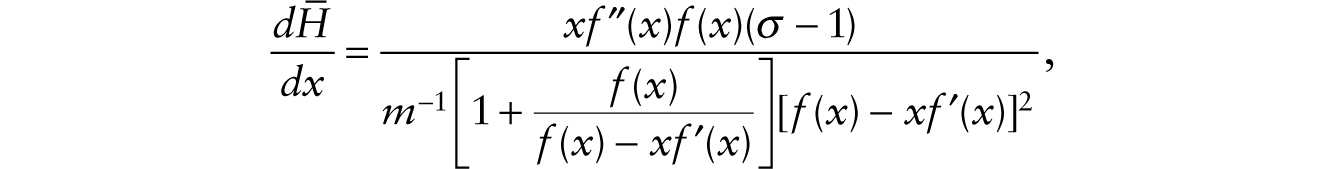
and
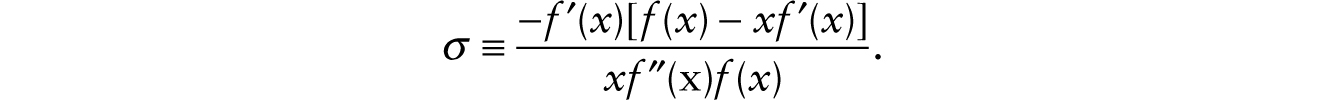
We get the result that, if the elasticity of substitution between physical structures and total effective labor (σ) is less than one, then, given T and m, a helicopter drop of multiplicative robots has an ambiguous effect on real wages but decreases aggregate employment. The real wage is pulled down by the fall in x but increased by the labor-augmenting effect of 1 + RM on human labor. If the elasticity of substitution between physical structures and total effective labor is less than one, the helicopter drop of multiplicative robots increases the consumption-wage ratio and thus contracts employment.

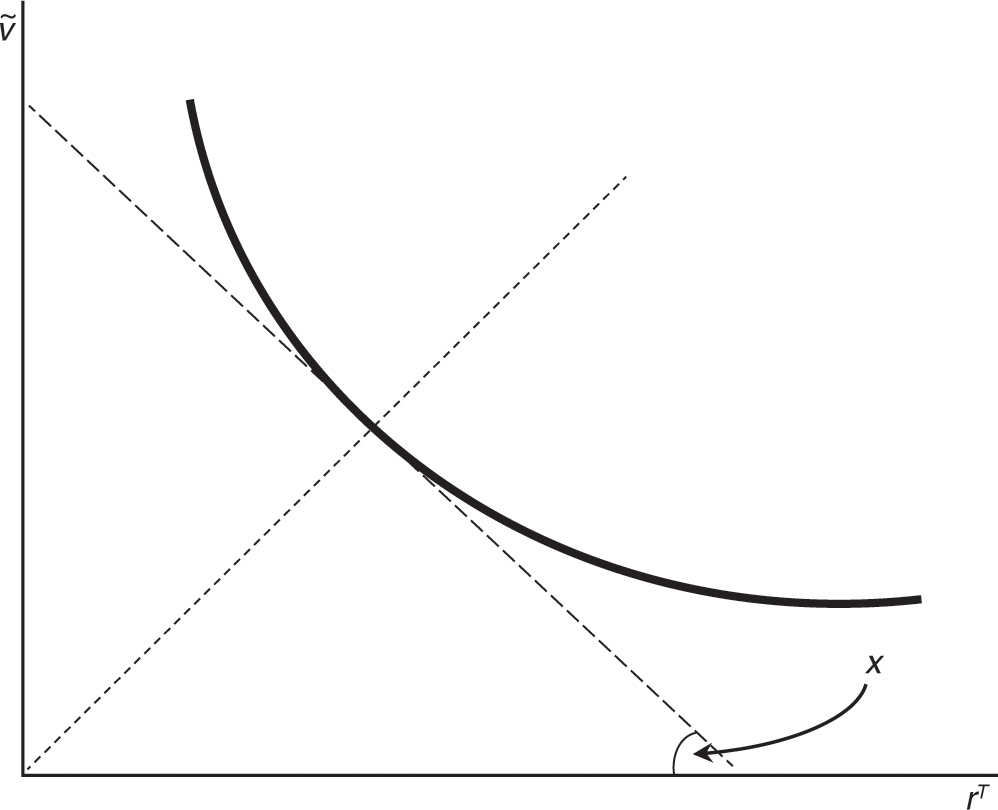
Figure 9.1a. Factor-price frontier.

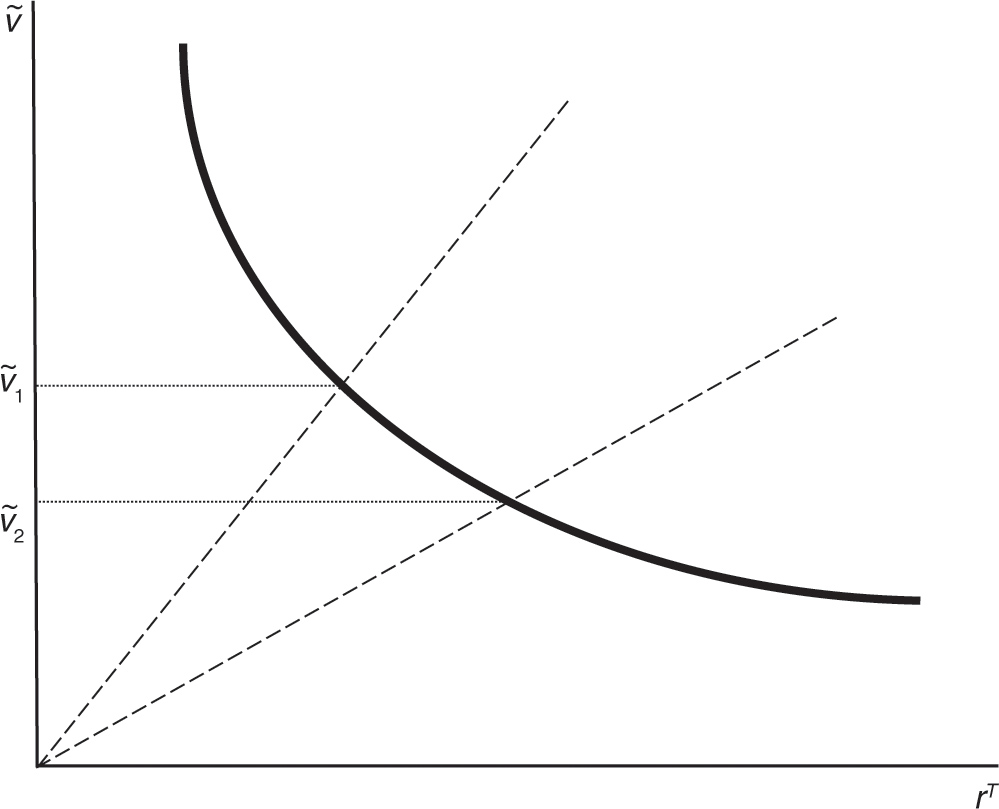
Figure 9.1b. Decrease in x due to introduction of robotics.

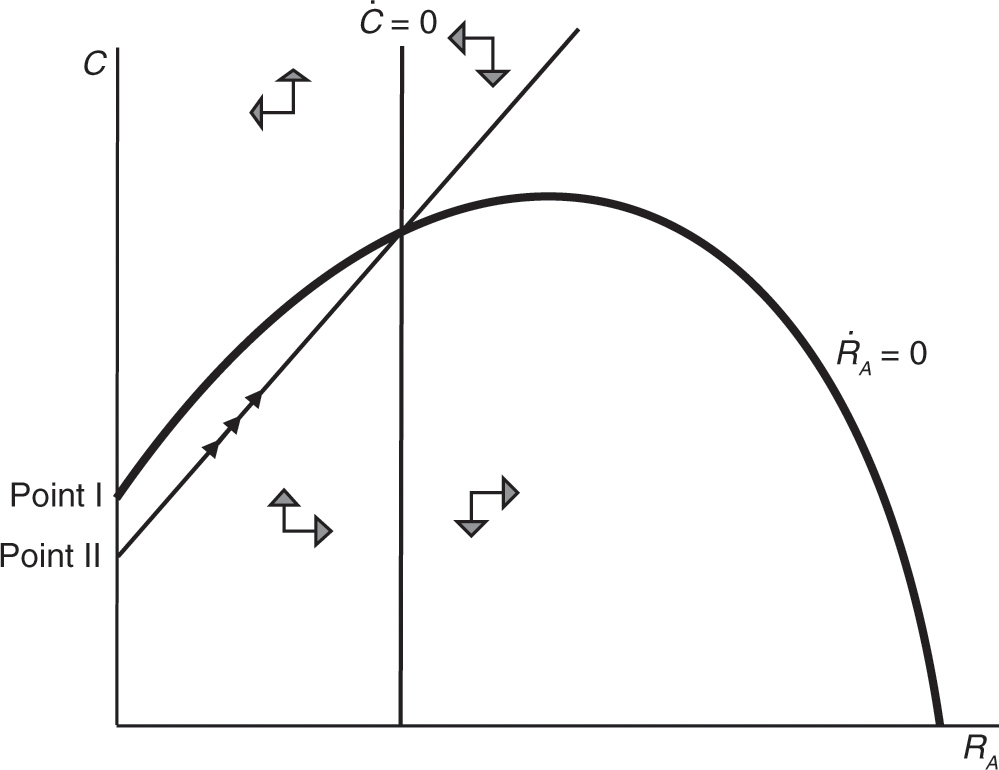
Figure 9.2a. Saddle-path stability in (RA, C) plane.

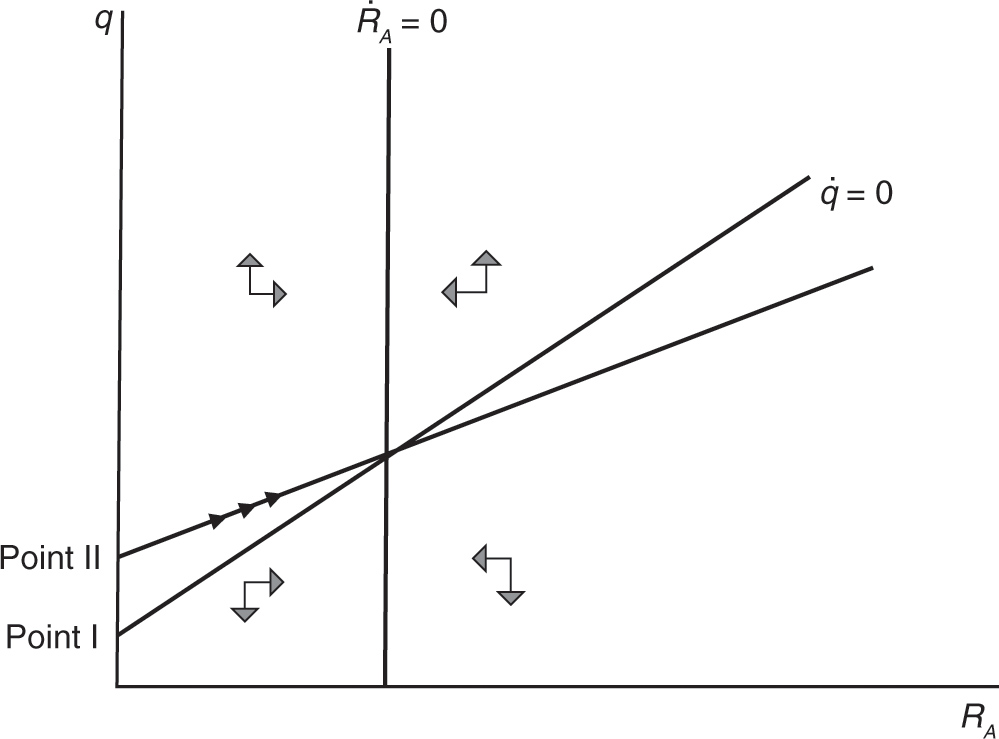
Figure 9.2b. Saddle-path stability in (RA, q) plane.