The Elliott wave principle was established by R. N. Elliott and was first published in a series of articles in Financial World in 1939. The basis of the Elliott wave theory developed from the observation that rhythmic regularity has been the law of creation since the beginning of time. Elliott noted that all cycles in nature, whether of the tide, the heavenly bodies, the planets, day and night, or even life and death, had the capability for repeating themselves indefinitely. Those cyclical movements were characterized by two forces: one building up and the other tearing down.
The principal part of the theory is concerned with form or wave patterns, but other aspects include ratio and time. In this case, pattern does not refer to the types of formation covered in earlier chapters, but to a waveform. Ratio refers to the concept of price retracements and time to the period separating important peaks and troughs.
Chapter 15 described several techniques based on the Fibonacci number sequence. This same sequence forms the basis for retracement and time development in Elliott theory.
This concept of natural law also embraces an extraordinary numerical series discovered by a thirteenth-century mathematician named Fibonacci. The series that carries his name is derived by taking the number 2 and adding to it the previous number in the series. Thus, 2 + 1 = 3, then 3 + 2 = 5, 5 + 3 = 8, 8 + 5 = 13, 13 + 8 = 21, 21 + 13 = 34, and so on. The series becomes 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, and so on. It has a number of fascinating properties, among which are the following:
1. The sum of any two consecutive numbers forms the number following them. Thus, 3 + 5 = 8 and 5 + 8 = 13, and so on.
2. The ratio of any number to its next higher is 61.8 to 100, and the ratio of any number to its next lower is 161.8 to 100.
3. The ratio 1.68 multiplied by the ratio 0.618 equals 1.
The connection between Elliott’s observation of repeating cycles of nature and the Fibonacci summation series is that the Fibonacci numbers and proportions are found in many manifestations of nature. For example, a sunflower has 89 curves, of which 55 wind in one direction and 34 in the opposite direction. In music, an octave comprises 13 keys on a piano, with 5 black notes and 8 white. Trees always branch from the base in Fibonacci series, and so on.
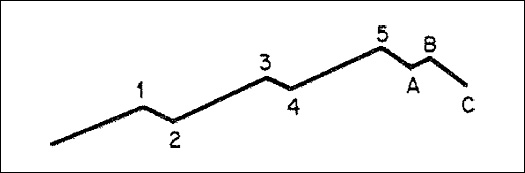
Combining his observation of natural cycles with his knowledge of the Fibonacci series, Elliott noted that the market moves forward in a series of five waves and then declines in a series of three waves. He concluded that a single cycle comprised eight waves, as shown in Figure A.1 (3, 5, and 8 are, of course, Fibonacci numbers).
FIGURE A.1 Typical Cycle

The upper part of the cycle consists of five waves. Waves 1, 3, and 5 are protrend moves and are called impulse waves. Waves 2 and 4, on the other hand, are called corrective waves because they correct waves 1 and 3. The declining part of the cycle consists of three waves, known as a, b, and c.
The longest cycle in the Elliott concept is called the grand supercycle. In turn, each grand supercycle can be subdivided into eight supercycle waves, each of which is then divided into eight cycle waves. The process continues to embrace primary, intermediate, minute, minuette, and subminuette waves. The various details are highly intricate, but the general picture is represented in Figures A.1 and A.2.
FIGURE A.2 Complete Cycle with Subwaves
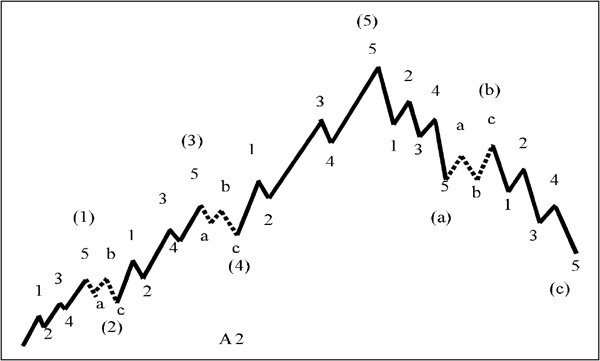
Figure A.2 shows a complete cycle with its subwaves. The determinant of whether a wave divides into five or three is the direction of the next largest wave. Corrections are always three-wave affairs.
Figures A.3 and A.4 show Elliott in historical perspective. Figure A.3 illustrates the first five waves of the grand supercycle, which Elliott deemed to have begun in 1800. Some Elliott wave theoreticians believe that the grand supercycle peaked at the end of the twentieth century.
FIGURE A.3 The Grand Supercycle
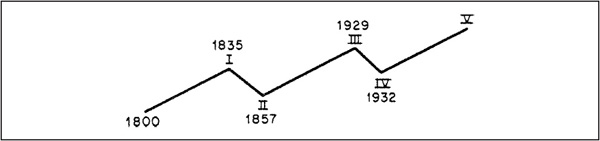
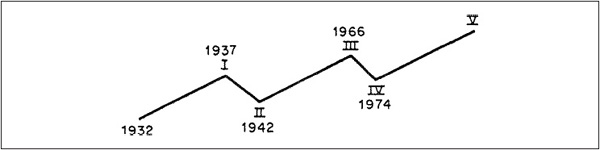
As the wave principle is one of form, there is no way to determine when the three corrective waves are likely to appear. However, the frequent recurrences of Fibonacci numbers representing time spans between peaks and troughs are probably beyond coincidence. These time spans are shown in Table A.1.
TABLE A.1 Time Spans Between Stock Market Peaks and Troughs
More recently, 8 years occurred between the 1966 and 1974 bottoms, the 1968 and 1976 tops, and the 1990 and 1998 bottoms. Also, there were 5 years between the 1968 and 1973 tops, for example. By the same token, there are many peaks and troughs that are not separated by numbers in this sequence.
It can readily be seen that the real problem with Elliott is interpretation. Indeed, every wave theorist (including Elliott himself) has at some time or another become entangled with the question of where one wave finished and another started. As far as the Fibonacci time spans are concerned, although these periods recur frequently, it is extremely difficult to use this principle as a basis for forecasting; there are no indications whether time spans based on these numbers will produce tops to tops or bottoms to tops, or something else, and the permutations are infinite.
We have hardly scratched the surface, and in some respects the old maxim “A little knowledge is a dangerous thing” applies probably more to Elliott than to any other market theorist. Its subjectivity in itself can be dangerous because the market is very subject to emotional influences. Consequently, the weight given to Elliott interpretations should probably be downplayed. Those wishing to pursue this theory in greater detail are referred to the classic text on the subject, by Frost and Prechter, called Elliott Wave Principle (Gainsville, GA, New Classics Library, 1978), since the theory has been described in this Appendix only in its barest outline.