Reading and Manipulating Data |
Traditional statistical computer packages such as SAS or SPSS are designed primarily to transform rectangular data sets into (sometimes very long) printed reports and graphs. A rectangular data set has rows representing observations and columns representing variables. In contrast, R is a programming language embedded in a statistical computing environment. It is designed to transform data objects into other data objects, (generally brief) printed reports, and graphs.
R supports rectangular data sets, in the form of data frames, but it also supports a variety of other data structures. One by-product of this generality is flexibility: Tasks not directly designed into the software are typically easier to carry out in R than in a statistical package. Another by-product of generality, however, is complexity. In this chapter, we attempt to eliminate some of the complexity:
Section 2.1 describes how to read data into R variables and data frames. Section 2.2 explains how to work with data stored in data frames. Section 2.3 introduces matrices, higher-dimensional arrays, and lists. Section 2.4 explains how to manipulate character data in R. Section 2.5 discusses how to handle large data sets in R. Finally, Section 2.6 deals more abstractly with the organization of data in R, explaining the notions of classes, modes, and attributes, and describing the problems that can arise with floating-point calculations.
2.1 Data Input
Although there are many ways to read data into R, we will concentrate on the most important ones: typing data directly at the keyboard, reading data from a plain-text (also known as ASCII) file into an R data frame, importing data saved by another statistical package, importing data from a spreadsheet, and accessing data from one of R’s many packages. In addition, we will explain how to generate certain kinds of patterned data. In Section 2.5.3, we will briefly discuss how to access data stored in a database management system.
| 2.1.1 | KEYBOARD INPUT |
Entering data directly into R using the keyboard can be useful in some circumstances. First, if the number of values is small, keyboard entry can be efficient. Second, as we will see, R has a number of functions for quickly generating patterned data. For large amounts of data, however, keyboard entry is likely to be inefficient and error-prone.
We saw in Chapter 1 how to use the c (c ombine) function to enter a vector of numbers:
> (x <− c(1, 2, 3, 4))
[1] 1 2 3 4
Recall that enclosing the command in parentheses causes the value of x to be printed. The same procedure works for vectors of other types, such as character data or logical data:
> (names <− c("John", "Sandy", ’Mary’))
[1] "John" "Sandy" "Mary"
> (v <− c(TRUE, FALSE))
[1] TRUE FALSE
Character strings may be input between single or double quotation marks: for example, ’John’ and "John" are equivalent. When R prints character strings, it encloses them within double quotes, regardless of whether single or double quotes were used to enter the strings.
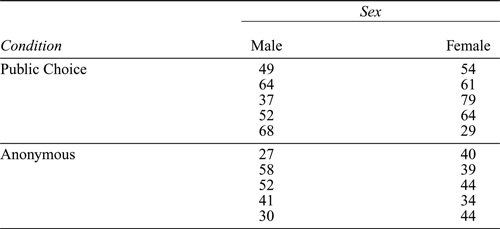
Table 2.1 Data from an experiment on anonymity and cooperation by Fox and Guyer (1978). The data consist of the number of cooperative choices made out of 120 total choices.

Entering data in this manner works well for very short vectors. You may have noticed in some of the previous examples that when an R statement is continued on additional lines, the > (greater than) prompt is replaced by the interpreter with the + (plus) prompt on the continuation lines. R recognizes that a line is to be continued when it is syntactically incomplete— for example, when a left parenthesis needs to be balanced by a right parenthesis or when the right argument to a binary operator, such as * (multiplication), has not yet been entered. Consequently, entries using c may be continued over several lines simply by omitting the terminal right parenthesis until the data are complete. It may be more convenient, however, to use the scan function, to be illustrated shortly, which prompts with the index of the next entry.
Consider the data in Table 2.1. The data are from an experiment (Fox and Guyer, 1978) in which each of 20 four-person groups of subjects played 30 trials of a prisoners’ dilemma game in which subjects could make either cooperative or competitive choices. Half the groups were composed of women and half of men. Half the groups of each sex were randomly assigned to a public-choice condition, in which the choices of all the individuals were made known to the group after each trial, and the other groups were assigned to an anonymous-choice condition, in which only the aggregated choices were revealed. The data in the table give the number of cooperative choices made in each group, out of 30 × 4 = 120 choices in all.
To enter the number of cooperative choices as a vector, we could use the c function, typing the data values separated by commas, but instead we will illustrate the use of the scan function:
1: 49 64 37 52 68 54
7: 61 79 64 29
11: 27 58 52 41 30 40 39
18: 44 34 44
21:
Read 20 items
[1] 49 64 37 52 68 54 61 79 64 29 27 58 52 41 30 40 39 44 34 44
The number before the colon on each input line is the index of the next observation to be entered and is supplied by scan ; entering a blank line terminates scan . We entered the data for the Male, Public-Choice treatment first, followed by the data for the Female, Public-Choice treatment, and so on.
We could enter the condition and sex of each group in a similar manner, but because the data are patterned, it is more economical to use the rep (replicate) function. The first argument to rep specifies the data to be repeated; the second argument specifies the number of repetitions:
> rep(5, 3)
[1] 5 5 5
> rep(c(1, 2, 3), 2)
[1] 1 2 3 1 2 3
When the first argument to rep is a vector, the second argument can be a vector of the same length, specifying the number of times each entry of the first argument is to be repeated:
> rep(1:3, 3:1)
[1] 1 1 1 2 2 3
In the current context, we may proceed as follows:
> (condition <− rep(c("public", "anonymous"), c(10, 10)))

Thus, condition is formed by repeating each element of c("public", "anonymous") 10 times.
> (sex <− rep(rep(c("male", "female"), c(5, 5)), 2))

The vector sex requires using rep twice, first to generate five "male" character strings followed by five "female" character strings, and then to repeat this pattern twice to get all 20 values.
Finally, it is convenient to put the three variables together in a data frame:
> (Guyer <− data.frame(cooperation, condition, sex))

The original variables condition and sex are character vectors. When vectors of character strings are put into a data frame, they are converted by default into factors, which is almost always appropriate for subsequent statistical analysis of the data. (The important distinction between character vectors and factors is discussed in Section 2.2.4.)
R has a bare-bones, spreadsheet-like data editor that may be used to enter, examine, and modify data frames. We find this editor useful primarily for modifying individual values—for example, to fix an error in the data. If you prefer to enter data in a spreadsheet-like environment, we suggest using one of the popular and more general spreadsheet programs such as Excel or OpenOffice Calc, and then importing your data into R.
To enter data into a new data frame using the editor, we may type the following:
> Guyer <− edit(as.data.frame(NULL))
This command opens the data editor, into which we may type variable names and data values. An existing data frame can be edited with the fix function, as in fix(Guyer) .
The fix function can also be used to examine an existing data frame, but the View function is safer and more convenient: safer because View cannot modify the data, and more convenient because the View spreadsheet window can remain open while we continue to work at the R command prompt. In contrast, the R interpreter waits for fix or edit to terminate before returning control to the command prompt.
| 2.1.2 | FILE INPUT TO A DATA FRAME |
DELIMITED DATA IN A LOCAL FILE
The previous example shows how to construct a data frame from preexisting variables. More frequently, we read data from a plain-text (ASCII) file into an R data frame using the read.table function. We assume that the input file is organized in the following manner:
This specification is more rigid than it needs to be, but it is clear and usually is easy to satisfy. Most spreadsheet, database, and statistical programs are capable of producing plain-text files of this format, or produce files that can be put in this form with minimal editing. Use a plain-text editor (such as Windows Notepad or a programming editor) to edit data files. If you use a word-processing program (such as Word or OpenOffice Writer), be careful to save the file as a plain-text file; read.table cannot read data saved in the default formats used by word-processing programs.
We use the data in the file Prestige.txt to illustrate.1 This data set, with occupations as observations, is similar to the Duncan occupational-prestige data employed as an example in the previous chapter. Here are a few lines of the data file (recall that the ellipses represent omitted lines—there are 102 occupations in all):
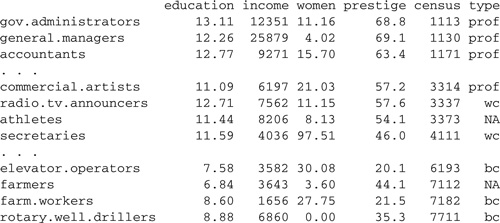
The variables in the data file are defined as follows:
To read the data into R, we enter:
> (Prestige <− read.table("D:/data/Prestige.txt", header=TRUE))
The first argument to read.table specifies the location of the input file, in this case the location in our local file system where we placed Prestige.txt. As we will see, with an active Internet connection, it is also possible to read a data file from a URL (web address). We suggest naming the data frame for the file from which the data were read and to begin the name of the data frame with an uppercase letter: Prestige .
Even though we are using R on a Windows system, the directories in the file system are separated by a / (forward slash) rather than by the standard Windows \ (back slash), because the back slash serves as a so-called escape character in an R character string, indicating that the next character has a special meaning: For example, \n represents a new-line character (i.e., go to the beginning of the next line), while \t is the tab character. Such special characters can be useful in creating printed output. A (single) back slash may be entered in a character string as \\.
You can avoid having to specify the full path to a data file if you first tell R where to look for data by specifying the working directory. For example, setwd("D:/data") sets the working directory to D:\data, and the command read.table("mydata.txt") would then look for the file mydata.txt in the D:\data directory. On Windows or Mac OS X, the command setwd(choose.dir()) allows the user to select the working directory interactively.2 The command getwd() displays the working directory.
Under Windows or Mac OS X, you can also browse the file system to find the file you want using the file.choose function:
> Prestige <− read.table(file.choose(), header=TRUE)
The file.choose function returns the path to the selected file as a character string, which is then passed to read.table .
The second argument, header=TRUE , tells read.table that the first line in the file contains variable names. It is not necessary to specify header= TRUE when, as here, the initial variable-names line has one fewer entry than the data lines that follow. The first entry on each data line in the file is an observation label. Nevertheless, it does not hurt to specify header=TRUE , and getting into the habit of doing so will save you trouble when you read a file with variable names but without row names.
If you have an active Internet connection, files can also conveniently be read from their URLs. For example, we can read the Canadian occupational-prestige data set from the website for the book:3
> Prestige <− read.table(
+ "http://socserv.socsci.mcmaster.ca/jfox/ books/Companion/data/Prestige.txt",
+ header=TRUE)
DEBUGGING DATA FILES
Not all data files can be read on the first try. Here are some simple steps to follow to correct a problematic data file.
Whenever you read a file for the first time, it is a good idea to run a few checks to make sure the file doesn’t have any problems. The summary function can be helpful for this purpose. For the Prestige data frame:
> summary(Prestige)
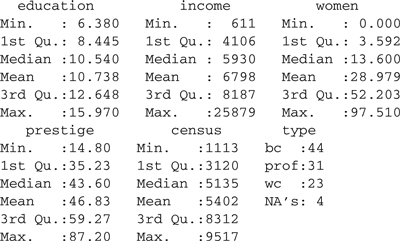
From this output, we see that all the variables except type are numeric, because numeric summaries are reported, while type is a factor with levels bc , wc , and prof ; furthermore, type has four missing values, given by the NA s.
If we had made an error in entering a numeric value—for example, typing the letter l (“ell”) instead of the numeral 1 (one), or the letter O (“oh”) instead of the numeral 0 (zero)—then the corresponding variable would have been made into a factor with many levels rather than a numeric variable, and we would have to correct the data in order to read them properly. Similarly, numbers with embedded commas, such as 2,000,000 , are treated as character values rather than as numeric data, and so the corresponding variables would be incorrectly read as factors. Finally, if a value of type were entered incorrectly as BC rather than bc , then the type factor would acquire the additional level BC .
In some instances, an error in the data will prevent a file from being read at all, a problem that is usually caused by having too many or too few values in a line of the data file. Too many values can be produced by embedded blanks: For example, the characters − 2.3 in an input line, with a space between the minus sign and 2.3 , would be read as two values, - and 2.3 , not as the intended negative number −2.3. Too few items can be produced by coding missing data with blanks rather than with a proper missing-value indicator such as NA .
To simulate too few values in input lines, we prepared a version of the Prestige.txt data file in which NAs were erroneously replaced by blanks. Trying to read this file yields the following result:
> file <−
+ "http://socserv.socsci.mcmaster.ca/jfox/ books/Companion/data/Prestige-bugged.txt"
> Prestige <− read.table(file, header=TRUE)
Error in scan(file = file, what = what, sep = sep, quote = quote, skip = 0, : line 34 did not have 7 elements
Because of the error, the data frame Prestige has not been created, and the error message tells us that at least one line in the file has the wrong number of elements. We can use the count.fields function to discover whether there are other errors as well, and, if there are, to determine their location:
> (counts <− count.fields(file))
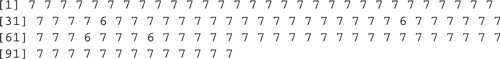
> which(counts != 7)
[1] 35 54 64 68
Once we know the location of the errors, it is simple to fix the input file in a text editor that keeps track of line numbers. Because the data file has column names in its first line, the 34th data line is the 35th line in the file.
FIXED-FORMAT DATA
Although they are no longer common, you may encounter fixed-format data files, in which the data values are not separated by white space or commas and in which variables appear in fixed positions within each line of the file. To illustrate the process of reading this kind of data, we have created a fixed-format version of the Canadian occupational-prestige data set, which we placed in the file Prestige-fixed.txt. The file looks like this:
gov.administrators | 13.111235111.1668.81113prof |
general.managers | 12.2625879 4.0269.11130prof |
12.77 927115.7063.41171prof | |
… | |
typesetters | 10.00 646213.5842.29511bc |
bookbinders | 8.55 361770.8735.29517bc |
The first 25 characters in each line are reserved for the occupation name, the next five spaces for the education value, the next five for income , and so on. Most of the data values run together, making the file difficult to decipher. If you have a choice, fixed-format input is best avoided. The read.fwf (read fixed- width- format) function can be used to read this file into a data frame:
> file <−
+ "http://socserv.socsci.mcmaster.ca/jfox/books/ Companion/data/Prestige-fixed.txt"
> Prestige <− read.fwf(file,
+ col.names=c("occupation", "education", "income", "women",
+ "prestige", "census", "type"),
+ row.names="occupation",
+ widths=c(25, 5, 5, 5, 4, 4, 4))
Our sample file does not have an initial line with variable names, and so the default value of header=FALSE is appropriate. The col.names argument to read.fwf supplies names for the variables, and the argument row.-names indicates that the variable occupation should be used to define row names. The widths argument gives the field width of each variable in the input file.
| 2.1.3 | IMPORTING DATA |
DATA FROM OTHER STATISTICAL PACKAGES
You are likely to encounter data sets that have been prepared in another statistical system, such as SAS or SPSS. If you have access to the other program, then exporting the data as a plain-text (ASCII) file for reading into R is generally quite straightforward. Alternatively, R provides facilities for importing data from other programs through functions in the foreign package, which is part of the standard R distribution. Currently, functions are available for importing data files from S version 3, SAS, SPSS, Minitab, Stata, and others. For example, the function read.spss is used to import SPSS data sets.
DATA FROM A SPREADSHEET
Raw data in a spreadsheet are probably the most common form of data that you will encounter. We can recommend three approaches to reading data from a spreadsheet. The simplest procedure may be to use the spreadsheet program to save the file in a format that can be read by read.table , usually a plaintext file with either white-space-delimited or comma-separated values. For this process to work, the data you want must be in the top-most worksheet of the spreadsheet, and the worksheet should look like a plain-text data file, with optional variable names in the first row, optional row names in the first column, and the row-by-column matrix of data values filled in completely. No extraneous information, such as variable labels requiring two rows, should be included.
The second approach is to copy the data you want to the clipboard and then to use an R function such as read.table to read the data from the clipboard. Select the data to be read in the spreadsheet program (e.g., by left-clicking and dragging the mouse over the data); the first row of the blocked data can contain variable names and the first column can contain row names. Next, copy the selected data to the clipboard (e.g., in Windows by the key combination Control-c and in Mac OS X by command-c). Finally, switch to R, and enter a command such as Data <− read.table("clipboard", header=TRUE) to read the data into the data frame Data . If the first selected row in the spreadsheet doesn’t contain variable names, omit the argument header=TRUE .
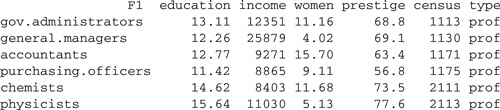
On Windows, the RODBC package4 can be used to read spreadsheets in Excel format directly. For example, the file Datasets.xls on the website for the book is an Excel file containing two worksheets: Duncan , with Duncan’s occupational-prestige data, and Prestige , with the Canadian occupational-prestige data. We placed this file in D:\data\Datasets.xls. To read the Prestige data into R,
> library(RODBC)
> channel <− odbcConnectExcel("D:/data/Datasets.xls")
> Prestige <− sqlQuery(channel, "select * from [Prestige$]")
> odbcClose(channel)
> head(Prestige) # first 6 rows
Recall that everything to the right of the # (pound sign) is a comment and is ignored by the R interpreter. For Excel 2007 files, use odbcConnect-Excel2007 in place of odbcConnectExcel .
The variable name "F1" was supplied automatically for the first column of the spreadsheet. We prefer to use this column to provide row names for the Prestige data frame:
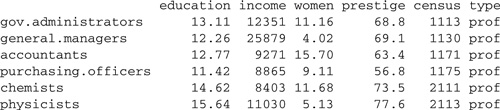
> rownames(Prestige) <− Prestige$F1
> Prestige$F1 <− NULL # remove F1 from Prestige
> head(Prestige)
> remove(Prestige) # clean up
The RODBC package can also be used to connect R to a database management system (a topic that we will discuss briefly in Section 2.5.3).
| 2.1.4 | ACCESSING DATA IN R PACKAGES |
Many R packages, including the car and alr3 packages, contain data sets. R provides two mechanisms for accessing the data in packages:
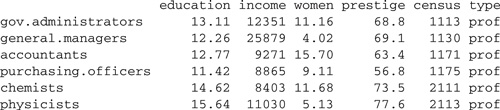
> data(Prestige, package="car")
> head(Prestige) # first 6 rows

> remove(Prestige) # clean up
Had the car package already been loaded, the package argument to data could have been omitted.
library(car)
…
> head(Prestige)
We have defined several variables in the course of this section, some of which are no longer needed, so it is time to clean up:
> objects()
![]()
> remove(channel, names, v, x)
> detach(package:RODBC)
We have retained the data frame Guyer and the vectors condition , cooperation , and sex for subsequent illustrations in this chapter. Because we are finished with the RODBC package, we have detached it.
| 2.1.5 | GETTING DATA OUT OF R |
We hope and expect that you will rarely have to get your data out of R to use with another program, but doing so is nevertheless quite straightforward. As in the case of reading data, there are many ways to proceed, but a particularly simple approach is to use the write.table or write.csv function to output a data frame to a plain-text file. The syntax for write.table is essentially the reverse of that for read.table . For example, the following command writes the Duncan data frame (from the attached car package) to a file:
> write.table(Duncan, "c:/temp/Duncan.txt")
By default, row labels and variable names are included in the file, data values are separated by blanks, and all character strings are in quotes, whether or not they contain blanks. This default behavior can be changed—see ?write.table .
The foreign package also includes some functions for exporting R data to a variety of file formats: Consult the documentation for the foreign package, help(package="foreign") .
2.2 Working With Data Frames
It is perfectly possible in R to analyze data stored in vectors, but we generally prefer to begin with a data frame, typically read from a file via the read.table function or accessed from an R package. Almost all the examples in this Companion use data frames from the car package.
In many statistical packages, such as SPSS, a single data set is active at any given time; in other packages, such as SAS, individual statistical procedures typically draw their data from a single source, which by default in SAS is the last data set created. This is not the case in R, where data may be used simultaneously from several sources, providing flexibility but with the possibility of interference and confusion.
There are essentially two ways to work with data in a data frame, both of which we will explain in this section:
New users of R generally prefer the first approach, probably because it is superficially similar to other statistical software in which commands reference an active data set. For reasons that we will explain, however, experienced users of R usually prefer not to attach data frames to the search path.
| 2.2.1 | THE SEARCH PATH |
When you type the name of a variable in a command, the R interpreter looks for an object of that name in the locations specified by the search path.We attach the Duncan data frame to the search path with the attach function and then use the search function to view the current path:
> attach(Duncan)
> search()

Now if we type the name of the variable prestige at the command prompt, R will look first in the global environment (.GlobalEnv ), the region of memory in which R stores working data. If no variable named prestige is found in the global environment, then the data frame Duncan will be searched, because it was placed by the attach command in the second position on the search list. There is in fact no variable named prestige in the working data, but there is a variable by this name in the Duncan data frame, and so when we type prestige , we retrieve the prestige variable from Duncan , as we may readily verify:
> prestige
![]()
![]()
Typing Duncan$prestige directly extracts the column named prestige from the Duncan data frame.6
Had prestige not been found in Duncan , then the sequence of attached packages would have been searched in the order shown, followed by a special list of objects (Autoloads ) that are loaded automatically as needed (and which we will subsequently ignore), and finally the R base package. The packages in the search path shown above, beginning with the stats package, are part of the basic R system and are loaded by default when R starts up.
Suppose, now, that we attach the Prestige data frame to the search path. The default behavior of the attach function is to attach a data frame in the second position on the search path, after the global environment:
> attach(Prestige)
The following object(s) are masked from Duncan :
education income prestige type
The following object(s) are masked from package:datasets :
women
> search()

Consequently, the data frame Prestige is attached before the data frame Duncan ; and if we now simply type prestige , then the prestige variable in Prestige will be located before the prestige variable in Duncan is encountered:
> prestige

The prestige variable in Duncan is still there—it is just being shadowed or masked (i.e., hidden) by prestige in Prestige , as the attach command warned us:
> Duncan$prestige
![]()
Because the variables in one data frame can shadow the variables in another, attaching more than one data frame at a time can lead to unanticipated problems and should generally be avoided. You can remove a data frame from the search path with the detach command:
> detach(Prestige) > search()

Calling detach with no arguments detaches the second entry in the search path and, thus, produces the same effect as detach(Prestige) .
Now that Prestige has been detached, prestige again refers to the variable by that name in the Duncan data frame:
> prestige
![]()
The working data are the first item in the search path, and so globally defined variables shadow variables with the same names anywhere else along the path. This is why we use an uppercase letter at the beginning of the name of a data frame. Had we, for example, named the data frame prestige rather than Prestige , then the variable prestige within the data frame would have been shadowed by the data frame itself. To access the variable would then require a potentially confusing expression, such as prestige$prestige .
Our focus here is on manipulating data, but it is worth mentioning that R locates functions in the same way that it locates data. Consequently, functions earlier on the path can shadow functions of the same name later on the path.
In Section 1.1.3, we defined a function called myMean , avoiding the name mean so that the mean function in the base package would not be shadowed. The base function mean can calculate trimmed means as well as the ordinary arithmetic mean; for example,
[1] 47.68889
> mean(prestige, trim=0.1)
[1] 47.2973
Specifying mean(prestige, trim=0.1) removes the top and bottom 10% of the data, calculating the mean of the middle 80% of observations. Trimmed means provide more efficient estimates of the center of a heavy-tailed distribution—for example, when outliers are present; in this example, however, trimming makes little difference.
Suppose that we define our own mean function, making no provision for trimming:
> mean <− function(x){ + warning("the mean function in the base package is shadowed") + sum(x)/length(x) + }
The first line in our mean function prints a warning message. The purpose of the warning is simply to verify that our function executes in place of the mean function in the base package. Had we carelessly shadowed the standard mean function, we would not have politely provided a warning:
> mean(prestige)
[1] 47.68889
Warning message:
In mean(prestige):the mean function in the base package is shadowed
The essential point here is that because our mean function resides in the global environment, it is encountered on the search path before the mean function in the base package. Shadowing the standard mean function is inconsequential as long as our function is equivalent; but if, for example, we try to calculate a trimmed mean, our function does not work:
> mean(prestige, trim=0.1)
Error in mean(prestige, trim = 0.1):unused argument(s)(trim = 0.1)
Shadowing standard R functions is a practice generally to be avoided. Suppose, for example, that a robust-regression function tries to calculate a trimmed mean, but fails because the standard mean function is shadowed by our redefined mean function. If we are not conscious of this problem, the resulting error message may prove cryptic.
We can, however, use the same name for a variable and a function, as long as the two do not reside in the working data. Consider the following example:
> mean <− mean(prestige) # uses then overwrites our mean function
> mean
[1] 47.68889
Specifying mean <− mean(prestige) causes our mean function to calculate the mean prestige and then stores the result in a variable called mean , which has the effect of destroying our mean function (and good riddance to it). The variable mean in the working data does not, however, shadow the function mean in the base package:
> mean(prestige, trim=0.1)
[1] 47.2973
Before proceeding, let us tidy up a bit:
> remove(mean)
> detach(Duncan)
2.2.2 AVOIDING attach
Here are some compelling reasons for not attaching data frames to the search path:
There are several strategies that we can use to avoid attaching a data frame:
> mean(Duncan$prestige)
[1] 47.68889
> (lm(prestige ~ income + education, data=Duncan))
Call:
lm(formula = prestige ~ income + education, data = Duncan)
![]()
> with(Duncan, mean(prestige))
[1] 47.68889
> with(Duncan, lm(prestige ~ income + education))
Call:
lm(formula = prestige ~ income + education)
Coefficients:
![]()
We will use with frequently in the rest of this Companion.
| 2.2.3 | MISSING DATA |
Missing data are a regrettably common feature of real data sets. Two kinds of issues arise in handling missing data:
As we have explained, on data input, missing values are typically encoded by the characters NA . The same characters are used to print missing information. Many functions in R know how to handle missing data, although sometimes they have to be explicitly told what to do.
To illustrate, let us examine the data set Freedman in the car package:
> head(Freedman) # first 6 rows

> dim(Freedman) # number of rows and columns
[1] 110 4
These data, on 110 U.S. metropolitan areas, were originally from the 1970 Statistical Abstract of the United States and were used by Freedman (1975) as part of a wide-ranging study of the social and psychological effects of crowding. Freedman argues, by the way, that high density tends to intensify social interaction, and thus the effects of crowding are not simply negative. The variables in the data set are as follows:
Some of Freedman’s data are missing—for example, the population and density for Albuquerque. Here are the first few values for density :
> head(Freedman$density, 20) # first 20 values
![]()
Suppose, now, that we try to calculate the median density ; as we will see shortly, the density values are highly positively skewed, so using the mean as a measure of the center of the distribution would be a bad idea:
> median(Freedman$density)
[1] NA
R tells us that the median density is missing. This is the pedantically correct answer: Several of the density values are missing, and consequently we cannot in the absence of those values know the median, but this is probably not what we had in mind when we asked for the median density .By setting the na.rm (NA -remove) argument of median to TRUE , we instruct R to calculate the median of the remaining, nonmissing values:
> median(Freedman$density, na.rm=TRUE)
[1] 412
Several other R functions that calculate statistical summaries, such as mean , var (variance), sd (standard deviation), and quantile (quantiles), also have na.rm arguments, but not all R functions handle missing data in this manner.
Most plotting functions simply ignore missing data. For example, to construct a scatterplot of crime against density , including only the observations with valid data for both variables, we enter
> with(Freedman, {
+ plot(density, crime)
+ identify(density, crime, row.names(Freedman))
+ })
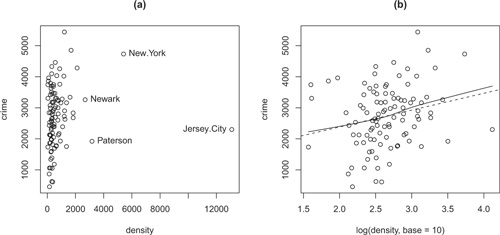
Figure 2.1 Scatterplot of crime by population density for Freedman’s data. (a) Original density scale, with a few high-density cities identified interactively with the mouse, and (b) log-density scale, showing linear least-squares (broken) and lowess nonparametric-regression (solid) lines. Cases with one or both values missing are silently omitted from both graphs.
The resulting graph, including several observations identified with the mouse, appears in Figure 2.1a. Recall that we identify observations by pointing at them with the mouse and clicking the left mouse button; exit from identify by pressing the esc key in Mac OS X or, in Windows, by clicking the right mouse button and selecting Stop. It is apparent that density is highly positively skewed, making the plot very difficult to read. We would like to try plotting crime against the log of density but wonder whether the missing data will spoil the computation.8 The log function in R behaves sensibly, however: The result has a missing entry wherever—and only where—there was a missing entry in the argument:
> log(c(1, 10, NA, 100), base=10)
[1] 0 1 NA 2
Other functions that compute on vectors in an element-wise fashion—such as the arithmetic operators—behave similarly.
We, therefore, may proceed as follows, producing the graph in Figure 2.1b:9
> with(Freedman, plot(log(density, base=10), crime))
This graph is much easier to read, and it now appears that there is a weak, positive relationship between crime and density . We will address momentarily how to produce the lines in the plot.
Statistical-modeling functions in R have a special argument, na.action , which specifies how missing data are to be handled; na.action is set to a function that takes a data frame as an argument and returns a similar data frame composed entirely of valid data (see Section 4.8.5). The default na.action is na.omit , which removes all observations with missing data on any variable in the computation. All the examples in this Companion use na.omit . An alternative, for example, would be to supply an na.action that imputes the missing values.
The prototypical statistical-modeling function in R is lm , which is described extensively in Chapter 4. For example, to fit a linear regression of crime on the log of density , removing observations with missing data on either crime or density , enter the command
> lm(crime ~ log(density, base=10), data=Freedman)
Call:
lm(formula = crime ~ log(density, base = 10), data = Freedman)
Coefficients:
(Intercept) log(density, base = 10)
1297.3 542.6
The lm function returns a linear-model object; because the returned object was not saved in a variable, the interpreter simply printed a brief report of the regression. To plot the least-squares line on the scatterplot in Figure 2.1:
> abline(lm(crime ~ log(density, base=10), data=Freedman), lty="dashed")
The linear-model object returned by lm is passed to abline , which draws the regression line; specifying the line type lty="dashed" produces a broken line.
Some functions in R, especially the older ones, make no provision for missing data and simply fail if an argument has a missing entry. In these cases, we need somewhat tediously to handle the missing data ourselves. A relatively straightforward way to do so is to use the complete.cases function to test for missing data, and then to exclude the missing data from the calculation.
For example, to locate all observations with valid data for both crime and density , we enter:
> good <− with(Freedman, complete.cases(crime, density))
> head(good, 20) # first 20 values
![]()
We then use good to select the valid observations by indexing (a topic described in Section 2.3.4). For example, it is convenient to use the lowess function to add a nonparametric-regression smooth to our scatterplot (Figure 2.1b), but lowess makes no provision for missing data:10
+ lines(lowess(log(density[good], base=10), crime[good], f=1.0)))
By indexing the predictor density and response crime with the logical vector good , we extract only the observations that have valid data for both variables. The argument f to the lowess function specifies the span of the lowess smoother—that is, the fraction of the data included in each local-regression fit; large spans (such as the value 1.0 employed here) produce smooth regression curves.
Suppose, as is frequently the case, that we analyze a data set with a complex pattern of missing data, fitting several statistical models to the data. If the models do not all use exactly the same variables, then it is likely that they will be fit to different subsets of nonmissing observations. Then if we compare the models with a likelihood ratio test, for example, the comparison will be invalid.11
To avoid this problem, we can first use na.omit to filter the data frame for missing data, including all the variables that we intend to use in our data analysis. For example, for Freedman’s data, we may proceed as follows, assuming that we want subsequently to use all four variables in the data frame:
> Freedman.good <− na.omit(Freedman)
> head(Freedman.good) # first 6 rows

A note of caution: Filtering for missing data on variables that we do not intend to use can result in discarding data unnecessarily. We have seen cases where students and researchers inadvertently and needlessly threw away most of their data by filtering an entire data set for missing values, even when they intended to use only a few variables in the data set.
Finally, a few words about testing for missing data in R: A common error is to assume that one can check for missing data using the == (equals) operator, as in
> NA == c(1, 2, NA, 4)
[1] NA NA NA NA
Testing equality of NA against any value in R returns NA as a result. After all, if the value is missing, how can we know whether it’s equal to something else? The proper way to test for missing data is with the function is.na :
[1] FALSE FALSE TRUE FALSE
For example, to count the number of missing values in the Freedman data frame:
> sum(is.na(Freedman))
[1] 20
This command relies on the automatic coercion of the logical values TRUE and FALSE to one and zero, respectively.
| 2.2.4 | NUMERIC VARIABLES AND FACTORS |
If we construct R data frames by reading data from text files using read.-table or from numeric and character vectors using data.frame , then our data frames will consist of two kinds of data: numeric variables and factors. Both read.table and data.frame by default translate character data and logical data into factors.
Before proceeding, let us clean up a bit:
> objects()
![]()
> remove(good, Freedman.good)
Near the beginning of this chapter, we entered data from Fox and Guyer’s (1978) experiment on anonymity and cooperation into the global variables cooperation , condition , and sex .12 The latter two variables are character vectors, as we verify for condition :
> condition

We can confirm that this is a vector of character values using the predicate function is.character , which tests whether its argument is of mode "character" :
> is.character(condition)
[1] TRUE
After entering the data, we defined the data frame Guyer , which also contains variables named cooperation , condition , and sex . We will remove the global variables and will work instead with the data frame:
> remove(cooperation, condition, sex)
Look at the variable condition in the Guyer data frame:
> Guyer$condition

> is.character(Guyer$condition)
[1] FALSE
> is.factor(Guyer$condition)
[1] TRUE
As we explained, condition in the data frame is a factor rather than a character vector. A factor is a representation of a categorical variable; factors are stored more economically than character vectors, and the manner in which they are stored saves information about the levels (category set) of a factor. When a factor is printed, its values are not quoted, as are the values of a character vector, and the levels of the factor are listed.
Many functions in R, including statistical-modeling functions such as lm , know how to deal with factors. For example, when the generic summary function is called with a data frame as its argument, it prints various statistics for a numeric variable but simply counts the number of observations in each level of a factor:
> summary(Guyer)

Factors have unordered levels. An extension, called ordered factors, is discussed, along with factors, in the context of linear models in Section 4.6.
| 2.2.5 | MODIFYING AND TRANSFORMING DATA |
Data modification in R usually occurs naturally and unremarkably. When we wanted to plot crime against the log of density in Freedman’s data, for example, we simply specified log(density, base=10) .13 Similarly, in regressing crime on the log of density , we just used log(density, base=10) on the right-hand side of the linear-model formula.
Creating new variables that are functions of other variables is straightforward. For example, the variable cooperation in the Guyer data set counts the number of cooperative choices out of a total of 120 choices. To create a new variable with the percentage of cooperative choices in each group:
> perc.coop <− 100*Guyer$cooperation/120
The new variable perc.coop resides in the working data, not in the Guyer data frame. It is generally advantageous to add new variables such as this to the data frame from which they originate: Keeping related variables together in a data frame avoids confusion, for example.
> Guyer$perc.coop <− 100*Guyer$cooperation/120
> head(Guyer) # first 6 rows

A similar procedure may be used to modify an existing variable in a data frame. The following command, for example, replaces the original cooperation variable in Guyer with the logit (log-odds) of cooperation:
> Guyer$cooperation <− with(Guyer, log(perc.coop/(100 − perc.coop)))
> head(Guyer)

The transform function can be used to create and modify several variables in a data frame at once. For example, if we have a data frame called Data with variables named a , b , and c , then the command
> Data <− transform(Data, c=-c, asq=a^2, a.over.b=a/b)
replaces Data by a new data frame in which the variables a and b are included unchanged, c is replaced by -c , and two new variables are added—asq , with the squares of a , and a.over.b , with the ratios of a to b .
Transforming numeric data is usually a straightforward operation—simply using mathematical operators and functions. Categorizing numeric data and recoding categorical variables are often more complicated matters. Several functions in R are employed to create factors from numeric data and to manipulate categorical data, but we will limit our discussion to three that we find particularly useful: (1) the standard R function cut , (2) the recode function in the car package, and (3) the standard ifelse function.
The cut function dissects the range of a numeric variable into class intervals, or bins. The first argument to the function is the variable to be binned; the second argument gives either the number of equal-width bins or a vector of cut points at which the division is to take place. For example, to divide the range of perc.coop into four equal-width bins, we specify
> Guyer$coop.4 <− cut(Guyer$perc.coop, 4)
> summary(Guyer$coop.4)
![]()
R responds by creating a factor, the levels of which are named for the end points of the bins. In the example above, the first level includes all values with Guyer$perc.coop greater than 22.5 (which is slightly smaller than the minimum value of Guyer$perc.coop ) and less than or equal to 33.3, the cut point between the first two levels. Because perc.coop is not uniformly distributed across its range, the several levels of coop.4 contain different numbers of observations. The output from the summary function applied to a factor gives a one-dimensional table of the number of observations in each level of the factor.
Suppose, alternatively, that we want to bin perc.coop into three levels containing roughly equal numbers of observations14 and to name these levels "low" , "med" , and "high" ; we may proceed as follows:
> Guyer$coop.groups <− with(Guyer, cut(perc.coop,
+ quantile(perc.coop, c(0, 1/3, 2/3, 1)),
+ include.lowest=TRUE,
+ labels=c("low", "med", "high")))
> summary(Guyer$coop.groups)
low med high
7 6 7
The quantile function is used to locate the cut points. Had we wished to divide perc.coop into four groups, for example, we would simply have specified different quantiles, c(0, .25, .5, .75, 1) , and of course supplied four values for the labels argument.
The recode function in the car package, which is more flexible than cut , can also be used to dissect a quantitative variable into class intervals: for example,
> (Guyer$coop.2 <− recode(Guyer$perc.coop, "lo:50=1; 50:hi=2"))
[1] 1 2 1 1 2 1 2 2 2 1 1 1 1 1 1 1 1 1 1 1
The recode function works as follows:
To provide a richer context for additional illustrations of the use of recode , we turn our attention to the Womenlf data frame from the car package:
> set.seed(12345) # for reproducibility
> (sample.20 <− sort(sample(nrow(Womenlf), 20))) # 20 random obs.
![]()
> Womenlf[sample.20, ] # 20 randomly selected rows
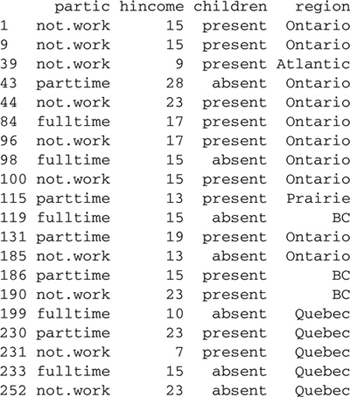
The sample function is used to pick a random sample of 20 rows in the data frame, selecting 20 random numbers without replacement from one to the number of rows in Womenlf ; the numbers are placed in ascending order by the sort function.15
We use the set.seed function to specify the seed for R’s pseudo-random number generator, ensuring that if we repeat the sample command, we will obtain the same sequence of pseudo-random numbers. Otherwise, the seed of the random-number generator will be selected unpredictably based on the system clock when the first random number is generated in an R session. Setting the random seed to a known value before a random simulation makes the result of the simulation reproducible. In serious work, we generally prefer to start with a known but randomly selected seed, as follows:
> (seed <− sample(2^31 − 1, 1))
[1] 974373618
> set.seed(seed)
The number 231 − 1 is the largest integer representable as a 32-bit binary number on most of the computer systems on which R runs (see Section 2.6.2).
The data in Womenlf originate from a social survey of the Canadian population conducted in 1977 and pertain to married women between the ages of 21 and 30, with the variables defined as follows:
Now consider the following recodes:

In all these examples, factors (either partic or region ) are recoded, and consequently, recode returns factors as results:
The standard R ifelse command (discussed further in Section 8.3.1) can also be used to recode data. For example,
> Womenlf$working.alt.2 <− factor(with(Womenlf,
+ ifelse(partic %in% c("parttime", "fulltime"), "yes", "no")))
> with(Womenlf, all.equal(working, working.alt.2))
[1] TRUE
> Womenlf$fulltime.alt <− factor(with(Womenlf,
+ ifelse(partic == "fulltime", "yes",
+ ifelse(partic == "parttime", "no", NA))))
> with(Womenlf, all.equal(fulltime, fulltime.alt))
[1] TRUE
The first argument to ifelse is a logical vector, containing the values TRUE and FALSE ; the second argument gives the value assigned where the first argument is TRUE ; and the third argument gives the value assigned when the first argument is FALSE . We used cascading ifelse commands to create the variable fulltime.alt , assigning the value "yes" to those working "fulltime" , "no" to those working "parttime" , and NA otherwise (i.e., where partic takes on the value "not.work" ).
We employed the matching operator, %in% , which returns a logical vector containing TRUE if a value in the vector before %in% is a member of the vector after the symbol and FALSE otherwise. See help("%in%") for more information; the quotes are required because of the % character. We also used the function all.equal to test the equality of the alternative recodings. When applied to numeric variables, all.equal tests for approximate equality, within the precision of floating-point computations (discussed in Section 2.6.2); more generally, all.equal not only reports whether two objects are approximately equal but, if they are not equal, provides information on how they differ.
An alternative to the first test is all(working == working.alt.2) , but this approach won’t work properly in the second test because of the missing data:
> with(Womenlf, all(fulltime == fulltime.alt))
[1] NA
We once more clean up before proceeding by removing the copy of Womenlf that was made in the working data:
> remove(Womenlf)
2.3 Matrices, Arrays, and Lists
We have thus far encountered and used several data structures in R:
In this section, we describe three other common data structures in R: matrices, arrays, and lists.
| 2.3.1 | MATRICES |
A matrix in R is a two-dimensional array of elements all of which are of the same mode—for example, real numbers, integers, character strings, or logical values. Matrices can be constructed using the matrix function, which reshapes its first argument into a matrix with the specified number of rows (the second argument) and columns (the third argument): for example,
> (A <− matrix(1:12, nrow=3, ncol=4))

>(B <− matrix(c("a", "b", "c"), 4, 3, byrow=TRUE))# 4 rows,3 columns
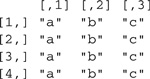
A matrix is filled by columns, unless the optional argument byrow is set to TRUE . The second example illustrates that if there are fewer elements in the first argument than are required, then the elements are simply recycled, extended by repetition to the required length.
A defining characteristic of a matrix is that it has a dim (d imension) attribute with two elements: the number of rows and the number of columns: 16
> dim(A)
[1] 3 4
> dim(B)
[1] 4 3
As we have seen before, a vector is a one-dimensional array of numbers. For example, here is a vector containing a random permutation of the first 10 integers:
> set.seed(54321) # for reproducibility
> (v <− sample(10, 10)) # permutation of 1 to 10
[1] 5 10 2 8 7 9 1 4 3 6
A vector has a length attribute but not a dim attribute:
> length(v)
[1] 10
> dim(v)
NULL
R often treats vectors differently than matrices. You can turn a vector into a one-column matrix using the as.matrix coercion function:
> as.matrix(v)
[,1] |
|
[1,] |
5 |
[2,] |
10 |
[3,] |
2 |
[4,] |
8 |
[5,] |
7 |
[6,] |
9 |
[7,] |
1 |
[8,] |
4 |
[9,] |
3 |
[10,] |
6 |
R includes extensive facilities for matrix computation, some of which are described later in this chapter and in Section 8.2.
| 2.3.2 | ARRAYS |
Higher-dimensional arrays of homogeneous elements are encountered much less frequently than matrices. If needed, higher-dimensional arrays may be created with the array function; here is an example generating a three-dimensional array:
> (array.3 <− array(1:24, dim=c(4, 3, 2))) # 4 rows, 3 columns, 2 layers
,,1

,,2

The order of the dimensions is row, column, and layer. The array is filled with the index of the first dimension changing most quickly—that is, row, then column, then layer.
| 2.3.3 | LISTS |
Lists are data structures composed of potentially heterogeneous elements. The elements of a list may be complex data structures, including other lists. Because a list can contain other lists as elements, each of which can also contain lists, lists are recursive structures. In contrast, the elements of an ordinary vector—such as an individual number, character string, or logical value—are atomic objects.
Here is an example of a list, constructed with the list function:
> (list.1 <− list(mat.1=A, mat.2=B, vec=v)) # a 3-item list

This list contains a numeric matrix, a character matrix, and a numeric vector. We named the arguments in the call to the list function; these are arbitrary names that we chose, not standard arguments to list . The argument names supplied became the names of the list elements.
Because lists permit us to collect related information regardless of its form, they provide the foundation for the class-based S3 object system in R.17 Data frames, for example, are lists with some special properties that permit them to behave somewhat like matrices.
| 2.3.4 | INDEXING |
A common operation in R is to extract some of the elements of a vector, matrix, array, list, or data frame by supplying the indices of the elements to be extracted. Indices are specified between square brackets, “[ ” and “] ”. We have already used this syntax on several occasions, and it is now time to consider indexing more systematically.
A vector can be indexed by a single number or by a vector of numbers; indeed, indices may be specified out of order, and an index may be repeated to extract the corresponding element more than once:
> v
[1] 5 10 2 8 7 9 1 4 3 6
> v[2]
[1] 10
> v[c(4, 2, 6)]
[1] 8 10 9
> v[c(4, 2, 4)]
[1] 8 10 8
Specifying negative indices suppresses the corresponding elements of the vector:
> v[-c(2, 4, 6, 8, 10)]
[1] 5 2 7 1 3
If a vector has a names attribute, then we can also index the elements by name:18
> names(v) <− letters[1:10]
> v
a b c d e f g h i j
5 10 2 8 7 9 1 4 3 6
> v[c("f", "i", "g")]
f i g
9 3 1
Finally, a vector may be indexed by a logical vector of the same length, retaining the elements corresponding to TRUE and omitting those corresponding to FALSE :
> v < 6
![]()
> v[v < 6] # all entries less than 6
5 2 1 4 3
Any of these forms of indexing may be used on the left-hand side of the assignment operator to replace the elements of a vector—an unusual and convenient feature of the R language: for example,
> (vv <− v) # make copy of v
a b c d e f g h i j
5 10 2 8 7 9 1 4 3 6
> vv[c(1, 3, 5)] <− 1:3
> vv
a b c d e f g h i j
1 10 2 8 3 9 1 4 3 6
> vv[c("b", "d", "f", "h", "j")] <− NA
> vv
a b c d e f g h i j
1 NA 2 NA 3 NA 1 NA 3 NA
> remove(vv)
INDEXING MATRICES AND ARRAYS
Indexing extends straightforwardly to matrices and to higher-dimensional arrays. Indices corresponding to the different dimensions of an array are separated by commas; if the index for a dimension is left unspecified, then all the elements along that dimension are selected. We demonstrate with the matrix A :
> A

> A[2, 3] # element in row 2, column 3
[1] 8
> A[c(1, 2), 2] # rows 1 and 2, column 2
[1] 4 5
> A[c(1, 2), c(2, 3)] # rows 1 and 2, columns 2 and 3
![]()
> A[c(1, 2), ] # rows 1 and 2, all columns
![]()
The second example above, A[2, 3] , returns a single-element vector rather than a 1 × 1 matrix; likewise, the third example, A[c(1, 2), 2] , returns a vector with two elements rather than a 2 × 1 matrix. More generally, in indexing a matrix or array, dimensions of extent one are automatically dropped. In particular, if we select elements in a single row or single column of a matrix, then the result is a vector, not a matrix with a single row or column, a convention that will occasionally give an R programmer headaches. We can override this default behavior with the argument drop=FALSE :
> A[,1]
[1] 1 2 3
> A[ , 1, drop=FALSE]
[,1] | |
[1,] | 1 |
[2,] | 2 |
[3,] | 3 |
In both of these examples, the row index is missing and is therefore taken to be all rows of the matrix.
Negative indices, row or column names (if they are defined), and logical vectors of the appropriate length may also be used to index a matrix or a higher-dimensional array:
> A[ , -c(1, 3)] # omit columns 1 and 3

> A[−1, −2] # omit row 1 and column 2
![]()
> rownames(A) <− c("one", "two", "three") # set row names
> colnames(A) <− c("w", "x", "y", "z") # set column names > A

> A[c("one", "two"), c("x", "y")]
![]()
> A[c(TRUE, FALSE, TRUE), ]
![]()
Used on the left of the assignment arrow, we may replace indexed elements in a matrix or array:
> (AA <− A) # make a copy of A
> AA[1, ] <− 0 # set first row to zeros
> AA

> remove(AA)
INDEXING LISTS
Lists may be indexed in much the same way as vectors, but some special considerations apply. Recall the list that we constructed earlier:

> list.1[c(2, 3)] # elements 2 and 3
$mat.2
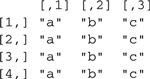
$vec
[1] 5 10 2 8 7 9 1 4 3 6
> list.1[2] # returns a one-element list
$mat.2

Even when we select a single element of the list, as in the last example, we get a single-element list rather than (in this case) a matrix. To extract the matrix in position 2 of the list, we can use double-bracket notation:
> list.1[[2]] # returns a matrix
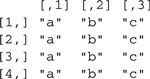
The distinction between a one-element list and the element itself is subtle but important, and it can trip us up if we are not careful.
If the list elements are named, then we can use the names in indexing the list:
> list.1["mat.1"] # produces a one-element list
$mat.1

> list.1[["mat.1"]] # extracts a single element

An element name may also be used—either quoted or, if it is a legal R name, unquoted—after the $ (dollar sign) to extract a list element:
> list.1$mat.1

Used on the left-hand side of the assignment arrow, dollar-sign indexing allows us to replace list elements, define new elements, or delete an element (by assigning NULL to the element):

Setting a list element to NULL is trickier:
> list.1["title"] <− list(NULL)
> list.1

$vec
[1] 5 10 2 8 7 9 1 4 3 6
$title
NULL
Once a list element is extracted, it may itself be indexed: for example,
> list.1$vec[3]
[1] 2
> list.1[["vec"]][3:5]
[1] 2 8 7
Finally, extracting a nonexistent element returns NULL :
> list.1$foo
NULL
This behavior is potentially confusing because it is not possible to distinguish by the value returned between a NULL element, such as list.1$title in the example, and a nonexistent element, such as list.1$foo .
Data frames may be indexed either as lists or as matrices. Recall the Guyer data frame:

Because no row names were specified when we entered the data, the row names are simply the character representation of the row numbers. Indexing Guyer as a matrix:

We require with in the last example to access the variables sex and condition , because the data frame Guyer is not attached to the search path. More conveniently, we can use the subset function to perform this operation:
> subset(Guyer, sex == "female" & condition == "public")

Alternatively, indexing the data frame Guyer as a list:

> head(Guyer["cooperation"]) # first six rows
cooperation |
|
1 |
-0.3708596 |
2 |
0.1335314 |
3 |
-0.8079227 |
4 |
-0.2682640 |
5 |
0.2682640 |
6 |
-0.2006707 |
Specifying Guyer["cooperation"] returns a one-column data frame rather than a vector.
As has become our habit, we clean up before continuing:
> remove(A, B, v, array.3, list.1)
2.4 Manipulating Character Data
One of the most underappreciated capabilities of R is its facility in handling text. Indeed, for many applications, R is a viable alternative to specialized text-processing tools, such as the PERL scripting language and the Unix utilities sed, grep, and awk. Most of the text-processing functions in R make use of so-called regular expressions for matching text in character strings. In this section, we provide a brief introduction to manipulating character data in R, primarily by example. More complete information may be found in the online help for the various text-processing functions; in ?regexp , which describes how regular expressions are implemented in R; and in the sources cited at the end of the chapter.
We’ll turn to the familiar “To Be or Not To Be” soliloquy from Shakespeare’s Hamlet, in the plain-text file Hamlet.txt, as a source of examples. We begin by using the readLines function to read the lines of the file into a character vector, one line per element:
> file <− "http://socserv.socsci.mcmaster.ca/jfox/ books/Companion/data/Hamlet.txt"
> Hamlet <− readLines(file)
> head(Hamlet) # first 6 lines
[1]"To be, or not to be: that is the question:"
[2]"Whether ’tis nobler in the mind to suffer"
[3]"The slings and arrows of outrageous fortune,"
[4]"Or to take arms against a sea of troubles,"
[5]"And by opposing end them? To die: to sleep;"
[6]"No more; and by a sleep to say we end"
> length(Hamlet) # number of lines
[1] 35
> nchar(Hamlet) # number of characters per line
[1] 42 41 44 42 43 37 46 42 40 50 47 43 39 36 48 49 44 38 41 38
[21] 43 38 44 41 37 43 39 44 37 47 40 42 44 39 26
> sum(nchar(Hamlet)) # number of characters in all
[1] 1454
The length function counts the number of character strings in the character vector Hamlet —that is, the number of lines in the soliloquy—while the nchar function counts the number of characters in each string—that is, in each line.
The paste function is useful for joining character strings into a single string. For example, to join the first six lines:
(lines.1_6 <− paste(Hamlet[1:6], collapse=" "))
[1] "To be, or not to be: that is the question: … to say we end"
Here, and elsewhere in this section, we’ve edited the R output where necessary so that it fits properly on the page. Alternatively, we can use the strwrap function to wrap the text (though this once again divides it into lines),
> strwrap(lines.1_6)
[1] "To be, or not to be: that is the question: Whether ’tis"
[2] "nobler in the mind to suffer The slings and arrows of"
[3] "outrageous fortune, Or to take arms against a sea of"
[4] "troubles, And by opposing end them? To die: to sleep; No"
[5] "more; and by a sleep to say we end"
and the substring function, as its name implies, to select parts of a character string—for example, to select the characters 1 through 42:
> substring(lines.1_6, 1, 42)
[1] "To be, or not to be: that is the question:"
Suppose, now, that we want to divide lines.1_6 into words. As a first approximation, let’s split the character string at the blanks:
> strsplit(lines.1_6, " ")

The strsplit (string-split) function takes two required arguments: (1) a character vector of strings to be split, here consisting of one element, and (2) a quoted regular expression specifying a pattern that determines where the splits will take place. In this case, the regular expression contains the single character " " (space). Most characters in regular expressions, including spaces, numerals, and lowercase and uppercase alphabetic characters, simply match themselves. The strsplit function returns a list as its result, with one element for each element of the first argument—in this case, a one-element list corresponding to the single string in lines.1_6 .
Our first attempt at dividing lines.1_6 into words hasn’t been entirely successful: Perhaps we’re willing to live with words such as “’tis ” (which is a contraction of “it is”), but it would be nice to remove the punctuation from "be:" , "troubles," and "them?" , for example.
Characters enclosed in square brackets in a regular expression represent alternatives; thus, for example, the regular expression "[ ,;:.?!]" will match a space, comma, semicolon, colon, period, question mark, or exclamation point. Because some words are separated by more than one of these characters (e.g., a colon followed by a space), we add the quantifier + (plus sign) immediately to the right of the closing bracket; the resulting regular expression, "[ ,;:.?!]+" , will match one or more adjacent spaces and punctuation characters:
> strsplit(lines.1_6, "[ ,;:.?!]+")[[1]]
[1] "To" "be" "or" "not"
[5] "to" "be" "that" "is" [9] "the" "question" "Whether" "’tis" … [49] "sleep" "to" "say" "we" [53] "end"
Other quantifiers in regular expressions include * (asterisk), which matches the preceding expression zero or more times, and ? (question mark), which matches the preceding expression zero or one time. Special characters, such as square brackets and quantifiers, that don’t represent themselves in regular expressions are called meta-characters. We can, for example, divide the text into sentences by splitting at any of . , ? ,or ! , followed by zero or more spaces:
> strsplit(lines.1_6, "[.?!] *")[[1]]
[1] "To be, or not to be: that is the question: … end them"
[2] "To die: to sleep; No more; and by a sleep to say we end"
And we can divide the text into individual characters by splitting at the empty string, "" :
> characters <− strsplit(lines.1_6, "")[[1]]
> length(characters) # number of characters
[1] 254
> head(characters, 20) # first 20 characters
[1] "T" "o" " " "b" "e" "," " " "o" "r" " " "n" "o" "t" " " "t"
[16] "o" " " "b" "e" ":"
Let us turn now to the whole soliloquy, dividing the text into words at spaces (a strategy that, as we have seen, is flawed):
> all.lines <− paste(Hamlet, collapse=" ")
> words <− strsplit(all.lines, " ")[[1]]
> length(words) # number of words
[1] 277
> head(words, 20) # first 20 words

We can fix the words that have extraneous punctuation by substituting the empty string for the punctuation, using the function sub (substitute):
> words <− sub("[,;:.?!]", "", words)
> head(words, 20)

The sub function takes three required arguments: (1) a regular expression matching the text to be replaced, (2) the replacement text (here, the empty string), and (3) a character vector in which the replacement is to be performed. If the pattern in the regular expression matches more than one substring in an element of the third argument, then only the first occurrence is replaced. The gsub function behaves similarly, except that all occurrences of the pattern are replaced:
> sub("me", "you", "It’s all, ’me, me, me’ with you!")
[1] "It’s all, ’you, me, me’ with you!"
> gsub("me", "you", "It’s all, ’me, me, me’ with you!")
[1] "It’s all, ’you, you, you’ with you!"
Returning to the soliloquy, suppose that we want to determine and count the different words that Shakespeare used. A first step is to use the tolower function to change all the characters to lowercase, so that, for example, "the" and "The" aren’t treated as distinct words:
> head(words <− tolower(words), 20) # first 20 words

> word.counts <− sort(table(words), decreasing=TRUE)
> word.counts[word.counts > 2] # words used more than twice

> head(sort(unique(words)), 20) # first 20 unique words

> length(unique(words)) # number of unique words
[1] 167
We used the table command to obtain the word counts, unique to remove duplicate words, and sort to order the words from the most to the least used and to arrange the unique words in alphabetical order. The alphabetized words reveal a problem, however: We’re treating the hyphen (“- ”) as if it were a word.
The function grep may be used to search character strings for a regular expression, returning the indices of the strings in a character vector for which there is a match. For our example,
> grep("-", words)
[1] 55 262
> words[grep("-", words)]
[1] "heart-ache" "-"
We found matches in two character strings: the valid, hyphenated word "heart-ache" and the spurious word "-" . We would like to be able to differentiate between the two, because we want to discard the latter from our vector of words but retain the former. We can do so as follows:
> grep("^-", words)
[1] 262
> words <− words[- grep("^-", words)] # negative index to delete
> head(sort(unique(words)), 20)

The meta-character ^ (caret) is an anchor representing the beginning of a text string, and thus, the regular expression "^-" only matches first-character hyphens. The meta-character $ is similarly an anchor representing the end of a text string:
> grep("!$", c("!10", "wow!"))
[1] 2
> grep("^and$", c("android", "sand", "and", "random"))
[1] 3
> grep("and", c("android", "sand", "and", "random"))
[1] 1 2 3 4
A hyphen (- ) may be used as a meta-character within square brackets to represent a range of characters, such as the digits from 0 through 9 ;19 in the following command, for example, we pick out the elements of a character vector that is composed of numerals, periods, and minus signs:
> data <− c("−123.45", "three hundred", "7550",
+ "three hundred 23", "Fred")
> data[grep("^[0-9.-]*$", data)]
[1] "−123.45" "7550"
Here, the hyphen before the closing bracket represents itself and will match a minus sign.
Used after an opening square bracket, the meta-character “^ ” represents negation, and so, for example, to select elements of the vector data that do not contain any numerals, hyphens, or periods:
> data[grep("^[^0-9.-]*$", data)]
[1] "three hundred" "Fred"
Parentheses are used for grouping in regular expressions, and the bar character (| ) means or. To find all the articles in the soliloquy, for example:
> words[grep("^(the|a|an)$", words)]
![]()
To see why the parentheses are needed here, try omitting them.
What happens if we want to treat a meta-character as an ordinary character? We have to escape the meta-character by using a back slash (\), and because the back slash is the escape character for R as well as for regular expressions, we must, somewhat awkwardly, double it: for example,
> grep("\\$", c("$100.00", "100 dollars"))
[1] 1
> remove(Hamlet, lines.1_6, characters, all.lines, word.counts, data)
2.5 Handling Large Data Sets in R*
R has a reputation in some quarters for choking on large data sets. This reputation is only partly deserved. We will explain in this section why very large data sets may pose a problem for R and suggest some strategies for dealing with such data sets.
The most straightforward way to write functions in R is to access data that reside in the computer’s main memory. This is true, for example, of the statistical-modeling functions in the standard R distribution, such as the lm function for fitting linear models (discussed in Chapter 4) and the glm function for fitting generalized linear models (Chapter 5). The size of computer memory then becomes a limitation on the size of statistical analyses that can be handled successfully.
A computer with a 32-bit operating system can’t address more than 4 GB (gigabytes) of memory, and depending on the system, not all this memory may be available to R.20 Computers with 64-bit operating systems can address vastly larger amounts of memory. The current version of R is freely available in 64-bit implementations for Linux, Mac OS X and Windows systems. As memory gets cheaper and 64-bit systems become more common, analyzing very large data sets directly in memory will become more practical.
Handling large data sets in R is partly a matter of programming technique. Although it is convenient in R to store data in memory, it is not necessary to do so. There are many R programs designed to handle very large data sets, such as those used in genomic research, most notably the R packages distributed by Bioconductor (at www.bioconductor.org ). Similarly, the biglm package on CRAN has functions for fitting linear and generalized linear models that work serially on chunks of the data rather than all the data at once. Moreover, some packages, such as biglm and the survey package for the analysis of data from complex sample surveys, are capable of accessing data in database management systems (see Section 2.5.3).
Inefficient programming, such as unnecessarily looping over the observations of a data set or allocating very large sparse matrices consisting mostly of zeros, can waste computer time and memory.21
Problems that are quite large by social science standards can be handled routinely in R, and don’t require any special care or treatment. In the following examples, we will fit linear least-squares and logistic regressions to a data set with 100,000 observations and 100 explanatory variables. All this is done on our 32-bit Windows Vista system, which has the maximum 4 GB of memory. By default, about 1.5 GB is allocated to the R process, and this is sufficient for the computations below. If necessary, the memory allocated to R can be increased: See ?memory.limit .
We begin by constructing a model matrix for the regression by sampling 100, 000 × 100 values from the standard-normal distribution and then reshaping these values into a matrix with 100,000 rows and 100 columns:
> set.seed(123456789) # for reproducibility >
X <− rnorm(100000*100)
> X <− matrix(X, 100000, 100)
Under Windows, the memory.size and memory.limit functions allow us to check the amount of memory in MB (megabytes—approximately 1 million bytes, or 0.001 of a GB) that we’ve used and the amount available to the R process, respectively:
> memory.size()
[1] 10.59
> memory.limit()
[1] 1535
Thus, we’ve used less than 10% of the memory available to R. Next, we generate values of the response variable y , according to a linear-regression model with normally distributed errors that have a standard deviation of 10:
> y <− 10 + as.vector(X %*% rep(1, 100) + rnorm(100000, sd=10))
In this expression, %*% is the matrix multiplication operator (see Section 8.2), and the coercion function as.vector is used to coerce the result to a vector, because matrix multiplication of a matrix by a vector in R returns a one-column matrix. The vector of population regression coefficients consists of ones—rep(1, 100) —and the regression intercept is 10.
To fit the regression model to the data,
> system.time(m <− lm(y ~ X))
![]()
> head(coef(m)) # first 6 coefficients
![]()
We print the first six regression coefficients: The intercept and the first five slopes are close to the population values of the coefficients, as we would expect in a sample of n =100,000 observations. The system.time command times the computation, which took about 6 seconds on our computer. More information on system.time is provided in Section 8.6.2.
For a logistic regression (see Section 5.3), we first generate the response vector yy of 0s and 1s according to a model with an intercept of 0 and slope coefficients of 1/4:
> p <− as.vector(1/(1 + exp(-X %*% rep(0.25, 100))))
> summary(p)
![]()
> yy <− rbinom(100000, 1, prob=p)
> table(yy)
yy
0 1
49978 50022
Then, to fit the model,
> system.time(m <− glm(yy ~ X, family=binomial))
![]()
> head(coef(m)) # first 6 coefficients
![]()
Again, the computation goes through in a reasonable amount of time (22 seconds) and in the available memory; the results are as expected.
2.5.2 SPEEDING UP read.table
In Section 2.1.2, we suggested using read.table to input data from ASCII files into R,but read.table can be very slow in reading large data sets. To provide a simple example, we create a data frame from our simulated data and output the data frame to an ASCII file with the write.table function:
> D <− data.frame(X, y, yy)
> dim(D)
[1] 100000 102
> object.size(D)
81611176 bytes
> write.table(D, "C:/temp/largeData.txt")
The data frame D consists of 100,000 rows and 102 columns, and uses about 80 MB of memory. To read the data back into memory from the ASCII file takes about 3 minutes on our Windows Vista computer:
> system.time(DD <− read.table("C:/temp/largeData.txt", header=TRUE))
![]()
The read.table function is slow because it has to figure out whether data should be read as numeric variables or as factors. To determine the class of each variable, read.table reads all the data in character form and then examines each column, converting the column to a numeric variable or a factor, as required. We can make this process considerably more efficient by explicitly telling read.table the class of each variable, via the col-Classes argument:
> system.time(DD <− read.table("C:/temp/largeData.txt", header=TRUE,
+ colClasses=c("character", rep("numeric", 102))))
![]()
Reading the data now takes about 30 seconds. The "character" class specified for the first column is for the row name in each line of the file created by write.table ; for example, the name of the first row is "1" (with the quotation marks included). For more details about specifying the col-Classes argument, see ?read.table .
The save function allows us to store data frames and other R objects in a non-human-readable format, which can be reread—using the load function— much more quickly than an ASCII data file. For our example, the time to read the data is reduced to only about 3 seconds:
> save(DD, file="C:/temp/DD.Rdata")
> remove(DD)
> system.time(load("C:/temp/DD.Rdata"))
![]()
> dim(DD)
[1] 100000 102
Before continuing, we clean up the workspace:
> remove(D, DD, p, X, y, yy)
| 2.5.3 | ACCESSING DATA IN DATABASES |
In large problems, the variables to be used at any given time are often many fewer than the variables available. For example, there may be hundreds of variables in a data set from a social survey with tens of thousands of observations, but a regression model fit to the data will likely use only a small fraction of these variables.
Very large data sets may not fit into the memory of a 32-bit system, and manipulating very large data sets in memory may well prove awkward and slow even on a 64-bit system. We could use read.table to input only the variables that we intend to use, but the process of specifying these variables is tedious and error-prone, and if we decide to add a variable to the analysis, we would have to read the data again.
A better solution is to store the data in a database management system (DBMS), retrieving subsets of the data as they are required. There are several packages on CRAN for interfacing R with DBMSs, including the RODBC package (which we introduced in Section 2.1.3 to import data from an Excel spreadsheet).
2.6 More on the Representation of Data in R*
This section deals more abstractly with data in R. We aim to introduce the topic rather than to cover it exhaustively. The information here is rarely needed in routine data analysis, but it is occasionally useful for programming in R; you may safely skip this section on first reading.
| 2.6.1 | LENGTH, CLASS, MODE, AND ATTRIBUTES |
All objects in R have a length,a class, and a mode.22 Consider the following examples.
> (x <− 1:5)
[1] 1 2 3 4 5
> length(x)
[1] 5
> class(x)
[1] "integer"
> mode(x)
[1] "numeric"
> (y <− log(x))
[1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379
> length(y)
[1] 5
> class(y)
[1] "numeric"
> mode(y)
[1] "numeric"
> (cv <− c("Abel", "Baker", "Charlie"))
[1] "Abel" "Baker" "Charlie" >
length(cv)
[1] 3
> class(cv)
[1] "character"
> mode(cv)
[1] "character"
> (lst <− list(x=x, y=y, cv=cv))
$x
[1] 1 2 3 4 5
$y
[1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379
$cv
[1] "Abel" "Baker" "Charlie" >
length(lst)
[1] 3
> class(lst)
[1] "list"
> mode(lst)
[1] "list"
> (X <− cbind(x, y))

[1] 10
> class(X)
[1] "matrix"
> mode(X)
[1] "numeric"
> head(Duncan)

> length(Duncan)
[1] 4
> class(Duncan)
[1] "data.frame"
> mode(Duncan)
[1] "list"
> Duncan$type

> length(Duncan$type)
[1] 45
> class(Duncan$type)
[1] "factor"
> mode(Duncan$type)
[1] "numeric"
> length(lm)
[1] 1
> class(lm)
[1] "function"
> mode(lm)
[1] "function"
> (mod <− lm(prestige ~ income + education, data=Duncan))
Call:
lm(formula = prestige ~ income + education, data = Duncan)
![]()
> length(mod)
[1] 12
> class(mod)
[1] "lm"
> mode(mod)
[1] "list"
The class of an object is most important in object-oriented programming in R (discussed in Sections 1.4 and 8.7), where generic functions are written to invoke different methods depending on the class of their arguments. A familiar example is the generic summary function, which works differently for vectors, data frames, and regression models, among other classes of objects.
Some objects have additional attributes, which store information about the object: for example,
> X # a matrix

> attributes(X)
$dim
[1] 5 2
$dimnames
$dimnames[[1]]
NULL
$dimnames[[2]]
[1] "x" "y"
> attributes(Duncan) # a data frame
$names
[1] "type" "income" "education" "prestige"
$class
[1] "data.frame"

There is an important distinction between the printed representation of an object (such as the linear-model object mod ) and its internal structure. That said, we do not normally interact directly with an object produced by a modeling function and therefore do not need to see its internal structure; interaction with the object is the province of functions created for that purpose (e.g., the generic summary function). The invaluable str function, however, allows us to examine the internal structure of an object in abbreviated form:
> str(Duncan) # a data frame

The output from str gives us a variety of information about the object: that it is a data frame composed of four variables, including the factor type , with levels "bc" , "wc" , and "prof" and initial values 2 2 2 2 2 2 2 2 3 2 ; and so on.23
Standard R functions exist to create data of different modes and for many classes (constructor functions), to test for modes and classes (predicate functions), and to convert data to a specific mode or class (coercion functions).
> (num <− numeric(5))# create numeric vector of 0s of length 5
[1] 0 0 0 0 0
> (fac <− factor(c("a","b","c","c","b","a")))# create factor
[1] a b c c b a
Levels: a b c
There is also the general constructor function vector , whose first argument specifies the mode of the object to be created and whose second argument specifies the object’s length :
> vector(mode="numeric", length=5)
[1] 0 0 0 0 0
> vector(mode="list", length=2)
[[1]]
NULL
[[2]]
NULL
> is.numeric(num) # predicate for mode numeric
[1] TRUE
> is.numeric(fac)
[1] FALSE
> is.factor(fac) # predicate for class factor
[1] TRUE
The general predicate is takes a class or mode as its second argument:
> is(fac, "factor")
[1] TRUE
> is(fac, "numeric")
[1] FALSE
> (char <− as.character(fac)) # coerce to mode character
[1] "a" "b" "c" "c" "b" "a"
> (num <− as.numeric(fac)) # coerce to mode numeric
[1] 1 2 3 3 2 1
> (as.factor(num)) # coerce to class factor
[1] 1 2 3 3 2 1
Levels: 1 2 3
> as.numeric(char)
[1] NA NA NA NA NA NA
Warning message:
NAs introduced by coercion
The last example illustrates that coercion may cause information to be lost.
There is also a general coercion function, as :
> as(fac, "character")
[1] "a" "b" "c" "c" "b" "a"
> as(fac, "numeric")
[1] 1 2 3 3 2 1
2.6.2 PITFALLS OF FLOATING-POINT ARITHMETIC
The designers of R have paid a great deal of attention to the numerical accuracy of computations in the language, but they have not been able to repeal the laws of computer arithmetic. We usually need not concern ourselves with the details of how numbers are stored in R; occasionally, however, these details can do us in if we’re not careful.
Integers—that is, the positive and negative whole numbers and zero— are represented exactly in R. There are, however, qualifications. Computers represent numbers in binary form, and on a typical computer, R uses 32 binary digits (bits) to store an integer, which usually means that integers from −231 = −2,147,483,648 to 231 − 1 = +2,147,483,647 can be represented. Smaller and larger integers can’t be represented. Moreover, just because a number looks like an integer doesn’t mean that it is represented as an integer in R:
> is.integer(2)
[1] FALSE
> is.integer(2L)
[1] TRUE
Integer constants are entered directly by appending the character L to the number.24 As well, some operations produce integers:
> is.integer(1:100)
[1] TRUE
Unlike in some programming languages, arithmetic involving integers in R doesn’t necessarily produce an integer result, even when the result could be represented exactly as an integer:
> is.integer(2L + 3L)
[1] TRUE
> is.integer(2L*3L)
[1] TRUE
> is.integer(4L/2L)
[1] FALSE
> is.integer(sqrt(4L))
[1] FALSE
Furthermore, R silently coerces integers to floating-point numbers (described below), when both kinds of numbers appear in an arithmetic expression:
[1] FALSE
Most numbers in R are represented as floating-point numbers. A floating-point number consists of three parts: a sign, either + or −;a significand;and an exponent. You’re probably already familiar with this idea from scientific notation; for example, the number −2.3 × 1012 has the sign −, significand 2.3, and exponent 12.
On a computer, floating-point numbers are represented in binary rather than in decimal form. R stores floating-point numbers as double-precision binary numbers, which typically use 64 bits for each number, including one bit for the sign, 11 bits for the exponent, and 52 bits for the significand. This allows R to represent numbers with magnitudes between about 5 × 10−324 and 2 × 10308. If you work with numbers outside this range, then you’re out of our league!
You’re probably also familiar with the idea that not all numbers have exact decimal representations. For example, the irrational numbers π ≈ 3.14159, e ≈ 2.71828, and ![]() ≈ 1.41421 cannot be represented exactly as decimal numbers. Even many rational numbers, such as 1/3 = 0.33333·, do not have exact decimal representations. The same is true in binary representation, where, for example, 1/10 does not have an exact representation because 10 is not a power of 2. This fact, and the fact that floating-point arithmetic can result in round-off errors, means that you cannot rely on R to produce exact floating-point results: for example,
≈ 1.41421 cannot be represented exactly as decimal numbers. Even many rational numbers, such as 1/3 = 0.33333·, do not have exact decimal representations. The same is true in binary representation, where, for example, 1/10 does not have an exact representation because 10 is not a power of 2. This fact, and the fact that floating-point arithmetic can result in round-off errors, means that you cannot rely on R to produce exact floating-point results: for example,
> (sqrt(2))^2 == 2
[1] FALSE
> (sqrt(2))^2 − 2
[1] 4.440892e−16
Recall that 4.440892e−16 represents 4.440892 × 10−16, a number very close to 0.
It is, consequently, not a good idea to test for exact equality of numbers produced by floating-point operations. The machine double-epsilon for a computer gives the maximum relative error that can result from rounding floating-point numbers and depends on the number of bits in the significand; thus, on a typical computer, the machine double-epsilon is 2−52 ≈ 2 × 10−16.
When comparing floating-point numbers for equality, we should allow for a tolerance of about the square root of the machine double-epsilon, that is, typically 2−26 ≈ 1.5 × 10−8. The all.equal function in R uses this tolerance by default:
> all.equal((sqrt(2))^2, 2)
[1] TRUE
Moreover, when objects are not essentially equal, all.equal tries to provide useful information about how they differ:
> all.equal(2, 4)
[1] "Mean relative difference: 1"
> all.equal(2, "2")
[1] "Modes: numeric, character"
[2] "target is numeric, current is character"
R can also represent and compute with complex numbers, which occasionally have statistical applications:
> (z <− complex(real=0, imaginary=1))
[1] 0+1i
> (w <− 2 + 2*z) # 2 is coerced to complex
[1] 2+2i
> w*z
[1] −2+2i
> w/z
[1] 2−2i
See ?complex for more information.
Finally, arithmetic operations can produce results that are not (ordinary) numbers:
> 1/0
[1] Inf
> −1/0
[1] -Inf
> 0/0
[1] NaN
where Inf stands for ∞ (infinity) and NaN stands for “N ot aN umber.”
We do not bother to clean up at the end of the current chapter because we will not save the R workspace. More generally, and as we mentioned in the Preface, in this book we assume that each chapter represents an independent R session.
2.7 Complementary Reading and References
_____________________________
1You can download this file and other data files referenced in this chapter from the website for the book, most conveniently with the carWeb function—see ?carWeb . The data sets are also available, with the same names, in the car package.
2Alternatively, you can use the menus to select File → Change dir under Windows or Misc → Change Working Directory under MacOSX.
3The character string specifying the URL for the file Prestige.txt is broken across two lines to fit on the page but in fact must be given as one long string. Similar line breaks appear later in the chapter.
4You can download and install this package from CRAN in the usual manner with the command install.packages("RODBC") or via the Packages menu. The RODBC package can also be made to work on other operating systems but not as conveniently as under Windows.
5Environments in R are discussed in Section 8.9.1.
6Information on indexing data frames is presented in Section 2.3.4.
7Notable packages for handling missing data include amelia, mi, mice,and norm, which perform various versions of multiple imputation of missing data.
8Transformations, including the log transformation, are the subject of Section 3.4.
9An alternative would have been to plot crime against density using a log axis for density : plot(density, crime, log="x") . See Chapters 3 and 7 for general discussions of plotting data in R.
10The lowess function is described in Section 3.2.1.
11How statistical-modeling functions in R handle missing data is described in Section 4.8.5.
12Variables created by assignment at the command prompt are global variables defined in the working data.
13We did not have to create a new variable, say log.density <− log(density, 10) , as one may be required to do in a typical statistical package such as SAS or SPSS.
14Roughly equal numbers of observations in the three bins are the best we can do because n = 20 is not evenly divisible by 3.
15If the objective here were simply to sample 20 rows from Womenlf , then we could more simply use the some function in the car package, some(Womenlf, 20) , but we will reuse this sample to check on the results of our recodes.
16More correctly, a matrix is a vector with a two-element dim attribute.
17Classes are described in Sections 2.6 and 8.7.
18The vector letters contains the 26 lowercase letters from "a" to "z" ; LETTERS similarly contains the uppercase letters.
19Using the hyphen to represent ranges of characters can be risky, because character ranges can vary from one locale to another—say between English and French. Thus, for example, we cannot rely on the range a-zA-Z to contain all the alphabetic characters that may appear in a word—it will miss the accented letters, for example. As a consequence, there are special character classes defined for regular expressions, including [:alpha:] , which matches all the alphabetic characters in the current locale.
20One gigabyte is a little more than 1 billion bytes, and 1 byte is 8 bits (i.e., binary digits); double-precision floating-point numbers in R are stored in 8 bytes (64 bits) each. In a data set composed of floating-point numbers, then, 4 GB corresponds to 4 × 10243/8, or somewhat more than 500 million data values.
21We describe how to avoid these problems in Sections 8.4.1 and 8.6.2.
22Objects also have a storage mode, but we will not make use of that.
23The str function is used extensively in Chapter 8 on programming in R.
24Integers in R are so-called long integers, occupying 32 bits, hence the L .