Mathematics for the Nonmathematician

LOGIC AND MATHEMATICS

Geometry will draw the soul toward truth and create the spirit of philosophy.

PLATO

Mathematics has its own ways of establishing knowledge, and the understanding of mathematics is considerably promoted if one learns first just what those ways are. In this chapter we shall study the concepts which mathematics treats; the method, called deductive proof, by which mathematics establishes its conclusions; and the principles or axioms on which mathematics rests. Study of the contents and logical structure of mathematics leaves untouched the subject of how the mathematician knows what conclusions to establish and how to prove them. We shall therefore present a brief and preliminary discussion of the creation of mathematics. This topic will recur as we examine the subject matter itself in subsequent chapters.

Since mathematics, as we conceive the subject today, was fashioned by the Greeks, we shall also attempt to see what features of Greek thought and culture caused these people to remodel what the Egyptians and Babylonians had pursued for several thousand years.

3–2 THE CONCEPTS OF MATHEMATICS

The first major step which the Greeks made was to insist that mathematics must deal with abstract concepts. Let us see just what this means. When we first learn about numbers we are taught to think about collections of particular objects such as two apples, three men, and so on. Gradually and rather subconsciously we begin to think about the numbers 2, 3, and other whole numbers without having to associate them with physical objects. We soon reach the more advanced stage of adding, subtracting, and performing other operations with numbers without having to handle collections of objects in order to understand these operations or to see that the results agree with experience. Thus we soon become convinced that 4 times 5 must be 20, whether these numbers represent quantities of apples, horses, or even purely imaginary objects. By this time we are really dealing with concepts or ideas, for the whole numbers do not exist in nature. Any whole number is rather an abstraction of a property which is common to many different collections or sets of objects.

The whole numbers then are ideas, and the same is true of fractions such as , , and so on. In the latter case, too, the formulation of the physical relationship of a part of an object to the whole, whether it refers to pies, bushels of wheat, or to a smaller monetary value in relation to a larger one, again leads to an abstraction. Mathematicians formulate operations with fractions, that is, combining parts of an object, taking one part away from the other, or taking a part of a part, in such a way that the result of any operation on abstract fractions agrees with the corresponding physical occurrence. Thus the mathematical process of, say adding and , which yields , expresses the addition of of a pie and of a pie, and the result tells us how many parts of a pie one would actually have.

Whole numbers, fractions, and the various operations with whole numbers and fractions are abstractions. Although this fact is rather easy to understand, we tend to lose sight of it and cause ourselves unnecessary confusion. Let us consider an example. A man goes into a shoe store and buys 3 pairs of shoes at 10 dollars per pair. The storekeeper reasons that 3 pairs times 10 dollars is 30 dollars and asks for 30 dollars in return for the 3 pairs of shoes. If this reasoning is correct, then it is equally correct for the customer to argue that 3 pairs times 10 dollars is 30 pairs of shoes and to walk out with 30 pairs of shoes without handing the storekeeper one cent. The customer may end up in jail, but he may console himself while he languishes there that his reasoning is as sound as the storekeeper’s.

The source of the difficulty is, of course, that one cannot multiply shoes by dollars. One can multiply the number 3 by the number 10 and obtain the number 30. The practical and no doubt obligatory physical interpretation of the answer in the above situation is that one must pay 30 dollars rather than walk out with 30 pairs of shoes. We see, therefore, that one must distinguish between the purely mathematical operation of multiplying 3 by 10 and the physical objects with which these numbers may be associated.

The same point is involved in a slightly different situation. Mathematically is equal to . But the corresponding physical fact may not be true. One may be willing to accept 4 half-pies instead of 2 whole pies, but no woman would accept 4 half-dresses in place of 2 dresses or 4 half-shoes in place of 1 pair of whole shoes.

The Egyptians and Babylonians did reach the stage of working with pure numbers dissociated from physical objects. But like young children of our civilization, they hardly recognized that they were dealing with abstract entities. By contrast, the Greeks not only recognized numbers as ideas but emphasized that this is the way we must regard them. The Greek philosopher Plato, who lived from 428 to 348 B.C. and whose ideas are representative of the classical Greek period, says in his famous work, the Republic,

We must endeavor that those who are to be the principal men of our State go and learn arithmetic, not as amateurs, but they must carry on the study until they see the nature of numbers with the mind only; . . . arithmetic has a very great and elevating effect, compelling the soul to reason about abstract number, and rebelling against the introduction of visible or tangible objects into the argument.

The Greeks not only emphasized the distinction between pure numbers and the physical applications of such numbers, but they preferred the former to the latter. The study of the properties of pure numbers, which they called arithmetica, was esteemed as a worthy activity of the mind, whereas the use of numbers in practical applications, logistica, was deprecated as a mere skill.

Geometrical thinking prior to the classical Greek period was even less advanced than thinking about numbers. To the Egyptians and Babylonians the words “straight line” meant no more than a stretched rope or a line traced in sand, and a rectangle was a piece of land of a particular shape. The Greeks began the practice of treating point, line, triangle, and other geometrical notions as concepts. They did of course appreciate that these mental notions are suggested by physical objects, but they stressed that the concepts differ from the physical examples as sharply as the concept of time differs from the passage of the sun across the sky. The stretched string is a physical object illustrating the concept of line, but the mathematical line has no thickness, no color, no molecular structure, and no tension.

The Greeks were explicit in asserting that geometry deals with abstractions. Speaking of mathematicians, Plato says,

And do you not know also that although they make use of the visible forms and reason about them, they are thinking not of these, but of the ideals which they resemble; not of the figures which they draw, but of the absolute square and the absolute diameter . . . they are really seeking to behold the things themselves, which can be seen only with the eye of the mind?

On the basis of elementary abstractions, mathematics creates others which are even more remote from anything real. Negative numbers, equations involving unknowns, formulas, and other concepts we shall encounter are abstractions built upon abstractions. Fortunately, every abstraction is ultimately derived from, and therefore understandable in terms of, intuitively meaningful objects or phenomena. The mind does play its part in the creation of mathematical concepts, but the mind does not function independently of the outside world. Indeed the mathematician who treats concepts that have no physically real or intuitive origins is almost surely talking nonsense. The intimate connection between mathematics and objects and events in the physical world is reassuring, for it means that we can not only hope to understand the mathematics proper, but also expect physically meaningful and valuable conclusions.

The use of abstractions is not peculiar to mathematics. The concepts of force, mass, and energy, which are studied in physics, are abstractions from real phenomena. The concept of wealth, an abstraction from material possessions such as land, buildings, and jewelry, is studied in economics. The concepts of liberty, justice, and democracy are familiar in political science. Indeed, with respect to the use of abstract concepts, the distinction between mathematics on the one hand and the physical and social sciences on the other is not a sharp one. In fact, the influence of mathematics and mathematical ways of thinking on the physical sciences especially has led to ever increasing use of abstract concepts including some, as we shall see, which may have no direct real counterpart at all, any more than a mathematical formula has a direct real counterpart.

The very fact that other studies also engage in abstractions raises an important question. Mathematics is confined to some abstractions, numbers and geometrical forms, and to concepts built upon these basic ones. Abstractions such as mass, force, and energy belong to physics, and still other abstractions belong to other subjects. Why doesn’t mathematics also treat forces, wealth, and justice? Certainly these concepts are also worthy of study. Did the mathematicians make an agreement with physicists, economists, and others to divide the concepts among themselves? The restriction of mathematics to numbers and geometrical forms is partly a historical accident and partly a deliberate decision made by the Greeks. Numbers and geometrical forms had already been introduced by the Egyptians and Babylonians, and their utility in daily life was established. Since the Greeks learned the rudiments of mathematics from these civilizations, the sheer weight of tradition might have caused them to continue the practice of regarding mathematics as the study of numbers and geometrical figures. But people as original and bold in thought as the Greeks would not have been bound merely by tradition, had they not found in numbers and geometrical forms sharp and clear notions which appealed to their delight in the processes of exact thinking. However, an even more compelling reason was their belief that numerical and geometrical properties and relationships were basic, that they underlay the phenomena of the physical world and the design of the entire universe. Hence to understand the world one should seek this mathematical essence. The brilliance and depth of their conception of the universe will be revealed more and more as we proceed.

When one compares the pre-Greek and Greek understanding of the concepts of mathematics and notes the sharp transition from the concrete to the abstract, another question presents itself. The Greeks eliminated the physical substance and retained only the idea. Why did they do it? Surely it is more difficult to think about abstractions than about concrete things. Also it would seem that an attempt to study nature by concentrating on just a few aspects of physical objects rather than on the objects themselves would fall far short of effectiveness.

Insofar as the emphasis on abstractions is concerned, the Greeks saw at once what any thinking people would see sooner or later. One advantage of treating abstractions is the gain in generality. When a child learns that 5 + 5 = 10, he acquires in one swoop a fact which applies to hundreds of situations. Likewise a theorem proved about the abstract triangle applies to a triangular piece of land, a musical percussion instrument, and a triangle determined by three heavenly bodies at any instant of time. It has been said that the process of abstraction amounts to giving the same name to different things, but this very recognition that different objects possess the common property named in the abstraction carries with it the implication that anything true of the abstraction will apply to the several objects. Part of the secret of the power of mathematics is that it deals with abstractions.

Another advantage of abstraction was also clear to the Greeks. Abstracting from a physical situation just those properties which are to be studied frees the mind from burdensome and irrelevant details and enables one to concentrate on the features of interest. When one wishes to determine the area of a piece of land, only shape and size are relevant, and it is desirable to think only about these and not about the fertility of the soil.

The emphasis on mathematical abstractions by the classical Greeks was part and parcel of their outlook on the entire universe. They were concerned with truths, and leading philosophical schools, notably the Pythagoreans and the Platonists, maintained that truths could be established only about abstractions. Let us follow their argument. The physical world presents various objects to the senses. But the impressions received by the senses are inexact, transitory, and constantly changing; indeed, the senses may be even deceived, as by mirages. However, truth, by its very meaning, must consist of permanent, unchanging, definite entities and relationships. Fortunately, the intelligence of man excited to reflection by the impressions of sensible objects may rise to higher conceptions of the realities faintly exhibited to the senses, and so man may rise to the contemplation of ideas. These are eternal realities and the true goal of thought, whereas mere “things are the shadows of ideas thrown on the screen of experience.”

Thus Plato would say that there is nothing real in a horse, a house, or a beautiful woman. The reality is in the universal type or idea of a horse, a home, or a woman. The ideas, among which Plato emphasized Beauty, Justice, Intelligence, Goodness, Perfection, and the State, are independent of the superficial appearances of things, of the flux of life, and of the biases and warped desires of man; they are in fact constant and invariable, and knowledge concerning them is firm and indestructible. Real and eternal knowledge concerns these ideas, rather than sensuous objects. This distinction between the intelligible world and the world revealed by the senses is all-important in Plato.

Fig. 3–1.
Polyclitus: Spear-bearer (Daryphorus). National Museum, Naples.

To put Plato’s doctrine in everyday language, fundamental knowledge does not concern itself with what John ate, Mary heard, or William felt. Knowledge must rise above individuals and particular objects and tell us about broad classes of objects and about man as a whole. True knowledge must therefore of necessity concern abstractions. Plato admits that physical or sensible objects suggest the ideas just as diagrams of geometry suggest abstract geometrical concepts. Hence there is a point to studying physical objects, but one must not lose himself in trivial and confusing minutiae.

The abstractions of mathematics possessed a special importance for the Greeks. The philosophers pointed out that, to pass from a knowledge of the world of matter to the world of ideas, man must train his mind to grasp the ideas. These highest realities blind the person who is not prepared to contemplate them. He is, to use Plato’s famous simile, like one who lives continuously in the deep shadows of a cave and is suddenly brought out into the sunlight. The study of mathematics helps make the transition from darkness to light. Mathematics is in fact ideally suited to prepare the mind for higher forms of thought because on the one hand it pertains to the world of visible things and on the other hand it deals with abstract concepts. Hence through the study of mathematics man learns to pass from concrete figures to abstract forms; moreover, this study purifies the mind by drawing it away from the contemplation of the sensible and perishable and leading it to the eternal ideas. These latter abstractions are on the same mental level as the concepts of mathematics. Thus, Socrates says, “The understanding of mathematics is necessary for a sound grasp of ethics.”

Fig. 3–2.
Bust of Caesar. Vatican.

To sum up Plato’s position we may say that while a little knowledge of geometry and calculation suffices for practical needs, the higher and more advanced portions tend to lift the mind above mundane considerations and enable it to apprehend the final aim of philosophy, the idea of the Good. Mathematics, then, is the best preparation for philosophy. For this reason Plato recommended that the future rulers, who were to be philosopher-kings, be trained for ten years, from age 20 to 30, in the study of the exact sciences, arithmetic, plane geometry, solid geometry, astronomy, and harmonics (music). The oft-repeated inscription over the doors of Plato’s Academy, stating that no one ignorant of mathematics should enter, fully expresses the importance he attached to the subject, although modern critics of Plato read into these words his admission that one would not be able to learn it after entering. This value of mathematical training led one historian to remark, “Mathematics considered as a science owes its origins to the idealistic needs of the Greek philosophers, and not as fable has it, to the practical demands of Egyptian economics.”

Fig. 3–3.
Parthenon, Athens.

The preference of the Greeks for abstractions is equally evident in the art of the great sculptors, Polyclitus, Praxiteles, and Phidias. One has only to glance at the face in Fig. 3–1 to observe that Greek sculpture of the classical period dwelt not on particular men and women but on types, ideal types. Idealization extended to standardization of the ratios of the parts of the body to each other. Polyclitus believed, in fact, that there were ideal numerical ratios which fix the proportions of the human body. Perfect art must follow these ideal proportions. He wrote a book, The Canon, on the subject and constructed the “Spear-bearer” to illustrate the thesis. These abstract types contrast sharply with what is found in numerous busts and statues of private individuals and military and political leaders made by Romans (Fig. 3–2).

Greek architecture also reveals the emphasis on ideal forms. The simple and austere buildings were always rectangular in shape; even the ratios of the dimensions employed were fixed. The Parthenon at Athens (Fig. 3–3) is an example of the style and proportions found in almost all Greek temples.

EXERCISES

1. Suppose 5 trucks pass by with 4 men in each. To answer the question of how many men there are in all the trucks, a person reasons that 4 men times 5 trucks is 20 men. On the other hand, if there are 4 men each owning 5 trucks, the total number of trucks is 20 trucks. Hence 4 men times 5 trucks yields 20 trucks. How do you know that the answer is 20 men in one case and 20 trucks in the other?

2. If the product of 25¢ and 25¢ is obtained by multiplying 0.25 by 0.25 the result is 0.0625 or 6 ¢. Does it pay to multiply money?

3. Can you suggest some abstract political or ethical concepts?

4. Suppose 30 books are to be distributed among 5 people. Since 30 books divided by 5 people yields 6 books, each person gets 6 books. Criticize the reasoning.

5. A store advertises that it will give a credit of $1 for each purchase amounting to $1. A man who spends $6 reasons that he should receive a credit of $6 times $1, or $6. But $6 is 600¢ and $1 is 100¢. Hence 600¢ times 100¢ is 60,000¢, or $600. It would seem that it is more profitable to operate with the almost worthless cent than with dollars! What is wrong?

6. What does the statement that mathematics deals with abstractions mean?

7. Why did the Greeks make mathematics abstract?

3–3 IDEALIZATION

The geometrical notions of mathematics are abstract in the sense that shapes are mental concepts which actual physical objects merely approximate. The sides of a rectangular piece of land may not be exactly straight nor would each angle be exactly 90°. Hence, in adopting such abstract concepts, mathematics does idealize. But in studying the physical world, mathematics also idealizes in another sense which is equally important. Very often mathematicians undertake to study an object which is not a sphere and yet choose to regard it as such. For example, the earth is not a sphere but a spheroid, that is, a sphere flattened at the top and bottom. Yet in many physical problems which are treated mathematically the earth is represented as a perfect sphere. In problems of astronomy a large mass such as the earth or the sun is often regarded as concentrated at one point.

In making such idealizations, the mathematician deliberately distorts or approximates at least some features of the physical situation. Why does he do it? The reason usually is that he simplifies the problem and yet is quite sure that he has not introduced any gross errors. If one is to investigate, for example, the motion of a shell which travels ten miles, the difference between the assumed spherical shape of the earth and the true spheroidal shape does not matter. In fact, in the study of any motion which takes place over a limited region, say one mile, it may be sufficient to treat the earth as a flat surface. On the other hand, if one were to draw a very accurate map of the earth, he would take into account that the shape is spheroidal. As another example, to find the distance to the moon, it is good enough to assume that the moon is a point in space. However, to find the size of the moon, it is clearly pointless to regard the moon as a point.

The question does arise, how does the mathematician know when idealization is justified? There is no simple answer to this question. If he has to solve a series of like problems, he may solve one using the correct figure, and another, using a simplified figure, and compare results. If the difference does not matter for his purposes, he may then retain the simpler figure for the remaining problems. Sometimes he can estimate the error introduced by using the simpler figure and may find that this error is too small to matter. Or the mathematician may make the idealization and use the result because it is the best he can do. Then he must accept experience as his guide in deciding whether the result is good enough.

To idealize by deliberately introducing a simplification is to lie a little, but the lie is a white one. Using idealizations to study the physical world does impose a limitation on what mathematics accomplishes, but we shall find that even where idealizations are employed, the knowledge gained is of immense value.

EXERCISES

1. Distinguish between abstraction and idealization.

2. Is it correct to assume that the lines of sight to the sun from two places A and B on the earth’s surface are parallel?

3. Suppose you wished to measure the height of a flagpole. Would it be wise to regard the flagpole as a line segment?

3–4 METHODS OF REASONING

There are many ways, more or less reliable, of obtaining knowledge. One can resort to authority as one often does in obtaining historical knowledge. One may accept revelation as many religious people do. And one may rely upon experience. The foods we eat are chosen on the basis of experience. No one determined in advance by careful chemical analysis that bread is a healthful food.

We may pass over with a mere mention such sources of knowledge as authority and revelation, for these sources cannot be helpful in building mathematics or in acquiring knowledge of the physical world. It is true that in the medieval period of Western European culture men did contend that all desirable knowledge of nature was revealed in the Bible. However in no significant period of scientific thought has this view played any role. Experience, on the other hand, is a useful source of knowledge. But there are difficulties in employing this method. We should not wish to build a fifty-story building in order to decide whether a steel beam of specified dimensions is strong enough to be used in the foundation. Moreover, even if one should happen to choose workable dimensions, the choice may be wasteful of materials. Of course, experience is of no use in determining the size of the earth or the distance to the moon.

Closely related to experience is the method of experiment which amounts to setting up and going through a series of purposive, systematic experiences. It is true that experimentation fundamentally is experience, but it is usually accompanied by careful planning which eliminates extraneous factors, and the experience is repeated enough times to yield reliable information. However, experimentation is subject to much the same limitations as experience.

Are authority, revelation, experience, and even experimentation the only methods of obtaining knowledge? The answer is no. The major method is reasoning, and within the domain of reasoning there are several forms. One can reason by analogy. A boy who is considering a college career may note that his friend went to college and handled it successfully. He argues that since he is very much like his friend in physical and mental qualities, he too should succeed in college work. The method of reasoning just illustrated is to find a similar situation or circumstance and to argue that what was true for the similar case should be true of the one in question. Of course, one must be able to find a similar situation and one must take the chance that the differences do not matter.

Another common method of reasoning is induction. People use this method of reasoning every day. Because a person may have had unfortunate experiences in dealing with a few department stores, he concludes that all department stores are bad to deal with. Or, for example, experimentation would show that iron, copper, brass, oil, and other substances expand when heated, and one consequently concludes that all substances expand when heated. Inductive reasoning is in fact the common method used in experimentation. An experiment is generally performed many times, and if the same result is obtained each time, the experimenter concludes that the result will always follow. The essence of induction is that one observes repeated occurrences of the same phenomenon and concludes that the phenomenon will always occur. Conclusions obtained by induction seem well warranted by the evidence, especially when the number of instances observed is large. Thus the sun is observed so often to rise in the morning that one is sure it has risen even on those mornings when it is hidden by clouds.

There is still a third method of reasoning, called deduction. Let us consider some examples. If we accept as basic facts that honest people return found money and that John is honest, we may conclude unquestionably that John will return money that he finds. Likewise, if we start with the facts that no mathematician is a fool and that John is a mathematician, then we may conclude with certainty that John is not a fool. In deductive reasoning we start with certain statements, called premises, and assert a conclusion which is a necessary or inescapable consequence of the premises.

All three methods of reasoning, analogy, induction, and deduction, and other methods we could describe, are commonly employed. There is one essential difference, however, between deduction on the one hand and all other methods of reasoning on the other. Whereas the conclusion drawn by analogy or induction has only a probability of being correct, the conclusion drawn by deduction necessarily holds. Thus one might argue that because lions are similar to cows and cows eat grass, lions also eat grass. This argument by analogy leads to a false conclusion. The same is true for induction: although experiment may indeed show that two dozen different substances expand when heated, it does not necessarily follow that all substances do. Thus water, for example, when heated from 0° to 4° centigrade * does not expand; it contracts.

Since deductive reasoning has the outstanding advantage of yielding an indubitable conclusion, it would seem obvious that one should always use this method in preference to the others. But the situation is not that simple. For one thing analogy and induction are often easier to employ. In the case of analogy, a similar situation may be readily available. In the case of induction, experience often supplies the facts with no effort at all. The fact that the sun rises every morning is noticed by all of us almost automatically. Furthermore, deductive reasoning calls for premises which it may be impossible to obtain despite all efforts. Fortunately we can use deductive reasoning in a variety of situations. For example, we can use it to find the distance to the moon. In this instance, both analogy and induction are powerless, whereas, as we shall see later, deduction will obtain the result quickly. It is also apparent that where deduction can replace induction based on expensive experimentation, deduction is preferred.

Because we shall be concerned primarily with deductive reasoning, let us become a little more familiar with it. We have given several examples of deductive reasoning and have asserted that the conclusions are inescapable consequences of the premises. Let us consider, however, the following example. We shall accept as premises that

All good cars are expensive

and

All Locomobiles are expensive.

We might conclude that

All Locomobiles are good cars.

Fig. 3–4.

Fig. 3–5.

The reasoning here is intended as deductive; that is, the presumption in drawing this conclusion is that it is an inevitable consequence of the premises. Unfortunately, the reasoning is not correct. How can we see that it is not correct? A good way of picturing deductive arguments which enables us to see whether or not they are correct is called the circle test.

We note that the first premise deals with cars and expensive objects. Let us think of all the expensive objects in this world as represented by the points of a circle, the largest circle in Fig. 3–4. The statement that all good cars are expensive means that all good cars are a part of the collection of expensive objects. Hence we draw another circle within the circle of expensive objects, and the points of this smaller circle represent all the good cars. The second premise says that all Locomobiles are expensive. Hence if we represent all Locomobiles by the points of a circle, this circle, too, must be drawn within the circle of expensive objects. However we do not know, on the basis of the two premises, where to place the circle representing all Locomobiles. It can, as far as we know, fall in the position shown in the figure. Then we cannot conclude that all Locomobiles are good cars, because if that conclusion were inevitable, the circle representing Locomobiles must fall inside the circle representing good cars.

Many people do conclude from the above premises that all Locomobiles are good cars and the reason that they err is that they confuse the premise “All good cars are expensive” with the statement that “All expensive cars are good.” Were the latter statement our first premise then the deductive argument would be valid or correct.

Let us consider another example. Suppose we take as our premises that

All professors are learned people

and

Some professors are intelligent people.

May we necessarily conclude that

Some intelligent people are learned?

It may or may not be obvious that this conclusion is correct. Let us use the circle test. We draw a circle representing the class of learned people (Fig 3–5). Since the first premise tells us that all professors are learned people, the circle representing the class of professors must fall within the circle representing learned people. The second premise introduces the class of intelligent people, and we now have to determine where to draw that circle. This class must include some professors. Hence the circle must intersect the circle of professors. Since the latter is inside the circle of learned people, some intelligent people must fall within the class of learned people.

These examples of deductive reasoning may make another point clear. In determining whether a given argument is correct or valid, we must rely only upon the facts given in the premises. We may not use information which is not explicitly there. For example, we may believe that learned people are intelligent because to acquire learning they must possess intelligence. But this belief or fact, if it is a fact, cannot enter into the argument. Nothing that one may happen to know or believe about learned or intelligent people is to be used unless explicitly stated in the premises. In fact, as far as the validity of the argument is concerned, we might just as well have considered the premises

All x’s are y’s,

Some x’s are z’s,

and the conclusion, then, is

Some z’s are y’s.

Here we have used x for professor, y for learned person, and z for intelligent person. The use of x, y, and z does make the argument more abstract and more difficult to retain in the mind, but it emphasizes that we must look only at the information in the premises and avoids bringing in extraneous information about professors, learned people, and intelligent people. When we write the argument in this more abstract form, we also see more clearly that what determines the validity of the argument is the form of the premises rather than the meaning of x, y, and z.

A great deal of deductive reasoning falls into the patterns we have been illustrating. There are, however, variations that should be noted. It is quite customary, especially in the geometry we learn in high school, to state theorems in what is called the “if . . . then” form. Thus one might say, if a triangle is isosceles, then its base angles are equal. One could as well say, all isosceles triangles have equal base angles; or, the base angles of an isosceles triangle are equal. All three versions say the same thing.

Connected with the “if . . . then” form of a premise is a related statement which is often misunderstood. The statement “if a man is a professor, he is learned” offers no difficulty. As noted in the preceding paragraph, it is equivalent to “all professors are learned.” However the statement “only if a man is a professor, is he learned” has quite a different meaning. It means that to be learned one must be a professor or that if a man is learned, he must be a professor. Thus the addition of the word only has the significance of interchanging the “if” clause and the “then” clause.

We shall encounter numerous instances of deductive reasoning in our work. The subject of deductive reasoning is customarily studied in logic, a discipline which treats more thoroughly the valid forms of reasoning. However, we shall not need to depend upon formal training in logic. In most cases, common experience will enable us to ascertain whether the reasoning is or is not valid. When in doubt, we can use the circle test. Moreover, mathematics itself is the superb field from which to learn reasoning and is the best exercise in logic. The laws of logic were in fact formulated by the Greeks on the basis of their experiences with mathematical arguments.

EXERCISES

1. A coin is tossed ten times and each time it falls heads. What conclusion does inductive reasoning warrant?

2. Characterize deductive reasoning.

3. What superior features does deductive reasoning possess compared with induction and analogy?

4. Can you prove deductively that George Washington was the best president of the United States?

5. Can one always apply deductive reasoning to prove a desired statement?

6. Can you prove deductively that monogamy is the best system of marriage?

7. Are the following purportedly deductive arguments valid?

a) All good cars are expensive. A Daffy is an expensive car. Therefore a Daffy is a good car.

b) All New Yorkers are good citizens. All good citizens give to charity. Therefore all New Yorkers give to charity.

c) All college students are clever. All young boys are clever. Therefore all young boys are college students.

d) The same premises as in (c), but the conclusion: All college students are young boys.

e) It rains every Monday and it is raining today; hence today must be Monday.

f) No decent people curse; Americans are decent; therefore Americans do not curse.

g) No decent people curse; Americans curse; therefore some Americans are not decent.

h) No decent people curse; some Americans are not decent; therefore some Americans curse.

i) No undergraduates have a bachelor-of-arts degree; no freshmen have a bachelor-of-arts degree. Therefore all freshmen are undergraduates.

8. If someone gave you a valid deductive argument but the conclusion was not true, where would you look for the difficulty?

9. Distinguish between the validity of a deductive argument and the truth of the conclusion.

3–5 MATHEMATICAL PROOF

We have seen so far in our discussion of reasoning that there are several methods of reasoning and that all are useful. These methods can be applied to mathematical problems. Let us suppose that one wished to determine the sum of the angles of a triangle. He could draw on paper many different triangles or construct some out of wood or metal and measure the angles. In each case he would find that the sum is as close to 180° as the eye and hand can determine. By inductive reasoning he could conclude that the sum of the angles in every triangle is 180°. As a matter of fact, the Babylonians and Egyptians did in effect use inductive reasoning to establish their mathematical results. They must have determined by measurement that the area of a triangle is one-half the base times the altitude and, having used this formula repeatedly and having obtained reliable results, they concluded that the formula is correct.

Fig. 3–6.
The mid-points of parallel chords lie on a straight line.

To see that reasoning by analogy can be used in mathematics, let us note first that the centers of a set of parallel chords of a circle lie on a straight line (Fig. 3–6a). In fact this line is a diameter of the circle. Now an ellipse (Fig. 3–6b) is very much like a circle. Hence one might conclude that the centers of a set of parallel chords of an ellipse also lie on a straight line.

Deduction is certainly applicable in mathematics. The proofs which one learns in Euclidean geometry are deductive. As another illustration we might consider the following algebraic argument. Suppose one wishes to solve the equation x − 3 = 7. One knows that equals added to equals give equals. If we added 3 to both sides of the preceding equation, we would be adding equals to an equality. Hence the addition of 3 to both sides is justified. When this is done, the result is x = 10, and the equation is solved.

Thus all three methods are applicable. There is a lot to be said for the use of induction and analogy. The inductive argument for the sum of the angles of a triangle can be carried out in a matter of minutes. The argument by analogy given above is also readily made. On the other hand, finding deductive proofs for these same conclusions might take weeks or might never be accomplished by the average person. As a matter of fact, we shall soon encounter some examples of conjectures for which the inductive evidence is overwhelming but for which no deductive proof has been thus far obtained even by the best mathematicians.

Despite the usefulness and advantages of induction and analogy, mathematics does not rely upon these methods to establish its conclusions. All mathematical proofs must be deductive. Each proof is a chain of deductive arguments, each of which has its premises and conclusion.

Before examining the reasons for this restriction to deductive proof, we might contrast the method of mathematics with those of the physical and social sciences. The scientist feels free to draw conclusions by any method of reasoning and, for that matter, on the basis of observation, experimentation, and experience. He may reason by analogy as, for example, when he reasons about sound waves by observing water waves or when he reasons about a possible cure for a disease affecting human beings by testing the cure on animals. In fact reasoning by analogy is a powerful method in science. The scientist may also reason inductively: if he observes many times that hydrogen and oxygen combine to form water, he will conclude that this combination will always form water. At some stages of his work the scientist may also reason deductively and, in fact, even employ the concepts and methods of mathematics proper.

To contrast further the method of mathematics with that of the scientist—and perhaps to illustrate just how stubborn the mathematician can be—we might consider a rather famous example. Mathematicians are concerned with whole numbers, or integers, and among these they distinguish the prime numbers. A prime is a number which has no integral divisors other than itself and 1. Thus 11 is a prime number, whereas 12 is not because it is divisible by 2 for example. Now by actual trial one finds that each of the first few even numbers can be expressed as the sum of two prime numbers. For example, 2 = 1 + 1; 4 = 2 + 2; 6 = 3 + 3; 8 = 3 + 5; 10 = 3 + 7; . . . . If one investigates larger and larger even numbers, one finds without exception that every even number can be expressed as the sum of two primes. Hence by inductive reasoning one could conclude that every even number is the sum of two prime numbers.

But the mathematician does not accept this conclusion as a theorem of mathematics because it has not been proved deductively from acceptable premises. The conjecture that every even number is the sum of two primes, known as Goldbach’s hypothesis because it was first suggested by the eighteenth-century mathematician Christian Goldbach, is an unsolved problem of mathematics. The mathematician will insist on a deductive proof even if it takes thousands of years, as it literally has in some instances, to find one. However a scientist would not hesitate to use this inductively well supported conclusion.

Of course, the scientist should not be surprised to find that some of his conclusions are false because, as we have seen, induction and analogy do not lead to sure conclusions. But it does seem as though the scientist’s procedure is wiser since he can take advantage of any method of reasoning which will help him advance his knowledge. The mathematician by comparison appears to be narrow-minded or shortsighted. He achieves a reputation for certainty, but at the price of limiting his results to those which can be established deductively. How wise the mathematician may be in his insistence on deductive proof we shall learn as we proceed.

The decision to confine mathematical proof to deductive reasoning was made by the Greeks of the classical period. And they not only rejected all other methods of proof in mathematics, but they also discarded all the knowledge which the Egyptians and Babylonians had acquired over a period of four thousand years because it had only an empirical justification. Why did the Greeks do it?

The intellectuals of the classical Greek period were largely absorbed in philosophy and these same men, because they possessed intellectual interests, were the very ones who developed mathematics as a system of thought. The Ionians, the Pythagoreans, the Sophists, the Platonists, and the Aristotelians were the leading philosophers who gave mathematics its definitive form. The credit for initiating this step probably belongs to one school of Greek philosopher-mathematicians, known as the Ionian school. However, if credit can be assigned to any one person, it belongs to Thales, who lived about 600 B.C. Though a native of Miletus, a Greek city in Asia Minor, Thales spent many years in Egypt as a merchant. There he learned what the Egyptians had to offer in mathematics and science, but apparently he was not satisfied, for he would accept no results that could not be established by deductive reasoning from clearly acceptable axioms. In his wisdom Thales perceived what we shall perceive as we follow the story of mathematics, that the obvious is far more suspect than the abstruse.

Thales probably supplied the proof of many geometrical theorems. He acquired great fame as an astronomer and is believed to have predicted an eclipse of the sun in 585 B.C. A philosopher-astronomer-mathematician might readily be accused of being an impractical stargazer, but Aristotle tells us otherwise. In a year when olives promised to be plentiful, Thales shrewdly cornered all the oil presses to be found in Miletus and in Chios. When the olives were ripe for pressing, Thales was in a position to rent out the presses at his own price. Thales might perhaps have lived in history as a leading businessman, but he is far better known as the father of Greek philosophy and mathematics. From his time onward, deductive proof became the standard in mathematics.

It is to be expected that philosophers would favor deductive reasoning. Whereas scientists select particular phenomena for observation and experimentation and then draw conclusions by induction or analogy, philosophers are concerned with broad knowledge about man and the physical world. To establish universal truths, such as that man is basically good, that the world is designed, or that man’s life has purpose, deductive reasoning from acceptable principles is far more feasible than induction or analogy. As Plato put it in his Republic, “If persons cannot give or receive a reason, they cannot attain that knowledge which, as we have said, man ought to have.”

There is another reason that philosophers favor deductive reasoning. These men seek truths, the eternal verities. We have seen that of all the methods of reasoning only deductive reasoning grants sure and exact conclusions. Hence this is the method which philosophers would almost necessarily adopt. Not only do induction and analogy fail to yield absolutely unquestionable conclusions, but many Greek philosophers would not have accepted as facts the data with which these methods operate, because these are acquired by the senses. Plato stressed the unreliability of sensory perceptions. Empirical knowledge, as Plato put it, yields opinion only.

The Greek preference for deduction had a sociological basis. Contrary to our own society wherein bankers and industrialists are respected most, in classical Greek society, the philosophers, mathematicians, and artists were the leading citizens. The upper class regarded earning a living as an unfortunate necessity. Work robbed man of time and energy for intellectual activities, the duties of citizenship and discussion. These Greeks did not hesitate to express their disdain for work and business. The Pythagoreans, who, as we shall see, delighted in the properties of numbers and applied numbers to the study of nature, derided the use of numbers in commerce. They boasted that they sought knowledge rather than wealth. Plato, too, maintained that knowledge rather than trade was the goal in studying arithmetic. Freemen, he declared, who allowed themselves to become preoccupied with business should be punished, and a civilization which is concerned mainly with the material wants of man is no more than a “city of happy pigs.” Xenophon, the famous Greek general and historian, says, “What are called the mechanical arts carry a social stigma and are rightly dishonored in our cities.” Aristotle wanted an ideal society in which citizens would not have to practice any mechanical arts. Among the Boeotians, one of the independent tribes of Ancient Greece, those who defiled themselves, with commerce were by law excluded from state positions for ten years.

Who did the daily work of providing food, shelter, clothing, and the other necessities of life? Slaves and free men ineligible for citizenship ran the businesses and the households, did unskilled and technical work, managed the industries, and carried on the professions such as medicine. They produced even the articles of refinement and luxury.

In view of this attitude of the Greek upper class towards commerce and trade, it is not hard to understand the classical Greek’s preference for deduction. People who do not “live” in the workaday world can learn little from experience, and people who will not observe and use their hands to experiment will not have the facts on which to base reasoning by analogy or induction. In fact the institution of slavery in classical Greek society fostered a divorce of theory from practice and favored the development of speculative and deductive science and mathematics at the expense of experimentation and practical applications.

Over and above the various cultural forces which inclined the Greeks toward deduction were a farsightedness and a wisdom which mark true genius. The Greeks were the first to recognize the power of reason. The mind was a faculty not only additional to the senses but more powerful than the senses. The mind can survey all the whole numbers, but the senses are limited to perceiving only a few at a time. The mind can encompass the earth and the heavens; the sense of sight is confined to a small angle of vision. Indeed the mind can predict future events which the senses of contemporaries will not live to perceive. This mental faculty could be exploited. The Greeks saw clearly that if man could obtain some truths, he could establish others entirely by reasoning, and these new truths, together with the original ones, enabled man to establish still other truths. Indeed the possibilities would multiply at an enormous rate. Here was a means of acquiring knowledge which had been either overlooked or neglected.

This was indeed the plan which the Greeks projected for mathematics. By starting with some truths about numbers and geometrical figures they could deduce others. A chain of deductions might lead to a significant new fact which would be labeled a theorem to call attention to its importance. Each theorem added to the stock of truths that could serve as premises for new deductive arguments, and so one could build an immense body of knowledge about the basic concepts.

Although the Greeks may have been guilty of overemphasizing the power of the mind unaided by experience and observation to obtain truths, there is no doubt that in insisting on deductive proof as the sole method, they rose above the practical level of carpenters, surveyors, farmers, and navigators. At the same time they elevated the subject of mathematics to a system of thought. Moreover the preference for reason which they exhibited gave this faculty the high prestige which it now enjoys and permitted it to exercise its true powers. When we have surveyed some of the creations of the mind that succeeding civilizations building on the Greek plan contributed, we shall appreciate the true depth of the Greek vision.

EXERCISES

1. Compare Greek and pre-Greek standards of proof in mathematics. Reread the relevant parts of Chapter 2.

2. Distinguish science and mathematics with respect to ways of establishing conclusions.

3. Explain the statement that the Greeks converted mathematics from an empirical science to a deductive system.

4. Are the following deductive arguments valid?

a) All even numbers are divisible by 4. Ten is an even number. Hence 10 is divisible by 4.

b) Equals divided by equals give equals. Dividing both sides of 3x = 6 by 3 is dividing equals by equals. Hence x = 2.

5. Does it follow from the fact that the square of any odd number is odd that the square of any even number is even?

6. Criticize the argument:

The square of every even number is even because 2² = 4, 4² = 16, 6² = 36, and it is obvious that the square of any larger even number also is even.

7. If we accept the premises that the square of any odd number is odd and the square of any even number is even, does it follow deductively that if the square of a number is even, the number must be even?

8. Why did the Greeks insist on deductive proof in mathematics?

9. Let us take for granted that if a triangle has two equal sides, the opposite angles are equal and that we have a triangle in which all three sides are equal. Prove deductively that all three angles are equal in the triangle under consideration. You may also use the premise that things equal to the same thing are equal to one another.

10. How did the Greeks propose to obtain new truths from known ones?

3–6 AXIOMS AND DEFINITIONS

From our discussion of deductive reasoning we know that to apply such reasoning we must have premises. Hence the question arises, what premises does the mathematician use? Since the mathematician reasons about numbers and geometrical figures, he must of course have facts about these concepts. These cannot be obtained deductively because then there would have to be prior premises, and if one continued this process backward, there would be no starting point. The Greeks readily found premises. It seemed indisputable, for example, that two points determine one and only one line and that equals added to equals give equals.

To the Greeks the premises on which mathematics was to be built were self-evident truths, and they called these premises axioms. Socrates and Plato believed, as did many later philosophers, that these truths were already in our minds at birth and that we had but to recall them. And since the Greeks believed that axioms were truths and since deductive reasoning yielded unquestionable conclusions, they also believed that theorems were truths. This view is no longer held, and we shall see later in this book why mathematicians abandoned it. We now know that axioms are suggested by experience and observation. Naturally, to be as certain as we can of these axioms we select those facts which seem clearest and most reliable in our experience. But we must recognize that there is no guarantee that we have selected truths about the world. Some mathematicians prefer to use the word assumptions instead of axioms to emphasize this point.

The mathematician also takes care to state his axioms at the outset and to be sure as he performs his reasoning that no assumptions or facts are used which were not so stated. There is an interesting story told by former President Charles W. Eliot of Harvard which illustrates the likelihood of introducing unwarranted premises. He entered a crowded restaurant and handed his hat to the doorman. When he came out, the doorman at once picked Eliot’s hat out of hundreds on the racks and gave it to him. He was amazed that the doorman could remember so well and asked him, “How did you know that was my hat?” “I didn’t,” replied the doorman. “Why, then, did you hand it to me?” The doorman’s reply was, “Because you handed it to me, sir.”

Undoubtedly no harm would have been done if the doorman had assumed that the hat he returned to President Eliot belonged to the man. But the mathematician interested in obtaining conclusions about the physical world might be wasting his time if he unwittingly introduced an assumption that he had no right to make

There is one other element in the logical structure of mathematics about which we shall say a few words now and return to in a later chapter (Chapter 20). Like other studies mathematics uses definitions. Whenever we have occasion to use a concept whose description requires a lengthy statement, we introduce a single word or phrase to replace that lengthy statement. For example, we may wish to talk about the figure which consists of three distinct points which do not lie on the same straight line and of the line segments joining these points. It is convenient to introduce the word triangle to represent this long description. Likewise the word circle represents the set of all points which are at a fixed distance from a definite point. The definite point is called the center, and the fixed distance is called the radius. Definitions promote brevity.

EXERCISES

1. What belief did the Greeks hold about the axioms of mathematics?

2. Summarize the changes which the Greeks made in the nature of mathematics.

3. Is it fair to say that mathematics is the child of philosophy?

3–7 THE CREATION OF MATHEMATICS

Because mathematical proof is strictly deductive and merely reasonable or appealing arguments may not be used to establish a conclusion, mathematics has been described as a deductive science, or as the science which derives necessary conclusions, that is, conclusions which necessarily or inevitably follow from the axioms. This description of mathematics is incomplete. Mathematicians must also discover what to prove and how to go about establishing proofs. These processes are also part of mathematics and they are not deductive.

How does the mathematician discover what to prove and the deductive arguments that lead to the conclusions? The most fertile source of mathematical ideas is nature herself. Mathematics is devoted to the study of the physical world, and simple experience or the more careful scrutiny of nature suggests idea after idea. Let us consider here a few simple examples. Once mathematicians had decided to devote themselves to geometric forms, it was only natural that such questions should arise as, what are the area, perimeter, and sum of the angles of common figures? Moreover, it is even possible to see how the precise statement of the theorem to be proved would follow from direct experience with physical objects. The mathematician might measure the sum of the angles of various triangles and find that these measurements all yield results close to 180°. Hence the suggestion that the sum of the angles in every triangle is 180° occurs as a possible theorem. To decide the question, which has more area, a polygon or a circle having the same perimeter, one might cut out cardboard figures and weigh them. The relative weights would suggest the statement of the theorem to be proved.

After some theorems have been suggested by direct physical problems, others are readily conceived by generalizing or varying the conditions. Thus knowing the problem of determining the sum of the angles of a triangle, one might ask, What is the sum of the angles of a quadrilateral, a pentagon, and so forth? That is, once the mathematician begins an investigation which is suggested by a physical problem, he can easily find new problems which go beyond the original one.

In the domains of arithmetic and algebra direct calculation with numbers, which is analogous to measurement in geometry, will suggest possible theorems. Anyone who has played with integers, for example, has doubtless observed the following facts:

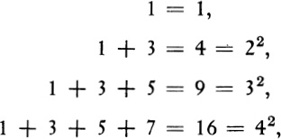
We note that each number on the right is the square of the number of odd numbers appearing on the left; thus in the fourth line, there are four numbers on the left side, and the right side is 4². The general result which these calculations suggest is that if the first n odd numbers were on the left side, then the sum would be n². Of course, this possible theorem is not proved by the above calculations. Nor could it ever be proved by such calculations, for no mortal man could make the infinite set of computations required to establish the conclusion for every n. The calculations do, however, give the mathematician something to work on.

These simple illustrations of how observation, measurement, and calculation suggest possible theorems are not too striking or very profound. We shall see in the course of later work how physical problems suggest more significant mathematical theorems. However, experience, measurement, calculation, and generalization do not include the most fertile source of possible theorems. And it is especially true in seeking methods of proof that more than routine techniques must be utilized. In both endeavors the most important source is the creative act of the human mind.

Fig. 3–7

Let us consider the matter of proof. Suppose one has discovered by measurements that the sum of the angles of various triangles is 180°. One must now prove this result deductively. No obvious method will do the job. Some new idea is required, and the reader who remembers his elementary geometry will recall that the proof is usually made by drawing a line through one vertex (A in Fig. 3–7) and parallel to the opposite side. It then turns out as a consequence of a previously established theorem on parallel lines that the angles 1 and 2 are equal, as are the angles 3 and 4. However the angles 1, 3, and the angle A of the triangle itself do add up to 180°, and so the same is true for the angles of the triangle. This method of proof is not routine. The idea of drawing the line through A must be supplied by the mind. Some methods of proof seem so devious and artificial that they have provoked critical comments. The philosopher Arthur Schopenhauer called Euclid’s proof of the Pythagorean theorem “a mouse-trap proof” and “a proof walking on stilts, nay, a mean, underhand proof.”

The above example has been offered to emphasize the fact that ingenious mathematical work must be done in finding methods of proofs even after the question of what to prove is disposed of. In the search for a method of proof, as in finding what to prove, the mathematician must use audacious imagination, insight, and creative ability. His mind must see possible lines of attack where others would not. In the domains of algebra, calculus, and advanced analysis especially, the first-rate mathematician depends upon the kind of inspiration that we usually associate with the creation of music, literature, or art. The composer feels that he has a theme which when properly developed will produce true music. Experience and a knowledge of music aid him in arriving at this conviction. Similarly, the mathematician surmises that he has a conclusion which will follow from the axioms of mathematics. Experience and knowledge may guide his thoughts into the proper channels. Modifications of one sort or another may be required before a correct proof and a satisfactory statement of the new theorem are achieved. But essentially both mathematician and composer are moved by an afflatus which enables them to see the final edifice before a single stone is laid.

We do not know just what mental processes may lead to correct insight any more than we know how it was possible for Keats to write fine poetry or why Rembrandt was able to turn out fine paintings. One might say of mathematical creation what P. W. Bridgman, the noted physicist, has said of scientific method, that it consists of “doing one’s damnedest with one’s mind, no holds barred.” There is no logic or infallible guide which tells the mind how to think. The very fact that many great mathematicians have tackled a problem and failed and that another comes along and solves it shows that the mind has something to contribute.

The preceding discussion of the creation of mathematics should correct several mistaken popular impressions. When creating a mathematical proof, the mind does not see the cold, ordered arguments which one reads in texts, but rather it perceives an idea or a scheme which when properly formulated constitutes the deductive proof. The formal proof, so to speak, merely sanctions the conquest already made by the intuition. Secondly, the deductive proof is not the preferable form by which to grasp the idea or method employed. In fact the deductive argument often conceals the idea because the logical form is not perspicuous to the intuition. At the very least the details of the arguments obscure the main threads. The value of the deductive organization of the proof is that it enables the creator and the reader to test the arguments by the standards of exact reasoning. Thirdly, there is the prevalent but mistaken notion that scientists and mathematicians must keep their minds open and unbiased in pursuing an investigation. They are not supposed to prejudge the conclusion. Actually the mathematician must first decide what to prove, and this conclusion not only does but must precede the search for the proof, or else he would not know where to head. This is not to say that the mathematician may not sometimes make a false conjecture. If he does, his search for a proof will fail or in the course of the search he will realize that he cannot prove what he is after, and he will correct his conjecture. But in any case he knows what he is trying to prove.

EXERCISES

1. Consider the parallelogram ABCD (Fig. 3–8). By definition, the opposite sides are parallel. Now introduce the diagonal BD. Does observation suggest a possible theorem relating the triangles ABD and BDC?

Fig. 3–8

Fig. 3–9

2. Consider any quadrilateral ABCD (Fig. 3–9) and the figure formed by joining the mid-points E, F, G, H of the sides of the quadrilateral. Does observation or intuition suggest any significant fact about the quadrilateral EFGH?

3. The formula n² − n + 41 is supposed to yield primes for various values of n. Thus when n = 1,

1² − 1 + 41 = 41,

and this is a prime. When n = 2,

2² − 2 + 41 = 43,

and this is a prime. Test the formula for n = 3 and n = 4. Are the resulting values of the formula primes? Have you proved, then, that the formula always yields primes?

4. Can you specify conditions under which two quadrilaterals will be congruent, that is, have the same size and shape?

5. The following lines show some calculations with the sum of the cubes of whole numbers:

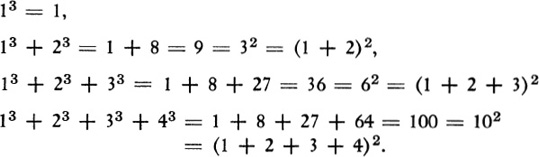
What generalization do these few calculations suggest?

REVIEW EXERCISES

1. What basis did the Egyptians and Babylonians have for believing in the correctness of their mathematical conclusions?

2. Compare Greek and pre-Greek understanding of the concepts of mathematics.

3. What was the Greek plan for establishing mathematical conclusions?

4. In what sense is mathematics a creation of the Greeks rather than of the Egyptians and the Babylonians?

5. Suppose we accept the premises that all professors are intelligent people and all professors are learned people. Which of the following conclusions is validly deduced?

a) Some intelligent people are learned.

b) Some learned people are intelligent.

c) All intelligent people are learned.

d) All learned people are intelligent.

6. Suppose we accept the premises that all college students are wise, and no professors are college students. Which of the following conclusions is validly deduced?

a) No professors are wise.

b) Some professors are wise.

c) All professors are wise.

7. Is the following argument valid?

All parallelograms are quadrilaterals, and figure ABCD is a quadrilateral. Hence figure ABCD is a parallelogram.

8. What conclusion can you deduce from the premises,

Every successful student must work hard,

and

John does not work hard?

9. Smith says,

If it rains I go to the movies.

If Smith went to the movies, what can you conclude deductively?

10. Smith says,

I go to the movies only if it rains.

If Smith went to the movies, what can you conclude deductively?

Topics for Further Investigation

To pursue any of these topics use the books listed below under Recommended Reading.

1. The life and work of the Pythagoreans

2. The life and work of Euclid

CHAPTER 3

LOGIC AND MATHEMATICS

3–1 INTRODUCTION

3–2 THE CONCEPTS OF MATHEMATICS

EXERCISES

3–3 IDEALIZATION

EXERCISES

3–4 METHODS OF REASONING

EXERCISES

3–5 MATHEMATICAL PROOF

EXERCISES

3–6 AXIOMS AND DEFINITIONS

EXERCISES

3–7 THE CREATION OF MATHEMATICS

EXERCISES

REVIEW EXERCISES

Topics for Further Investigation

Recommended Reading