One must do no violence to nature, nor model it in conformity to any blindly formed chimaera;. . .
JOHN BOLYAI
The most significant revolutions in this world are not political. Political revolutions hardly change the daily life of man or, if they do, exert a short-term effect which may even be reversed by subsequent revolutions. The significant upheavals are caused by new ideas; these far more effectively, powerfully, and lastingly alter the lives of civilized human beings. For example, the beliefs in the importance of the human being and in his right to life, liberty, and the pursuit of happiness have permanently and radically changed the lives and aspirations of hundreds of millions of human beings. Indeed, many political revolutions were inspired by the desire to realize these ideas. The two concepts which have most profoundly revolutionized our intellectual development since the nineteenth century are evolution and non-Euclidean geometry. The theory of evolution is generally well recognized as a prime influence, but non-Euclidean geometry, despite its more fundamental and more far-reaching effects, seems to escape attention.
In this chapter we shall examine the nature of non-Euclidean geometry, its value for science, its implications for the nature of mathematics, and, finally, its influence on our culture.
Euclidean geometry, as well as developments such as arithmetic, algebra, and calculus, rests upon axioms. The Greeks, who formulated the axioms of Euclidean geometry, believed that human minds immediately recognized some truths about the geometrical properties of physical objects and of space. Thus, it seemed indubitable that two points determined one and only one line, and that equal line segments added to another pair of equal line segments gave equal sums. For two thousand years the entire intellectual world accepted the Greek doctrine that the axioms of Euclidean geometry and of mathematics in general, were truths about the physical world, truths so clear and so evident that no one in his right mind could question them. Of course, since the axioms of geometry were truths, and since the theorems were logically necessary consequences of the axioms, the entire body of Euclidean geometry constituted a collection of indubitable truths about idealized objects and phenomena of the physical world.
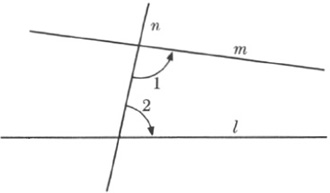
One slight blemish seemed to mar the collection of axioms. Euclidean geometry deals with parallel lines. By definition, two lines in the same plane are parallel if they do not meet, that is, if they do not contain any point in common. This last statement expresses what we mean by parallel lines and so is not objectionable. In itself it does not assert that there are any parallel lines. But Euclidean geometry contains an axiom which implies the existence of parallel lines, and our present discussion centers about the nature of this axiom. As stated by Euclid, the axiom asserts that if two lines m and l (Fig. 20–1), meet a third line, n, so as to make the sum of angles 1 and 2 less than 180°, then the lines m and l meet on that side of the line n on which the angles 1 and 2 lie. Euclid then proves, for example, that if the sum of angles 1 and 2 is 180°, then m and l are parallel. This axiom is a bit involved, and there is some reason to believe that even Euclid himself was not too happy about it. Neither he nor later mathematicians up to the nineteenth century really doubted the truth of this axiom; that is, they had no doubt that it was a correct idealization of the behavior of actual or physical lines. What bothered Euclid and his successors was that the axiom was not quite so self-evident as the axiom, say, that any two right angles are equal.
Fig. 20–1.
Euclid’s parallel axiom.
Fig. 20–2.
Playfair’s parallel axiom.
From Greek times on mathematicians sought to replace this axiom with an equivalent one. An equivalent axiom is one which, together with the other nine axioms of Euclid, will make it possible to derive the same body of theorems that Euclid deduced. Many equivalent axioms were proposed. One of these, known as Playfair’s axiom fit was adopted by the mathematician John Playfair (1748–1819)], is the one we usually learn in high school. Playfair’s axiom states that, given a line l (Fig. 20–2) and a point P not on that line, there is one and only one line m in the plane of P and l which passes through P and does not meet l. From Playfair’s parallel axiom and the other nine axioms of Euclid one can deduce all the theorems of Euclidean geometry.
Playfair’s axiom appears intuitively convincing. That is, it does seem as though straight lines in physical space possess the property asserted. However, mathematicians were not satisfied with Playfair’s axiom or other proposed equivalents of Euclid’s parallel axiom. They recognized that every proposed substitute involved directly or indirectly an assertion about what happened far off in space. Thus, Playfair’s axiom asserts that the line m through P will not meet l even in the very distant space to which these lines extend. As a matter of fact, Euclid’s axiom is superior in this respect because it does not assert that lines will not meet, but states conditions under which they will meet at some finite distance.
What is objectionable about axioms which assert what happens far out in space? The answer is that they transcend experience. The axioms of Euclidean geometry are supposed to be immediately convincing statements about the properties of space. But how can one be sure of what happens millions of miles away? How can one be sure that it is possible to extend straight lines indefinitely far out into physical space, without the lines ever being forced to meet? Thus the efforts made to find a simpler statement than Euclid’s did succeed insofar as simplicity of statement was concerned, but bred doubts about the truth of any assertion regarding the existence of parallel lines.
By the eighteenth century some mathematicians decided to try a new tack. Euclid’s set contained ten axioms. Perhaps nine sufficed; that is, perhaps one could prove an assertion about parallel lines by deduction from the other nine axioms. If this should be possible, then there would be no further problem, because the assertion about parallel lines would be a necessary consequence of the nine entirely acceptable axioms. However, all these efforts failed.
One of these efforts, though, deserves special attention. The Jesuit priest Girolamo Saccheri (1667–1733) decided to apply the indirect method of proof. Euclid’s parallel axiom asserts, in effect, the existence of one and only one line through P and parallel to l. To establish the truth of this statement by contradiction, two alternatives are available: no line parallel to l through P or more than one. Saccheri’s plan was to assume in turn that each alternative to Euclid’s parallel axiom was true and, with this alternative and the other nine axioms of Euclid, show that deductions would lead to a contradiction. He could then proclaim that the only questionable assumption, namely the alternative to Euclid’s parallel axiom, must be false. After doing this with each of the two alternatives, he could then assert that the only remaining possibility, Euclid’s axiom, must be true. As a matter of history, the alternative asserting that there were no parallels to l through P produced a contradiction. However, from the second alternative (there is more than one parallel to l through P) Saccheri derived a number of strange theorems but no contradiction.
The strangeness of the theorems he obtained was enough to convince Saccheri that this second alternative could not be true, and hence that Euclid’s parallel axiom must be true because it was the only possible alternative. And so in 1733 he published a book entitled Euclid Vindicated From All Dejects. Of course, strangeness of theorems and logical contradiction are quite different matters, and Saccheri was not justified in substituting one for the other. But he was tied to his time and, in drawing the conclusion that Euclid’s assertion on parallel lines was a necessary consequence of the other nine axioms, he showed merely that if a man sets out to establish something of which he is already convinced, he will satisfy at least himself that he has proved its truth regardless of the facts.
The first to draw the conclusion which Saccheri should have drawn was Karl Friedrich Gauss (1777–1855). Gauss was one of the greatest mathematicians of all times. His father was a bricklayer who expected his son to adopt the same trade. However, Gauss showed his precocity in elementary school, and his teachers saw to it that he received a good education. At the University of Göttingen his teachers were hard put to keep up with him. At 22 Gauss submitted his doctoral thesis to the University of Helmstedt. In this thesis he proved what is often called the fundamental theorem of algebra, namely, that every algebraic equation of any degree has at least one root. At the age of 30 he was appointed professor of astronomy at the University of Göttingen. He discouraged students from attending his lectures.
Gauss’s scientific interests, like those of Archimedes and Newton, were unbelievably broad. He was, for example, a great inventor. He designed many instruments for use in geodesy and was one of the inventors of the electric telegraph. He devised methods of making maps, was an excellent astronomical observer, and set up systems of insurance. At the request of the Elector of Hannover he made a survey of the principality. In addition to devising instruments for the measurement of the earth’s magnetic field, he himself studied the variation in the strength of this field over the earth. The unit now used to measure the strength of magnetic fields is called the gauss.
Inspired by his scientific and practical interests, Gauss contributed to a number of major branches of mathematics. In fact, he would not think of separating mathematics from its application to science. Though his greatest achievements were in mathematics and he is therefore most often described as a mathematician, it would be more appropriate to call him a student of nature. His motto read:
Thou, nature, art my goddess; to thy laws
My services are bound. . .
A famous phrase, Mathematics, Queen of the Sciences, is due to him.
One of Gauss’s greatest creations and certainly the most momentous from the standpoint of its implications is his non-Euclidean geometry. Gauss started his thinking on this subject as a boy and, like others before him, he began by trying to replace Euclid’s parallel axiom by a more acceptable one, that is, one which did not involve any assertion about what must happen far off in space. But he did not succeed. He also appreciated at the age of 15, as he told his friend Schumacher, that one could not hope to prove an assertion about parallel lines on the basis of the other nine axioms. That is, he realized that these nine axioms did not in themselves dictate the form of the parallel axiom. Gauss was too brilliant a man to overlook the implication of this fact. If there was some freedom in the choice of a parallel axiom, then one might choose an axiom different from Euclid’s and build a new kind of geometry. Gauss did just this. He pursued the logical implications of a system of axioms which included the assumption that more than one parallel to a given line passed through a given point, and thus created non-Euclidean geometry. (Gauss himself finally adopted the term non-Euclidean after having called his system anti-Euclidean geometry, and later astral geometry.)
Though Gauss realized that such a geometry could conceivably apply to physical space and hence was indeed significant, he did not publish his results. Gauss was far ahead of his times in concluding that Euclidean geometry was not necessarily the correct description of physical space and that some non-Euclidean geometry might prove as accurate. Hence he feared that he would be laughed at. In a letter written in 1829 to his friend, the mathematician Friedrich Wilhelm Bessel, Gauss confessed that he feared the clamor of the Boeotians, a figurative reference to the dull-witted, for the Boeotians had been one of the more simple-minded Greek tribes. Gauss’s work on non-Euclidean geometry was found among his papers after his death in 1855.
The men who usually receive credit for creating non-Euclidean geometry because they published their results are Nicholas I. Lobachevsky (1793–1856) and John Bolyai (1802–1860). Lobachevsky, born to a poor family and displaying brightness even as a youngster, attended the University of Kazan in Russia. One of his teachers was the German mathematician J. M. C. Bartels, a friend of Gauss, and it is very likely that the problem of the parallel axiom was called to Lobachevsky’s attention by Bartels. Lobachevsky became a professor at Kazan at the age of 23 and continued to work on the problem. By 1823 he realized that there can be other geometries and that Euclidean geometry need not be the correct description of physical space. He said later that two thousand years of fruitless attempts to put the parallel axiom on an unquestionable basis had led him to suspect that it could not be done. From 1829 on Lobachevsky published books and papers in which he expounded the theorems that hold in his non-Euclidean geometry. Despite valuable services to mathematics, his university, and the Russian government, he was dismissed in 1846, but continued to work in his field until his death.
Bolyai, a Hungarian, was an Austrian army officer. He learned mathematics from his father, Wolfgang Bolyai, who set his son thinking about the parallel axiom. In 1823 John arrived at the same conclusion that had been reached by Gauss and Lobachevsky, namely, that the Euclidean parallel axiom cannot be proved and that, in fact, it was but one alternative. He proceeded to develop a non-Euclidean geometry and published his work as an appendix to his father’s book on mathematics which appeared in 1833. Knowing Gauss’s interest in the subject of non-Euclidean geometry, Wolfgang sent a copy of his son’s work to Gauss. The latter replied,
If I commenced by saying that 1 am unable to praise this work, you would certainly be surprised for a moment. But 1 cannot say otherwise. To praise it would be to praise myself. Indeed, the whole contents of the work, the path taken by your son, the results to which he is led, coincide almost entirely with my meditations, which have occupied my mind partly for the last thirty or thirty-five years.
Though Wolfgang was pleased to learn that his son’s thinking paralleled that of the great Gauss, John was not, for, like others who had found that Gauss had beaten them to a discovery, he felt cheated of the glory. The irony of the situation was compounded further. Although Lobachevsky and Bolyai are now credited with the discovery of non-Euclidean geometry because they were the first to publish on the subject, the mathematical world of the 1830’s and 1840’s ignored their publications until Gauss’s notes on non-Euclidean geomtry were found among his papers after his death. The name of Gauss attached to the idea made the mathematical world grant the proper importance to the subject.
On the surface, the history of non-Euclidean geometry seems remarkable because after two thousand years of futile work, three men suddenly saw the parallel axiom and Euclidean geometry in the proper light. However, while such coincidences of history are by no means uncommon, the present one is perhaps less remarkable than is ordinarily believed. Gauss did not hesitate to tell his mathematical friends of his radical views on the parallel axiom and of his doubts about the necessary truth of Euclidean geometry. Both Bartels and Wolfgang Bolyai were in this circle of friends, and they may have communicated Gauss’s views to their respective charges. The mere derivation of theorems from new parallel axioms, though a considerable technical achievement, goes back to Saccheri, and numerous minor and major mathematicians had done similar work in the intervening one hundred-year period. But the correct evaluation of the significance of these logical developments was a new step, and this seems to have been made first by Gauss. However, Wolfgang Bolyai, perhaps to defend the originality of his son’s thoughts, said of the work by the three men,
. . . because it seems to be true that many things have, as it were, an epoch in which they are discovered in several places simultaneously, just as the violets appear on all sides in the springtime.
1. What is the definition of parallel lines?
2. What objection did Euclid’s successors have to Euclid’s axiom on parallel lines?
3. What objections were there to axioms such as Playfair’s which replaced Euclid’s parallel axiom by simpler assumptions?
4. Describe Saccheri’s plan to establish the truth of Euclid’s parallel axiom.
5. Did Saccheri arrive at the concept of a non-Euclidean geometry?
6. What advances did Gauss, Lobachevsky, and Bolyai make over Saccheri with respect to the nature of geometry?
To appreciate the significance of what Gauss, Lobachevsky, and Bolyai created, we must look into the specific mathematical facts of their work. For brevity we shall, at present, refer to their geometry as Gauss’s geometry. The main idea conceived by the three men asserted that one was logically free to adopt a parallel axiom which differs fundamentally from Euclid’s, and that one could construct a new geometry which would be as valid as Euclid’s and which might even be a good description of physical space.
What was the new parallel axiom? Euclid’s parallel axiom, at least in the equivalent form which Playfair had given, stated that given a line l and a point P, there is one and only one line in the plane of l and P which passes through P and does not meet l (Fig. 20–2). Gauss, Lobachevsky, and Bolyai assumed that there are two lines, m and n, through P (Fig. 20–3) which are parallel to l, that is, these two lines through P do not meet l, and that any line through P falling within the angle MPN does meet l. Of course, any line such as q which passes through P and lies within the angle NPR cannot meet l because to do so, q would have to cross m or n and therefore meet m or n in a second point. But since two lines can intersect in at most one point, it follows that all lines through P which lie within the angle NPR will not meet l. Hence the assumption that there are at least two parallels to l implies that there is an infinite number of parallels.
The term parallel lines was reserved by Gauss, Lobachevsky, and Bolyai for m and n, whereas lines such as q were called nonintersecting lines. For this reason, their geometry is often described as a geometry with two parallel lines, although, in the Euclidean sense of the term parallel lines (two lines in a plane which have no point in common), it contains an infinite number of parallels. We shall use the terminology chosen by Gauss, Bolyai, and Lobachevsky.
Fig. 20–3. Gauss’s parallel axiom.
Fig. 20–4
Before proceeding to draw conclusions from this new parallel axiom and the other nine Euclidean axioms, let us dispel in advance any doubts about the common sense of the material we are about to present. We are so accustomed to Euclidean geometry (those of us who did not take our high-school geometry very seriously may be in a better position) that the idea of adopting a new parallel axiom and of proving theorems seems ridiculous. Euclid’s geometry is truth to us, and to defy the truth and pursue the consequences of this folly seem a waste of time. There are two counterarguments. We can admit that from a practical standpoint the effort required to develop such a new system is pointless. Nevertheless, we should be able to comprehend that it is logically possible to investigate the consequences of a new set of axioms. What we are about to do is analogous to changing one of the articles in the Constitution of the United States while retaining the others, just to see what changes might follow in our laws. Thus we might decide to replace an elected president by a monarch and yet continue to elect congressmen and retain the institution of a Supreme Court. The second counterargument is based on the fact that Gauss, Bolyai, and Lobachevsky doubted the truth of Euclidean geometry and were ready to consider an alternative geometry as a description of physical space. To what extent their doubts were justified and whether the new geometry could serve in physical applications will be clearer when we know what theorems actually resulted from the new set of axioms.
We shall describe, but not prove, the theorems of the new geometry. The methods of proofs are precisely the same as in Euclidean geometry; however, one must be careful to use only the new axioms to support any assertions.
Many theorems of the new geometry are precisely the same as those of Euclidean geometry. Indeed those theorems of Euclidean geometry which are proved with the aid of only the first nine axioms of Euclid, that is, those theorems which do not depend upon the Euclidean parallel axiom, must also be theorems of the new geometry because these nine axioms are retained in the new system. Thus the theorems which assert when two triangles are congruent, the theorem asserting that the base angles of an isosceles triangle are equal, the theorem stating that an exterior angle of a triangle is greater than either remote interior angle, and the theorem postulating that from a point off a line, there is one and only one perpendicular to that line, are all valid in the new geometry.
But now let us examine some theorems of the new geometry which are different from those of Euclidean geometry. Suppose that the point P and the line l (Fig. 20–4) are given. In the new geometry, the parallel axiom states that there are two lines, m and n, through P which are parallel to l. Let us now drop a perpendicular p from P to l. Then in this new geometry the angle A between p and n is no longer a right angle, although n and l are parallel lines. Angle A is in fact an acute angle. Moreover, the size of angle A depends upon the length of p. The shorter p is, the larger does angle A become, and as p approaches zero, angle A approaches 90° in size. Of course, in Euclidean geometry angle A is a right angle and this holds no matter how large p is. A key theorem of the new geometry asserts that the sum of the angles of a triangle is always less than 180°, whereas it is exactly 180° in Euclidean geometry. Further, in the new geometry the sum of the angles of a triangle varies with the area of the triangle. The smaller the area, the closer is the angle sum to 180°. A very surprising theorem of the new geometry states that if the three angles of one triangle equal, respectively, the three angles of another, the triangles are congruent. Of course, in Euclidean geometry two such triangles would be similar, and one could be very much larger than the other. There are many more interesting consequences of the new axioms, but we have seen enough to obtain some indication of the nature of the new geometry.
1. Describe the parallel axiom adopted by Gauss, Bolyai, and Lobachevsky.
2. Distinguish between the Euclidean use of the term parallel lines and the usage in Gauss’s geometry.
3. State three theorems which are common to Euclidean geometry and Gauss’s non-Euclidean geometry.
4. State three theorems of Gauss’s geometry which do not hold in Euclidean geometry.
5. Suppose that one triangle has an angle sum of 170° and another, of 175°. Which has the larger area in Gauss’s geometry?
6. Given two triangles, one with angles of 30°, 40°, and 100° and another with angles of 35°, 45°, and 90°. What does Gauss’s geometry say about their area?
7. Suppose that the angles of one triangle are equal, respectively, to the angles of another. What may you conclude about these triangles on the basis of Gauss’s geometry?
We saw in the preceding section that it is possible to investigate a new set of geometrical axioms and to deduce logical consequences. Perhaps we are not satisfied as yet that such an investigation is of value, but we shall reserve our final judgment until we have looked into one more mathematical creation in the field of non-Euclidean geometry.
Invesugations of the parallel axiom had led mathematicians to question its truth because it made assertions about what must happen in physical space far beyond man’s experience. Having become aware of this shortcoming, mathematicians examined the remaining axioms and soon found another which suffered from the same failing. Euclid’s second axiom asserts that a straight line extends indefinitely far in either direction. This axiom attracted the attention of the nineteenth-century mathematical giant, Georg Friedrich Bernhard Rie-mann (1826–66). Riemann, the son of a Lutheran pastor, was born sickly and precocious. He became a student of Gauss at the University of Göttingen, and was later appointed professor at the same institution. Like Gauss, and most mathematicians for that matter, he was keenly interested in science and in the applicability of mathematics to the physical world.
Riemann observed that experience suggests not the infinite extent of the straight line but rather its endlessness. He accordingly distinguished between endlessness, or unboundedness, and infinite length. The simplest example of that distinction is furnished by the circle. One can traverse the circle endlessly, yet its length is finite. Hence Riemann proposed to replace the Euclidean axiom that a straight line extends indefinitely far by the axiom that it is unbounded.
Riemann also observed that experience does not vouch for the existence of any parallel lines. Within the limits of experience, we could equally well assume that any two lines meet. Hence Riemann proposed this axiom as an alternative to Euclid’s parallel axiom. It may be recalled that Saccheri had considered the same possibility, but had found that it led to contradictions. However, Saccheri had combined this axiom with the other nine Euclidean axioms, whereas Riemann proposed an additional change, namely the unboundedness of the straight line, and had therefore reason to believe that he, unlike Saccheri, would not encounter any contradictions.
Since Riemann did retain some of Euclid’s axioms, he arrived at some theorems identical to those of Euclidean geometry. Thus the theorem that two triangles are congruent when two sides and the included angle of one are equal to the corresponding parts of the other is a theorem of Riemann’s geometry, as are other familiar congruence theorems.
The striking theorems of Riemann’s geometry are, of course, those which differ markedly from Euclid’s results. One Riemannian theorem asserts that every straight line has the same finite length. Another asserts that all perpendiculars to a line meet in one point. In Riemann’s geometry the sum of the angles of a triangle is always greater than 180°. Moreover the sum varies with the area of the triangle and decreases to 180° as the area approaches zero. Two similar triangles are necessarily congruent (this is also the case in Gauss’s geometry). These theorems are, of course, just a representative selection from a vast number.
1. Why did Riemann question the Euclidean axiom that a straight line extends indefinitely far in either direction?
2. What axiom on parallel lines did Riemann adopt?
3. Some theorems of Gauss’s and Riemann’s non-Euclidean geometries are identical with Euclidean theorems. Why does this occur?
4. Which of the two non-Euclidean geometries would you expect to have more theorems in common with Euclidean geometry and why?
5. Compare the Euclidean, Gaussian, and Riemannian theorems about the sum of the angles of a triangle.
6. State three theorems peculiar to Riemann’s geometry.
7. What is non-Euclidean geometry?
8. What happens to the Euclidean distinction between congruent and similar triangles in non-Euclidean geometry?
The very fact that there can be geometries other than Euclid’s, that one can formulate axioms fundamentally different from Euclid’s and prove theorems, was in itself a remarkable discovery. The concept of geometry was considerably broadened and this suggested that mathematics might be something more than the study of the implications of the self-evident truths about number and geometrical figures. However, the very existence of these new geometries caused mathematicians to take up a deeper and more disturbing question, one which had already been raised by Gauss. Could any one of these new geometries be applied? Could the axioms and theorems fit physical space and perhaps even prove more accurate than Euclidean geometry? Why should one continue to believe that physical space was necessarily Euclidean?
At first blush the idea that either of these strange geometries could possibly supersede Euclidean geometry seems absurd. That Euclidean geometry is the geometry of physical space, that it is the truth about space is so ingrained in people’s minds that any contrary thoughts are rejected. The mathematician Georg Cantor spoke of a law of conservation of ignorance. A false conclusion once arrived at is not easily dislodged. And the less it is understood, the more tenaciously is it held. In fact, for a long time non-Euclidean geometry was regarded as a logical curiosity. Its existence could not be denied, but mathematicians maintained that the real geometry, the geometry of the physical world, was Euclidean. They refused to take seriously the thought that any other geometry could be applied. However, they ultimately realized that their insistence on Euclidean geometry was merely a habit of thought and not at all a necessary belief. Those few who failed to see this were shocked into the realization when the theory of relativity actually made use of non-Euclidean geometry.
It is important to see how and why a non-Euclidean geometry can fit physical space. Let us recall, first of all, why Gauss, Bolyai, and Lobachevsky doubted the truth of the Euclidean parallel axiom. They realized that this axiom and all of the simpler forms which might serve as substitutes contained assertions about what happens in space far beyond the range of man’s experience. Hence experience does not support such axioms. As a matter of fact, if the lines m and n of Fig. 20–3 and all lines, such as q, falling within the angle NPR should have almost the direction of l, then they would certainly not meet l within a short distance from the point P. Hence Gauss’s axiom is as much in accord with experience as Euclid’s. Our intuition is seemingly violated by such a thought, but this intuition may be conditioned by our familiarity with Euclidean geometry. In other words, insofar as experience is concerned, one can adopt Gauss’s or Riemann’s alternative axioms.
In view of our inability to decide a priori which of the several alternative axioms fits physical space, we might consider another approach to the problem. The theorems of any geometry are logical consequences of the axioms. Perhaps it would be easier to discriminate among these geometries by seeing how well their respective theorems fit physical space. This thought had already occurred to Gauss. He noted that in his geometry the sum of the angles of a triangle must be less than 180°, whereas in Euclidean geometry it is exactly 180°. Hence he had three observers stand on three mountain peaks and directed each one to measure the angle between his lines of sight to the other two observers. The sum of the angles of the triangle formed by the three peaks turned out to be 170°59′58″; that is, it was within 2″ of 180°.
This result might be interpreted as a victory for Euclidean geometry, but the situation is not so simple. In Gauss’s geometry the sum of the angles of a triangle increases as the area of the triangle decreases, and the sum approaches 180° as the area approaches zero. In Riemann’s geometry, the sum of the angles of a triangle is always larger than 180°, but the sum again appproaches 180° as the area of the triangle decreases. Hence for small triangles, all three geometries call for an angle sum close to 180°. Had Gauss’s measurement of the angles formed by the mountain peaks been exact, he might have been able to assert that his result was less than, equal to, or more than 180°, and so his test would have been decisive. However, every measurement contains an error because the eye and hand are not precise. We may safely suppose that the error in Gauss’s measurement was more than 2″. Thus, in view of his result, the true angle sum could have been anything from a little more than 180° to a little less. Hence the result was consistent with any one of the three geometries.
For a large triangle, the angle sum should be significantly less than 180° in Gauss’s geometry and significantly more in Riemann’s. Hence, by using a large triangle, say one formed by three celestial bodies at some instant, one might be able to obtain a result which would fit only one of the three geometries, provided the error of measurement were kept small. Thus, a result of 175°, with an error of measurement of less than 5°, would certainly establish the physical correctness of Gauss’s geometry. However, in the nineteenth century, no such result was obtained. Gauss, Lobachevsky, and Bolyai realized that, at least in their day and with the instruments at their disposal, measurement would not decide the question.
Since a test based on the sum of the angles of a triangle does not succeed in establishing which of the geometries fits physical space, one might cast about for another theorem which would serve the purpose. He might then hit upon the theorem which holds in both non-Euclidean geometries, namely the theorem stating that two similar triangles must be congruent. Here a decisive test seems likely, for it appears quite obvious that one can construct a small and a large triangle and make them similar. One only has to ensure that the angles of the small triangle equal the angles of the large one, and the similarity of the two triangles necessarily follows. Only Euclidean geometry fits this physical situation. The argument, however, has a flaw since one cannot be sure that the corresponding angles of the two triangles are really equal. After all, measurement is approximate, and at least one angle of one triangle might differ from the corresponding angle of the other triangle. If this happened, the triangles would not be similar.
The substance of the above arguments is that there is no simple test which points to one geometry rather than to another. However, if an application involved a truly large triangle, as astronomical investigations do, one might be able to determine which geometry fits better. As a matter of fact, this possibility has been realized. In the theory of relativity, Einstein employed a non-Euclidean geometry (though one more complicated than those we have studied), and the agreement between his predictions and observations was better than the result obtained by means of Euclidean geometry.
1. Does measurement help us to show that objects in physical space are better described by the theorems of one rather than another geometry?
2. Could we use Gauss’s or Riemann’s non-Euclidean geometry for engineering and architecture?
3. Why did Gauss’s measurement of the sum of the angles of a triangle fail to show that space is or is not Euclidean?
Thus far we have considered the applicability of non-Euclidean geometry to our physical space, with the understanding that the physical meaning of a straight line is the stretched string or the ruler’s edge. Even when we visualize a straight line so long that we could never construct it, for example, a line from the earth to the moon, we picture a long taut string or an imaginary long straight stick. However, we must now realize that the mathematical straight line is not limited to this physical or geometrical figure. Let us consider an example.
Suppose that we begin with a flat sheet of paper which can be imagined to extend indefinitely far in all directions. Now let us suppose that the paper is bent so that it curves upward to the right and to the left (Fig. 20–5) and, of course, continues to extend indefinitely far out in all directions. In mathematics, incidentally, this shape is known as a cylindrical surface. (One can form a limited cylindrical surface by merely bending upward the sides of a sheet of paper.) As a consequence of the change from a plane to a cylindrical surface, many of the straight lines of the plane become curves on the surface. Thus AC in Fig. 20–5 is an arc of a curve which, if the surface were flattened, would become a segment of a straight line. Curves which derive from straight lines we shall continue to call lines. Angles in the plane become, under the bending, angles on the surface. A triangle in the plane corresponds to a triangle formed by arcs of curves on the surface. A circle in the plane becomes a new curve on the surface which we shall continue to call a circle.
Fig. 20–5.
Euclidean geometry on a cylindrical surface.
Now let us note that the bending of the plane into the cylindrical surface does not change lengths or angles, because the plane neither stretches nor contracts as one forms the surface. Hence a distance between two points measured along the surface is the same as the distance between the two points when on the plane.
Since lengths and angles do not change, it follows that if the figures in the plane satisfy the axioms of Euclidean geometry, then so do the figures on the surface, provided the meaning of lines, angles, and circles on the surface is as specified above. And since theorems are logical consequences of axioms, it follows that the Euclidean theorems, too, retain their validity for figures on the surface. Thus the sum of the angles of triangle ABC in Fig. 20–5 is 180°. These last few assertions appear at first to be incredible. Our triangles are no longer formed by straight line segments, and yet the Euclidean theorems continue to hold. How is it possible to apply the word line of the Euclidean axioms and theorems to the curves that are no longer straight lines?
The answer to this question involves a major point about geometry and indeed about mathematics in general. In our review of Euclidean geometry in Chapter 6, we briefly mentioned that Euclid’s definitions of point, line, plane, and other concepts were not quite satisfactory. The full story is that his definitions of these concepts are meaningless. He defined curve as length without breadth, but he did not say what he understood by length and breadth. He then defined the straight line as a curve which lies evenly between the ends, but he did not indicate what “lies evenly” meant. Euclid was relying on our intuitive understanding of these terms, but intuitive understanding cannot be part of a logical treatment. Mathematics does not rest logically on physical meanings. What then is the alternative? It is not possible to begin the process of developing any new branch of mathematics by defining the initial notions,’ for definition requires that one provide descriptions in terms of other concepts whose meaning is already established. But obviously the initial concepts cannot be defined in terms of prior ones since there are no prior ones. The point, then, is that the initial concepts cannot be defined. They must remain undefined.
This assertion raises another question. If point, line, plane, and other basic concepts are undefined, how shall we know what we mean by them and how shall we know how to treat them? The answer is that the axioms of Euclidean geometry tell us what properties these concepts possess. These properties and only these may be used in establishing the proofs. The concepts are therefore limited only to the extent that they must satisfy the axioms.
Now, as far as we can determine, physical straight lines, such as rulers’ edges and stretched strings, do satisfy the axioms of Euclidean geometry. In fact, historically, the axioms were formulated by observing the properties of rulers’ edges and stretched strings. What is surprising, however, is that one may encounter other “lines” which also satisfy the axioms. If they do, they are legitimate interpretations or realizations of the axioms and hence of the theorems. This is the case for the lines of our cylindrical surface. We know that they satisfy the Euclidean axioms because in deforming the plane into the cylindrical surface, we did not disturb any of the properties asserted by the axioms. Consequently, Euclidean geometry as a whole applies to the points, lines, triangles, polygons, circles, and other figures on the cylindrical surface.
The significance, then, of the entire discussion about the cylindrical surface is that it is possible to associate a totally new picture with Euclidean geometry. In other words, we see that Euclidean geometry applies to more physical situations than we had previously suspected. But if one can put Euclidean geometry to new uses by adopting a new view of the straight line, perhaps one can do the same for the non-Euclidean geometries, and hence these, too, may be more valuable and more meaningful than we have hitherto suspected. We shall now show that it is possible to give a very simple and practical interpretation of Riemann’s non-Euclidean geometry.
Fig. 20–6.
A spherical triangle formed by arcs of great circles.
Fig. 20–7.
A circle on a sphere.
Let us consider the surface of the earth and let us suppose that we were assigned the task of developing a geometry that would fit the surface of the earth. We would, of course, choose as points the idealization of the usual physical points. We would most likely cast about next for the figure which would play the role of the straight line. Now straight lines in the usual sense do not exist on the surface of the earth because the surface is curved. Hence our line cannot be the rulers’ edge or a stretched string. The most useful curve to choose would be the curve which connects two points by the shortest path. The shortest path between any two points on a sphere is the shorter arc of the great circle through these points.* Hence it seems reasonable to choose great circles on the sphere as our lines. A triangle on the sphere would be the figure formed by three arcs of three great circles (Fig. 20–6). A circle on the sphere would be the set of all points at a given distance from a fixed point (Fig. 20–7). (This distance between the fixed point and any point on the circle would, of course, be measured along the great circle through the two points.) We could, in fact, describe a variety of geometrical figures in terms of points and lines on the sphere.
The next step in the construction of our geometry would be to determine the axioms which our points, lines, and geometrical figures satisfy. Now our lines are great circles. These lines are not infinite in extent. However, each is unbounded; that is, there is no beginning or end. Hence our axiom should assert merely that a line is unbounded. We note next that two points which are not on opposite ends of a diameter determine a unique great circle. However two points which are on opposite ends of a diameter do not determine a unique great circle. Consequently we cannot adopt the axiom that any two points determine a unique line. Let us look next into the subject of an axiom on parallel lines. Any two great circles on a sphere do meet; in fact, they meet at two points which are diametrically opposite. Hence the parallel axiom should read that any two lines meet; that is, there are no parallel lines. We shall not go further in selecting axioms for our system of geometry, for the conclusion toward which we are heading is now obvious. The axioms we would have to adopt to make our geometry fit the surface of the sphere would be exactly those which Riemann adopted for his non-Euclidean geometry.
Since the axioms of Riemann’s geometry hold for the sphere, the theorems must also hold. Hence the geometry on the surface of a sphere is an application of Riemann’s non-Euclidean geometry. Merely to satisfy ourselves, let us see whether a few theorems of Riemann’s geometry really do apply. Let us consider the theorem that all perpendiculars to a line meet in a point. Figure 20–8 illustrates this theorem, and we see at once that it does apply. Another theorem asserts that the sum of the angles of a triangle is always greater than 180°. To verify that this theorem holds for every triangle on a sphere, we would have to call upon a theorem proved in spherical geometry which asserts that the sum of the angles of any spherical triangle is always between 180° and 540°. However, we can see at once in particular cases that Riemann’s theorem does apply. Let us consider triangle ABC of Fig. 20–8. Angles A and B are each 90°. Hence, whatever the size of angle C, the sum of the three angles is larger than 180°. We could, of course, verify that all theorems of Riemann’s geometry hold for the sphere.
Fig. 20–8.
The sum of the angles of a spherical triangle is greater than 180°.
Fig. 20–9
The major point, then, which emerges from our discussion of the geometry on a sphere is that we have found a new use for Riemann’s non-Euclidean geometry. It applies directly to the surface of a sphere, provided that straight line means great circle on the sphere.
Consideration of this last fact does lead to a question: Since Riemann’s geometry applies so naturally to the surface of a sphere, why did not mathematicians hit upon non-Euclidean geometry in Greek times? Why did the realization that there can be non-Euclidean geometries take so long to strike home? The answer is that the Greeks, no doubt influenced by the Egyptians and Babylonians, had chosen the stretched string or ruler’s edge as the physical straight line and the Euclidean axioms as the basis for their geometry. Such choices were very natural for people whose experiences were limited to a small part of the earth’s surface. When they came to consider the sphere among the various surfaces, they had to approach it through concepts and axioms already adopted and hence described its properties in Euclidean terms. Thus great circles were treated as curves. As we have already noted in another connection, the Greeks and all mathematicians up to 1800 were so sure that Euclidean geometry was the true geometry of physical space that the idea of approaching the sphere directly and building a special geometry for it would have seemed nonsensical. They already possessed the true geometry and could not break what we can now see clearly was just a habit of thought.
It is possible to exhibit a surface to which the axioms and theorems of Gauss’s non-Euclidean geometry apply, provided that the curves chosen as the lines on that surface are, as in the case of the sphere, those which connect two points by the shortest path. However, this surface is not widely used, and so we shall not devote any time to it. It will be more profitable to turn to the reconsideration of our familiar physical space.
We have grown accustomed to the idea that the reasonable and convenient physical interpretation of the straight line is the ruler’s edge or a stretched string. Even with this interpretation we found that experience in limited regions did not enable us to exclude the non-Euclidean geometries as possible descriptions of physical space. We should now note that the ruler’s edge and stretched string are, indeed, not the major physical interpretation of the mathematical straight line, and that we commonly and necessarily use another. Let us consider how surveyors determine distances. They begin by adopting a convenient base line AB (Fig. 20–9) whose length is measured by actually applying a tape measure. To determine the distance AC, a surveyor measures angle A by sighting point C in his telescope stationed at A and then swings the telescope around until he sights point B. On his theodolite he has a scale which tells him how much he has rotated his telescope, and hence he knows angle A. In a similar manner, he measures angle B. By means of trigonometry he can now calculate AC and BC. The surveyor proceeds on the assumption that the light rays which travel from C to A and from B to A follow the straight-line (stretched string) paths between those pairs of points, and, since the axioms of Euclidean geometry fit stretched strings, he applies Euclidean geometry or trigonometry to calculate AC and BC. However, the surveyor may be mistaken. The light ray from C to A may have followed the broken-line path shown in Fig. 20–9, and the surveyor at A would have to point his telescope tangentially to the light ray in order to receive the light. Hence the telescope would really be pointed to C′ although the surveyor sees the point C in his telescope. Consequently, the angle he actually measures is C′AB and not CAB. Thus the use of Euclidean geometry may have led to erroneous results for AC and BC.
What then should he have done? He should have applied a geometry whose axioms fit the behavior of light rays since these are the straight lines he really used. But do not light rays follow truly straight paths? We certainly know of situations in which they do not. We have had occasion to note (Chapter 1) that when light from the sun passes through the earth’s atmosphere, it is bent by the refractive effect of the atmosphere. Hence there is some question of what path light rays do follow. Observation and measurement show that over short distances along or near the earth’s surface light rays follow straight paths closely enough, but over larger distances this is certainly not true.
The above example may serve to suggest a major point. In astronomical measurements we necessarily depend entirely on light rays to measure angles. Since these rays travel over long distances, the paths they follow may not be truly straight, and we cannot check the true paths by laying down a tape measure or ruler. Hence we cannot be sure whether we should use Euclidean geometry.
We could try to solve this difficulty in one of two ways. We could attempt to determine by physical investigations what paths light rays follow, and, even though we may find that these are curved, treat them as if they were curves in Euclidean geometry. This is what physicists do when they study the behavior of light near the surface of the earth. The law of refraction tells us how light behaves, and all the reasoning in formulating and in applying this law is based on Euclidean geometry. Alternatively we can regard the paths of light rays as lines and construct a geometry which fits the convention that the light rays are to be the lines of that geometry. How to construct such a geometry is not obvious. One would have to determine some facts about the behavior of light rays, which would become the axioms of that geometry, and then deduce theorems. The resulting geometry might very well be non-Euclidean and might even differ from those developed by Gauss and Riemann.
All discussion of the possibility of applying non-Euclidean geometry is in a sense outdated. One of the basic current theories of science, the theory of relativity, does presuppose that our space is non-Euclidean and on this basis obtains better agreement between theory and experiment than the older theory of Newtonian mechanics based on Euclidean geometry was able to do. For reasons too lengthy to be discussed in this brief survey of the applicability of non-Euclidean geometry, the theory of relativity requires that the position as well as the time of events be treated together so that an object or event is described not only by the coordinates x, y, and z which denote position, but also by the value of the time t at which the object or event occurs at position x, y, z. In other words, the relevant geometry is four-dimensional. This fact in itself does not imply that we must resort to a non-Euclidean geometry. However, in attempting to explain the phenomenon of gravitational attraction, it is necessary to regard the four-dimensional space-time as a nonhomogeneous geometry. This means that the nature of space-time varies from region to region, just as a two-dimensional mountainous surface changes its geometrical character from region to region. In the geometry of general relativity, it is also the presence of physical masses which determines the character of the geometry in any region, these masses being the earth, the moon, the sun, and other heavenly bodies. Moreover, the geometry is constructed in such a way that the “straight lines” are the shortest “paths” of that space-time. Light rays do take the shortest “paths” in the space-time system. Hence, while the straight line is not defined in terms of light rays in the non-Euclidean geometry of relativity, it is nevertheless significant that light rays do take such paths.
1. Can you explain how it is that Euclidean geometry applies to a cylindrical surface even though the lines of that geometry do not have the shape of stretched strings?
2. Why must there be undefined concepts in the initial stages of any branch of mathematics?
3. Under what conditions does Riemann’s non-Euclidean geometry prove to be the correct geometry on the surface of a sphere?
4. Should we distinguish between the geometries created by mathematicians and the geometry of physical space?
5. Does science really use the stretched string as its physical model of the mathematical straight line?
6. Imagine people living in a mountainous region who wish to construct a geometry for that region. They agree to consider the shortest path between two points as the line of that geometry. What kind of geometry might they arrive at?
7. Imagine people living in a mountainous region who wish to construct a geometry for that region. Since they travel by foot, using the shortest path to get from one place to another might require more time than some indirect path, because the shortest path may involve difficult mountain climbing. These people therefore agree to take as the line joining two points the path requiring least travel time. What kind of geometry might these people arrive at?
The existence of non-Euclidean geometries which can fit physical space, to say nothing of the actual use of one of these non-Euclidean geometries in the theory of relativity, has had profound implications for mathematics itself, for science, and for some segments of our culture. In this section we shall discuss the implications for mathematics.
The most important effect of this creation has been the realization that mathematics does not offer truths. The Greeks adopted the axioms of Euclidean geometry because they believed that they were self-evident truths about our physical space. The axioms appealed to their minds as necessary truths which anyone must grant, even without experience. Since theorems are obtained by deductive reasoning and so are inescapable consequences of the axioms, the Greeks believed that the theorems, too, were truths. The observed agreement between the theorems deduced from these axioms and experience reinforced their certainty that the axioms were truths. The belief that mathematics offers truths was firmly held by every thinking being until the creation of non-Euclidean geometry. But if several geometries which contradict one another all fit physical space, then it becomes very obvious, indeed, that all of these cannot be the truth, and, worse yet, one can no longer be sure that any of these is the truth.
We see more clearly now that one must distinguish between mathematical space and physical space. Mathematicians and scientists believe that a physical world exists outside of and independently of human beings, and they seek to understand it by adopting axioms which seem to fit this physical space and then deducing theorems from these axioms. We now recognize that we have no reason to identify the mathematical construction with physical space. Indeed, several different mathematical theories may fit equally well. Mathematical theories of space are like any scientific theories; that is, the mathematical system used is the one which at the time best fits experience. If, as experience widens, it becomes clear that another geometry will fit experience better, then the older theory of space is discarded, and a new one adopted. This is precisely what happened when the theory of relativity sought to account for phenomena to an accuracy which would surpass that of the older scientific work.
The remarks we have made thus far about truth in mathematics and the provisional character of mathematical theories have been based on the developments in geometry. But the reader may have an objection. He may admit that geometry no longer offers truths, but continue to be convinced that our arithmetic, algebra, and other developments based on our number system do constitute truths. We shall devote Chapter 21 to this point and perhaps then see more clearly that with respect to truth the domain of number does not differ from geometry.
If the various branches of mathematics have only a more or less useful correspondence with physical experience, does then mathematics differ in any way from science? Mathematics had always been distinguished from science because mathematical axioms were regarded as truths, whereas the axioms of science were clearly recognized to be generalizations from limited experience or experiments. Scientists recognized that their researches produced only theories which did not provide a veridical description of what occurred in nature, but which might have to be altered to fit new facts. Is this not precisely what we now perceive to apply also to mathematics?
Insofar as the study of the physical world is concerned, mathematics has the same character as any of the sciences. It offers nothing but theories. And, as in science, new mathematical theories may replace older ones when experience or experiment shows that a new theory provides closer correspondence than an older one. As Einstein put it,
So far as the theories of mathematics are about reality, they are not certain; so far as they are certain, they are not about reality.
Yet there are basic distinctions between mathematics and science. Mathematics confines its work to numbers, geometrical figures, and relationships which obtain among numbers and among geometrical figures. All other concepts and relationships of mathematics are derived from numbers and geometry. Science deals with mass, velocity, force, energy, molecular structure, chemical processes, the structure of plants, animals, and humans, and hundreds of other concepts. That is, the subject matter of mathematics differs from that of science.
A second difference is that mathematics will always insist on deductive proof, whereas the sciences, even though they aim to be deductive, will continue to utilize any experimental or observational fact as a basis for conclusions; that is, the sciences do not insist on a thoroughly deductive structure based on a fixed number of axioms stated at the outset. There are many hypotheses of mathematics, such as, for example, that every even number is the sum of two primes, for which the inductive evidence is most conclusive. No scientist would hesitate to use an assertion so well supported by evidence. But the mathematician continues to search for a deductive proof. This difference between mathematics and science is perhaps one of degree or method of operation. Having chosen his axioms, the mathematician proceeds to derive as many conclusions as possible from them. The scientist will not hesitate to introduce new axioms if such a step seems warranted by inductive evidence.
A third difference between mathematics and science was, peculiarly, accentuated by the creation of non-Euclidean geometry. Mathematics, like science, had been devoted primarily to the exploration of nature. Yet mathematicians had always felt free to develop the implications of the axioms of number and Euclidean geometry even though there was no immediate application for any of the results pursued. Number and Euclidean geometry were regarded as so important in the study of nature that almost any information about them was welcomed. However, non-Euclidean geometry, which, at the outset and for a long time thereafter, seemed to concern axioms which could not possibly apply to the physical world, had finally proved useful in the study of the physical world. Thus history teaches us that mathematicians should feel free to investigate axioms which have no immediate or obvious bearing on the physical world. Consequently, mathematics has been given a new dimension of freedom, the freedom to explore what the mind wishes to explore, and has been released from bondage to the axioms of number and Euclidean geometry. One could say that the creation of non-Euclidean geometry had the effect of divorcing mathematics from science. By the end of the nineteenth century, Georg Cantor, one of the great mathematical minds of modern times and the creator of a strange and revolutionary theory, the theory of transfinite numbers, was able to say, “The essence of mathematics is its freedom.” The enormous expansion in mathematical activity in the last century is partly the consequence of the new freedom.*
1. Why does the existence of non-Euclidean geometry show that mathematics does not offer truths?
2. What distinction should one make between a mathematical space and physical space?
3. Is it proper to regard mathematics as one of the sciences?
In view of the role which mathematics plays in science and the implications of scientific knowledge for all of our beliefs, revolutionary changes in man’s understanding of the nature of mathematics could not but mean revolutionary changes in his understanding of science, doctrines of philosophy, religious and ethical beliefs, and, in fact, all intellectual disciplines.
Let us consider first the effect on scientific thought. Although scientists had more or less recognized that their theories in various branches of science were not the final word, in the back of their minds they continued to believe that true accounts of the various phenomena of nature were possible and that they were working toward these goals. Indeed, in the fields of astronomy and mechanics, the eighteenth-century thinkers proclaimed with certainty that they had found the true laws of nature. The influence of Newtonian mechanics on almost all thought was profound, precisely because the intellectual leaders of the eighteenth century were convinced that the mathematical account of nature’s behavior was correct. The creation of non-Euclidean geometry affected scientific thought in two ways. First of all, the major facts of mathematics, i.e., the axioms and theorems about triangles, squares, circles, and other common figures are used repeatedly in scientific work and had been for centuries accepted as truths—indeed, as the most accessible truths. Since these facts could no longer be regarded as truths, all conclusions of science which depended upon strictly mathematical theorems also ceased to be truths. Or, to broaden our statement, since scientific structures were and are in large part just series of mathematical chains of reasoning, the appearance of non-Euclidean geometries raised doubts about the very framework of these structures.
Secondly, the debacle in mathematics led scientists to question whether man could ever hope to find a true scientific theory. The Greek and Newtonian views put man in the role of one who merely uncovers the design already incorporated in nature. However, scientists have been obliged to recast their goals. They now believe that the mathematical laws they seek are merely approximate descriptions and, however accurate, no more than man’s way of understanding and viewing nature.
Even on the level of engineering a serious question emerged. Since bridges, buildings, dams, and other works were based on Euclidean geometry, was there not some danger that these structures would collapse? Actually there is no guarantee that they will not. But this thought did not alarm the scientists and engineers of the nineteenth century, who, despite the existence of non-Euclidean geometry, did not believe that the geometry of physical space could be other than Euclidean. The other geometries they dismissed as logical curiosities. The behavior of these scientists and even mathematicians illustrates what has been called the law of inertia in the world of ideas. Just as a body at rest or in motion exhibits inertia or unwillingness to change its velocity, so do human beings balk at changing their ideas. However, the advent of the theory of relativity drove home the point that Euclidean geometry is not necessarily the best geometry for applications. Why then do engineers continue to use Euclidean geometry for ordinary projects? They do so because on the basis of experience Euclidean geometry has been known to be reliable. This is their only assurance. For engineering involving motion with high velocities such as modern accelerators of electrons or neutrons develop, the theory of relativity is used.
In the realm of philosophy, all doctrines built on science were necessarily affected. The most majestic development of the seventeenth and eighteenth centuries, Newtonian mechanics, fostered and supported the view that the world is designed and determined in accordance with mathematical laws. The discovery of more laws in fields such as electricity and light during the early nineteenth century reinforced the belief in a highly mechanistic and deterministic universe. But once non-Euclidean geometry destroyed the belief in mathematical truth and revealed that science offered merely theories about how nature might behave, the strongest reason for belief in determinism was shattered.
Perhaps even more devastating to philosophy was the realization that man can no longer be sure of his ability to acquire truths. Through philosophy man has sought knowledge of ultimate realities, knowledge which would enable him to live wisely, and knowledge which would answer irrepressible questions about the meaning and purpose of his existence on this earth. All people, prior to non-Euclidean geometry, had shared the fundamental belief that man can obtain certainties. The solid basis for this belief had been that man had already obtained some truths—witness, mathematics. No system of thought has ever been so widely and completely accepted as Euclidean geometry. To preceding generations it was the “rock of ages” in the realm of truth. Tradition buttressed self-evidence, and experience bolstered “common sense.” Men such as Plato and Descartes were convinced that mathematical truths were innate in human beings. Kant based his entire philosophy on the existence of mathematical truths. But now philosophy is haunted by the specter that the search for truths may be a search for phantoms.
The implication of non-Euclidean geometry, namely, that man may not be able to acquire truths, affects all thought. Past ages have sought absolute standards in law, ethics, government, economics, and other fields. They believed that by reasoning one could determine the perfect state, the perfect economic system, the ideals of human behavior, and the like. The standards sought were not just the most effective ones, but the unique, the correct ones. This belief in absolutes was based on the conviction that there were truths in the respective spheres. But in depriving mathematics of its claim to truth, the non-Euclidean geometries destroyed the shining knight of truth and shattered man’s hope of ever attaining any truths. When the anchor of truth was lost, all bodies of knowledge were cast adrift. Apparently the intellectual process does not lead to certainties. In Henri Bergson’s words, “One can always reason with reason.”
Our own century is the first to feel the impact of non-Euclidean geometry because the theory of relativity brought it into prominence. It is very likely that the abandonment of absolutes has seeped into the minds of all intellectuals. We no longer search for the ideal political system or ideal code of ethics but rather for the most workable. It is almost commonplace to hear people say that one cannot expect perfection. This attitude contrasts sharply with those of the eighteenth century and the Victorian age.
Perhaps the greatest import of non-Euclidean geometry is the insight it offers into the workings of the human mind. No episode of history is more instructive. The view that mathematics is a body of truths, which obtained prior to non-Euclidean geometry, was accepted at face value by every thinking being for 2000 years, in fact, practically throughout the entire existence of Western culture. This view, of course, proved to be wrong. We see therefore, on the one hand, how powerless the mind is to recognize the assumptions it makes. It would be more appropriate to say of man that he is surest of what he believes, than to claim that he believes what is sure. Apparently we should constantly re-examine our firmest convictions, for these are most likely to be suspect. They mark our limitations rather than our positive accomplishments. On the other hand, non-Euclidean geometry also shows the heights to which the human mind can rise. In pursuing the concept of a new geometry, it defied intuition, common sense, experience, and the most firmly entrenched philosophical doctrines just to see what reasoning would produce.
1. What would you regard as the most serious implication of the creation of non-Euclidean geometry?
2. How does the existence of non-Euclidean geometry affect the goals of scientists?
3. Develop the analogy between different systems of geometry and different bodies of law.
4. Does the existence of non-Euclidean geometry augment the power of science to provide rational comprehension of natural phenomena?
1. The history of attempts to find a simpler parallel postulate.
2. The work of Girolamo Saccheri.
3. The life of Carl Friedrich Gauss.
4. The use of non-Euclidean geometry in the theory of relativity.
BELL, ERIC T.: Men of Mathematics, Chaps. 14 and 16, Simon and Schuster, Inc., New York, 1937.
BONOLA, ROBERTO: Non-Euclidean Geometry, A Critical and Historical Study of Its Development, Dover Publications, Inc., New York, 1955.
CARSLAW, H. S.: Non-Euclidean Plane Geometry and Trigonometry, Chelsea Publishing Co., New York, 1959.
DUNNINGTON, G. W.: Carl Friedrich Gauss: Titan of Science, Exposition Press, New York, 1955.
DURELL, CLEMENT V.: Readable Relativity, G. Bell and Sons Ltd., London, 1931.
FRANK, PHILIPP: Philosophy of Science, Chap. 3, Prentice-Hall, Inc., Englewood Cliffs, N.J., 1957.
GAMOW, GEORGE: One Two Three. . . Infinity, Chaps. 4 and 5, The New American Library, Mentor Books, New York, 1947.
KLINE, MORRIS: Mathematics in Western Culture, Chap. 27, Oxford University Press, New York, 1953.
POINCARÉ, HENRI: Science and Hypothesis, Chaps. 3 to 5, Dover Publications, Inc., New York, 1952.
RUSSELL, BERTRAND: The ABC of Relativity, Harper and Bros., New York, 1926.
SOMMERVILLE, D. M. Y.: The Elements of Non-Euclidean Geometry, Dover Publications, Inc., New York, 1958.
WOLFE, HAROLD E.: Introduction to Non-Euclidean Geometry, The Dryden Press, New York, 1945.
YOUNG, JACOB W. A.: Monographs on Topics of Modern Mathematics, Chap. 3, Dover Publications, Inc., New York, 1955.
* The concept of great circle was explained in Chapter 7.
* However, see Section 24–4.