And wisely tell what hour o’ the day
The clock doth strike, by Algebra
SAMUEL BUTLER
We have seen that mathematics contains several geometries and that the very existence of these geometries has profound implications for the nature of mathematics and for the relationship of geometry to our physical world. It is therefore only natural to ask whether there are also many algebras, and whether the existence of these algebras has comparable implications for mathematics and its relation to the physical world. This question is vital not only because algebra plays a most important role in physical applications but because, after non-Euclidean geometry had taught mathematicians that geometry does not offer truths, many turned to the ordinary number system and the developments built upon it and maintained that this part of mathematics still offered truths. The same thought is often expressed today by people who, wishing to give an example of an unquestionable truth, quote 2 + 2 = 4.
Examination of the relationship between our ordinary number system and the physical situations to which it is applied will show that it does not offer truths. We shall then see that other algebras do exist and are useful, just as non-Euclidean geometries are useful.
Mathematicians are, of course, free to introduce the symbols 1, 2, 3, 4, . . . , where 2 means 1 + 1, 3 means 2 + 1, 4 means 3 + 1, and so on. Moreover, as we pointed out in Chapter 4, experience suggests that for any three numbers a, b, and c, (a + b) + c = a + (b + c), and so this associative property is adopted as an axiom. We may now prove readily that 2 + 2 = 4 because, first of all, by the very meaning of 2, we have
2 + 2 = 2 + (1 + 1).
From the associative axiom it follows that
2 + (1 + 1) = (2 + 1) + 1.
According to the definition of 3,
(2 + 1) + 1 = 3 + 1,
and, according to the definition of 4,
3 + 1 = 4.
And now, by applying the axiom that things equal to the same thing are equal to one another, we can assert that 2 + 2 = 4.
Thus by a purely logical process which employs definitions and axioms we have proved that 2 + 2 = 4. But the question we seek to answer is not whether the mathematician can set up definitions and axioms and deduce conclusions. We grant that arithmetic is a valid deductive system. We wish to know whether this system necessarily expresses truths about the physical world.
A possible denial might be entered at once on the ground that the only justification for the associative axiom was limited experience with simple numbers, whereas the axiom asserts something about all whole numbers. There is force to this argument because a generalization on the basis of limited experience may be erroneous. However, there are many thinkers who would assert that whether or not the associative axiom was suggested by experience, it is clearly a truth. Of course, the burden of proof then rests on those who proclaim truths. We shall not insist on this point, since there are weaker links between arithmetic and the physical world.
If a farmer has two herds consisting of 10 and 25 heads of cows, respectively, he knows by adding 10 and 25 that the total number of cows is 35. That is, he need not count the cows. Suppose, however, he brings the two herds of cows to market where they are selling for $100 apiece. Will a herd of 10 cows which might bring in $1000 and a herd of 25 cows which might bring in $2500 together bring in $3500? Every businessman knows that when supply exceeds demand, the price may drop, and hence 35 cows may bring in only $3000. In some idealized world the value of the cows may continue to be $3500, but in actual situations this need not be true.
Let us consider next whether some of the slightly deeper results of arithmetic apply to the physical world. Certainly the statement that 
is arithmetically correct. But do two half-sheets of paper make one whole sheet and do two half-shoes make one whole shoe? Clearly two physical halves never make one whole unless they can be joined in such a way that the halves merge into one whole. Two half-dollars, in general, equal one whole dollar in purchasing power, but in areas where silver is preferred to bills two half-dollars are worth more. To know whether the arithmetic is applicable, we must examine the physical situation.
Let us consider the addition of velocities. If a river flows at the rate of 3 miles per hour and a man capable of rowing at 5 miles per hour in still water rows downstream, his velocity relative to some fixed point in the river is the sum of 3 and 5, that is, 8 miles per hour. But if Mr. A walks along a road at the rate of 3 miles per hour and Mr. B walks along at the rate of 5 miles per hour, then B’s velocity relative to some fixed point is not 8 miles per hour. Of course not, we would say. But why do we add the 3 and 5 in one case and not in the other? It is the physical situation which tells us when to add and when not to do so.
In all of the above examples we must examine the particular physical situation to determine whether the mathematical result fits. But if we must resort to experience to decide when the results of our arithmetic apply, then it is not the truth of arithmetic on which we rely.
Let us test further the applicability of arithmetic. Suppose that we measure two boards and find them to be 3 and 4 feet long, respectively. If we place these boards end to end, will the result be 7 board feet? Probably not. All measurement is approximate, and our statement that the individual boards are 3 and 4 feet long merely means that we are unable to detect any difference between the actual lengths of the boards and the 3- and 4-foot marks on our measuring device. But the first may be 3.01 feet, and the second 4.01 feet. Together they are then 7.02 feet, and we may be able to detect a difference of 0.02 feet. One may object here and say that the trouble is due to the limitations of our senses. This is indeed true; however, can we continue to claim that 3 + 4 = 7 applies to the physical world, insofar at least as situations involving measurement are concerned?
We learn in chemistry that when one mixes hydrogen and oxygen, he obtains water. More precisely, if one takes 2 volumes, say 2 cubic centimeters, of hydrogen and 1 volume of oxygen, he obtains 2 volumes of water vapor. Likewise 1 volume of nitrogen and 3 volumes of hydrogen yield 2 volumes of ammonia. We happen to know the physical explanation of these surprising arithmetic relationships. By Avogadro’s hypothesis, equal volumes of any gas, under the same conditions of temperature and pressure, contain the same number of particles. If, then, a given volume of oxygen contains 10 molecules, the same volume of hydrogen will also contain 10 molecules. Then there are 20 molecules in 2 volumes of hydrogen. Now it happens that the molecules of oxygen and hydrogen are diatomic; that is, each contains two atoms. Each of these 20 diatomic hydrogen molecules combines with one atom of oxygen to form 20 molecules of water or 2 volumes of water.* The chemistry is interesting, but the main point we wish to make is that ordinary arithmetic fails to describe correctly the result of combining gases by volume.
Suppose, next, that one raindrop is added to another raindrop. Do we now have two raindrops? If one cloud is joined to another cloud do we now have two clouds? One may protest that in these examples the merged objects have lost their identity, and that the addition process of arithmetic does not contemplate such loss. And precisely for this reason, arithmetic in the normal sense no longer applies.
All of the above examples lead to two general conclusions. One is that there are many physical situations where ordinary arithmetic does not apply; that is, ordinary arithmetic is unable to express proper quantitative truths about these situations. The second conclusion is that even though there are a few situations to which ordinary arithmetic does apply, such as, for example, adding herds of cattle, we must depend upon experience with those very situations to know this fact. If herds of cattle behaved like volumes of gases or like raindrops, then the arithmetic would not apply, and it is only through experience that we learn how they do behave. Hence we have no guarantee that arithmetic per se represents truths about the physical world.
1. If we place the length of one 10-ft ladder on top of the length of another, do we obtain a 20-ft ladder? What is the point of the question?
2. Since measurement is approximate, can we say that pouring two 10-lb packages of flour into one bag will produce one 20-lb package of flour?
3. If we balance two objects in the pans of a scale and then add 5 lb to each pan, will the scale still balance? What axiom of arithmetic is applicable to this situation?
4. If an object is thrown downward with a velocity of 100 ft/sec and acquires a velocity due to gravity of 32t ft/sec, is its total downward velocity (100 + 32t)ft/sec? Justify your answer.
5. If we superimpose a sinusoidal sound wave of frequency 100 cycles per second on one which has a frequency of 50 cycles per second, do we obtain a sound wave of frequency 150 cycles per second?
6. If one mixes two equal volumes of water, one having a temperature of 40°F and the other of 50°F, what is the temperature of the mixture?
Mathematics does not have at its disposal special arithmetics to treat all of the situations in which ordinary arithmetic fails. For example, there is no arithmetic which tells us how volumes of gases combine. Each distinct combination must be analyzed on the basis of physical knowledge about the molecules involved. But there are situations which warrant the introduction of special arithmetical concepts and operations. If an arithmetic, that is, the concepts and operations, accurately describes physical events and permits prediction of future behavior, just as ordinary addition predicts the result of combining two herds of cattle, then it is worth creating.
Our first example of an arithmetic different from the ordinary arithmetic does not serve any deep scientific purposes, but it does fill a need which many millions of Americans experience. These people seem to be very much excited by the batting averages of baseball players. Let us look into this matter. Suppose a player goes to bat 3 times in one game and 4 times in another. How many times in all did he go to bat? There is no difficulty here. He went to bat a total of 7 times. Suppose he hit the ball successfully, that is, got to first base or farther, 2 times in the first game and 3 times in the second. How many hits did he achieve in both games. Again there is no difficulty. The total number of hits is 2 + 3 or 5.
What the audience and the player himself are usually most interested in is the batting average, that is, the ratio of the number of hits to the number of times at bat. In the first game this ratio was 2/3; in the second game the ratio was 3/4. And now suppose the player or a baseball fan wishes to use these two ratios to compute the batting average for both games. One would think that all one had to do would be to add the two fractions. That is,
Of course this result is absurd. The player could not get 17 hits in 12 times at bat. Evidently the ordinary method of adding fractions does not give the batting average for both games by adding the batting averages for the separate games.
How can we obtain the correct batting average for the two games from those of the separate games? The answer is to use a new method of adding fractions. We know that the average for both games is 5/7 and the separate batting averages are 2/3 and 3/4. We see that if we add the numerators and add the denominators of the separate fractions and then form the new fraction, we get the correct answer. That is,
provided this plus sign means adding the numerators and adding the denominators.
We now have the makings of a new arithmetic. The addition of integers will be the usual one. However, the addition of fractions is to obey the definition
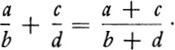
We can introduce subtraction of one integer from another and subtraction of one fraction from another. In the latter case, the definition is
Though we have no significant physical interpretation for negative integers and negative fractions, at least in terms of the baseball situation, there would be no objection mathematically to introducing them. Likewise, though the physically significant fractions so far as baseball is concerned would be less than 1 or 1, we could introduce any quotient a/b even when a is greater than b. One could even introduce the usual multiplication of fractions and all of the ideas associated with this operation.
The laws of this new arithmetic would, in many instances, be the familiar ones. As to the basic operation of addition, whether of integers or fractions, let us note that the commutative law (see Section 4–5) holds, that is,
the associative law holds, that is
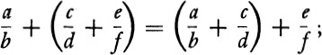
and, if we were to introduce the usual multiplication of fractions, then the distributive law holds, that is
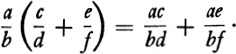
Nevertheless, the arithmetic will have some peculiarities. Let us note a few of these. Ordinarily 
. However in adding two fractions, say,
it would not do to replace 
by 
, for the answer in one case is 
and in the other 
, and these two answers are not equal. Further, in the normal arithmetic, fractions such as 
and 
behave exactly as do the integers 5 and 7. However, if We add and as fractions in the new arithmetic, we do not obtain 
but 
.
We shall not pursue further this arithmetic of baseball because it does not have any broad mathematical significance. What we should learn from it is that given a physical situation we can invent an arithmetic to fit it. The arithmetic is man-made. Moreover, when we apply this arithmetic to any physical situation we have no guarantee in advance, any more than we do in the case of ordinary arithmetic, that the arithmetic will work, that is, will predict what happens. Insofar as the arithmetic has been designed to fit a particular situation, the computation of batting averages, it will work, but this is not surprising or due to any inherent truth in arithmetic.
1. Is a batting average of the same as or 
for the purpose of computing the batting average for several games?
2. Show that under the definition of addition of fractions discussed in the text and the usual product definition, the distributive law holds.
3. What fraction added to 
gives 0 in this baseball arithmetic?
4. Suppose a salesman selling vacuum cleaners on a house-to-house basis makes 3 sales in 10 calls on one day, 4 sales in 11 calls the next day, and so on. Could he compute his “batting average” by adding fractions in the manner described in the above text?
An entirely different arithmetic from the normal one or the arithmetic of baseball is suggested by our system of recording the time of the day. Six hours after 10 o’clock is not 16 o’clock but 4 o’clock; that is, in this system,
10 + 6 = 4.
Similarly, 6 hours before 3 o’clock is 9 o’clock; that is,
3 − 6 = 9.
The idea which this system of telling time suggests is that if two numbers differ by 12 or a multiple of 12, then they are equal. Thus 26 = 2 because 26 − 2 = 2 · 12, and 9 = −3 because 9 − (−3) = 12. Clearly the equality sign here does not mean the same as in ordinary arithmetic; hence we use the symbol = and write our new equations, which are now called congruences, as follows:
26 ≡ 2, modulo 12; 9 ≡ − 3, modulo 12.
The phrase “modulo 12” after each equation repeats, in shorthand form, the condition stated above, namely, that the equation holds if and only if we neglect multiples of 12.
In this arithmetic, which is usually limited to whole numbers, any number larger than 12 is congruent to some number less than 12 because we can always subtract from the larger number some multiple of 12 to obtain a number less than 12. Thus, if we start with 35, we can subtract 2 · 12 and obtain 11. Then
35 ≡ 11, modulo 12.
The number 12 itself is congruent to 0 because 12 − 0 = 1 · 12. Hence
12 ≡ 0, modulo 12.
Similarly, any negative number is congruent to some positive number less than 12. For example, −25 ≡ 11 because 11 − (−25) = 3·12, or if one prefers, −25 − 11 = −3·12. Thus in the arithmetic modulo 12 we need deal only with positive integers from 0 to 11. We also regard any positive integer less than 12 to be congruent to itself because the difference of the two integers is zero times 12. Thus
7 ≡ 7, modulo 12.
Let us see what the results of simple addition and multiplication are in this modular arithmetic. For example,
9 + 6 ≡ 3, modulo 12.
Also
9 + 3 ≡ 0, modulo 12,
and
9 × 4 ≡ 0, modulo 12.
Here, then, is an arithmetic in which the sum and the product of two positive numbers can be zero, although the summands and the factors are not zero.
We see that addition and multiplication are possible in this arithmetic modulo 12. It is mathematically significant to ask, Do the inverse operations exist? That is, can one subtract any number from another or divide one number by another in this arithmetic? In discussing the answers to these questions let us keep in mind that the only numbers we need to consider are from 0 to 11.
Let us consider subtraction. We should like to know, given a and b, whether there is some quantity x such that
a − b ≡ x, modulo 12
or, by the meaning of subtraction as the inverse of addition,
a ≡ b + x, modulo 12.
If we take x to be 12 − b + a, then we shall have
a ≡ b + 12 − b + a or a ≡ 12 + a or a ≡ a.
Just to see what this means, suppose a = 3 and b = 7. Then x = 12 − 7 + 3 or 8. Hence
3 − 7 ≡ 8, modulo 12
which is certainly correct because −4 ≡ 8 modulo 12. Thus we can subtract any number from any other in the system of numbers 0 to 11, modulo 12.
And now let us consider division. Here we ask, given a and b with b not zero, is there a number in our collection such that
or, by the meaning of division as the inverse of multiplication,
a ≡ bx, modulo 12?
If we were to try to prove that there always is such an x, we would not succeed. Indeed we can show by an example, that such an x does not always exist. Consider
1 = 3x, modulo 12.
The possible values of x are 0 to 11, and trial of all these values shows that not one will satisfy the equation. Thus we cannot divide 1 by 3.
This example does not prove that division is never possible. For example, it is possible to divide 3 by 9 because
3 = 9·3, modulo 12,
so that 3 divided by 9 is 3, modulo 12. Let us also note that
3 ≡ 9·7, modulo 12,
so that in this case of 3 divided by 9 there are at least two answers: 7 and 3.
Modular arithmetics are numerous. Another one is suggested by the fact that there are 7 days in the week. If one wanted to know what the day of the week will be 26 days from a Wednesday, say, he could of course determine it by pursuing the sequence, Thursday, Friday, etc., until he had counted 26 days. However, he could recognize that every 7 days brings him back to Wednesday and that all he need to do is count 5 days from Wednesday. In other words, so far as days of the week are concerned, any multiple of 7 can be neglected. This fact suggests an arithmetic modulo 7.
Thus we have
5 + 4 ≡ 2, modulo 7 and 5 · 4 = 6, modulo 7.
In the system of arithmetic modulo 12, it was necessary to consider only the numbers from 0 to 11. Analogously, in the system modulo 7 it is necessary to consider only the numbers from 0 to 6. The properties of this latter system are very similar to those of the former but they differ in one essential respect. It was not possible to divide any specific number by any other given number in the modulo 12 system and where division was possible the answer was in some cases not unique. It is possible to divide any number from 0 to 6 by any other from 1 to 6 (division by 0 is excluded) in the modulo 7 system and the answer is unique. Thus 2 divided by 5 is 6 because
2 ≡ 5 · 6, modulo 7.
The fact that division is always possible is easy enough to check by actual trial and so we shall not prove the general fact. We note that the operation of division behaves more normally in the modulo 7 system than in the modulo 12 system. The difference is due to the fact that 7 is a prime number, whereas 12 is not.
When a mathematician investigates an arithmetic and its algebra he attempts to ascertain what basic properties the members of the system obey. We have already done some of this. For example, we have investigated subtraction and division for the modular systems. The mathematician would also investigate whether the basic operations of addition and multiplication are commutative and associative and whether multiplication is distributive with respect to addition. We shall leave some of these matters to the exercises and consider others.
We know that in ordinary arithmetic we can add one equality to another and the sums are equal. Is this true for congruences? Thus if
and
is it true that
a + c = b + d, modulo m?
Let us see if we can prove this.
The statement that a ≡ b, modulo m means that
a − b = pm,
where p is some whole number. Likewise the statement that c ≡ d, modulo m means that
c − d = qm,
where q is some whole number. If we add these two ordinary equations we find that
a − b + c − d = pm + qm
or
a + c − (b + d) = (p + q)m.
This last statement says that the difference between a + c and b + d is a multiple of m. But this can be written as
Thus we can add congruences with respect to the same modulus.
It is likewise possible to prove that if
a ≡ b, modulo m
and
c ≡ d, modulo m,
then
We shall leave this proof to an exercise.
We can use these two simple theorems on addition and multiplication of congruences to make an application to ordinary arithmetic. We know that
Multiplying this congruence by itself, we obtain
Multiplication of the two above congruences yields
Obviously we could continue to higher and higher powers of ten.
Now let us consider any number, say 457. This number actually is 4·100 + 5·10 + 7. We may certainly state that
Since
we can multiply equations (9) and (5) and obtain
Similarly, from 4 ≡ 4, modulo 9, and from (6), we obtain by multiplication of congruences:
Statement (3) says that we can add congruences, modulo the same number; hence, let us add the congruences (8), (10), and (11). The result is
4 · 100 + 5 · 10 + 7 = 4 + 5 + 7, modulo 9,
or
457 ≡ 4 + 5 + 7, modulo 9.
What this result says is that a number and the sum of its digits are congruent. Hence a number minus the sum of its digits must be a multiple of 9. To test this statement for the number 457 itself, we note that 457 − (4 + 5 + 7), or 441, is 49 times 9.
This result is, of course, of interest to those who like to play with numbers, but it also provides a useful method of checking the ordinary arithmetic operations of addition, subtraction, and multiplication. For example, let us consider the product of 457 and 892. We know that
457 ≡ 4 + 5 + 7, modulo 9, and 892 ≡ 8 + 9 + 2, modulo 9.
Moreover, 4 + 5 + 7, or 16, is congruent to 7, modulo 9, and 8 + 9 + 2, or 19, is congruent to 1, modulo 9. Hence
457 ≡ 7, modulo 9,
and
892 ≡ 1, modulo 9.
In view of (4), we may multiply these congruences and state that
457 · 892 ≡ 7 · 1, modulo 9.
Then the product of 457 and 892 is congruent to 7, modulo 9. That is, the actual product and the product of the sums of the digits in the two factors are congruent. But the actual product is also congruent to the sum of its digits. Hence the sum of the digits in the product is congruent to the product of the sums of the digits in the factors. We have therefore a check on the correctness of the multiplication, which is known as the rule for casting out nines.* But we did not prove and so cannot conclude that if the congruence does hold, then the multiplication is correct.
We shall not pursue further the subject of modular arithmetics. These are studied extensively in the branch of mathematics known as the theory of numbers, wherein they are often classified under congruences. Our objective in studying them is primarily to see that there are alternative arithmetics and their algebras. We have also been concerned to see that there is no one necessary arithmetic whose applicability to the physical world is guaranteed. Let us note that in arithmetic modulo 4, 2 + 2 = 0. Hence 2 + 2 does not always make 4.
1. Make up the addition table for the arithmetic, modulo 7.
2. Make up the multiplication table for the arithmetic, modulo 7.
3. By trials with actual numbers decide whether it is possible to subtract any whole number from another and obtain an answer in the arithmetic, modulo 7.
4. Are there any answers to the problem of dividing 4 by 2 in the arithmetic, modulo 6? of dividing 3 by 2?
5. Answer the same questions as in Exercise 4, but applied to the arithmetic, modulo 7. Does any significant conclusion suggest itself from a comparison of the answers in this exercise with those of Exercise 4?
6. Solve the equation x + 5 ≡ 2 in the arithmetic, modulo 12.
7. Prove that if a ≡ b, modulo m, and c ≡ d, modulo m, then a − c ≡ b − d, modulo m.
8. Prove that if a ≡ b, modulo m, and c ≡ d, modulo m, then ac ≡ bd, modulo m. [Suggestion: Since a = b, modulo m, a = b + pm.]
9. We know that 16 ≡ 4, modulo 6, and 4 ≡ 4, modulo 6. By dividing the first congruence by the second one, we obtain 4 ≡ 1, modulo 6. What conclusion do you draw?
10. What is the analogue for congruences of the usual axiom that things equal to the same thing are equal to each other?
11. Check the addition of 578 and 642 by the rule of casting out nines.
12. Check the multiplication of 578 and 642 by the rule of casting out nines.
13. a) Does the commutative law of addition hold for congruences modulo m, that is, is a + b ≡ b + a, modulo m?
b) Does the associative law of addition hold for congruences modulo m?
c) Does the distributive law of multiplication with respect to addition hold for congruences modulo m?
14. What is the answer to each of the following division problems in the arithmetic modulo 7?
a) 
b)
c) 
d) 
e) 
f) 
15. Obtain all possible solutions of the following equations in the arithmetic system modulo 6.
a) 2x ≡ 2
b) 3x ≡ 0
c) 3x ≡ 3
We shall now examine still another algebra. Suppose that a man has inherited two different libraries of books. It would be very natural for him to merge them into one library in which, contrary to the case of inheriting dollar bills, he would not want any duplicates. He is, then, combining the two libraries and hence, mathematically speaking, he is adding one to the other. However, since he will reject any duplicates, he will not add in the usual arithmetic sense. For example, if there are 100 books in one library and 200 in the other, the combined library may contain fewer than 300 books. Indeed, if there are 50 titles in one of the collections that duplicate titles in the other, the unified library will contain only 250 books. Thus, to represent the operation of combining two libraries, we need an addition which permits 100 + 200 to equal 250.
Mathematicians have devised an arithmetic and algebra whose addition processes represent precisely what happens in the combining of the two libraries. The system is called the algebra of sets. The arithmetic arid algebra are both so simple that we may as well discuss the algebra at once.
Let A and B be any two sets of objects. Thus A and B might be the two libraries discussed above. To indicate the addition of B to A in the sense in which the libraries were to be joined, that is, an object common to A and B is to be taken only once, we write A ∪ B and this combination of A and B is called the union of A and B. The operation we have just introduced implies: a book is in A ∪ B if it is in A, or in B, or in both, but if it is in both, it is counted only once.
Fig. 21–1.
The union of two sets.
Before proceeding, let us illustrate what the new operation of addition amounts to. Let us suppose that the books in library A are represented as points, and that the entire library consists of all points inside some curve. The set of books in library B can also be represented as the set of points inside some other curve (Fig. 21–1). Since the two libraries contain duplicate titles, these two regions will overlap. The union A ∪ B in the sense defined above will then be represented by the collection of points inside both curves, i.e., by the entire shaded area in Fig. 21–1. Of course, the points common to the two regions, the crosshatched area in Fig. 21–1, count only once in the union, but this just means that the union is represented by the points in the entire shaded area.
We thus have a new concept, the union of sets. Just as in the case of ordinary addition, for any A and B,
A ∪ B = B ∪ A
because the same collection is formed whether we add collection B to collection A or A to B, that is, the commutative property (Chapter 4) holds for this new operation of union.
Further, the associative property holds for the union of sets. Thus if we have three collections, A, B, and C, we may form A ∪ B and then add C to A ∪ B to obtain (A ∪ B) ∪ C, or we may begin with B ∪ C and add this sum to A to obtain A ∪ (B ∪ C). Both procedures yield the same total collection. In other words, for this new concept of addition, we have
(A ∪ B) ∪ C = A ∪ (B ∪ C),
whether or not the sets overlap (Fig. 21–2).
It is because these familiar properties of commutativity and associativity hold for the new concept of union that some people use the term addition and the usual plus sign, although the operation of combining the two libraries while rejecting duplicate titles is not the same as the usual combination of collections of cows or dollars. We should, however, note that there are essential differences between the new concept of union and the usual addition. Suppose, for example, that all titles in library B are also in A. Then our new concept of union requires that (Fig. 21–3)
A ∪ B = A.
Moreover, if we add collection A to itself, we obtain A. That is
A ∪ A = A.
The algebra of sets also has a concept somewhat analogous to multiplication. Suppose that the man combining the two libraries were interested in determining how many titles were common to the two libraries. For example, he might wish to know how many books can be sold. The set of titles common to the two libraries A and B is called the intersection of A and B and is denoted by A ∩ B or simply, as in ordinary algebra, by AB. If the books in the sets A and B are again pictured as the points inside two curves (Fig. 21–4), then the intersection is represented by the area common to the sets of points A and B, the shaded area in the figure.
Fig. 21–2.
Fig. 21–3
A ∪ B = A.
Fig. 21–4.
A ∩ B.
Fig. 21–5
This concept of intersection differs from the ordinary concept of multiplication in that intersection in set algebra usually produces a much smaller set than is contained in either of the factors A or B. Yet the fundamental properties of the intersection of sets are the same as for ordinary multiplication. For example, it is certainly true for the intersection of sets that
A ∩ B = B ∩ A
because the same final set, for example, the books common to both libraries, is obtained whether we consider the objects common to A and B or to B and A. Similarly, it is true that
(A ∩ B) ∩ C = A ∩ (B ∩ C)
for, if we select the objects common to A and B (Fig. 21–5) and then those common to A ∩ B and C, we surely obtain the same set as if we selected the objects common to B and C and then the titles common to A and B ∩ C. In either case, we obtain the set of objects in all three sets, A, B, and C. Thus the commutative and associative properties hold for this new concept of intersection.
There are, however, essential conceptual differences between the intersection of sets of objects and the product for ordinary numbers. If in our library example the set B consists of titles which are all in A, then (Fig. 21–3)
A ∩ B = B,
because the books common to A and B are those in B. Also, the intersection of A and A is A; that is,
A ∩ A = A.
Finally, suppose that A and B have no objects in common. What is the set of objects common to A and B? Physically, there is none. Mathematically we introduce the symbol 0 to represent an empty set of objects* and write
A ∪ B = 0.
The symbol 0 possesses many of the usual properties of the number zero. Thus, by the above definitions of union and intersection for sets, it is true that
A ∪ 0 = A
and
A ∩ 0 = 0.
There are other interesting concepts and operations in the algebra of sets. For example, one may be concerned with all books that exist in the world. Then this entire collection of books is called the universe of discourse, and the entire collection is denoted by 1. It follows, unlike ordinary algebra, that
A ∪ 1 = 1.
On the other hand, as in ordinary algebra, we have
A ∩ 1 = A.
We need not explore the entire theory of the algebra of sets to appreciate that this algebra is quite distinct from the algebra of ordinary numbers. However, we shall note that while there is a concept of subtraction, it is not the inverse of addition. Normally 7 – 4 is a number which when added to 4 gives 7, and we say that subtraction is the inverse of addition because the result of the subtraction when added to the subtrahend or the quantity subtracted gives the original quantity. Given any two sets A and B, the difference A − B is, by definition, the set of objects in A which are not in B. Thus if A and B are the two sets of points enclosed by the respective circles in Fig. 21–6, A − B consists of the shaded portion of A. If we join B to A − B, the union is not A but A ∪ B. Thus the concept of subtraction is not the usual one. As for division of one set by another it is not possible to make a definition which will yield a quotient for any two sets A and B.
Fig. 21–6
Historically, one of the motivations for the study of the algebra of sets was provided by the study of logic. Mathematicians, notably Descartes and Leibniz, were so much impressed by the usefulness of ordinary algebra that they conceived the idea of inventing an algebra for reasoning in all fields of thought. The concepts of ethics, politics, economics, and philosophy would be the analogues of numbers, and the relationships among these concepts would be the analogues of the operations of arithmetic. They referred to this plan as a universal algebra. The work of Descartes and Leibniz was not successful because they undertook too much. (One can hardly imagine learned Republican and Democratic algebraists sitting down to calculate the solution of a vexing political problem by means of some system of algebra.) It is not likely that the ideas of disciplines such as philosophy and economics can be compactly represented by symbols and the reasoning performed by suitable algebraic operations. However, about 1850, George Boole, one of the founders of mathematical logic, showed that the reasoning processes themselves, which are studied in logic, can be formalized and carried out by an algebra of logic which is identical with the algebra of sets.
Boole’s first idea was that in ordinary reasoning we deal with classes or sets of objects. The statement that all students are wise deals with the class of students and the class of wise people. Moreover, the statement itself says that the class of students is included in the class of wise people. If we let A be the class of all students and B the class of all wise people, then the statement that A is included in B can be expressed by the fact that the intersection of A and B is A. Thus the symbolic equivalent is
The statement that no wise people ignore mathematics can also be expressed symbolically. We let C denote the class of people who ignore mathematics. Since the statement says that there is no person common to the class B of wise people and the class C of those who ignore mathematics, then, in symbols, the statement says
These two premises should lead to a conclusion about students and people who ignore mathematics. Hence let us derive an equation involving A and C. Since the left and right sides of (12) and (13) are identical sets, we have
The associative property of intersection tells us that we may arbitrarily group any two factors, just as in the product (3 · 4) (5 · 6) we may group the 4 and 5 and write 3(4 · 5)6. Then
(A ∩ B) ∩ (B ∩ C) = A ∩ (B ∩ B) ∩ C.
However, B ∩ B = B. Hence
(A ∩ B) ∩ (B ∩ C) = A ∩ B ∩ C.
But by (12) A ∩ B = A. Therefore
From (14) and (15) it now follows that
Translated into words, this conclusion states that the class of students and the class of people who ignore mathematics have no members in common, or no student ignores mathematics. We have thus arrived at a conclusion by purely algebraic means.
This example illustrates how Boole used the symbols and algebraic operations of the algebra of sets to perform ordinary reasoning. With his algebra of logic Boole hoped not only to facilitate reasoning but to impart precision to the logical methods of reasoning. His ideas were taken up by others and became the basis of the subject now known as symbolic logic.
The algebra of sets and symbolic logic will not be pursued further. Neither is central in mathematics. The algebra of sets is used in a few advanced branches of mathematics, although even there it is a subsidiary notion. Symbolic logic is another very specialized field, somewhat apart from the main body of mathematics. It is used mainly by logicians who are seeking to clarify problems of logic and the relationship of mathematics to logic. The algebra of sets has been presented here only to help illustrate the variety of algebras in mathematics.
1. If A and B are sets and A ∪ B = B, what may you infer about the objects in A and B?
2. If A and B are sets and A ∩ B = A, what may you infer about the objects in A and B?
3. The operation of union of sets has a different meaning from the addition of ordinary numbers. Why might one use the word addition and the symbol “+” for sets?
4. Evaluate in the algebra of sets: A ∪ (A ∩ A).
5. Suppose A and B contain no objects in common. Evaluate: A ∩ (B ∪ A).
6. Given the premises that all professors are intelligent and that no students are intelligent, translate these premises into the algebra of sets and deduce a conclusion about the relationship of students to professors.
7. Show that the distributive law A ∩ (B ∪ C) = A ∩ B ∪ A ∩ C applies to set multiplication and addition.
8. Show that for any two sets A and B,
a) A ∪ (A ∩ B) = A,
b) A ∩ (A ∪ B) = A,
c) (A − B) ∪ B = A ∪ B.
9. Show that if A and B are any two sets, it is impossible to find a set X such that A/B = X or A = B ∩ X.
Our study of non-Euclidean geometries and of exotic algebras may have prepared us to see that mathematics is a somewhat different activity from what man had presumed on the basis of the study of ordinary arithmetic and Euclidean geometry alone. The development of the latter two subjects had given rise to the belief that mathematics takes over certain truths about the physical world, adopts these as axioms, and then proceeds to study the physical world by deducing the implications of the axioms. Men did not question that the axioms were truths about the world but tried instead to account for their possession of truths by theories of knowledge or by crediting God with implanting these truths in human minds. However, as mathematicians undertook to study and encompass new classes of physical phenomena or to represent more accurately a previously studied phenomenon such as physical space, they were forced to recognize the need for new concepts and new sets of axioms.
The mathematician really creates models of reality. The concepts, axioms, and theorems of an algebra or a geometry are a model with which to think about some aspect of the physical world. Each model has a limited applicability. Moreover, one must distinguish between the mathematical model and the physical world or between mathematical theories and physical reality.
1. Modular arithmetics.
2. The properties of the algebra of sets.
3. The algebra of logic.
4. The nature of symbolic logic.
BELL, ERIC T.: Men of Mathematics, Chap. 23, Simon and Schuster, Inc., New York, 1937.
BOOLE, GEORGE: An Investigation of the Laws of Thought, Chaps. 1 to 7, Dover Publications, Inc., New York, 1951.
COURANT, R. and H. ROBBINS: What is Mathematics?, pp. 31–40, 108–116, Oxford University Press, New York, 1941.
LANGER, SUSANNE K.: An Introduction to Symbolic Logic, 2nd ed., Dover Publications, Inc., New York, 1953.
NEWMAN, JAMES R.: The World of Mathematics, Vol. III, pp. 1852–1900 (selections on symbolic logic), Simon and Schuster, Inc., New York, 1956.
SAWYER, W. W.: Prelude to Mathematics, Chaps. 7, 8, 13, and 14, Penguin Books Ltd., Harmondsworth, England, 1955.
* This phenomenon is clearly explained in Francis T. Bonner and Melba Phillips: Principles of Physical Science, Addison-Wesley Publishing Co., Inc., 1957, p. 149.
* If two numbers are congruent modulo 9, then they must have the same remainders upon division by 9, for the difference must be an exact multiple of 9. Hence the rule for casting out nines is sometimes stated as follows: the product of two numbers and the product of the sums of the digits must have the same remainder upon division by 9.
* Some books use the symbol φ.
