I now propose to set forth those properties which belong to a body whose motion is compounded of two other motions, namely, one uniform and one naturally accelerated; these properties, well worth knowing, I propose to demonstrate in a rigorous manner.
GALILEO
We saw in the preceding chapter that simple functions can be used to express physical principles and that by applying algebra to the formulas which express the functions symbolically, we can obtain new physical knowledge. To some extent, then, we have come to recognize the broader significance and usefulness of functions and mathematical processes for science in general. However, we have hardly penetrated as yet the mathematical domain of functions nor have we learned enough applications to sense its real power.
In this chapter we shall extend slightly the use of functions. In Chapter 13, we represented the acceleration and speed attained and distance traveled by a falling body by using one formula for each physical quantity. We were enabled thereby to study motion along straight-line paths. We shall now examine motion along curved paths, for example, the motion of an object dropped from a moving plane, or the motion of a projectile shot out from a cannon. It was again Galileo who perceived the basic principle underlying the phenomenon of curvilinear motion. He presented the concept and its mathematical treatment to the world in the Dialogues Concerning Two New Sciences, the very same book in which he treated motion in a straight line. Galileo’s purpose in investigating curvilinear motion was to study the behavior of cannon balls, or projectiles in general. The cannon, introduced in the fourteenth century, had undergone such improvement by Galileo’s time that it could fire a projectile over several miles. However, the theory of projectile motion was not well understood before Galileo’s work because mathematicians and physicists had attempted to apply Aristotle’s laws of motion, and these were not correct.
The problems that Galileo treated, e.g., the motion of cannon balls, unfortunately did not lose their importance in the succeeding centuries. In fact, they have become even more common and more complicated in our times, since such phenomena as the motion of bombs dropped from moving airplanes, the trajectories of death-dealing projectiles capable of traveling thousands of miles, and similar problems of modern “civilization,” also fall within the puissance of Galileo’s method. However, the value of this phase of Galileo’s work is not limited to meting out death and destruction. Aside from using his results as an illustration of the power of mathematics, we shall see in the space of one chapter how an extension of Galileo’s ideas on projectile motion led, in the hands of Newton, to the greatest advance in science which our civilization has achieved.
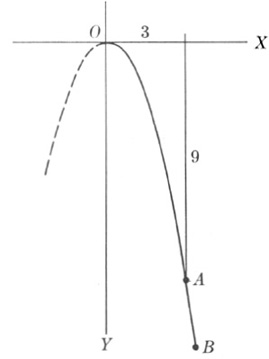
Let us suppose that a stone is thrown out horizontally from the top O of a cliff (Fig. 14–1). We know from physical experience that the stone will travel out and down and follow the curved path OAB. If we introduce a set of coordinate axes on which the positive direction of the Y-axis is downward, then we know from our work in coordinate geometry that this curve can be represented by an equation. Let us suppose, for definiteness, that this equation is y = x2. Then it follows from equation (9) of Chapter 12 that the path is part of a parabola opening downward. We shall call y = x2, which is, of course, also the formula that tells us how y changes when x changes, the direct relationship between x and y.
Fig. 14–1.
The path of a stone thrown out horizontally from the top O of a cliff.
As the stone travels out and down, the horizontal distance and the downward distance which it travels from the point O keep changing with time. Thus, at the point A, the horizontal distance traveled may be 3, and since y = x2, the vertical distance must be 9. At the point B, the horizontal distance may be 4, in which case the vertical distance must be 16.
The direct relationship between x and y is frequently useful, but it does not involve the time that the object is in motion. We may wish instead to utilize the equation which gives the relationship between horizontal distance traveled and time and the equation which relates vertical distance and time. Let us suppose for the moment that the stone travels straight out at the rate of 3 ft/sec. Then the relationship between horizontal distance and time is x = 3t. Since y = x2, then in terms of t, y = (3t)2 or y = 9t2.
are called the parametric equations of the curve OAB. They describe the curve OAB just as well as does the single equation y = x2, provided that we understand how parametric equations are to be used. For each value of t, equations (1) yield a value of x and a value of y. These values of x and y which belong to the same value of t are the coordinates of one point on the curve OAB. Thus for t = 1, x = 3, and y = 9. Then (3, 9) are the coordinates of a point on the curve, namely, the point A, which we discussed earlier. For ![]() , x = 4 and y = 16, and (4, 16) are the coordinates of the point B.
, x = 4 and y = 16, and (4, 16) are the coordinates of the point B.
We may also say that the two formulas x = 3t and y = 9t2 are equivalent to the single formula y = x2. Whether we speak of equations of curves or formulas is really immaterial. The word formula emphasizes the idea of change because formulas are relationships among variables, and we often like to think of what happens to one variable as another, related variable changes. On the other hand, when a curve is given in its entirety, the concept of change may not be relevant, and then we speak of the equation of the curve.
If the two formulas in (1) are entirely equivalent to the single formula y = x2, why do we bother with two formulas instead of one? There are two reasons: (1) When one argues from physical principles, it is often easier to arrive at the parametric representation of a given phenomenon, and (2) it is easier to study the phenomenon by working with parametric equations. We shall recognize the utility of parametric representations as we study the next few sections.
There is one more mathematical detail. Suppose that we find the parametric formulas describing a motion and we wish to determine the direct relationship between x and y. Can we do this? Yes indeed. For example, if x = 3t and y = 4t2 are the parametric formulas, we can solve the first one for t and obtain t = x/3. We substitute this value of t in y = 4t2 and obtain
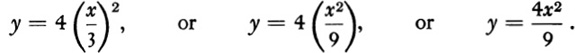
This is the direct relationship between x and y.
1. If the parametric formulas representing a phenomenon are x = 2t and y = 3t, what is the direct relationship between x and y? What curve represents the parametric formulas or the direct relationship?
2. If the parametric formulas are x = 4t and y = 5t2, what is the direct relationship between x and y? What curve represents the direct relationship?
3. Suppose the parametric formulas are x = 2t and y = 10t + 4t2. What is the direct relationship between x and y and what curve describes it?
4. Suppose x = 3t and ![]() are the parametric equations of a curve. Sketch the the curve by using the parametric equations only.
are the parametric equations of a curve. Sketch the the curve by using the parametric equations only.
Let us see now how parametric formulas arise in the study of physical phenomena and how they can be useful in deducing new information about the phenomena. Suppose a bomb is released from an airplane which is flying horizontally at 60 miles per hour (an unrealistic figure used for computational convenience). If there were no gravity, the bomb would continue to move forward alongside the airplane at the rate of 60 miles per hour. This fact seems surprising, but it is a consequence of the first law of motion, which states that if an object is in motion and no force is applied to alter that motion, then the object will continue to move indefinitely at the speed it already has. Since the bomb has been moving with the airplane, it already possesses a horizontal speed of 60 miles per hour. We have assumed that no forces are acting on the bomb and hence it will continue to move forward at that speed. There are more familiar analogous situations which may make the truth of what was just said a little more acceptable. Suppose that a person rides in an automobile which is moving at the rate of 60 miles per hour and the driver suddenly applies the brakes. The automobile’s motion is then checked, but the passenger’s motion is not, and he continues to move forward at 60 miles per hour, at least until he hits the windshield.
Let us return to the motion of the bomb released from the plane. We had assumed that gravity was not acting. But it does act and it pulls the bomb downward at the same time as the bomb moves forward so that the bomb follows a curved path. Here Galileo made a discovery applying to projectile motion, namely, that one could study its horizontal and vertical motions as though they were occurring separately, and that the position of the bomb at any time could be determined by finding how far it had traveled horizontally and vertically. This idea was new and radical in Galileo’s time. Aristotle had argued that one motion would interfere with the other, and that only one could operate at any given time. Thus he would have said that the violent motion imparted to the bomb by the airplane would prevail until the acting force was used up, and then the natural motion downward would take over and cause the bomb to fall straight down.
Let us apply Galileo’s way of analyzing the motion. The bomb moves horizontally at the constant speed of 60 miles per hour, or 88 feet per second. If we measure time from the instant the bomb is released from the plane, and if we measure horizontal distance from the point at which it is released, then the horizontal distance x covered by the bomb in t seconds is given by the formula
This formula describes the horizontal motion.
According to Galileo, the vertical motion downward takes place as though it were independent of the horizontal motion. But the vertical motion is due to gravity only, and we know that an object which falls straight down under the action of gravity and starts with zero speed falls 16t2 feet in t seconds. Hence, if we let y represent the distance downward from the point at which the bomb is released, then
Formulas (2) and (3) together describe the entire motion. We observe that x and y, the horizontal and vertical distances traveled, are given in terms of a third variable, t. In fact, they are the parametric formulas for the motion in question. To draw the graph of the path described by the bomb, we may adopt either of two methods. We can choose various values of t, say t = 0, 1, 2, 3, and so on, and calculate the values of x and y for each value of t. Thus when t = 1, x = 88 and y = 16; then (88, 16) are the coordinates of one point on the curve. Calculating many such sets of coordinates will give us some idea of the shape of the curve (Fig. 14–2).
Or we may proceed by the second method, that is, determine the direct relationship between x and y. Solving equation (2) for t, we have t = x/88. Substituting this expression for t in (3) yields
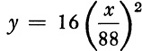
or
Fig. 14–2.
Path of a bomb released from an airplane flying horizontally.
From formula (9) of Chapter 12 we know that the curve is a parabola. We have thus called upon our knowledge of curve and equation to determine that the curve is a parabola. If we had not been familiar with the curve of equation (4), we would have had to analyze the equation or plot points whose coordinates satisfy (4) and thereby determine the curve. In other words, we would have been faced with a problem of coordinate geometry.
We should note that only part of the parabola is of physical interest. The full parabola extends to the right and left of the Y-axis. However, only the part to the right, that is, the half corresponding to positive x-values, represents the motion of the bomb. And of this right-hand half, which mathematically extends downward indefinitely, only an are is of physical interest, namely the are from O to the ground.
We have learned so far that the path of the bomb released from an airplane traveling horizontally is an are of a parabola. Let us now see whether we can use mathematics to derive more information about the motion of bombs or, in general, about objects which move outward and downward. Suppose that two airplanes flying horizontally at speeds of 60 and 120 miles per hour, respectively, release bombs from the same point at the same instant of time. Which of these bombs would reach the ground sooner? The reader might try to answer this question by using his intuition before resorting to the use of mathematics.
Both bombs must fall the same vertical distance to reach the ground. The vertical motion is independent of the horizontal motion and is governed by formula (3). Hence this formula applies to both bombs. When they reach the ground, the value of y will be the same for both bombs. It follows that the value of t will also be the same for both. That is, both bombs will reach the ground at the same time.
Fig. 14–3.
Paths of two bombs released from two airplanes with different horizontal speeds.
How does the difference in the speeds of the two airplanes affect the motion? The plane flying at 60 miles per hour gives its bomb a horizontal speed of 60 miles per hour, or 88 feet per second, and the plane flying at 120 miles per hour imparts to its bomb a speed of 120 miles per hour, or 176 feet per second. Hence the bombs move with different horizontal speeds, and in the same time, t, the second one will travel farther horizontally. Thus OCD, the path of the second bomb, will be a wider parabola than OAB, the path traveled by the first bomb (Fig. 14–3).
1. Suppose that there were no force of gravity, and that an object is released from an airplane flying horizontally at the rate of 100 mi/hr. Describe the subsequent motion of the object.
2. One object is dropped from an airplane flying horizontally at the rate of 100 mi/hr and another from a plane flying horizontally at 200 mi/hr. Both planes are at the same altitude. Compare the times required for the two objects to reach the ground. What principle is involved?
3. From a cliff 500 ft high a stone is thrown horizontally with a speed of 100 ft/sec. How long does it take the stone to reach the ground below? What horizontal distance has the stone traveled by the time it strikes the ground?
4. A gun installed in a plane which is flying in a horizontal line at a speed of 2000 ft/sec fires a bullet in the direction of the plane’s motion at the initial speed of 1000 ft/sec. What is the horizontal speed of the bullet relative to the ground?
5. A bullet fired horizontally hits a point on a wall 300 ft away. The point is 1 ft below the level at which the bullet is fired. What is the horizontal speed of the bullet?
6. A plane is traveling in a horizontal line at a speed of 300 ft/sec and at an altitude of 1 mi. Where (at what horizontal distance from the target) should the gunner release a bomb to hit a given point on the ground?
7. Suppose that a plane flying in a horizontal line at the rate of 200 ft/sec releases a bomb and continues to fly horizontally at the same rate. Where is the plane in relation to the bomb when the bomb strikes the ground?
A slight extension of the mathematics just introduced to treat the motion of bombs dropped from airplanes will enable us to handle the motion of projectiles shot out from cannons inclined at some angle to the ground. It was this latter problem which Galileo investigated in the seventeenth century. We shall see how neatly mathematics answers a variety of problems raised by such motions.
Suppose that a cannon inclined at an angle of 30° to the ground fires a shell with a velocity* of 1000 ft/sec (Fig. 14–4). What is the subsequent motion of the shell? We know from intuition or experience with balls thrown at a similar angle of elevation that the shell will travel out and up along some curved path and will then return to the ground. This qualitative knowledge is not, of course, sufficient to answer significant questions about the motion.
The initial velocity of the shell is in the direction which makes an angle of 30° to the ground. To treat the motion of the shell, it is mathematically simpler to consider its horizontal and vertical motions separately, that is, to obtain the parametric formulas. For this purpose we must know the horizontal and vertical velocities of the shell.
Fig. 14–4.
Shell fired with an initial velocity of 1000 ft/sec from a cannon inclined at an angle of 30° to the ground.
Suppose that the shell travels for one second in the direction OR in which it is fired. How far will it travel horizontally and vertically in that second? Let us drop a perpendicular from R onto the X-axis and from R onto the Y-axis. Thus we determine the lengths OP and OQ, respectively. The length OP is the horizontal distance which the shell travels in one second and the length OQ is the corresponding vertical distance. Since OP and OQ are distances traveled in one second, they also represent the horizontal and vertical velocities.
The horizontal and vertical velocities are then OP and OQ. What are their magnitudes? We see from Fig. 14–4 that
![]()
or
OP = ·1000 cos 30° = 1000(0.8660) = 866 ft/sec.
Similarly,
![]()
or
PR = 1000 sin 30° = 1000(0.5000) = 500 ft/sec.
Since PR = OQ, the horizontal and vertical velocities of the shell are 866 ft/sec and 500 ft/sec, respectively.
We now utilize the physical fact that the horizontal and vertical motions can be treated independently. Let us begin with the horizontal motion. The shell has an initial horizontal velocity of 866 ft/sec, and no force acts to accelerate or decelerate the horizontal motion. Hence the shell will continue to move horizontally at a constant speed of 866 ft/sec, and the horizontal distance x traveled in time t is given by
Next we consider the vertical motion of the shell. Gravity gives the shell a constant acceleration downward of 32 ft/sec2. Since the upward direction has been chosen to be positive, the downward acceleration must be written
The downward velocity acquired in time t is − 32t. However, the shell has an initial upward velocity of 500 ft/sec which, by the first law of motion, would continue indefinitely, were it not affected by gravity. The net velocity υ is then (compare Section 13–7)
To obtain the distance traveled upward in any time t, we use the same reasoning as in the preceding chapter. If only the velocity of 500 ft/sec were acting, the distance traveled upward in t seconds would be 500t. But in that time gravity pulls the shell downward a distance of 16t2. Hence y, the net height above the ground, is
Formulas (5) and (8) give the horizontal and vertical distances from the starting point O. We note that once more motion is represented by parametric formulas.
Several questions about the motion arise in practice. The first is, What path does the shell take? We may save ourselves the work of plotting the curve by determining the direct relationship between x and y, provided we recognize the curve of the resulting equation. Let us try this. Solving (5) for t yields t = x/866. We substitute this value of t in (8) and obtain
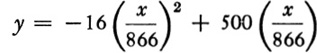
or
In Section 12–5 we discussed equations of the form (9)—albeit by means of numerically simpler examples. We could have proved the quite general statement that an equation of the form
where a and b are any positive numbers, represents a parabola which opens downward and passes through the origin. (See Exercise 3 of Section 12–5, which is a special case.) Hence with just a little more work in coordinate geometry, we could have proved what we shall now state without proof, namely, that equation (9) describes a parabola. Thus the parabola, as Galileo readily established, appears once more as the path of a projectile.
What is the range of the shell? That is, how far from the starting point will the projectile strike the ground again? The answer is important because it tells us whether a given target on the ground can be reached. Unfortunately neither formula (5) nor formula (8) answers this question directly. However, when the shell reaches the ground, the value of y in (8) should be zero. Let us determine, then, the value of t, say t1, when y = 0. From (8)
Equation (11), which is of the second degree in t1, is rather easy to solve. Applying the distributive axiom, we may write
The right side of (12) equals zero when either factor is zero, that is, when t1 = 0 and when
–16t1 + 500 = 0.
The second alternative leads to
The first value, t1 = 0, corresponds to the instant when the shell first starts its flight. Then the second value, 125/4, must be the time when the shell returns to the ground.
To determine the range, one more step is necessary. Formula (5) tells us how far the shell travels horizontally in any time t. Since the shell travels 125/4 seconds by the time it reaches the ground, we have but to substitute this value of t in (5) to get the range. If x1 denotes the range, then (see Fig. 14–5)
We might also like to know how high the shell will go in its flight and how long it takes to reach that height. These questions are readily answered. At the highest point in its flight, the vertical velocity is zero, else the shell would continue to rise. Formula (7) gives us the vertical velocity at any time t. Let us ask for the value of t, say t2, when v = 0. Then
0 = – 32t2 + 500
or
Fig. 14–5.
Path of a shell shot from a cannon.
Hence it takes 125/8 seconds for the shell to reach the highest point. Now formula (8) tells us how high the shell is at any time t. Let us therefore find the height, y2, when t = 125/8. We substitute 125/8 for t in (8) and obtain
![]()
or
Hence the shell reaches a maximum height of 3906 feet above the ground.
Another interesting question is whether the shell takes as long to travel from the cannon to its maximum height as it does to return from the latter position to the ground. Or, to fit the situation shown in Fig. 14–5, we may restate the question and ask, Does it take as long for the shell to travel from O to A as from A to B? We considered an analogous problem in the preceding chapter while discussing the motion of an object thrown straight up into the air and found that the two time intervals were equal. What does intuition suggest as the answer in the present case?
We can show at once that the time required to get from O to A is the same as the time required to travel from A to B. Equation (13) supplies the time it takes the shell to reach B, that is, to travel the path OAB. Equation (15) gives the time required to travel the path O A. We see at once that the value of t1 is twice the value t2. Hence the time of travel along path AB must equal the time of travel along path O A.
1. Suppose that a shell is fired in a direction making an angle of 40° with the ground and with a velocity of 300 ft/sec. What are the horizontal and vertical velocities of the shell? What are the parametric equations describing the motion?
2. Suppose that the parametric formulas for the motion of a projectile are x = 20t and y = −16t2 + 30t. What is the direct relationship between x and y? What is the nature of the curve represented by the direct relationship between x and y?
3. Suppose that the parametric formulas for the motion of a projectile are x = 3t and y = −16t2 + 5t. Working with these formulas, plot a few points of the path.
4. Find the range of the projectile whose motion is described in Exercise 2.
5. Find the maximum height of the projectile whose motion is described in Exercise 2.
6. What velocity does the shell whose motion is treated in Section 14–4 have on striking the ground? How does this terminal velocity compare with the initial velocity?
In the preceding section we saw how we could study the motion of a shell fired from a cannon which is inclined at an angle of 30° to the ground. The initial velocity of the shell in this direction was 1000 ft/sec. Since the angle of fire and initial velocity given in our example are representative values, the example teaches a great deal about the phenomenon of projectile motion. However, suppose that we sought to answer such questions as: What is the effect of the initial velocity on the range and on the maximum height attained by the projectile? What is the effect of the angle of fire on the range and on the maximum height of the projectile? At what angle should one fire a projectile to hit a given target? One could repeat the procedures pursued in the preceding section, using different initial velocities and angles of fire, and thus perhaps obtain answers to some of these questions. But the work would be considerable and still leave us with the problem of trying to infer a general conclusion from a number of special cases. The mathematician would not proceed in this way. He would suppose that the initial velocity is an arbitrary value, V, and that the angle of fire is an arbitrary angle, A, and then study the motion with these arbitrary values V and A. He might thereby obtain conclusions about all such motions because his results would hold for any initial velocity and any angle of fire.
Fig. 14–6.
Shell fired with an initial velocity of V ft/sec from a cannon inclined at an angle A to the ground.
Let us pursue this general investigation of projectile motion. Suppose that a shell is fired from a cannon which is inclined at an angle A to the ground (Fig. 14–6), and that the initial velocity of the shell is V ft/sec. What is the subsequent motion of the shell?
We shall follow the procedure of the preceding section. The first major point to remember is the physical principle that the horizontal and vertical motions of the projectile can be studied as though the motions were taking place independently. Hence let us find the initial horizontal and vertical velocities of the shell. By the very same argument that we used in Section 14–4, we know that the components of the velocity OR in the horizontal and vertical direction (Fig. 14–6) are obtained by dropping a perpendicular from R onto the X- and Y-axes, respectively. Thus OP is the horizontal velocity, and OQ is the vertical velocity. Now
![]()
Hence
OP = OR cos A
or
Since
![]()
and since OQ = PR, we have
OQ = OR sin A
or
Formulas (17) and (18) give us the initial horizontal and vertical velocities, respectively. We must now see what happens when the shell is in motion. The horizontal motion is uniform; i.e., no force acts to speed it up or slow it down. The shell will therefore continue to travel indefinitely in the horizontal direction at the velocity given by (17). Let us use vx to indicate the velocity in the X-direction. Then at any time t,
Since the velocity in the horizontal direction is constant, the distance traveled is velocity multiplied by time. Then
x = (V cos A)t.
This expression is best written as
so that there is no confusion about the fact that the quantity whose cosine is to be taken is A, whereas if we had written V cos At, one might think that the quantity is At. Formula (20) is a generalization of formula (5), for the 866 in (5) is just 1000 cos 30°.
To obtain the vertical velocity of the shell we must take into account the fact that gravity does produce a vertical acceleration which affects the vertical velocity. This vertical acceleration is 32 ft/sec2 and is downward. Since we have chosen the upward direction as positive, we have
a = − 32.
Because the acceleration is constant, the downward velocity gained by the shell in t seconds is − 32t. However the shell has an upward initial velocity of V sin A. Hence the net vertical velocity vy is
Next we use an old argument to determine the vertical height attained by the shell in t seconds. If only the velocity V sin A were acting, then in t seconds the shell would reach the height (V sin A)t or Vt sin A. However, in these t seconds gravity pulls the shell downward a distance of 16t2. The net height, y, of the shell therefore is
Formulas (19) through (22) supply the general equations of projectile motion. We are now in a position to answer with respect to the arbitrary values V and A the same questions that were discussed in the preceding section for a specific numerical example. Thus, by solving (20) for t and substituting this result in (22), we could find the direct relationship between x and y. We could then see that for any fixed value of V and any fixed value of A, the path is a parabola. Similarly, we could obtain general expressions for the maximum height reached by the shell, the time required to reach that height, and, say, the time required for the shell to return to the ground. In other words, we could reproduce for any V and A the results derived in the preceding section for special values of V and A.
Let us turn instead to answering questions which we could not treat before. Let us study the effect of the initial velocity, V, and angle of fire, A, on the range of the cannon. To do this we must first determine the general expression for the range. The method is the same as the one used in the preceding section.
We begin with the physical fact that when the shell strikes the ground, the y-value of its position is zero. Hence let t1 be the value of t when y = 0. Setting y = 0 in (22), we have
![]()
We may apply the distributive axiom to write
0 = t1(− 16t1 + V sin A).
Now the right side is zero when t1 = 0 and when
Since t1 = 0 corresponds physically to the instant when the shell starts its motion, it follows that the value given by (23) is the value of t at the instant the shell strikes the ground. If we solve (23) for t1, we find
To determine the shell’s range, that is, its horizontal distance from the starting point at the instant when t1 has the value just found, we use formula (20). Thus, if x1 is the value of x when t has the value t1 then
![]()
or the range is
Formula (25) answers one question immediately. If the angle A is held fixed, then the range depends upon V2. If V is increased, then x1 increases, and indeed x1 increases rapidly because it depends upon V2 rather than upon just V. Also, if we wished to attain a given range with a given angle of fire, that is, if x1 and A were specified, we could use (25) to calculate the necessary initial velocity, V.
The more practical problem is to study the dependence of range upon angle of fire, for it is easier to change the angle of fire of a cannon than it is to change the initial velocity of the shells. Let us suppose, then, that the initial velocity V is fixed and ask the question, What is the maximum range that can be obtained by varying angle A? Since V is fixed, our question, in view of (25), amounts to: For what value of A is the product sin A cos A a maximum? A little mathematics provides the answer.
We know from our work on the trigonometric ratios that sin A and cos A are certain ratios of sides of a right triangle. The size of the right triangle used to determine sin A and cos A does not matter because all possible right triangles containing a definite angle A are similar and therefore the ratio of two particular sides in any one of these triangles is always the same.* Hence let us choose a right triangle whose hypotenuse AB (Fig. 14–7) is the diameter of a definite circle. The vertex of the right angle of this right triangle must lie on the circle because a theorem of plane geometry states that the vertices of all right triangles with vertex C and hypotenuse AB must lie on a circle with AB as diameter. Let us denote the sides of the right triangle ABC by a, b, and c. We draw the perpendicular CD and denote it by h. Then, using the right triangle ADC, we obtain
![]()
From the right triangle ABC we have
![]()
So far, then, we have found that
Fig. 14–7
We may vary angle A and continue to regard it as an angle of a right triangle with hypotenuse AB because, as we noted above, the size of the right triangle is immaterial. Of course, variations in the angle A will produce changes in the position of C, but for the reason given earlier, C will continue to be a point on the circle with diameter AB. Hence we can consider all possible acute angles A by considering all triangles ABC with AB fixed and C varying on the circle. Let us now look at (26) again. Since the quantity c is fixed, sin A cos A will be a maximum when h is a maximum, and h is greatest when it is the radius of the circle. But when h is the radius, C is directly above the center of the circle. Then AC = BC. In this case angle A = 45° because the right triangle ABC is isosceles. Hence
sin A cos A
is a maximum when angle A = 45°.
We may now return to formula (25). We have found that when V is fixed, the maximum range, that is, the maximum possible value of x1, is obtained when A = 45°. Since for A = 45°, sin ![]() , the maximum range is given by the formula
, the maximum range is given by the formula
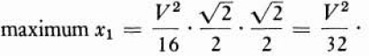
This famous result was first proved by Galileo.
1. Formulas (20) and (22) give the parametric representation of the motion of a projectile. Find the direct relationship between x and y.
2. Derive the formula in terms of V and A for the time it takes a projectile to reach its maximum height.
3. What is the formula in terms of V and A for the maximum height reached by a projectile?
4. Show generally that it takes as long for a projectile to return from its highest position to the ground as it does to travel from the cannon to the highest position.
5. What is the range of a projectile which is fired with an initial velocity of 2000 ft/sec and at an angle of 40° to the ground?
6. What is the maximum range of a projectile fired with an initial velocity of 800 ft/sec?
7. How long does it take for a projectile fired with an initial velocity of 2000 ft/sec to reach a target located at maximum range?
8. Show that the highest point which a gun can reach for all possible angles of fire but with the same initial velocity is attained by firing straight up.
In this chapter we have seen how the simultaneous application of two simple formulas, the parametric formulas, makes it possible to represent an entire class of curves which physically happen to be the paths of projectiles. The value of the parametric formulas is, then, that they enable us to answer readily a variety of questions about projectile motion. To appreciate how much mathematics accomplishes in this area, one might consider how he would proceed experimentally to find, for example, the dependence of the range of a projectile on the angle of fire. One would have to fire at least dozens of projectiles at different angles, making certain that other factors, such as the velocity with which the projectiles are fired, the shape of the projectiles, and the state of the atmosphere, are constant, and accurately measure the range and angle each time. With all these precautions taken and the information secured, the experimenter might obtain some limited results. He might, for example, learn that as the angle of fire increases in l°-degree steps from 1° to 40°, the range increases steadily, but he might miss the all-important fact that above 45° the range decreases. The dependence of range upon velocity would still be entirely unknown and require further experimentation. But we have seen how a little mathematics costing only pencil and paper can supply the full story of the dependence of range upon angle of fire and initial velocity.
Thus the present chapter, too, illustrates how the combination of mathematics and simple physical axioms, such as the fact that the acceleration of bodies near the surface of the earth is 32 ft/sec2, the first law of motion, and the independence of the horizontal and vertical motions, permits us to deduce a vast amount of knowledge about our physical world. The knowledge referred to at the moment concerns projectile motion under idealized conditions; that is, the resistance of air is neglected; the earth is assumed to be flat over the short distances which the projectiles cover; and the projectiles are limited to travel near the surface of the earth. One might regard the whole story as of minor interest because it deals with just one phenomenon and one which seems limited to bombs and guns. However, the study of this phenomenon has proved to be of immeasurable scientific importance. First of all, the deductions made from the physical axioms mentioned above can be checked experimentally. If the deductions agree with experience we have some reason to believe that the axioms are correct. We must remember in this connection that physical axioms are generalizations from limited experience and that our confidence in them depends upon how well they continue to lead to new physical facts. Secondly, the study of motions near the surface of the earth, projectile motion in particular, led to the most important advance in science since 1600, namely Newtonian mechanics. The step to the broad science of mathematical mechanics will be taken in the next chapter.
1. Sketch the curves whose parametric equations are given below.
a) x = 3t, y = 7t
b) x = 3t, y = 5t2
c) x = 3t2, y = 5t
d) x = 3t + 7, y = 5t + 9
e) x = 5 cos θ, y = 5 sin θ
f) x = 2t, y = 5 t2 + 3t
2. Find the direct equations in parts (a), (b), (c), and (d) of Exercise 1.
3. Suppose a bomb is released from an airplane which is flying horizontally at a speed of 240 mph.
a) Write the parametric equations of motion of the bomb.
b) If the airplane is one mile above the ground, how long will it take the bomb to strike the ground?
c) Suppose the airplane flies at 300 mph instead of 240. How long will it take the bomb to strike the ground?
d) Suppose the airplane is 2 mi above the ground and flies at 240 mph. How long will it take the bomb to reach the ground?
e) How far from the point on the ground directly below the point at which the bomb is released does the bomb strike the ground?
4. Suppose a shell is shot from a cannon inclined at an angle of 45° with the ground and the shell is given an initial velocity of 2000 ft/sec.
a) What are the horizontal and vertical velocities of the shell?
b) Write the parametric equations of the motion of the shell.
c) Find the range of the shell.
d) What is the maximum height above the ground attained by the shell during its flight?
GALILEI, GALILEO: Dialogues Concerning Two New Sciences, pp. 234 through 282, Dover Publications, Inc., New York, 1952.
HOLTON, GERALD and DUANE H. D. ROLLER: Foundations of Modern Physical Science, Chap. 3, Addison-Wesley Publishing Co., Inc., Reading, Mass., 1958.
KLINE, MORRIS: Mathematics and the Physical World, Chap. 14, T. Y. Crowell Co., New York, 1959. Also in paperback, Doubleday and Co., New York, 1963.
* The terms speed and velocity are often used interchangeably. However, the word velocity implies that direction as well as magnitude of the speed are under discussion.
* The reader can review this point in Chapter 7, where it was first mad,