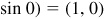CHAPTER 2
Trigonometric Functions of a General Angle
2.1 Coordinates on a Line
A directed line is a line on which one direction is taken as positive and the other as negative. The positive direction is indicated by an arrowhead.
A number scale is established on a directed line by choosing a point O (see Fig. 2.1) called the origin and a unit of measure 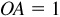 . On this scale, B is 4 units to the right of O (that is, in the positive direction from O) and C is 2 units to the left of O (that is, in the negative direction from O). The directed distance
. On this scale, B is 4 units to the right of O (that is, in the positive direction from O) and C is 2 units to the left of O (that is, in the negative direction from O). The directed distance 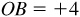 and the directed distance
and the directed distance 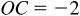 . It is important to note that since the line is directed,
. It is important to note that since the line is directed, 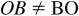 and
and  The directed distance BO = –4, being measured contrary to the indicated positive direction, and the directed distance
The directed distance BO = –4, being measured contrary to the indicated positive direction, and the directed distance 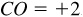 . Then
. Then 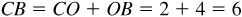 and
and 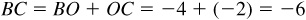 .
.

Fig. 2.1
2.2 Coordinates in a Plane
A rectangular coordinate system in a plane consists of two number scales (called axes), one horizontal and the other vertical, whose point of intersection (origin) is the origin on each scale. It is customary to choose the positive direction on each axis as indicated in the figure, that is, positive to the right on the horizontal axis or x axis and positive upward on the vertical or y axis. For convenience, we will assume the same unit of measure on each axis.
By means of such a system the position of any point P in the plane is given by its (directed) distances, called coordinates, from the axes. The x-coordinate of a point P (see Fig. 2.2) is the directed distance 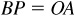 and the y-coordinate is the directed distance
and the y-coordinate is the directed distance 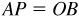 . A point P with x-coordinate x and y- coordinate y will be denoted by P (x, y).
. A point P with x-coordinate x and y- coordinate y will be denoted by P (x, y).
Fig. 2.2
The axes divide the plane into four parts, called quadrants, which are numbered (in a counterclockwise direction) I, II, III, and IV. The numbered quadrants, together with the signs of the coordinates of a point in each, are shown in Fig. 2.3.
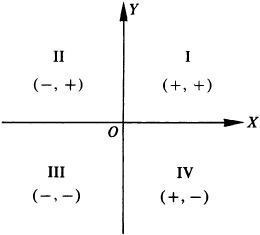
Fig. 2.3
The undirected distance r of any point P(x, y) from the origin, called the distance of P or the radius vector of P, is given by
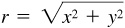
Thus, with each point in the plane, we associate three numbers: x, y, and r.
(See Probs. 2.1 to 2.3.)
2.3 Angles in Standard Position
With respect to a rectangular coordinate system, an angle is said to be in standard position when its vertex is at the origin and its initial side coincides with the positive x axis.
An angle is said to be a first-quadrant angle or to be in the first quadrant if, when in standard position, its terminal side falls in that quadrant. Similar definitions hold for the other quadrants. For example, the angles 30°, 59°, and –330° are first-quadrant angles [see Fig. 2.4(a)]; 119° is a second-quadrant angle; –119° is a third-quadrant angle; and –10° and 710° are fourth-quadrant angles [see Fig. 2.4(b)].
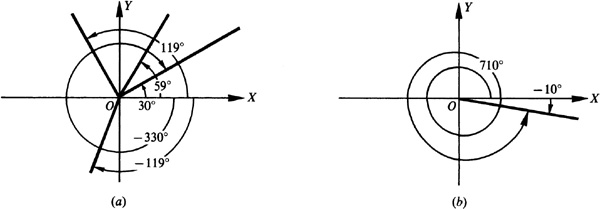
Fig. 2.4
Two angles which, when placed in standard position, have coincident terminal sides are called coterminal angles. For example, 30° and –330°, and –10° and 710° are pairs of coterminal angles. There is an unlimited number of angles coterminal with a given angle. Coterminal angles for any given angle can be found by adding integer multiples of 360° to the degree measure of the given angle.
(See Probs. 2.4 to 2.5.)
The angles 0°, 90°, 180°, and 270° and all the angles coterminal with them are called quadrantal angles.
2.4 Trigonometric Functions of a General Angle
Let θ be an angle (not quadrantal) in standard position and let P(x, y) be any point, distinct from the origin, on the terminal side of the angle. The six trigonometric functions of θ are defined, in terms of the x-coordinate, y-coordinate, and r (the distance of P from the origin), as follows:
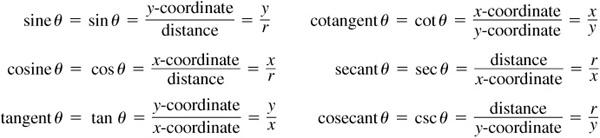
As an immediate consequence of these definitions, we have the so-called reciprocal relations:
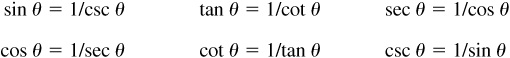
Because of these reciprocal relationships, one function in each pair of reciprocal trigonometric functions has been used more frequently than the other. The more frequently used trigonometric functions are sine, cosine, and tangent.
It is evident from the diagrams in Fig. 2.5 that the values of the trigonometric functions of θ change as θ changes. In Prob. 2.6 it is shown that the values of the functions of a given angle θ are independent of the choice of the point P on its terminal side.

Fig. 2.5
2.5 Quadrant Signs of the Functions
Since r is always positive, the signs of the functions in the various quadrants depend on the signs of x and y. To determine these signs, one may visualize the angle in standard position or use some device as shown in Fig. 2.6 in which only the functions having positive signs are listed.
(See Prob. 2.7.)

Fig. 2.6
When an angle is given, its trigonometric functions are uniquely determined. When, however, the value of one function of an angle is given, the angle is not uniquely determined. For example, if sin 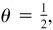 then
then
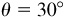 , 150°, 390°, 510°, …. In general, two possible positions of the terminal side are found; for example, the terminal sides of 30° and 150° in the above illustration. The exceptions to this rule occur when the angle is quadrantal.
, 150°, 390°, 510°, …. In general, two possible positions of the terminal side are found; for example, the terminal sides of 30° and 150° in the above illustration. The exceptions to this rule occur when the angle is quadrantal.
(See Probs. 2.8 to 2.16.)
2.6 Trigonometric Functions of Quadrantal Angles
For a quadrantal angle, the terminal side coincides with one of the axes. A point P, distinct from the origin, on the terminal side has either 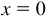 and
and 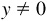 , or
, or 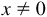 and
and 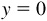 . In either case, two of the six functions will not be defined. For example, the terminal side of the angle 0 coincides with the positive x axis and the y-coordinate of P is 0. Since the x-coordinate occurs in the denominator of the ratio defining the cotangent and cosecant, these functions are not defined. In this book, undefined will be used instead of a numerical value in such cases, but some authors indicate this by writing cot
. In either case, two of the six functions will not be defined. For example, the terminal side of the angle 0 coincides with the positive x axis and the y-coordinate of P is 0. Since the x-coordinate occurs in the denominator of the ratio defining the cotangent and cosecant, these functions are not defined. In this book, undefined will be used instead of a numerical value in such cases, but some authors indicate this by writing cot 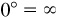 , and others write cot
, and others write cot 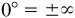 . The following results are obtained in Prob. 2.17.
. The following results are obtained in Prob. 2.17.

2.7 Undefined Trigonometric Functions
It has been noted that cot 0° and csc 0° are not defined since division by zero is never allowed, but the values of these functions for angles near 0° are of interest. In Fig. 2.7(a), take θ to be a small positive angle in standard position and on its terminal side take P(x, y) to be at a distance r from O. Now x is slightly less than r, and y is positive and very small; then cot 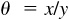 and csc
and csc 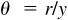 are positive and very large. Next let θ decrease toward 0° with P remaining at a distance r from O. Now x increases but is always less than r, while y decreases but remains greater than 0; thus cot θ and csc θ become larger and larger. (To see this, take r = 1 and compute csc θ when
are positive and very large. Next let θ decrease toward 0° with P remaining at a distance r from O. Now x increases but is always less than r, while y decreases but remains greater than 0; thus cot θ and csc θ become larger and larger. (To see this, take r = 1 and compute csc θ when 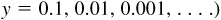 This state of affairs is indicated by “If θ approaches 0°+, then cot θ approaches + ∞,” which is what is meant when writing cot
This state of affairs is indicated by “If θ approaches 0°+, then cot θ approaches + ∞,” which is what is meant when writing cot  .
.

Fig. 2.7
Next suppose, as in Fig. 2.7(b), that θ is a negative angle close to 0°, and take P(x, y) on its terminal side at a distance r from O. Then x is positive and slightly smaller than r, while y is negative and has a small absolute value. Both cot θ and csc θ are negative with large absolute values. Next let θ increase toward 0° with P remaining at a distance r from O. Now x increases but is always less than r, while y remains negative with an absolute value decreasing toward 0°; thus cot θ and csc θ remain negative, but have absolute values that get larger and larger. This situation is indicated by “If θ approaches 0°–, then cot θ approaches –∞,” which is what is meant when writing cot 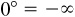 .
.
In each of these cases, cot 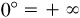 and cot
and cot 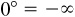 , the use of the = sign does not have the standard meaning of “equals” and should be used with caution, since cot 0° is undefined and ∞ is not a number. The notation is used as a short way to describe a special situation for trigonometric functions.
, the use of the = sign does not have the standard meaning of “equals” and should be used with caution, since cot 0° is undefined and ∞ is not a number. The notation is used as a short way to describe a special situation for trigonometric functions.
The behavior of other trigonometric functions that become undefined can be explored in a similar manner. The following chart summarizes the behavior of each trigonometric function that becomes undefined for angles from 0° up to 360°.

(NOTE: The + means the value is greater than the number stated; 180°+ means values greater than 180°. The – means the value is less than the number stated; 90°– means values less than 90°.)
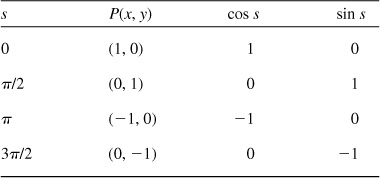
2.8 Coordinates of Points on a Unit Circle
Let s be the length of an arc on a unit circle 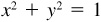 ; each s is paired with an angle θ in radians (see Sec. 1.4). Using the point (1, 0) as the initial point of the arc and P(x, y) as the terminal point of the arc, as in Fig. 2.8, we can determine the coordinates of P in terms of the real number s.
; each s is paired with an angle θ in radians (see Sec. 1.4). Using the point (1, 0) as the initial point of the arc and P(x, y) as the terminal point of the arc, as in Fig. 2.8, we can determine the coordinates of P in terms of the real number s.
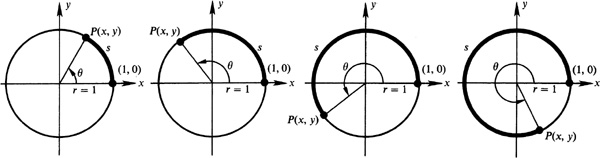
Fig. 2.8
For any angle θ, 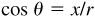 and
and 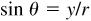 . On a unit circle,
. On a unit circle, 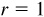 and the arc length
and the arc length 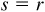
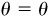 and
and 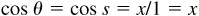 and
and 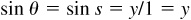 . The point P associated with the arc length s is determined by
. The point P associated with the arc length s is determined by 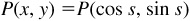 . The wrapping function W maps real numbers s onto points P of the unit circle denoted by
. The wrapping function W maps real numbers s onto points P of the unit circle denoted by

Some arc lengths are paired with points on the unit circle whose coordinates are easily determined. If 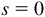 , the point is (1, 0); for
, the point is (1, 0); for 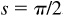 , one-fourth the way around the unit circle, the point is (0, 1);
, one-fourth the way around the unit circle, the point is (0, 1); 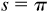 is paired with (–1, 0); and
is paired with (–1, 0); and 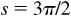 is paired with (0, –1). (See Sec. 1.5.) These values are summarized in the following chart.
is paired with (0, –1). (See Sec. 1.5.) These values are summarized in the following chart.
2.9 Circular Functions
Each arc length s determines a single ordered pair (cos s, sin s) on a unit circle. Both s and cos s are real numbers and define a function (s, cos s) which is called the circular function cosine. Likewise, s and sin s are real numbers and define a function (s, sin s) which is called the circular function sine. These functions are called circular functions since both cos s and sin s are coordinates on a unit circle. The circular functions sin s and cos s are similar to the trigonometric functions sin θ and cos θ in all regards, since, as shown in Chap. 1, any angle in degree measure can be converted to radian measure, and this radian-measure angle is paired with an arc s on the unit circle. The important distinction for circular functions is that since (s, cos s) and (s, sin s) are ordered pairs of real numbers, all properties and procedures for functions of real numbers apply to circular functions.
The remaining circular functions are defined in terms of cos s and sin s.
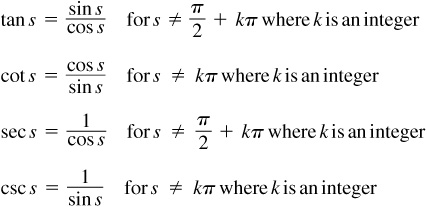
It should be noted that the circular functions are defined everywhere that the trigonometric functions are defined, and the values left out of the domains correspond to values where the trigonometric functions are undefined.
In any application, there is no need to distinguish between trigonometric functions of angles in radian measure and circular functions of real numbers.
SOLVED PROBLEMS
2.1 Using a rectangular coordinate system, locate the following points and find the value of r for each:
A(1, 2), B (–3, 4), 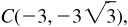 D (4, –5) (see Fig. 2.9).
D (4, –5) (see Fig. 2.9).
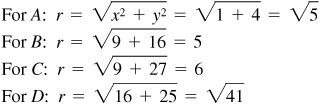
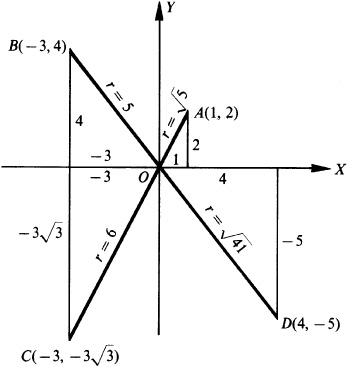
Fig. 2.9
2.2 Determine the missing coordinate of P in each of the following:
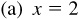 ,
, 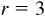 , P in the first quadrant
, P in the first quadrant
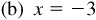 ,
, 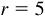 , P in the second quadrant
, P in the second quadrant
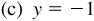 ,
,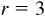 , P in the third quadrant
, P in the third quadrant
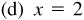 ,
, 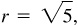 P in the fourth quadrant
P in the fourth quadrant
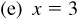 ,
, 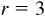
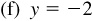 ,
, 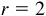
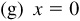 ,
, 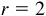 , y positive
, y positive
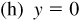 ,
, 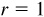 , x negative
, x negative
(a) Using the relation 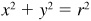 , we have
, we have 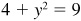 ; then
; then 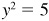 and
and 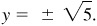
Since P is in the first quadrant, the missing coordinate is 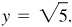
(b) Here 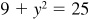 ,
, 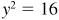 , and
, and 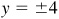 .
.
Since P is in the second quadrant, the missing coordinate is 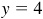 .
.
(c) We have 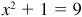 ,
, 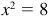 , and
, and 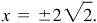
Since P is in the third quadrant, the missing coordinate is 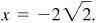
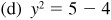 and
and 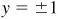 . Since P is in the fourth quadrant, the missing coordinate is
. Since P is in the fourth quadrant, the missing coordinate is 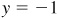 .
.
(e) Here 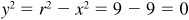 and the missing coordinate is y = 0.
and the missing coordinate is y = 0.
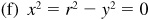 and x = 0.
and x = 0.
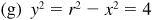 and
and 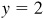 is the missing coordinate.
is the missing coordinate.
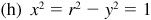 and
and 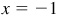 is the missing coordinate.
is the missing coordinate.
2.3 In what quadrants may P(x, y) be located if
(a) x is positive and 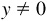 ?
?
(b) y is negative and 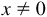 ?
?
(c) y/r is positive?
(d) r/x is negative?
(e) y/x is positive?
(a) In the first quadrant when y is positive and in the fourth quadrant when y is negative
(b) In the fourth quadrant when x is positive and in the third quadrant when x is negative
(c) In the first and second quadrants
(d) In the second and third quadrants
(e) In the first quadrant when both x and y are positive and in the third quadrant when both x and y are negative
2.4 (a) Construct the following angles in standard position and determine those which are coterminal: 125°, 210°, –150°, 385°, 930°, –370°, –955°, –870°
(b) Give five other angles coterminal with 125°.
(a) The angles in standard position are shown in Fig. 2.10. The angles 125° and –955° are coterminal since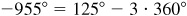 (or since
(or since 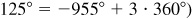 . The angles 210°, –150°, 930°, and –870° are coterminal since
. The angles 210°, –150°, 930°, and –870° are coterminal since 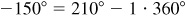 ,
, 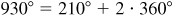 . and
. and 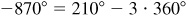 . From Fig. 2.10, it can be seen that there is only one first-quadrant angle, 385°, and only one fourth-quadrant angle, –370°, so these angles cannot be coterminal with any of the other angles.
. From Fig. 2.10, it can be seen that there is only one first-quadrant angle, 385°, and only one fourth-quadrant angle, –370°, so these angles cannot be coterminal with any of the other angles.
(b) Any angle coterminal with 125° can be written in the form 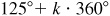 where k is an integer. Therefore,
where k is an integer. Therefore, 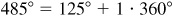 ,
, 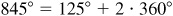 ,
, 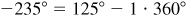 ,
, 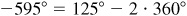 , and
, and  are angles coterminal with 125°.
are angles coterminal with 125°.
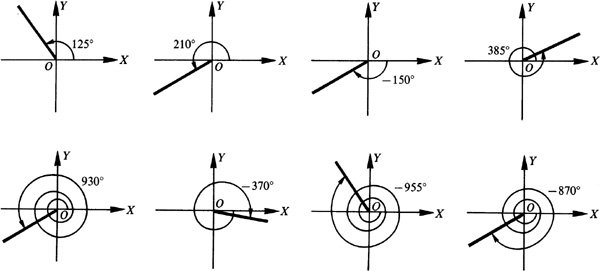
Fig. 2.10
2.5 State a positive angle and a negative angle coterminal with each radian-measure angle:
(a) π/6,
(b) 5π/4,
(c) 0,
(d) –17π/6,
(e) –10π/3,
(f) 7π/2
k. 360° = k (2π radians) = 2kπ where k is an integer
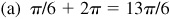 ;
; 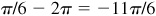
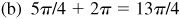 ;
; 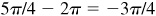
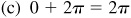 ;
; 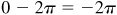
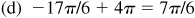 ;
; 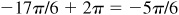
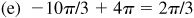 ;
; 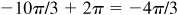
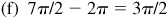 ;
; 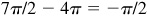
2.6 Show that the values of the trigonometric functions of an angle θ do not depend on the choice of the point P selected on the terminal side of the angle.
On the terminal side of each of the angles of Fig. 2.11, let P and P′ have coordinates as indicated and denote the distances OP and OP′ by r and r′, respectively. Drop the perpendiculars AP and A′ P′ to the x axis. In each of the diagrams in Fig. 2.11, the triangles OAP and OA′ P′, having sides a, b, r, and a′, b′, r′, respectively, are similar; thus, using Fig. 2.11(a),
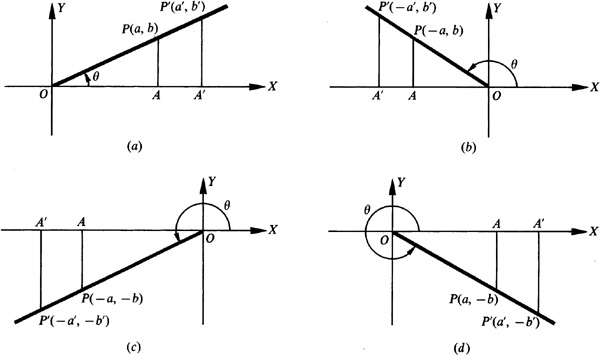
Fig. 2.11

Since the ratios are the trigonometric ratios for the first-quadrant angle, the values of the functions of any first-quadrant angle are independent of the choice of P.
From (1) and Fig. 2.11(b) it follows that
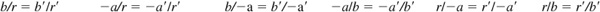
Since these are the trigonometric ratios for the second-quadrant angle, the values of the functions of any second-quadrant angle are independent of the choice of P.
From (1) and Fig. 2.11 (c), it follows that
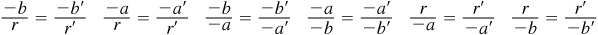
Since the ratios are the trigonometric ratios for the third-quadrant angle, the values of the functions of any third-quadrant angle are independent of the choice of P.
From (1) and Fig. 2.11 (d), it follows that
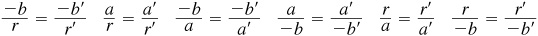
Since the ratios are the trigonometric ratios for the fourth-quadrant angle, the values of the functions of any fourth-quadrant angle are independent of the choice of P.
2.7 Determine the signs of the functions sine, cosine, and tangent in each of the quadrants.
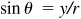 . Since y is positive in quadrants I and II and negative in quadrants III and IV and r is always positive, sin is positive in quadrants I and II and negative in quadrants III and IV.
. Since y is positive in quadrants I and II and negative in quadrants III and IV and r is always positive, sin is positive in quadrants I and II and negative in quadrants III and IV.
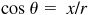 . Since x is positive in quadrants I and IV and negative in quadrants II and III, cos θ is positive in quadrants I and IV and negative in quadrants II and III.
. Since x is positive in quadrants I and IV and negative in quadrants II and III, cos θ is positive in quadrants I and IV and negative in quadrants II and III.
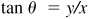 . Since x and y have the same signs in quadrants I and III and opposite signs in quadrants II and IV, tan θ is positive in quadrants I and III and negative in quadrants II and IV.
. Since x and y have the same signs in quadrants I and III and opposite signs in quadrants II and IV, tan θ is positive in quadrants I and III and negative in quadrants II and IV.
(NOTE: The reciprocal of a trigonometric function has the same sign in each quadrant as the function.)
2.8 Determine the values of the trigonometric functions of angle θ (smallest positive angle in standard position) if P is a point on the terminal side of θ and the coordinates of P are
(a) P (3, 4),
(b) P (–3, 4),
(c) P (–1, –3)
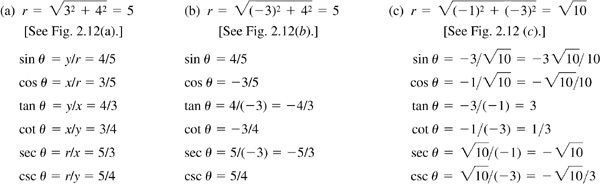
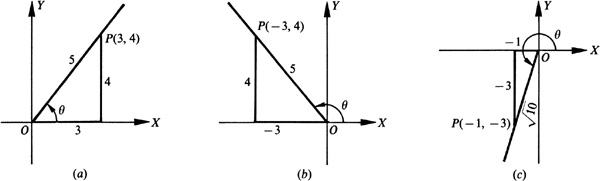
Fig. 2.12
Note the reciprocal relationships. For example, in (b)
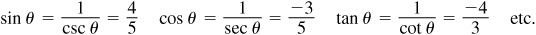
Note in (c) the rationalizing of the denominators:
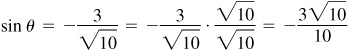
and
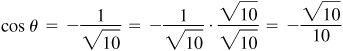
Whenever the denominator of a fraction is an irrational number, an equivalent fraction with a rational denominator will be given as well.
2.9 In what quadrant will θ terminate, if
(a) sin θ and cos θ are both negative?
(b) sin θ and tan θ are both positive?
(c) sin θ is positive and sec θ is negative?
(d) sec θ is negative and tan θ is negative?
(a) Since 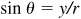 and
and 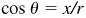 , both x and y are negative. (Recall that r is always positive.) Thus, θ is a third-quadrant angle.
, both x and y are negative. (Recall that r is always positive.) Thus, θ is a third-quadrant angle.
(b) Since sin θ is positive, y is positive; since 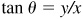 is positive, x is also positive. Thus, θ is a first-quadrant angle.
is positive, x is also positive. Thus, θ is a first-quadrant angle.
(c) Since sin θ is positive, y is positive; since sec θ is negative, x is negative. Thus, θ is a second-quadrant angle.
(d) Since sec θ is negative, x is negative; since tan θ is negative, y is then positive. Thus, θ is a second-quadrant angle.
2.10 In what quadrants may θ terminate if
(a) sin θ is positive?
(b) cos θ is negative?
(c) tan θ is negative?
(d) sec θ is positive?
(a) Since sin θ is positive, y is positive. Then x may be positive or negative, and θ is a first- or second-quadrant angle.
(b) Since cos θ is negative, x is negative. Then y may be positive or negative, and θ is a second- or third-quadrant angle.
(c) Since tan θ is negative, either y is positive and x is negative, or y is negative and x is positive. Thus, θ may be a second- or fourth-quadrant angle.
(d) Since sec θ is positive, x is positive. Thus, θ may be a first- or fourth-quadrant angle.
2.11 Find the values of cos θ and tan θ, given 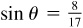 and θ in quadrant I.
and θ in quadrant I.
Let P be a point on the terminal line of θ. Since cos 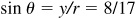 , we take
, we take 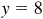 and
and 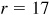 . Since θ is in quadrant I, x is positive; thus
. Since θ is in quadrant I, x is positive; thus
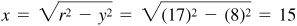
To draw the figure, locate the point P (15, 8), join it to the origin, and indicate the angle θ. (See Fig. 2.13.)
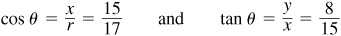
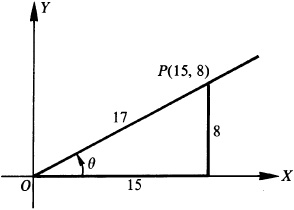
Fig. 2.13
The choice of 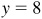 and
and 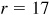 is one of convenience. Note that
is one of convenience. Note that 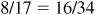 and we might have taken
and we might have taken 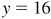 ,
, 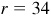 . Then
. Then 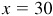 , cos θ = 30/34 = 15/17 and
, cos θ = 30/34 = 15/17 and 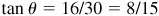 .
.
(See Prob. 2.6.)
2.12 Find the values of sin θ and tan θ, given 
Since cos θ is positive, θ is in quadrant I or IV.
Since 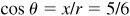 , we take
, we take 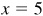 and
and 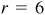 ;
; 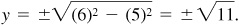
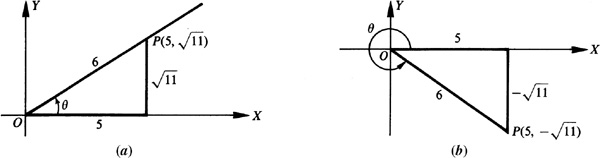
Fig. 2.14
(a) For θ in quadrant I [Fig. 2.14(a)] we have 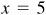 ,
,  and
and  ; then
; then
(b) For θ in quadrant IV [Fig. 2.14(b)] we have 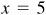 ,
, 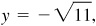 and
and 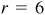 ; then
; then
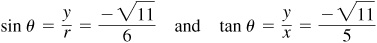
2.13 Find the values of sin θ and cos θ, given 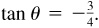
Since tan θ = y/x is negative θ, is in quadrant II (take 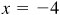 and
and 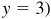 or in quadrant IV (take
or in quadrant IV (take 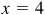 and
and 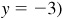 . In either case
. In either case 
(a) For θ in quadrant II [Fig. 2.15(a)], 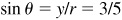 and
and 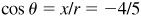 .
.
(b) For θ in quadrant IV [Fig. 2.15(b)], 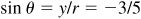 and cos
and cos 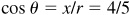 .
.
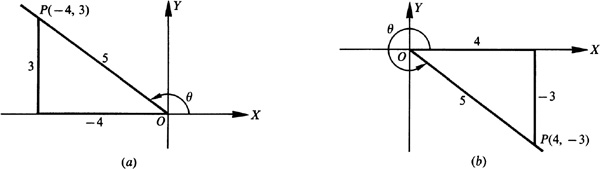
Fig. 2.15
2.14 Find sin θ, given cos 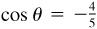 and that tan θ is positive.
and that tan θ is positive.
Since 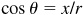 is negative, x is negative. Since also
is negative, x is negative. Since also 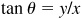 is positive, y must be negative. Then θ is in quadrant III. (See Fig. 2.16.)
is positive, y must be negative. Then θ is in quadrant III. (See Fig. 2.16.)
Take 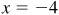 and
and 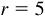 ; then
; then 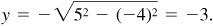 Thus,
Thus, 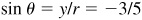 .
.

Fig. 2.16
2.15 Find the values of the remaining functions of θ, given 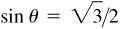 and
and 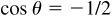 .
.
Since 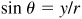 is positive, y is positive. Since
is positive, y is positive. Since 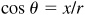 is negative, x is negative. Thus θ, is in quadrant II. (See Fig. 2.17.)
is negative, x is negative. Thus θ, is in quadrant II. (See Fig. 2.17.)
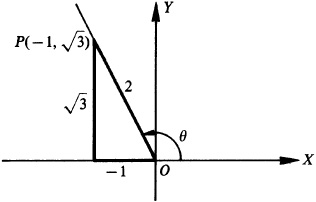
Fig. 2.17
Taking 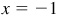 ,
, 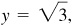 and
and 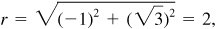 we have
we have
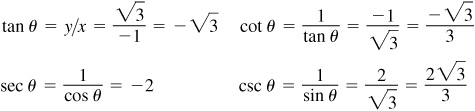
2.16 Determine the values of cos θ and tan θ if 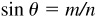 , a negative fraction.
, a negative fraction.
Since sin θ is negative, θ is in quadrant III or IV.
(a) In quadrant III: Take 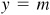 ,
,  ,
, 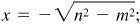 then
then
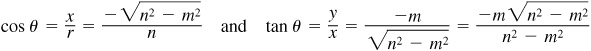
(b) In quadrant IV: Take 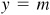 ,
,  ,
, 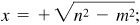 then
then
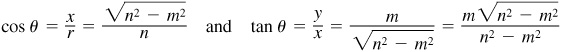
2.17 Determine the values of the trigonometric functions of
(a) 0°,
(b) 90°,
(c) 180°,
(d) 270°
Let P be any point except the origin on the terminal side of θ. When  ,
,  and y = 0; when
and y = 0; when  , x = 0 and
, x = 0 and 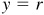 ; when
; when 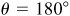 ,
, 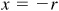 and y = 0; and when
and y = 0; and when 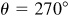 , x = 0 and
, x = 0 and 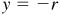 .
.


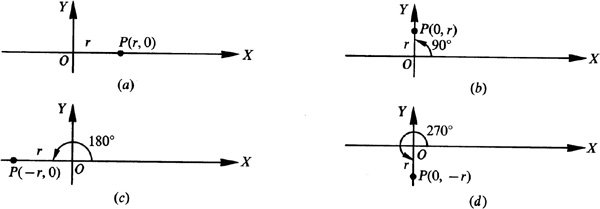
Fig. 2.18
2.18 Evaluate:
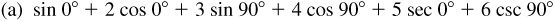
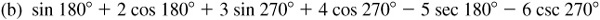
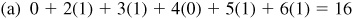
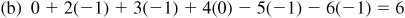
2.19 Using a protractor, construct an angle of 20° in standard position. With O as center, describe an arc of radius 10 units intersecting the terminal side at point P. From P drop a perpendicular to the x axis, meeting it in A. By actual measurement, 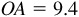 ,
, 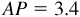 , and P has coordinates (9.4, 3.4). Then find the trigonometric functions of 20° (see Fig. 2.19).
, and P has coordinates (9.4, 3.4). Then find the trigonometric functions of 20° (see Fig. 2.19).
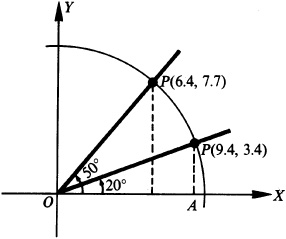
Fig. 2.19

2.20 Obtain the trigonometric functions of 50° as in Prob. 2.19. Refer to Fig. 2.19.
By actual measurement, P, on the terminal side at a distance 10 units from the origin, has coordinates (6.4, 7.7). Then

SUPPLEMENTARY PROBLEMS
2.21 State the quadrant in which each angle terminates and the signs of the sine, cosine, and tangent of each angle.
(a) 125°,
(b) 75°,
(c) 320°,
(d) 212°,
(e) 460°,
(f) 750°,
(g) –250°,
(h) –1000°
Ans.
(a) II; +, –, –;
(b) I; +, +, +;
(c) IV; –, +, –;
(d) III; –, –, +;
(e) II; +, –, –;
(f) I; +, +, +;
(g) II; +, –, –;
(h) I; +, +, +
2.22 In what quadrant will θ terminate if
(a) sin θ and cos θ are both positive?
(b) cos θ and tan θ are both positive?
(c) sin θ and sec θ are both negative?
(d) cos θ and cot θ are both negative?
(e) tan θ is positive and sec θ is negative?
(f) tan θ is negative and sec θ is positive?
(g) sin θ is positive and cos θ is negative?
(h) sec θ is positive and csc θ is negative?
Ans.
(a) I,
(b) I,
(c) III,
(d) II,
(e) III,
(f) IV,
(g) II,
(h) IV
2.23 Denote by θ the smallest positive angle whose terminal side passes through the given point, and find the trigonometric functions of θ:
(a) P (–5, 12),
(b) P (7, –24),
(c) P (2, 3),
(d) P (–3, –5)
Ans. Answers listed in the order sin θ, cos θ, tan θ, cot θ, sec θ, csc θ
(a) 12/13, –5/13, –12/5, –5/12, –13/5, 13/12
(b) –24/25, 7/25, –24/7, –7/24, 25/7, –25/24
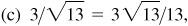
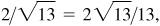 3/2, 2/3,
3/2, 2/3, 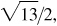
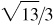
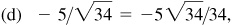
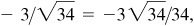 5/3, 3/5
5/3, 3/5 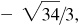
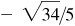
2.24 Find the values of the trigonometric functions of θ, given:
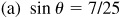
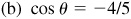
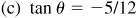
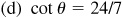
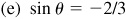
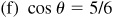
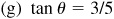
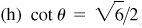
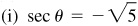
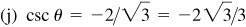
Ans. Answers listed in the order sin θ, cos θ, tan θ, cot θ, sec θ, csc θ
(a) I: 7/25, 24/25, 7/24, 24/7, 25/24, 25/7
II: 7/25, –24/25, –7/24, –24/7, –25/24, 25/7
(b) II: 3/5, –4/5, –3/4, –4/3, –5/4, 5/3
III: –3/5, –4/5, 3/4, 4/3, –5/4, –5/3
(c) II: 5/13, –12/13, –5/12, –12/5, –13/12, 13/5
IV: –5/13, 12/13, –5/12, –12/5, 13/12, –13/5
(d) I: 7/25, 24/25, 7/24, 24/7, 25/24, 25/7
III: –7/25, –24/25, 7/24, 24/7, –25/24, –25/7
(e) III: –2/3, 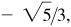
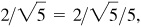
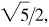
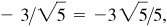 –3/2
–3/2
IV: 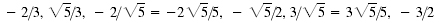
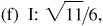 5/6,
5/6, 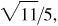
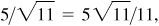 6/5,
6/5, 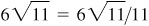
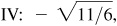 5/6,
5/6, 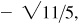
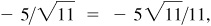 6/5,
6/5, 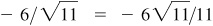
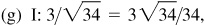
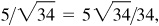 3/5, 5/3,
3/5, 5/3, 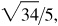
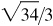
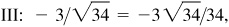
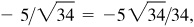 3/5, 5/3,
3/5, 5/3, 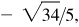
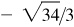
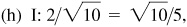
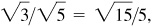
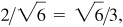
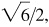
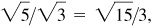
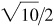
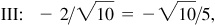
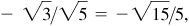
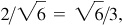
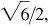
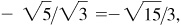
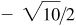
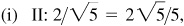
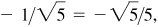 –2, –1/2,
–2, –1/2, 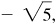
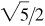
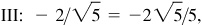
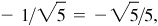 2, 1/2,
2, 1/2, 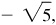
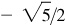
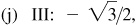 –1/2,
–1/2, 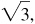
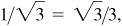 –2,
–2, 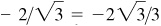
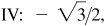 1/2,
1/2, 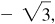
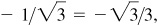 2,
2, 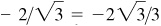
2.25 Evaluate each of the following:
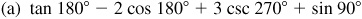
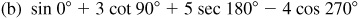
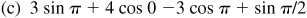
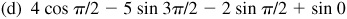
Ans.
(a) 0,
(b) –5,
(c) 6,
(d) 3
2.26 State the quadrant in which each angle in radian measure terminates:
(a) π/4,
(b) 5π/6,
(c) 11π/3,
(d) –3π/4,
(e) 8π/3,
(f) 17π/6,
(g) 23π/6
Ans.
(a) I,
(b) II,
(c) IV,
(d) III,
(e) II,
(f) II,
(g) IV
2.27 State the point on the unit circle that corresponds to each real number.
(a) 17π,
(b) –13π/2,
(c) 7π/2,
(d) 28π
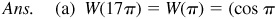
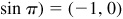
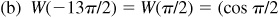 ,
, 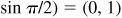
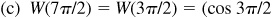 ,
, 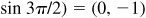
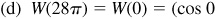 ,
, 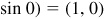
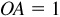 . On this scale, B is 4 units to the right of O (that is, in the positive direction from O) and C is 2 units to the left of O (that is, in the negative direction from O). The directed distance
. On this scale, B is 4 units to the right of O (that is, in the positive direction from O) and C is 2 units to the left of O (that is, in the negative direction from O). The directed distance 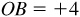 and the directed distance
and the directed distance 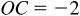 . It is important to note that since the line is directed,
. It is important to note that since the line is directed, 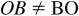 and
and  The directed distance BO = –4, being measured contrary to the indicated positive direction, and the directed distance
The directed distance BO = –4, being measured contrary to the indicated positive direction, and the directed distance 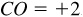 . Then
. Then 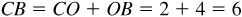 and
and 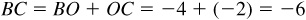 .
.
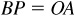 and the y-coordinate is the directed distance
and the y-coordinate is the directed distance 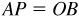 . A point P with x-coordinate x and y- coordinate y will be denoted by P (x, y).
. A point P with x-coordinate x and y- coordinate y will be denoted by P (x, y).

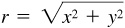

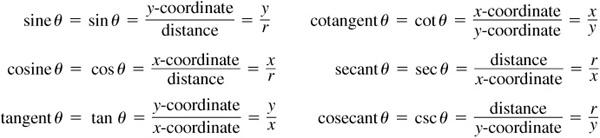
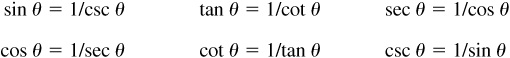


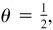 then
then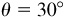 , 150°, 390°, 510°, …. In general, two possible positions of the terminal side are found; for example, the terminal sides of 30° and 150° in the above illustration. The exceptions to this rule occur when the angle is quadrantal.
, 150°, 390°, 510°, …. In general, two possible positions of the terminal side are found; for example, the terminal sides of 30° and 150° in the above illustration. The exceptions to this rule occur when the angle is quadrantal. and
and  , or
, or 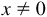 and
and 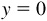 . In either case, two of the six functions will not be defined. For example, the terminal side of the angle 0 coincides with the positive x axis and the y-coordinate of P is 0. Since the x-coordinate occurs in the denominator of the ratio defining the cotangent and cosecant, these functions are not defined. In this book, undefined will be used instead of a numerical value in such cases, but some authors indicate this by writing cot
. In either case, two of the six functions will not be defined. For example, the terminal side of the angle 0 coincides with the positive x axis and the y-coordinate of P is 0. Since the x-coordinate occurs in the denominator of the ratio defining the cotangent and cosecant, these functions are not defined. In this book, undefined will be used instead of a numerical value in such cases, but some authors indicate this by writing cot 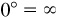 , and others write cot
, and others write cot 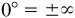 . The following results are obtained in Prob.
. The following results are obtained in Prob. 
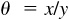 and csc
and csc 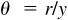 are positive and very large. Next let θ decrease toward 0° with P remaining at a distance r from O. Now x increases but is always less than r, while y decreases but remains greater than 0; thus cot θ and csc θ become larger and larger. (To see this, take r = 1 and compute csc θ when
are positive and very large. Next let θ decrease toward 0° with P remaining at a distance r from O. Now x increases but is always less than r, while y decreases but remains greater than 0; thus cot θ and csc θ become larger and larger. (To see this, take r = 1 and compute csc θ when 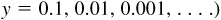 This state of affairs is indicated by “If θ approaches 0°+, then cot θ approaches + ∞,” which is what is meant when writing cot
This state of affairs is indicated by “If θ approaches 0°+, then cot θ approaches + ∞,” which is what is meant when writing cot 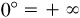 .
.
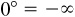 .
.
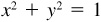 ; each s is paired with an angle θ in radians (see
; each s is paired with an angle θ in radians (see 
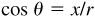 and
and 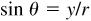 . On a unit circle,
. On a unit circle, 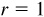 and the arc length
and the arc length 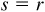
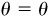 and
and 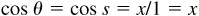 and
and 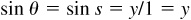 . The point P associated with the arc length s is determined by
. The point P associated with the arc length s is determined by 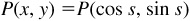 . The wrapping function W maps real numbers s onto points P of the unit circle denoted by
. The wrapping function W maps real numbers s onto points P of the unit circle denoted by
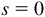 , the point is (1, 0); for
, the point is (1, 0); for 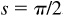 , one-fourth the way around the unit circle, the point is (0, 1);
, one-fourth the way around the unit circle, the point is (0, 1); 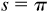 is paired with (–1, 0); and
is paired with (–1, 0); and 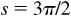 is paired with (0, –1). (See
is paired with (0, –1). (See 
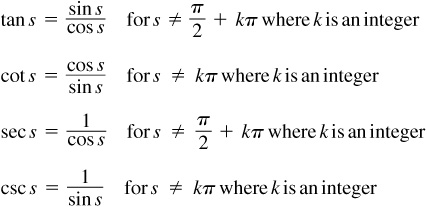
 D (4, –5) (see
D (4, –5) (see 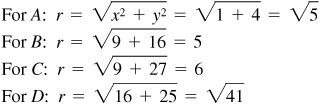

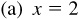 ,
, 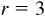 , P in the first quadrant
, P in the first quadrant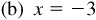 ,
, 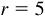 , P in the second quadrant
, P in the second quadrant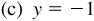 ,
,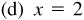 ,
, 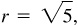 P in the fourth quadrant
P in the fourth quadrant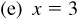 ,
, 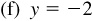 ,
, 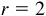
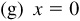 ,
, 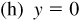 ,
, 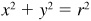 , we have
, we have 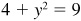 ; then
; then 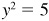 and
and 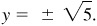
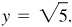
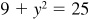 ,
, 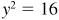 , and
, and 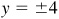 .
.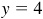 .
.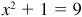 ,
, 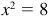 , and
, and 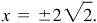
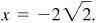
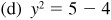 and
and 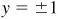 . Since P is in the fourth quadrant, the missing coordinate is
. Since P is in the fourth quadrant, the missing coordinate is 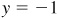 .
.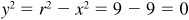 and the missing coordinate is y = 0.
and the missing coordinate is y = 0.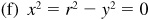 and x = 0.
and x = 0.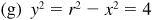 and
and 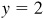 is the missing coordinate.
is the missing coordinate.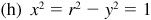 and
and 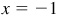 is the missing coordinate.
is the missing coordinate.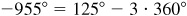 (or since
(or since 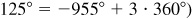 . The angles 210°, –150°, 930°, and –870° are coterminal since
. The angles 210°, –150°, 930°, and –870° are coterminal since 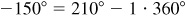 ,
, 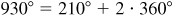 . and
. and 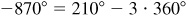 . From
. From 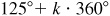 where k is an integer. Therefore,
where k is an integer. Therefore, 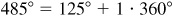 ,
, 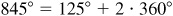 ,
, 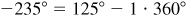 ,
, 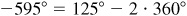 , and
, and 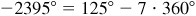 are angles coterminal with 125°.
are angles coterminal with 125°.
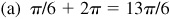 ;
; 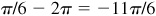
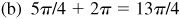 ;
; 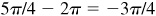
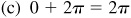 ;
; 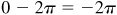
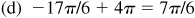 ;
; 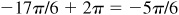
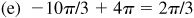 ;
; 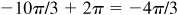
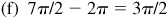 ;
; 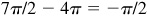


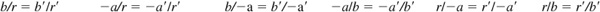
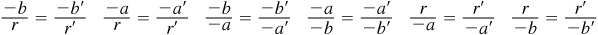
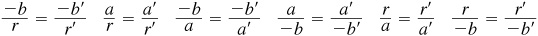
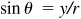 . Since y is positive in quadrants I and II and negative in quadrants III and IV and r is always positive, sin is positive in quadrants I and II and negative in quadrants III and IV.
. Since y is positive in quadrants I and II and negative in quadrants III and IV and r is always positive, sin is positive in quadrants I and II and negative in quadrants III and IV.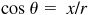 . Since x is positive in quadrants I and IV and negative in quadrants II and III, cos θ is positive in quadrants I and IV and negative in quadrants II and III.
. Since x is positive in quadrants I and IV and negative in quadrants II and III, cos θ is positive in quadrants I and IV and negative in quadrants II and III.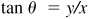 . Since x and y have the same signs in quadrants I and III and opposite signs in quadrants II and IV, tan θ is positive in quadrants I and III and negative in quadrants II and IV.
. Since x and y have the same signs in quadrants I and III and opposite signs in quadrants II and IV, tan θ is positive in quadrants I and III and negative in quadrants II and IV.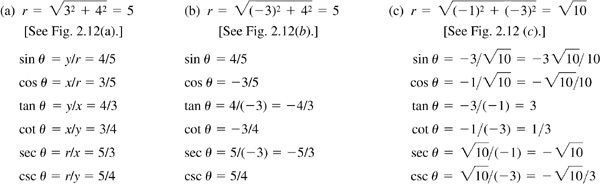

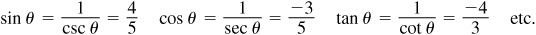
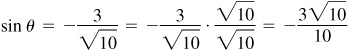
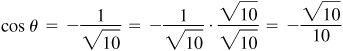
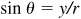 and
and 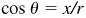 , both x and y are negative. (Recall that r is always positive.) Thus, θ is a third-quadrant angle.
, both x and y are negative. (Recall that r is always positive.) Thus, θ is a third-quadrant angle.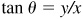 is positive, x is also positive. Thus, θ is a first-quadrant angle.
is positive, x is also positive. Thus, θ is a first-quadrant angle.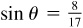 and θ in quadrant I.
and θ in quadrant I.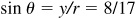 , we take
, we take 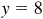 and
and 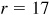 . Since θ is in quadrant I, x is positive; thus
. Since θ is in quadrant I, x is positive; thus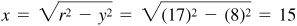
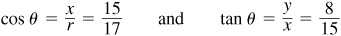

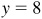 and
and 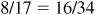 and we might have taken
and we might have taken 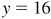 ,
, 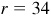 . Then
. Then 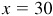 , cos θ = 30/34 = 15/17 and
, cos θ = 30/34 = 15/17 and 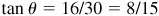 .
.
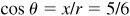 , we take
, we take 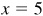 and
and 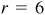 ;
; 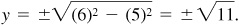

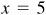 ,
, 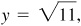 and
and 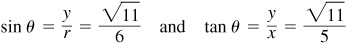
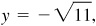 and
and 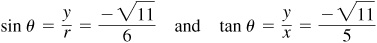
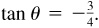
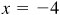 and
and 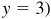 or in quadrant IV (take
or in quadrant IV (take 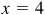 and
and 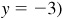 . In either case
. In either case 
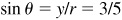 and
and 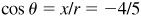 .
.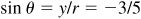 and cos
and cos 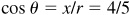 .
.
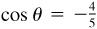 and that tan θ is positive.
and that tan θ is positive.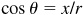 is negative, x is negative. Since also
is negative, x is negative. Since also 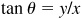 is positive, y must be negative. Then θ is in quadrant III. (See
is positive, y must be negative. Then θ is in quadrant III. (See 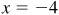 and
and 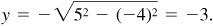 Thus,
Thus, 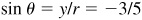 .
.
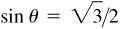 and
and 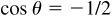 .
.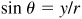 is positive, y is positive. Since
is positive, y is positive. Since 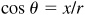 is negative, x is negative. Thus θ, is in quadrant II. (See
is negative, x is negative. Thus θ, is in quadrant II. (See 
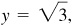 and
and 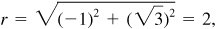 we have
we have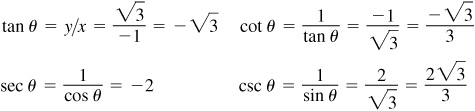
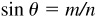 , a negative fraction.
, a negative fraction.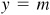 ,
,  ,
, 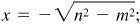 then
then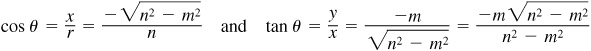
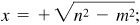 then
then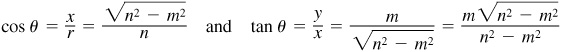
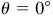 ,
, 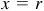 and y = 0; when
and y = 0; when 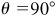 , x = 0 and
, x = 0 and 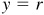 ; when
; when 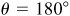 ,
, 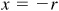 and y = 0; and when
and y = 0; and when 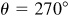 , x = 0 and
, x = 0 and 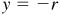 .
.


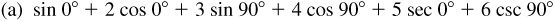
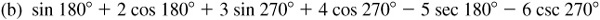
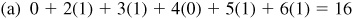
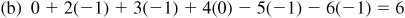
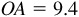 ,
, 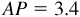 , and P has coordinates (9.4, 3.4). Then find the trigonometric functions of 20° (see
, and P has coordinates (9.4, 3.4). Then find the trigonometric functions of 20° (see 


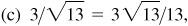
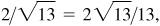 3/2, 2/3,
3/2, 2/3, 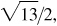
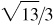
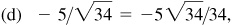
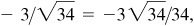 5/3, 3/5
5/3, 3/5 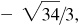
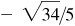
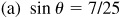
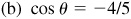
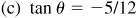
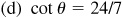
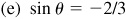
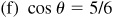
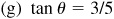
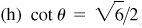
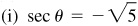
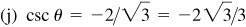
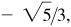
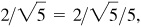
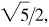
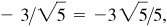 –3/2
–3/2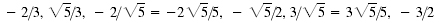
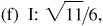 5/6,
5/6, 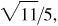
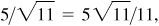 6/5,
6/5, 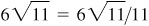
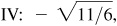 5/6,
5/6, 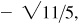
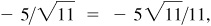 6/5,
6/5, 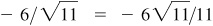
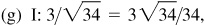
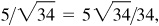 3/5, 5/3,
3/5, 5/3, 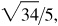
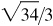
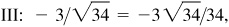
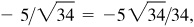 3/5, 5/3,
3/5, 5/3, 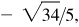
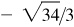
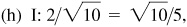
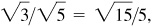
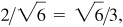
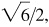
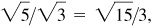
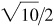
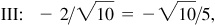
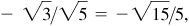
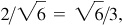
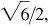
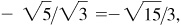
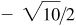
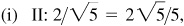
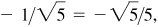 –2, –1/2,
–2, –1/2, 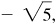
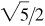
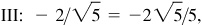
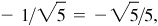 2, 1/2,
2, 1/2, 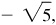
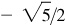
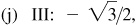 –1/2,
–1/2, 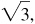
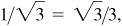 –2,
–2, 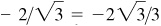
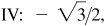 1/2,
1/2, 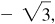
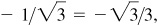 2,
2, 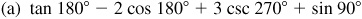
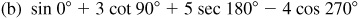
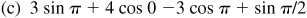
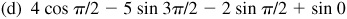
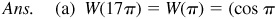
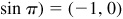
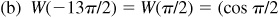 ,
, 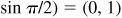
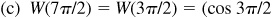 ,
, 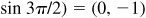
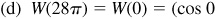 ,
,