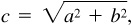 then the trigonometric functions of angle A may be defined in terms of the sides of the right triangle, as follows:
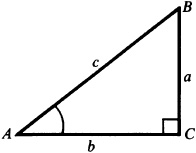
then the trigonometric functions of angle A may be defined in terms of the sides of the right triangle, as follows:In dealing with any right triangle, it will be convenient (see Fig. 3.1) to denote the vertices as A, B, and C with C the vertex of the right angle; to denote the angles of the triangles as A, B, and C, with C = 90°; and to denote the sides opposite the angles; as a, b, and c, respectively. With respect to angle A, a will be called the opposite side and b will be called the adjacent side; with respect to angle B, b will be called the opposite side and a the adjacent side. Side c will always be called the hypotenuse.
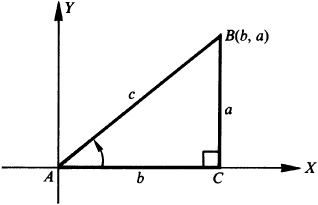
If now the right triangle is placed in a coordinate system (Fig. 3.2) so that angle A is in standard position, the point B on the terminal side of angle A has coordinates (b, a), and the distance 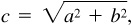 then the trigonometric functions of angle A may be defined in terms of the sides of the right triangle, as follows:
then the trigonometric functions of angle A may be defined in terms of the sides of the right triangle, as follows:
The acute angles A and B of the right triangle ABC are complementary; that is,  . From Fig. 3.1, we have
. From Fig. 3.1, we have

These relations associate the functions in pairs—sine and cosine, tangent and cotangent, secant and cosecant—each function of a pair being called the cofunction of the other.
Thus, any function of an acute angle is equal to the corresponding cofunction of the complementary angle.
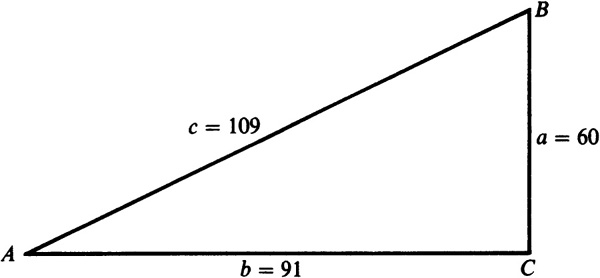
EXAMPLE 3.1 Find the values of the trigonometric functions of the angles of the right triangle ABC in Fig. 3.3.

The special acute angles 30°, 45°, and 60° (see App. 1, Geometry) have trigonometric function values that can be computed exactly. The following results are obtained in Probs. 3.8 and 3.9. For each fraction that had an irrational number denominator, only the equivalent fraction with a rational number denominator is stated in the table.
For many application problems, values of trigonometric functions are needed for angles that are not special angles. These values may be found in tables of trigonometric functions or by using a scientific calculator. Problems 3.10 to 3.15 illustrate a number of simple applications of trigonometric functions. For these problems, a two-decimal-place table is included below.
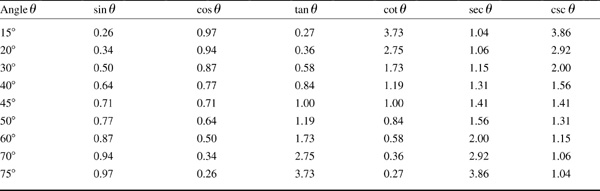
When using a calculator to find values for trigonometric functions, be sure to follow the procedure indicated in the instruction manual for your calculator. In general the procedure is (1) make sure the calculator is in degree mode, (2) enter the number of degrees in the angle, (3) press the key for the trigonometric function wanted, and (4) read the function value from the display.
EXAMPLE 3.2 Find tan 15° using a calculator. With the calculator in degree mode, enter 15 and press the (tan) key. The number 0.267949 will appear on the display; thus  . The number of digits that are displayed depends on the calculator used, but most scientific calculators show at least six digits. In this book if the value displayed on a calculator is not exact, it will be rounded to six digits when stated in a problem or example. Rounding procedures for final results will be introduced as needed.
. The number of digits that are displayed depends on the calculator used, but most scientific calculators show at least six digits. In this book if the value displayed on a calculator is not exact, it will be rounded to six digits when stated in a problem or example. Rounding procedures for final results will be introduced as needed.
Using a calculator to find an acute angle when the value of a trigonometric function is given requires the use of the inverse (inv) key or the second function (2nd) key. The value of the function is entered, the (inv) key is pressed, and then the trigonometric function key is pressed. The degree mode is used to get answers in degree measure.
EXAMPLE 3.3 Find acute angle A when  . With the calculator in degree mode, enter .2651 and press the (inv) key and the (sin) key. The number 15.3729 on the display is the degree measure of acute angle A. Thus to the nearest degree
. With the calculator in degree mode, enter .2651 and press the (inv) key and the (sin) key. The number 15.3729 on the display is the degree measure of acute angle A. Thus to the nearest degree  .
.
When using approximate numbers, the results need to be rounded. In this chapter, we will report angles to the nearest degree and lengths to the nearest unit. If a problem has intermediate values to be computed, wait to round numbers until the final result is found. Each intermediate value should have at least one more digit than the final result is to have so that each rounding does not directly involve the unit of accuracy.
In finding a side of a right triangle when an angle and a side are known, there are two trigonometric functions which can be used, a function and its reciprocal. When manually solving the problem, the choice is usually made so the unknown side is in the numerator of the fraction. This is done so that the operation needed to solve the equation will be multiplication rather than division. Most tables of values of trigonometric functions do not include values for secant and cosecant. You will need to use cosine instead of secant and sine instead of cosecant, when your tables only include values for sine, cosine, tangent, and cotangent. When a calculator is used, the function selected is sine, cosine, or tangent, since these functions are represented by keys on the calculator.
EXAMPLE 3.4 A support wire is anchored 12 m up from the base of a flagpole, and the wire makes a 15° angle with the ground. How long is the wire?
From Fig. 3.4, it can be seen that both sin 15° and csc 15° involve the known length 12 m and the requested length x. Either function can be used to solve the problem. The manual solution, that is, using tables and not a calculator, is easier using csc 15°, but not all trigonometric tables list values for secant and cosecant. The calculator solution will use sin 15° since there is no function key for cosecant.
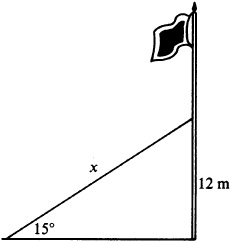

The wire is 46 m long.
In each solution, the result to the nearest meter is the same, but the results of the computations are different because of the rounding used in determining the value of the function used. Rounding to a few decimal places, as in the table provided in this section, often leads to different computational results. Using the four-decimal-place tables in App. 2 will result in very few situations where the choice of functions affects the results of the computation. Also, when these tables are used, the results will more frequently agree with those found using a calculator.
For the problems in this chapter, a manual solution and a calculator solution will be shown and an answer for each procedure will be indicated. In later chapters, an answer for each method will be indicated only when the two procedures produce different results.
The decision to use or not to use a calculator is a personal one for you to make. If you will not be able to use a calculator when you apply the procedures studied, then do not practice them using a calculator. Occasionally there will be procedures discussed that are used only with tables, and others that apply to calculator solutions only. These will be clearly indicated and can be omitted if you are not using that solution method.
An angle of depression is the angle from the horizontal down to the line of sight from the observer to an object below. The angle of elevation is the angle from the horizontal up to the line of sight from the observer to an object above.
In Fig. 3.5, the angle of depression from point A to point B is α and the angle of elevation from point B to point A is β. Since both angles are measured from horizontal lines, which are parallel, the line of sight AB is a transversal, and since alternate interior angles for parallel lines are equal, 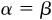 (See App. 1, Geometry.)
(See App. 1, Geometry.)
SOLVED PROBLEMS
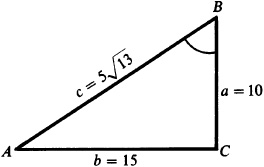
3.1 Find the trigonometric functions of the acute angles of the right triangle ABC, Fig. 3.6, given  and
and  .
.
Since  ,
, 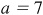 . Then
. Then

and

3.2 Find the values of the trigonometric functions of the acute angles of the right triangle ABC, Fig. 3.7, given 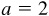 and
and 

Since  ,
,  . Then
. Then

3.3 Find the values of the trigonometric functions of the acute angle A, given  .
.
Construct the right triangle ABC, Fig. 3.8, with 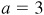 ,
, 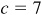 , and
, and  units. Then
units. Then

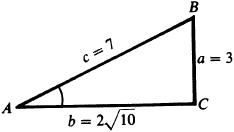
3.4 Find the values of the trigonometric functions of the acute angle B, given 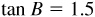 .
.
Refer to Fig. 3.9. Construct the right triangle ABC having  and
and  units. (Note that
units. (Note that 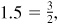 and therefore a right triangle with
and therefore a right triangle with  and
and 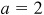 will serve equally well.)
will serve equally well.)
Then  and
and

3.5 If A is acute and sin 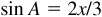 , determine the values of the remaining functions.
, determine the values of the remaining functions.
Construct the right triangle ABC having  and
and  , as in Fig. 3.10
, as in Fig. 3.10
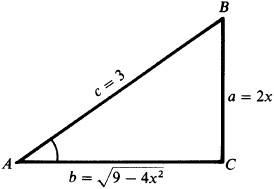
Then  and
and

3.6 If A is acute and tan 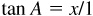 , determine the values of the remaining functions.
, determine the values of the remaining functions.
Construct the right triangle ABC having 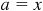 and
and 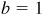 , as in Fig. 3.11. Then
, as in Fig. 3.11. Then  and
and


(a) Why is  ?
?
(b) When is 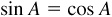 ?
?
(c) Why is  ?
?
(d) Why is 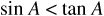 ?
?
(e) When is 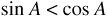 ?
?
(f) When is 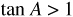 ?
?
In the right triangle ABC:
(a) Side a < side c; therefore 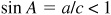 .
.
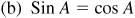 when
when 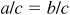 ; then
; then 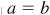 ,
, 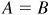 , and
, and  .
.
 (above) and
(above) and  .
.
 ,
, 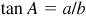 , and
, and  ; therefore
; therefore 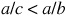 or
or 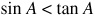 .
.
 when
when 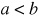 ; then
; then  or
or 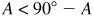 and
and  .
.
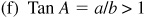 when
when  ; then
; then  and
and  .
.
3.8 Find the exact values of the trigonometric functions of 45°. (See Fig. 3.12.)

In any isosceles right triangle ABC,  and
and  . Let
. Let 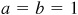 ; then
; then 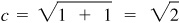 and
and
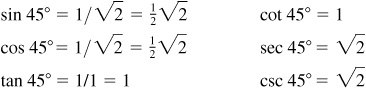
3.9 Find the exact values of the trigonometric functions of 30° and 60°. (See Fig. 3.13.)

In any equilateral triangle ABD, each angle is 60°. The bisector of any angle, like B, is the perpendicular bisector of the opposite side. Let the sides of the equilateral triangle be of length 2 units. Then in the right triangle ABC, 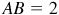 ,
,  , and
, and 

(NOTE: In Probs. 3.10 to 3.15 two solution procedures are shown, one for manual solution and one for calculator solution, whenever the two are different. Which one you use depends upon your access to a calculator during your problem-solving work. If your access to a calculator is restricted, then focus only on the manual solutions. In the calculator solutions, steps are shown to illustrate the procedures rather than as a guide to work steps that need to be shown. The steps shown in each solution are to allow you to see all the details of the procedure used.)
3.10 When the sun is 20° above the horizon, how long is the shadow cast by a building 50 m high?
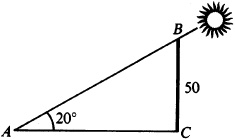
In Fig. 3.14,  ,
, 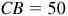 , and AC is to be found.
, and AC is to be found.

(NOTE: The difference in the answers for the two procedures is because cot 20° was rounded to two decimal places in the table. Each answer is the correct one for that procedure.)
3.11 A tree 100 ft tall casts a shadow 120 ft long. Find the angle of elevation of the sun.
In Fig. 3.15, 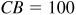 ,
, 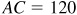 , and we want to find A.
, and we want to find A.
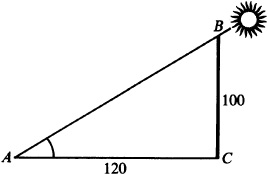

(Since tan 40° has the closest value to 0.83, we used 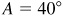 .)
.)
3.12 A ladder leans against the side of a building with its foot 12 ft from the building. How far from the ground is the top of the ladder and how long is the ladder if it makes an angle of 70° with the ground?
From Fig. 3.16, 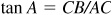 ; then
; then 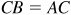

 . The top of the ladder is 33 ft above the ground. Manual:
. The top of the ladder is 33 ft above the ground. Manual:  ; then
; then 
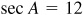
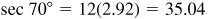 . The calculator solution procedure is the same.
. The calculator solution procedure is the same.
Calculator: 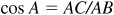 ; then
; then 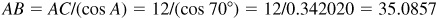 .
.
The ladder is 35 ft long.
3.13 From the top of a lighthouse 120 m above the sea, the angle of depression of a boat is 15°. How far is the boat from the lighthouse?
In Fig. 3.17, the right triangle ABC has 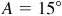 and
and 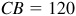 .
.
Manual: 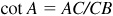 and
and 

 .
.
Calculator:  and
and 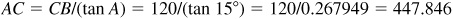 .
.
The boat is 448 m from the lighthouse.
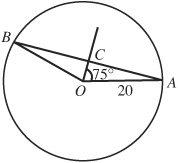
3.14 Find the length of the chord of a circle of radius 20 cm subtended by a central angle of 150°.
In Fig. 3.18, OC bisects ∠AOB. Then  and OCA is a right triangle.
and OCA is a right triangle.
Manual: In ΔOAC,  and
and 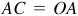
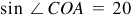
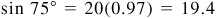 ;
; 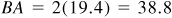 .
.
Calculator: 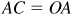
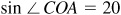
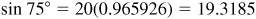 ;
; 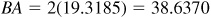 .
.
The length of the chord is 39 cm.
3.15 Find the height of a tree if the angle of elevation of its top changes from 20° to 40° as the observer advances 75 ft toward its base. See Fig. 3.19.
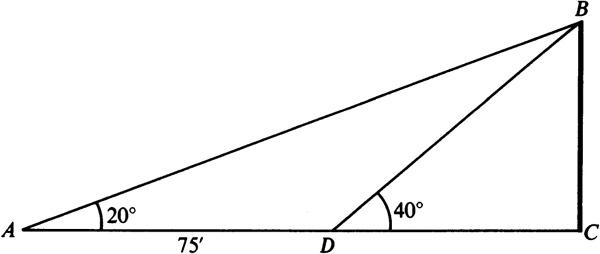
In the right triangle ABC, 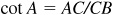 ; then
; then 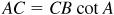 or
or 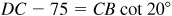 .
.
In the right triangle DBC,  ; then
; then 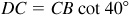 .
.
Manual:

and
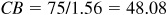
Calculator:
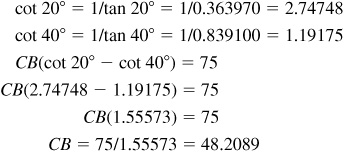
The tree is 48 ft tall.
3.16 A tower standing on level ground is due north of point A and due west of point B, a distance c ft from A. If the angles of elevation of the top of the tower as measured from A and B are α and β, respectively, find the height h of the tower.
In the right triangle ACD of Fig. 3.20, 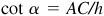 ; and in the right triangle BCD,
; and in the right triangle BCD,  . Then
. Then  and
and  .
.
Since ABC is a right triangle, 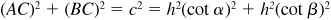 and
and
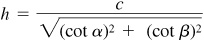

3.17 If holes are to be spaced regularly on a circle, show that the distance d between the centers of two successive holes is given by 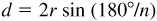 , where r = the radius of the circle and n = the number of holes. Find d when
, where r = the radius of the circle and n = the number of holes. Find d when  in and
in and 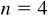 .
.
In Fig. 3.21, let A and B be the centers of two consecutive holes on the circle of radius r and center O. Let the bisector of the angle O of the triangle AOB meet AB at C. In right triangle AOC,
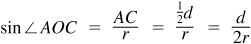
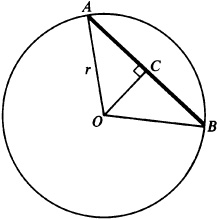
Then
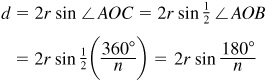
When 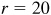 and
and  ,
, 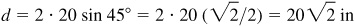 .
.
SUPPLEMENTARY PROBLEMS
3.18 Find the exact values of the trigonometric functions of the acute angles of the right triangle ABC, given:
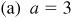 ,
, 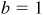 ;
;
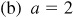 ,
, 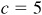 ;
;
 ,
, 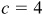
Ans. Answers are in the order sine, cosine, tangent, cotangent, secant, and cosecant.



(a) sin 55° or cos 55°
(b) sin 40° or cos 40°
(c) tan 15° or cot 15°
(d) sec 55° or csc 55°
Ans. (a) sin 55°,
(b) cos 40°,
(c) cot 15°,
(d) sec 55°
3.20 Find the exact value of each of the following.
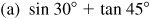
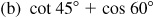

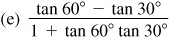
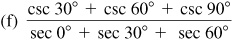
Ans.
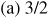 ,
,
 ,
,
(c) 1,
(d) 0,
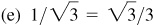 ,
,
(f) 1
3.21 A man drives 500 m along a road which is inclined 20° to the horizontal. How high above his starting point is he?
Ans. Manual: 170 m; calculator: 171 m (manual answer differs because of rounding of table values).
3.22 A tree broken over by the wind forms a right triangle with the ground. If the broken part makes an angle of 50° with the ground and the top of the tree is now 20 ft from its base, how tall was the tree?
Ans. 55 ft
3.23 Two straight roads intersect to form an angle of 75°. Find the shortest distance from one road to a gas station on the other road that is 1000 m from the intersection.
Ans. Manual: 3730 m; calculator: 3732 (manual answer differs because of rounding of table values).
3.24 Two buildings with flat roofs are 60 m apart. From the roof of the shorter building, 40 m in height, the angle of elevation to the edge of the roof of the taller building is 40°. How high is the taller building?
Ans. 90 m
3.25 A ladder with its foot in the street makes an angle of 30° with the street when its top rests on a building on one side of the street and makes an angle of 40° with the street when its top rests on a building on the other side of the street. If the ladder is 50 ft long, how wide is the street?
Ans. 82 ft
3.26 Find the perimeter of an isosceles triangle whose base is 40 cm and whose base angle is 70°.
Ans. 157 cm