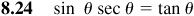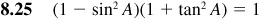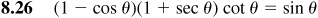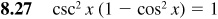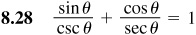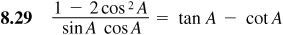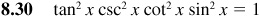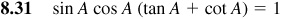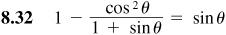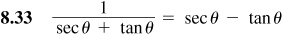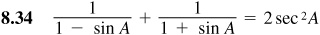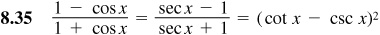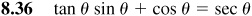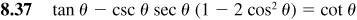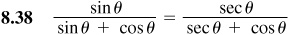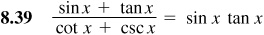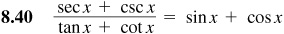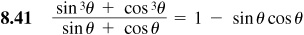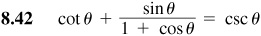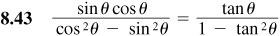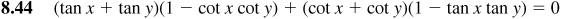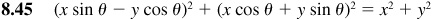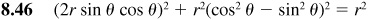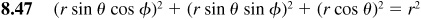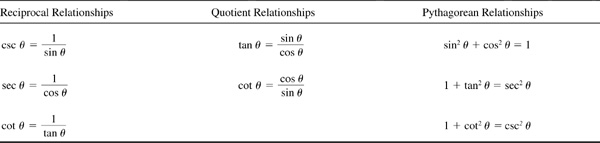

The basic relationships hold for every value of θ for which the functions involved are defined.
Thus, 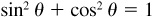 holds for every value of
holds for every value of 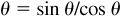 holds for all values of θ for which tan θ is defined, i.e., for all
holds for all values of θ for which tan θ is defined, i.e., for all 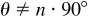 where n is odd. Note that for the excluded values of θ, cos
where n is odd. Note that for the excluded values of θ, cos 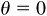 and sin
and sin 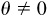 .
.
For proofs of the quotient and Pythagorean relationships, see Probs. 8.1 and 8.2. The reciprocal relationships were treated in Chap. 2.
(See also Probs. 8.3 to 8.6.)
It is frequently desirable to transform or reduce a given expression involving trigonometric functions to a simpler form.
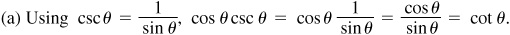
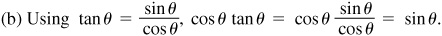
EXAMPLE 8.2 Using the relation 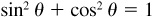 ,
,
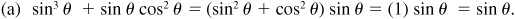
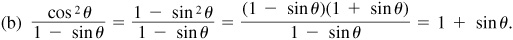
(NOTE: The relation 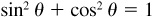 may be written as
may be written as 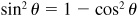 and as
and as 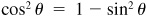 . Each form is equally useful. In Example 8.2 the second of these forms was used.)
. Each form is equally useful. In Example 8.2 the second of these forms was used.)
(See Probs. 8.7 to 8.9.)
An equation involving the trigonometric functions which is valid for all values of the angle for which the functions are defined is called a trigonometric identity. The eight basic relationships in Sec. 8.1 are trigonometric identities; so too are
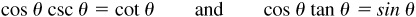
of Example 8.1.
A trigonometric identity is verified by transforming one member (your choice) into the other. In general, one begins with the more complicated side. In some cases each side is transformed into the same new form.
General Guidelines for Verifying Identities
1. Know the eight basic relationships and recognize alternative forms of each.
2. Know the procedures for adding and subtracting fractions, reducing fractions, and transforming fractions into equivalent fractions.
3. Know factoring and special product techniques.
4. Use only substitution and simplification procedures that allow you to work on exactly one side of an equation.
5. Select the side of the equation that appears more complicated and attempt to transform it into the form of the other side of the equation. (See Example 8.3.)
6. If neither side is uncomplicated, transform each side of the equation, independently, into the same form. (See Example 8.4.)
7. Avoid substitutions that introduce radicals.
8. Use substitutions to change all trigonometric functions into expressions involving only sine and cosine and then simplify. (See Example 8.5.)
9. Multiply the numerator and denominator of a fraction by the conjugate of either. (See Example 8.6.)
10. Simplify a square root of a fraction by using conjugates to transform it into the quotient of perfect squares. (See Example 8.7.)
EXAMPLE 8.3 Verify the identity 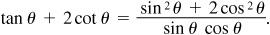
We shall attempt to convert the right side of the possible identity into the left side by using the properties of fractions and substitutions using basic trigonometric relationships.
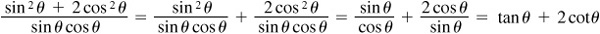
Thus, 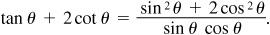
EXAMPLE 8.4 Verify the identity 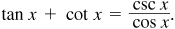
We transform the left side of the possible identity into a simpler form and then transform the right side into that same form.
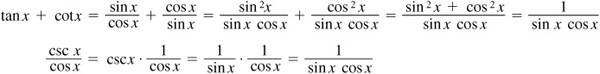
Thus, 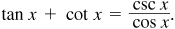
EXAMPLE 8.5 Verify the identity 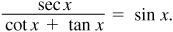
We transform the left side of the possible identity into an expression in sine and cosine and then simplify.
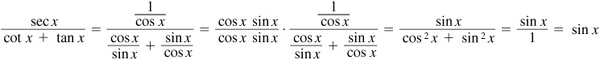
Thus, 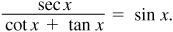
EXAMPLE 8.6 Verify the identity 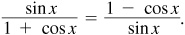
We multiply the numerator and denominator on the left side by 1 – cos x, which is the conjugate of the denominator. (The conjugate of a two-term expression is the expression determined when the sign between the two terms is replaced by its opposite.) The only time we use this procedure is when the product of the expression and its conjugate gives us a form of a Pythagorean relationship.
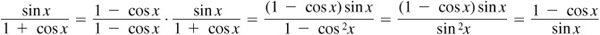
Thus, 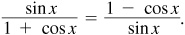
EXAMPLE 8.7 Verify the identity 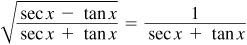
Since the left side has the radical, we want to multiply the numerator and denominator of the fraction under the radical by the conjugate of either. We will use the conjugate of the numerator since this will make the denominator the square of the value we want in the denominator.
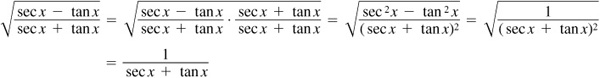
Thus, 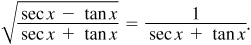
Practice makes deciding which substitutions to make and which procedures to use much easier. The procedures used in Examples 8.3, 8.4, and 8.5 are the ones most frequently used.
(See Probs. 8.10 to 8.18.)
8.1 Prove the quotient relationships 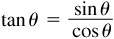 and
and 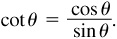
For any angleθ, sin 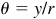 ,
, 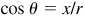 , tan
, tan 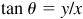 , and
, and 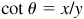 , where P(x, y) is any point on the terminal side of θ at a distance r from the origin.
, where P(x, y) is any point on the terminal side of θ at a distance r from the origin.
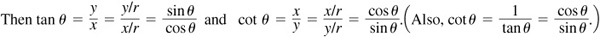
8.2 Prove the Pythagorean relationships 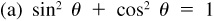 ,
, 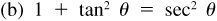 , and
, and 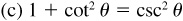 .
.
For P(x, y) defined as in Prob. 8.1, we have 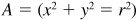 .
.
(a) Dividing A by r2, 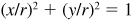 and
and 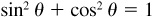 .
.
(b) Dividing A by x2, 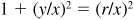 and
and 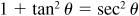 .
.
Also, dividing 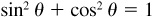 by cos2θ,
by cos2θ, 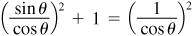 or
or 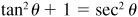
(c) Dividing A by y2, 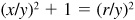 and
and 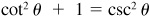 .
.
Also, dividing 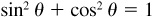 by sin2θ, 1
by sin2θ, 1 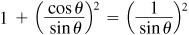 or
or 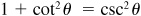
8.3 Express each of the other functions of θ in terms of sin θ.
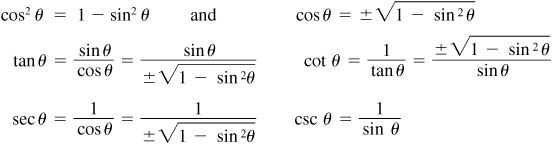
Note that 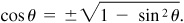 Writing
Writing 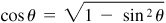 limits angle θ to those quadrants (first and fourth) in which the cosine is positive.
limits angle θ to those quadrants (first and fourth) in which the cosine is positive.
8.4 Express each of the other functions of θ in terms of tan θ.
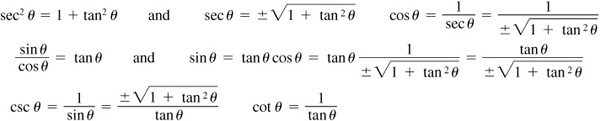
8.5 Using the basic relationships, find the values of the functions of θ, given 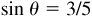 .
.
From 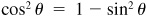 ,
, 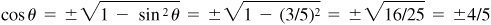 .
.
When θ is a first-quadrant angle sin θ and cos θ are both positive, while sin θ is positive and cos θ is negative when θ is a second-quadrant angle. Thus,

8.6 Using the basic relationships, find the values of the functions of θ, given 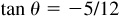 .
.
Since tan θ is negative, θ is either a second- or fourth-quadrant angle.

8.7 Perform the indicated operations.
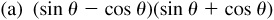
(b) (sin A + cos A)2
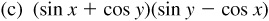
(d) (tan2 A – cot A)2
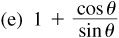
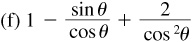
(a) sin2θ – cos2θ
(b) sin2 A + 2 sin A cos A + cos2 A
(c) sin x sin y – sin x cos x + sin y cos y – cos x cos y
(d) tan4 A –2 tan2 A cot A + cot2 A
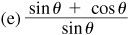
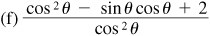
(a) sin2θ – sin θ cos θ
(b) sin2θ + sin2θ cos2θ
(c) sin2θ + sin θ sec θ –6 sec2θ
(d) sin3θ cos2θ – sin2θ cos3θ + sin θ cos2θ
(e) sin4θ – cos4θ
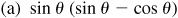
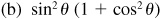
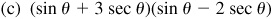
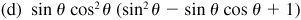
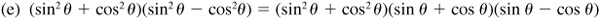
8.9 Simplify each of the following.
(a) sec θ – sec θ sin2θ
(b) sin θ sec θ cot θ
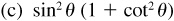
(d) sin2θ sec2θ – sec2θ
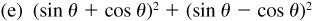
(f) tan2θ cos2θ + cot2θ sin2θ
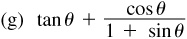
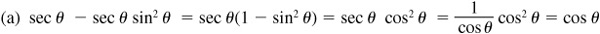
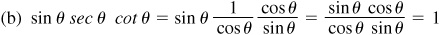
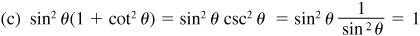
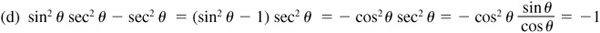
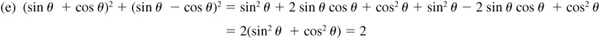
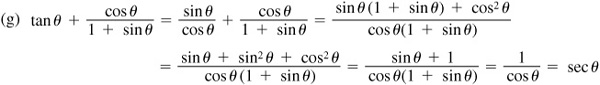
Verify the following identities.
or
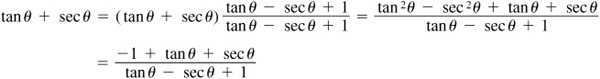
(NOTE: When expressed in terms of sin θ and cos θ, this identity becomes that of Prob. 8.17.)
SUPPLEMENTARY PROBLEMS
8.19 Find the values of the trigonometric functions of θ, given 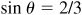 .
.
Ans. Quad I: 2/3, 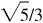 ,
, 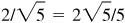 ,
, 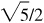 ,
, 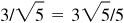 , 3/2
, 3/2
Quad II: 2/3, 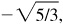
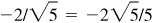 ,
, 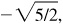
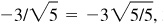 3/2
3/2
8.20 Find the values of the trigonometric functions of θ, given 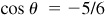 .
.
Ans. Quad II: 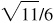 , –5/6,
, –5/6, 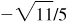 ,
, 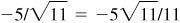 , –6/5,
, –6/5, 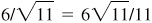
Quad III: 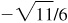 , –5/6,
, –5/6, 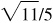 ,
, 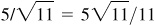 , –6/5,
, –6/5, 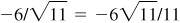
8.21 Find the values of the trigonometric functions of θ, given 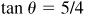 .
.
Ans. Quad I: 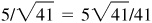 ,
, 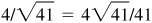 , 5/4, 4/5,
, 5/4, 4/5, 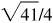 ,
, 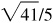
Quad III: 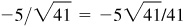 ,
, 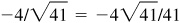 , 5/4, 4/5,
, 5/4, 4/5, 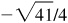 ,
, 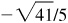
8.22 Find the values of the trigonometric functions of θ, given 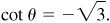
Ans. Quad II: 1/2, 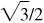 ,
, 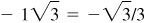 ,
, 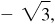
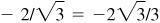 , 2
, 2
Quad IV: –1/2, 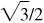 ,
, 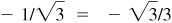 ,
, 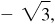
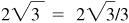 , –2
, –2
Ans. Quad II: 23/5; Quad IV: 34/35
Verify the following identities.