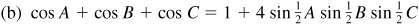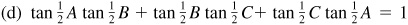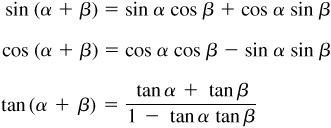
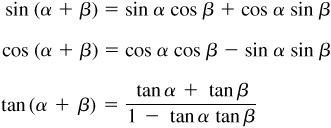
For a proof of these formulas, see Probs. 9.1 to 9.3.
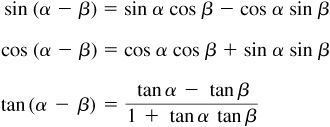
For a proof of these formulas, see Prob. 9.4.
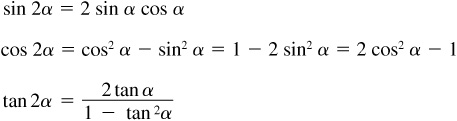
For a proof of these formulas, see Prob. 9.14.
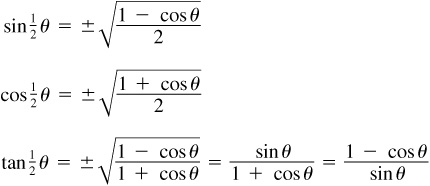
For a proof of these formulas, see Prob. 9.15.
SOLVED PROBLEMS
and 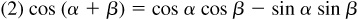 when α and β are positive acute angles.
when α and β are positive acute angles.
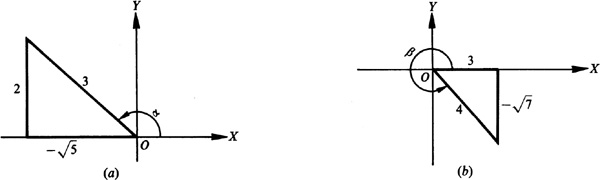
Let α and β be positive acute angles such that 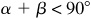 [Fig. 9.1(a)] and
[Fig. 9.1(a)] and 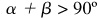 [Fig. 9.1(b)].
[Fig. 9.1(b)].

To construct these figures, place angle α in standard position and then place angle β with its vertex at O and its initial side along the terminal side of angle α. Let P be any point on the terminal side of angle (α + β). Draw PA perpendicular to OX, PB perpendicular to the terminal side of angle α, BC perpendicular to OX, and BD perpendicular to AP.
Now 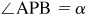 since corresponding sides (OA and AP, and OB and BP) are perpendicular. Then
since corresponding sides (OA and AP, and OB and BP) are perpendicular. Then
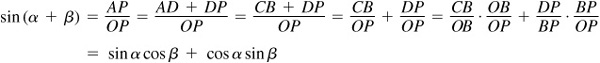
and
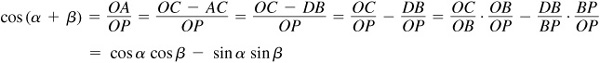
9.2 Show that (1) and (2) of Prob. 9.1 are valid when α and β are any angles.
First check the formulas for the case  and
and 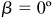 . Since
. Since
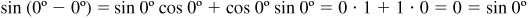
and
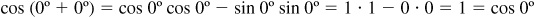
the formulas are valid for this case.
Next, it will be shown that if (1) and (2) are valid for any two given angles α and β, the formulas are also valid when, say, α is increased by 90°. Let α and β be two angles for which (1) and (2) hold and consider
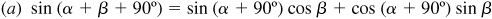
and
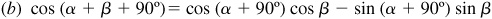
From the graphs in Sec. 7.3 we see that  and
and 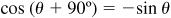 . It follows that sin
. It follows that sin 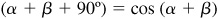 and
and 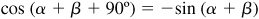 . Then (a) and (b) reduce to
. Then (a) and (b) reduce to
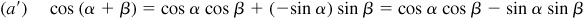
and
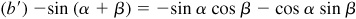
or
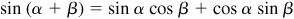
which, by assumption, are valid relations. Thus, (a) and (b) are valid relations.
The same argument may be made to show that if (1) and (2) are valid for two angles α and β, they are also valid when β is increased by 90°. Thus, the formulas are valid when both α and β are increased by 90°. Now any positive angle can be expressed as a multiple of 90° plus θ, where θ is either 0° or an acute angle. Thus, by a finite number of repetitions of the argument, we show that the formulas are valid for any two given positive angles.
It will be left for the reader to carry through the argument when, instead of an increase, there is a decrease of 90° and thus to show that (1) and (2) are valid when one angle is positive and the other negative, and when both are negative.
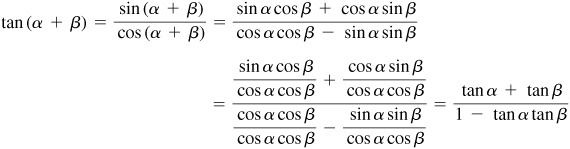
9.4 Prove the subtraction formulas.
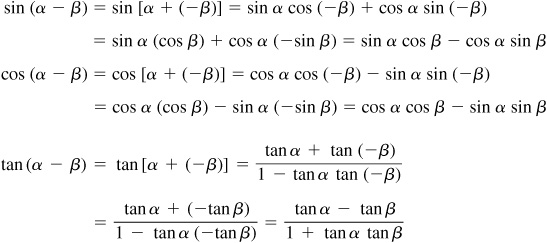
9.5 Find the values of the sine, cosine, and tangent of 15°, using 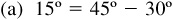 and
and 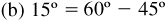 .
.
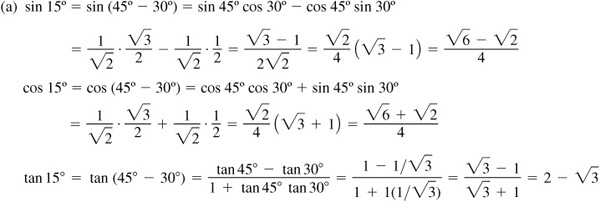
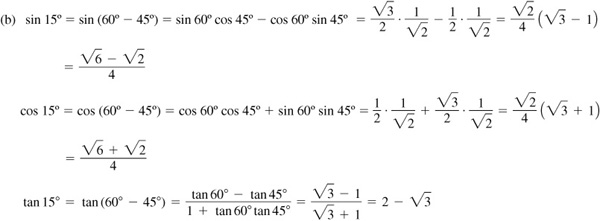
9.6 Find the values of the sine, cosine, and tangent of π/12 radians.
Since π/3 and π/4 are special angles and 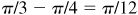 , they can be used to find the values needed.
, they can be used to find the values needed.
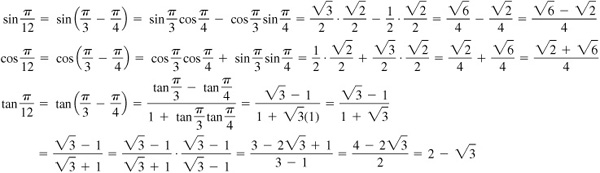
9.7 Find the values of the sine, cosine, and tangent of 5π/12 radians.
Since π/6 and π/4 are special angles and 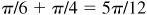 , they can be used to find the values needed.
, they can be used to find the values needed.

9.8 Rewrite each expression as a single function of an angle.
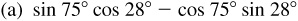
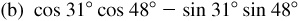
(c) 2 sin 75° cos 75°
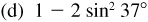
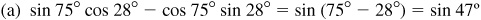
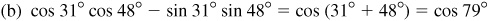
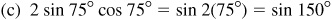
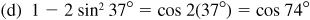
9.9 Rewrite each expression as a single function of an angle.
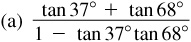

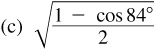

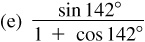
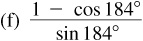
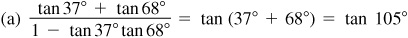
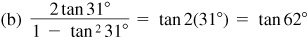
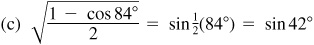
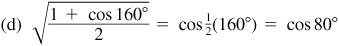
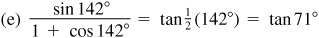
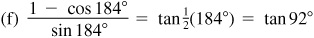
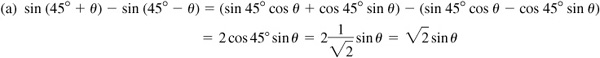
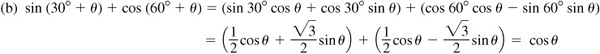
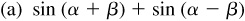


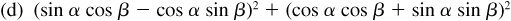
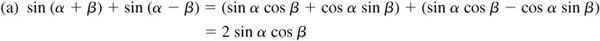
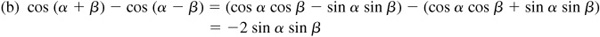
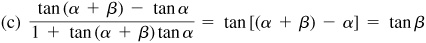
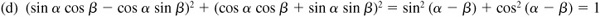
9.12 Find  ,
,  ,
,  , and
, and  and determine the quadrants in which
and determine the quadrants in which 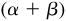 and
and  terminate, given
terminate, given
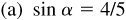 ,
, 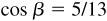 ; α and β in quadrant I
; α and β in quadrant I
 ,
, 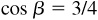 ; α in quadrant II, β in quadrant IV
; α in quadrant II, β in quadrant IV
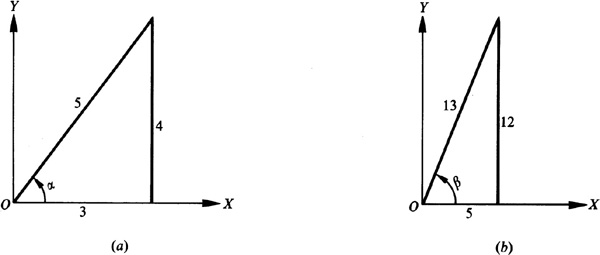
 , see Fig. 9.2(a), and
, see Fig. 9.2(a), and 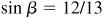 , see Fig. 9.2(b).
, see Fig. 9.2(b).
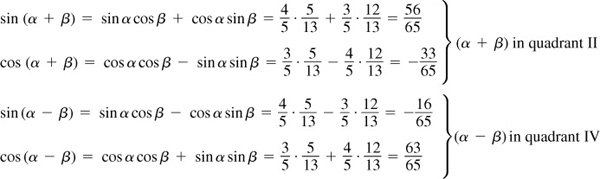
 see Fig. 9.3(a), and
see Fig. 9.3(a), and  see Fig. 9.3(b).
see Fig. 9.3(b).

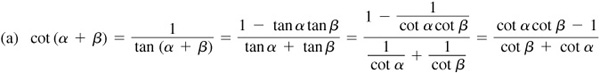
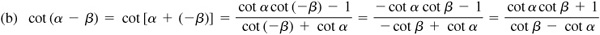
9.14 Prove the double-angle formulas.
In sin 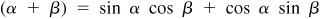 ,
, 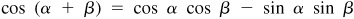 , and
, and 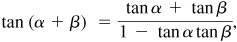 put
put 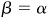 . Then
. Then
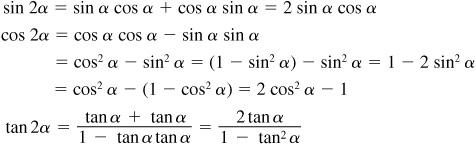
9.15 Prove the half-angle formulas.
In 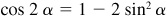 , let
, let 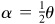 . Then
. Then
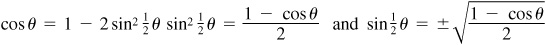
In 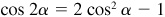 , let
, let 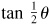 . Then
. Then
Finally,
The signs ± are not needed here since  and sin θ always have the same sign (Prob. 6.8, Chap. 6) and
and sin θ always have the same sign (Prob. 6.8, Chap. 6) and  is always positive.
is always positive.
9.16 Using the half-angle formulas, find the exact values of (a) sin 15°,  and (c) sin π/8.
and (c) sin π/8.
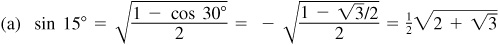
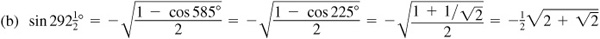
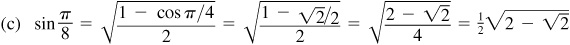
9.17 Find the values of the sine, cosine, and tangent of 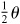 , given
, given 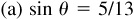 , θ in quadrant II and
, θ in quadrant II and 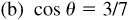 , θ in quadrant IV.
, θ in quadrant IV.
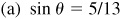 ,
, 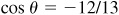 , and
, and 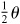 in quadrant I, see Fig. 9.4(a).
in quadrant I, see Fig. 9.4(a).

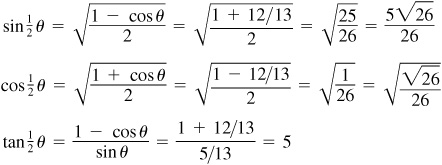
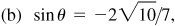
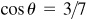 , and
, and 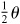 in quadrant II, see Fig. 9.4(b).
in quadrant II, see Fig. 9.4(b).
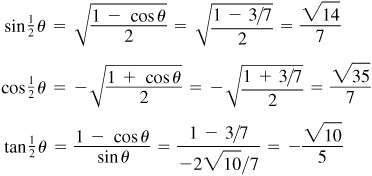
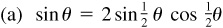
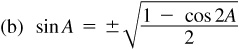
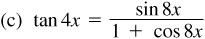
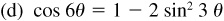
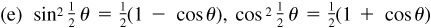
(a) This is obtained from 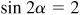 sin α cos α by putting
sin α cos α by putting 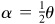 .
.
(b) This is obtained from 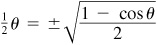 by putting
by putting 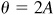 .
.
(c) This is obtained from 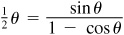 by putting
by putting 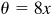 .
.
(d) This is obtained from 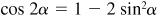 by putting
by putting 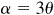 .
.
(e) These formulas are obtained by squaring 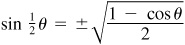 and
and 
9.19 Express (a) sin 3α in terms of sin α and (b) cos 4α in terms of cos α.
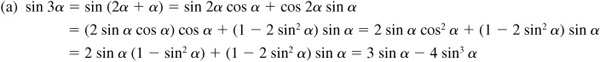
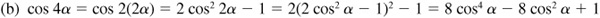
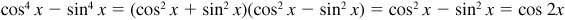
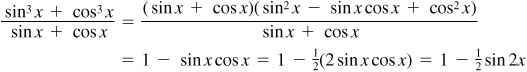
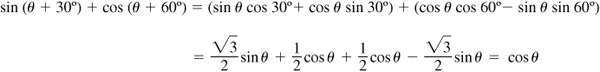
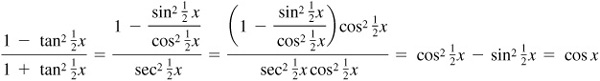
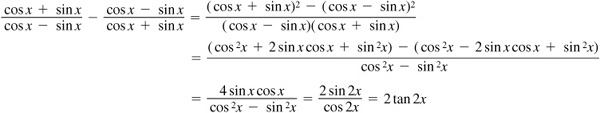
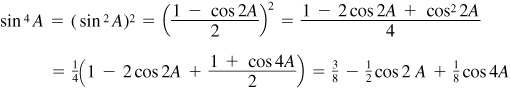
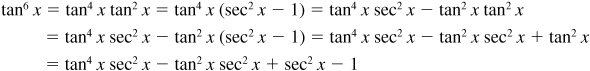
Since 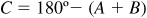 ,
,

Since 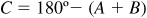 ,
,
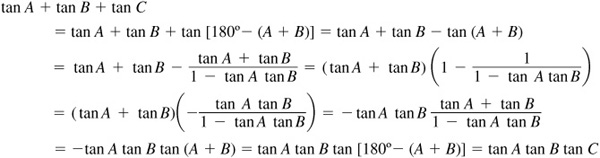
SUPPLEMENTARY PROBLEMS
9.29 Find the values of the sine, cosine, and tangent of (a) 75° and (b) 255°.
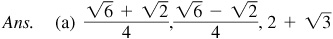

9.30 Find the values of the sine, cosine, and tangent of (a) 7π/12 and (b) 11π/12.

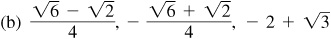
9.31 Rewrite each expression as a single function of an angle.

9.32 Find the values of  ,
,  , and
, and 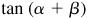 , given:
, given:

9.33 Find the values of  ,
,  , and
, and 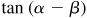 , given:
, given:

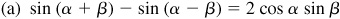
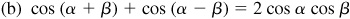
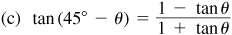
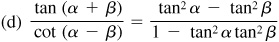
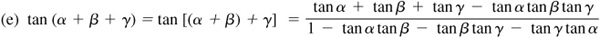
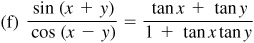
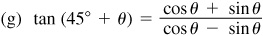
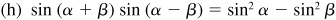
9.35 If A and B are acute angles, find 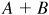 , given:
, given:
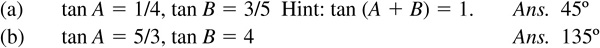
9.37 Find the values of sin 2θ, cos 2θ, and tan 2θ, given:


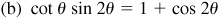
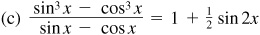
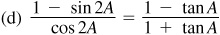
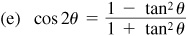
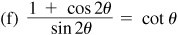
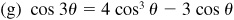
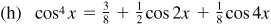
9.39 Find the values of the sine, cosine, and tangent of
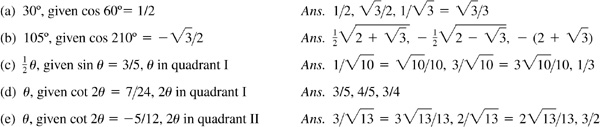
9.40 Find the values of the sine, cosine, and tangent of
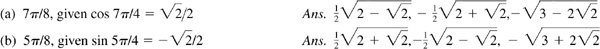

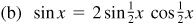
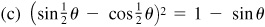
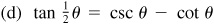
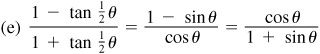

9.42 In the right triangle ABC in which C is the right angle, prove:
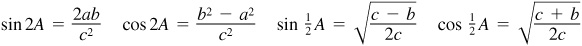
9.44 If A + B + C = 180°, prove: