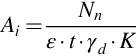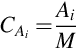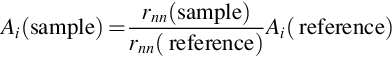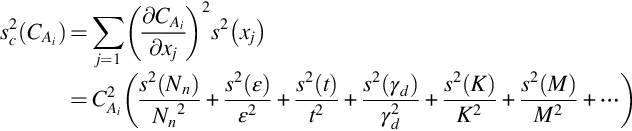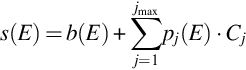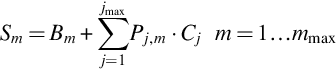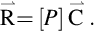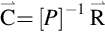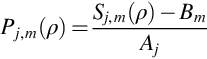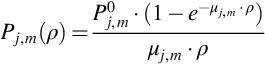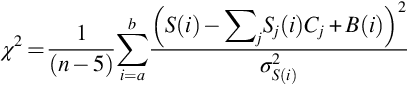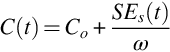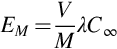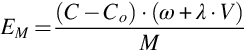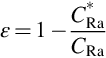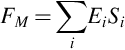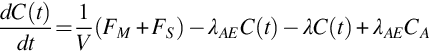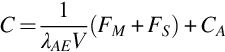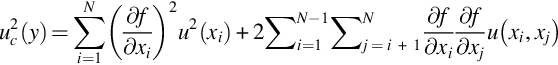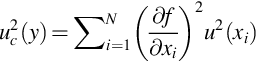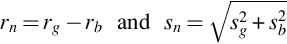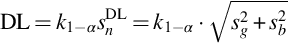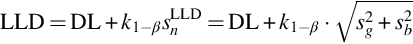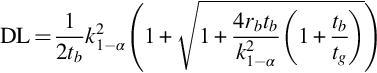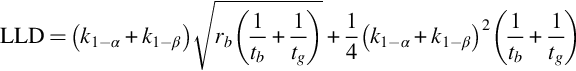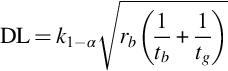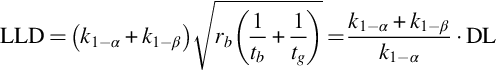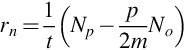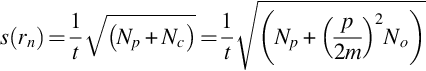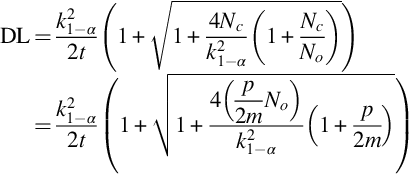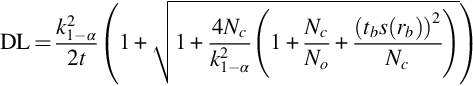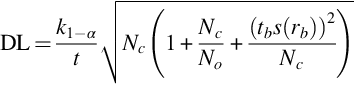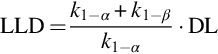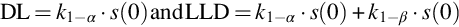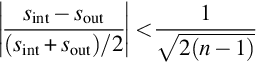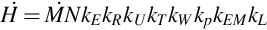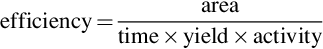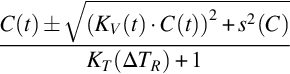Measurement of NORM
H. Friedmann*; C. Nuccetelli†; B. Michalik‡; M. Anagnostakis§; G. Xhixha¶; K. Kovler**; G. de With††; C. Gascó‡‡; W. Schroeyers§§; R. Trevisi¶¶; S. Antropov***; A. Tsapalov***; C. Kunze†††; N.P. Petropoulos§ * University of Vienna, Vienna, Austria
† National Institute of Health, Rome, Italy
‡ Glowny Instytut Gornictwa, Katowice, Poland
§ National Technical University of Athens, Athens, Greece
¶ University of Tirana, Tirana, Albania
** Technion – Israel Institute of Technology, Haifa, Israel
†† Nuclear Research and consultancy Group (NRG), Arnhem, The Netherlands
‡‡ CIEMAT, Unidad de Radiactividad Ambiental y Vigilancia Radiológica, Madrid, Spain
§§ Hasselt University, CMK, NuTeC, Diepenbeek, Belgium
¶¶ National Institute for Insurance against Accidents at Work (INAIL), Rome, Italy
*** Scientific and Technical Centre “AMPLITUDA”, Moscow, Russia
††† IAF-Radioökologie GmbH, Radeberg, Germany
Abstract
This chapter describes the most important measure methods to determine the activity concentration of gamma emitting radionuclides, the measurement of dose rates, and the determination of radon concentrations as well as radon exhalation rates. Several aspects concerning sampling, detector calibration, and uncertainty estimation are discussed.
Keywords
NORM; Gamma spectrometry; Calibration procedures in gamma spectrometry; Dosimetry of NORM; Radon emanation and exhalation; Uncertainty in gamma spectrometry
5.1 Introduction
Measurements are necessary to verify the compliance of building materials with the requirements of the European Union (EU) Basic Safety Standards (EU-BSS) (EU, 2014; Chapter 4) and national regulations. There are two items concerning the radioactivity of building material which need to be verified:
(a) The application of a reference level for the external exposure to gamma radiation (<1 mSv per year). It has to be noted that in many cases it is not possible to estimate directly the annual gamma dose rate to a single person of the public as caused by building materials. For such cases the EU BSS offers the possibility to comply with the dose limit by regulating the building materials radionuclides concentration.
(b) The application of a reference level of radon (222Rn) in indoor air (<300 Bqm−3). This is usually achieved by determining the radon exhalation rate associated to the materials and subsequently controlling it to below the rate that leads to radon concentrations greater than the reference level. In some cases this could be alternatively accomplished by regulating the 226Ra concentration in the materials.
5.2 Measurements by gamma-ray spectrometry
The activity concentration of a radionuclide in NORM, raw materials, and building products is usually measured by gamma-ray spectrometry. The main advantages of this method are the possibility to measure many radionuclides simultaneously and the limited needs concerning sample preparation. Moreover, well developed software analyzing gamma-ray spectra are commercially available. Up to date gamma spectrometers, depending on configuration, can be widely applied for precise laboratory quantitative measurement as well as for qualitative screening or monitoring. However, this method does not allow the measurement of radionuclides which are pure alpha or beta emitters.
Gamma-ray spectrometry relies on the generation of a measurable pulse, either electrical or optical, by a photon (a gamma-ray) in a radiation detector. Independent of the detector type employed, the detector output signal must be converted into a current or voltage pulse that is proportional in magnitude to the gamma-ray emission energy produced by the decay of the radioactive material being measured. The amplitude of a registered pulse must be measured, usually by means of an analogue-to-digital converter (ADC) and the measured pulses are then sorted by their amplitude into the so-called channels of a multichannel analyzer (MCA). The number of channels necessary for the MCA should be as much as of the ADC resolution; common values include consecutive nonnegative powers of two (i.e., 512, 1024, 2048, 4096, 8192, or 16,384 channels). All pulses registered in channels create a sample spectrum with characteristic peaks (photopeaks) that reflect energies of gamma-rays emitted by radionuclides enclosed in a sample (Fig. 5.1). Each gamma-emitting radionuclide has its own characteristic gamma-ray energy emissions and these can be used both to establish the presence of the radionuclide in a sample and to quantitatively determine its activity concentration in the sample.
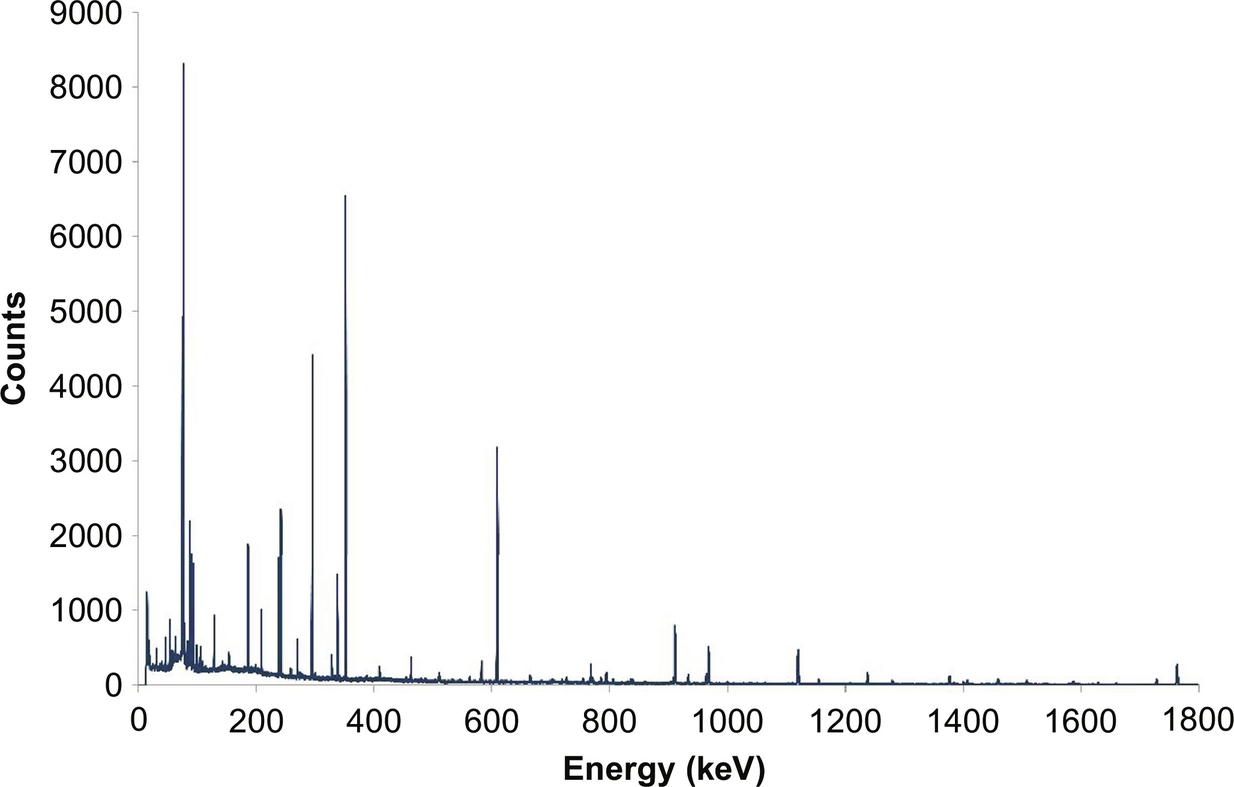
Modern systems are typically of the all-in-one design and operated via computer software applications. The advantage of these systems is that the package provides for the system control (high voltage for the detector system and amplifier settings and monitoring), MCA energy and efficiency calibration, photopeak detection and identification (including multiplet peak deconvolution), and provision of activity concentration and uncertainty calculations.
However, the spectrum analysis software available is not always up to the task and sometimes fails to detect radionuclides actually present in samples; therefore, some caution should be exercised when the spectrum analysis is performed fully automatically.
Generally, gamma-ray spectrometry does not allow for the absolute activity (concentration) determination. A calibration of the spectrometer is needed using a standard sample containing well-known activity concentration of some radionuclides. Moreover, results depend not only on detector types and parameters but also on electronics components, e.g., amplifier noise, ADC and MCA resolution and others. Measurement conditions, most notably sample shape and size (the measurement geometry), self-absorption of gamma-rays within the sample, and the gamma-rays radiation background, also influence the measurement results.
A specific type of calibration methods are based on numerical calculations that allow the modeling of the interactions of gamma-ray radiation in the sample and detector mass and the theoretical calculation of adequate calibration factors.
Gamma-ray spectroscopy is a very useful tool for the measurement of natural radioactivity, which usually consists of several different radioactive nuclides. From the point of view of possible radiation risk, Potassium-40 and two natural decay series, namely, the Uranium and Thorium series are the most important (see Fig. 3.1 in Chapter 3).
5.2.1 Semiconductor spectrometry
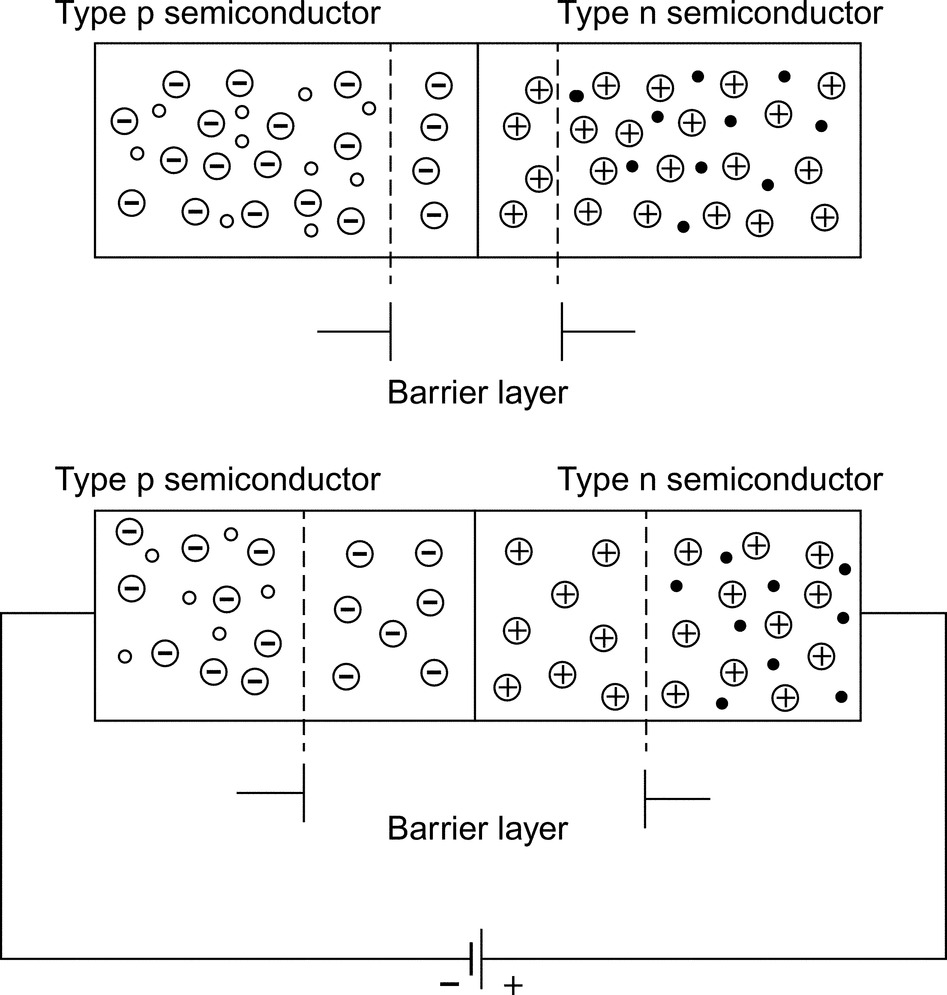
To construct a semiconductor detector, it is necessary to form a connection between n-type (electron donor) and p-type (electron acceptor) semiconductor materials the so-called p-n junction. An n-type semiconductor has a higher concentration of electrons than a p-type semiconductor; consequently, diffusion of electrons from n-type to p-type materials is observed after formation of a p-n junction. This diffusion of electrons leaves positively-charged ions in the n-type material. In the p-type material, negative ions are formed respectively. This mechanism causes separation of electrical charge: negative charge concentrated in p-type semiconductor region and positive charge in the n-type region. Such a charge separation results in an electric field between the two types of semiconductor. This field helps to eliminate free charge carriers from the area around p-n junction. A layer with no free charge carriers results and is called “depletion layer.” If some free charges are created in this volume, they are almost immediately removed by the electric field within a time scale of 10−12–10−11 s. This removal is accompanied by a small electrical signal, a disruption of the electric field, which, in principle could be detected. This phenomenon can be used for the detection of ionizing radiation and gamma-rays in particular, due to the obvious fact that ionizing radiation traversing through depletion layer around a p-n junction could ionize atoms and create free electric charge carriers. However, the electric field of the p-n junction, alternatively called as the contact potential, is usually very small, being typically around 1 V. This field is not enough to effectively produce a detectable electric signal from the charge carriers created by ionization radiation. Within such a small field all ions will recombine and the crucial information about the ionizing radiation will be lost.
To eliminate this problem, the p-n junction is further polarized using an externally imposed potential. This also increases the size of the depletion layer to what is called the active volume. The potential in question depends on the type of detector and is typically in the order of a few kilovolts (kV). A simplified schematic of a p-n junction with and without external potential is given in Fig. 5.2.
The semiconductor detectors contemporarily used for gamma-ray spectrometry usually consist of pure germanium monocrystals (High Purity Germanium, or HPGe). The efficiency (i.e., the detection probability for a photon when passing through the detector) of such detectors depends much on the active volume size and the energy of the gamma-rays and it is generally lower than that of solid scintillation detectors of the same volume. It is, however, possible to make monocrystals with such a large volume that their efficiency may exceed the efficiency of a smaller scintillation detector.
Modern germanium detectors demonstrate very good energy resolution. Combined with an appropriate set of signal preamplifier, signal amplifier, ADC, and MCA, the collection of gamma-ray spectra with the ability to distinguish even very closely located gamma-ray photopeaks is enabled. Such detectors have typically a full width at half maximum (FWHM) resolution of approximately 2 keV at the 1332 keV photopeak of cobalt-60, and a few hundred eV at lower energies. This is far better than the 40–60 keV resolution of a typical NaI(Tl) detector. Therefore, high-resolution gamma-ray spectrometry with semiconductor detectors provides the detection of photopeaks that may not have been able to be resolved using scintillation detectors. Furthermore, modern germanium detectors have a useful energy range from around 5 keV to several MeV, and may have a relative detection efficiency, compared to the industry standard of the 3″×3″ sized NaI(Tl) detector, of greater than 100%.
5.2.1.1 Activity and uncertainty calculation
The determination of activity concentrations in samples comprises the preparation of the sample, the measurement and the calculation of activity concentration from the measurement results. In all these steps contribution to the uncertainty budget exist. This chapter deals with high resolution γ-spectrometry but some parts concern low resolution γ-spectrometry too.
The general sequence in this kind of analysis is shown in Fig. 5.3:
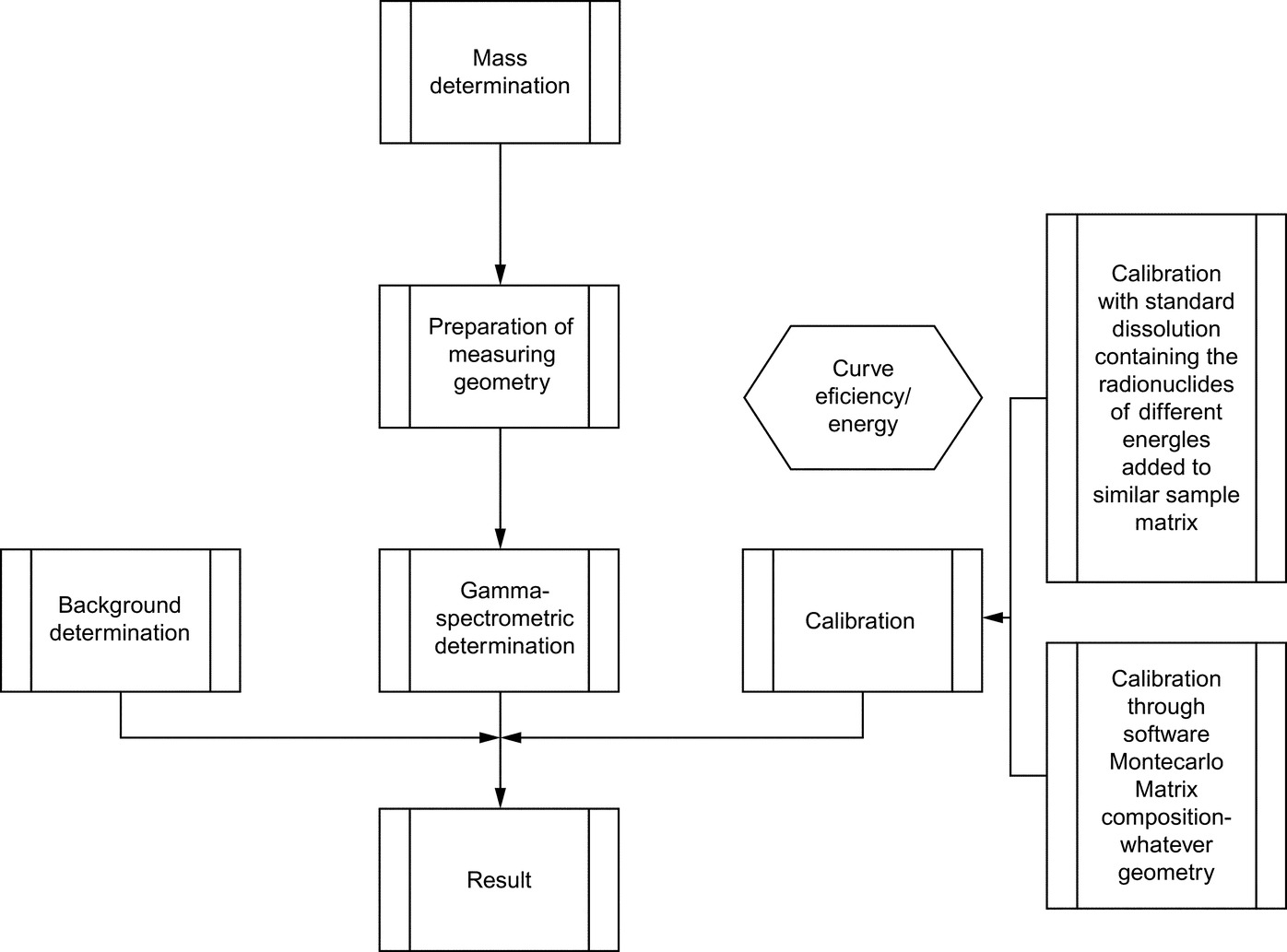
Therefore, the general approach is:
• Sample preparation: The sample has to be prepared homogeneous and in the same shape as the reference sample. The reference sample is either a real sample with known activity concentration or a virtual sample for which the detector efficiency for certain gammy peak energies is computed. Uncertainty contributions result from deviations from the reference sample which are not adjusted by correction factors involving detector efficiency and from the uncertainties of the correction factors. The correction factors concern mainly the density and the atomic composition of the sample compared with the reference sample. These correction factors are energy dependent.
• Measurement: Before starting a measurement the equipment should be checked, especially the electronic part should be adjusted for optimal resolution (time constant, baseline-restorer etc.). In NORM the determination of the activity concentration of a nuclide is often done indirectly by the determination of a progeny. In such a case it is essential to assure radioactive equilibrium between the relevant nuclides. This necessitates that intermediate decay products (such as 222Rn or 220Rn) remain in the sample. Any deviation from the radioactive equilibrium, if not corrected, will lead to an additional uncertainty. The aim of high resolution γ-spectrometry is to determine the counts within peaks that are only due to the investigated sample. Within the spectral interval which comprises the peak to be determined the following contributions must be considered and, where necessary, corrected: (1) unstructured background: counts from Compton scattered photons with higher energies, (2) structured background: counts from peaks from the surrounding radioactivity. This is especially relevant for the measurement of samples with natural radioactivity. Further corrections may be necessary for (3) coincident photon transitions (summing corrections), (4) for double peaks, and (5) for the dead-time of the ADC. The latter can usually be avoided when using live-time data acquisition which means the MCA stops the timer when the ADC is busy in a conversion and is not ready to accept an input signal.
• Calculation of the activity concentration:
The measurand is the nuclide activity concentration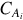 
in Bq/kg based on the peak at energy E:
where Ai=activity of nuclide i (Bq); Nn=background corrected net peak area; ɛ = detector efficiency; t=live time (s) (measurement time during which the digitally converted detector-pulses can be recorded); γd = branching ratio of this nuclide (γ conversion considered); M=mass of sample (kg); K=decay correction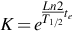 
for the nuclide if it is applicable; T1/2 = half-life time of the nuclide; te=elapsed time between the mid of acquisition and the time of sample collection.
The simplest way to determine the activity of the sample is to calculate the ratio of equivalent well separated peaks between the sample and a real reference sample. Then the activity of the sample at the time of the measurement can easily be calculated by:
with rnn… “net-net count rate” as defined in Annex A—Uncertainties, Decision Threshold (Decision Limit) and Detection Limit (Lower Limit of Detection), i.e., the net peak count rate of the sample (or reference) minus the net peak count rate in the background.
If necessary correction factors for density and atomic composition have to be applied. The uncertainty can be calculated in the usual way using the uncertainty propagation law. Only in case of high count rates (≫104 counts/s) a correction for random coincidences must be applied.
Often it makes sense to use more than one peak to determine an activity concentration. In such a case calculations for all used peaks should be performed and finally combined by a weighted mean with the inverse standard deviations as weights.
In case of calculated detector efficiencies several additional circumstances must be observed. For all peaks used for the determination of the activity concentration the gamma emission probabilities and the related uncertainties must be known. Further, coincident gamma transitions lead to summing peaks and consequently to a reduction in the peak areas of the single peaks. The size of this effect depends essentially on the geometry and efficiency, respectively, of the measurement setup. All the above-mentioned variables and effects are associated with uncertainties. In most cases the determination of these uncertainties is not easy and needs a lot of experience. All the uncertainties have to be combined by the uncertainty propagation law to the final uncertainty, which is an integral element of the final result.
Therefore, the estimation of uncertainties contains the following steps (see Fig. 5.23):
• Exploration of all factors influencing the measurement;
• Quantification of the uncertainty (standard uncertainty s(xj)) connected to each factor xj by measurement results or by expert judgment if applicable;
• Estimation of overall uncertainty of the measurement (standard uncertainty sc(CAi)).
The international standards (BIPM/ISO/IEC Guide 98-3, 2008; ISO, 11929, 2010) describe the methods for calculating these uncertainties in a practical way with some examples. The main components of uncertainty for the measurements using semiconductor detectors are listed in Annex A and Annex B.
5.2.1.2 In situ spectrometry
Strategy of measurements
In situ gamma spectroscopy is a well-known technique introduced by Beck et al. (1972) to determine the concentration of natural and artificial radionuclides in soil, the relevant ambient gamma dose rate in the air above, and the relative contribution of the radionuclides from the 238U and 232Th series and 40K to the dose rate. This technique soon appeared to be a powerful tool to provide rapid and spatially representative estimates of environmental radioactivity. It basically consists of the elaboration of the full absorption peak areas multiplied by ad hoc calibration coefficients calculated according to two fundamental assumptions:
(1) the source—in this case the soil—can be modeled as an infinite half-space (so-called 2π geometry);
(2) the vertical distribution of radionuclides can be reasonably assumed (e.g., uniform distribution for natural radionuclides and exponential distribution for artificial ones).
Under these conditions it is possible to use a standard point source calibration performed in the laboratory (Beck et al., 1972; Cutshall and Larsen, 1986). With this calibration and the coefficients elaborated following Beck's method, the dose rate—produced by the unscattered and scattered fluence of gamma rays—can be estimated, and the radionuclide inventory calculated.
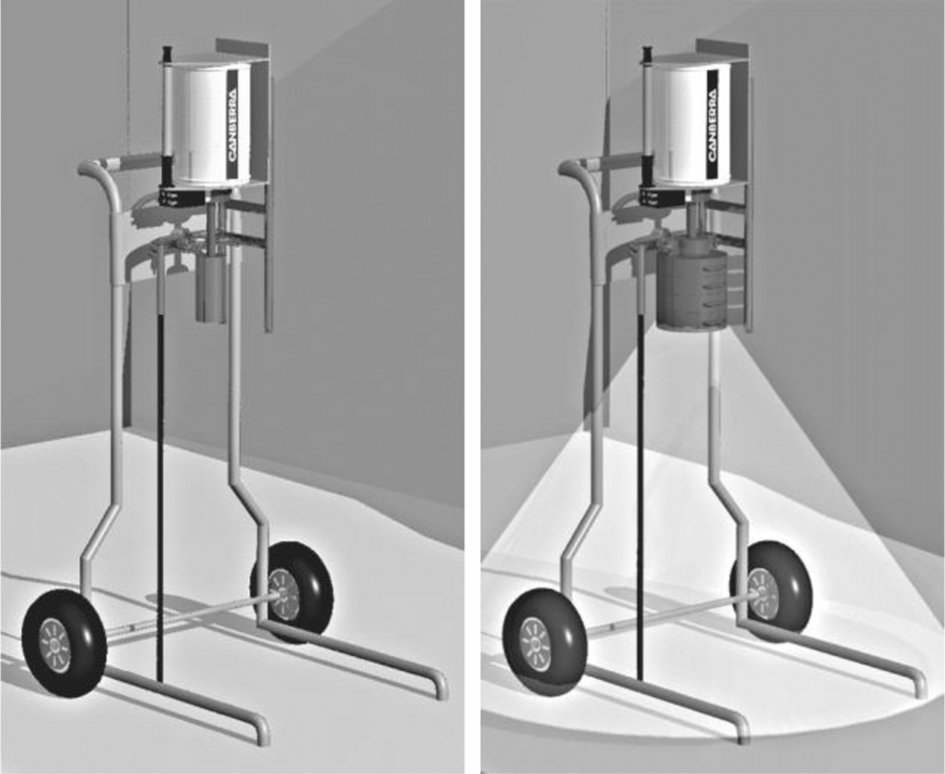
In view of the above features, in situ gamma spectroscopy can be a useful support to measure surface flat soils for many research or institutional activities, for example, to characterize sites in terms of natural background radiation or perform surveys to study sites contaminated by artificial radionuclides and/or NORM (ICRU, 1994; ISO, 18589-7, 2013) (Fig. 5.4). Further applications are the assessment of routine and accidental releases from nuclear facilities, and monitoring of soil contamination level in the different phases of environmental restoration projects. In short, in situ gamma spectroscopy is a very versatile and efficient tool for studying environmental radioactivity, but has some limits mainly associated to the need of a priori assumptions about the distribution of nuclides in the soil, an important source of uncertainties of activity concentration estimates and dose rate evaluations, since dose rate is obtained as a sum of different radionuclide contributions to unscattered and scattered gamma flux at the detector. Moreover, the original method cannot be used for all kinds of source geometry, e.g., indoors or urban outdoors, because it is not feasible to elaborate the build-up factors—taking into account the scattered gamma flux and necessity to determine the gamma dose rate from photopeaks in a recorded spectrum—or produce calibration curves from which to derive the radionuclide activity concentrations in the source. In the 1990s many studies were devoted to further widen the use of this method and overcome the above limitations, rendering in situ gamma spectrometry “independent” of source geometry. This research task yielded important outcomes such as indoor and outdoor build-up factors and the estimate of the actual radionuclide distribution in soil. These results have been obtained following two approaches: (1) Monte Carlo simulation and (2) the use of algorithms aimed to the direct elaboration of spectra. With these new methodologies the applications of in situ gamma spectroscopy have been improved and/or extended to indoor environments, and to outdoor environments not easily represented with a model, such as forests (Gering et al., 2002), urban and industrial outdoor areas (Medeiros and Yoshimura, 2005), and large areas (Cresswell et al., 2006). In particular, indoor utilization provides interesting information on building material characteristics as source of population exposure to natural radionuclides. With different approaches—e.g., Monte Carlo (Clouvas et al., 2000), elaboration of spectra (Bochicchio et al., 1994), computation plus room model (Nuccetelli and Bolzan, 2001; Nuccetelli, 2008)—the use of in situ gamma spectroscopy indoors allows the evaluation of, and the relative contribution of the various nuclides to, the total gamma dose rates. In some countries an indoor methodology was also applied to perform surveys in order to get not only information on population exposure from building materials, but a more detailed description of the sources as well (Clouvas et al., 2004; Svoukis and Tsertos, 2007). Indoor applications of in situ gamma spectroscopy can also provide interesting information about building materials as sources of radon, thoron, and gamma rays (Nuccetelli and Bolzan, 2001; Clouvas et al., 2003) and provide quantitative estimates about the activity concentrations of radionuclides in building materials.
Measurement results and uncertainty
The field-of-view of a detector, a parameter that is defined by the soil surface area from which 90% of the unscattered detected photons originate, limits the direct application of in situ gamma spectrometry in cases when the measured area cannot be modeled as an infinite half-space (Fig. 5.5). In these cases a correction factor (parameter) has to be applied. This parameter depends on the characteristics of the detector, the measurement height (distance from the source), and the distribution of the radionuclide of interest on the measured area. A gamma detector has a nearly 360° field-of-view, and can be used for 4π counting that needs a special calibration procedure which, when used indoor, must be prepared individually for almost each case of application (e.g., see differences in Fig. 5.5). However, the field-of-view can be reduced by adding a shield and collimators. A collimator can limit the field-of-view of the detector to the area of interest and to a certain size of this area. It allows filtering the flux of photons from outside of the measurement area of concern (Fig. 5.6). Finally, the calibration procedure either using calibration sources or mathematical calculation is easier and more accurate when the field-of-view is reduced.
5.2.1.3 Laboratory gamma-ray spectrometry
Sampling of NORM raw materials and by-products
The term NORM covers a wide variety of different materials that can either occur naturally in different forms or are created as a result of various technological processes. The final form of NORM occurrence is one of the most important parameters determining the sampling method that should be applied in order to collect laboratory samples representing the tested material properties at an acceptable level of confidence. Furthermore, sampling and measurement of NORM need to focus on different purposes depending on specific situations. When considering all possible situations, NORM could be sampled for:
• classification in the frame of regulatory control;
• identification of the contamination source or the contamination origin, including a contamination plume;
• identification of NORM related to high background areas;
• contamination inventory and NORM affected land classification including the risk assessment to humans and/or biota;
• land reclamation effectiveness assessment (in case of potential release from regulatory control); and
• existing exposure monitoring (e.g., in case of legacy sites).
All possible combinations of NORM occurrence forms and sampling and measurement purposes create a multiplicity of sampling and measurements scenarios. Therefore, it seems very difficult to develop a common and universal approach to sampling. At the moment as of 2017, there is no standard concerning NORM sampling; however, there often exists the possibility to apply sampling approaches developed for artificial radionuclides, e.g., like these described by Scott et al. (2008). In many cases existing contamination related to NORM can be monitored using principles set in standards dealing with soil sampling [see for example in ISO 18589-2 (ISO, 18589-2, 2015)] or methods developed for monitoring of soil general quality (Brus and de Gruijter, 1997; Judeza et al., 2006) and other relevant available standards like ISO 11074-2 (ISO, 11074-2, 2008), ISO 10381-1 (ISO, 10391-1, 2002), and ISO 10381-2 (ISO, 10381-2, 2002).
However, when applying these standards it is necessary to consider the differences existing between NORM and artificial radionuclides as well as classical pollutants, i.e., contamination source geometry, the location, the accumulation processes, and possible dispersion models. Actually, typical NORMs are either natural raw materials (ores) or, in case of residues, have the appearance of common waste dumps and in this case tend to have more in common with industrial waste than with wastes from the nuclear fuel cycle or the disposal of radioactive sources like those described in standard ISO 21238 (ISO, 21238, 2007). Moreover, natural radionuclides are chemical elements similar to other elements occurring naturally (e.g., heavy metals, noble gases) and their radioactivity does not significantly influence their behavior in the environment. Hence, due to the lack of specific recommendations and standards developed for NORM sampling, standards prepared for sampling of common waste can be applied [see for example PD CEN/TR 15310 (PD CEN/TR, 15310, Parts 1-5, 2006) and BS EN 14899 (BS EN, 14899, 2005)].
The sampling and measurement of NORM in order to release them from regulatory control towards their use in the construction industry is a specific aspect of the general regulatory overview. The screening levels of natural radioactivity content for NORM (despite the fact that these are not actually limits) intended to be used as an additive to building materials in construction industry as set in the EU-BSS (EU, 2014) are much more restrictive than the limits allowing release of NORM from regulatory control. This influences significantly the sampling procedures, which have to be more accurate than in the case of ordinary regulatory control. Considering that the content of natural radioactivity of NORM is only one parameter among many which are important from the point of view of the construction industry, NORMs that are intended for use in this industry must be well characterized and strict ways to prepare an appropriate characterisation are required. These requirements limit the variety of NORM available for consideration in construction industry to situations when their use could be justified from both, the economic and also from the technical point of view.
Therefore, the most suitable NORMs for this purpose are the residues created on regular basis as a result of a well-specified technological process or already accumulated in sufficient quantities (Fig. 5.7). Several typical cases are described in Chapter 6. In such cases initial data concerning the total quantities of NORM existing or expected along with homogeneity characteristics and relevant radionuclides content might be more readily available. Furthermore, usually there already exist sampling methods, used by the NORM processing industries, that could provide, besides their main purpose, also reliable information about the NORM properties for the construction industry. These sampling methods could be applied for the NORM radioactivity content identification and control as well. Moreover, standards developed either for quality monitoring of ordinary raw materials used in the construction industry or for final products can also be effectively adapted to radioactivity measurements. However, the presumable lack of homogeneity of NORM intended to be used as components for construction materials must be always taken into consideration when organizing a sampling campaign.
Provided that initial data do exist to account for the:
• homogeneity characterization of NORM to be used as input in processes or NORM found in residues,
• expected suite of radionuclides, and
• the total amount of available or produced NORM
a sampling campaign could be organized.
Based on general rules of sampling the first step of a sampling campaign organization is to prepare a sampling strategy specifying the density and spatial distribution of sampling points. This process allows for the definition of a sampling unit. Sampling unit may be defined as a part of the sampling area or as a portion of the NORM of concern. The boundaries of a sampling unit could be either physical or even virtual (see Fig. 5.7). In turn, the sampling unit size may be defined using statistics or geostatistics in case of NORM as illustrated in Fig. 5.7, or it might depend on the homogeneity of the sampled material or, to some extent, on the technological process involved. For example, in the case of an existing NORM deposition the sampling size should be decided, taking into consideration if the deposition as a whole should be subject to sampling or if it is enough to check some portions according to the current use. Then the spatial distribution of the sampling area can be replaced by temporal distribution according to the actual use of the material to be exploited.
Having defined the sampling unit, a next step is to fix the sampling density. At this stage technical possibilities and financial restrictions should be considered as well as the sampling unit size, the number of sampling units and the required quality of results. In general, the sampling density should be defined according to the sampling method chosen, taking into consideration that the method should allow for a sound statistical analysis. The sampling method of choice could be:
• Random sampling: collecting samples from the sampling units at randomly selected sites in space and time.
• Systematic sampling: collecting samples from the sampling units by some systematic method in space and time.
• Random systematic sampling: collecting samples at random from each sampling unit from a set of systematically defined sampling units.
Finally, a sampling strategy must be formulated in a way that the collected samples sent to laboratory for analysis (laboratory samples) are representative of the whole material. This means that the distribution of the tested parameter (e.g., 232Th-concentration) in the bulk material is mirrored in the laboratory samples. A sampling strategy presents a certain level of generality and can be applied to a particular type of NORM or for specific branches of industry. Specific applications of an adopted sampling strategy need an associated and precise protocol, which is usually called a sampling plan that, depending on the principles of the strategy, must include:
• Details of sampling method, such as:
• The method of sample collection based on individual sampling action resulting in the final sample that is investigated:
- Increment: the portion of material collected in a single action using a sampling device.
- Subsample: the sample in which the material of interest is randomly distributed in parts of equal or unequal size, a subsample may consist of one or more increments.
- Single sample: the representative quantity of the material, presumed to be homogeneous, taken from a sampling unit (or at least from the borders of a sampling unit), kept and treated separately from all other samples (Fig. 5.8); a single sample may consist of one or more subsamples.
- Composite sample—two or more increments or subsamples or single samples mixed in appropriate proportions, either discretely or continuously (blended composite sample), from which the average value representative of a desired characteristic may be obtained (Fig. 5.9).
• The spatial distribution (i.e., sampling pattern—system of sampling locations based on the results of statistical procedures) and/or the temporal distribution (frequency), of individual sampling action.
• The quantities sampled and the laboratory sample sizes preparation.
• The human and technical resources to be used for sampling.
• The necessary documentation (sampling report, sample identification and traceability, and Chain of Custody).
• The QA/QC procedures to be applied.
The preparation of a laboratory sample is one of the most important parts of a sampling plan and finally decides on the total number of samples intended to be analyzed. There is no strict recommendation concerning a laboratory sample preparation. Based on the previously defined sampling actions, an individual increment, a subsample as well as a composite sample can constitute a laboratory sample, providing that there is enough quantity of sampled material for the intended analysis. This means that in extreme cases the number of laboratory samples could be equal to the number of individual increments or on the other end there could exist only one composite sample as a representative of the whole tested NORM. Both approaches should give the same average quantity. However, limiting the number of laboratory samples reduces the direct information concerning the variability of the tested material.
The total number of laboratory samples is usually a compromise between the expected level of confidence of obtained results and available resources. In general, when sampled material is characterized by high variability in the parameter to be measured (such as natural radioactivity content), it is preferred to use a single sample as a laboratory sample, otherwise a composite sample obtained by mixing of some single samples could be representative enough. Apart from the expected quality of the analytical results that can be evaluated using a statistical procedure, other circumstances should be taken into account with regard to the technical feasibility of samples collection and the balance of costs related to samples collection and analysis.
Usually sampling does not involve very specific equipment and in the majority of cases a shovel can be good enough or other simple tools can be used (Fig. 5.10). However, it must be kept in mind that in some cases a sampling operation can be hindered by the conditions existing in a particular industry, e.g., access limitation to the material during the technological process or the need for specialized sampling devices. A special case exists when a whole depository of NORM must be characterized. In such a situation deep core samples must be taken most often by using drilling rigs.
Each stage of a sampling operation must be properly documented in order to prove the sample representativeness and sample traceability. If the documentation system applied is specific to a particular case, it should be described in details in the sampling plan.
Sampling is a source of an additional uncertainty contributing significantly to the total uncertainty of planned analysis. Hence, relevant QA/QC procedures must be applied in order to provide all data necessary to evaluate the uncertainty related to sampling. The easiest and most commonly applied way to deal with this problem is the collection of duplicate or even multiple samples. However, this method, apart from extra cost, needs advanced statistics in order to be used effectively.
The afore described suggestions for conduct regarding NORM sampling, though not mature, seems constituting the general framework for a uniform approach to the preparation of sampling operations for NORM intended to be used as additives to building materials. In summary, when preparing a sampling strategy and a sampling plan, much consideration should be given to optimization and the balancing of costs and the risk of manufacturing unacceptable final products.
However, in the light of the lack of either direct regulations or recommendations concerning sampling of NORM dedicated for use in construction industry, not disputable sampling procedures trusted by all stakeholders, should be developed.
Application
An accurate activity concentration can be obtained by using gamma spectrometry under laboratory conditions. In the case of high-resolution semiconductor detector, a laboratory gamma spectrometry system consists of the high purity germanium detector (HPGe) mounted in a cryostat (maintained at approximately 83 K by either liquid nitrogen or electrically by Peltier thermoelectric cells) to reduce electronic noise, an integrated preamplifier, a high voltage supply, an amplifier, and a MCA. Modern systems tend to incorporate the high voltage supply, a digital amplifier, and MCA in a single unit operated via an external computer. The detector element in a basic system is enclosed by a passive environmental radiation shield to decrease interference from external radiation sources (such as natural background radiation). The shield is made from low background lead (typically a few centimeters thick, 5–15 cm) and may include an additional internal graded shield of tin and copper to attenuate the lead (and tin) fluorescent X-rays produced within the shield. Selected ultra-low background construction materials for the detector chassis, low background noise preamplifier, and low background environments (e.g., under damp walls, underground tunnels or caves) including efficient ventilation system eliminating radon progeny may also be used to further increase the sensitivity of a gamma spectrometry system (Fig. 5.11).
5.2.2 Scintillation spectrometry
A scintillation detector consists of a scintillator which emits light pulses when exposed to radiation and a device, usually a photomultiplier tube (PM), which transforms these light pulses into electrical signals. A scintillation spectrometer has a lower energy resolution than a semiconductor detector. However, despite the low energy resolution, scintillation detectors are widely used in routine monitoring tasks of building materials. The reason for this is a high sensitivity of the detector at a low cost and its ease of use—the detector does not require cooling to liquid nitrogen temperature, and the spectrometer generally has a lower weight and smaller dimensions (Fig. 5.12).
Still the most used type of scintillation detector for γ-spectrometry is the NaI(Tl) detector. The detector crystal with housing, photomultiplier, and base is relatively easily available even in large sizes. Portable versions with high voltage supply, amplifier, and MCA, all powered by batteries, can be purchased from several suppliers.
Fig. 5.13A shows spectra, registered by the scintillation detector from sources containing 40K, 238U, and 232Th in radioactive equilibrium, while Fig. 5.13B shows the spectrum of a mixture of these radionuclides.
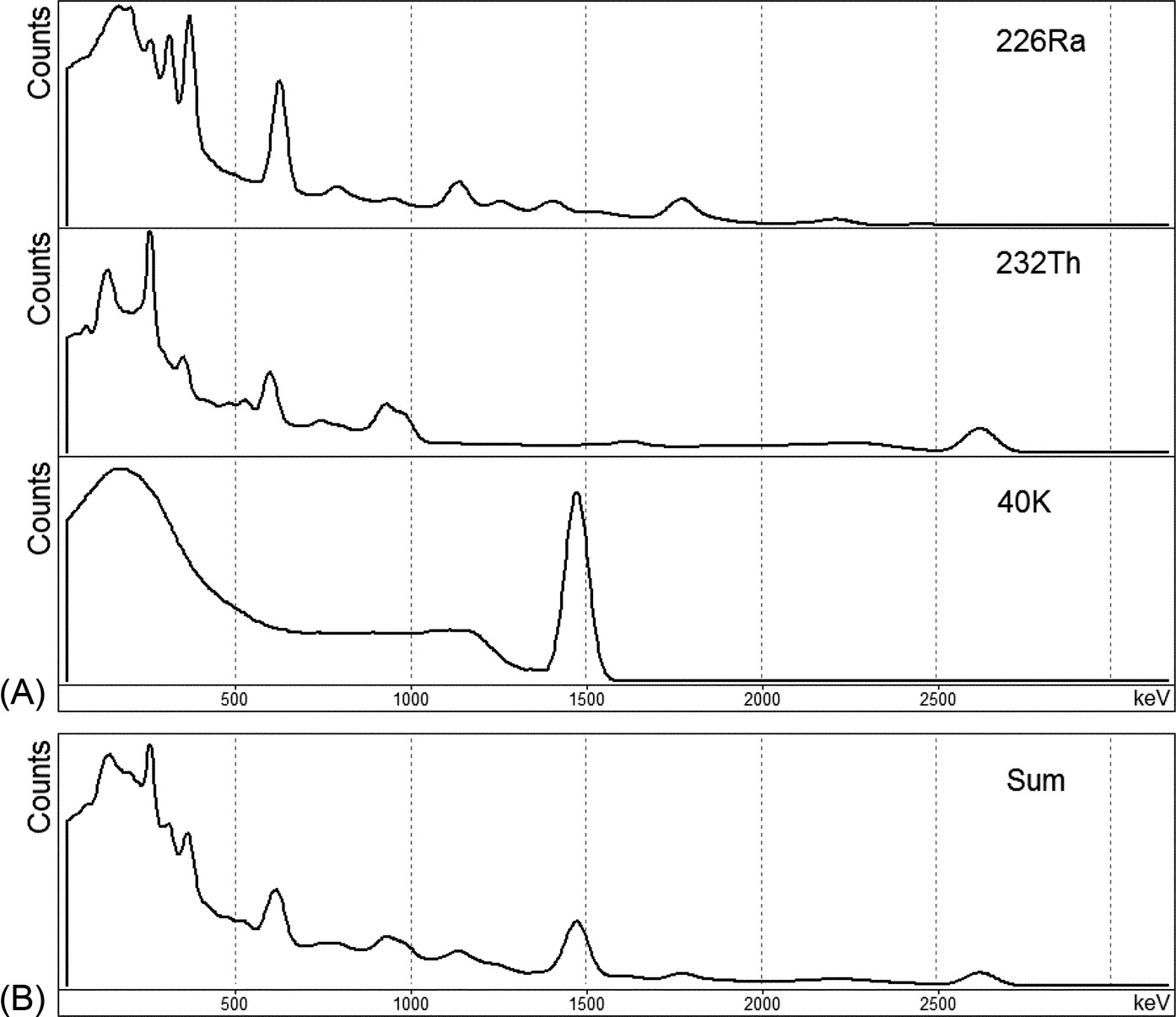
Special software was developed to overcome the drawbacks of low energy resolution of these detectors. It does not allocate single peaks for every radionuclide, but represents the whole measured spectrum as a sum of the images due to the contributions of these radionuclides. The spectra shown in Fig. 5.13A are determined during calibration of the spectrometer and represent the device response to radiation of unit activity of a radionuclide. The software automatically adjusts the image to the difference in densities of a test sample from the samples used in the calibration.
The conventional approach of spectra analysis is to calibrate broad spectral windows during the analysis for the main natural isotopes (Verdoya et al., 2009; Desbarats and Killeen, 1990). Generally, these windows are chosen around the photopeaks of 40K (1460 keV), of 214Bi (1765 keV), and of 208Tl (2614 keV). Three typical energy intervals for in situ measurements are: 1370–1570 keV; 1660–1860 keV; and 2410–2810 keV (IAEA, 2003). The concentration of 238U and 232Th are then evaluated detecting the γ-rays produced by 214Bi and 208Tl respectively. The assumption of secular equilibrium of the decay chains is required in order to use this approach. In addition to the above-mentioned radionuclides, the three-windows method has been extended to the measurement of 137Cs by Cresswell et al. (2006) and Sanderson et al. (1989).
The model of measurement assumes that the detected energy spectrum of gamma radiation is the sum of independent contributions due to background radiation and radiation of jmax radionuclides, which are present in the counting sample:
with s(E), detected energy spectrum, imp/(s keV), (imp=impulses); b(E), background energy spectrum, imp/(s⋅keV); pj(E), the fundamental energy spectra of the 1 Bq of element j, imp/(s⋅keV⋅Bq); Cj, the concentration of the element j, Bq; j, the index, which stands for K, Th, U, and eventually for 137Cs (if this artificial radionuclide is of interest in building materials and products).
The integration of the Eq. (5.5) in mmax different energy intervals (mmax>=jmax) leads to a system of mmax equations
where Sm (sample count rate in the energy interval m), Bm (background count rate in the energy interval m), and Pj,m (sensitivity of the detector to irradiation of radionuclide j in the energy interval m) are the integral by energy within the interval m from the functions s(E), b(E), and pj(E), respectively.
The relation Eq. (5.6) can be written in matrix notation Eq. (5.7) with Rm=Sm−Bm (net sample count rate i.e., sample count rate corrected for background) where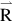 
is a vector with m components, 
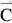is a vector with j components and [P] is a jmax×mmax matrix.
In the simplest case, with only three energy intervals, as mentioned before, only about 5% of all impulses are registered. This low number of counts leads to an unnecessary large statistical uncertainty.
An example of the sensitivity matrix estimated for a 3″×3″ (cylindrical form: height 7.64 cm, diameter 7.64 cm) NaI(Tl) for pads used for ground measurements (3 m in diameter, 50 cm thickness, and 2.25 g/cm3 density) is given in Table 5.1 (IAEA, 2003). Because there is only one single line from potassium, no crossover occurs to the uranium and thorium window. Vice versa, uranium and thorium progeny produce γ-emission with many different energies causing also counts in the other windows.
Table 5.1
Example for a sensitivity matrix [P]
| [S] | Potassium window | Uranium window | Thorium window |
| cps/%K | 3.360 | 0.000 | 0.000 |
| cps/ppm eUa | 0.250 | 0.325 | 0.011 |
| cps/ppm eTha | 0.062 | 0.075 | 0.128 |
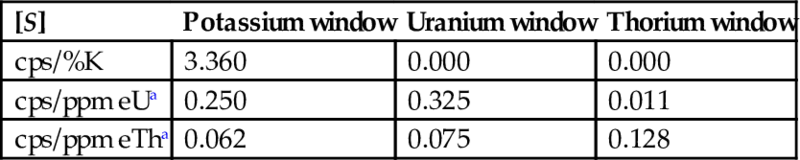
a Because U and Th concentrations are estimated by their decay products, the results are reported in equivalent uranium (ppm eU) and equivalent thorium (ppm eTh).
It has become a conventional representation for in situ measurements, at least for geological purposes, to express the concentrations of natural radioisotopes in their respective abundances, where K is given in % weight while eU and eTh are given in ppm.
The unknown concentration of K, U, and Th in a sample then can be calculated by
with [P]−1 the inverse matrix of the sensitivity matrix [P]. However, the inverse matrix is defined only for a quadratic matrix which means for three radionuclides only three windows can be chosen (jmax=mmax).
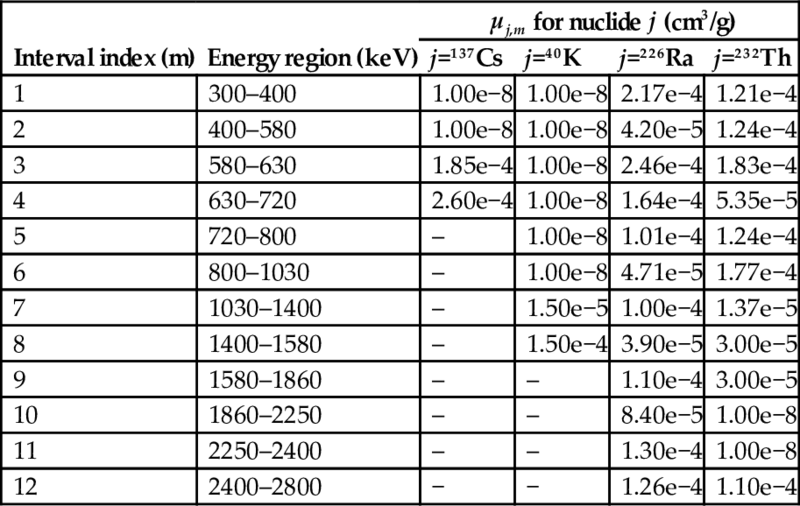
To increase the measurement accuracy more energy intervals can be used. A set of 12 energy intervals at the energy range 300–2800 keV proposed recently (Kovler et al, 2013) is listed in Table 5.2. To use this model either special software is necessary, or the software can be integrated in simpler computing facilities, such as in portable spectrometers.
Table 5.2
Coefficient μj,m for the 1 L Marinelli geometry
| Interval index (m) | Energy region (keV) | μj,m for nuclide j (cm3/g) | |||
| j=137Cs | j=40K | j=226Ra | j=232Th | ||
| 1 | 300–400 | 1.00e−8 | 1.00e−8 | 2.17e−4 | 1.21e−4 |
| 2 | 400–580 | 1.00e−8 | 1.00e−8 | 4.20e−5 | 1.24e−4 |
| 3 | 580–630 | 1.85e−4 | 1.00e−8 | 2.46e−4 | 1.83e−4 |
| 4 | 630–720 | 2.60e−4 | 1.00e−8 | 1.64e−4 | 5.35e−5 |
| 5 | 720–800 | – | 1.00e−8 | 1.01e−4 | 1.24e−4 |
| 6 | 800–1030 | – | 1.00e−8 | 4.71e−5 | 1.77e−4 |
| 7 | 1030–1400 | – | 1.50e−5 | 1.00e−4 | 1.37e−5 |
| 8 | 1400–1580 | – | 1.50e−4 | 3.90e−5 | 3.00e−5 |
| 9 | 1580–1860 | – | – | 1.10e−4 | 3.00e−5 |
| 10 | 1860–2250 | – | – | 8.40e−5 | 1.00e−8 |
| 11 | 2250–2400 | – | – | 1.30e−4 | 1.00e−8 |
| 12 | 2400–2800 | − | − | 1.26e−4 | 1.10e−4 |
In the extreme case, the energy intervals coincide with channels of the measured spectrum. In this case, the coefficient Sm is the value of the count rate recorded in channel m during the sample measurement and the number of equations in the system Eq. (5.6) is equal to the number of channels in the energy range used for processing. This method has been developed in different approaches (Maučec et al., 2009; Hendriks et al., 2001; Minty, 1992; Crossley and Reid, 1982; Smith et al., 1983) and was found to be a successful tool for spectrum analysis.
On one hand, the inclusion of as many channels as possible into the working range of the energy decreases the statistical measurement uncertainty. On the other hand, inclusion of the low energy region into the working area will increase the systematic component of the measurement uncertainty. Self-absorption of the radiation or of a portion of its energy in a sample substance by photoelectric effect or by Compton scattering at low energies contribute significantly to the shape of the spectrum s(E). If the probability for Compton scattering slightly depends on the atomic numbers present in the sample, and is determined mainly by the density of the sample, the probability for the photoelectric effect depends strongly on the atomic numbers present in the sample, which in practice is not always possible to consider. Therefore, the spectrum usually is only analyzed above an energy of 300 keV.
To account for the self-absorption processes of gamma-radiation the detector sensitivity is expressed as a function of the sample density. For that purpose, volume sources with different density ρ and known activity are used.
For every source the value of sensitivity Pj,m to the radiation of the radionuclide j in the interval m is
where Sj,m, count rate in the interval m registered from the source with density ρ; Bm, background count rate in the interval m; Aj, activity of nuclide j.
The function
is used to approximate the sensitivity depending on the sample mass.
Pj,m0 is the sensitivity for a zero density sample. It is derived in the calibration process by extrapolation. μj,m characterizes the effect of absorption and scattering of gamma radiation in the sample. It depends on the measurement geometry and is used to calculate a correction factor to the sensitivity of the detector, taking into account the difference between the density of the sample and the density of the calibration source. Table 5.2 shows the values of coefficient μj,m for the 1 L Marinelli geometry.
The activity concentrations are deduced applying the least square algorithm by minimizing the reduced χ2 according to Eq. (5.11):
where S(i) are the counts in the channel i; Cj are the concentration of the element j; Pj(i) are the associated counts to the fundamental spectrum of the element j in the channel i; B(i) are the counts in the channel i due to the intrinsic background; and the index j stands for K, Th, U, and eventually for 137Cs.
S(i) is considered Poisson distributed (then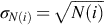 
) and n=b−a is the number of channels in the spectrum used in the analysis (the selected energetic range is typically 300–2900 keV: There is a strong presence of backscattering events below 300 keV, which depend on the atomic number and density of the surrounding materials; while above 2900 keV only the cosmic ray contribution is present).
The χ2 minimization without any further conditions can generate sensitive spectra having energy regions with negative events. To overcome this problem the NNLS (nonnegative least square) constraint was introduced. For details see (Lawson and Hanson, 1995; Désesquelles et al., 2009; Boutsidis and Drineas, 2009).
In the work of Kovler et al. (2013) the accuracy of activity determination by analyzing a spectrum by different methods is compared. For this purpose, different processing algorithms have been implemented for a certain detector. The algorithms differ by the number and width of energy ranges:
- energy intervals correspond to analyzer channels in energy range 300–2800 keV;
- 12 energy intervals according to Table 5.2;
- 4 intervals: 600–720; 1350–1560; 1640–1880; and 2500–2750 keV.
Measurements uncertainty values obtained for a coverage factor of k=2 are given in Table 5.3 describing the results obtained for a NaI(Tl) 2.5×2.5″ scintillation detector, measurement duration of 1 h and Marinelli 1 L geometry.
Table 5.3
Dependence of the expanded measurement uncertainty (twice the standard deviation of the measurement results) for low activity sample from processing method
| No. | Processing method | Expanded uncertainty (k=2), Bq | |||
| 137Cs | 40K | 226Ra | 232Th | ||
| 1 | Energy intervals correspond to analyzer channels in energy range 300–2800 keV (with more than 1000 intervals) | 1.1 | 16.4 | 2.1 | 2.5 |
| 2 | 12 energy intervals in energy range 300–2800 keV | 1.6 | 24.8 | 2.7 | 2.2 |
| 3 | 4 energy intervals | 1.6 | 25.3 | 4.6 | 3.1 |
Accuracy for all processing methods is sufficient to determine compliance of building materials with radiation safety criteria. Significantly lower cost makes this type of detector competitive in routine monitoring of large numbers and large volumes of construction materials.
The main advantage of the semiconductor detector, associated with its high-energy resolution, is the ability to identify the radionuclides in the samples with a complex radionuclide composition. This feature is not so relevant for the problem of measuring building materials—radionuclide composition of the sample is known a priori and is limited to natural radionuclides in a state of radioactive equilibrium. Exceptions are quite rare cases of imbalance (including in a chain of 232Th) by chemical processing of natural materials or ore dressing. Proper evaluation of the activity of individual radionuclides of 232Th chain in the absence of radioactive equilibrium can be carried out only with the semiconductor detector.
The most important limit of this method is that it is blind to any unexpected signal (anthropic isotopes). Other limitations are the low accuracy for short time acquisitions and the physical restriction of poor intrinsic energetic resolution of the NaI(Tl) detector.
It should be noted that the scintillation spectrometer software allows revealing cases of presence of additional radionuclides in the sample or imbalance between daughter radionuclides of 232Th chain. To do this, the software approximates the measured spectrum by a weighted sum of the fundamental spectra Pj(E) (model spectrum). If the model spectrum differs from the measured spectrum, the software displays a warning that a more detailed study of the sample would be indicated, including a high energy resolution semiconductor analysis (Fig. 5.14).
Today, some newer scintillation detectors are available which generally show better energy resolutions, e.g., LaCI3:Ce(0.9), CeBr3, BGO, CdWO4, and PbWO4. To analyze the spectra of these detectors usually smaller windows around the main photopeaks can be chosen, thus the crosstalk between the different isotopes is substantially reduced. These detectors stand in the energy resolution and therefore in the analysis procedures between the NaI(Tl) and the semiconductor detectors. A problem for low-level measurements is in some cases the low but nevertheless existing intrinsic radioactivity of these newer scintillation detector materials.
5.2.3 Calibration and metrological assurance
To transfer the results of a measurement (e.g., counts/s) into activity or activity concentration a calibration of the spectrometer is necessary. Usually a linear relation between measurement result and the activity (concentration) exist. The proportionality factor is called efficiency which depends on the geometry of the measurement and the sample properties as density and composition. For semiconductor detectors usually the efficiency for the photopeak as a function of energy (efficiency curve) is determined (see Annex B) for a specific geometry and sample properties. For scintillation detectors the sensitivity matrix [P] (Eq. 5.8) or matrix Pj,m0 and μj,m (Eq. 5.10) are determined.
The calibration of semiconductor spectrometer can either be done by (1) using a reference source with known activity or (2) by a calculation using the detector characteristics as well as the foreseen measurement geometry and sample properties.
The first method allows metrological traceability which in some countries is demanded by law. The second method usually uses Monte Carlo codes but does not formally provide traceability of the results to a primary standard. The correct use of this method produces accurate results and in some cases (e.g., in certain situations of in situ measurements) it is the only possible method of calibration. Further details can be found in Annex B.
Calibration of a scintillation detector is usually a little more complicated, and includes not only the determination of the efficiency of the detector, but also the form of the Compton part of the spectrum. Unlike semiconductor detectors that are calibrated directly in the measurement laboratory, scintillation detectors are often calibrated by the equipment manufacturer. The user is supplied with a system of coefficients for different geometries or can directly adjust the used measurement geometry in the unit's software.
5.2.4 EU proposal of a harmonized standard for building products
5.2.4.1 Background
The European Commission decided to harmonize, promote, and consolidate the main recommendations concerning NORM, introducing them into a new Council Directive (EU, 2014) laying down basic safety standards for the protection against the dangers arising from exposure to ionizing radiation, the so called EU Basic Safety Standards, or EU-BSS. This BSS directive was officially issued in Jan. 2014 and is described in more detail in Chapter 4. Member States were given four years to transpose and implement this directive and according to the Euratom Treaty, members shall before then communicate to the Commission their existing and draft provisions. The Commission shall then make appropriate recommendations for harmonizing the provisions amongst member States.
Requirements of this directive dealing with building materials need to be taken into account along with the 2011 EU regulation laying down harmonized conditions for the marketing of construction products (EU, 2011) so called construction product regulation, or CPR, containing many relevant articles which complement the aforesaid BSS directive. Both EU regulatory documents constitute the new basis for building material radiation protection regulation and should be soon followed by more detailed EU guidance and standards (see Chapter 4). Subsequently, the European Commission (EC) has mandated the CEN to establish EU harmonized standards regarding the determination of the activity concentrations of natural nuclides in construction products using gamma-ray spectrometry. Such standards should be robust enough not to give a chance to be challenged in the future; and they should be adopted by all Member States as soon as the BSS will come into force.
5.2.4.2 Scope
Under this mandate (M/366) a Technical Specification (TS) has been prepared by Technical Committee CEN/TC 351 Construction products—Assessment of release of dangerous substances'. The TS provides a measurement (test) method for the determination of the activity concentrations of the radionuclides 226Ra, 232Th, and 40K in construction products using gamma-ray spectrometry.
This TS describes the measurement method starting with the pretreatment of a laboratory sample, the test specimen preparation and the measurement by gamma-ray spectrometry. The description of measurement includes collection and analysis of a spectrum, background subtraction, energy and efficiency calibration, calculation of the activity concentrations with the associated uncertainties, the decision threshold and detection limit, and reporting of the results. Collection of product samples and the preparation of the laboratory sample from the initial product sample lie outside the scope of the TS. For that purpose rules described in product standards are suggested to be used. However, in case of NORM no strict recommendations exist and the adaptation of existing product standards is not always possible. Hence, individual approaches for NORM sampling based on general rules as described in the previous section are often required.
Authors of the TS have well identified major limitations and obstacles characteristic for gamma spectrometry and, additionally, this TS describes, in the normative part, the following:
• method for the determination of the radon-tightness of a test specimen container,
• preparation of standardized calibration sources,
• method for the determination of the activity concentration in a composite product, and
• determination of the dry matter content in the tested material and calculation of a related correction factor.
The TS is intended to be nonproduct-specific in scope, however, there are a limited number of product-specific elements such as the preparation of the test specimen and drying of the test sample that are not fitting to the generally requested procedures. The method is applicable to samples from products consisting of single or multiple material components, however special attention must be paid to proper preparation of representative test specimen when the testing material consists of more than one component.
Furthermore, the information within this TS is intended to be used for purposes of CE marking and evaluation/attestation of conformity. Product specification, standardization of representative sampling, and procedures for any product-specific laboratory sample preparation are the responsibility of product TCs and are not covered in this TS.
This TS supports existing regulations and standardized practices, and is based on methods described in standards, such as ISO 10703 (ISO, 10703, 2015), ISO 18589-2 (ISO, 18589-2, 2015), ISO 18589-3 (ISO, 18589-3, 2015), and NEN 5697 (NEN 5697, 2001).
5.2.4.3 The robustness testing
The draft of the TS 00351014 (Construction products—Assessment of release of dangerous substances—Determination of activity concentrations of radium-226, thorium-232, and potassium-40 in construction products using gamma-ray spectrometry) has undergone meticulous tests under real conditions in a gamma spectrometry laboratory according to the scenario developed by CEN/TC 351/WG 3 [“Revised work program for the robustness validation of draft TS 00351014” (N 116)]. The work program identified 14 parameters or measurement circumstances, respectively, that influence the results obtained by gamma spectrometry when applying the procedures set forth in the TS. However, all of these factors result from only a few physical phenomena and consequently the carried out tests were focused on:
• self-attenuation in an analyzed sample,
• radon leakage from measurement beakers,
• a temporary lack of secular equilibrium between radium and radon, and
• (long-term) lack of secular equilibrium inside uranium and/or thorium decay series.
All parameters influencing sample self-attenuation in all possible stages of the measurement process are presented in detail and one should give special consideration at any particular stage to these effects, which are summarized in Fig. 5.15.
The most important conclusions from the tests concerning the application of the TS are:
• According to the TS the activity concentrations of the gamma-emitting radionuclides in construction products should be determined by using high resolution gamma-ray spectrometry. A spectrometer with MCA with at least 4096 channels is required. This implies the use of high purity germanium detectors (HPGe), but this is not explicitly mentioned in the TS. That is why the question remains whether other detectors can be used without the risk not to comply with the standard requirements.
• As the TS requires, for 226Ra and 232Th the activity concentration should be determined using a progeny nuclide, while for 40K the concentration is based on the photopeak from the nuclide itself. Despite the application of high-resolution gamma spectrometry the TS assumes that only the four (most intensive) photo peaks with the gamma-ray energies 352 keV (214Pb, parent 226Ra), 583 keV (208Tl, parent 228Th), 911 keV (228Ac, parent 228Ra), and 1461 keV (40K) are used to determine the activity concentration of the radionuclides. However, when high resolution gamma spectrometry is applied, as required, there is no reason to use only one energy peak for the evaluation of a nuclide activity concentration. A weighted average from the use of more than one peak for the determination of the activity concentrations for a particular radionuclide will reduce the size of the uncertainty and will minimize the possibility of measurement errors. Existing practice showed that almost every professional gamma spectrometry laboratory is acting in this way.
• As was expected, all problems related to sample density, container shape, and volume can be solved by proper calibration using reference materials, which reflect the chemical and physical properties of the material, prepared as described in the standard. Separate standard samples are recommended for calibration of construction materials which are significantly different in chemical composition from materials of mineral origin commonly measured (e.g., for wooden materials). Therefore, the TS should not limit future user with materials made from raw materials of mineral origin for standard sample preparation as it is stated in the normative part of the current TS.
• In those cases, where the activity is determined using a progeny nuclide, a secular equilibrium between the progeny nuclide and its originating nuclide is necessary. To reach such equilibrium the test specimen is stored in a radon-tight container for a period of at least three weeks in order to ensure there is a secular equilibrium reached between 226Ra, 214Pb, and 214Bi inside the container. Additionally, the TS requires that it must be proved that no degradation in the equilibrium due to a leakage of radon from a beaker has happened. For this purpose the TS includes in the normative part a test for the determination of the tightness of the sealed measurement beaker. This test and applied criteria are questionable and can be replaced by a much simpler test. Moreover, including this test in normative part of the future standard would seriously limit its application due to the fact that not so many gamma laboratories have the required resources to carry out this test. Obviously, the solution for this problem is to make the standard a sealed beaker used multiple times.
• Despite the required waiting time of three weeks a disequilibrium in the 232Th decay chain can be present. Such disequilibrium is caused by different physio-chemical behavior between thorium and radium, the particular hydrogeological history and effects of industrial processes. Such disequilibrium is mirrored by a significant difference in the radioactivity concentrations of 228Th and 228Ra. In case of such a disequilibrium, the TS requires the use of available alternative measurement techniques or procedures for the determination of the 232Th activity. But this is outside the scope of this document. However, taking into account the behavior patterns of the above-mentioned radionuclides in the 232Th chain as described in Chapter 3, the specific observed ratio of 228Ra and 228Th radioactivity concentration, as well as supporting information concerning the origin of the NORM, allows the estimation of the 232Th activity concentration. 232Th does not contribute to the external dose because it is a pure α-emitter. But its direct progeny 228Ra is of importance for the external gamma dose. Therefore, exact information about the activity concentration of 232Th would be necessary when the observed 228Ra to 228Th ratio is bigger than one, otherwise it is almost sure that 228Th is not present in the sample at all (see Figs. 3.3 and 3.4 from Chapter 3). This limits the necessity of direct measurement of 232Th activity concentration significantly; however, this fact is not mentioned in the TS.
5.2.4.4 Summary
Currently (as of Jan. 2017) the relevant European standard is under development and the final form is still uncertain. However, experience collected by many gamma spectrometry laboratories involved in measurement of construction materials shows that the discussed version of Technical Specification presented by Technical Committee CEN/TC 351 “Construction products—Assessment of release of dangerous substances” for the determination of the activity concentrations of the radionuclides 226Ra, 232Th, and 40K in construction products using gamma-ray spectrometry does not need significant changes. However, some part of the future standard, as discussed in the previous section, should allow users more flexibility in their choice of options provided by the state of the art in gamma spectrometry.
The full report from the robustness validation of draft TS 00351014, prepared by Silesian Centre for Environmental Radioactivity (GIG, Poland) will be available for the public on CEN web site.
5.3 Dose rate measurement
5.3.1 Preliminaries
According to the EU BSS the annual gamma dose rate to a single person of the public caused by building material should not exceed 1 mSv. Generally this cannot be measured directly and therefore several assumptions are necessary. These assumptions concern the personal habits and the construction of the dwelling, the person lives in. Investigations have shown that people spend about 80% of their life indoors. With this assumption ambient dose rate measurements can be used to estimate the annual dose inside a house and check it for compliance with annual dose reference level of 1 mSv. This rather easy-sounding procedure has several difficulties and drawbacks. The difficulties will be discussed in detail below while the drawback of the method is obvious: The measurement is done after building a house with certain building materials. Constant ambient dose-rates are usually measured by active dose-rate meters, based either on ionization-chambers, Geiger-counters, or scintillation counters. For legal purposes these devices must be calibrated and in some countries it is necessary to have them stamped by a national metrology institute. In such a certification the conditions for the use of the measurement device are specified and the uncertainty of the reading is given when used within the limits of the conditions of use. Often also correction factors are given for a use outside the limits of the conditions of use. Typical conditions concern ambient temperature, humidity, power supply voltage, air pressure, linearity etc. which usually are not problematic. Much more difficulties come with energy dependence and angle dependence which will be discussed below. In most cases it is not necessary to correct for the natural background because it can be assumed that the shielding of the building reduces the background to a nonsignificant level. However, this is not always the case, e.g., at the ground floor in areas with enhanced Uranium or Thorium concentration in the soil or bedrock.
5.3.2 Energy dependence
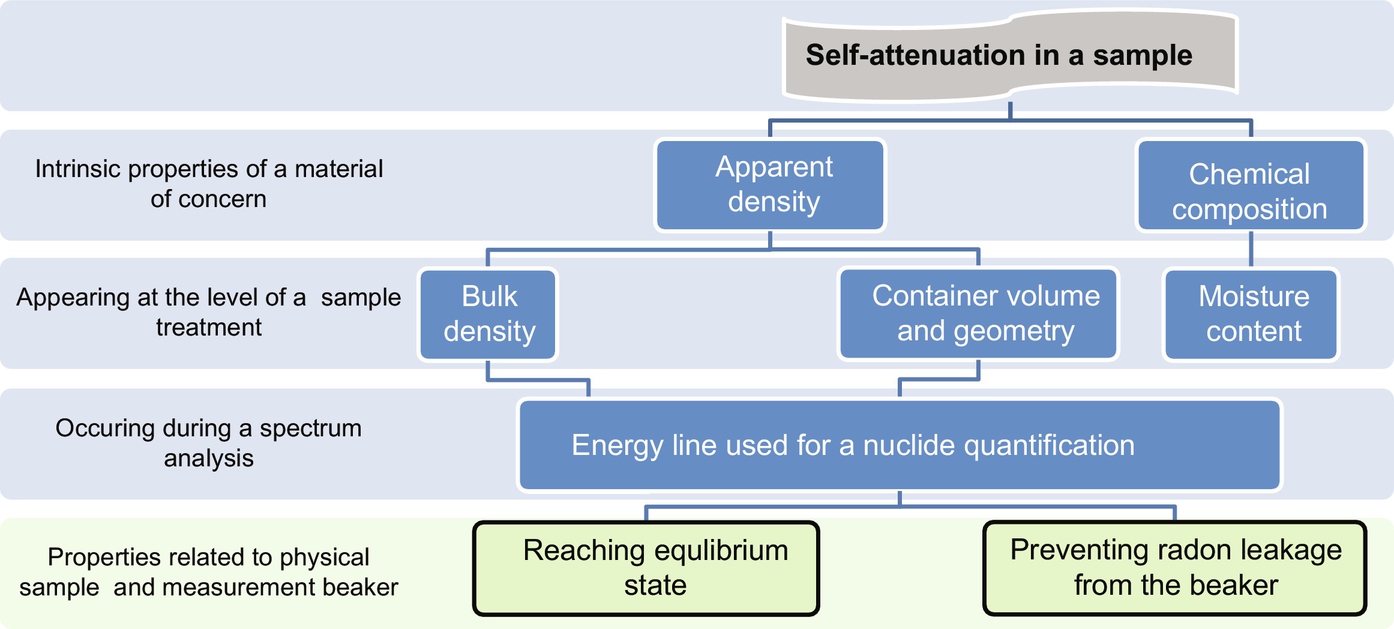
It is a good practice of the producer to supply dose-rate meters with a diagram concerning the dependence of the reading from the gamma energy (a typical example can be seen in Fig. 5.16). In other cases only the conditions for use are given, e.g., reading is valid within ±15% between 50 keV and 2 MeV. When dealing with radioactivity in building materials the three naturally occurring decay chains from 238U, 235U, and 232Th as well as 40K have to be regarded. 40K is not a problem because there is only one gamma energy of about 1.4 MeV which usually is within the conditions of use for most gamma dose-rate meters. However, gamma energies below 50 keV exist in the decay schemes. In case of radioactive equilibrium the contribution of gamma rays with energies below 50 keV is negligible, but in building materials radioactive equilibrium cannot be assumed, particularly in materials containing NORM residues, and then gamma and X-rays with energies below 50 keV may contribute substantially to the dose-rate. Because of the relatively low energies the radiation is partly shielded by the building material itself. Therefore, it is of importance, if the radioactivity is part of the bulk material or if it is part of a surface layer, e.g., tiles. It is not only the density which has to be considered but also the elemental composition which influences the self-absorption within the building material. If low energy radiation is essential, also the shielding by the person who measures can be a problem. Generally, when the interval of energies to be measured is known, then the correction factor can be taken as the mean between maximum and minimum of the correction factor within the energies of interest. For the uncertainty (coverage factor=1 means one standard deviation) half of the difference between maximum and minimum of the correction factor is a good choice.
5.3.3 Angle dependence
Dose-rate detectors are calibrated for a certain direction and the conditions for a correct reading (within the given uncertainties) include a certain angle from this main direction. The efficiency of the detector and consequently the dose-rate reading decrease sometimes relatively fast (often to less than 30%) outside of this angle. This is especially important for the typical construction of hand-held dose-rate meters, which combine the detector and the electronics in one single box. The change in efficiency with angle is energy dependent too. In most cases, if at all, this dependence is only given for a certain energy (e.g., 662 keV). The angle dependence is caused by the construction of the device and, as mentioned above, there is also the effect of shielding by the person who measures the dose rate.
Thus, only in case of well-documented angle dependence it is possible to determine the ambient dose-rate by subsequent measurements in all directions. If this is not the case the dose rate must be determined for all parts of a building separately. The determination of the dose rate caused by one building product can be applied for building material control at the stage of production too. Taking into consideration that building material dose-rates are rather small, measurement devices with low detection limits are necessary which may be expensive. Many dose-rate meters can be switched to integrate the dose-rate over time, which allows extending the lower limit of detection (LLD) to lower values. Such an instrument can be used to quantify the dose-rate during the production of building materials without a specific determination of the isotopes contributing to the radioactivity. Moreover, the dose-rate will probably be more precise than that deduced from the concentration of the respective isotopes causing the gamma radiation. Thus, it can be imagined that if a measured dose rate from a building material extrapolated to a room construction (4π) remains below 1 mSv/y this building material can be used anywhere.
Another method for the measurement of ambient dose-rates is the use of specially developed integrating detectors, e.g., thermo-luminescence detectors (TLD). Such detectors may consist of more than one TLD crystal and may be calibrated for radiation from all angles. But even for these detectors it is necessary to observe the conditions of use (energy dependence).
5.4 Radon measurement
5.4.1 Basic information on radon and progeny
Radon is a radioactive noble gas formed by the decay of radium. As discussed in Chapter 3 two isotopes are relevant for the radioactive exposure, namely 222Rn (“radon (Rn)”) and 220Rn (“thoron (Tn)”). The radon isotopes form chains of daughter decay products (or progeny), which have the properties of metals and release considerable energy by alpha, beta, and gamma radiation (see Fig. 3.1 and Tables 3.4 and 3.5).
Because of the different half-life times, the behaviors of 222Rn (T1/2=3.82 days) and 220Rn (T1/2=55.8 s) are different. Generally, when speaking of radon 222Rn is assumed. The relative long half-life time allows 222Rn to distribute more or less uniformly in closed rooms, producing the short living decay products 218Po (T1/2=3.09 min), 214Pb (T1/2=26.8 min), 214Bi (T1/2=19.9 min), and 214Po (T1/2=164 μs) anywhere in the rooms. In a sealed volume a satisfactory radioactive equilibrium between 222Rn and its short-lived decay products (equilibrium factor), as well as their decay in the case of instantaneous removal of radon, is obtained within 2–3 h, because the effective half-life time of the mixture of the short-lived radon decay products is about 40 min. Therefore, the activity concentration of short-lived decay products in the air is in general controlled by the radon behavior. In real rooms, a part of the short-lived progeny is removed as a result of ventilation and plate-out on walls, furniture etc. but the rest remains in the air and is responsible for the internal dose. The indoor equilibrium factor generally ranges from 0.2 to 0.7 (see Chapter 3). The atmospheric content of the long-lived radon decay products 210Pb (T1/2=22.3 years), 210Bi (T1/2=5.01 days), 210Po (T1/2=138 days), and 206Pb (stable) is extremely low due to the very long half-life of 210Pb and the almost complete precipitation of this progeny from the atmosphere to some surfaces. The contribution of the long-lived radon progeny to the radiation dose is very small; and therefore will not be considered here.
220Rn decays relatively quickly and shows its highest concentration close to its source, e.g., close to the walls. In radioactive equilibrium the formed decay products of 220Rn, which are 216Po (T1/2=0.15 s), 212Pb (T1/2=10.6 h), 212Bi (T1/2=60.5 min), 212Po (T1/2=0.30 μs), and 208Tl (T1/2=3.06 min) cause higher doses than the decay products of 222Rn for the same concentration. Nevertheless, in many cases the contribution to the internal dose from 220Rn can be neglected because its progeny often plate-out substantially on the walls from where 220Rn is emitted and the exhalation rate of the 220Rn from walls' surface usually is much less than that of 222Rn (see Chapter 3).
In the internal dose formation by thoron decay chain, the decisive role belongs to 212Pb, which has a half-life of more than 10 h—significantly longer than that of 220Rn and all other progeny, and longer than usual air exchange rates. Besides deposition on walls, the remaining part of 212Pb is removed from the room air due to ventilation. Therefore, there is a significant shift of radioactive equilibrium in this chain, indoors and outdoors, where the equilibrium factors drops to 0.01 or even lower values.
5.4.2 Radon and radon progeny measurement methods
Due to the significantly different lifetimes between 222Rn and 220Rn, an activity of 1 Bq corresponds to 476,600 222Rn atoms and 80 220Rn atoms. Therefore, usually the 220Rn contribution to the internal dose can be neglected and the focus in this section is concentrated on 222Rn measurements. However, if a substantial contribution of 220Rn is expected, it is necessary to control 220Rn or rather its progeny too. In addition, the presence of 220Rn can significantly distort the measurement results, when continuous or integrated radon measurements are conducted, which do not take into account the contribution of thoron and its progeny.
5.4.2.1 Classification of the methods
The international standard of ISO (ISO, 11665-1, 2012) proposed a classification of radon and its progeny measurement methods (Table 5.4). According to this standard, the sampling duration is important for achieving the measurement objective and the required uncertainty. For the sake of presentation, the measurement methods can therefore be distinguished based on the duration of the sampling phase: (a) integrated measurement methods, (b) continuous measurement methods including measurements with registration periods from 1 to 6 h, and (c) spot measurement methods. The information that is provided by these three different types of measurement is described briefly below.
Table 5.4
Classification of the methods to measure radon and its progeny
| Radon detection principle | Measurement method (usual sampling duration) | |||||||
| Spot (<1 h) | Continuous (variable) | Integrated | ||||||
| Short-term (few days) | Long-term (several months) | |||||||
| Sampling characteristics | ||||||||
| Active | Active | Passive | Active | Passive | Active | Passive | ||
| Ionization chamber | Rn,Tna | Rn,Tna | Rn | – | – | – | – | |
| ZnS(Ag) scintillation | Rn,Tna | Rn,Tna | Rn | – | – | – | – | |
| Gamma spectrometry (or gamma and beta radiometry) | Activatedcharcoal | Rn | – | – | – | Rn | – | – |
| Liquid scintillation | ||||||||
| Alpha spectrometry | Filter | RnP,TnP | RnP,TnPa | – | – | – | – | – |
| Electrostatic precipitation | Rn, Tna | Rn,Tna | Rn | – | – | – | – | |
| SSNTD+Filter | – | – | – | RnP,TnP | RnP,TnP | |||
| Electret | – | – | – | – | Rn,Tna | – | Rn,Tna | |
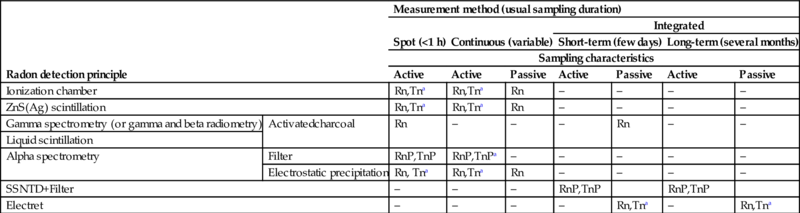
Notations: Rn, measurement of radon activity concentration; Tn, measurement of thoron activity concentration; RnP, measurement of radon progeny activity concentration, as EEC or PAEC (conversion between EEC and PAEC can be found in the Glossary); TnP, measurement of thoron progeny activity concentration, as EEC or PAEC.
a Measurements are not supported by metrological assurance, so the uncertainty of measurement results is unknown.
(a) Integrated measurement method
This method gives indications for measuring the average radon activity concentration or the average potential alpha energy concentration (PAEC) or the equilibrium equivalent concentration (EEC) of radon progeny in the air over periods varying from a few days to one year. Long-term integrated measurement methods are applicable in assessing human exposure to radon and its decay products.
(b) Continuous measurement method
This continuous monitoring enables the assessment of temporal changes in radon activity concentration in the environment, in public buildings, in homes and in workplaces, as a function of ventilation, and/or meteorological conditions.
(c) Spot measurement method
This method gives indications for spot measuring, at the scale of a few minutes at a given point, of the radon activity concentration or the PAEC or EEC radon progeny in open and confined atmospheres.
Table 5.4 addresses different types of sampling. Active sampling means continuously or intermittently forced pumping air through detector, filter, etc. Passive sampling does not use a forced pumping; in this case radon penetrates into measuring chamber, the sorption column, etc. by diffusion.
5.4.2.2 Radon detection principles
The radon detection principles mentioned in Table 5.4 are as follows ISO 11665-1 (ISO, 11665-1, 2012):
(a) Ionization chamber
When travelling through air, each alpha particle creates several tens of thousands of ion pairs which, under some experimental conditions, produces an ionization current. Although very low, this current may be measured using an ionization chamber that gives the activity concentration of radon and its decay products. When the sampling is performed through a filtering medium, only radon diffuses into the ionization chamber and the signal is proportional to the radon activity concentration.
(b) ZnS(Ag) scintillation (silver-activated zinc sulfide)
Some electrons in scintillating media, such as ZnS(Ag), have the particular feature of emitting light photons by returning to their ground state when they are excited by an alpha particle. These light photons can be detected using a photomultiplier. This is the principle adopted for scintillation cells, such as Lucas cells.
(c) Gamma spectrometry (or gamma and beta radiometry)
The radon, adsorbed on activated charcoal encapsulated in a container, is determined by gamma-ray spectrometry or gamma and beta radiometry of its short-lived decay products after their equilibrium is reached.
(d) Liquid scintillation
The radon, adsorbed on activated charcoal placed in a vial, is measured following the addition of a scintillation cocktail by counting alpha and beta particles emitted by the radon and its short-lived decay products after their equilibrium is reached
(e) Alpha spectrometry (based on the semiconductor detector)
A semiconductor detector (made of silicon) converts the energy from an incident alpha particle into electric charges. These are converted into pulses with amplitudes proportional to the energy of the alpha particles emitted by the radon or thoron decay products. This progeny is concentrated either near the front of the detector in case of sampling on a filter, or are precipitated directly onto the surface of the detector due to the electric field created specially in the measuring chamber.
(f) Solid-state nuclear track detectors (SSNTD)
An alpha particle triggers ionization as it passes through some polymer nuclear detectors (such as cellulose nitrate). Ion recombination is not complete after the particle has passed through. Appropriate etching acts as a developing agent. The detector then shows the tracks as etching holes or cones, in a quantity proportional to the number of alpha particles that have passed through the detector.
(g) Electret (discharge of polarized surface inside an expositional chamber)
A polytetrafluoroethylene (PTFE) disc with a positive electric potential is inserted into an ionization chamber, of a given volume, made of plastic conductive material. The electrostatic field, thus created inside the chamber, collects the ions formed during the disintegration of the radon and its decay products on this disc. After the ions have been collected, the electric potential of the disc decreases according to the radon activity concentration. An electrometer measures this potential difference, which is directly proportional to the radon activity concentration during the exposure period.
When thoron activity concentration is measured by SSNTD or Electret methods, two detectors are simultaneously exposed to thoron; one of them provides a diffusion barrier to eliminate the penetration of thoron in the exposition chamber. The difference between the measurement results obtained on these detectors is associated with the thoron activity concentration, but the uncertainty of this assessment is questionable due to the lack of metrological assurance for measurements of the thoron activity concentration.
5.4.3 Measurement of indoor radon concentration
The EU-BSS establishes reference levels for indoor radon concentrations. No distinction is made between building materials and the soil as sources of radon.
In this section the measurement of indoor radon concentration, as required by the EU-BSS, is discussed. Although the contribution of building materials to the indoor radon concentration is not regulated separately by the EU-BSS, and in spite of the fact, that it is indeed difficult to distinguish between building materials or the soil as sources of radon, but understanding how building materials contribute to the overall indoor radon, and how to limit this contribution by means of controlling radon exhalation from the surface of building materials, taking into account numerous different factors influencing indoor radon, is an important task, especially in the contest of the present book.
Indoor radon concentrations vary usually in a wide range, especially in rooms with high content of radon (relative to outdoor radon), as shown in Fig. 5.17. This is mainly due to the variations of air exchange rates caused by the ventilation mode, behavior of the inhabitants or workers, and changing weather conditions (mainly, temperature, wind).
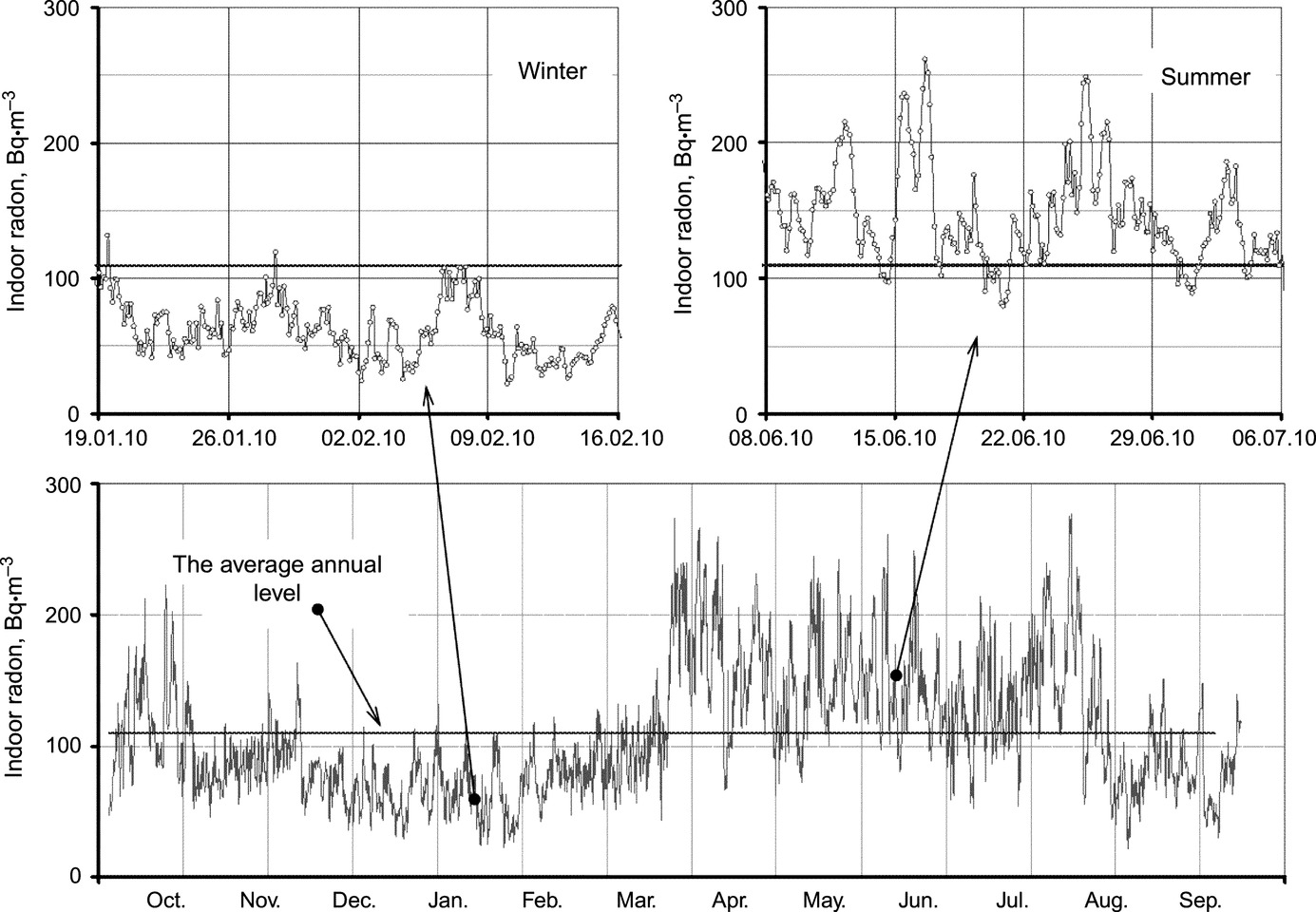
This section does not deal with radon exhalation from the soil, its further transport into the dwelling and the resistance of building materials to the radon inflow from the soil into the living space, because this problem is rather complicated and is out of the scope of NORM4Building. At the same time, it is well known that in most cases the indoor radon concentration is mainly determined by the inflow of radon from the ground below a building. For that reason and because of the wide variability of the indoor radon concentration, the measurement of the indoor radon concentration is usually not appropriate to estimate the contribution from the building material.
Significant variability of the indoor radon concentration due to a large number of influencing factors is the main problem in the interpretation of measurement results and reliable prediction of annual average indoor radon concentration.
When the average indoor radon concentration exceeds the level of outdoor radon by 5–10 times or more, usually both diurnal and seasonal variations of radon are observed. The amplitude of the temporal radon variation in buildings with a low radon concentration (at level of outdoor radon or slightly higher, but not more than 2–3 times higher) is significantly lower, and their regularity is less expressed.
Many researchers try to study the correlation between short-term and long-term measurement results. The unknown uncertainty of the annual average radon concentration using the measurements of different duration (both short- and long-term testing) prevents making reliable estimation. Obviously, the most accurate estimate of the average indoor radon concentration may be achieved, if the measurements were carried out during the whole year. However, only <2% of indoor radon measurements conducted, for example, in the US are made using long-term devices (George, 2015). The decrease of measurement duration will obviously tend to higher uncertainty of annual average estimates. In practice, the measurement duration varies usually from a few days to 1–2 weeks (short-term and continuous measurements), but sometimes can last 1–3 months and even longer (long-term and continuous measurements). Moreover, different countries use various measurement strategies and the corresponding traditional methods of estimating the annual average indoor radon concentration (WHO, 2009), including the measurement protocol for radon control applied in the USA. This protocol is based exclusively on a traditional experience approach (ANSI/AARST MAH, 2014). However, none of these methods, including those standardized by ISO (ISO, 11665-8, 2012), provides an estimate of the uncertainty of annual average indoor radon concentration.
An interesting method allowing to estimate quantitatively the uncertainty of measuring indoor radon is described in Annex C.
In most cases, indoor 220Rn is not of importance, however when enhanced concentrations exist, then the building material can certainly be the source. Therefore, sometimes its measurement is necessary, if the research object contains materials with a high activity concentration of 232Th or 228Ra. To evaluate the contribution to the effective dose the PAEC or the EEC of thoron progeny concentration should be measured, because a significant shift of radioactive equilibrium within the thoron decay chain always occurs indoors and outdoors. Therefore, the relation between the thoron activity concentration and the EEC (or PAEC) is difficult to determine correctly.
5.4.4 Measurements of radon emanation and exhalation
The basic parameter characterizing the rate of radon release from the surface of materials is the radon surface exhalation rate ES (Bq/m2/s). Another parameter is the radon mass exhalation rate EM (Bq/kg/s). But when only EM is known, one should take into account that, depending on the dimensions of the product and diffusion coefficient of radon in the material, only a part of free radon generated in the product is able to escape into the ambient air. The values of ES and EM can be obtained either by direct measurement, or by calculation in accordance with (3.13)–(3.15), if the values of the 226Ra activity concentration CRa (Bq/kg), the coefficient of emanation ɛ (rel), the density ρ (kg/m3), and the radon diffusion coefficient in the material D (m2/s) are known. Therefore, this section reports the methods of measurements of all of these three parameters: radon surface exhalation rate (ES), radon mass exhalation rate (EM), and radon emanation coefficient (ɛ). The value of CRa is determined by gamma spectrometry, as reported in detail before. Determination of D is a standard procedure, according to the future ISO standards ISO 11665-12 (ISO/TS, 11665-12, 2017) and ISO 11665-13 (ISO/TS, 11665-13, 2017). The standard (ISO 11665-12), in particular, proposed a rapid method for measuring the radon diffusion coefficient in various kinds of materials, which allows to reduce the duration of the test to 18 h. Further details about this method are available in Tsapalov et al. (2014).
The calculation formulas (3.8)–(3.15) describing the laws of emanation, transport, and exhalation of radon from materials are also valid to thoron, but have to consider the restrictions listed in Chapter 3 (Section 3.5.2).
5.4.4.1 Radon surface exhalation rate
The measurement of radon exhalation rates of building materials can be made by different methods (Kovler, 2012). Three fundamentally different methods of measuring radon surface exhalation rate are known. They are based on the analysis of radon release rate from the surface of the well-known area limited by sampling container (chamber). The features of the measurement principles depend on the different methods of sampling (passive or active), as well as on the design and composition of the sampling container (open or closed). Taking into account these differences, the measurement principles of the radon exhalation measurement have been suggested.
The Closed-Chamber Method (passive accumulation of radon in a closed container) is the most common method of measurement. It is based on the principle of radon accumulation in a closed container (usually of cylinder shape, with a diameter of 0.1–0.5 m and a volume of 1–10 L), which is mounted on the surface of the soil (IAEA, 2013) or the building material. The measurement of accumulating radon in the container is carried out in different ways, using (a) electrets (Kotrappa et al., 1993), (b) radon radiometers with either active (Lehmann et al., 2003) or passive (Lopez-Coto et al., 2009) sampling, or (c) activated charcoal, followed by measuring the activity of gamma radiation progeny of radon which accumulated in the activated charcoal (Duenas et al., 2007).
The international standard ISO 11665-7 (ISO, 11665-7, 2012) based on the Closed-Chamber Method gives guidelines for estimating the radon-222 surface exhalation rate over a short period (a few hours), at a given place, at the interface of the medium (soil, rock, laid building material, walls, etc.) and the atmosphere. The measurements are limited in time due to the growing influence of the closed chamber on the object of study with increasing duration of its exposure.
The essence of the Closed-Chamber Method, according to ISO 11665-7 (ISO, 11665-7, 2012), is to determine in the region of linear increase of the radon activity concentration, the rate of the increase in a closed container, which is purged by a clean atmospheric air (or better nitrogen) prior to the measurement after its installation on the investigated surface.
Starting from certain time after purging the container (depending on its height), the growth of radon activity concentration shows nearly a linear increase and later an asymptotic behavior: it slows down, ending in an equilibrium value. In this ideal steady-state mode (without leakage) the flow of radon into the container is practically absent. The calculation of ES (Bq/m2/s) is performed by measurements of radon activity concentration in the nonsteady state mode (during linear growth) by the formula:
with ΔC, change in the radon activity concentration in the container in the linear region, Bq/m3; Δt, time interval changes in the radon activity concentration, s; V, effective volume, m3; S, container base area, m2.
The ISO standard (ISO, 11665-7, 2012) addresses additional factors causing a disturbance in the free surface exhalation rate, which can significantly influence the final estimations:
(a) The variations in conditions (pressure, temperature, humidity) inside and outside the accumulation container: To minimize these effects, accumulation is specified in the standard to take place over a period of time with little variation in the external and internal container conditions (heavy rain and showers shall be avoided). However, the accumulation container may be thermally insulated.
(b) Inadequate air tightness (leakages) and back diffusion induce radon loss. To minimize the effect of leakages, improving air tightness is recommended. To minimize the effect of back diffusion, the container should be purged with radon-free air before beginning the accumulation process, and the calculation of the exhalation rate should be based on the initial slope of the curve of accumulation. It has to be clarified that the concept of “back diffusion” is often used in the professional literature and even in the ISO standard, although this term is not clearly defined and lacks the scientific basis. In this case, it should be understood that reduction of the radon diffusion into a closed container is due to the decrease of a gradient of radon activity concentration at the boundary, according to the Fick's law.
(c) The significant activity concentration of thoron in the soil pores.
Finally, the ISO standard ISO 11665-7 (ISO, 11665-7, 2012) provides the algorithms for estimating radon exhalation rate for different methods of measuring radon concentration in the container. However, as far as the implementation of these estimates is concerned, the standard procedure does not guarantee the reliability and accuracy of the measurements, because this standard does not define the calibration procedure of the measurements of radon surface exhalation rate.
The Open Charcoal Chamber Method (passive accumulation of radon in an open chamber with activated charcoal), in contrast to the Closed-Chamber Method, has a metrological assurance and passed the appropriate tests (Tsapalov et al, 2016a). However, this method is mainly used only for measuring the radon exhalation rate from the soil surface. Furthermore, this method is little known in the world, although is widespread in Russia and is used to control radon hazard of construction sites already for more than 20 years (Tsapalov et al, 2016a).
The Active Open-Chamber Method (continuous pumping of air through an open container) has not yet received wide practical application, because it is little known and rarely used in studies (Pearson at al., 1965; Pearson and Jones, 1966). Here, the measurement chamber is continuously purged with a fixed flow rate of the atmospheric or ambient air with a low radon concentration Co. The radon concentration in the container (or pumped air) is given by
with ω being the rate of air pumping in m3/s (here the radioactive decay is neglected). The advantage of this method is that the influence of back diffusion as well as the influence of other factors, e.g., the change of vapor pressure inside a closed chamber is avoided. The disadvantage of this method is the necessary high sensitivity of the radon detector, especially when the radon exhalation rates are low. According to Jonassen (Jonassen, 1983), the difference between 2 in series connected chambers as described above can be applied for the determination of the exhalation rate for thoron [see e.g., (Tuccimei, et al., 2006; Ujic, et al., 2008; De With, et al., 2014)].
Generally, direct methods for measuring the thoron exhalation rate are more complex (Ujic et al., 2008) and not widespread, however the Dutch standard NEN 5699 (NEN 5699, 2001; De Jong et al., 2005) exists.
5.4.4.2 Radon mass exhalation rate
Two methods of measuring radon mass exhalation rate, which are different only in methods of sampling, as reported in (IAEA, 2013) are shown in Fig. 5.18.
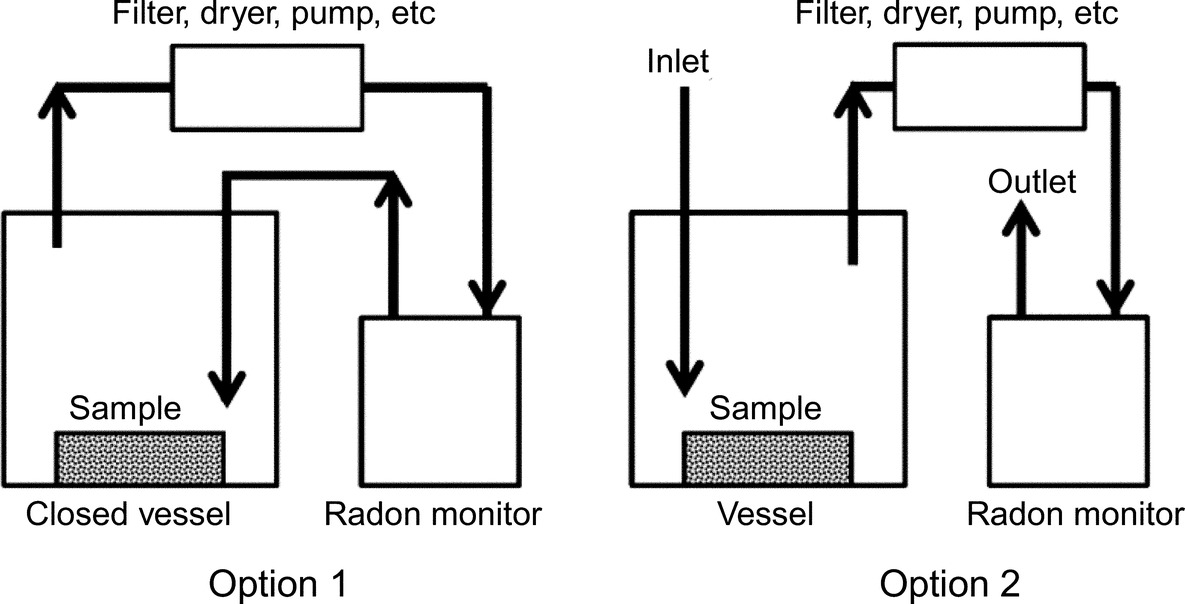
In the option 1, the sample is kept in a sealed vessel at least 4 weeks to establish radioactive equilibrium between radon and radium parent. Then the activity of radon freely released from the sample is determined, for example, by measuring the radon activity concentration in the whole volume of the measuring system, including the vessel, the measuring chamber device, tubes, and other adaptations. Finally, EM (Bq/kg/s) is calculated by the formula:
where,C∞ measured radon activity concentration, Bq/m3; V effective volume, m3; M sample weight, kg; λ radon decay constant, equal to 2.09×10−6 s−1.
In the option 2 (similar to the Active Open-Chamber Method) air (or better nitrogen) with the low Rn concentration Co is continuously pumped at a constant flow rate, through the vessel with a sample and the measuring device chamber. The radon activity concentration in the air flow is simultaneously measured, which corresponds to the rate of release of free radon activity from the sample per unit time taking into account the known volume rate of air flow and the radon concentration in the carrier gas.
Then, EM (Bq/kg/s) can be calculated as:
where ω is the volume rate of the pumped air, m3/s. In most cases ω≫λV and λV can be neglected.
It should be noted that the option 2 allows for quickly obtaining the result, but the uncertainty of such result will be significantly higher, than in the option 1 because of the low radon concentration to be measured. Therefore, the most sensitive methods for measuring radon activity concentration, have to be used, e.g., activated charcoal with liquid scintillation counting. In this case, the radon released from the sample is absorbed by (cooled) activated charcoal for a certain time, and then the radon activity in this charcoal is measured, according to the ISO standard (ISO, 11665-9, 2016).
5.4.4.3 Radon emanation coefficient
The measurements of the emanation coefficient are always conducted in the laboratory. A sample of the test material must be crushed to a fraction of the single grains not exceeding 8–10 mm by size, in order to let the free radon to be completely released into the ambient air due to diffusion even at the lowest values of the radon diffusion coefficient in material, taking into account its thickness, according to Fig. 3.5. The crushed sample should be dried naturally to the air-dry state. For this purpose the sample is kept in a dispersed state under room conditions, while free radon is naturally removed—this stage is called “deemanation” of the sample.
Determination of the emanation coefficient, ɛ (rel), may be carried out by analogy with the measurement of the value of EM (see the previous section). In this case, determination of the radium concentration CRa in the sample is additionally required, then the value of ɛ can be calculated from Eq. (3.15) taking into account Eqs. (5.14) and (5.15), respectively.
Another method to determine the emanation coefficient is achieved by means of gamma-spectrometry (IAEA, 2013). In principle two measurements are necessary: The first measurement concerns the sample at “deemanation state” that means all “free” radon and its progeny outside the sample are removed (kept in open air) so that only the activity concentration of the remaining “bond” radon and its progeny in the sample is measured and then converted to a virtual radium-concentration CRa*. The second measurement is carried out after keeping the sample in a hermetically sealed condition for at least 4 weeks for determining the radium activity concentration CRa which corresponds to the total activity of the “free” and “bond” radon. The value of ɛ is determined by Eq. (3.8) or (5.16)
Usually the determination of CRa* and CRa is performed by repeated measurements (recommended are at least three) and the uncertainty of the radon emanation coefficient is calculated according to ISO/IEC Guide 98-3 (BIPM/ISO/IEC Guide 98-3, 2008).
The Gamma-Method can be also used to determine the thoron emanation coefficient too, but the sample of test material must be crushed to powder. Deemanation of such sample is carried out by keeping that powder at a layer not thicker than 2 mm during at least two days to free air. The second measurement is performed in at least two days after sealing the sample.
5.4.5 Modeling indoor radon concentration from radon exhalation
Given the radon surface exhalation rates Ei (corresponds to ES in Bq/m2/s) for different building materials in a room the total inflow of radon in Bq/s can be calculated as
with Si (m2) being the surface area of the building material with the exhalation surface rate Ei. The air exchange rate λAE (s−1) is usually given as room volumes exchanged per hour. For example, λAE=1 h−1=1/3600 s−1 means that the amount of external air equal to the volume of the room V (m3) enters the room within 1 h (nowadays new houses with tight windows often have exchange rates of far below 1 h−1). The balance of the indoor radon activity concentration C (Bq/m3) in a nonsteady state mode is described by the equation
The first term at the right side is the total flux from building materials and soil (FS, Bq/s) divided by the total volume of the room; the second term is the reduction of the radon concentration caused by the air exchange rate; the third term accounts for radon reduction due to the radon decay with the decay constant λ=2.09×10−6 s−1 and the last term accounts for radon inflow from atmospheric air CA (Bq/m3). In the steady state condition C=constant for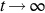 
, then 
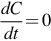, and the Eq. (5.18) can be easily solved given that λ≪λAE:
One has to realize that in most cases the ground below the building is the main source of indoor radon. Still, it is necessary to assure that building material with NORM ingredients will not contribute substantially to the indoor radon concentration. This is achieved by controlling and limiting (if necessary) the value of ES.
5.4.6 Estimation of the contribution from the building material to the indoor radon concentration
To estimate the contribution of building material to the indoor radon concentration, Eqs. (5.17) and (5.19) can be used. The member of FS in formula Eq. (5.19), considering the balance of radon only for the rooms of upper floors of buildings, will not be taken into account. The volume of the room and the area of the enclosing structures exhaling radon can be easily determined. Therefore, according to these formulas, the main components of uncertainty are the values of λAE and the surface exhalation rate ES.
The uncertainty of the ES-value can be estimated on the basis of formula (3.14), where the main sources of uncertainty are two quantities—ɛ and CRa, each of which can be determined in the lab with the accuracy of (30%–40%). Thus, the maximum uncertainty of the ES-value does not exceed 60% (the square root from a sum of squares of components of the combined uncertainty). In the case of direct measurements of the ES-value using the methods described in Section 5.4.4, even more accurate results can be obtained, if these methods have a reliable metrology assurance.
The value of λAE has an even larger uncertainty, but it does not exceed 100%. Indeed, taking into account the requirements for the design of modern buildings, most appropriately for modeling as the annual average would be to assume λAE=0.5 h−1. Then, with a high probability one can expect that the confidence interval of the λAE-value will be equal to 0.25–1.0 h−1 (i.e., the uncertainty of guaranteeing the optimum air exchange rate in premises of modern buildings roughly corresponds to 100%). It has to be noted that in premises with the annual air exchange rate of lower than 0.25 h−1 it would be difficult to guarantee a good indoor air quality and comfortable environment for long-term stay of building occupants, because the necessary hygienic requirements are violated. For example, air humidity increases, as well as the concentration of carbon dioxide and other nonradioactive gases released from building materials and interior items. As far as the high annual air exchange rate—exceeding 1 h−1, is concerned, it also does not provide a comfortable environment—differential pressures and powerful airflows in the rooms are developed. In addition, the energy efficiency of building is reduced.
Thus, the combined uncertainty of the evaluation of the annual indoor radon concentration obtained by modeling consists of two components (60% and 100%) and does not exceed 120%.
The obtained value of uncertainty exceeding 100% is generally perceived as unacceptably high. However, comparing the reference level of indoor radon (CR) to the level of average contribution from building materials (CM), it is quite acceptable that the modeling uncertainty may be so high. Indeed, according to the Eqs. (3.14), (5.17), and (5.19), and using the following parameter values: S/V=1.4 m−1, λAE=0.5 h−1, d=0.2 m, ρ=2400 kg/m3, ɛ=0.1 (see Table 3.5), and CRa=32 Bq/kg1 (the average concentration in the earth's crust), results in CM=16 Bq/m3. The reference values 300 or even 100 Bq/m3 are many times greater than the obtained value of CM. Analogous calculation shows that the indicated reference levels of the annual indoor radon in the upper floors of buildings confirm with the contribution from building materials, if the value of CRa is equal to 600 or 200 Bq/kg, respectively. Note that popular building materials can have a high activity concentration of radium, as seen from Table 3.6.
Thus, based on the above presented considerations and quantitative assessments a principle of appropriate restriction (standardization) of radon exhalation from building materials is justified.
From the above example it can be seen that the determination of ES could be important in case of an enhanced concentration of 226Ra. In case of a 226Ra concentration below, say 100 Bq/kg, and a nonhighly porous building material, radon from the building material should not lead to a radon concentration beyond the reference values.
5.5 Conclusions and recommendations
This chapter gives an overview on many aspects on measuring and how measurement results should be used to test the compliance of building materials (EU, 2011) with the EU Basic Safety Standards (BSS) (EU, 2014). However, all this information may be confusing to people who are not so familiar with radionuclide measurements, which is the case for the vast majority of people involved in either construction industry or construction materials manufacturing. Moreover, all parameters describing quality and expected mechanical properties crucial for construction materials (and hence controlled) have nothing in common with radioactivity.
Therefore, member states have not yet enforced requirements concerning radioactivity content in construction materials and seem not to be prepared to face the new challenges set in the directive. However, each member state has more or less well developed systems of nuclear safety and radiation protection with the relevant infrastructure as well as qualified personnel using all the measurement techniques discussed in this chapter. Therefore, it is not necessary to build a new measurement infrastructure from scratch. At the first stage, it is enough to introduce specific measurement procedures and engage existing resources. Such approach is justified also from an economic point of view because the necessary equipment is rather expensive and needs trained personnel. Taking into account the existing situation the concerns of the construction industry related to the technical and economic consequences of the introduction of the new measurement techniques are not well-founded.
A final modus operandi for monitoring radioactivity in building material will depend on the existing necessities and possibilities (i.e., number of construction materials types, number of samples, actually available resources, and related costs). It is not yet clear if the number of sample measurements with the demanded uncertainty of the results (measurement time related) can be managed by the existing laboratories as they do measurements for other purposes. One can imagine simplifying measurement of radioactivity of construction materials in comparison to the gamma spectrometry prepared for monitoring environmental radioactivity in all types of samples. Besides that certain laboratories can specialize in radioactivity measurements of construction materials. This approach is also supported by the state-of-the art requirements concerning quality management systems that have become obligatory in all laboratories involved in measurement of any parameter somehow related to the occupational or health risk assessment.
In principle it is possible for construction material producers to control themselves for all the used material in advance and during the production but the end product should be controlled by certified laboratories.
A slightly different situation exists when considering existing capabilities of radon measurement. The exposure to radon is significant in confined spaces, but existing measurement methods do not allow a known and sufficient accuracy to estimate the average annual indoor radon concentration if measurement duration of less than month, because the indoor radon concentration usually varies substantially in time. At the same time, the simulation based on the known radiation and physical properties of materials (defined under laboratory conditions) allows more accurate prediction of the contribution of the radon exhalation from building materials to the annual radon concentration in modern buildings. It is important that the accuracy of such assessment is practically not reduced, if the restriction of radon exhalation from building materials is mitigated only by setting the reference level of radium activity concentration (perhaps, considering also the thickness or dimensions of the end product). Thus, the control and restriction of the contribution of radon exhalation from building materials in the annual level of indoor radon can be provided by the results of the same laboratory gamma-ray measurements. In other words, it is not necessary to use a special equipment and measurement method.
NORM residues, which have radioactivity concentrations significantly exceeding the clearance level can be used for the production of construction materials as raw materials and other components are not subject to the requirements set in the EU directive. However, from a radiation protection point of view, occupational risk to workers involved in the process of construction materials manufacture is usually negligible, even if the concentration of natural radionuclides in raw materials exceeds either limits set for construction material or clearance level set for NORM. However, in some special situations when NORM is used as raw material then occupation exposure can be important. The reason can be either gamma radiation from large amounts of material or incorporation of dust or radon (progeny). Thus, several recommendations should be given for companies, which intend to process NORM above clearance level as set in the EU BSS directive.
Firstly, radiation protection concerns the workers in the production process and all people using the products. Usually, it should be possible by organizing provisions to avoid that workers become rated as radiation workers. This can be done by separating storage areas (large amounts of NORM) from working areas and/or limiting working time in areas with enhanced radiation. Cheap and simple measurement instruments are available to check for the ambient dose rate. In critical areas such dose-rate meters should be installed to survey these areas. According to the results of these measurements, the working time in such areas should be limited to assure less than a maximum effective dose of below 1 mSv/year to the workers. If radon concentration above 300 Bq/m3 is measured in some working places, then increased ventilation should be provided or, if possible, the emanating materials should be moved to some other places, either outside or to the locations where the workers do not remain the whole working day. An initial investigation should be performed by a specialist, especially to check if the material used is the source of radon or if it is the soil/rock beneath the production areas. Later a permanent but cheap measurement system, e.g., by SSNTD, with exposure times of at least 1 month in cold and warm seasons of the year can be used. Finally, it should be checked, if incorporation of NORM via dust particles is possible. In such case, action has to be taken to mitigate exposure of workers. This can be a modification of storage areas or production procedures, increased ventilation or as a last solution the use of dust protection masks.
Besides the occupational risk issues companies processing NORM residues should pay special attention to control the end-product parameters before the final test in a laboratory. In order to assure the positive result of the final test of a construction material product the following recommendations can be followed:
• The concentration of natural radionuclides in the raw materials must be determined, or the information must be supplied by the producer/importer. Taking a representative sample is essential.
• From this information the radionuclide concentration can be calculated for the end product, taking into account the mixing ratios, as well as the mass changes according to chemical/physical procedures during the production processes. The resultant index should be significantly (about two standard deviations) below the limit to be sure that small variations in the mixing ratios will not lead to exceedance of the limit.
• As a final check, a dose-rate meter with an alarm level can be installed at the end of the production line. Such a measurement device must be installed in a way that the background radiation remains constant (no storage of raw materials or other products in the vicinity of the meter, shielding against other directions in a way that only the end product contributes to the measurement). A first calibration should be done by determining the index of the end product and comparing it with the background corrected reading of the dose-rate meter. In this way a cheap and reliable internal QA is possible.
• The measurement and the interpretation of the measurement results of the radon exhalation from the end product is a rather difficult job, however the control of radon exhalation from building materials can be carried out by the results of a laboratory measurements of the radium activity concentration. It should be noted that the problem of reliable sealing the measured sample is not completely solved yet, and more research is needed.
• Any equipment (for all types of measurements) must be adequate to the problem to be solved, e.g., the sensitivity must be sufficient to measure the low radiation levels, the device must be robust enough to be used in industrial workshops, etc. This seems self-evident, however, such quality characteristics have often been overseen especially when the problem is new to a company. In addition, the equipment and measurement methods should be a reliable metrological assurance and conform to international standards.
• All measurements and all measures in connection with radiation protection must be documented and the documents must be stored according to the national regulations. To some extent all of these recommendations are valid also for construction material manufacturers that do not process NORM with high content of radioactivity because the compliance with the requirements of the European BSS is in force and must be checked for all building materials.
Annex A Uncertainties, decision threshold (decision limit), and detection limit (lower limit of detection)
A1 Uncertainty in gamma-spectrometry
The result of a measurement is only an approximation or estimate of the value of the specific quantity subject to measurement. The result of every measurement consists of two values: the value of the measured quantity (measurand) and a quantitative statement of its uncertainty. The uncertainty is a value which characterizes the range within which the true or expected value of a measurand lies with a defined probability. It is inherently connected with the statistical behavior of the measurement process and the measurand. A comprehensive description of how to treat uncertainties can be found in the “Guide to express uncertainties in measurement” (BIPM/ISO/IEC Guide 98-3, 2008: GUM—Evaluation of measurement data—Guide to the expression of uncertainty in measurement.)
The uncertainties in the measurement process consist of several components that can be grouped into two categories:
(A) those which are evaluated by statistical methods (e.g., counting) and
(B) those which are evaluated by other means.
The evaluation of both components “A” and “B” may be based on any statistical method for treating data or scientific judgments using relevant information available, respectively. In the case of component “A”: standard deviation of the mean of a series of independent observations or method of least squares to fit a curve and to estimate the parameters of the curve and their standard deviation or analysis of variance (ANOVA) to identify and quantify random effects in certain kinds of measurements. In the case of component “B”: previous measurement data, general knowledge of the behavior and property of relevant materials and instruments, manufacturer's specifications, data provided in calibration, and uncertainties assigned to reference data taken from handbooks.
The final uncertainty of the measurement result could be a combination of several components of both kinds “A” and “B”. When the measurand is not directly determined but is calculated through a function the law of propagation of uncertainty has to be used.
Let
be the outcome of a value derived from different inputs xi with known uncertainties u(xi). Then combined uncertainty of the measurement result y, designed by uc2(y) can be calculated as (Gaussian uncertainty propagation law)
In case of uncorrelated inputs xi the covariances u(xi, xj) are zero and Eq. (5.21) reduces to
Usually the uncertainties are given in standard deviations sc, si multiplied with some coverage factor. If the probability density distribution for the result y follows a Gaussian distribution then the probability for the true value of the result y lies between y−sc and y+sc is 68% (double-sided confidence level). If a higher probability is necessary a higher coverage factor has to be used, e.g., the probability is 95% for the range y−2sc to y+2sc (coverage factor k=2).
In contrast to the term “uncertainty”, an error means a “wrong decision”. For legal purposes it is often necessary to answer the question whether a sample contains a certain radionuclide. If a radioactivity measurement of the sample results in a value which is larger than the uncertainty of the measurement result then one decides that the sample contains a certain radioactivity. However, if this is not the case, then an error has been made. The size of the used uncertainty (the standard deviation and the used coverage factor) determines the probability for that error.
Besides statistical uncertainties there are a lot of possibilities for introducing additional uncertainties into the results of measurements. Fortunately many of them are small or can easily be compensated and some are not relevant in connection with the compliance for legal requirements. Especially for gamma spectrometry two points should be mentioned:
• Peak area determination: Generally, the background on both sides of a peak in the spectrum is used to estimate the background below the peak. Usually a linear extrapolation is used but in certain situations (e.g., adjacent to a Compton edge) a polynomial fit of the order 2 or 3 may simulate the background below the peak better. Additional attention must also be paid to overlapping peaks. Finally, HPGe detectors produce peaks with a relatively long tail at the low energy side. This is no problem if the sample peak is compared with a peak in a reference sample in an identical measurement situation. However, if only the efficiency of the detector is determined then one has to realize that outside the usually used interval for the determination of the peak area (usually 2–3 FWHM) approx. 2%–3% (depending of the size of the detector) of the peak area on the low energy side of the peak are not within the used interval (older Ge(Li) detectors do not show such effects). If the counting time is measured only when the MCA is ready to convert events (live-time measurement) no dead time correction is necessary.
• Sample effects: Generally a correction for sample density can be applied (the relevant correction factors should be determined during the calibration of the device), however also the atomic composition modifies the self-absorption in the sample because Compton scattering, photo effect, and (above 1 MeV) pairing effect are depending on some exponents of the atomic number Z. In most cases building material does not vary very much concerning the atomic numbers of its ingredients but in some cases (e.g., Ba-concrete) this may be of concern. Also the homogeneity of the samples can be of interest. A typical example is the measurement of liquid samples (e.g., leaching tests). Tiny solid parts, sometimes even invisible, can settle on the bottom of the sample container and this inhomogeneity of the radioactivity in the sample cannot be used to determine the activity by comparing with a homogeneous reference material.1
In any measurement it is a good practice not to rely only on automatic analyzer systems but to think about all steps during the determination of an activity concentration and to realize what really happens and what uncertainties can be present in the process.
A2 Decision threshold and detection limit in gamma spectrometry
It is often necessary to decide if materials comply with legal requirements or not. However, all measurements are connected with uncertainties, thus, every decision may be erroneous. The only possibility is to limit such false decisions to a certain probability. To deal with such problems the decision threshold (or decision limit, DL) and detection limit (called hereafter LLD were introduced).
In case of low level measurements two decisions are of importance:
• to decide that a sample contains a certain radionuclide and
• to decide between the cases of radioactivity below or above a reference value.
Both decisions should be made with a certain low probability for a wrong decision which means low probabilities of error. It is obvious that the probability for an error essentially depends on the uncertainties of the measurements.
In the theory of statistics a certain hypothesis is called null-hypothesis (in the case to decide if a sample contains a certain radionuclide the null-hypothesis is usually the hypothesis that the sample does not contain the nuclide) while the other case is called antithesis. Then four possibilities exist and are shown in Table 5.5.
Table 5.5
Definition of “Error of the first kind” and “Error of the second kind”
| Null-hypothesis is true: the sample does not contain the radionuclide | Antithesis is true: the sample contains the radionuclide | |
| Decision: Sample does not contain the radionuclide (null-hypothesis is accepted) | Correct decision | Error of the second kind |
| Decision: Sample contains the radionuclide (antithesis is accepted) | Error of the first kind | Correct decision |
Thus, the “Error of the first kind” is a false accepted antithesis (false decision that the sample is radioactive), while the “Error of the second kind” is a false accepted null-hypothesis (false decision that the sample is not radioactive).
Now the question arises how to determine the probability of the error in the decision if a sample contains a certain radionuclide or vice versa, which net effect is necessary to decide that a sample contains that radionuclide and the probability of a wrong decision being lower than a required probability. To avoid the measurement time in the calculation only rates and their uncertainties are used below. The radioactivity determination comprises in principle two measurements: the measurements of the sample (gross rate rg with standard deviation sg) and the measurement of the background (background rate rb with standard deviation sb). The required result is the net rate rn with its standard deviation sn which can easily be calculated:
Now we can introduce the decision limit DL (decision threshold): If the value of the result of a physical effect exceeds the decision threshold then one decides that the physical effect is present. At the limit of decision the probability for the error of the first kind is equal to α (e.g., Donn and Wolke, 1977).
In Fig. 5.19 the probability density distribution for rn for a sample without the physical effect of radioactivity is shown. The decision limit will be chosen as DL=k1−αsn. e.g., a coverage factor k1−α=2 leads to a (single-sided) probability α=0.0228 for rn when assuming a Gaussian probability density distribution. With such a choice the error for a wrong decision is 2.28%. The choice of the value for the decision limit depends on the acceptable probability α for a wrong decision. (In earlier papers the DL was often called limit of detection or LLD, while today the LLD is defined differently (Altshuler and Pasternack, 1963)—see Table 5.6.)
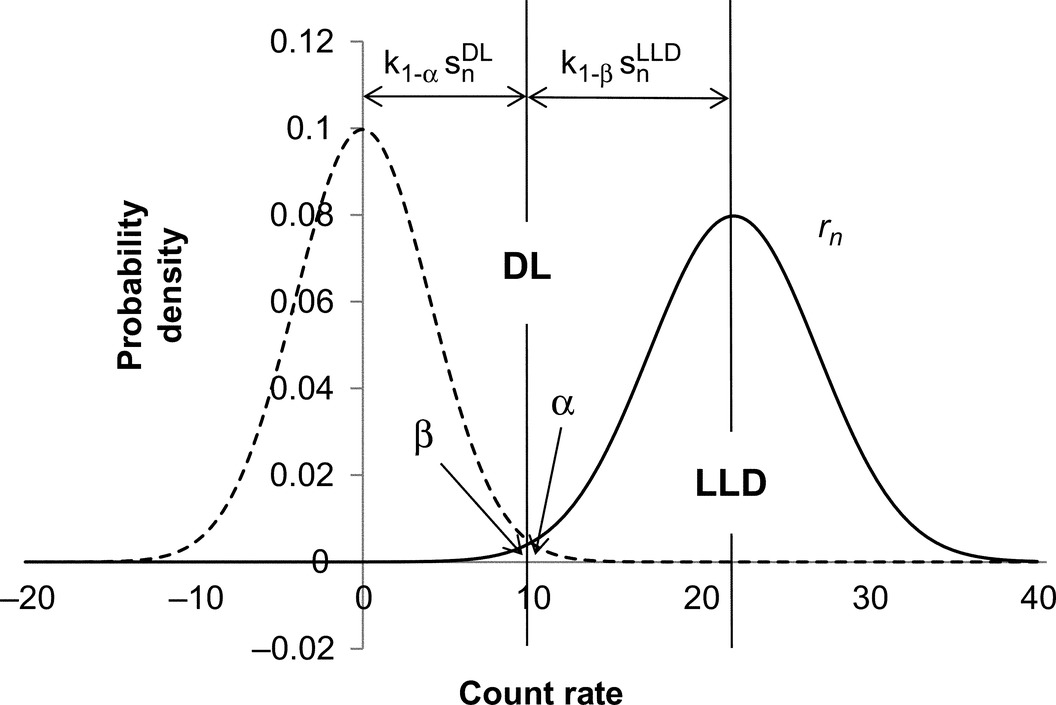
Table 5.6
Single-sided confidence level and single-sided significance level for different coverage factors for a Gaussian frequency density distributiona
| Coverage factor k1−α, k1−β | Confidence level 1−α, 1−β | Significance level α, β |
| 1000 | 0.8414 | 0.1586 |
| 1282 | 0.9000 | 0.1000 |
| 1645 | 0.9500 | 0.0500 |
| 1960 | 0.9750 | 0.0250 |
| 2000 | 0.9772 | 0.0228 |
| 2326 | 0.9900 | 0.0100 |
| 2576 | 0.9950 | 0.0050 |
| 3000 | 0.9986 | 0.0014 |
| 3090 | 0.9990 | 0.0010 |
a For a very low number of counts the Poissonian distribution cannot be approximated by a Gaussian distribution and the difference between two Poissonian distributions is not a Poissonian distribution. Therefore, special tables have to be used (e.g., Helene, 1984).
Thus, the general expression for the decision limit can be written as
with sg the standard deviation of the gross measurement results for a sample at the decision limit and sb the standard deviation of the background (which has to be subtracted from the gross measurement result). In most cases the approximation to compute sg for the background is sufficient. In any case, the decision limit is—apart from the selected coverage factor-only dependent on the background (and the measurement circumstances, e.g., measurement time, etc.).
To achieve a value from the measurement which can be compared with a reference value or a limit it is not sufficient only to proof the existence of a radionuclide in a sample. For this task the LLD is introduced. The LLD is defined as the expectation value for the random variable (measured variable) with a given probability for a value below the decision limit (see Fig. 5.19).
The LLD can be written as
with sg being the standard deviation of the gross measurement result for a sample at the LLD and sb the standard deviation of the background.
What is the meaning of the LLD? Let us assume a sample with a true activity equal to the LLD. Then a single measurement will result in a value below the DL with a probability β. This means with a probability β it cannot be decided at a 1–α level that the sample shows any contribution of the radionuclide. Therefore, the LLD of the measurement procedure must be lower than the reference level or the limit to which the sample should be tested. If this is not the case the measurement procedure is not adequate to test the compliance with the reference value or limit.
In the case of a simple counting measurement, e.g., gross beta counting, the DL and LLD can be calculated according to
where rb is the background count rate, rg is the gross count rate, and tb and tg the corresponding measuring times. For rbtb>50 one can use the following approximation:
A3 Application of DL and LLD in gamma-spectrometry
For a spectrometric measurement the determination of the DL and the LLD is more complicated [see ISO-11929 (ISO-11929, 2010) and ISO-28218 (ISO-28218, 2010)].
The simplest way to calculate the net count rate in a peak is a linear approximation of the background from the data left and right of the peak (Fig. 5.20). When using the same number of channels (m) for the background on both sides of the peak, then the net peak rate (rn) is
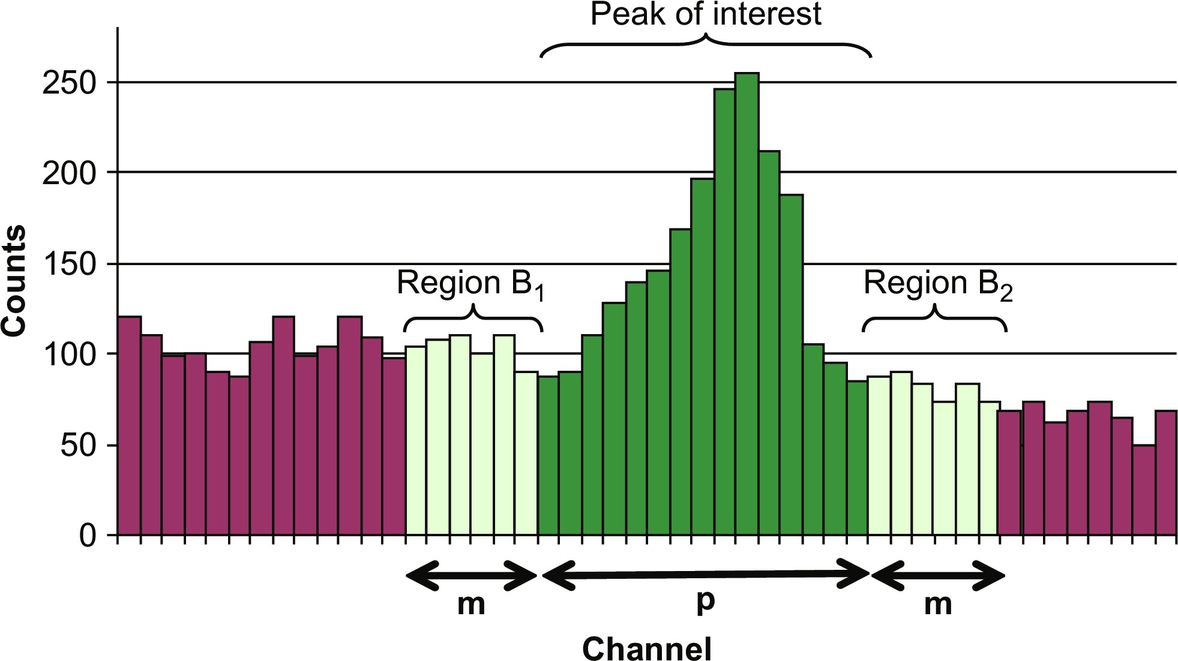
with Np being the number of counts in range p (channels) of the peak, No the sum of then number of counts in the background areas B1 and B2, and t the counting time. If it is not possible to select the same number of channels on both sides of the peak then Eq. (5.30) has to be slightly modified. Generally, from the counts in the range p the counts Nc of the pedestal below the peak have to be subtracted. Usually, Nc is computed by a linear fit from the background left and right from the peak, thus leading to equation (5.30).
Because counting statistics follows a Poissonian distribution the standard deviations of Np and No are their square roots. With the uncertainty propagation law and considering that time and channel ratio has no significant uncertainty one gets
At the DL Np can be calculated from Eqs. (5.30)and (5.31) and substituted in Eq. (5.24). This results in an implicit equation for DL with the result
In case that there is no background peak below the analyzed peak the DL as determined according to Eq. (5.32) can be directly converted into a DL for the activity of the sample by dividing by the efficiency ɛ.
In the measurement of NORM the problem arises that in a separate background measurement usually peaks exist at the same position as those to be measured. Therefore, Eq. (5.32) cannot be used directly. Usual software supplied with the spectrometer often includes the determination of DL and LLD, however, these values concern only the situation with no background peak at the same position. The correct procedure to be applied is the following:
(a) Determination of the net count rate in the peak from the sample and its standard deviation;
(b) Determination of the net count rate in the peak in the background spectrum rb (counting time tb) at the same position and its standard deviation s(rb);
(c) Calculation of the “net-net-count” rate rnn=rn−rb (difference between net count rate from the sample and the net count rate from the background spectrum) and its (net–net) standard deviation;
(d) The (net–net) standard deviation s(rnn) calculated this way can be used to calculate the DL according to Eq. (5.33). A measured net-net-count rate can then be compared with DL (and with LLD). To achieve the DL (and LLD) in units of activity a division by the efficiency (and other factors) is necessary.
For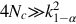 
which in most cases is fulfilled then Eq. (5.33) can be simplified to
In analogy to the formulas derived for the DL, the formula for the LLD can be found. The result is even more complicated but for 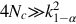one gets in good approximation
The above described methods are the correct procedures to determine DL and LLD. In case that the peak does not stick up considerably from the background (low-level measurement) then DL and LLD can be calculated as:
where s(0) is the null measurement standard uncertainty which means the standard uncertainty of a measurement where the specified peak area is zero. For a coinciding peak in the background but a low contribution of the sample, then the calculation of s(0) must include the peak in the background too.
The procedure to determine the DL and the LLD is in principle similar if more than one peak is used to determine the activity of a sample.
The DL and the LLD as derived in this chapter take only statistical uncertainties into account. Sample selection, preparation, etc. have to be separately analyzed and their uncertainties have to be included into the uncertainty budget of the result and used to determine the DL and LLD.
Another method to determine the activity of samples uses library spectra for single radionuclides with well-known activities and combines such spectra linearly with the background spectrum as in multivariate analysis. For this type of analyzes Pasternack and Harley (1971)) developed a method to compute the decision limits for different nuclides. Such methods are mainly applied when using detectors with lower energy resolution than Ge-detectors, e.g., NaI-detectors.
Because of some problems especially in sample selection, preparation etc. the ISO 11929 (ISO, 11929, 2010) does not use frequency statistics as derived above but the Bayesian statistics to determine DL and LLD (see ISO 11929 (ISO, 11929, 2010) and references therein (e.g., Weise, et al., 2006). In most cases there are no or only very small differences in DL and LLD between the different ways of calculation, thus, a determination of DL and LLD as explained above seems to be sufficient in practice.
Just to give an example for Bayesian statistics in radioactivity measurement: It is possible that the count rate of a sample is lower than the count rate in the background. This leads to a negative net-count rate which is physically not possible. An “a priori” information (radioactivity cannot be negative) can be used to cut the distribution of the net count rate at zero and to use the centroid of the tail of the distribution above zero to determine a positive net-count rate and its variance. This “a priori” information (only positive net-count rates are possible) is only one possibility (e.g., see Little, 1982).
A4 Example for the determination of peak area, DL and LLD
Commercial γ-spectrometry software usually includes the calculation of DL and LLD. Such software assumes that below the investigated peak no background peak exists. This is usually not the case when measuring NORM. An example for the procedure to calculate the net count rate in a peak with a peak at the same position in the background spectrum is shown below step by step (see Fig. 5.21), as well as the exact determination of DL and LLD.
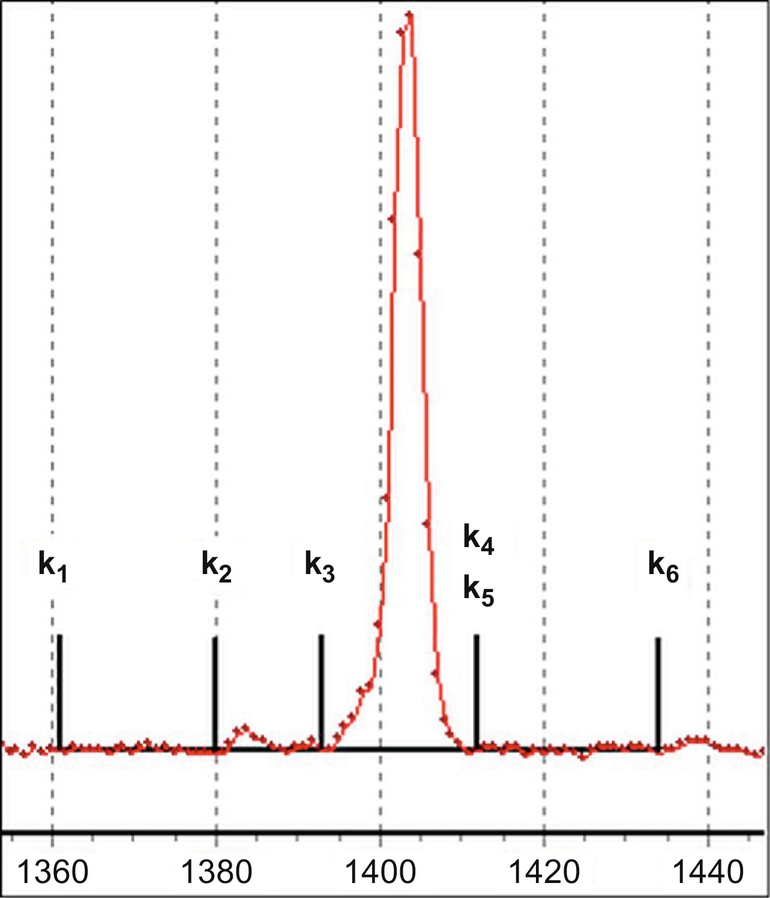
• The intervals for the determination of background and peak have to be defined. It is not always possible to define the intervals for the background determination back to back and equally sized on both sides of the peak interval as shown in Fig. 5.20. Thus, the channel numbers for the left background area (B1) from k1 to k2, the peak interval should be from k3 to k4 and the right background (B2) comprises the channels k5 to k6.
• The left background counts are NL=Σni with i from k1 to k2, the right background counts are NR=Σni with i from k5 to k6 and the counts in the peak area are NP=Σni with i from k3 to k4.
• The computed background below the peak NC area is determined by a linear fit based on the left and right background areas.
• Then the net peat area is Nn=NP−NC.
• The standard uncertainty is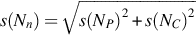 
. Because of the Poissonian distribution and the assumption that the relative uncertainty of NC is approximately equal to the relative uncertainty of NL+NR, this can be written as 
.
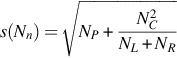• The net count-rate and its uncertainty are then calculated by a division by the measured (live) time t: rn=Nn/t and s(rn)=s(Nn)/t.
In NORM it can be assumed that below the observed peak from the sample the same nuclide from the environment causes a peak in the background at the identical position. A structured background can be neglected only in case of an extremely good shielding. Therefore, the same procedure as described above should be applied for the background. Thus, the count rate in a peak which is due only to the sample (rnn) is the difference between the net count rates from the sample and the count rate from the background.
• rnn=rn(sample)−rn(background) and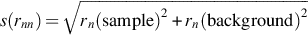 
.
• According to Eqs. (5.33) or (5.34) and (5.35) the DL and the LLD can be determined.
Numerical realization: Sample measurement time t=20,000 s.
• Selected intervals: k1=1361, k2=1380, k3=1393, k4=1412, k5=1412, k6=1434. The left background area was selected not directly adjacent to the peak interval because of a possible additional peak.
• The background counts from k1 to k2 (NL=9966) and from k5 to k6 (NR=11,538) are used to calculate the unstructured background within the interval k3 to k4. The total counts in the peak interval are NP=32,793 counts and in the background intervals No=NL+NR=9966+11,538=21,504 counts.
• The linear fit results in NC=10005.2 counts.
• The net peak area is Nn=32,793-10005.2=22787.8 counts.
• The standard uncertainty computes to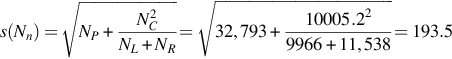
• Thus, the net count rate and its uncertainty is rn(sample)=1.14 counts/s and s(rn)=0.01 counts/s.
A measurement (measurement time tb=40,000 s) without the sample shows a peak at the same position as the peak to be investigated. The same procedure as above gives rn(background)=(0.02±0.01)counts/s.
• rnn=rn(sample)−rn(background)=1.14−0.02=1.12 counts/s and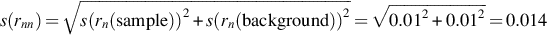
. In this case the peak in the background spectrum does not really change the uncertainty in the net peak count rate.
• 
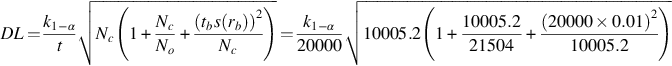For k1−α=2 we get DL=0.023 counts/s and with k1−β=2 we have LDD=0.05 counts/s.
• The uncertainty in the net count rate is in the order of 1% which means that in such a case this statistical uncertainty (uncertainty of category A) usually can be neglected in comparison with all other uncertainties appearing during the determination of the activity concentration in a sample.
• When using the simplified Eq. (5.36) then s(0) must be determined: From rnn=rn(sample)−rn(background)=rP(sample)−rC(sample)−rn(background) we get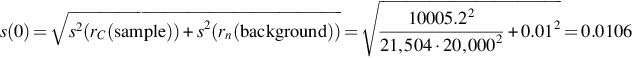
. For k1−α=2 we get DL=0.021 counts/s and with k1−β=2 we have LDD=0.04 counts/s. Thus, DL and LLD do not differ much compared with the exact formulas.
Fig. 5.22 shows a general scheme for identifying possible sources of uncertainties in γ-spectrometry and estimating their size.
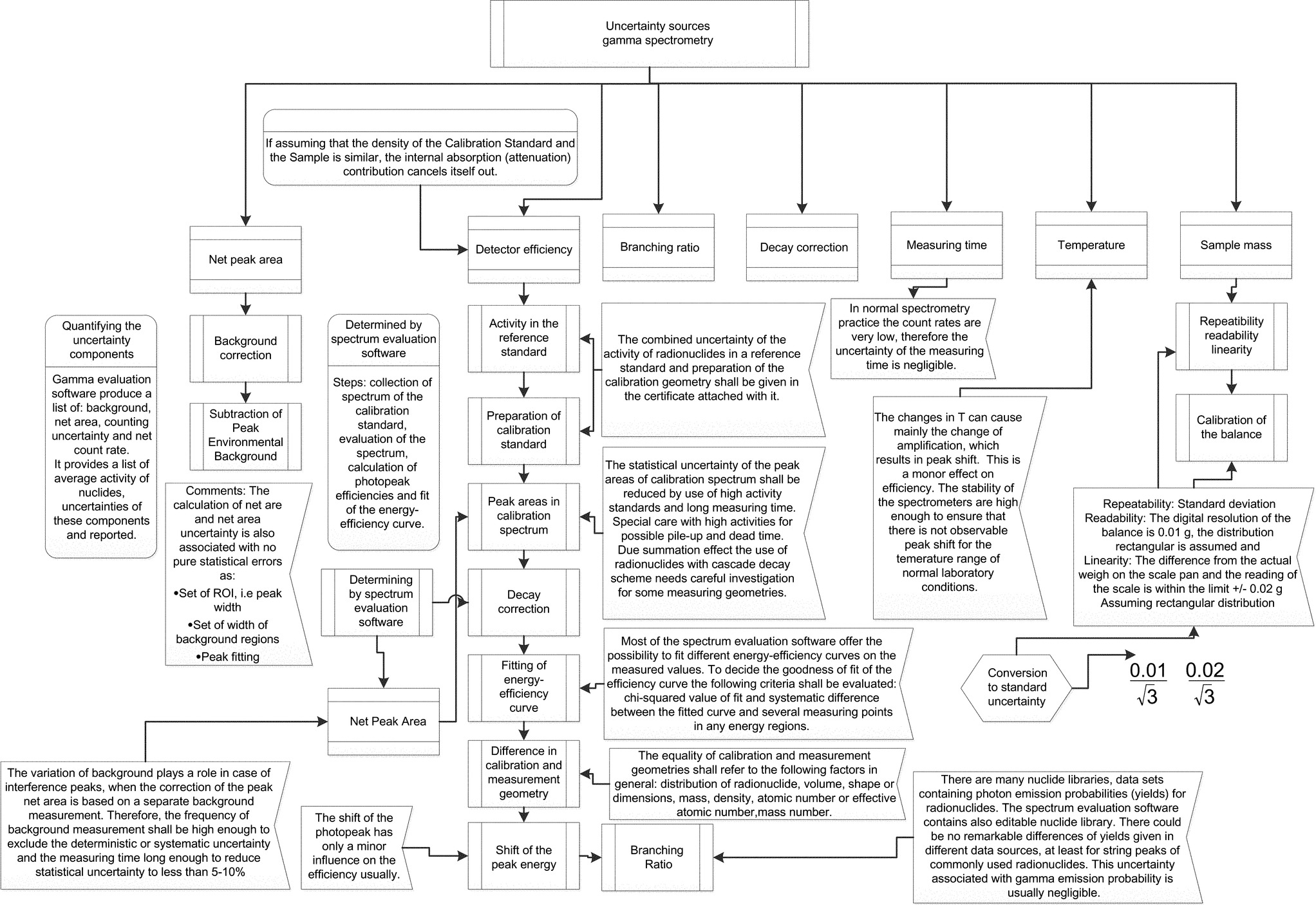
A general test for the integrity of the measurement equipment which can be applied to all types of counting measurements relies on the comparison of the results of repeated measurements and the result of an analysis of summing up the data of all measurements: Any results of counting measurements should follow a Poissonian distribution. This means that the number of counts is equal to the variance of the measurement result. Thus, the uncertainty of repeated measurements with the same counting time can be determined by calculating the standard uncertainty of the mean in the usual way (outer uncertainty sout) and compare this standard uncertainty with the standard uncertainty of the sum of all measurements (inner uncertainty sin). The standard deviations should agree within
with n being the number of measurements (comparison of inner and outer uncertainty). A similar procedure can be applied when more than one gamma peak are used to determine the concentration of a radionuclide in a sample.
A5 Uncertainties in dosimetry
The ambient dose H or dose rate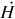 
can be calculated from the reading of a measurement device M, its calibration factor N and correction factors kj for the different influencing quantities which do not modify the reading but the result of the measurement:
Correction factors kj are necessary to correct measurements which are not made under the reference conditions (conditions for calibration). Main correction factors are listed in Table 5.7.
Table 5.7
Influencing parameters and correction factors for ambient dose-rate measurements
| Influencing parameter | Correction factor |
| Photon energy | kE |
| Direction of incidence | kR |
| Supply voltage | kU |
| Ambient temperature | kT |
| Relative humidity | kW |
| Air pressure | kp |
| Electromagnetic disturbances | kEM |
| Linearity | kL |
The calculation of the standard uncertainty must include all uncertainties from the correction factors too. The simplest case is a measurement with a calibrated device at reference conditions. Then the calibration factor is N=1 and all correction factors are unity. If a national metrology institute has verified the calibration, it usually testifies the compliance with the national standard within e.g., 20% assuming a rectangle probability density distribution.2 This means a standard uncertainty of 0.2/√3=0.115. Let us assume repeated measurements at reference conditions with a mean and a standard uncertainty for the reading M=(15.28±0.17)μSv/h then the measurement result and its standard uncertainty becomes 
μSv/h (coverage factor k=1) by using the uncertainty propagation law.
If the instrument was calibrated a calibration factor with an uncertainty is given, e.g., N=1.05±0.20. If the reading is about 15 μSv/h but the calibration was performed at 25 μSv/h then estimation of the uncertainty of kL is necessary. The correction factor for the linearity should not exceed the interval between 0.95 and 1.05 (rectangle distribution). This gives a standard uncertainty for kL as 0.05/√3=0.03. More important is the uncertainty for the correction factor for the photon energy kE. Fig. 5.16 shows a typical behavior for kE when the reference energy was 662 keV (137Cs). Let the actually measured energy vary between 50 and 1000 keV. Then the mean correction factor is kE=0.95 and it varies between 0.8 and 1.1. Thus a good choice would be a rectangle distribution with a width of ±0.15. This means that the standard deviation for kE is 0.15/√3=0.087 and with kE=0.95±0.09 and kL=1.00±0.03 the final result and its standard deviation can be computed. In the case of M=(15.28±0.17) μSv/h, N=1.05±0.20, kE=0.95±0.09, and kL=1.00±0.03 and all other correction factors are unity then the result becomes 
μSv/h (coverage factor k=1).
For a measurement outside the reference conditions all correction factors with their uncertainties have to be considered. For most ambient dose rate monitors the correction factor for the direction of incidence is of main importance and its uncertainty becomes the largest of all correction factors. Even in the example above which represents a typical situation the standard uncertainty is about 20%. When the direction of gamma radiation incidence is not clearly known as it is usually the case in ambient dose-rate measurements then the standard uncertainty becomes even larger. This should always be kept in mind when ambient dose-rate measurement results are used to check for compliance with legal requirements.
The circumstances are much better when dose-rate measurements are made in a standard situation (geometry and energy) which can easily be corrected to the reference conditions or when only relative measurements are necessary. Such a situation is possible when the same type of product is surveyed at the end of a production process.
Annex B Calibration and metrological assurance for semiconductor detectors
The most common way of detector efficiency calibration in gamma spectrometry is experimentally using certified mixed radionuclide solutions. These calibration solutions typically contain a series of radionuclides emitting photons to cover the energy region 59—1836 keV, where photons emitted by most of the radionuclides usually found in the environmental samples can be registered. The mixed radionuclide solution is used for the preparation of a calibration source having the same geometry as the sample to be analyzed. If samples of different geometries are to be analyzed, more calibration sources have to be prepared. It is therefore possible to calculate the detector full energy peak efficiency for each photon energy emitted by the calibration source and for the specific source-to-detector geometry by the formula:
where yield is the specific photon emission probability and activity is the corresponding radionuclide radioactivity at the day of the analysis. A series of correction factors may be required further for the efficiency calibration to take into consideration self-attenuation of low energy photons, coincidence summing corrections etc.
Unfortunately reality often shows that radionuclides other than those ones actually present in a standard sample available need to be measured. In this case calibration coefficients obtained for radionuclides present in a standard sample are used to calculate a detector efficiency curve, which is a function of energy. Obtained efficiency curves can be used for the evaluation of calibration coefficients for radionuclides that were not present in a standard sample but need to be measured in a test sample (Canberra, 2016) (Fig. 5.23).
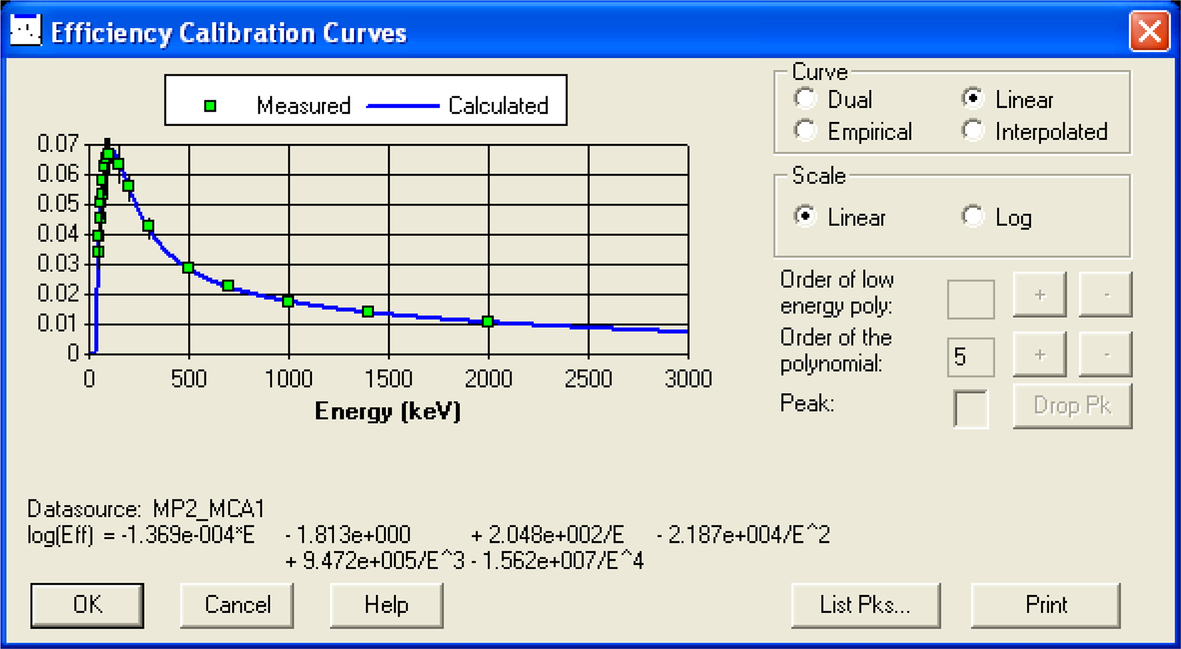
Besides the calibration of the detector done using a standard sample containing well known content of some radionuclides, the most important aspect is self-attenuation of gamma radiation within a sample. According to the interaction of radiation with matter part of the radiation is attenuated in the sample. This phenomenon depends of radiation energy, sample density, and chemical composition. Its impact on measurement results is included in the efficiency curve obtained during calibration and there is no problem when a tested sample has the same properties as the reference sample. As it is unlikely that separate standard (and calibration curve) is available for each and every kind of sample intended to be measured, additional correction is necessary for a sample that significantly differs from the used standard. A practical approach to solve this problem is to prepare a set of standards reflecting a range of typical samples measured. With a sufficiently large set of different calibration standards it is possible to calculate correction factors for a sample with particular properties. It is important to note that the calculated correction factors should cover the entire spectral range of gamma energies measured.
The radiation self-absorption in a sample can also be determined by the “transmission method”: An additional source containing the radionuclide of concern is placed directly on the tested sample to enable direct measurement of the self-attenuation in the sample (when compared with the measurement made without the tested sample). This method is mainly used for measurement of radionuclides emitting low energy radiation, as for this method not only the sample density is important but also its chemical composition. In practice this method is used mainly for the measurement of 210Pb (Cutshall et al., 1983; Bonczyk et al., 2016).
Over the last few years an extensive use of computational methods—often combined with experimental ones—for efficiency calibration has been observed. Most of them are based on Monte Carlo simulation. Progress in computational calibration was mainly due to the development of powerful computers—including parallel processing—and user-friendly graphical interfaces. Two types of Monte Carlo computer codes are used for computational calibrations:
A. General-purpose Monte Carlo (M-C) simulation computer codes that can be also used for detector calibrations. Typical codes are: MCNP, GEANT, ETRAN, PENELOPE, EGS4, etc. For these codes to be used for detector efficiency calibration, the user has to describe as accurately as possible the source-to-detector geometry, using a series of mathematically described surfaces. By using these surfaces, the detector, source, shielding and all other bodies existing in the detector system can be described. The existence of user-friendly graphical interfaces and computer programs like gview3d allow the user to display the geometry on the computer screen. After the geometry has been described the code simulates a large amount of “histories” that may reach or exceed 109, each of them corresponding to a single photon emitted by the source and its interaction with the source material and the detector. The software ensures that the photons are emitted randomly inside the source. Simulation codes normally incorporate “virtual detectors” that are used for recording several parameters during the simulation, the most important being the energy deposition detector (EDD). By defining an EDD with the same geometry as the actual detector under calibration, it is possible to record the amount of energy which is deposited in the detector for each simulated photon of energy E emitted by the source. For this purpose the energy region from zero to E is divided in energy windows (bins) of user-defined width. The simulation of a large amount of photons results in the probability distribution function of the photon energy deposited on the detector, which corresponds to the actual spectrum collected by the detector. It is therefore possible to use information from this probability distribution function to calculate the full energy peak efficiency or the total efficiency of the detector.
Though the whole procedure seems rather straightforward, there are some details that may significantly affect the quality of the simulation results. One of them is detector geometry. Only part of the detector geometry is accurately known or can be directly determined by the user. In most cases the user relies on the geometrical characteristics provided by the detector manufacturer which may not be entirely accurate. A typical case is that of HPGe detectors, where the user cannot actually see the detector as it is enclosed inside the detector housing. The detector manufacturer provides some of the external geometrical characteristics of the detector (e.g., height, diameter, etc.) and an estimation of the thickness of the detector's insensitive layer (dead layer), which however cannot be measured. Furthermore, the detector and the dead layer may not be homogenous. Another issue is the inhomogeneity of the electric field inside the detector which may affect the charge collection and the corresponding signal produced in the detector. It is clear that these problems should be taken into consideration for the simulation results to be meaningful and accurate.
The way to deal with these problems is the experimental determination of the detector geometrical characteristics, a process described as “detector characterization”. For this purpose an iterative procedure is introduced, consisting of the following steps: (i) The full energy peak efficiency for the detector is experimentally determined using sources emitting various photon energies. (ii) Monte Carlo simulations of these experiments are conducted using the best available detector geometrical characteristics, subsequently calculating full energy peak efficiencies using the simulation results. (iii) Experimental and simulation results are compared and simulations are repeated with slightly modified geometrical characteristics aiming at the convergence between experimental and simulation results. The whole procedure is repeated until acceptable convergence is reached (e.g., an error margin of 2%–3%). As a result, a set of new detector geometrical characteristics is obtained which are then used for the determination of detector efficiency for energies and geometries where no experimental data exist. It should be noted that: (i) this set of geometrical characteristics is not necessarily the actual detector geometrical characteristics, (ii) this set of geometrical characteristics may strongly depend on the source geometry and distance from detector, and (iii) the whole process introduces a systematic (Type B) uncertainty, originating from the difference between experimental and simulation results, which should be further taken into consideration during efficiency uncertainty determination.
Another important issue is the simulation results interpretation. This was clearly demonstrated in an International Intercomparison of Monte Carlo codes in gamma spectrometry (Vidmar, et al., 2008), where the efficiency calibration of an HPGe detector for three well-defined source-to-detector-geometries was required. It was found that, even when the same computer code was used, significant differences in the full energy peak efficiencies were observed, depending on the selection of various simulation parameters—mainly the cut-off energies—and the interpretation of the simulation results. In a real spectrum, the photopeaks do not contain the full energy of all photons that contribute to a given photopeak. Some of these photons may have lost a small part of their energy content as a result of prior interaction (e.g., small angle Compton scattering inside the source) and deliver a reduced amount of energy to the detector. Additionally, the charge collection can marginally be incomplete. This is particularly important for low energy photons (e.g., 46.5 keV of 210Pb) where a distortion of the photopeak and a low energy tail are occasionally observed. It is therefore of great importance for the simulation to select an energy bin width that will record all of the photon energies that are actually recorded under the real photopeak in the corresponding gamma spectrum. For this purpose the detector energy resolution should be taken into consideration.
B. Dedicated computer codes for detector efficiency calibration. Several such codes have been developed over the last few years for the calibration of Germanium detectors, some of which are based on analytical calculations, others on M-C simulation and still others on a combination of both. Besides the efficiency calibration some of the codes are also calculating correction factors for self-absorption or true coincidence. A list of such codes include:
i. ANGLE is commercially available software for the efficiency calibration of Ge detectors. The program uses a technique called “efficiency transfer”. ANGLE calculates a transfer function between the absolute efficiency data for a detector-sample-matrix geometry which is experimentally determined (the “reference geometry”) and the new detector-sample geometry (the “sample”). The semiempirical approach used in ANGLE differs from absolute methods, in that ANGLE starts from a measured calibration which is then “transferred” to the new geometry by calculation of the transfer function, rather than starting with a Monte Carlo model of the detector and then correcting the model via measurement (detector characterization). Obviously, the closer the calibration source is to the sample geometry, the better the result.
ii. GESPECOR is a Monte Carlo based software developed for the calculation of full energy and total efficiency, as well as correction factors to take into consideration matrix effects (self-attenuation) and coincidence summing. The code can be used for coaxial, well-type HPGe or Ge(Li) detectors, and for various types of sources, including point, cylindrical, spherical sources or Marinelli beakers. Since the exact geometrical characteristics of the detector may not be accurately known, the users are advised to check the calculated values of the full energy peak efficiency for some geometry against experimental values. It is also possible to use the efficiency transfer method for the calculation of the full energy peak efficiency. The results obtained using the efficiency transfer method are less sensitive to the uncertainty of the detector geometrical characteristics than the results obtained by a direct computation of the efficiency. Therefore, if the reference measurement was made using high quality standard sources, the efficiency transfer method should be preferred. The code is capable of using the results of transmission experiments carried out with uncollimated point sources for the estimation of the linear attenuation coefficient which is needed for self-attenuation correction.
iii. ETNA is a computer code that has been developed at the Laboratoire National Henri Becquerel for computing the efficiency transfer and coincidence summing corrections for gamma-ray spectrometry. The code uses a numerical method and requires the decay scheme of the radionuclide emitting the photons of interest, as well as the experimentally determined full energy and total efficiency for the corresponding photon energy for at least one source-to-detector geometry. The code is available from the developer upon request.
iv. LabSOCS (Laboratory Sourceless Calibration System) is a commercially available computer code for the calculation of the full energy peak efficiency of voluminous sources. Efficiency for a specific source is calculated by integrating the response over the volume of the source. For this purpose the detector is previously characterized by the manufacturer, the detector model is determined using the MCNP code and compared to experimental results using five different traceable sources of different geometries. A large number of efficiency data sets for point sources in vacuum at various positions around the detector is then obtained and a calibration grid of the detector is created. It should be mentioned however that the user has to rely on a factory calibrated detector and therefore experimental verification of detector calibration should be conducted.
v. EFFTRAN (EFFiciency TRANsfer) is a computer code for the transfer of full energy peak efficiency from one geometry to another and for coincidence summing correction calculations in gamma ray spectrometry. It is limited to coaxial detectors and cylindrical sources including point sources. The program calculates the total efficiencies for the required source geometry and a reference point source geometry applying the Monte-Carlo integration method. For this purpose the detector geometrical characteristics provided by the detector manufacturer are used. For the calculation of the full energy peak efficiency for the required source geometry the efficiency for the reference point source geometry must experimentally be determined.
For example ISOCS (In Situ Object Counting System) provided by CANBERRA has been designed in order to limit the field-of-view of a detector to 30, 90, and nearly 180 degrees by simply sliding the appropriate shield components on the mounting rails (Canberra, 2016) (Fig. 5.24).
The ISOCS is connected with a calibration software package making gamma in situ assay simpler and more effective by eliminating the need for traditional calibration sources during the efficiency calibration process. The detector characterization produced by the MCNP (Monte Carlo N-Particle; https://mcnp.lanl.govc/, accessed 02.11.16) modeling code, mathematical geometry templates, physical (shape and size) parameters of measured objects, and its chemical composition are necessary. Using these data, the ISOCS Calibration Software provides the ability to get accurate calibration of a spectrometric system used for most any object type and size (Canberra, 2016) (Fig. 5.25).
Despite the principal possibility of in situ measurements, HPGe gamma spectrometry is traditionally used in a laboratory environment to determine the activity concentrations in sample materials using a predefined geometry. Rather to the contrary, the use of low resolution scintillation techniques as an alternative to HPGe gamma spectrometry in field applications is even more often met than its laboratory use. The main advantage of scintillation-based techniques is its simple ability to perform measurements on site as well as the purchase and operational costs that are considerably lower when compared against HPGe, which needs to be cooled during operation to a temperature about liquid nitrogen (Kovler et al., 2013). The drawback of scintillation detectors such as NaI(Tl), CeBr, or LaBr is their low energy resolution. The energy resolution is expressed in terms of a FWHM. For scintillation detectors the FWHM in the energy regions of interest is in the order of 5%–10%; in comparison the FWHM for an HPGe detector is well below 1%. As a result, the energy peaks in the spectrum do not appear as discrete lines but show a more diffuse and wider peak instead. When dealing with NORM the spectrum is characterized by many individual peaks coming from the photons emitted by radium, thorium, and its progeny at many different energy. As a consequence, the individual energy peaks in the spectrum will interfere with each other making it difficult to achieve an accurate assessment of the peak content and its associated activity concentration in the sample.
Annex C Uncertainties in estimation of annual average indoor radon concentration
The absence of information about the measurement uncertainty of annual average indoor radon concentration does not allow performing correctly its comparison with the normative (control, or action) level, as well as to optimize the measurement duration. For example, it is extremely inefficient to carry out the measurements in houses with a radon concentration far below the reference value for several months for checking compliance with the reference. Moreover, in cases where the upper limit of confidence interval does not differ from the normative level, the measurement should be continued longer, even beyond the three months of continuous monitoring. Furthermore, the results of repeated measurements with certain confidence intervals can be correctly averaged, using the inverse uncertainties as weights, which is particularly important in the development of radon hazard maps.
An interesting and promising method of estimating the confidence interval of the average annual indoor radon concentration, depending on the duration of the measurement, has been recently suggested through the following expression (Tsapalov et al., 2016b):
where C(t) …average indoor radon activity concentration measured for a sampling duration time t, Bq/m3; s(C) …instrumental standard uncertainty of radon concentration measurement, Bq/m3; KV(t) …radon variation coefficient depending on a sampling duration, (rel); KT(ΔTR) …the thermal influence function, (rel).
The coefficients KV(t) and KT(ΔTR) are determined by statistical processing of the results of annual continuous monitoring of the radon activity concentration and temperature in rooms with enhanced radon concentrations at typical ventilation mode. These coefficients have been defined for the premises of the buildings located in Russia (Moscow region), and their values are given in Tsapalov and Marennyy (2014). However, for buildings located in other climatic zones and geological conditions, the values of the coefficients may vary. Therefore, there is a need to conduct appropriate studies in order to clarify the values of these coefficients.
As already reported in Section 5.4.3, the uncertainty of assessment of the annual average indoor radon depends on the measurement duration. The longer the measurements are, the more accurate the assessment is. For example, Table 5.8 provides the values of radon variation coefficient for the rooms, which are equipped with systems of natural ventilation and operating without any restrictions. In this table the values of variation coefficient, according to Eq. (5.39) for the measurement duration of no longer than several weeks, correspond to the combined uncertainty of the annual average indoor radon.
Table 5.8
The values of radon variation coefficient depending on the measurement duration
| Measurement duration (days) | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 14 | Minimum duration of one of the two long-term measurementsa | Continuous measurement during 1 year | ||
| 1 month | 2 months | 3 months | |||||||||||
| KV (t), % | 240 | 220 | 200 | 180 | 160 | 150 | 140 | 140 | 140 | 40 | 30 | 20 | 0 |
a Two measurements are performed in different seasons—cold and warm.