Level 6: Mathematics & Physics
Well, I won’t sugar coat it: we’re in trouble. The Lucky Dare Game Jam Competition is 50% over, and it turns out we wasted the entire first day working on entirely the wrong project. We need to pivot and somehow transform our spooky maze crawler into something physics-based.
This means emulating the forces that act in the world around us. Good physics can increase player immersion and make a game world feel fluid, natural, and dynamic. Game physics can range from simple (often exaggerated) approximations to elaborate simulations. In this chapter, we’ll cover essential math concepts for game development and use them to implement some widely applicable game physics.
As always, game development is 90% smoke and mirrors. If you’re creating the next Kerbal Space Program, you’ll want to dust of your physics textbooks. If you’re making something more, uh, out-of-this-world—such as Sos Sosowski’s Mosh Pit Simulator then reality is not the goal. Accuracy and realism is often undesirable for crafting the user experience we want to provide. All we need is something that feels like physics, is fun to control, and meets our artistic needs.

Jump Everybody, Jump
Being on a deadline, it seems unwise to completely throw away our Bravedigger maze crawler from the end of the last chapter. We’re agile (and lazy) and can adapt it to work with the new theme. Instead of a top-down maze explorer, it becomes a side-on platform game à la Super Mario Bros. All we need is a bit of gravity and we can call it Bravedigger II!
Rather than have Bravedigger’s vertical position determined by the keyboard (that is, via controls.y) it’ll be powered by a jump force (applied when the player hits the space bar) combined with an opposing downward force. Imagine an apple. It falls from a nearby tree and lands on your head. In retaliation to the inanimate object, you pick it up and hurl it into the sky. What does its trajectory look like?
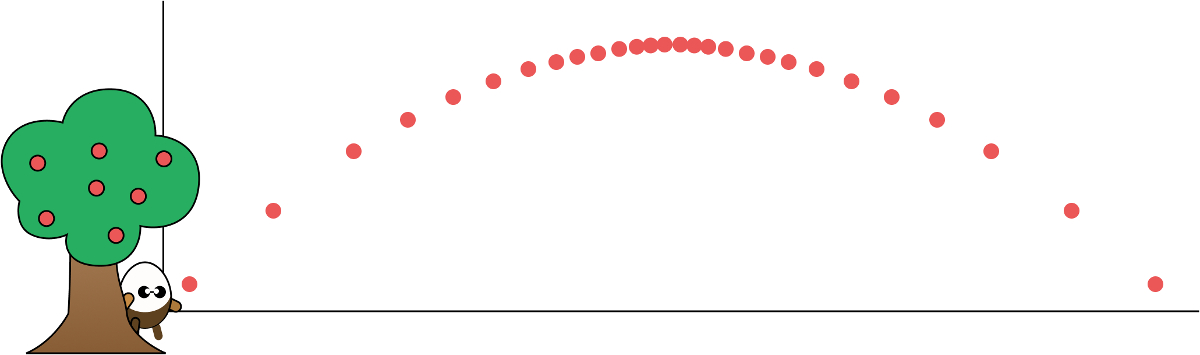
The apple starts around ground level. After one instant of time (say, 16.66 milliseconds) it has traveled upwards a large distance. If we drew it on screen it would move, say, -10 pixels in the vertical direction. But its vertical speed isn’t constant. Because gravity is pushing down on the apple, the movement in the next instant will be reduced—say -9.5 pixels. Then after that even less—perhaps -8.7 pixels—and so on.
The apple is still moving upwards, but it’s slowing down each frame. Eventually, it will be moving vertically by ~0 pixels, only its horizontal position appearing to change. From this point on, the apple starts falling back to the ground, at first slowly—say +0.1 pixels—but with the force accumulating. It falls faster and faster and faster as it approaches the ground. This sounds vaguely like gravity!
Faking Gravity
It’s time to fake some fundamental universal forces. I say “faking” because we won’t worry about air resistance, or which planet we’re on, or even how heavy we are. We just need something that looks gravity-like. Starting with a minimal new project, we now have to think “side on” rather than “top down”. This means removing the ability to move up and down with the keyboard (unless your game also happens to feature a jetpack):
const { x } = controls; // Removed `y`!
const xo = x * dt * speed;
let yo = 0;
// Apply some gravity
...
pos.x += xo; // horizontal influenced by the keyboard
pos.y += yo; // vertical influenced by "gravity"
The left–right keys still determine the horizontal movement, but now yo can only be influenced by gravity. The player is suspended permanently on a vertical plane wherever they spawn. To get them airborne, add some properties for leaping and falling:
this.jumping = false;
this.vel = 0;
jumping is a flag to track if the player is currently airborne. They can only start a jump if they’re not already jumping. Otherwise, they could spam the “jump” button and fly right out of the top of the screen.
The other property is the player’s velocity—vel for short. For now, this is a scalar value, a one-dimensional force (we’ll go 2D later in the chapter) that tracks the player’s y offset, as influenced by gravity. When a jump commences, velocity is set to a large negative number (-10 pixels, for example). This is our launch force—the only thing that can get us off the ground. Gravity will reduce the force until we hang in the air and then start falling—just like an apple.
if (!this.jumping && controls.action) {
// Jump!
this.vel = -10; // Launch force
this.jumping = true;
}
Pressing the space bar triggers a jump and sets the launch velocity. Whenever the sprite is in the process of jumping, any force accumulated in vel is added to our temporary variable yo. Remember that this amount is finally summed with the player’s position, therefore affecting vertical motion on screen.
Now the player is moving upwards, but they are dutifully respecting Newton’s First Law of Motion: a body in motion will remain in motion unless it is acted upon by an external force. If there were no change to vel, the player would rapidly depart the top of the screen at a speed of -10 pixels per frame. It’s time for gravity to flex its muscles and assert some force over vel:
if (this.jumping) {
this.vel += 32 * dt;
yo += this.vel;
}
Here gravity is also a scalar: 32 pixels per second. Every frame, it gets added to velocity. The player’s initial launch velocity is -10. After one frame that velocity is increased by 32 * dt to about -9.46 (depending on dt). Like our apple, the player is still moving upwards—but a tiny, tiny bit slower. This accumulates every frame, until velocity is positive and the player starts “falling”. The result is a nice arcing trajectory.
Gravitational Constant
“32” is our game’s gravitational constant. But 32 is not the actual gravitational constant of earth. (It’s about 9.81 meters per second on Earth, at 45 degrees latitude). So what is 32? It’s a number I chose because it felt pretty good. 50 felt too heavy, 10 felt too floaty. Test things out, but don’t overthink it!
Having applied our force, the final step is to actually stop it when the player is on the ground. In the real world, gravity is relentless and unceasing. In the game world it’s whatever we want it to be. Real-world forces can be hard to control in the game world, so we’ll simplify things. When we decide the player is on “the ground”, the jump is finished and gravity no longer exists:
// Check if hit ground
if (player.pos.y > h / 2) {
player.pos.y = h / 2;
player.jumping = false;
}

As well as ending the jump, we also set the y position to be exactly level with the ground plane (h / 2). This is necessary, as the player may be moving very quickly when they land, and could end up with their feet stuck below the floor.
For homework, you should test out various launch velocities and the gravity constants. You’ll see they tremendously alter the feel of the player—from moon-like, floaty leaps to heavy, lead-balloon trajectories. What works for you will depend completely on your requirements, and might even change throughout your game.
Jumping Platformer
At this point we have something that passes for gravity, but we need to try it out in a real game environment to see if it plays well. In our game we need the tile map to be the judge of when the player is on the ground (rather than some arbitrary ground plane). But last chapter’s top-down, procedurally generated maze is no longer appropriate for a side-view platformer. We have to undo the cool maze generation code and create an artisanal, hand-crafted ASCII map that’s purpose-built to accommodate a jumping character:
const ascii = `
# # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # #
# # # B # # #
# # # # # #
# # # # # # # # # # #
# # # # # # #
# B # # # # #
# # # # # T
# # # # # # T # # # # # # #
# # # # # # #
# # # # # # #
# # # # #
# # # # # # # # # # # # # #
# # # # # # # # # T # # # # # # # # # #
# X # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # #`;
Hand-rolling level maps inside code files is pretty good fun. If you squint you can see what the level will look like. The ASCII characters in the string get sliced up into rows and columns. Each cell is converted into the relevant TileSprite index that defines the cavernous level. Where there’s a # will be a solid wall tile. A space will be a walkable tile. The mapping from character to TileSprite is completely up to you. The scattered letters will generate spawn points: X is where the player spawns, B is where the bats will spawn, and T where the Totems spawn.
switch (cell) {
case "#":
return 1; // Wall tile
case "B":
spawns.bats.push({ x, y }); // Create a bat!
return 0; // Empty tile
...
case " ":
return 0; // Empty tile
}

Aesthetic Tweaks
In the top-down version I did a second pass over the generated level and changed the tiles to look more “3D”. For the side-on version I took exactly the same approach, but looked for any tiles that had a non-walkable tile above them. These were then changed to the grass-topped tile to give it some visual interest.
ASCII maps are quick and effective for testing (and learning), but they don’t “scale up” well. They’re limited in functionality and are hard to edit. Once you’re sick of hand-rolling maps, spend some time looking at Tile map editors. These are GUI applications where you can select your tiles from a palette and paint your world. You can have multiple layers, as well as attach data to layers or individual tiles. Tile data can be integrated into your game code—so things like “player start positions”, or “enemy types” can be defined in the editor, rather than hardcoded in your game. We’ll integrate the popular Tiled Editor in Chapter 8.
In the initial “jumping” test, the sprite falls until it touches the ground plane arbitrarily defined as “halfway down the game screen”. In a tile-based level, how can we know when the player is on the ground? Conceptually, it’s when the player’s “feet” have collided with the top of the ground beneath them. It turns out we already check this exact scenario in the bowels of our wallslide collision detection function: if (y > 0 && !(bl && br)).
If the player is falling (y > 0) and their feet (bottom-left or bottom-right corners) are not free to move, they must have hit the ground. We’ll augment wallslide to note which edge of the entity has collided with a tile in the direction it wants to move:
const hits = { up: false, down: false, left: false, right: false };
We’ll then pass this information back from a collision check for use in our game logic:
return { x: xo, y: yo, hits };
The hit directions all default to false and will only be true if a collision occurs in the given direction. In the movement collision tests, when we test if the entity hits its “head”, we now also record this in the hits map:
// Hit your head
if (y < 0 && !(tl && tr)) {
hits.up = true;
...
}
The same goes for the feet (down), and left and right. We now understand the nature of the collision. We know when the player touches the ground, hits their head, or bumps into edges. This will be useful for other game mechanics too, such as wall jumping.
Wall Jumping
Wall jumping is a standard platform-game mechanic where the players jump, hit a wall, and jump again from midair—allowing them to go higher, rather than just sliding down to the ground. To implement it in your game, you could check if the player is pressing jump in the same frame that hits.left or hits.right is true and re-trigger a jump. We’ll explore this more in Chapter 8.
Back in the main game code, we reset the jumping flag (and velocity) whenever hits tells us there’s a solid tile beneath us:
const r = wallslide(this, map, xo, yo);
if (r.hits.down) {
this.jumping = false;
this.vel = 0;
}
So far, so good. But now we have a levitational issue: gravity is only applied when the player is jumping—and jumping is only enabled when the player presses the jump button. If the player wanders off the edge of a ledge, there will be no gravity and they can walk on air. You probably don’t want this. Check if the ground isn’t actually there (r.hits.down is not true) any time the player is not jumping.
To make it feel a bit more natural, we also give a little push downwards (three units) so they don’t “float” off the edge too much. This was just a trial-and-error figure that felt pretty good:
// Check if falling
if (!this.jumping && !r.hits.down) {
this.jumping = true;
this.vel = 3;
}
Not Quite Natural
Why not just apply gravity all the time, like in the real world? You can! Though one tiny issue is that for each frame, gravity will push down, while collision detection will push back—giving it a small vertical jiggle. This is a bug, because we flip between hits.down true/false every frame. We’ll fix this soon, by checking underneath the player. More importantly, though, not applying unnecessary forces makes it easier for us to precisely control what is going on—rather than leaving it up to the laws of “nature”.
There’s one final subtle issue with our jumping code. If the player tries to jump in a confined area, they smash their head on the roof above them. You’d expect them to rebound and fall directly back to the ground, but because the regular jumping trajectory is still being calculated, the player sticks to the roof until velocity gets high enough to push them down. To avoid this, velocity must be neutralized as soon as the player hits their head:
if (r.hits.up) {
this.vel = 0;
}
Notice how easy it is to mess with physical laws in our game world! Once you understand how to implement things realistically, you can start thinking about how to bend the rules. Perhaps velocity doesn’t get neutralized when you hit your head, and “roof sliding” across gaps is a core mechanic of your game? Always be experimenting and prototyping with the rules and values!
Fixing Our Time Step
We’re back on track for the game jam, but our platform game has just exposed a major issue with our game loop. If you play the game on a slow computer (or your computer suddenly undertakes a CPU-intensive task) the player’s jump height changes! They might not even be able to jump high enough to get up on a platform! That’s not good. We glossed over this in Chapter 2 (for simplicity’s sake) but we can’t ignore it when implementing forces that depend on a consistent delta time.
Simulating High CPU Load
To mimic a high load, you can write a loop that outputs a lot of console.log messages in the game’s main update. For example, for (let i = 0; i < 1000; i++) console.log(i);. Now play the game and hold down the space bar: notice the jump height can dip below the platform!
The reason for the inconsistency is this: the force we apply for a jump is constant and instantaneous, but the amount of gravity we apply is dependent on the time that has passed between each frame. On a slow computer more time passes, so dt is higher and gravity is heavier. We could compensate by considering dt when applying a launch force. But dt varies; if jumping happens on a fast frame, there wouldn’t be much power. If it’s during a lag, the player would get a mega jump—possibly getting stuck in a tile above them!
One solution is to use a fixed time step for our physics system where each update is given a constant dt. When there’s a lag, a lot of time has passed between frames, so we call update multiple times with the constant dt to make up for it. We only render once after the updates are complete. Rendering is generally the most expensive part of a game loop, so splitting apart updating and rendering gives us a way to keep the game physics correct without overtaxing slow computers.
The core game loop logic in Game.js is the same as before: determine the time between the previous and current frames (capped at some maximum length based on STEP: the frame rate we desire). However, now the dt is accumulated rather than just assigned. (That is, where previously we had dt = Math.min(...), we now have dt += Math.min(...).)
// Updates and render
const t = ms / 1000; // Let's work in seconds
dt += Math.min(t - last, MAX_FRAME);
last = t;
The accumulation is used to store the amount of time that gets “carried over” from the last loop. Then comes the crux of a fixed time step loop: the amount of time carried over, plus the length of time between the frame, is divided into STEP-sized chunks. This is the number of updates that need to be done. For each chunk, our scene is updated and the gameUpdate function is called:
while (dt >= STEP) {
this.scene.update(STEP, t);
gameUpdate(STEP, t);
dt -= STEP;
}
this.renderer.render(this.scene);
After the STEP-sized updates are done, the scene is rendered once. In a perfect world, there would only ever be one update per frame. But if there’s lag in the browser, it may be two or even three (up to our maximum). But each update is a fixed size, so our physics calculations will behave more predictably. The elapsed time won’t be exactly the size of a step, but whatever is left over gets saved for the next frame.
In addition to having a stable game loop, we also have more control over when our update and render functions are called. It can be enhanced with additional features such as “slow motion”. The game will think it’s running at 60 frames per second, but we can speed it up or slow it down so that time is mystically dilated. Add another couple of global variables at the to of Game.js:
const MULTIPLIER = 1;
const SPEED = STEP * MULTIPLIER;
The MULTIPLIER will be the ratio to dilate time by. Greater than 1 and time will slow, less than 1 and time will speed up. SPEED uses the multiplier to determine the rate that the game should be updated. For now, the MULTIPLIER is a constant, but later we’ll expose it so we can modify it in real time:
while (dt >= SPEED) {
this.scene.update(STEP, t / MULTIPLIER);
gameUpdate(STEP, t / MULTIPLIER);
dt -= SPEED;
}
The number of updates we do depends now on SPEED (which is a function of the step size and the multiplier). Each update still receives the normal STEP size, so despite the modified frames per second, internally the game will be consistent as when running at normal speed. Even if you don’t want time manipulation as part of your game, setting MULTIPLIER to a large number can be invaluable for debugging game logic. We’ll cover this in Chapter 9.
The final change to our game loop is not related to fixed time steps (or physics) at all. There’s an issue with how our loop values are initialized. When we first call the loopy function via requestAnimationFrame, the timestamp (ms) is not zero. Depending on what your scripts are doing it can sometimes be 100 milliseconds or more. This means our delta value for the first frame is way too high.
To prevent update being called multiple times unnecessarily, we’ll have a separate function that properly initializes the variable.
const loopy = ms => {
// ... main loop logic
};
// Initialize the timer
const init = ms => {
last = ms / 1000;
requestAnimationFrame(loopy);
};
requestAnimationFrame(init); // Call "init" instead of "loopy"
Game will schedule a call to the init function. This sets the real last value and then schedules a call to loopy. Problem fixed!
While we’re here I also converted loopy to be an arrow function: because I know we’ll need to be in the correct Game scope later, when we implement screen transitions. Our core loop is now rock-solid, and ready to be the backbone of our physics-enabled games.
Triangles and Vectors
Trigonometry is all about the relationships of lengths and angles in triangles. When you start squinting, triangles are everywhere—and recognizing characteristics and behaviors of triangles is extremely important in game development. They turn up in AI for path finding and human-like behavioral responses, in simple physical properties like bouncing and reflecting, and in visual effects like lighting and particles. It’s all triangles!
Thankfully, we don’t have to dive too deep into math to reap some compelling rewards. Even the shallow end of the math pool gets us a long way when making games.
Building a Vector Library
Vector spaces (for the purposes of gamedev, at least) represent the game universe where things exist. Vectors are objects that model certain aspects of our game world. Pragmatically, we often use them to represent points in space and physical forces. There are some wonderful mathematical properties of (and operations we can perform on) vectors that benefit us while making games.
For example, combining vectors is an elegant way to implement physical forces (jumping force + gravity force = player trajectory). Or another example, if you apply the algebraic operation known as the dot product on vectors that represent the positions of, say, a bad guy and the player, the result will tell you if the bad guy is facing the player. Which has some obvious use cases for enemy AI. Vectors are a way of neatly modeling the world around us in code.
Vectors are often visualized by an arrow that has a length (called its magnitude) and a direction. Throughout this book, we’ve been representing points in screen space using the 2D vector pos. This has an x and y component that together show where an entity should be drawn. If we wanted to, we could also consider pos a vector that starts at the origin (often written (0, 0), where x = 0 and y = 0) and points to x and y:
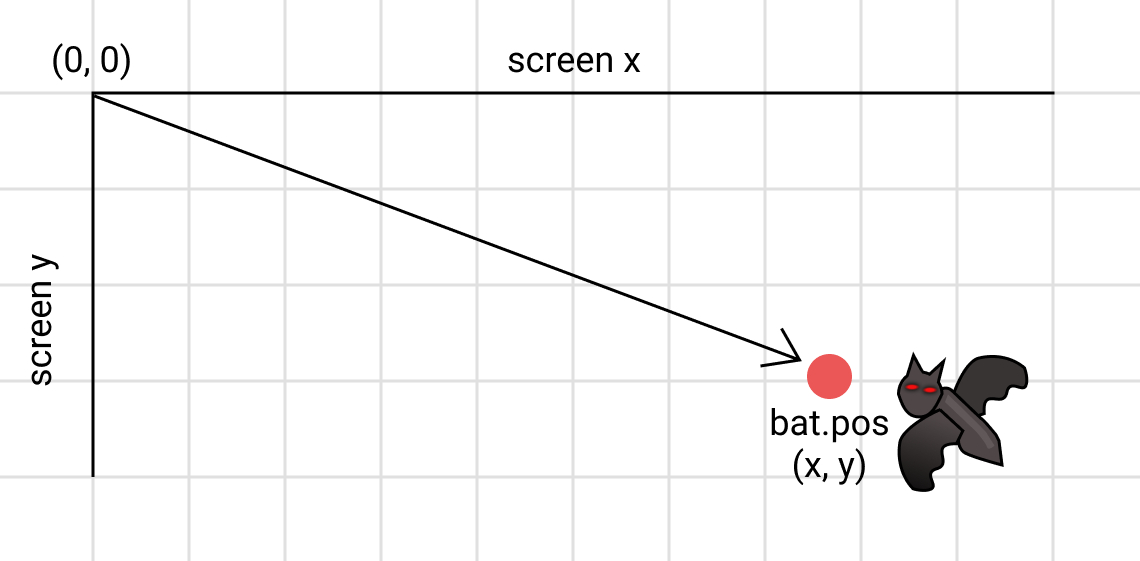
The line from the origin (0, 0) to (x, y) is the magnitude (length) of the vector. An advantage of treating pos as a vector is that we can abstract common vector operations into a reusable library. We no longer need to apply every operation separately to the x and y components. We write less code, and our intentions are clearer.
So let’s make a vector library that will encapsulate the concept of vectors. In this section, we’ll create the library (a library inside our library!) and add some helpful methods. Then, in the rest of the chapter, we’ll use the vector library to simplify and extend our physics code. The library will live in Pop in the utils folder, and will henceforth be known as Vec.js. At its core, it’s a container that (optionally) sets x and y values:
class Vec {
constructor(x = 0, y = 0) {
this.x = x;
this.y = y;
}
}
Throughout the book, we’ve created many objects that would be better modeled as a Vec. The most obvious is the pos of our base library elements. We can store pos as a Vec, rather than maintain the individual x and y properties ourselves. For example, let’s convert a Sprite’s pos into a vector:
import Vec from "./utils/Vec.js";
class Sprite {
constructor(texture) {
this.pos = new Vec();
...
}
}
For the moment, nothing has changed: a sprite’s position can still be altered by modifying pos.x or pos.y. Any time we need a point-like object such as pos, we can create a new Vec(). If we want to default it to a value, we can pass that in at creation time: new Vec(10, 10).
Vectors can be used for more than just modeling points. A vector often represents an entity with a direction and a magnitude. In the previous image, you can see that the vector’s origin point is (0, 0). The direction is the angle of the hypotenuse of the right triangle formed from the origin and the point. The magnitude is the length of the hypotenuse. Sound familiar? It’s Pythagoras again—just like our math.distance function. Determining the magnitude of a vector comes in handy, so it becomes the first helper method on Vec:
mag() {
const { x, y } = this;
return Math.sqrt(x * x + y * y);
}
The Vec class can also be extended with methods that manipulate vectors. A simple but useful one for us is set, which updates both components at the same time:
set(x, y) {
this.x = x;
this.y = y;
return this;
}
Any Sprite’s position can be updated with a single call—pos.set(10, 10). Not a huge difference, but conceptually we’re now thinking about position in terms of a single tangible concept (and we can set pos with a one-liner, instead of two!).
Enabling Method Chaining
Many of the methods in the Vec library will return this. this represents the current instance of the Vec. By returning itself, we end up back where we started after the function is complete. From here we can call another function, and another. For example, pos.set(x, y).add(velocity) would first set the position and then add a velocity vector to the original position. This method chaining can result in a very readable API when we need to perform multiple operations in a sequence.
Many times we want to set an entity’s location to some existing value (for example, its spawn location). A bullet should originate at the player’s current location when they press fire, or a bad guy should spawn at a location defined in our level map editor. Rather than setting positions by hand, we could copy an existing vector:
copy({x, y}) {
this.x = x;
this.y = y;
return this;
}
The copy method works with any object that has an x and y property (it doesn’t have to be an instance of Vec). Just like set, we can now use a single call rather than setting properties manually:
map.spawns.bats.forEach(spawn => {
const bat = bats.add(new Bat());
bat.pos.copy(spawn);
});
I think that looks a lot nicer. Let’s take it even further. Once our Vec library becomes more powerful, we’ll want to be able to use any object (that has an x and y property) as a vector source. We could create a new Vec and use copy to set the values with new Vec().copy(objWithXY), but it’s a bit ugly: it doesn’t clearly show our intent to create a new Vec from a source. A nicer solution is to provide a shortcut (via a static method) at the top of the Vec.js class:
static from (v) {
return new Vec().copy(v);
}
Then we can create a vector via Vec.from(objWithXY) without requiring the new operator. Handy!
Static Methods and Properties
Static methods and properties are shared between all instances of the class. As a property, this makes sense when all instances need to globally share some information (perhaps a count of all created instances). For methods, it’s nice in cases where you don’t need access to the instance properties, such as our from helper.
Having a raft of ways of initialized vector values, it’s finally time to do some vector manipulation. The most common vector operation is to add two vectors together. What doing vector addition means depends on the use of the vector itself. If we’re using it to denote a position in space, then addition is a translation from a current position to a new position. However, if the vector is a force, then it’s the combination of forces.
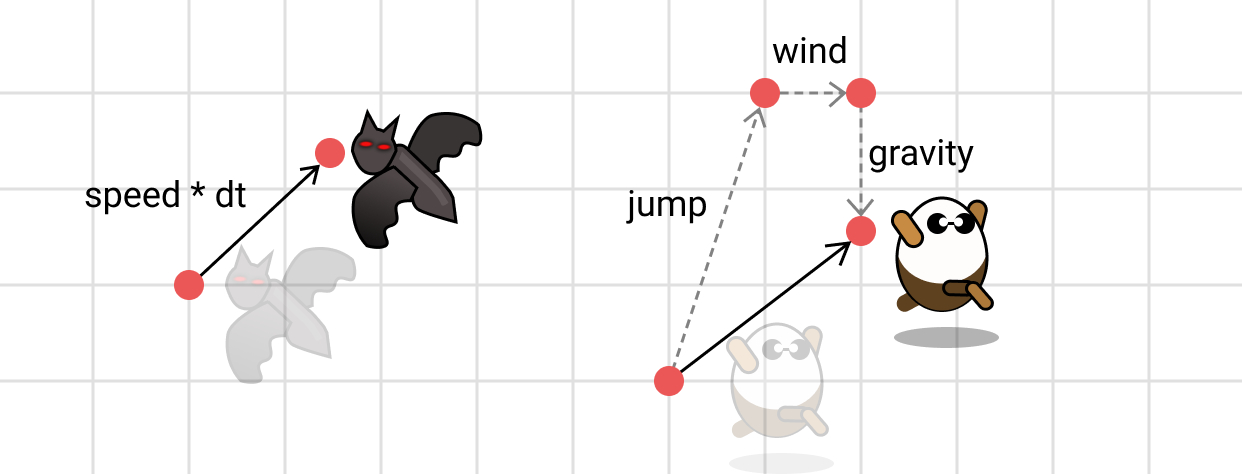
To add two vectors together, we sum the corresponding x and y components. Our API accepts a vector as an argument (actually, anything with x and y properties) and adds this to the current vector. This modifies the current vector:
add({ x, y }) {
this.x += x;
this.y += y;
return this;
}
We can make a complimentary subtract method too. If we want to translate a sprite, we can add or subtract a translation vector to it. For example, we currently do this every time after we check for tile-map collisions. The result from wallslide is the amount to translate the sprite by—in the form of an object with x and y components that we can now treat as a vector:
const response = wallslide(this, map, xo, yo);
pos.add(response);
Another common operation is vector scaling. Scaling a vector means to make its magnitude larger or smaller by some factor. For example, if we had a vector Vec(5, 0) and wanted to scale it by a factor of two, we’d expect to end up with the result Vec(10, 0). The magnitude of the vector has doubled.
To calculate the new vector, we multiply it by a scaling ratio. Because we want it to scale proportionately on both axes, the multiplication factor is a scalar value (single number) rather than a vector:
multiply(s) {
this.x *= s;
this.y *= s;
return this;
}
To test that our vector has been correctly scaled, we can measure its magnitude before and after scaling:
const vec = new Vec(5, 0);
console.log(vec.mag()); // 5
vec.multiply(2);
console.log(vec.mag()); // 10
But what does it mean to scale a vector? Again, it depends on the context. If the vector is a force, scaling it will either strengthen or weaken the force. If the vector is a position, scaling will project the position along the path from the origin to the current location. For example, we could find the midpoint between two entities by adding their positions and then scaling by half:
player.pos
.add(badguy.pos)
.multiply(0.5);
The midpoint between two entities might be of practical use in your game. Perhaps you want to show a warning indicator half-way between you and some approaching aliens, or deploy a fancy shield that blocks incoming missiles. However, there’s an issue with our operation. The add function modifies the original vector. Calculating the midpoint would result in the player’s sprite being teleported to the midpoint! This is because our vector library is mutable: all changes are done in place on existing vectors. If we want to use the result somewhere else, we first need to clone the original vector:
clone() {
return Vec.from(this);
}
Cloning will create a new Vec object and initialize it with the current x and y values:
const midpoint = player.pos
.clone()
.add(badguy.pos)
.multiply(0.5);
Normalizing, and the Dot Product
There are several additional operations that are frequently required when making games. One is the concept of normalizing a vector. Normalizing scales a vector so that its magnitude is exactly 1. To do this, take the current magnitude and divide each axis by that amount:
normalize() {
const mag = this.mag();
if (mag > 0) {
this.x /= mag;
this.y /= mag;
}
return this;
}
The result of normalizing is a unit vector (because it would touch the perimeter of a unit circle—a circle with radius 1). Normalizing gives us the essence of the direction of a vector. Once you have the essence, you can manipulate this in consistent ways. For example, a normalized vector can be rescaled to get a specific magnitude in the given direction. Here’s how to find the point exactly 50 pixels away from the player, in the direction the bad guy:
player.pos.clone()
.add(badguys.pos)
.normalize()
.multiply(50)
The last operation we’ll look at is a weird one, but one that often appears in AI behaviors—the dot product. The dot product is the sums of the products of corresponding components. It’s calculated like this:
dot({x, y}) {
return this.x * x + this.y * y;
}
The result of the dot product is the x components multiplied together, plus the y components multiplied together—a scalar value. Intuitively, this might seem like a strange idea, but it has some interesting properties with regards to the angle between the two vectors.
When two vectors are pointing in the same direction, their dot product is positive. This seems reasonable enough: if you took the dot product of a vector with itself, it would be the squared length of the vector. The opposite case also seems reasonable: when the vectors point away from each other, the result will be negative. And the point where they’re exactly perpendicular to each other? There’s nothing in common between the vectors, so the dot product returns 0!
The dot product is proportionate to how closely the vectors are pointing in the same direction. This sounds valuable when we think about applying it in our games. “If the bad guy’s facing away from the player, wander around. If they’re facing the player, ATTACK!”
The Need for Speed (and Direction)
Having implemented some vector manipulation, it’s time to see what we can do with our new skills. Many of the properties and forces we’ll use to simulate the world around us can be nicely modeled with vectors. “Roughly” simulating the world is our goal here. Mario doesn’t fall back to the ground at a rate of 9.80665 meters per second for a reason: it’s not as fun!
Unless you're trying to create a realistic simulation, you should consider tweaking and exaggerating your physics to make things exciting and compelling. If you’re playing a futuristic racing game and the cars move as they do on Earth, it feels good … but if the cars slide around and accelerate like a rocket, it feels awesome. If the cars handle like souped-up old jalopies, you'd better have some other interesting mechanic (get it?) to make it enjoyable!

Pausing Bravedigger
For the next few sections, we’ll put Bravedigger on the back burner and start fresh with a minimal test project. The goal of this project is to implement and validate a physics system with velocity, acceleration, gravity, and friction. Once we’ve confirmed our system is solid, we’ll integrate it back into our physics-based platform game.
Velocity
It all starts with velocity. Velocity is a vector quantity that describes an object’s speed and direction. We’ve been setting the player’s velocity all along—based on a combination of the user’s keyboard controls and a constant “speed” amount. Because we independently update an entity’s x and y coordinates, we’ve been able to move in any direction. As we switch to a physics-based approach, we’ll stop directly modifying pos and instead apply a “force” that will indirectly affect it.
Our project will feature a brave test pilot—an intrepid Sprite called CrashTestDummy.js. CrashTestDummy is our guinea pig while we work out kinks in the physics system. The main GameScreen consists of a CrashTestDummy, along with some debugging Text for displaying timing information to validate our physics values.

class CrashTestDummy extends TileSprite {
constructor(vel) {
super(texture, 48, 48);
this.vel = new Vec(vel, 0);
}
}
The key here is the creation of the velocity vector, vel. It’s a Vec initialized with a y value of 0 (so it won’t move up or down) and an x value assigned from the outside world. This will be the speed of our CrashTestDummy test subject.
The velocity of an object is the rate of change of its position with respect to time. To calculate the new position of an entity (to apply the vector force and displace our sprite) we add the individual components of the vectors, multiplied by time, to the original position.
update(dt) {
const { pos, vel } = this;
// Move in the direction of the path
pos.x += vel.x * dt;
pos.y += vel.y * dt;
}
Using an Old Approach
We’re back to individually updating properties again (rather than using .add() and .multiply()). Why? Multiplying the velocity vector by dt would mutate vel, but we need it to remain unchanged. We could clone it with pos.add(vel.clone().multiply(dt)), but then we have to create a new Vec object every frame, and the result is harder to read. I just decided to do it the old way.
To test velocity within our new project, in GameScreen create a new CrashTestDummy and assign it a velocity based on the width of the screen. By doing this, we know how long the Sprite should take to get from one side of the screen to the other, and we can set a timer to confirm that our velocity calculations are correct:
const velocity = this.w / 3; // Should be three seconds to cross the screen
this.ctd = this.add(new CrashTestDummy(velocity));
Every frame, we check if the CrashTestDummy has made it to the finish line. If so, we stop the timer running. (I also added in a reset switch so you can hit the space bar to re-start the test.)
if (ctd.pos.x >= w) {
this.running = false;
}
if (running) {
this.time += dt;
timer.text = `${this.time.toFixed(3)}`;
}
This looks correct. Good enough at least! Our CrashTestDummy takes exactly three seconds to get from the left to the right side of the 800-pixel-wide screen, at a velocity of 266.67 pixels per second. Try modifying the frames per second (STEP size) in our main game loop to ensure we’re running correctly at all frame rates. (Spoiler: this also seems fine.)
Velocity Bounce
The sprite’s position is now the result of applying velocity. If we don’t modify velocity after we initially set it, CrashTestDummy will fly off the screen, never to return. It would be nice if it bounced back when it hit an edge. Reflecting an arbitrary angle (bouncing off a surface) can sometimes be tricky—but not so much in our simple world. Because the screen edges are perpendicular, we only need to invert the entity’s velocity on the axis that it collides with. Velocity can be inverted by multiplying it by -1:
// Bounce off the walls
if (pos.x < 0 || pos.x > bounds.w - w) {
vel.x *= -1;
}
if (pos.y < 0 || pos.y > bounds.h - h) {
vel.y *= -1;
}
The bounds is the bounding area of the entire game screen. We’ll make the main game area quite large, and pass the bounds to the CrashTestDummy when it’s instantiated. Our CrashTestDummy can now bounce. To test this, have the CrashTestDummy choose its own position (within the bounds) and velocity (between -300 and 300 pixels per second on both axes). Because the velocities are random for both x and y, it will also move in a random direction:
this.pos.set(bounds.w / 2, bounds.h / 2);
this.vel = new Vec(
math.rand(-300, 300),
math.rand(-300, 300));
Now we can apply the sacred rule for showing off gamedev features: “Why have one, when you can have 30?” More is more! Add a pod of crash test dummies to a Container in GameScreen and set them free:
const bounds = { x: 0, y: 0, w: this.w, h: this.h };
for (let i = 0; i < 30; i++) {
this.add(new CrashTestDummy(bounds));
}

Having direction controlled via velocity starts to yield some fruit.
Acceleration
Moving things with velocity alone is fine, but acceleration is how we make things supercool. Where velocity represented the rate of change of position, acceleration represents the rate of change of velocity. Rather than just adding a constant to an entity’s position, we add the amount of acceleration to velocity and accumulate it every frame. This accumulation is what gives the feeling of naturally “speeding up”:
this.vel = new Vec();
this.acc = new Vec();
Acceleration is a vector just like velocity. It can be applied independently in the x and y directions. For our initial tests, we’ll only apply it in the horizontal direction inside CrashTestDummy’s update (at a rate of 200 pixels per second):
const ACCELERATION = 200;
acc.x += ACCELERATION;
// Update velocity and position
...
acc.set(0, 0);
At the end of the update loop, acc is reset back to 0. Otherwise, we’d be accelerating acceleration! Now we can do our physics integration:
vel.x += acc.x * dt;
vel.y += acc.y * dt;
pos.x += vel.x * dt;
pos.y += vel.y * dt;
Acceleration is the rate of change of velocity with delta time, and velocity is the rate of change of position with delta time. First we add acceleration to velocity, then update position from velocity as usual. Now on each frame the value of velocity becomes larger, rather than remaining a constant. The CrashTestDummy starts very slowly, getting faster and faster until it hits the other side of the screen, then rebounds back elastically.
It looks pretty groovy—and that’s often good enough. But to ensure we’re accumulating velocity correctly, we could test it against the physics formula for displacement from acceleration—s = ut + ½at2—where s is where our sprite should end up on the screen, u is the initial velocity, a is acceleration and t is time. Because we start from a dead stop, ut can be ignored, and we end up with this:
const expectedPos = 0.5 * ACCELERATION * this.time * this.time;
In the game screen, we’ll add a timer and some text and freeze it after two seconds to see if we’re correct. In our tests (running at 60 frames per second) we saw that, after 2.017 seconds, the sprite had moved 410 pixels. Plugging that into the equation gives 0.5 * 200 * 2.017 * 2.017 = 406. That seems pretty close—only a few pixels off. But still, not perfect. And if we try dropping the frame rate in Game.js, the margin of error gets larger.
Integration
The reason for the discrepancy is due to our method of integration. Adding acceleration with time to velocity, then velocity with time to position, is called the “Semi-implicit Euler method”. It’s simple, efficient, and matches our verbal definitions of acceleration nicely, but it’s only as accurate as the delta step time, and is subject to rounding errors.
More Advanced Physics
If you want to build a serious physics engine, you should study integration algorithms like Vertlet integration and the 4th-order Runge-Kutta method (RK4). These are stable and will work well even when it comes time to implement advanced physics topics.
We don’t need our engine to be too advanced, but we’d like it to work even consistently at very low frame rates. We’ll tweak our integration to use an approach called Velocity Vertlet integration. Because this is something we’ll want to do on many of our entities, it’s time to drop some physics into Pop in a new file called utils/physics.js:
function integrate(e, dt) {
const { pos, vel, acc } = e;
// integrate!
...
acc.set(0, 0);
}
export default {
integrate
};
This method is doing exactly what we did earlier. It’s a function that accepts an entity and the delta time that has elapsed and then applies acceleration and velocity to position (and finally resets acceleration to 0). Before this, we perform the Velocity Vertlet integration:
const vx = vel.x + acc.x * dt;
const vy = vel.y + acc.y * dt;
const x = (vel.x + vx) / 2 * dt;
const y = (vel.y + vy) / 2 * dt;
pos.add({ x, y });
vel.set(vx, vy);
This integration method looks a bit hairier than Euler’s method, but it’s not too different. It’s still adding acceleration by time to velocity, then velocity by time to position. But now it’s averaging the acceleration over frames—applying half now, and the other half next frame. The position update is calculated in the middle of an integration step, rather than on the edge, resulting in more stable updates even at very low frame rates.
Now that we can easily integrate, we should also make it easy to add forces to an entity. The CrashTestDummy is currently powered by a mysterious force pushing on it to the right, and that’s it. The beauty of controlling entities via forces is that they can easily be combined to make more interesting results. For example, the mysterious force on CrashTestDummy is probably a jetpack, but crash test dummies could also be subject to gravitational forces—or perhaps intermittent wind forces. Each can be added independently without knowing about the others.
For us, applying a force simply means adding it to the amount of acceleration to calculate. If you think back to physics classes, you may recall Newton’s Second Law of Motion: F = ma. Force equals mass times acceleration. If we want to figure out acceleration, we have to solve for it. Acceleration equals force divided by mass. Most of the time, we’ll omit mass from the entity and just assume everything has mass 1, but feel free to play around and changing it!
function applyForce (e, force) {
const { acc, mass = 1 } = e;
acc.x += force.x / mass;
acc.y += force.y / mass;
};
Notice that we add the result to acc. Acceleration is accumulated with each force we apply. That’s why we needed to reset acc to 0 at the end of the integration, rather than just assign it fresh at the start of each loop. Each force is applied, then finally we integrate:
// Jetpack!
physics.applyForce(this, { x: 200, y: 0 });
// Gravity!
physics.applyForce(this, { x: 0, y: 100 });
physics.integrate(this, dt);
Impulse Forces
Accelerate is slowly build up velocity over time. Not all forces work this way: if you get shot out of a cannon, you don’t take much time to get to your maximum speed! In our games, we’ll frequently want to give an entity an instant boost to have them moving at the correct rate. We do this with an impulse force. Rather than something that accumulates over frames, it’s a one-off injection:
const applyImpulse = (e, force, dt) => {
applyForce(e, { x: force.x / dt, y: force.y / dt });
};
Applying an impulse is similar to a regular force, except you must also pass in the delta time for the current frame. The applyImpulse method removes the time that would normally get multiplied inside the integrate method; the force gets directly transformed into velocity. You use an impulse wherever you want a one-off kick, rather than a constant buildup:
if (mouse.released) {
physics.applyImpulse(this, {
x: 400,
y: 0
}, dt);
}
For example, a bullet will instantly be moving at its maximum speed as soon as the player clicks the fire button. Applying an impulse uses the regular applyForce under the hood. Therefore, other forces that affect the bullet (impulses or regular) still work as expected.
Friction
Without an opposing force, our sprites would keep accelerating and drifting though the void of space forever. Even with small amounts of acceleration, that will quickly become uncontrollably fast! Something needs to slow us down, and that something will be friction. For games that aren’t set in space, we need to calculate the friction generated when an entity is in contact with a surface.
The formula for friction is F = -1µNv, where F is friction, µ is a coefficient for resistance of the surface, N is the normal vector (perpendicular force) of the surface, and v is the velocity vector. That’s a lot of things to do just to slow us down a bit. Time to “fake it until we make it” again (we’ll figure it out correctly in the next section).
How about, instead of real friction, we temporarily violate our rule of messing with vel directly and apply a dampening force. It’s not really a force as we know it; it’s just a trick to scale down the final velocity vector by a value from 0 to 1. The closer the value is to 1, the lower the friction. (We’ll put physics constants at the top of the file so you can quickly tweak them.)
const FRICTION = 0.95;
...
vel.multiply(FRICTION)
The value you choose radically changes how the sprites move. Very close to 1 feels like you’re skating on ice. Lower, and you’re suddenly stuck in mud. You also may have to increase the acceleration power to fight the opposing friction. Striking a perfect balance between power and friction is the key to making something that handles nicely. Optimum values vary dramatically depending on the requirements of your game.
Figuring Out the Best Values
Figuring out the best values for our faux-physics system is great fun and can result in some happy, unexpected accidents. Don’t forget the tip “double or halve it!” when hunting for interesting settings.
More Accurate Friction
The dampening method for applying friction is simple and easy, but really it’s a cheat. Gamedev is all about cheating when you can get away with it, but there are some serious problems with our fake friction. A big one is that it doesn’t consider the timestep at all. If you’re running at a low frame rate, friction will be calculated less often, and the sprites will slide around more.
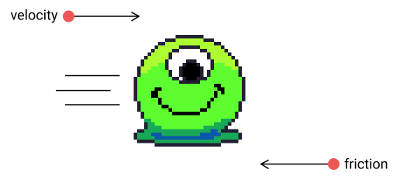
Let’s move closer to the original equation for calculating kinetic friction force, F = -1µNv. -1 is the inverse. µ is fine too: it’s the coefficient constant we want to resist by. Higher equals more resistance. v is the direction of velocity. The only thing left is N, the surface normal. In the image above, the surface normal is a vector pointing perpendicular to the ground. Our ground is flat, so the surface normal points straight up and doesn’t affect the horizontal force. We’ll ignore it.
The idea is to get the vector that’s pointing in the opposite direction to the sprite (that’s why it’s -1), and apply a set resistance force in that direction. We can find the “opposite direction” by scaling the velocity vector by -1: vel.clone().multiply(-1). If we used that, the equal-and-opposite force would stop the sprite dead. To apply a specific µ value, we first need to normalize to get the unit vector and then multiply by our friction coefficient:
const friction = vel.clone()
.multiply(-1)
.normalize()
.multiply(200);
physics.applyForce(this, friction);
Velocity isn’t being modified directly, but through a force. Our entities will slide the same regardless of frame rates. Other real-world forces can be emulated in the same manner. The beauty of a physics-based system is this ability to combine simple rules to define the overall complex behavior of your game world. In many games, you’ll just want to keep things simple: friction, gravity, maybe some air resistance. But you get to be God here, and you write the rules. Don’t forget to go crazy from time to time.
Gravity-based Platformer
We have all the tools to integrate physics into our games. As we saw earlier, gravity is a downward force (a force with no x component). Of course, it doesn’t have to be downwards, or constant; you can make gravity work however you want! But now, thanks to friction, when the CrashTestDummy reflects off the bottom of the screen it will struggle to return to its original position. Force is being dissipated and our crash test dummies “bounce”.
const friction = vel.clone().multiply(-1).normalize().multiply(200);
const gravity = { x: 0, y: 500 };
physics.applyForce(this, friction);
physics.applyForce(this, gravity);
physics.integrate(this, dt);
Having covered velocity, acceleration, and friction, we can reintroduce these concepts into Bravedigger. Our game’s forces of nature will affect how the player moves. However, forces are not the only things that affect the player in the games we’ve been making.
Our level’s tile map is made of solid bricks; gravity shouldn’t be strong enough to push us right through the ground. We need our physics integration to work together with our wallslide (and related collision detection functions) to put entities in their correct spots.
Skipping the Physics
You can think of the wallslide collision detection method as being the opposing ground reaction force to our character’s contact force. But it’s not implemented as a force at all: it’s just cheating and using our old system of modifying the pos variable manually. You could model it with a real force—but honestly, because of the simple nature of a platformer world, it’s much easier to get the precise feel you’re after by taking manual control.
Remember that our collision detection algorithms work by us providing a displacement amount we want to move. In return, it tells us how much we can move. Rather than updating pos directly in integrate, we need to get the amount we want to move back from it so we can pass it to wallslide:
const vx = vel.x + acc.x * dt;
const vy = vel.y + acc.y * dt;
const x = (vel.x + vx) / 2 * dt;
const y = (vel.y + vy) / 2 * dt;
vel.set(vx, vy);
acc.set(0, 0);
return { x, y };
The result from the integration is where physics thinks we should go. Wallslide considers this and returns its own opinion. That is the displacement amount we add to pos:
let r = physics.integrate(this, dt);
r = wallslide(this, map, r.x, r.y);
pos.add(r);
With physics and tile-map collision working together, the only remaining challenge is choosing the physics constants that feel good in the game. It can be “fun” getting values that work exactly how you’d like. It’s the double-edged sword of using a physics system: having the world dictate how everything moves is magical and powerful, but comes with the cost of surrendering precise and exact control.
It’s best not to be too dogmatic. Where possible, you shouldn’t modify velocities and positions directly … but gamedev rules were meant to be broken! If you need to stop velocity dead in its tracks to get a sensation or effect you desire, then break the rules. If it feels good, do it.
Billiard Ball Physics
Adding basic physical properties to your games gives fluidity to platformers and shoot-’em-ups. But it can be taken further! If you take the simulation further—and your game’s core mechanics rely on it—then you have a physics game. In physics games, generally all forces and responses are determined by the physics engine. (For example, we don’t delegate responsibility out to a wallslide, like a collision handler.)
Implementing a system to handle arbitrary shapes in our library (like polygon sprites and convex terrain) is beyond the scope of this book. (In the next section, we’ll cheat and use a third-party library to do it for us.) But if we impose some restrictions, we can implement some nice physics-based mechanics without getting into “hard math” territory.
Our primary restriction is that we have to treat all entities as circles, rather than rectangles. Circles are just easier to deal with: we don’t have to worry about detecting collisions with rotated rectangles. With that in mind, we’ll implement a simulation of balls moving on a billiard table, pinging and reflecting off each other as they collide.
The setup will be a handful of crash test dummies placed randomly around the screen:
this.bounds = { x: 0, y: 0, w: this.w, h: this.h };
this.balls = this.add(new Container());
for (let i = 0; i < 30; i++) {
const b = this.balls.add(new CrashTestDummy(this.bounds));
b.pos.set(
math.rand(48, this.w - 96),
math.rand(48, this.h - 96)
);
}
The bulk of the collision detection and resolution is done in the GameScreen’s update. Here we loop over all of the balls and check them for collisions against all other balls. We do with this in a nested for loop:
const balls = this.balls.children;
for (let i = 0; i < balls.length; i++) {
const a = balls[i];
for (let j = i + 1; j < balls.length; j++) {
const b = balls[j];
// Check for collisions
...
}
}
This nested loop is an efficient way to check each child against all others. The inner loop starts from i + 1 so that we only check each pair of balls against each other once. Now we can do collision detection and resolution. The first step is detection:
// Check for collisions
const diff = b.pos.clone().subtract(a.pos);
if (diff.mag() > a.radius + b.radius) {
continue;
}
This is our standard circle-based collision test. We say there’s a “collision” if the magnitude of the position offsets (a.pos and b.pos) are less than the sum of the circle’s radii—just like our shoot-’em-up in Chapter 3. If there’s no collision, we’ll move on to the next pair of balls.
Collision Resolution
Now comes the tricky part. The two entities are colliding. Up till now, when things have collided we’ve made them explode and die—problem solved. But now we need them to react less violently. We need to adjust their positions so they’re not colliding, and adjust their velocities so they’re moving away from each other—in the correct direction, with the correct speed.
The first step is to separate the two entities so they no longer overlap. To do this, take the vector between them, find the point exactly in the middle of that vector, then adjust each position relative to the midpoint such that they’re no longer overlapping.
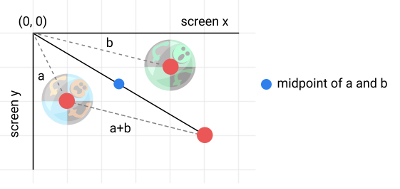
To acquire the midpoint between the two balls, add the positions together and divide by two:
const mid = a.pos.clone().add(b.pos).divide(2);
const normal = diff.normalize();
To move the balls apart, first normalize the diff vector between the balls and displace them away from the midpoint. Remember that normalizing gives us only the direction between the two points, with its magnitude scaled to 1. We can use this to move an exact number of pixels in that direction. Multiplying by radius gives us the correct amount to move. For the first ball, we add this to the midpoint; for the second ball, we subtract it. In pseudo-code it would look like this:
a.pos = mid - (a.radius * normal)
b.pos = mid + (b.radius * normal)
If we did these calculations with our vector library, there would be lot of cloning for the midpoint and normal vectors. This would be costly in terms of unnecessary objects, and wouldn’t read very nicely either. It’s another case where it’s probably better to do it ourselves:
a.pos.set(mid.x - normal.x * a.radius, mid.y - normal.y * a.radius);
b.pos.set(mid.x + normal.x * b.radius, mid.y + normal.y * a.radius);
The a entity has been moved a bit in one direction, the b in the other. Because they both moved apart radius pixels, they no longer overlap and sit just next to each other. Now the balls are in the right spot, but their velocities still have them moving on their original courses. To rectify this, we take the difference between their current velocities, projected along the normal vector between them:
let power = (a.vel.x - b.vel.x) * normal.x;
power += (a.vel.y - b.vel.y) * normal.y;
Taking the sum of the axes’ power, we alternatively add and subtract it to the entities’ velocities—just as we did for adjusting the positions. They now reflect off each other and ricochet away.
const displacement = normal.multiply(power);
a.vel.subtract(displacement);
b.vel.add(displacement);

Using principles of vector manipulation, we can create some satisfying real-world effects. At the very least we could make a good game of snooker.
Polar Coordinates
We’ve seen how using vector properties can help us model real-world moving objects … but what do the components of our velocity vectors actually represent? At what speed is something moving if its velocity vector is {x: 150, y: 85}? At what angle is it traveling if its velocity is {x: 0.7, y: 0.7}?
In our bouncing billiard balls example, some sprites were moving at, say, a 30 degree angle. So there must be some value of x and y we can use to move in any desired direction. Yes! It turns out it’s about {x: 0.866, y: -0.5} to move at 30 degrees at a speed of 1. This x/y representation is referred to as the Cartesian coordinate system (specifically as the rectangular coordinate system because we’re in two dimensions).
In the real world, we don’t talk in terms of xs and ys. We like to think about things in terms of more familiar angles and speeds. We need a different representation—namely, the polar coordinate system.
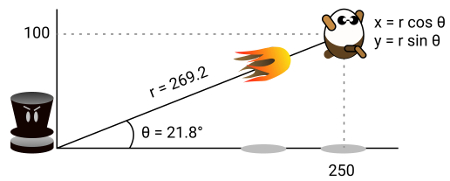
Thankfully, converting between the two systems is straightforward. When we have a scalar that is the radius (the magnitude, or speed to move by) and an angle (in radians), we retrieve Cartesian components like so:
x = r cos θ
y = r sin θ
And when we want to convert back from Cartesian to polar coordinates, there are two distinct operations—both of which we’ve used before in the “Moving, and Shooting, Towards a Target” section from Chapter 5:
r = √ x² + y²
θ = atan2(y, x)
Using Pythagoras’ theorem, we can calculate the hypotenuse of the triangle formed (which represents the radius, or speed, or distance) by our coordinates. This just happens to be our math.distance function. Similarly, the angle is calculated by taking the arc tangent of the coordinates, and is our math.angle function. We can use whichever representation is more natural for the task at hand:
this.dir = math.randf(Math.PI * 2);
this.speed = math.rand(50, 150);
In this example, our CrashTestDummy sprites are assigned a random direction between 0 and 2π (0 to 360 degrees), and a random speed. They aren’t moved by a velocity vector, but via their angles and speed. We use the formula above to convert them into x and y values to add to position:
pos.add({
x: Math.cos(dir) * speed * dt,
y: Math.sin(dir) * speed * dt
});
And we’ll sync the sprite’s rotation to match the direction:
this.rotation = this.dir + Math.PI / 4;
Offsetting Rotation
The rotation property is offset by the amount π / 4. This is because the graphics file was drawn with “up” facing 45 degrees away from 0 radians. The offset syncs the sprites so they’re facing forwards as they move.

`x` and `y` versus speed and angle are two ways of representing the same thing. Which you choose to work with depends on the situation. For example, polar coordinates are more natural when we want our entities to be controlled by steering, like a car: turning the steering wheel doesn’t move the vehicle, it only changes its direction.
this.dir += controls.x * 0.8 * dt;
Increasing or decreasing the dir property is all we have to do to steer! If you combine this with the acceleration we implemented earlier, you can create some extremely satisfying car sliding mechanics.
Physics All the Things
“Hey, hey, MomPop Games!” It’s Guy. Again. “Did you recover from your false start? Got a game to show me?” he enquires as he takes over your laptop and starts playing. “Hmm, what’s with all this platform-game nonsense? What kind of sport is that?”
He looks at your blank stare.
“I told you the theme was ‘Let’s get PHYSICAL’, right? It’s supposed to be about sports. That’s the pun—physics, physical … Sports. You get it? Oh man, that’s a shame. You should really read the website instead of listening to me, you know.”
He has a point.
You consider your situation—having to start all over again at this late stage in the competition. It’d be hard to transform Bravedigger into some kind of sport. You reply, “Oh, this—no, this is just the base for an idea I’m fleshing out. It’s, um, golf, but with … penguins. Penguin Golf. It’s called Pengolfin’, and it’s fully physics-based.”
He looks at you suspiciously, with a raised eyebrow, as he rises and silently moonwalks out the door. Forget about him, we still have time to get an entry done for this game jam! We just need a little bit of third-party help.
Physics Libraries
Recreating accurate, real-world physics is not an easy task. So far, our efforts have been fairly simple approximations of how things “kind of” move. If we were to continue to build on our custom system, we’d quickly hit some really difficult (albeit, quite interesting) problems around collision resolution, and how to accurately detect collisions between rotated entities.
If we had more time, we might start delving into these meaty topics (look up the Separating Axis Theorem if you’re keen)—but we’re in the middle of a game jam, so we we’ll repeat a well-worn gamedev adage: “Make games, not engines!”
There are some excellent JavaScript options for us when it comes to simulating a rigid-body system. Rigid-body means the points that make up the object don’t get deformed by external forces—but we’ll think of it as “our player object is solid, has mass, and will react appropriately when hit by another object”. Many game frameworks have real physics options baked in, so we’ll need a stand-alone library that we can integrate with Pop.
Do You Need a Real Physics Engine?
You should consider carefully if your game really needs a full-blown physics engine. They simulate chaos; they’re unpredictable. If you’ve ever played Angry Birds, you’ll likely have encountered a time where the game declares “LEVEL FAILED” even though you know the teetering pillars will topple given a couple more seconds. With a physics system, it’s hard to know when things are stable, and it’s hard to control exactly how everything will interact together.
One of the most common physics libraries known in 2D game development is a C++ project called Box2D. This has been ported to many languages, including several efforts in JavaScript. Of these, Planck.js is a well maintained effort.
However, I feel that Box2D tends to feel very “C++”-ish and verbose in JavaScript. There are a few more modern and idiomatic options available to us. P2.js and Matter.js are two great projects that have been under active development for a long time. We’re going to run with Matter.js. It’s well maintained, fun to use, and easy to integrate. It’s important to note that the basic concepts and features apply to nearly all physics engines. Once you master one, it doesn’t require a lot of effort to get up to speed with any other.
Penguin Golf
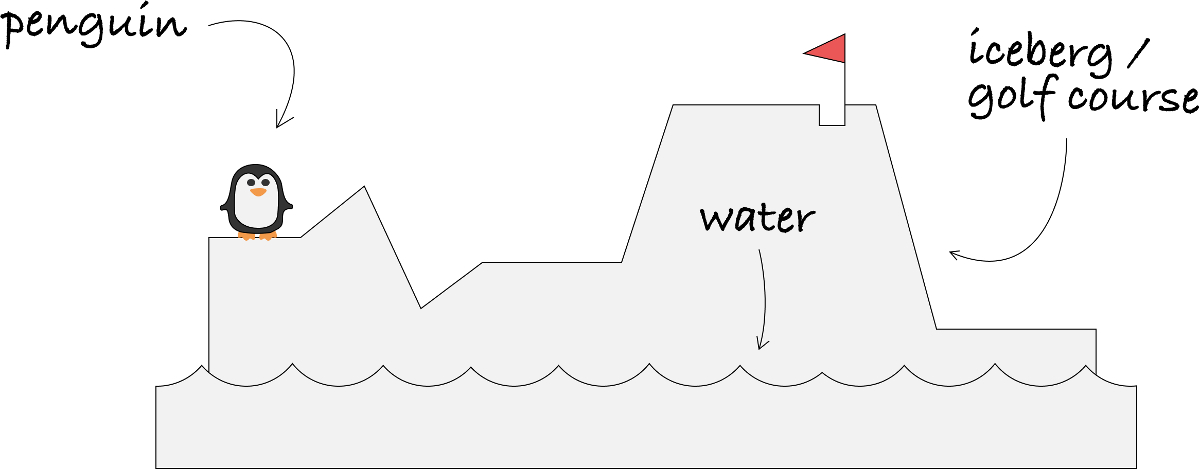
We don’t have a lot of time left in the game jam, so we need to think fast. Something simple, but fun and addictive. Pengolfin’ will involve a side-view, mountainous golf course. The player will angle and fire their penguin and try to get it in the hole in as few “strokes” as possible. To make it more interesting, we’ll also make randomly generated terrain. To maintain the penguin theme, the terrain will actually be icebergs—so badly aimed strokes will land the penguin ball in the ocean, after which it’s returned to the tee.
Matter.js
To get a feel for what a physics engine can do, we’re going to start with a minimal version without even using our Pop library at all. Matter.js includes its own renderer that’s perfect for debugging. Once we’re satisfied it can produce the results we want, we’ll figure out how to sync up the Matter.js models with our sprites to be rendered with our renderer. That’s essentially our goal: syncing the bodies from a physics library to Pop entities. The physics library does the heavy lifting, and we draw sprites on top of it.
Starting from scratch, we’ll pull in the components we need from Matter, and spin up a new engine:
import { Engine, Bodies, World, Render } from "matter-js";
const w = 800;
const h = 400;
// Set up the physics engine
const engine = Engine.create();
Engine.run(engine);
Engine is the main workhorse of Matter.js. It performs all the calculations for physical interactions and responses between Bodies (objects like circles, rectangles, and other polygons) in the World. Matter is designed both to be used standalone, or in other game libraries such as Pop. In standalone mode (or when debugging) we can use its Render object to render wireframes of the physics bodies:
// Debug render it
const render = Render.create({
element: document.querySelector("#board"),
engine: engine,
options: {
width: w,
height: h,
showAngleIndicator: true
}
});
Render.run(render);
A renderer requires an element in the HTML page as a container, the engine we created, and accepts a bunch of options that affect how the world works. We’ll specify the width and height of the world as well as showing some extra debugging indicators. If you run the code, you’ll have a full-fledged physics engine—but there’s nothing in the world yet.
// Create some bodies
const course = Bodies.rectangle(400, 30, 300, 50, { isStatic: true });
The Matter.Bodies object contains a collection of factory methods for creating physics bodies. You can create circles, rectangles, trapezoids, polygons, and complex shapes from vertices. The factory methods all also accept an options object for specifying a body’s physical properties, like mass, density, friction levels—all sorts of goodies that simulate objects in the real world.
Our rectangular body we have created (with Bodies.rectangle) is located at coordinates (400, 300). It’s 300 pixels wide and 50 pixels tall. The only extra option we’ve specified is isStatic. A static body is not affected by physical collisions, and it doesn’t fall to the ground under the pressure of gravity. It’s as solid as a rock.
Now that we have the earth beneath our feet, we’ll drop a whole boatload of bouncy balls on it, just to see what happens:
const balls = [...Array(50)].map(() => {
const radius = Math.random() * 25 + 5;
const x = Math.random() * w;
const y = Math.random() * -1000;
const options = {
restitution: 0.7
};
return Bodies.circle(x, y, radius, options);
});
A circle body requires an x/y location, as well as a radius. As far as options go, we set the ball to have a restitution of 0.7. Restitution means how elastic and bouncy a body is. 0 means the body is perfectly inelastic—it doesn’t bounce at all. 1 means the object will bounce back with 100% of its kinetic energy … and is ludicrously bouncy.
Other Stuff to Play With
“Restitution” is just one of the fun properties we can play with. Check out the properties on Matter.Body in the documentation and see how messed up you can make things!
Bodies need to be added to the world before they’re processed in the engine. To set our balls in motion, add everything to engine.world, passing an array to Matter.World.add:
// Add them to the world
World.add(engine.world, [course, ...balls]);
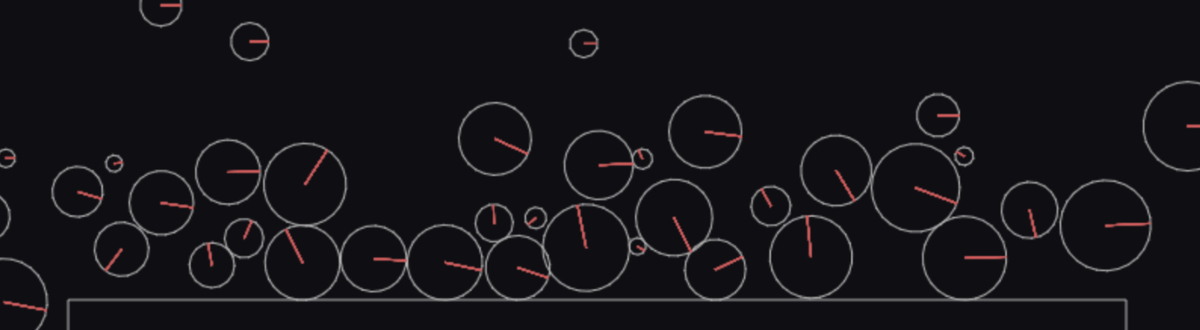
I’d say that was a successful test. Now let’s see how this might integrate with a Pop game. To establish a base for Pengolfin', start a new project using the familiar GameScreen approach. Create some mouse controls too—because our game will be controlled largely by mouse. Also give GameScreen a way to restart a level:
// Main.js
...
const game = new Game(800, 400);
const controls = {
keys: new KeyControls(),
mouse: new MouseControls(game.renderer.view)
};
function playHole() {
game.scene = new GameScreen(game, controls, playHole);
}
playHole();
game.run();
Main.js is, as always, the entry point for the game. We’ll keep track of the score here too, but now the Matter.js engine creation code we played around with will become part of the responsibility of GameScreen.
Syncing with Our Library
The physics engine is doing all the hard work of figuring out where things go and how they move. All we have to do is draw it all. To marry Pop and Matter.js we’ll create entities as usual with Pop, but also give each entity a corresponding Matter body.
The Matter body will be created and attached to the Pop entity as a property called body. In an entity’s update method (that runs every frame) we’ll set the rotation and pos properties to match the values of the Matter body. The physics system calculates where things should be, and we copy the results back to our Pop entity. To get things started, we’ll make the boring-est golf course ever—a flat rectangle:
import { Bodies, Body } from "matter-js";
class Course extends Rect {
constructor(pos) {
super(1000, 20, { fill: "#eee" });
// Step 1: Create the body
...
// Step 2: Sync the body and the Rect
...
this.body = body; // store the Matter body reference
}
}
One major difference between Matter’s coordinate system and our coordinate system is where the pivot and anchor points are set. In Pop, an entity’s position is where the top-left pixel should be located. In Matter, it’s where the center of the body should be located. Likewise, the default pivot point is top left in Pop, but center in Matter. We need to account for this and offset the entity’s pivot and anchor points accordingly:
this.pivot = {
x: this.w / 2,
y: this.h / 2
};
this.anchor = Vec.from(this.pivot).multiply(-1);
const body = Bodies.rectangle(0, 0, this.w, this.h, { isStatic: true });
Body.setPosition(body, pos);
First, we adjust the pivot point to the center, and then copy that point and invert it—thus giving the correct drawing offset. This now matches Matter’s system. The Matter Body is a rectangle and the Pop entity is a Rect. To make the two match up, we copy the position and rotation from the Body to the Rect:
// Sync the Rect
this.rotation = body.angle;
pos.copy(body.position);
For non-static bodies, we have to copy the body.position and the body.rotation every frame in the entity’s update function. That’s all it takes to get Pop and Matter in sync! Now we can do the same for the golf-ball penguin. It’s a TileSprite that lives in entities/Penguin.js:
class Penguin extends TileSprite {
constructor(pos) {
super(texture, 32, 32);
this.pivot.x = this.w / 2;
this.pivot.y = this.h / 2;
this.anchor = Vec.from(this.pivot).multiply(-1);
this.body = Bodies.circle(pos.x, pos.y, 10, {
restitution: 0.7
});
this.body.torque = 0.002;
}
}
Just as with the ground, to make a physics-enabled Penguin we offset the pivot and anchor points of the penguin and then create a Body—this time a circle. We’ve adjusted the default torque of the Matter.js body. Torque is a measure of how much rotational force is acting on a body. By applying a bit of torque as the penguin is created, it rolls slightly to the right. It just looks cool—that’s all. Penguin.js has the same update function as the ground plane, which syncs the TileSprite’s pos to body.position and rotation to body.angle.
import { Engine, Events, World } from "matter-js";
class GameScreen extends Container {
constructor(game, controls, onHole) {
// ...
this.ready = false; // Can the player shoot yet?
const course = new Course({ x: 450, y: 300 });
const penguin = new Penguin({ x: this.w / 2, y: -32 });
// Add everyone to the game
this.penguin = this.add(penguin);
this.course = this.add(course);
}
}
At the end of the GameScreen constructor, we put the engine creation code (which I cut and pasted from our initial Matter.js tests from earlier). All that remains is to add the penguin and the golf course bodies to the new World:
World.add(this.engine.world, [penguin.body, course.body]);
Everything is in sync! Whenever the physics bodies move, the corresponding Pop entity follows. This is just one way of many to proxy the properties of a physics body to our entities. If you have a preferred way to accomplish this task, don’t be afraid to roll your own.
Event Systems
One of the big challenges when making physics games is deciding when a given “turn” or “play” has completed. In a complex system of interacting bodies, 99% of entities could all be at a standstill and at rest. Then one kinetic-energy-filled smart alec makes a final move that triggers a whole new chain reaction. Waiting for everything to be 100% stable can take a very long time—often far longer than your impatient player is willing to wait to keep playing.
Generally, there’s no easy solution to this. You’ll just have to “call it” at some point. In our golf game, life’s a little easier: there’s only one body we have to worry about (the penguin) and it’s essential that it comes to a complete stop before we let the player shoot again.
How do we determine if the penguin is at rest? Perhaps we could just check its speed every frame and see if it’s close to zero? You could do that by polling body.motion, which is a number representing the amount of movement a body currently has. If it’s very close to zero, the penguin isn’t moving. Unfortunately, that’s not enough. If the penguin is shot straight upwards, at the peak of its trajectory its body.motion will also be close to 0. Luckily, Matter supplies us with a module to help out—Matter.Sleeping.
Not Every Game Needs Sleeping
Not every game will care when bodies are sleeping, so to avoid unnecessary computations, it’s not enabled by default. This is why we had to add enableSleeping: true as an option when creating the main engine.
A body is sleeping when it has no motion and there are no pending forces acting on it. We can check our penguin and see if it’s awake or asleep with the property isSleeping:
if (penguin.body.isSleeping) {
// Player can shoot again!
this.ready = true;
}
Alternatively, we could use the Matter event system. An event system is a way to manage communication between different parts of your game without each part needing explicit knowledge of the other. In this case, our Penguin can be informed about something that happens in the Matter.Sleeping system without knowing anything specific about the system itself. The Penguin doesn’t care who decides it’s sleeping; it just wants to know when it happens. This is achieved through an event listener, specifically via the sleepStart and sleepEnd events:
Matter.Events.on(penguin.body, "sleepStart", () => {
this.ready = true;
});
The event is registered once in GameScreen initialization. It’s the same as how we register event listeners for mouse or keyboard events from the DOM. When the Sleeping module determines the penguin is sleeping, it will fire the event and call our callback function, enabling the player to shoot again.
Available Events
There are many events available for us to listen to; have a look at the Matter event examples on the Matter.js website for more. If you want to listen to multiple events for the same body, you can separate them via spaces: Events.on(body, "sleepStart collisionStart", (e) => {}). Generally, you’ll only listen to similar events in each Events.on statement, because the event information passed to the callback will be specific to that event. For example, collision events will have a member e.pairs—with bodyA and bodyB properties for the bodies involved in the collision.
Now that the sleeping logic has been delegated to the event listener, the only actual game logic we need to handle in the GameScreen is to check if the penguin has fallen off the edge of the screen, and if the player fired the penguin:
const { penguin, h, mouse } = this;
// Gone off the edge?
if (penguin.pos.y > h) {
this.onHole();
}
// Player taken a shot?
if (mouse.released) {
// Fire!
}
mouse.update();
If the penguin’s y position is greater than the height of the game screen, we assume it fell off the edge and call the onHole method. This in turn calls the playHole function from main.js—which restarts the game.
Another way we could implement “falling off the edge of the world” would be to create additional Matter bodies and position them around the edges of the screen. If we got a collisionStart message from any of them, we’d know the Penguin went out of bounds. It’s not really necessary here, as our entity check is much simpler, but it highlights the benefit of mixing and matching the power of Matter.js and Pop.
Applying Forces
Just like our home-brew physics solution, Matter.js supplies a method for applying a force to a body. It’s slightly more complicated than our version, because in addition to specifying the force, you must also specify the position in the world you’re applying the force from.
Matter.Body.applyForce(body, position, force)
In our simple Pop physics, position isn’t relevant. In a real physics system, it changes how the amount of power and torque gets applied to the body. For our golf game, it means we can hit the ball (penguin) slightly above center, so torque is applied in a clockwise direction and it gets a nice forward roll to keep it coasting after it lands:
fire(angle, power) {
const { body } = this;
Body.applyForce(
body,
{ x: body.position.x, y: body.position.y - 10 },
{ x: Math.cos(angle) * power, y: Math.sin(angle) * power }
);
}
We put the call to applyForce in a helper function that accepts an angle to fire at, along with the power of the shot. We convert the angle and power to Cartesian coordinates (see the earlier “Polar Coordinates” section). These inputs will eventually be supplied by dragging and releasing the mouse, but to test it out we’ll just hardcode it in the main game after a mouse click:
if (mouse.released) {
// Fire!
const angle = -Math.PI / math.randf(1.75, 2.25);
const power = 0.01;
penguin.fire(angle, power);
}
The angle is a random upwards value (-Math.PI / 2 is straight up). As it stands, you can spam the mouse button to apply the force repeatedly to make a flying penguin. It might be unrealistic (penguins can’t fly: their wings are tiny!), but it’s pretty funny.

Dragging Indicator
In our golf game, the player fires the penguin into the air by clicking somewhere on the screen, then dragging in the opposite direction they want to fire—as if pulling back a slingshot. We have to implement a slingshot.
The amount of power is determined by the distance the mouse is dragged. To model this (as well as visually show the player what they’re doing), we create a new entity Arrow. It will hold the positions and states of the mouse clicks as well as draw a couple of thin rectangles for a power-and-direction bar:
class Arrow extends Container {
constructor(max = 100) {
super();
this.background = this.add(
new Rect(max, 4, { fill: "rgba(0, 0, 0, 0.1)" })
);
this.arrow = this.add(new Rect(0, 4, { fill: "#FDA740" }));
...
}
}
The rectangles will rotate to show the direction of the shot. The background rectangle shows the full power range available, and the arrow rectangle will change width depending on the current stroke power. For the drag state, we have to track the start position where the mouse was clicked, the maximum width the display can be (this is also the constant width of the background rectangle), and the maximum drag distance—the amount of pixels to drag to have 100%-power shot:
this.pos = new Vec();
this.max = max;
this.maxDragDistance = 80;
A golf shot in our game is made up of two parts: clicking, and dragging. When the player clicks, we provide a start method to register the position and move the arrow:
start(pos) {
this.pos.copy(pos);
}
Any dragging that’s done now is in relation to this start position. This relationship is used to calculate the angle and power:
drag(drag) {
const { arrow, pos, max, maxDragDistance } = this;
// Calculate angle and power
...
// Set the display
this.rotation = angle;
arrow.w = power * max;
return { angle, power };
}
Every frame the player drags, the visualization will be updated and the angle/power data returned. The power is a number from 0 to 1, where 0 is “no power” and 1 is “full power”. To calculate these we use some hopefully now-familiar math friends math.angle and math.distance to convert to polar coordinates:
// Calculate angle and power
const angle = math.angle(pos, drag);
const dist = math.distance(pos, drag);
const power = Math.min(1, dist / maxDragDistance);
The distance between the drag position and the start position is used to calculate the amount of power. If we drag further than maxDragDistance, the power is capped to 1 (by taking the minimum). Because we have a normalized value, we can use that to set the display width of the power bar.
The arrow is now ready to be used in GameScreen. When the player first presses their mouse button, we call start to register the position:
// Start your stroke
if (mouse.pressed) {
arrow.start(mouse.pos);
}
Then we have some logic to do. We can only drag and shoot when the penguin body is sleeping and we’re ready to go. If it’s all good, we check that the mouse is either being held down (mouse.isDown) or just released (mouse.released). In either case, we update the arrow with arrow.drag, passing the current mouse position:
if (this.ready) {
if (mouse.isDown || mouse.released) {
const { angle, power } = arrow.drag(mouse.pos);
if (mouse.released) {
this.fireAway(angle, power * 0.021);
}
}
}
When the player has finalized their shot, they release the mouse button and we can call this.fireAway with the returned angle and a scaled power. (It’s scaled down because power is a ratio from 0 to 1, and a Matter.js force of 1 will send our penguin flying miles off the golf course!)
The fireAway method calls fire on the penguin, and also sets this.ready = false so the player can’t apply more force to the penguin until it comes to rest. To give this golf game a point, we’ll also create an entity that’s the hole to try and get the penguin in. This can live in GameScreen: it’s just a regular Pop entity on which we’ll do a regular bounding-box collision test, to see if the penguin is touching it as it goes to sleep:
const hole = this.add(new Rect(20, 10, { fill: "#FDA740" }));
hold.pos.set(this.w - 100, 300);
When the penguin stops, we check if it’s touching the hole (it doesn’t count if the penguin bounces in the hole and then bounces out again). If it’s touching, the hole is completed successfully. Again, we’re mixing and matching our Pop and Matter.js logic: we could have also made the hole a Matter body and checked for collisions with Matter. Whatever works, works!
If there’s a collision, we’ll pass a flag (true) to indicate the hole was completed successfully, as opposed to the penguin falling off the edge of the world:
Events.on(penguin.body, "sleepStart", () => {
if (entity.hit(penguin, hole)) {
this.onHole(true);
}
this.ready = true;
});
That’s the core of our game working. You can aim and fire a penguin; when it hits the hole, we’re done! It’s not very fun though. The problem is that the course is very flat and very repetitive. Physics games are only fun when things bounce around and interact with the environment. Let’s build some more challenging courses.
Procedurally Generated Terrain
The exciting part about minigolf-style games is the wacky courses. Our game will be side-on, so the challenge needs to be in getting the penguin in the hole despite some mountainous icebergs standing in the way. There are several ways we could accomplish this.
To be honest, for the first pass when making this prototype, I took a different approach. I created a course out of several rotated rectangles that fit together snuggly. This worked fine (better than I expected, actually) but it had a couple of issues. Making levels by hand was pretty easy, but when trying to procedurally generate new levels, the math got pretty gnarly. Secondly, it was very hard to render these nicely on the screen. There’s no way to “fill in” the space between the rectangles, so there were big holes in the middle of the iceberg courses.
I decided to bite the bullet and introduce a new renderable entity into Pop: a path. A path is series (an array) of point coordinates that join together like connect-the-dot puzzles, with the last point connecting back to the first to form an arbitrary polygon.

HTML5 Canvas has the concept of a path as part of its API, so it’s easy to integrate into our Canvas renderer. But it’s not something native to Matter.js: there’ll be a couple of hoops to jump through to make that work. Additionally, when it comes time to make our WebGL Renderer, it will complicate things there too! Ah well, that’s the beauty of rolling your own library: you can add things as you need them, and adapt to the situation at hand.
To display the path on screen, we need to add support to Pop’s CanvasRender.js. The renderer will expect a “path” element to have a path property that’s an array containing two or more points defining the path. It also expects it to have a style property that optionally defines a fill color (defaulting to #fff) to paint the polygon:
else if (child.path) {
const [head, ...tail] = child.path;
if (tail.length > 0) {
// Draw the path
}
}
The path is split into two parts: the “head” (first element) and the “tail” (the rest). To draw a path in Canvas, you start with a call to beginPath, then moveTo the position defined by head. From here, you lineTo each proceeding point, and finally call closePath to join up the path:
ctx.fillStyle = child.style.fill || "#fff";
ctx.beginPath();
ctx.moveTo(head.x, head.y);
tail.forEach(({x, y}) => ctx.lineTo(x, y));
ctx.closePath();
ctx.fill();
Now that we can render a path, we have to figure out how to procedurally generate our golf course, and cut that up for Matter.js. The way we’ll approach it is to slice the course up into vertical segments. Each segment will either be flat, slope up, or slope down a random amount. The first segment will be the tee, and we’ll choose a random segment to be the hole. Both of these will have to be flat.
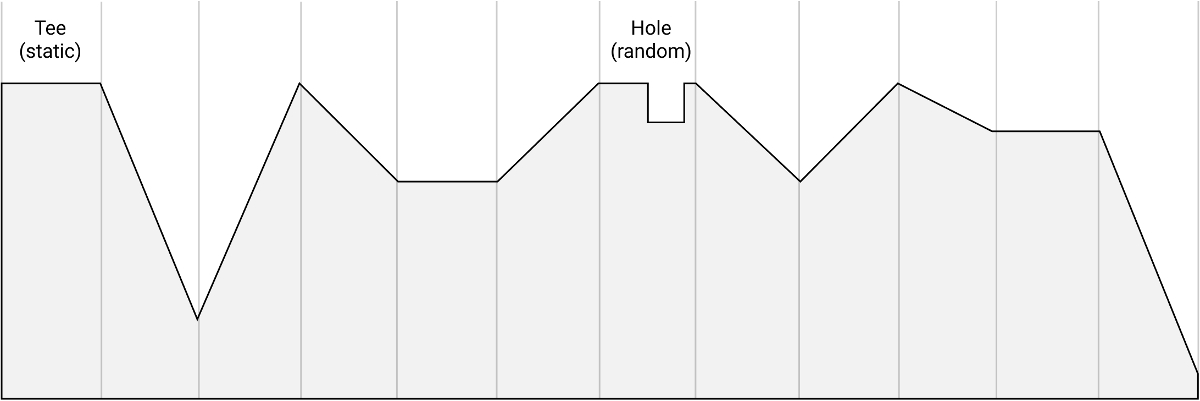
class Course extends Container {
constructor(gameW, gameH) {
...
const segments = 13;
const segmentWidth = 64;
const xo = 15;
let yo = math.randOneFrom([32, 128, 300]);
let minY = yo;
let maxY = yo;
let holeSegment = math.rand(segments - 7, segments);
}
}
The number of segments, and the segment width, have been chosen to fit nicely in the screen space. The xo and yo properties are the initial offsets for the first segment. We keep track of the height of each segment and make sure the course doesn’t get too high or too low:
const terrainData = [...Array(segments)].map((_, i) => {
const mustBeFlat = i <= 1 || i === holeSegment;
if (!mustBeFlat) {
// Randomly move up or down
...
}
return { x: i * segmentWidth, y: yo };
});
const tee = terrainData[0];
const hole = terrainData[holeSegment];
Some JS Trickery
The code [...Array(segments)].map() is a handy JavaScript trick for creating an array of a given size that can be mapped over. If you create an array “normally” with new Array(segments), the entries will be empty and are not passed to .map(). By destructuring the empty array we get a list of undefined elements that do get passed to .map().
We create a new object for each segment to store the x and y positions of the segment point. The x (horizontal position) is calculated by taking the current array index (i) and multiplying it by the segmentWidth. The y (vertical position) depends on whether or not the segment is flat. If it’s flat, the yo offset remains the same and adjoining points will be on the same vertical plane.
// Randomly move up or down
const drop = math.randOneFrom([32, 64, 152]);
const dir = math.randOneFrom([-1, 0, 1]);
// Random go down
if (dir === 1 && yo - drop > 0) {
yo -= drop;
}
//Random go up
if (dir === -1 && yo + drop < 320) {
yo += drop;
}
if (yo > maxY) maxY = yo;
if (yo < minY) minY = yo;
If the segment is not flat, we choose a random elevation and direction for the slope—ensuring we never get too high (yo must be less than 320), and never dive right through the bottom of the iceberg (yo must be greater or equal to 0). The maximum and minimum levels are recorded so we can calculate the total course height later.
This gives us the top surface of the golf course. To finish it off, we have to “carve” a small rectangular area as the hole. It needs to be big enough for the penguin to fall into, but not too big as to make the game too easy! We’ll splice in four additional points on the flat surface of the hole segment. The four points are the corners of the hole:
// Add the hole
terrainData.splice(
holeSegment,
0,
{ x: hole.x - 30, y: hole.y },
{ x: hole.x - 30, y: hole.y + 25 },
{ x: hole.x - 10, y: hole.y + 25 },
{ x: hole.x - 10, y: hole.y }
);
With the top surface of the course complete, we now add two more points (the bottom-right point of the iceberg and the bottom-left point of the iceberg) to create a “base” for the course. This is calculated by going straight down from the top surface to the maxY value we calculated earlier. We also add an extra 52 pixels so the bottom of the course can never be too close to the water. The final point aligns horizontally with the first point (x = 0) so when the path is closed we get nice rectangular edges:
// Add the base, close the path
const { x } = terrainData[terrainData.length - 1];
maxY += 52; // "base" height
terrainData.push({ x, y: maxY });
terrainData.push({ x: 0, y: maxY });
The last step is to figure out the total final height of the iceberg so it can be positioned on screen correctly:
const h = gameH - (maxY - minY);
this.path = terrainData;
this.pos = new Vec(xo, h - minY);
The final terrain data points are stored on the entity as this.path. The CanvasRenderer will see the path and fill it in for us.

We have an infinite golf course! Refreshing the screen gives us a new challenge each time. While we’re here, we can also add in the spawn locations for the tee and the hole. We’ll use these in the main GameScreen to position the Penguin and the target hole graphics:
this.hole = Vec.from(hole).add({ x: -15, y: h - minY });
this.tee = Vec.from(tee)
.add({ x: xo + segmentWidth / 2, y: h - minY - 5 });
Having all of this information is no good if the penguin has no physics bodies to interact with. The iceberg level is just an image; the penguin will fall straight through it and the game will reset. We need to be able to convert our path into Matter.js bodies. To achieve this, we use the Bodies factory method called fromVertices:
const terrain = Bodies.fromVertices(0, 0, terrainData, { isStatic: true });
Bodies.fromVertices takes the path and chops it into a body. Sounds exactly like what we need. Only, by default, it works with convex polygons. A convex polygon is one where, if you drew any straight line through the shape, it would hit exactly two borders. If our golf course was a triangle or a simple rectangle, this would be true. But we have all sorts of dips and peaks. Our course is concave.
If Matter encounters a concave path, it will try to decompose the path into multiple convex polygons. But to do this it needs an additional library, poly-decomp.js, which we need to make available as a global function. The easiest way to do this is to put it in our /vendor folder and link to it from the main HTML:
<script src="vendor/decomp.min.js"></script>
The golf course will be chopped up into multiple convex polygons that work perfectly with Matter.js. If you want to see the triangles that poly-decomp creates, re-add the debug Matter renderer. It’s pretty impressive. With a course full of convex polygons, Penguin will bounce around just like a real penguin golf ball. Like all of our Matter bodies, we need to adjust it so it aligns with the Pop image, and now our penguin is once again forced to obey our laws of nature!
// Create the geometry
Body.setPosition(terrain, {
x: -terrain.bounds.min.x + xo,
y: h - terrain.bounds.min.y
});
this.body = terrain;
We’re rapidly running out of time, but we have everything we need to turn this into a game now. Using the hole and tee positions, we can set the start and end points of each hole.
Then the game could use a few finishing touches. First, a score system. How about this: each shot the player takes will add one stroke to their score? Makes sense. Annnd, if they fall off the edge of the world, they get, say, a five-stroke penalty.
To make our game more aesthetically pleasing, we’ll add a couple of arctic-themed touches. A solid blue rectangle at the bottom of the screen represents water. Each frame, this can bob up and down via a sine wave to look like a rising and falling arctic ocean:
waves.pos.y = Math.sin(t / 800) * 7 + this.h - 20;
In the dying seconds of the game jam, we’ll add a CSS gradient background in main.css to represent the skyline … aaaand time is well and truly up!

When you model aspects of your game using physical forces—whether through rolling your own, or via a full-featured physics engine—they become part of a system. System-based games can be extremely interesting from both a player’s and a developer’s perspective, as they allow for emergent behavior—interactions between simple rules that combine into complex, fascinating, and unexpected results. That means deeper gameplay for the player, and more hours lost tinkering with things for the developer. How about extending Pengolfin’ with some more obstacles … such as moving targets to bounce things off … mountain-side trampolines … penguin multi-ball?
We Got Physical
As you consider the possibilities, there’s a kerfuffle at your door, as Guy Shifty and a dozen of his minions push into your office at the same time. Guy stands before them, looking immaculate as ever. It was only one grueling weekend, but you look like you’ve been lost in the woods for a month. How does he do it?
“I just brought my people down here to show them an example of poor planning. I assume you got nothing done for the Lucky Dare Game Jam Competition in the end?”
You let the minions play some Pengolfin’. They try not to smile as they play.
Shifty looks moody. “Hmm, better than nothing, I suppose. But no music or sounds, no polish. And like I told you all”, he barks, as he snatches the mouse from the current player and starts ushering the crew back out the door, “it’s got no chance at this year’s IGC.”
You roll your eyes, but decide to indulge him. “What’s IGC?”
“You don’t know about the Independent Game Competition?” he replies, feigning surprise. “It’s only the biggest indie game competition of the year. I’m entering my ‘indie division’ (the people I don’t pay). First prize is $10,000.” He looks at you coldly as he exits. “You could use that money to help you find a new place to work.”
I don’t know what he means by that, but it can’t be good. He’s right about one thing, though: having games systems and good core mechanics is not enough. We need start polishing our games. We need music, special effects, explosions, and sounds. It’s time to roll up our sleeves and begin the grind of transforming our prototypes into games. It’s time to take it to the next level!