Instruction Set Principles
Wilkes and Renwick, Selection from the List of 18 Machine, Instructions for the EDSAC (1949)
This appendix concentrates on instruction set architecture—the portion of the computer visible to the programmer or compiler writer. This appendix introduces the wide variety of design alternatives available to the instruction set architect. In particular, it focuses on four topics. First, it presents a taxonomy of instruction set alternatives and gives some qualitative assessment of the advantages and disadvantages of various approaches. Second, it presents and analyzes some instruction set measurements that are largely independent of a specific instruction set. Third, it addresses the issue of languages and compilers and their bearing on instruction set architecture. Finally, the “Putting It All Together” section shows how these ideas are reflected in the MIPS instruction set, which is typical of RISC architectures. It concludes with fallacies and pitfalls of instruction set design.
A.1 Introduction
A.2 Classifying Instruction Set Architectures
A.3 Memory Addressing
A.4 Type and Size of Operands
A.5 Operations in the Instruction Set
A.6 Instructions for Control Flow
A.7 Encoding an Instruction Set
A.8 Crosscutting Issues: The Role of Compilers
A.9 Putting It All Together: The MIPS Architecture
A.10 Fallacies and Pitfalls
A.11 Concluding Remarks
A.12 Historical Perspective and References
A.1 Introduction
In this appendix we concentrate on instruction set architecture—the portion of the computer visible to the programmer or compiler writer. Most of this material should be review for readers of this book; we include it here for background. This appendix introduces the wide variety of design alternatives available to the instruction set architect. In particular, we focus on four topics. First, we present a taxonomy of instruction set alternatives and give some qualitative assessment of the advantages and disadvantages of various approaches. Second, we present and analyze some instruction set measurements that are largely independent of a specific instruction set. Third, we address the issue of languages and compilers and their bearing on instruction set architecture. Finally, the “Putting It All Together” section shows how these ideas are reflected in the MIPS instruction set, which is typical of RISC architectures. We conclude with fallacies and pitfalls of instruction set design.
To illustrate the principles further, Appendix K also gives four examples of general-purpose RISC architectures (MIPS, PowerPC, Precision Architecture, SPARC), four embedded RISC processors (ARM, Hitachi SH, MIPS 16, Thumb), and three older architectures (80×86, IBM 360/370, and VAX). Before we discuss how to classify architectures, we need to say something about instruction set measurement.
Throughout this appendix, we examine a wide variety of architectural measurements. Clearly, these measurements depend on the programs measured and on the compilers used in making the measurements. The results should not be interpreted as absolute, and you might see different data if you did the measurement with a different compiler or a different set of programs. We believe that the measurements in this appendix are reasonably indicative of a class of typical applications. Many of the measurements are presented using a small set of benchmarks, so that the data can be reasonably displayed and the differences among programs can be seen. An architect for a new computer would want to analyze a much larger collection of programs before making architectural decisions. The measurements shown are usually dynamic —that is, the frequency of a measured event is weighed by the number of times that event occurs during execution of the measured program.
Before starting with the general principles, let’s review the three application areas from Chapter 1. Desktop computing emphasizes the performance of programs with integer and floating-point data types, with little regard for program size. For example, code size has never been reported in the five generations of SPEC benchmarks. Servers today are used primarily for database, file server, and Web applications, plus some time-sharing applications for many users. Hence, floating-point performance is much less important for performance than integers and character strings, yet virtually every server processor still includes floating-point instructions. Personal mobile devices and embedded applications value cost and energy, so code size is important because less memory is both cheaper and lower energy, and some classes of instructions (such as floating point) may be optional to reduce chip costs.
Thus, instruction sets for all three applications are very similar. In fact, the MIPS architecture that drives this appendix has been used successfully in desktops, servers, and embedded applications.
One successful architecture very different from RISC is the 80×86 (see Appendix K). Surprisingly, its success does not necessarily belie the advantages of a RISC instruction set. The commercial importance of binary compatibility with PC software combined with the abundance of transistors provided by Moore’s law led Intel to use a RISC instruction set internally while supporting an 80×86 instruction set externally. Recent 80×86 microprocessors, such as the Pentium 4, use hardware to translate from 80×86 instructions to RISC-like instructions and then execute the translated operations inside the chip. They maintain the illusion of 80×86 architecture to the programmer while allowing the computer designer to implement a RISC-style processor for performance.
Now that the background is set, we begin by exploring how instruction set architectures can be classified.
A.2 Classifying Instruction Set Architectures
The type of internal storage in a processor is the most basic differentiation, so in this section we will focus on the alternatives for this portion of the architecture. The major choices are a stack, an accumulator, or a set of registers. Operands may be named explicitly or implicitly: The operands in a stack architecture are implicitly on the top of the stack, and in an accumulator architecture one operand is implicitly the accumulator. The general-purpose register architectures have only explicit operands—either registers or memory locations. Figure A.1 shows a block diagram of such architectures, and Figure A.2 shows how the code sequence C = A + B would typically appear in these three classes of instruction sets. The explicit operands may be accessed directly from memory or may need to be first loaded into temporary storage, depending on the class of architecture and choice of specific instruction.
Figure A.1 Operand locations for four instruction set architecture classes. The arrows indicate whether the operand is an input or the result of the arithmetic-logical unit (ALU) operation, or both an input and result. Lighter shades indicate inputs, and the dark shade indicates the result. In (a), a Top Of Stack register (TOS) points to the top input operand, which is combined with the operand below. The first operand is removed from the stack, the result takes the place of the second operand, and TOS is updated to point to the result. All operands are implicit. In (b), the Accumulator is both an implicit input operand and a result. In (c), one input operand is a register, one is in memory, and the result goes to a register. All operands are registers in (d) and, like the stack architecture, can be transferred to memory only via separate instructions: push or pop for (a) and load or store for (d).
Figure A.2 The code sequence for C = A + B for four classes of instruction sets. Note that the Add instruction has implicit operands for stack and accumulator architectures and explicit operands for register architectures. It is assumed that A, B, and C all belong in memory and that the values of A and B cannot be destroyed. Figure A.1 shows the Add operation for each class of architecture.
As the figures show, there are really two classes of register computers. One class can access memory as part of any instruction, called register-memory architecture, and the other can access memory only with load and store instructions, called load-store architecture. A third class, not found in computers shipping today, keeps all operands in memory and is called a memory-memory architecture. Some instruction set architectures have more registers than a single accumulator but place restrictions on uses of these special registers. Such an architecture is sometimes called an extended accumulator or special-purpose register computer.
Although most early computers used stack or accumulator-style architectures, virtually every new architecture designed after 1980 uses a load-store register architecture. The major reasons for the emergence of general-purpose register (GPR) computers are twofold. First, registers—like other forms of storage internal to the processor—are faster than memory. Second, registers are more efficient for a compiler to use than other forms of internal storage. For example, on a register computer the expression (A * B) – (B * C) – (A * D) may be evaluated by doing the multiplications in any order, which may be more efficient because of the location of the operands or because of pipelining concerns (see Chapter 3). Nevertheless, on a stack computer the hardware must evaluate the expression in only one order, since operands are hidden on the stack, and it may have to load an operand multiple times.
More importantly, registers can be used to hold variables. When variables are allocated to registers, the memory traffic reduces, the program speeds up (since registers are faster than memory), and the code density improves (since a register can be named with fewer bits than can a memory location).
As explained in Section A.8, compiler writers would prefer that all registers be equivalent and unreserved. Older computers compromise this desire by dedicating registers to special uses, effectively decreasing the number of general-purpose registers. If the number of truly general-purpose registers is too small, trying to allocate variables to registers will not be profitable. Instead, the compiler will reserve all the uncommitted registers for use in expression evaluation.
How many registers are sufficient? The answer, of course, depends on the effectiveness of the compiler. Most compilers reserve some registers for expression evaluation, use some for parameter passing, and allow the remainder to be allocated to hold variables. Modern compiler technology and its ability to effectively use larger numbers of registers has led to an increase in register counts in more recent architectures.
Two major instruction set characteristics divide GPR architectures. Both characteristics concern the nature of operands for a typical arithmetic or logical instruction (ALU instruction). The first concerns whether an ALU instruction has two or three operands. In the three-operand format, the instruction contains one result operand and two source operands. In the two-operand format, one of the operands is both a source and a result for the operation. The second distinction among GPR architectures concerns how many of the operands may be memory addresses in ALU instructions. The number of memory operands supported by a typical ALU instruction may vary from none to three. Figure A.3 shows combinations of these two attributes with examples of computers. Although there are seven possible combinations, three serve to classify nearly all existing computers. As we mentioned earlier, these three are load-store (also called register-register), register-memory, and memory-memory.
Figure A.3 Typical combinations of memory operands and total operands per typical ALU instruction with examples of computers. Computers with no memory reference per ALU instruction are called load-store or register-register computers. Instructions with multiple memory operands per typical ALU instruction are called register-memory or memory-memory, according to whether they have one or more than one memory operand.
Figure A.4 shows the advantages and disadvantages of each of these alternatives. Of course, these advantages and disadvantages are not absolutes: They are qualitative and their actual impact depends on the compiler and implementation strategy. A GPR computer with memory-memory operations could easily be ignored by the compiler and used as a load-store computer. One of the most pervasive architectural impacts is on instruction encoding and the number of instructions needed to perform a task. We see the impact of these architectural alternatives on implementation approaches in Appendix C and Chapter 3.
Figure A.4 Advantages and disadvantages of the three most common types of general-purpose register computers. The notation (m, n) means m memory operands and n total operands. In general, computers with fewer alternatives simplify the compiler’s task since there are fewer decisions for the compiler to make (see Section A.8). Computers with a wide variety of flexible instruction formats reduce the number of bits required to encode the program. The number of registers also affects the instruction size since you need log2 (number of registers) for each register specifier in an instruction. Thus, doubling the number of registers takes 3 extra bits for a register-register architecture, or about 10% of a 32-bit instruction.
Summary: Classifying Instruction Set Architectures
Here and at the end of Sections A.3 through A.8 we summarize those characteristics we would expect to find in a new instruction set architecture, building the foundation for the MIPS architecture introduced in Section A.9. From this section we should clearly expect the use of general-purpose registers. Figure A.4, combined with Appendix C on pipelining, leads to the expectation of a load-store version of a general-purpose register architecture.
With the class of architecture covered, the next topic is addressing operands.
A.3 Memory Addressing
Independent of whether the architecture is load-store or allows any operand to be a memory reference, it must define how memory addresses are interpreted and how they are specified. The measurements presented here are largely, but not completely, computer independent. In some cases the measurements are significantly affected by the compiler technology. These measurements have been made using an optimizing compiler, since compiler technology plays a critical role.
Interpreting Memory Addresses
How is a memory address interpreted? That is, what object is accessed as a function of the address and the length? All the instruction sets discussed in this book are byte addressed and provide access for bytes (8 bits), half words (16 bits), and words (32 bits). Most of the computers also provide access for double words (64 bits).
There are two different conventions for ordering the bytes within a larger object. Little Endian byte order puts the byte whose address is “x … x000” at the least-significant position in the double word (the little end). The bytes are numbered:
Big Endian byte order puts the byte whose address is “x … x000” at the most-significant position in the double word (the big end). The bytes are numbered:
When operating within one computer, the byte order is often unnoticeable—only programs that access the same locations as both, say, words and bytes, can notice the difference. Byte order is a problem when exchanging data among computers with different orderings, however. Little Endian ordering also fails to match the normal ordering of words when strings are compared. Strings appear “SDRAWKCAB” (backwards) in the registers.
A second memory issue is that in many computers, accesses to objects larger than a byte must be aligned. An access to an object of size s bytes at byte address A is aligned if A mod s = 0. Figure A.5 shows the addresses at which an access is aligned or misaligned.
Figure A.5 Aligned and misaligned addresses of byte, half-word, word, and double-word objects for byte-addressed computers. For each misaligned example some objects require two memory accesses to complete. Every aligned object can always complete in one memory access, as long as the memory is as wide as the object. The figure shows the memory organized as 8 bytes wide. The byte offsets that label the columns specify the low-order 3 bits of the address.
Why would someone design a computer with alignment restrictions? Misalignment causes hardware complications, since the memory is typically aligned on a multiple of a word or double-word boundary. A misaligned memory access may, therefore, take multiple aligned memory references. Thus, even in computers that allow misaligned access, programs with aligned accesses run faster.
Even if data are aligned, supporting byte, half-word, and word accesses requires an alignment network to align bytes, half words, and words in 64-bit registers. For example, in Figure A.5, suppose we read a byte from an address with its 3 low-order bits having the value 4. We will need to shift right 3 bytes to align the byte to the proper place in a 64-bit register. Depending on the instruction, the computer may also need to sign-extend the quantity. Stores are easy: Only the addressed bytes in memory may be altered. On some computers a byte, half-word, and word operation does not affect the upper portion of a register. Although all the computers discussed in this book permit byte, half-word, and word accesses to memory, only the IBM 360/370, Intel 80×86, and VAX support ALU operations on register operands narrower than the full width.
Now that we have discussed alternative interpretations of memory addresses, we can discuss the ways addresses are specified by instructions, called addressing modes.
Addressing Modes
Given an address, we now know what bytes to access in memory. In this subsection we will look at addressing modes—how architectures specify the address of an object they will access. Addressing modes specify constants and registers in addition to locations in memory. When a memory location is used, the actual memory address specified by the addressing mode is called the effective address.
Figure A.6 shows all the data addressing modes that have been used in recent computers. Immediates or literals are usually considered memory addressing modes (even though the value they access is in the instruction stream), although registers are often separated since they don’t normally have memory addresses. We have kept addressing modes that depend on the program counter, called PC-relative addressing, separate. PC-relative addressing is used primarily for specifying code addresses in control transfer instructions, discussed in Section A.6.
Figure A.6 Selection of addressing modes with examples, meaning, and usage. In autoincrement/-decrement and scaled addressing modes, the variable d designates the size of the data item being accessed (i.e., whether the instruction is accessing 1, 2, 4, or 8 bytes). These addressing modes are only useful when the elements being accessed are adjacent in memory. RISC computers use displacement addressing to simulate register indirect with 0 for the address and to simulate direct addressing using 0 in the base register. In our measurements, we use the first name shown for each mode. The extensions to C used as hardware descriptions are defined on page A-36.
Figure A.6 shows the most common names for the addressing modes, though the names differ among architectures. In this figure and throughout the book, we will use an extension of the C programming language as a hardware description notation. In this figure, only one non-C feature is used: The left arrow (←) is used for assignment. We also use the array Mem as the name for main memory and the array Regs for registers. Thus, Mem[Regs[R1]] refers to the contents of the memory location whose address is given by the contents of register 1 (R1). Later, we will introduce extensions for accessing and transferring data smaller than a word.
Addressing modes have the ability to significantly reduce instruction counts; they also add to the complexity of building a computer and may increase the average clock cycles per instruction (CPI) of computers that implement those modes. Thus, the usage of various addressing modes is quite important in helping the architect choose what to include.
Figure A.7 shows the results of measuring addressing mode usage patterns in three programs on the VAX architecture. We use the old VAX architecture for a few measurements in this appendix because it has the richest set of addressing modes and the fewest restrictions on memory addressing. For example, Figure A.6 on page A-9 shows all the modes the VAX supports. Most measurements in this appendix, however, will use the more recent register-register architectures to show how programs use instruction sets of current computers.
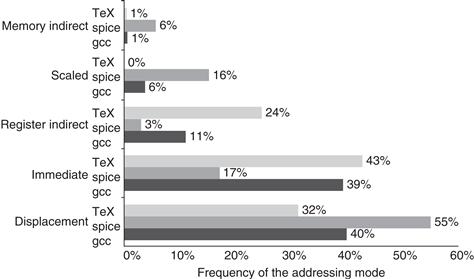
Figure A.7 Summary of use of memory addressing modes (including immediates). These major addressing modes account for all but a few percent (0% to 3%) of the memory accesses. Register modes, which are not counted, account for one-half of the operand references, while memory addressing modes (including immediate) account for the other half. Of course, the compiler affects what addressing modes are used; see Section A.8. The memory indirect mode on the VAX can use displacement, autoincrement, or autodecrement to form the initial memory address; in these programs, almost all the memory indirect references use displacement mode as the base. Displacement mode includes all displacement lengths (8, 16, and 32 bits). The PC-relative addressing modes, used almost exclusively for branches, are not included. Only the addressing modes with an average frequency of over 1% are shown.
As Figure A.7 shows, displacement and immediate addressing dominate addressing mode usage. Let’s look at some properties of these two heavily used modes.
Displacement Addressing Mode
The major question that arises for a displacement-style addressing mode is that of the range of displacements used. Based on the use of various displacement sizes, a decision of what sizes to support can be made. Choosing the displacement field sizes is important because they directly affect the instruction length. Figure A.8 shows the measurements taken on the data access on a load-store architecture using our benchmark programs. We look at branch offsets in Section A.6—data accessing patterns and branches are different; little is gained by combining them, although in practice the immediate sizes are made the same for simplicity.
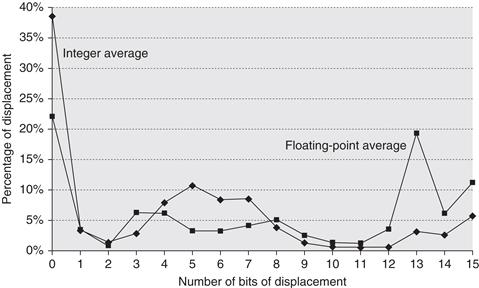
Figure A.8 Displacement values are widely distributed. There are both a large number of small values and a fair number of large values. The wide distribution of displacement values is due to multiple storage areas for variables and different displacements to access them (see Section A.8) as well as the overall addressing scheme the compiler uses. The x -axis is log2 of the displacement, that is, the size of a field needed to represent the magnitude of the displacement. Zero on the x- axis shows the percentage of displacements of value 0. The graph does not include the sign bit, which is heavily affected by the storage layout. Most displacements are positive, but a majority of the largest displacements (14+ bits) are negative. Since these data were collected on a computer with 16-bit displacements, they cannot tell us about longer displacements. These data were taken on the Alpha architecture with full optimization (see Section A.8) for SPEC CPU2000, showing the average of integer programs (CINT2000) and the average of floating-point programs (CFP2000).
Immediate or Literal Addressing Mode
Immediates can be used in arithmetic operations, in comparisons (primarily for branches), and in moves where a constant is wanted in a register. The last case occurs for constants written in the code—which tend to be small—and for address constants, which tend to be large. For the use of immediates it is important to know whether they need to be supported for all operations or for only a subset. Figure A.9 shows the frequency of immediates for the general classes of integer and floating-point operations in an instruction set.
Figure A.9 About one-quarter of data transfers and ALU operations have an immediate operand. The bottom bars show that integer programs use immediates in about one-fifth of the instructions, while floating-point programs use immediates in about one-sixth of the instructions. For loads, the load immediate instruction loads 16 bits into either half of a 32-bit register. Load immediates are not loads in a strict sense because they do not access memory. Occasionally a pair of load immediates is used to load a 32-bit constant, but this is rare. (For ALU operations, shifts by a constant amount are included as operations with immediate operands.) The programs and computer used to collect these statistics are the same as in Figure A.8.
Another important instruction set measurement is the range of values for immediates. Like displacement values, the size of immediate values affects instruction length. As Figure A.10 shows, small immediate values are most heavily used. Large immediates are sometimes used, however, most likely in addressing calculations.
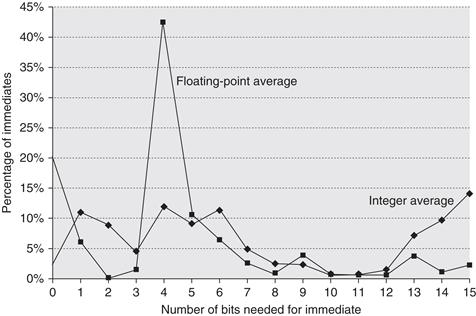
Figure A.10 The distribution of immediate values. The x-axis shows the number of bits needed to represent the magnitude of an immediate value—0 means the immediate field value was 0. The majority of the immediate values are positive. About 20% were negative for CINT2000, and about 30% were negative for CFP2000. These measurements were taken on an Alpha, where the maximum immediate is 16 bits, for the same programs as in Figure A.8. A similar measurement on the VAX, which supported 32-bit immediates, showed that about 20% to 25% of immediates were longer than 16 bits. Thus, 16 bits would capture about 80% and 8 bits about 50%.
Summary: Memory Addressing
First, because of their popularity, we would expect a new architecture to support at least the following addressing modes: displacement, immediate, and register indirect. Figure A.7 shows that they represent 75% to 99% of the addressing modes used in our measurements. Second, we would expect the size of the address for displacement mode to be at least 12 to 16 bits, since the caption in Figure A.8 suggests these sizes would capture 75% to 99% of the displacements. Third, we would expect the size of the immediate field to be at least 8 to 16 bits. This claim is not substantiated by the caption of the figure to which it refers.
Having covered instruction set classes and decided on register-register architectures, plus the previous recommendations on data addressing modes, we next cover the sizes and meanings of data.
A.4 Type and Size of Operands
How is the type of an operand designated? Normally, encoding in the opcode designates the type of an operand—this is the method used most often. Alternatively, the data can be annotated with tags that are interpreted by the hardware. These tags specify the type of the operand, and the operation is chosen accordingly. Computers with tagged data, however, can only be found in computer museums.
Let’s start with desktop and server architectures. Usually the type of an operand—integer, single-precision floating point, character, and so on—effectively gives its size. Common operand types include character (8 bits), half word (16 bits), word (32 bits), single-precision floating point (also 1 word), and double-precision floating point (2 words). Integers are almost universally represented as two’s complement binary numbers. Characters are usually in ASCII, but the 16-bit Unicode (used in Java) is gaining popularity with the internationalization of computers. Until the early 1980s, most computer manufacturers chose their own floating-point representation. Almost all computers since that time follow the same standard for floating point, the IEEE standard 754. The IEEE floating-point standard is discussed in detail in Appendix J.
Some architectures provide operations on character strings, although such operations are usually quite limited and treat each byte in the string as a single character. Typical operations supported on character strings are comparisons and moves.
For business applications, some architectures support a decimal format, usually called packed decimal or binary-coded decimal —4 bits are used to encode the values 0 to 9, and 2 decimal digits are packed into each byte. Numeric character strings are sometimes called unpacked decimal, and operations—called packing and unpacking —are usually provided for converting back and forth between them.
One reason to use decimal operands is to get results that exactly match decimal numbers, as some decimal fractions do not have an exact representation in binary. For example, 0.1010 is a simple fraction in decimal, but in binary it requires an infinite set of repeating digits: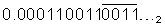 
. Thus, calculations that are exact in decimal can be close but inexact in binary, which can be a problem for financial transactions. (See Appendix J to learn more about precise arithmetic.)
Our SPEC benchmarks use byte or character, half-word (short integer), word (integer), double-word (long integer), and floating-point data types. Figure A.11 shows the dynamic distribution of the sizes of objects referenced from memory for these programs. The frequency of access to different data types helps in deciding what types are most important to support efficiently. Should the computer have a 64-bit access path, or would taking two cycles to access a double word be satisfactory? As we saw earlier, byte accesses require an alignment network: How important is it to support bytes as primitives? Figure A.11 uses memory references to examine the types of data being accessed.
Figure A.11 Distribution of data accesses by size for the benchmark programs. The double-word data type is used for double-precision floating point in floating-point programs and for addresses, since the computer uses 64-bit addresses. On a 32-bit address computer the 64-bit addresses would be replaced by 32-bit addresses, and so almost all double-word accesses in integer programs would become single-word accesses.
In some architectures, objects in registers may be accessed as bytes or half words. However, such access is very infrequent—on the VAX, it accounts for no more than 12% of register references, or roughly 6% of all operand accesses in these programs.
A.5 Operations in the Instruction Set
The operators supported by most instruction set architectures can be categorized as in Figure A.12. One rule of thumb across all architectures is that the most widely executed instructions are the simple operations of an instruction set. For example, Figure A.13 shows 10 simple instructions that account for 96% of instructions executed for a collection of integer programs running on the popular Intel 80×86. Hence, the implementor of these instructions should be sure to make these fast, as they are the common case.
Figure A.12 Categories of instruction operators and examples of each. All computers generally provide a full set of operations for the first three categories. The support for system functions in the instruction set varies widely among architectures, but all computers must have some instruction support for basic system functions. The amount of support in the instruction set for the last four categories may vary from none to an extensive set of special instructions. Floating-point instructions will be provided in any computer that is intended for use in an application that makes much use of floating point. These instructions are sometimes part of an optional instruction set. Decimal and string instructions are sometimes primitives, as in the VAX or the IBM 360, or may be synthesized by the compiler from simpler instructions. Graphics instructions typically operate on many smaller data items in parallel—for example, performing eight 8-bit additions on two 64-bit operands.
Figure A.13 The top 10 instructions for the 80×86. Simple instructions dominate this list and are responsible for 96% of the instructions executed. These percentages are the average of the five SPECint92 programs.
As mentioned before, the instructions in Figure A.13 are found in every computer for every application––desktop, server, embedded––with the variations of operations in Figure A.12 largely depending on which data types that the instruction set includes.
A.6 Instructions for Control Flow
Because the measurements of branch and jump behavior are fairly independent of other measurements and applications, we now examine the use of control flow instructions, which have little in common with the operations of the previous sections.
There is no consistent terminology for instructions that change the flow of control. In the 1950s they were typically called transfers. Beginning in 1960 the name branch began to be used. Later, computers introduced additional names. Throughout this book we will use jump when the change in control is unconditional and branch when the change is conditional.
We can distinguish four different types of control flow change:
We want to know the relative frequency of these events, as each event is different, may use different instructions, and may have different behavior. Figure A.14 shows the frequencies of these control flow instructions for a load-store computer running our benchmarks.
Figure A.14 Breakdown of control flow instructions into three classes: calls or returns, jumps, and conditional branches. Conditional branches clearly dominate. Each type is counted in one of three bars. The programs and computer used to collect these statistics are the same as those in Figure A.8.
Addressing Modes for Control Flow Instructions
The destination address of a control flow instruction must always be specified. This destination is specified explicitly in the instruction in the vast majority of cases—procedure return being the major exception, since for return the target is not known at compile time. The most common way to specify the destination is to supply a displacement that is added to the program counter (PC). Control flow instructions of this sort are called PC-relative. PC-relative branches or jumps are advantageous because the target is often near the current instruction, and specifying the position relative to the current PC requires fewer bits. Using PC-relative addressing also permits the code to run independently of where it is loaded. This property, called position independence, can eliminate some work when the program is linked and is also useful in programs linked dynamically during execution.
To implement returns and indirect jumps when the target is not known at compile time, a method other than PC-relative addressing is required. Here, there must be a way to specify the target dynamically, so that it can change at runtime. This dynamic address may be as simple as naming a register that contains the target address; alternatively, the jump may permit any addressing mode to be used to supply the target address.
These register indirect jumps are also useful for four other important features:
■ Case or switch statements, found in most programming languages (which select among one of several alternatives)
■ Virtual functions or methods in object-oriented languages like C++ or Java (which allow different routines to be called depending on the type of the argument)
■ High-order functions or function pointers in languages like C or C++ (which allow functions to be passed as arguments, giving some of the flavor of object-oriented programming)
■ Dynamically shared libraries (which allow a library to be loaded and linked at runtime only when it is actually invoked by the program rather than loaded and linked statically before the program is run)
In all four cases the target address is not known at compile time, and hence is usually loaded from memory into a register before the register indirect jump.
As branches generally use PC-relative addressing to specify their targets, an important question concerns how far branch targets are from branches. Knowing the distribution of these displacements will help in choosing what branch offsets to support, and thus will affect the instruction length and encoding. Figure A.15 shows the distribution of displacements for PC-relative branches in instructions. About 75% of the branches are in the forward direction.
Figure A.15 Branch distances in terms of number of instructions between the target and the branch instruction. The most frequent branches in the integer programs are to targets that can be encoded in 4 to 8 bits. This result tells us that short displacement fields often suffice for branches and that the designer can gain some encoding density by having a shorter instruction with a smaller branch displacement. These measurements were taken on a load-store computer (Alpha architecture) with all instructions aligned on word boundaries. An architecture that requires fewer instructions for the same program, such as a VAX, would have shorter branch distances. However, the number of bits needed for the displacement may increase if the computer has variable-length instructions to be aligned on any byte boundary. The programs and computer used to collect these statistics are the same as those in Figure A.8.
Conditional Branch Options
Since most changes in control flow are branches, deciding how to specify the branch condition is important. Figure A.16 shows the three primary techniques in use today and their advantages and disadvantages.
Figure A.16 The major methods for evaluating branch conditions, their advantages, and their disadvantages. Although condition codes can be set by ALU operations that are needed for other purposes, measurements on programs show that this rarely happens. The major implementation problems with condition codes arise when the condition code is set by a large or haphazardly chosen subset of the instructions, rather than being controlled by a bit in the instruction. Computers with compare and branch often limit the set of compares and use a condition register for more complex compares. Often, different techniques are used for branches based on floating-point comparison versus those based on integer comparison. This dichotomy is reasonable since the number of branches that depend on floating-point comparisons is much smaller than the number depending on integer comparisons.
One of the most noticeable properties of branches is that a large number of the comparisons are simple tests, and a large number are comparisons with zero. Thus, some architectures choose to treat these comparisons as special cases, especially if a compare and branch instruction is being used. Figure A.17 shows the frequency of different comparisons used for conditional branching.
Figure A.17 Frequency of different types of compares in conditional branches. Less than (or equal) branches dominate this combination of compiler and architecture. These measurements include both the integer and floating-point compares in branches. The programs and computer used to collect these statistics are the same as those in Figure A.8.
Procedure Invocation Options
Procedure calls and returns include control transfer and possibly some state saving; at a minimum the return address must be saved somewhere, sometimes in a special link register or just a GPR. Some older architectures provide a mechanism to save many registers, while newer architectures require the compiler to generate stores and loads for each register saved and restored.
There are two basic conventions in use to save registers: either at the call site or inside the procedure being called. Caller saving means that the calling procedure must save the registers that it wants preserved for access after the call, and thus the called procedure need not worry about registers. Callee saving is the opposite: the called procedure must save the registers it wants to use, leaving the caller unrestrained. There are times when caller save must be used because of access patterns to globally visible variables in two different procedures. For example, suppose we have a procedure P1 that calls procedure P2, and both procedures manipulate the global variable x. If P1 had allocated x to a register, it must be sure to save x to a location known by P2 before the call to P2. A compiler’s ability to discover when a called procedure may access register-allocated quantities is complicated by the possibility of separate compilation. Suppose P2 may not touch x but can call another procedure, P3, that may access x, yet P2 and P3 are compiled separately. Because of these complications, most compilers will conservatively caller save any variable that may be accessed during a call.
In the cases where either convention could be used, some programs will be more optimal with callee save and some will be more optimal with caller save. As a result, most real systems today use a combination of the two mechanisms. This convention is specified in an application binary interface (ABI) that sets down the basic rules as to which registers should be caller saved and which should be callee saved. Later in this appendix we will examine the mismatch between sophisticated instructions for automatically saving registers and the needs of the compiler.
Summary: Instructions for Control Flow
Control flow instructions are some of the most frequently executed instructions. Although there are many options for conditional branches, we would expect branch addressing in a new architecture to be able to jump to hundreds of instructions either above or below the branch. This requirement suggests a PC-relative branch displacement of at least 8 bits. We would also expect to see register indirect and PC-relative addressing for jump instructions to support returns as well as many other features of current systems.
We have now completed our instruction architecture tour at the level seen by an assembly language programmer or compiler writer. We are leaning toward a load-store architecture with displacement, immediate, and register indirect addressing modes. These data are 8-, 16-, 32-, and 64-bit integers and 32- and 64-bit floating-point data. The instructions include simple operations, PC-relative conditional branches, jump and link instructions for procedure call, and register indirect jumps for procedure return (plus a few other uses).
Now we need to select how to represent this architecture in a form that makes it easy for the hardware to execute.
A.7 Encoding an Instruction Set
Clearly, the choices mentioned above will affect how the instructions are encoded into a binary representation for execution by the processor. This representation affects not only the size of the compiled program but also the implementation of the processor, which must decode this representation to quickly find the operation and its operands. The operation is typically specified in one field, called the opcode. As we shall see, the important decision is how to encode the addressing modes with the operations.
This decision depends on the range of addressing modes and the degree of independence between opcodes and modes. Some older computers have one to five operands with 10 addressing modes for each operand (see Figure A.6). For such a large number of combinations, typically a separate address specifier is needed for each operand: The address specifier tells what addressing mode is used to access the operand. At the other extreme are load-store computers with only one memory operand and only one or two addressing modes; obviously, in this case, the addressing mode can be encoded as part of the opcode.
When encoding the instructions, the number of registers and the number of addressing modes both have a significant impact on the size of instructions, as the register field and addressing mode field may appear many times in a single instruction. In fact, for most instructions many more bits are consumed in encoding addressing modes and register fields than in specifying the opcode. The architect must balance several competing forces when encoding the instruction set:
1. The desire to have as many registers and addressing modes as possible.
2. The impact of the size of the register and addressing mode fields on the average instruction size and hence on the average program size.
3. A desire to have instructions encoded into lengths that will be easy to handle in a pipelined implementation. (The value of easily decoded instructions is discussed in Appendix C and Chapter 3.) As a minimum, the architect wants instructions to be in multiples of bytes, rather than an arbitrary bit length. Many desktop and server architects have chosen to use a fixed-length instruction to gain implementation benefits while sacrificing average code size.
Figure A.18 shows three popular choices for encoding the instruction set. The first we call variable, since it allows virtually all addressing modes to be with all operations. This style is best when there are many addressing modes and operations. The second choice we call fixed, since it combines the operation and the addressing mode into the opcode. Often fixed encoding will have only a single size for all instructions; it works best when there are few addressing modes and operations. The trade-off between variable encoding and fixed encoding is size of programs versus ease of decoding in the processor. Variable tries to use as few bits as possible to represent the program, but individual instructions can vary widely in both size and the amount of work to be performed.
Figure A.18 Three basic variations in instruction encoding: variable length, fixed length, and hybrid. The variable format can support any number of operands, with each address specifier determining the addressing mode and the length of the specifier for that operand. It generally enables the smallest code representation, since unused fields need not be included. The fixed format always has the same number of operands, with the addressing modes (if options exist) specified as part of the opcode. It generally results in the largest code size. Although the fields tend not to vary in their location, they will be used for different purposes by different instructions. The hybrid approach has multiple formats specified by the opcode, adding one or two fields to specify the addressing mode and one or two fields to specify the operand address.
Let’s look at an 80×86 instruction to see an example of the variable encoding:
add EAX,1000(EBX)
The name add means a 32-bit integer add instruction with two operands, and this opcode takes 1 byte. An 80×86 address specifier is 1 or 2 bytes, specifying the source/destination register (EAX) and the addressing mode (displacement in this case) and base register (EBX) for the second operand. This combination takes 1 byte to specify the operands. When in 32-bit mode (see Appendix K), the size of the address field is either 1 byte or 4 bytes. Since 1000 is bigger than 28, the total length of the instruction is
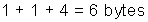
The length of 80×86 instructions varies between 1 and 17 bytes. 80×86 programs are generally smaller than the RISC architectures, which use fixed formats (see Appendix K).
Given these two poles of instruction set design of variable and fixed, the third alternative immediately springs to mind: Reduce the variability in size and work of the variable architecture but provide multiple instruction lengths to reduce code size. This hybrid approach is the third encoding alternative, and we’ll see examples shortly.
Reduced Code Size in RISCs
As RISC computers started being used in embedded applications, the 32-bit fixed format became a liability since cost and hence smaller code are important. In response, several manufacturers offered a new hybrid version of their RISC instruction sets, with both 16-bit and 32-bit instructions. The narrow instructions support fewer operations, smaller address and immediate fields, fewer registers, and the two-address format rather than the classic three-address format of RISC computers. Appendix K gives two examples, the ARM Thumb and MIPS MIPS16, which both claim a code size reduction of up to 40%.
In contrast to these instruction set extensions, IBM simply compresses its standard instruction set and then adds hardware to decompress instructions as they are fetched from memory on an instruction cache miss. Thus, the instruction cache contains full 32-bit instructions, but compressed code is kept in main memory, ROMs, and the disk. The advantage of MIPS16 and Thumb is that instruction caches act as if they are about 25% larger, while IBM’s CodePack means that compilers need not be changed to handle different instruction sets and instruction decoding can remain simple.
CodePack starts with run-length encoding compression on any PowerPC program and then loads the resulting compression tables in a 2 KB table on chip. Hence, every program has its own unique encoding. To handle branches, which are no longer to an aligned word boundary, the PowerPC creates a hash table in memory that maps between compressed and uncompressed addresses. Like a TLB (see Chapter 2), it caches the most recently used address maps to reduce the number of memory accesses. IBM claims an overall performance cost of 10%, resulting in a code size reduction of 35% to 40%.
Hitachi simply invented a RISC instruction set with a fixed 16-bit format, called SuperH, for embedded applications (see Appendix K). It has 16 rather than 32 registers to make it fit the narrower format and fewer instructions but otherwise looks like a classic RISC architecture.
Summary: Encoding an Instruction Set
Decisions made in the components of instruction set design discussed in previous sections determine whether the architect has the choice between variable and fixed instruction encodings. Given the choice, the architect more interested in code size than performance will pick variable encoding, and the one more interested in performance than code size will pick fixed encoding. Appendix E gives 13 examples of the results of architects’ choices. In Appendix C and Chapter 3, the impact of variability on performance of the processor will be discussed further.
We have almost finished laying the groundwork for the MIPS instruction set architecture that will be introduced in Section A.9. Before we do that, however, it will be helpful to take a brief look at compiler technology and its effect on program properties.
A.8 Crosscutting Issues: The Role of Compilers
Today almost all programming is done in high-level languages for desktop and server applications. This development means that since most instructions executed are the output of a compiler, an instruction set architecture is essentially a compiler target. In earlier times for these applications, architectural decisions were often made to ease assembly language programming or for a specific kernel. Because the compiler will significantly affect the performance of a computer, understanding compiler technology today is critical to designing and efficiently implementing an instruction set.
Once it was popular to try to isolate the compiler technology and its effect on hardware performance from the architecture and its performance, just as it was popular to try to separate architecture from its implementation. This separation is essentially impossible with today’s desktop compilers and computers. Architectural choices affect the quality of the code that can be generated for a computer and the complexity of building a good compiler for it, for better or for worse.
In this section, we discuss the critical goals in the instruction set primarily from the compiler viewpoint. It starts with a review of the anatomy of current compilers. Next we discuss how compiler technology affects the decisions of the architect, and how the architect can make it hard or easy for the compiler to produce good code. We conclude with a review of compilers and multimedia operations, which unfortunately is a bad example of cooperation between compiler writers and architects.
The Structure of Recent Compilers
To begin, let’s look at what optimizing compilers are like today. Figure A.19 shows the structure of recent compilers.
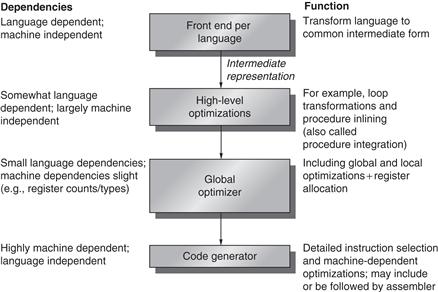
Figure A.19 Compilers typically consist of two to four passes, with more highly optimizing compilers having more passes. This structure maximizes the probability that a program compiled at various levels of optimization will produce the same output when given the same input. The optimizing passes are designed to be optional and may be skipped when faster compilation is the goal and lower-quality code is acceptable. A pass is simply one phase in which the compiler reads and transforms the entire program. (The term phase is often used interchangeably with pass.) Because the optimizing passes are separated, multiple languages can use the same optimizing and code generation passes. Only a new front end is required for a new language.
A compiler writer’s first goal is correctness—all valid programs must be compiled correctly. The second goal is usually speed of the compiled code. Typically, a whole set of other goals follows these two, including fast compilation, debugging support, and interoperability among languages. Normally, the passes in the compiler transform higher-level, more abstract representations into progressively lower-level representations. Eventually it reaches the instruction set. This structure helps manage the complexity of the transformations and makes writing a bug-free compiler easier.
The complexity of writing a correct compiler is a major limitation on the amount of optimization that can be done. Although the multiple-pass structure helps reduce compiler complexity, it also means that the compiler must order and perform some transformations before others. In the diagram of the optimizing compiler in Figure A.19, we can see that certain high-level optimizations are performed long before it is known what the resulting code will look like. Once such a transformation is made, the compiler can’t afford to go back and revisit all steps, possibly undoing transformations. Such iteration would be prohibitive, both in compilation time and in complexity. Thus, compilers make assumptions about the ability of later steps to deal with certain problems. For example, compilers usually have to choose which procedure calls to expand inline before they know the exact size of the procedure being called. Compiler writers call this problem the phase-ordering problem.
How does this ordering of transformations interact with the instruction set architecture? A good example occurs with the optimization called global common subexpression elimination. This optimization finds two instances of an expression that compute the same value and saves the value of the first computation in a temporary. It then uses the temporary value, eliminating the second computation of the common expression.
For this optimization to be significant, the temporary must be allocated to a register. Otherwise, the cost of storing the temporary in memory and later reloading it may negate the savings gained by not recomputing the expression. There are, in fact, cases where this optimization actually slows down code when the temporary is not register allocated. Phase ordering complicates this problem because register allocation is typically done near the end of the global optimization pass, just before code generation. Thus, an optimizer that performs this optimization must assume that the register allocator will allocate the temporary to a register.
Optimizations performed by modern compilers can be classified by the style of the transformation, as follows:
■ High-level optimizations are often done on the source with output fed to later optimization passes.
■ Local optimizations optimize code only within a straight-line code fragment (called a basic block by compiler people).
■ Global optimizations extend the local optimizations across branches and introduce a set of transformations aimed at optimizing loops.
■ Register allocation associates registers with operands.
■ Processor-dependent optimizations attempt to take advantage of specific architectural knowledge.
Register Allocation
Because of the central role that register allocation plays, both in speeding up the code and in making other optimizations useful, it is one of the most important—if not the most important—of the optimizations. Register allocation algorithms today are based on a technique called graph coloring. The basic idea behind graph coloring is to construct a graph representing the possible candidates for allocation to a register and then to use the graph to allocate registers. Roughly speaking, the problem is how to use a limited set of colors so that no two adjacent nodes in a dependency graph have the same color. The emphasis in the approach is to achieve 100% register allocation of active variables. The problem of coloring a graph in general can take exponential time as a function of the size of the graph (NP-complete). There are heuristic algorithms, however, that work well in practice, yielding close allocations that run in near-linear time.
Graph coloring works best when there are at least 16 (and preferably more) general-purpose registers available for global allocation for integer variables and additional registers for floating point. Unfortunately, graph coloring does not work very well when the number of registers is small because the heuristic algorithms for coloring the graph are likely to fail.
Impact of Optimizations on Performance
It is sometimes difficult to separate some of the simpler optimizations—local and processor-dependent optimizations—from transformations done in the code generator. Examples of typical optimizations are given in Figure A.20. The last column of Figure A.20 indicates the frequency with which the listed optimizing transforms were applied to the source program.
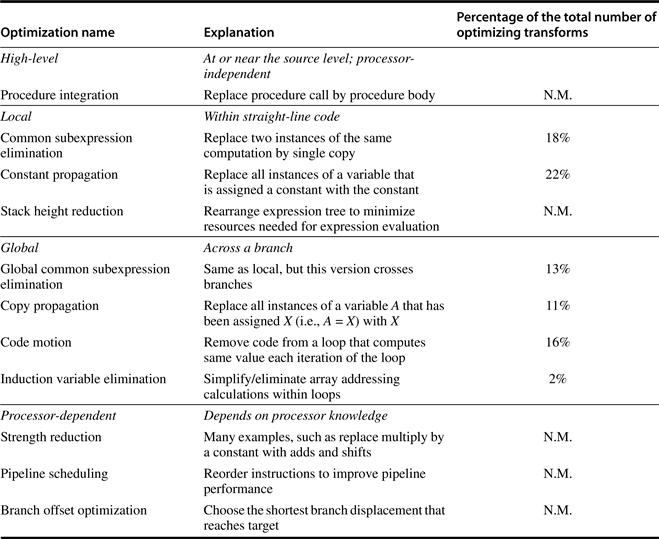
Figure A.20 Major types of optimizations and examples in each class. These data tell us about the relative frequency of occurrence of various optimizations. The third column lists the static frequency with which some of the common optimizations are applied in a set of 12 small Fortran and Pascal programs. There are nine local and global optimizations done by the compiler included in the measurement. Six of these optimizations are covered in the figure, and the remaining three account for 18% of the total static occurrences. The abbreviation N.M. means that the number of occurrences of that optimization was not measured. Processor-dependent optimizations are usually done in a code generator, and none of those was measured in this experiment. The percentage is the portion of the static optimizations that are of the specified type. Data from Chow [1983] (collected using the Stanford UCODE compiler).
Figure A.21 shows the effect of various optimizations on instructions executed for two programs. In this case, optimized programs executed roughly 25% to 90% fewer instructions than unoptimized programs. The figure illustrates the importance of looking at optimized code before suggesting new instruction set features, since a compiler might completely remove the instructions the architect was trying to improve.
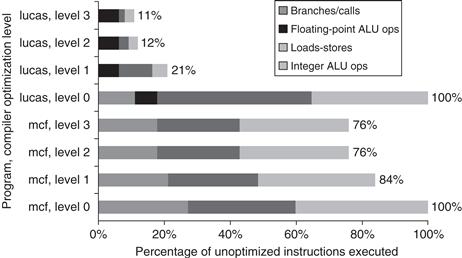
Figure A.21 Change in instruction count for the programs lucas and mcf from the SPEC2000 as compiler optimization levels vary. Level 0 is the same as unoptimized code. Level 1 includes local optimizations, code scheduling, and local register allocation. Level 2 includes global optimizations, loop transformations (software pipelining), and global register allocation. Level 3 adds procedure integration. These experiments were performed on Alpha compilers.
The Impact of Compiler Technology on the Architect’s Decisions
The interaction of compilers and high-level languages significantly affects how programs use an instruction set architecture. There are two important questions: How are variables allocated and addressed? How many registers are needed to allocate variables appropriately? To address these questions, we must look at the three separate areas in which current high-level languages allocate their data:
■ The stack is used to allocate local variables. The stack is grown or shrunk on procedure call or return, respectively. Objects on the stack are addressed relative to the stack pointer and are primarily scalars (single variables) rather than arrays. The stack is used for activation records, not as a stack for evaluating expressions. Hence, values are almost never pushed or popped on the stack.
■ The global data area is used to allocate statically declared objects, such as global variables and constants. A large percentage of these objects are arrays or other aggregate data structures.
■ The heap is used to allocate dynamic objects that do not adhere to a stack discipline. Objects in the heap are accessed with pointers and are typically not scalars.
Register allocation is much more effective for stack-allocated objects than for global variables, and register allocation is essentially impossible for heap-allocated objects because they are accessed with pointers. Global variables and some stack variables are impossible to allocate because they are aliased —there are multiple ways to refer to the address of a variable, making it illegal to put it into a register. (Most heap variables are effectively aliased for today’s compiler technology.)
For example, consider the following code sequence, where &; returns the address of a variable and * dereferences a pointer:
p = &a-- gets address of a in p
a = ...-- assigns to a directly
*p = ...-- uses p to assign to a
...a...-- accesses a
The variable a could not be register allocated across the assignment to *p without generating incorrect code. Aliasing causes a substantial problem because it is often difficult or impossible to decide what objects a pointer may refer to. A compiler must be conservative; some compilers will not allocate any local variables of a procedure in a register when there is a pointer that may refer to one of the local variables.
How the Architect Can Help the Compiler Writer
Today, the complexity of a compiler does not come from translating simple statements like A = B + C. Most programs are locally simple, and simple translations work fine. Rather, complexity arises because programs are large and globally complex in their interactions, and because the structure of compilers means decisions are made one step at a time about which code sequence is best.
Compiler writers often are working under their own corollary of a basic principle in architecture: Make the frequent cases fast and the rare case correct. That is, if we know which cases are frequent and which are rare, and if generating code for both is straightforward, then the quality of the code for the rare case may not be very important—but it must be correct!
Some instruction set properties help the compiler writer. These properties should not be thought of as hard-and-fast rules, but rather as guidelines that will make it easier to write a compiler that will generate efficient and correct code.
■ Provide regularity —Whenever it makes sense, the three primary components of an instruction set—the operations, the data types, and the addressing modes—should be orthogonal. Two aspects of an architecture are said to be orthogonal if they are independent. For example, the operations and addressing modes are orthogonal if, for every operation to which one addressing mode can be applied, all addressing modes are applicable. This regularity helps simplify code generation and is particularly important when the decision about what code to generate is split into two passes in the compiler. A good counterexample of this property is restricting what registers can be used for a certain class of instructions. Compilers for special-purpose register architectures typically get stuck in this dilemma. This restriction can result in the compiler finding itself with lots of available registers, but none of the right kind!
■ Provide primitives, not solutions —Special features that “match” a language construct or a kernel function are often unusable. Attempts to support high-level languages may work only with one language or do more or less than is required for a correct and efficient implementation of the language. An example of how such attempts have failed is given in Section A.10.
■ Simplify trade-offs among alternatives —One of the toughest jobs a compiler writer has is figuring out what instruction sequence will be best for every segment of code that arises. In earlier days, instruction counts or total code size might have been good metrics, but—as we saw in Chapter 1—this is no longer true. With caches and pipelining, the trade-offs have become very complex. Anything the designer can do to help the compiler writer understand the costs of alternative code sequences would help improve the code. One of the most difficult instances of complex trade-offs occurs in a register-memory architecture in deciding how many times a variable should be referenced before it is cheaper to load it into a register. This threshold is hard to compute and, in fact, may vary among models of the same architecture.
■ Provide instructions that bind the quantities known at compile time as constants —A compiler writer hates the thought of the processor interpreting at runtime a value that was known at compile time. Good counterexamples of this principle include instructions that interpret values that were fixed at compile time. For instance, the VAX procedure call instruction (calls ) dynamically interprets a mask saying what registers to save on a call, but the mask is fixed at compile time (see Section A.10).
Compiler Support (or Lack Thereof) for Multimedia Instructions
Alas, the designers of the SIMD instructions (see Section 4.3 in Chapter 4) basically ignored the previous subsection. These instructions tend to be solutions, not primitives; they are short of registers; and the data types do not match existing programming languages. Architects hoped to find an inexpensive solution that would help some users, but often only a few low-level graphics library routines use them.
The SIMD instructions are really an abbreviated version of an elegant architecture style that has its own compiler technology. As explained in Section 4.2, vector architectures operate on vectors of data. Invented originally for scientific codes, multimedia kernels are often vectorizable as well, albeit often with shorter vectors. As Section 4.3 suggests, we can think of Intel’s MMX and SSE or PowerPC’s AltiVec as simply short vector computers: MMX with vectors of eight 8-bit elements, four 16-bit elements, or two 32-bit elements, and AltiVec with vectors twice that length. They are implemented as simply adjacent, narrow elements in wide registers.
These microprocessor architectures build the vector register size into the architecture: the sum of the sizes of the elements is limited to 64 bits for MMX and 128 bits for AltiVec. When Intel decided to expand to 128-bit vectors, it added a whole new set of instructions, called Streaming SIMD Extension (SSE).
A major advantage of vector computers is hiding latency of memory access by loading many elements at once and then overlapping execution with data transfer. The goal of vector addressing modes is to collect data scattered about memory, place them in a compact form so that they can be operated on efficiently, and then place the results back where they belong.
Vector computers include strided addressing and gather/scatter addressing (see Section 4.2) to increase the number of programs that can be vectorized. Strided addressing skips a fixed number of words between each access, so sequential addressing is often called unit stride addressing. Gather and scatter find their addresses in another vector register: Think of it as register indirect addressing for vector computers. From a vector perspective, in contrast, these short-vector SIMD computers support only unit strided accesses: Memory accesses load or store all elements at once from a single wide memory location. Since the data for multimedia applications are often streams that start and end in memory, strided and gather/scatter addressing modes are essential to successful vectorization (see Section 4.7).
Having short, architecture-limited vectors with few registers and simple memory addressing modes makes it more difficult to use vectorizing compiler technology. Hence, these SIMD instructions are more likely to be found in hand-coded libraries than in compiled code.
Summary: The Role of Compilers
This section leads to several recommendations. First, we expect a new instruction set architecture to have at least 16 general-purpose registers—not counting separate registers for floating-point numbers—to simplify allocation of registers using graph coloring. The advice on orthogonality suggests that all supported addressing modes apply to all instructions that transfer data. Finally, the last three pieces of advice—provide primitives instead of solutions, simplify trade-offs between alternatives, don’t bind constants at runtime—all suggest that it is better to err on the side of simplicity. In other words, understand that less is more in the design of an instruction set. Alas, SIMD extensions are more an example of good marketing than of outstanding achievement of hardware–software co-design.
A.9 Putting It All Together: The MIPS Architecture
In this section we describe a simple 64-bit load-store architecture called MIPS. The instruction set architecture of MIPS and RISC relatives was based on observations similar to those covered in the last sections. (In Section L.3 we discuss how and why these architectures became popular.) Reviewing our expectations from each section, for desktop applications:
■ Section A.2 —Use general-purpose registers with a load-store architecture.
■ Section A.3 —Support these addressing modes: displacement (with an address offset size of 12 to 16 bits), immediate (size 8 to 16 bits), and register indirect.
■ Section A.4 —Support these data sizes and types: 8-, 16-, 32-, and 64-bit integers and 64-bit IEEE 754 floating-point numbers.
■ Section A.5 —Support these simple instructions, since they will dominate the number of instructions executed: load, store, add, subtract, move register-register, and shift.
■ Section A.6 —Compare equal, compare not equal, compare less, branch (with a PC-relative address at least 8 bits long), jump, call, and return.
■ Section A.7 —Use fixed instruction encoding if interested in performance, and use variable instruction encoding if interested in code size.
■ Section A.8 —Provide at least 16 general-purpose registers, be sure all addressing modes apply to all data transfer instructions, and aim for a minimalist instruction set. This section didn’t cover floating-point programs, but they often use separate floating-point registers. The justification is to increase the total number of registers without raising problems in the instruction format or in the speed of the general-purpose register file. This compromise, however, is not orthogonal.
We introduce MIPS by showing how it follows these recommendations. Like most recent computers, MIPS emphasizes
■ A simple load-store instruction set
■ Design for pipelining efficiency (discussed in Appendix C), including a fixed instruction set encoding
MIPS provides a good architectural model for study, not only because of the popularity of this type of processor, but also because it is an easy architecture to understand. We will use this architecture again in Appendix C and in Chapter 3, and it forms the basis for a number of exercises and programming projects.
In the years since the first MIPS processor in 1985, there have been many versions of MIPS (see Appendix K). We will use a subset of what is now called MIPS64, which will often abbreviate to just MIPS, but the full instruction set is found in Appendix K.
Registers for MIPS
MIPS64 has 32 64-bit general-purpose registers (GPRs), named R0, R1,…, R31. GPRs are also sometimes known as integer registers. Additionally, there is a set of 32 floating-point registers (FPRs), named F0, F1,…, F31, which can hold 32 single-precision (32-bit) values or 32 double-precision (64-bit) values. (When holding one single-precision number, the other half of the FPR is unused.) Both single- and double-precision floating-point operations (32-bit and 64-bit) are provided. MIPS also includes instructions that operate on two single-precision operands in a single 64-bit floating-point register.
The value of R0 is always 0. We shall see later how we can use this register to synthesize a variety of useful operations from a simple instruction set.
A few special registers can be transferred to and from the general-purpose registers. An example is the floating-point status register, used to hold information about the results of floating-point operations. There are also instructions for moving between an FPR and a GPR.
Data Types for MIPS
The data types are 8-bit bytes, 16-bit half words, 32-bit words, and 64-bit double words for integer data and 32-bit single precision and 64-bit double precision for floating point. Half words were added because they are found in languages like C and are popular in some programs, such as the operating systems, concerned about size of data structures. They will also become more popular if Unicode becomes widely used. Single-precision floating-point operands were added for similar reasons. (Remember the early warning that you should measure many more programs before designing an instruction set.)
The MIPS64 operations work on 64-bit integers and 32- or 64-bit floating point. Bytes, half words, and words are loaded into the general-purpose registers with either zeros or the sign bit replicated to fill the 64 bits of the GPRs. Once loaded, they are operated on with the 64-bit integer operations.
Addressing Modes for MIPS Data Transfers
The only data addressing modes are immediate and displacement, both with 16-bit fields. Register indirect is accomplished simply by placing 0 in the 16-bit displacement field, and absolute addressing with a 16-bit field is accomplished by using register 0 as the base register. Embracing zero gives us four effective modes, although only two are supported in the architecture.
MIPS memory is byte addressable with a 64-bit address. It has a mode bit that allows software to select either Big Endian or Little Endian. As it is a load-store architecture, all references between memory and either GPRs or FPRs are through loads or stores. Supporting the data types mentioned above, memory accesses involving GPRs can be to a byte, half word, word, or double word. The FPRs may be loaded and stored with single-precision or double-precision numbers. All memory accesses must be aligned.
MIPS Instruction Format
Since MIPS has just two addressing modes, these can be encoded into the opcode. Following the advice on making the processor easy to pipeline and decode, all instructions are 32 bits with a 6-bit primary opcode. Figure A.22 shows the instruction layout. These formats are simple while providing 16-bit fields for displacement addressing, immediate constants, or PC-relative branch addresses.
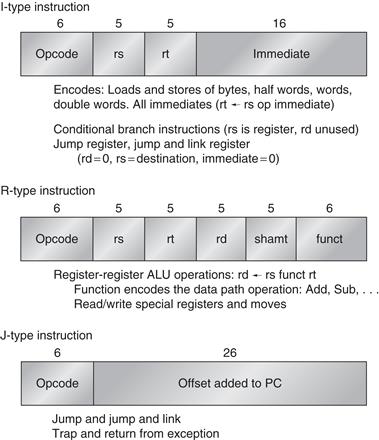
Figure A.22 Instruction layout for MIPS. All instructions are encoded in one of three types, with common fields in the same location in each format.
Appendix K shows a variant of MIPS––called MIPS16––which has 16-bit and 32-bit instructions to improve code density for embedded applications. We will stick to the traditional 32-bit format in this book.
MIPS Operations
MIPS supports the list of simple operations recommended above plus a few others. There are four broad classes of instructions: loads and stores, ALU operations, branches and jumps, and floating-point operations.
Any of the general-purpose or floating-point registers may be loaded or stored, except that loading R0 has no effect. Figure A.23 gives examples of the load and store instructions. Single-precision floating-point numbers occupy half a floating-point register. Conversions between single and double precision must be done explicitly. The floating-point format is IEEE 754 (see Appendix J). A list of all the MIPS instructions in our subset appears in Figure A.26 (page A-40).
Figure A.23 The load and store instructions in MIPS. All use a single addressing mode and require that the memory value be aligned. Of course, both loads and stores are available for all the data types shown.
Figure A.26 Subset of the instructions in MIPS64. Figure A.22 lists the formats of these instructions. SP = single precision; DP = double precision. This list can also be found on the back inside cover.
To understand these figures we need to introduce a few additional extensions to our C description language used initially on page A-9:
■ A subscript is appended to the symbol ← whenever the length of the datum being transferred might not be clear. Thus, ←n means transfer an n -bit quantity. We use x, y ← z to indicate that z should be transferred to x and y.
■ A subscript is used to indicate selection of a bit from a field. Bits are labeled from the most-significant bit starting at 0. The subscript may be a single digit (e.g., Regs[R4]0 yields the sign bit of R4) or a subrange (e.g., Regs[R3] 56..63 yields the least-significant byte of R3).
■ The variable Mem, used as an array that stands for main memory, is indexed by a byte address and may transfer any number of bytes.
■ A superscript is used to replicate a field (e.g., 048 yields a field of zeros of length 48 bits).
■ The symbol ## is used to concatenate two fields and may appear on either side of a data transfer.
As an example, assuming that R8 and R10 are 64-bit registers:
Regs[R10] 32..63 ← 32 (Mem[Regs[R8]]0)24 ## Mem[Regs[R8]]
means that the byte at the memory location addressed by the contents of register R8 is sign-extended to form a 32-bit quantity that is stored into the lower half of register R10. (The upper half of R10 is unchanged.)
All ALU instructions are register-register instructions. Figure A.24 gives some examples of the arithmetic/logical instructions. The operations include simple arithmetic and logical operations: add, subtract, AND, OR, XOR, and shifts. Immediate forms of all these instructions are provided using a 16-bit sign-extended immediate. The operation LUI (load upper immediate) loads bits 32 through 47 of a register, while setting the rest of the register to 0. LUI allows a 32-bit constant to be built in two instructions, or a data transfer using any constant 32-bit address in one extra instruction.
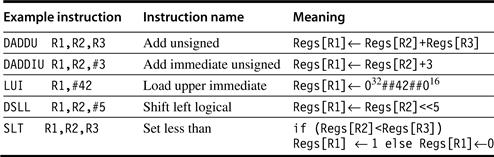
Figure A.24 Examples of arithmetic/logical instructions on MIPS, both with and without immediates.
As mentioned above, R0 is used to synthesize popular operations. Loading a constant is simply an add immediate where the source operand is R0, and a register-register move is simply an add where one of the sources is R0. (We sometimes use the mnemonic LI, standing for load immediate, to represent the former, and the mnemonic MOV for the latter.)
MIPS Control Flow Instructions
MIPS provides compare instructions, which compare two registers to see if the first is less than the second. If the condition is true, these instructions place a 1 in the destination register (to represent true); otherwise, they place the value 0. Because these operations “set” a register, they are called set-equal, set-not-equal, set-less-than, and so on. There are also immediate forms of these compares.
Control is handled through a set of jumps and a set of branches. Figure A.25 gives some typical branch and jump instructions. The four jump instructions are differentiated by the two ways to specify the destination address and by whether or not a link is made. Two jumps use a 26-bit offset shifted 2 bits and then replace the lower 28 bits of the program counter (of the instruction sequentially following the jump) to determine the destination address. The other two jump instructions specify a register that contains the destination address. There are two flavors of jumps: plain jump and jump and link (used for procedure calls). The latter places the return address—the address of the next sequential instruction—in R31.
Figure A.25 Typical control flow instructions in MIPS. All control instructions, except jumps to an address in a register, are PC-relative. Note that the branch distances are longer than the address field would suggest; since MIPS instructions are all 32 bits long, the byte branch address is multiplied by 4 to get a longer distance.
All branches are conditional. The branch condition is specified by the instruction, which may test the register source for zero or nonzero; the register may contain a data value or the result of a compare. There are also conditional branch instructions to test for whether a register is negative and for equality between two registers. The branch-target address is specified with a 16-bit signed offset that is shifted left two places and then added to the program counter, which is pointing to the next sequential instruction. There is also a branch to test the floating-point status register for floating-point conditional branches, described later.
Appendix C and Chapter 3 show that conditional branches are a major challenge to pipelined execution; hence, many architectures have added instructions to convert a simple branch into a conditional arithmetic instruction. MIPS included conditional move on zero or not zero. The value of the destination register either is left unchanged or is replaced by a copy of one of the source registers depending on whether or not the value of the other source register is zero.
MIPS Floating-Point Operations
Floating-point instructions manipulate the floating-point registers and indicate whether the operation to be performed is single or double precision. The operations MOV.S and MOV.D copy a single-precision (MOV.S) or double-precision (MOV.D) floating-point register to another register of the same type. The operations MFC1, MTC1, D MFC1, and D MTC1 move data between a single or double floating-point register and an integer register. Conversions from integer to floating point are also provided, and vice versa.
The floating-point operations are add, subtract, multiply, and divide; a suffix D is used for double precision, and a suffix S is used for single precision (e.g., ADD.D, ADD.S, SUB.D, SUB.S, MUL.D, MUL.S, DIV.D, DIV.S). Floating-point compares set a bit in the special floating-point status register that can be tested with a pair of branches: BC1T and BC1F, branch floating-point true and branch floating-point false.
To get greater performance for graphics routines, MIPS64 has instructions that perform two 32-bit floating-point operations on each half of the 64-bit floating-point register. These paired single operations include ADD.PS, SUB.PS, MUL.PS, and DIV.PS. (They are loaded and stored using double-precision loads and stores.)
Giving a nod toward the importance of multimedia applications, MIPS64 also includes both integer and floating-point multiply-add instructions: MADD, MADD.S, MADD.D, and MADD.PS. The registers are all the same width in these combined operations. Figure A.26 contains a list of a subset of MIPS64 operations and their meanings.
MIPS Instruction Set Usage
To give an idea of which instructions are popular, Figure A.27 shows the frequency of instructions and instruction classes for five SPECint2000 programs, and Figure A.28 shows the same data for five SPECfp2000 programs.
Figure A.27 MIPS dynamic instruction mix for five SPECint2000 programs. Note that integer register-register move instructions are included in the or instruction. Blank entries have the value 0.0%.
Figure A.28 MIPS dynamic instruction mix for five programs from SPECfp2000. Note that integer register-register move instructions are included in the or instruction. Blank entries have the value 0.0%.
A.10 Fallacies and Pitfalls
Architects have repeatedly tripped on common, but erroneous, beliefs. In this section we look at a few of them.
Pitfall Designing a “high-level” instruction set feature specifically oriented to supporting a high-level language structure.
Attempts to incorporate high-level language features in the instruction set have led architects to provide powerful instructions with a wide range of flexibility. However, often these instructions do more work than is required in the frequent case, or they don’t exactly match the requirements of some languages. Many such efforts have been aimed at eliminating what in the 1970s was called the semantic gap. Although the idea is to supplement the instruction set with additions that bring the hardware up to the level of the language, the additions can generate what Wulf, Levin, and Harbison [1981] have called a semantic clash:
… by giving too much semantic content to the instruction, the computer designer made it possible to use the instruction only in limited contexts. [p. 43]
More often the instructions are simply overkill—they are too general for the most frequent case, resulting in unneeded work and a slower instruction. Again, the VAX CALLS is a good example. CALLS uses a callee save strategy (the registers to be saved are specified by the callee), but the saving is done by the call instruction in the caller. The CALLS instruction begins with the arguments pushed on the stack, and then takes the following steps:
2. Push the argument count on the stack.
3. Save the registers indicated by the procedure call mask on the stack (as mentioned in Section A.8). The mask is kept in the called procedure’s code—this permits the callee to specify the registers to be saved by the caller even with separate compilation.
4. Push the return address on the stack, and then push the top and base of stack pointers (for the activation record).
5. Clear the condition codes, which sets the trap enable to a known state.
6. Push a word for status information and a zero word on the stack.
The vast majority of calls in real programs do not require this amount of overhead. Most procedures know their argument counts, and a much faster linkage convention can be established using registers to pass arguments rather than the stack in memory. Furthermore, the CALLS instruction forces two registers to be used for linkage, while many languages require only one linkage register. Many attempts to support procedure call and activation stack management have failed to be useful, either because they do not match the language needs or because they are too general and hence too expensive to use.
The VAX designers provided a simpler instruction, JSB, that is much faster since it only pushes the return PC on the stack and jumps to the procedure. However, most VAX compilers use the more costly CALLS instructions. The call instructions were included in the architecture to standardize the procedure linkage convention. Other computers have standardized their calling convention by agreement among compiler writers and without requiring the overhead of a complex, very general procedure call instruction.
Fallacy There is such a thing as a typical program.
Many people would like to believe that there is a single “typical” program that could be used to design an optimal instruction set. For example, see the synthetic benchmarks discussed in Chapter 1. The data in this appendix clearly show that programs can vary significantly in how they use an instruction set. For example, Figure A.29 shows the mix of data transfer sizes for four of the SPEC2000 programs: It would be hard to say what is typical from these four programs. The variations are even larger on an instruction set that supports a class of applications, such as decimal instructions, that are unused by other applications.
Figure A.29 Data reference size of four programs from SPEC2000. Although you can calculate an average size, it would be hard to claim the average is typical of programs.
Pitfall Innovating at the instruction set architecture to reduce code size without accounting for the compiler.
Figure A.30 shows the relative code sizes for four compilers for the MIPS instruction set. Whereas architects struggle to reduce code size by 30% to 40%, different compiler strategies can change code size by much larger factors. Similar to performance optimization techniques, the architect should start with the tightest code the compilers can produce before proposing hardware innovations to save space.
Figure A.30 Code size relative to Apogee Software Version 4.1 C compiler for Telecom application of EEMBC benchmarks. The instruction set architectures are virtually identical, yet the code sizes vary by factors of 2. These results were reported February–June 2000.
Fallacy An architecture with flaws cannot be successful.
The 80×86 provides a dramatic example: The instruction set architecture is one only its creators could love (see Appendix K). Succeeding generations of Intel engineers have tried to correct unpopular architectural decisions made in designing the 80×86. For example, the 80×86 supports segmentation, whereas all others picked paging; it uses extended accumulators for integer data, but other processors use general-purpose registers; and it uses a stack for floating-point data, when everyone else abandoned execution stacks long before.
Despite these major difficulties, the 80×86 architecture has been enormously successful. The reasons are threefold: First, its selection as the microprocessor in the initial IBM PC makes 80×86 binary compatibility extremely valuable. Second, Moore’s law provided sufficient resources for 80×86 microprocessors to translate to an internal RISC instruction set and then execute RISC-like instructions. This mix enables binary compatibility with the valuable PC software base and performance on par with RISC processors. Third, the very high volumes of PC microprocessors mean Intel can easily pay for the increased design cost of hardware translation. In addition, the high volumes allow the manufacturer to go up the learning curve, which lowers the cost of the product.
The larger die size and increased power for translation may be a liability for embedded applications, but it makes tremendous economic sense for the desktop. And its cost-performance in the desktop also makes it attractive for servers, with its main weakness for servers being 32-bit addresses, which was resolved with the 64-bit addresses of AMD64 (see Chapter 2).
Fallacy You can design a flawless architecture.
All architecture design involves trade-offs made in the context of a set of hardware and software technologies. Over time those technologies are likely to change, and decisions that may have been correct at the time they were made look like mistakes. For example, in 1975 the VAX designers overemphasized the importance of code size efficiency, underestimating how important ease of decoding and pipelining would be five years later. An example in the RISC camp is delayed branch (see Appendix K). It was a simple matter to control pipeline hazards with five-stage pipelines, but a challenge for processors with longer pipelines that issue multiple instructions per clock cycle. In addition, almost all architectures eventually succumb to the lack of sufficient address space.
In general, avoiding such flaws in the long run would probably mean compromising the efficiency of the architecture in the short run, which is dangerous, since a new instruction set architecture must struggle to survive its first few years.
A.11 Concluding Remarks
The earliest architectures were limited in their instruction sets by the hardware technology of that time. As soon as the hardware technology permitted, computer architects began looking for ways to support high-level languages. This search led to three distinct periods of thought about how to support programs efficiently. In the 1960s, stack architectures became popular. They were viewed as being a good match for high-level languages—and they probably were, given the compiler technology of the day. In the 1970s, the main concern of architects was how to reduce software costs. This concern was met primarily by replacing software with hardware, or by providing high-level architectures that could simplify the task of software designers. The result was both the high-level language computer architecture movement and powerful architectures like the VAX, which has a large number of addressing modes, multiple data types, and a highly orthogonal architecture. In the 1980s, more sophisticated compiler technology and a renewed emphasis on processor performance saw a return to simpler architectures, based mainly on the load-store style of computer.
The following instruction set architecture changes occurred in the 1990s:
■ Address size doubles —The 32-bit address instruction sets for most desktop and server processors were extended to 64-bit addresses, expanding the width of the registers (among other things) to 64 bits. Appendix K gives three examples of architectures that have gone from 32 bits to 64 bits.
■ Optimization of conditional branches via conditional execution —In Chapter 3, we see that conditional branches can limit the performance of aggressive computer designs. Hence, there was interest in replacing conditional branches with conditional completion of operations, such as conditional move (see Appendix H), which was added to most instruction sets.
■ Optimization of cache performance via prefetch —Chapter 2 explains the increasing role of memory hierarchy in the performance of computers, with a cache miss on some computers taking as many instruction times as page faults took on earlier computers. Hence, prefetch instructions were added to try to hide the cost of cache misses by prefetching (see Chapter 2).
■ Support for multimedia —Most desktop and embedded instruction sets were extended with support for multimedia applications.
■ Faster floating-point operations — Appendix J describes operations added to enhance floating-point performance, such as operations that perform a multiply and an add and paired single execution. (We include them in MIPS.)
Between 1970 and 1985 many thought the primary job of the computer architect was the design of instruction sets. As a result, textbooks of that era emphasize instruction set design, much as computer architecture textbooks of the 1950s and 1960s emphasized computer arithmetic. The educated architect was expected to have strong opinions about the strengths and especially the weaknesses of the popular computers. The importance of binary compatibility in quashing innovations in instruction set design was unappreciated by many researchers and textbook writers, giving the impression that many architects would get a chance to design an instruction set.
The definition of computer architecture today has been expanded to include design and evaluation of the full computer system—not just the definition of the instruction set and not just the processor—and hence there are plenty of topics for the architect to study. In fact, the material in this appendix was a central point of the book in its first edition in 1990, but now is included in an appendix primarily as reference material!
Appendix K may satisfy readers interested in instruction set architecture; it describes a variety of instruction sets, which are either important in the marketplace today or historically important, and it compares nine popular load-store computers with MIPS.
A.12 Historical Perspective and References
Section L.4 (available online) features a discussion on the evolution of instruction sets and includes references for further reading and exploration of related topics.
Exercises by Gregory D. Peterson
A.1 [15] <A.9> Compute the effective CPI for MIPS using Figure A.27. Assume we have made the following measurements of average CPI for instruction types:
| Instruction | Clock Cycles |
| All ALU instructions | 1.0 |
| Loads-stores | 1.4 |
| Conditional branches | |
| Taken | 2.0 |
| Not taken | 1.5 |
| Jumps | 1.2 |
Assume that 60% of the conditional branches are taken and that all instructions in the “other” category of Figure A.27 are ALU instructions. Average the instruction frequencies of gap and gcc to obtain the instruction mix.
A.3 [15] <A.9> Compute the effective CPI for MIPS using Figure A.27 and the table above. Average the instruction frequencies of gzip and perlbmk to obtain the instruction mix.
1.2 [20] <A.9> Compute the effective CPI for MIPS using Figure A.28. Assume we have made the following measurements of average CPI for instruction types:
| Instruction | Clock Cycles |
| All ALU instructions | 1.0 |
| Loads-stores | 1.4 |
| Conditional branches: | |
| Taken | 2.0 |
| Not taken | 1.5 |
| Jumps | 1.2 |
| FP multiply | 6.0 |
| FP add | 4.0 |
| FP divide | 20.0 |
| Load-store FP | 1.5 |
| Other FP | 2.0 |
Assume that 60% of the conditional branches are taken and that all instructions in the “other” category of Figure A.28 are ALU instructions. Average the instruction frequencies of lucas and swim to obtain the instruction mix.
A.4 [20] <A.9> Compute the effective CPI for MIPS using Figure A.28 and the table above. Average the instruction frequencies of applu and art to obtain the instruction mix.
A.5 [10] <A.8> Consider this high-level code sequence of three statements:
A = B + C;
B = A + C;
D = A – B;
Use the technique of copy propagation (see Figure A.20) to transform the code sequence to the point where no operand is a computed value. Note the instances in which the transformation has reduced the computational work of a statement and those cases where the work has increased. What does this suggest about the technical challenge faced in trying to satisfy the desire for optimizing compilers?
A.6 [30] <A.8> Compiler optimizations may result in improvements to code size and/or performance. Consider one or more of the benchmark programs from the SPEC CPU2006 suite. Use a processor available to you and the GNU C compiler to optimize the program using no optimization, –O1, –O2, and –O3. Compare the performance and size of the resulting programs. Also compare your results to Figure A.21.
A.7 [20/20] <A.2, A.9> Consider the following fragment of C code:
for (i = 0; i <= 100; i++)
{ A[i] = B[i] + C; }
Assume that A and B are arrays of 64-bit integers, and C and i are 64-bit integers. Assume that all data values and their addresses are kept in memory (at addresses 1000, 3000, 5000, and 7000 for A, B, C, and i, respectively) except when they are operated on. Assume that values in registers are lost between iterations of the loop.
a. [20] <A.2, A.9> Write the code for MIPS. How many instructions are required dynamically? How many memory-data references will be executed? What is the code size in bytes?
b. [20] <A.2> Write the code for ×86. How many instructions are required dynamically? How many memory-data references will be executed? What is the code size in bytes?
A.8 [10/10/10] <A.2, A.7> For the following we consider instruction encoding for instruction set architectures.
a. [10] <A.2, A.7> Consider the case of a processor with an instruction length of 12 bits and with 32 general-purpose registers so the size of the address fields is 5 bits. Is it possible to have instruction encodings for the following?
■ 3 two-address instructions
■ 30 one-address instructions
■ 45 zero-address instructions
b. [10] <A.2, A.7> Assuming the same instruction length and address field sizes as above, determine if it is possible to have
■ 3 two-address instructions
■ 31 one-address instructions
■ 35 zero-address instructions
c. [10] <A.2, A.7> Assume the same instruction length and address field sizes as above. Further assume there are already 3 two-address and 24 zero-address instructions. What is the maximum number of one-address instructions that can be encoded for this processor?
A.9 [10/15] <A.2> For the following assume that values A, B, C, D, E, and F reside in memory. Also assume that instruction operation codes are represented in 8 bits, memory addresses are 64 bits, and register addresses are 6 bits.
a. [10] <A.2> For each instruction set architecture shown in Figure A.2, how many addresses, or names, appear in each instruction for the code to compute C = A + B, and what is the total code size?
b. [15] <A.2> Some of the instruction set architectures in Figure A.2 destroy operands in the course of computation. This loss of data values from processor internal storage has performance consequences. For each architecture in Figure A.2, write the code sequence to compute:
C = A + B
D = A – E
F = C + D
In your code, mark each operand that is destroyed during execution and mark each “overhead” instruction that is included just to overcome this loss of data from processor internal storage. What is the total code size, the number of bytes of instructions and data moved to or from memory, the number of overhead instructions, and the number of overhead data bytes for each of your code sequences?
A.10 [20] <A.2, A.7, A.9> The design of MIPS provides for 32 general-purpose registers and 32 floating-point registers. If registers are good, are more registers better? List and discuss as many trade-offs as you can that should be considered by instruction set architecture designers examining whether to, and how much to, increase the number of MIPS registers.
A.11 [5] <A.3> Consider a C struct that includes the following members:
struct foo {
char a;
bool b;
int c;
double d;
short e;
float f;
double g;
char * cptr;
float * fptr;
int x;
};
For a 32-bit machine, what is the size of the foo struct? What is the minimum size required for this struct, assuming you may arrange the order of the struct members as you wish? What about for a 64-bit machine?
A.12 [30] <A.7> Many computer manufacturers now include tools or simulators that allow you to measure the instruction set usage of a user program. Among the methods in use are machine simulation, hardware-supported trapping, and a compiler technique that instruments the object code module by inserting counters. Find a processor available to you that includes such a tool. Use it to measure the instruction set mix for one of the SPEC CPU2006 benchmarks. Compare the results to those shown in this chapter.
A.13 [30] <A.8> Newer processors such as Intel’s i7 Sandy Bridge include support for AVX vector/multimedia instructions. Write a dense matrix multiply function using single-precision values and compile it with different compilers and optimization flags. Linear algebra codes using Basic Linear Algebra Subroutine (BLAS) routines such as SGEMM include optimized versions of dense matrix multiply. Compare the code size and performance of your code to that of BLAS SGEMM. Explore what happens when using double-precision values and DGEMM.
A.14 [30] <A.8> For the SGEMM code developed above for the i7 processor, include the use of AVX intrinsics to improve the performance. In particular, try to vectorize your code to better utilize the AVX hardware. Compare the code size and performance to the original code.
A.15 [30] <A.7, A.9> SPIM is a popular simulator for simulating MIPS processors. Use SPIM to measure the instruction set mix for some SPEC CPU2006 benchmark programs.
A.16 [35/35/35/35] <A.2–A.8> gcc targets most modern instruction set architectures (see www.gnu.org/software/gcc/). Create a version of gcc for several architectures that you have access to, such as ×86, MIPS, PowerPC, and ARM.
a. [35] <A.2–A.8> Compile a subset of SPEC CPU2006 integer benchmarks and create a table of code sizes. Which architecture is best for each program?
b. [35] <A.2–A.8> Compile a subset of SPEC CPU2006 floating-point benchmarks and create a table of code sizes. Which architecture is best for each program?
c. [35] <A.2–A.8> Compile a subset of EEMBC AutoBench benchmarks (see www.eembc.org/home.php) and create a table of code sizes. Which architecture is best for each program?
d. [35] <A.2–A.8> Compile a subset of EEMBC FPBench floating-point benchmarks and create a table of code sizes. Which architecture is best for each program?
A.17 [40] <A.2–A.8> Power efficiency has become very important for modern processors, particularly for embedded systems. Create a version of gcc for two architectures that you have access to, such as ×86, MIPS, PowerPC, and ARM. Compile a subset of EEMBC benchmarks while using EnergyBench to measure energy usage during execution. Compare code size, performance, and energy usage for the processors. Which is best for each program?
A.18 [20/15/15/20] Your task is to compare the memory efficiency of four different styles of instruction set architectures. The architecture styles are
■ Accumulator—All operations occur between a single register and a memory location.
■ Memory-memory—All instruction addresses reference only memory locations.
■ Stack—All operations occur on top of the stack. Push and pop are the only instructions that access memory; all others remove their operands from the stack and replace them with the result. The implementation uses a hardwired stack for only the top two stack entries, which keeps the processor circuit very small and low cost. Additional stack positions are kept in memory locations, and accesses to these stack positions require memory references.
■ Load-store—All operations occur in registers, and register-to-register instructions have three register names per instruction.
To measure memory efficiency, make the following assumptions about all four instruction sets:
■ All instructions are an integral number of bytes in length.
■ The opcode is always one byte (8 bits).
■ Memory accesses use direct, or absolute, addressing.
■ The variables A, B, C, and D are initially in memory.
a. [20] <A.2, A.3> Invent your own assembly language mnemonics (Figure A.2 provides a useful sample to generalize), and for each architecture write the best equivalent assembly language code for this high-level language code sequence:
A = B + C;
B = A + C;
D = A – B;
b. [15] <A.3> Label each instance in your assembly codes for part (a) where a value is loaded from memory after having been loaded once. Also label each instance in your code where the result of one instruction is passed to another instruction as an operand, and further classify these events as involving storage within the processor or storage in memory.
c. [15] <A.7> Assume that the given code sequence is from a small, embedded computer application, such as a microwave oven controller, that uses a 16-bit memory address and data operands. If a load-store architecture is used, assume it has 16 general-purpose registers. For each architecture answer the following questions: How many instruction bytes are fetched? How many bytes of data are transferred from/to memory? Which architecture is most efficient as measured by total memory traffic (code + data)?
d. [20] <A.7> Now assume a processor with 64-bit memory addresses and data operands. For each architecture answer the questions of part (c). How have the relative merits of the architectures changed for the chosen metrics?
A.19 [30] <A.2, A.3> Use the four different instruction set architecture styles from above, but assume that the memory operations supported include register indirect as well as direct addressing. Invent your own assembly language mnemonics (Figure A.2 provides a useful sample to generalize), and for each architecture write the best equivalent assembly language code for this fragment of C code:
for (i = 0; i <= 100; i++)
{ A[i] = B[i] + C; }
Assume that A and B are arrays of 64-bit integers, and C and i are 64-bit integers.
The second and third columns contain the cumulative percentage of the data references and branches, respectively, that can be accommodated with the corresponding number of bits of magnitude in the displacement. These are the average distances of all the integer and floating-point programs in Figures A.8 and A.15.
A.20 [20/20/20] <A.3> We are designing instruction set formats for a load-store architecture and are trying to decide whether it is worthwhile to have multiple offset lengths for branches and memory references. The length of an instruction would be equal to 16 bits + offset length in bits, so ALU instructions will be 16 bits. Figure A.31 contains data on offset size for the Alpha architecture with full optimization for SPEC CPU2000. For instruction set frequencies, use the data for MIPS from the average of the five benchmarks for the load-store machine in Figure A.27. Assume that the miscellaneous instructions are all ALU instructions that use only registers.
a. [20] <A.3> Suppose offsets are permitted to be 0, 8, 16, or 24 bits in length, including the sign bit. What is the average length of an executed instruction?
b. [20] <A.3> Suppose we want a fixed-length instruction and we chose a 24-bit instruction length (for everything, including ALU instructions). For every offset of longer than 8 bits, additional instructions are required. Determine the number of instruction bytes fetched in this machine with fixed instruction size versus those fetched with a byte-variable-sized instruction as defined in part (a).
c. [20] <A.3> Now suppose we use a fixed offset length of 24 bits so that no additional instruction is ever required. How many instruction bytes would be required? Compare this result to your answer to part (b).
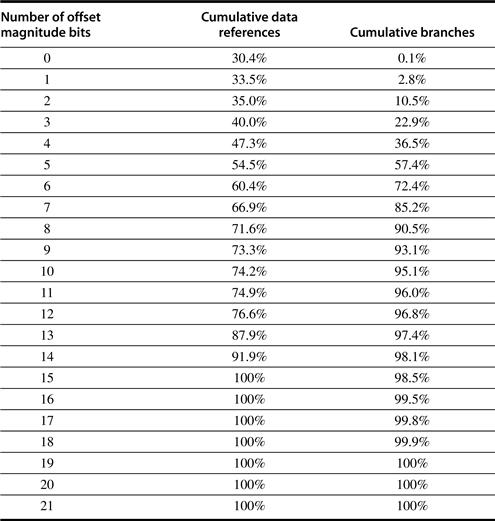
Figure A.31 Data on offset size for the Alpha architecture with full optimization for SPEC CPU2000.
A.21 [20/20] <A.3, A.6, A.9> The size of displacement values needed for the displacement addressing mode or for PC-relative addressing can be extracted from compiled applications. Use a disassembler with one or more of the SPEC CPU2006 benchmarks compiled for the MIPS processor.
a. [20] <A.3, A.9> For each instruction using displacement addressing, record the displacement value used. Create a histogram of displacement values. Compare the results to those shown in this chapter in Figure A.8.
b. [20] <A.6, A.9> For each branch instruction using PC-relative addressing, record the displacement value used. Create a histogram of displacement values. Compare the results to those shown in this chapter in Figure A.15.
A.22 [15/15/10/10] <A.3> The value represented by the hexadecimal number 434F 4D50 5554 4552 is to be stored in an aligned 64-bit double word.
a. [15] <A.3> Using the physical arrangement of the first row in Figure A.5, write the value to be stored using Big Endian byte order. Next, interpret each byte as an ASCII character and below each byte write the corresponding character, forming the character string as it would be stored in Big Endian order.
b. [15] <A.3> Using the same physical arrangement as in part (a), write the value to be stored using Little Endian byte order, and below each byte write the corresponding ASCII character.
c. [10] <A.3> What are the hexadecimal values of all misaligned 2-byte words that can be read from the given 64-bit double word when stored in Big Endian byte order?
d. [10] <A.3> What are the hexadecimal values of all misaligned 4-byte words that can be read from the given 64-bit double word when stored in Little Endian byte order?
A.23 [Discussion] <A.2–A.12> Consider typical applications for desktop, server, cloud, and embedded computing. How would instruction set architecture be impacted for machines targeting each of these markets?