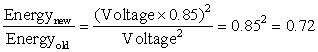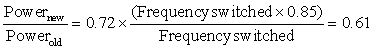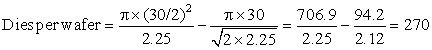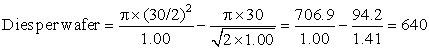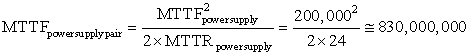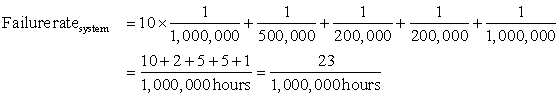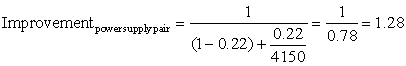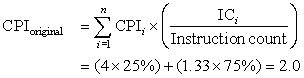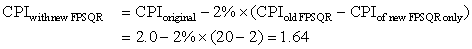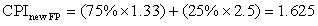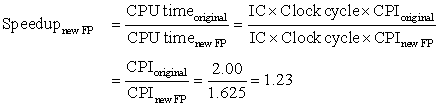1

Fundamentals of Quantitative Design and Analysis

I think it’s fair to say that personal computers have become the most empowering tool we’ve ever created. They’re tools of communication, they’re tools of creativity, and they can be shaped by their user.

Bill Gates, February 24, 2004

1.1 Introduction

1.2 Classes of Computers

1.3 Defining Computer Architecture

1.4 Trends in Technology

1.5 Trends in Power and Energy in Integrated Circuits

1.6 Trends in Cost

1.7 Dependability

1.8 Measuring, Reporting, and Summarizing Performance

1.9 Quantitative Principles of Computer Design

1.10 Putting It All Together: Performance, Price, and Power

1.11 Fallacies and Pitfalls

1.12 Concluding Remarks

1.13 Historical Perspectives and References

Case Studies and Exercises by Diana Franklin

1.1 Introduction

Computer technology has made incredible progress in the roughly 65 years since the first general-purpose electronic computer was created. Today, less than $500 will purchase a mobile computer that has more performance, more main memory, and more disk storage than a computer bought in 1985 for $1 million. This rapid improvement has come both from advances in the technology used to build computers and from innovations in computer design.

Although technological improvements have been fairly steady, progress arising from better computer architectures has been much less consistent. During the first 25 years of electronic computers, both forces made a major contribution, delivering performance improvement of about 25% per year. The late 1970s saw the emergence of the microprocessor. The ability of the microprocessor to ride the improvements in integrated circuit technology led to a higher rate of performance improvement—roughly 35% growth per year.

This growth rate, combined with the cost advantages of a mass-produced microprocessor, led to an increasing fraction of the computer business being based on microprocessors. In addition, two significant changes in the computer marketplace made it easier than ever before to succeed commercially with a new architecture. First, the virtual elimination of assembly language programming reduced the need for object-code compatibility. Second, the creation of standardized, vendor-independent operating systems, such as UNIX and its clone, Linux, lowered the cost and risk of bringing out a new architecture.

These changes made it possible to develop successfully a new set of architectures with simpler instructions, called RISC (Reduced Instruction Set Computer) architectures, in the early 1980s. The RISC-based machines focused the attention of designers on two critical performance techniques, the exploitation of instruction-level parallelism (initially through pipelining and later through multiple instruction issue) and the use of caches (initially in simple forms and later using more sophisticated organizations and optimizations).

The RISC-based computers raised the performance bar, forcing prior architectures to keep up or disappear. The Digital Equipment Vax could not, and so it was replaced by a RISC architecture. Intel rose to the challenge, primarily by translating 80x86 instructions into RISC-like instructions internally, allowing it to adopt many of the innovations first pioneered in the RISC designs. As transistor counts soared in the late 1990s, the hardware overhead of translating the more complex x86 architecture became negligible. In low-end applications, such as cell phones, the cost in power and silicon area of the x86-translation overhead helped lead to a RISC architecture, ARM, becoming dominant.

Figure 1.1 shows that the combination of architectural and organizational enhancements led to 17 years of sustained growth in performance at an annual rate of over 50%—a rate that is unprecedented in the computer industry.

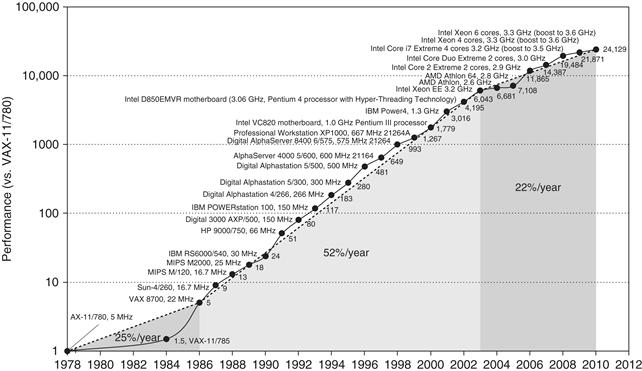
Figure 1.1 Growth in processor performance since the late 1970s. This chart plots performance relative to the VAX 11/780 as measured by the SPEC benchmarks (see Section 1.8). Prior to the mid-1980s, processor performance growth was largely technology driven and averaged about 25% per year. The increase in growth to about 52% since then is attributable to more advanced architectural and organizational ideas. By 2003, this growth led to a difference in performance of about a factor of 25 versus if we had continued at the 25% rate. Performance for floating-point-oriented calculations has increased even faster. Since 2003, the limits of power and available instruction-level parallelism have slowed uniprocessor performance, to no more than 22% per year, or about 5 times slower than had we continued at 52% per year. (The fastest SPEC performance since 2007 has had automatic parallelization turned on with increasing number of cores per chip each year, so uniprocessor speed is harder to gauge. These results are limited to single-socket systems to reduce the impact of automatic parallelization.) Figure 1.11 on page 24 shows the improvement in clock rates for these same three eras. Since SPEC has changed over the years, performance of newer machines is estimated by a scaling factor that relates the performance for two different versions of SPEC (e.g., SPEC89, SPEC92, SPEC95, SPEC2000, and SPEC2006).

The effect of this dramatic growth rate in the 20th century has been fourfold. First, it has significantly enhanced the capability available to computer users. For many applications, the highest-performance microprocessors of today outperform the supercomputer of less than 10 years ago.

Second, this dramatic improvement in cost-performance leads to new classes of computers. Personal computers and workstations emerged in the 1980s with the availability of the microprocessor. The last decade saw the rise of smart cell phones and tablet computers, which many people are using as their primary computing platforms instead of PCs. These mobile client devices are increasingly using the Internet to access warehouses containing tens of thousands of servers, which are being designed as if they were a single gigantic computer.

Third, continuing improvement of semiconductor manufacturing as predicted by Moore’s law has led to the dominance of microprocessor-based computers across the entire range of computer design. Minicomputers, which were traditionally made from off-the-shelf logic or from gate arrays, were replaced by servers made using microprocessors. Even mainframe computers and high-performance supercomputers are all collections of microprocessors.

The hardware innovations above led to a renaissance in computer design, which emphasized both architectural innovation and efficient use of technology improvements. This rate of growth has compounded so that by 2003, high-performance microprocessors were 7.5 times faster than what would have been obtained by relying solely on technology, including improved circuit design; that is, 52% per year versus 35% per year.

This hardware renaissance led to the fourth impact, which is on software development. This 25,000-fold performance improvement since 1978 (see Figure 1.1) allowed programmers today to trade performance for productivity. In place of performance-oriented languages like C and C++, much more programming today is done in managed programming languages like Java and C#. Moreover, scripting languages like Python and Ruby, which are even more productive, are gaining in popularity along with programming frameworks like Ruby on Rails. To maintain productivity and try to close the performance gap, interpreters with just-in-time compilers and trace-based compiling are replacing the traditional compiler and linker of the past. Software deployment is changing as well, with Software as a Service (SaaS) used over the Internet replacing shrink-wrapped software that must be installed and run on a local computer.

The nature of applications also changes. Speech, sound, images, and video are becoming increasingly important, along with predictable response time that is so critical to the user experience. An inspiring example is Google Goggles. This application lets you hold up your cell phone to point its camera at an object, and the image is sent wirelessly over the Internet to a warehouse-scale computer that recognizes the object and tells you interesting information about it. It might translate text on the object to another language; read the bar code on a book cover to tell you if a book is available online and its price; or, if you pan the phone camera, tell you what businesses are nearby along with their websites, phone numbers, and directions.

Alas, Figure 1.1 also shows that this 17-year hardware renaissance is over. Since 2003, single-processor performance improvement has dropped to less than 22% per year due to the twin hurdles of maximum power dissipation of air-cooled chips and the lack of more instruction-level parallelism to exploit efficiently. Indeed, in 2004 Intel canceled its high-performance uniprocessor projects and joined others in declaring that the road to higher performance would be via multiple processors per chip rather than via faster uniprocessors.

This milestone signals a historic switch from relying solely on instruction-level parallelism (ILP), the primary focus of the first three editions of this book, to data-level parallelism (DLP) and thread-level parallelism (TLP), which were featured in the fourth edition and expanded in this edition. This edition also adds warehouse-scale computers and request-level parallelism (RLP). Whereas the compiler and hardware conspire to exploit ILP implicitly without the programmer’s attention, DLP, TLP, and RLP are explicitly parallel, requiring the restructuring of the application so that it can exploit explicit parallelism. In some instances, this is easy; in many, it is a major new burden for programmers.

This text is about the architectural ideas and accompanying compiler improvements that made the incredible growth rate possible in the last century, the reasons for the dramatic change, and the challenges and initial promising approaches to architectural ideas, compilers, and interpreters for the 21st century. At the core is a quantitative approach to computer design and analysis that uses empirical observations of programs, experimentation, and simulation as its tools. It is this style and approach to computer design that is reflected in this text. The purpose of this chapter is to lay the quantitative foundation on which the following chapters and appendices are based.

This book was written not only to explain this design style but also to stimulate you to contribute to this progress. We believe this approach will work for explicitly parallel computers of the future just as it worked for the implicitly parallel computers of the past.

1.2 Classes of Computers

These changes have set the stage for a dramatic change in how we view computing, computing applications, and the computer markets in this new century. Not since the creation of the personal computer have we seen such dramatic changes in the way computers appear and in how they are used. These changes in computer use have led to five different computing markets, each characterized by different applications, requirements, and computing technologies. Figure 1.2 summarizes these mainstream classes of computing environments and their important characteristics.

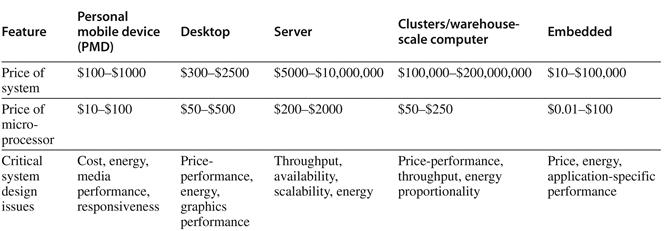
Figure 1.2 A summary of the five mainstream computing classes and their system characteristics. Sales in 2010 included about 1.8 billion PMDs (90% cell phones), 350 million desktop PCs, and 20 million servers. The total number of embedded processors sold was nearly 19 billion. In total, 6.1 billion ARM-technology based chips were shipped in 2010. Note the wide range in system price for servers and embedded systems, which go from USB keys to network routers. For servers, this range arises from the need for very large-scale multiprocessor systems for high-end transaction processing.

Personal Mobile Device (PMD)

Personal mobile device (PMD) is the term we apply to a collection of wireless devices with multimedia user interfaces such as cell phones, tablet computers, and so on. Cost is a prime concern given the consumer price for the whole product is a few hundred dollars. Although the emphasis on energy efficiency is frequently driven by the use of batteries, the need to use less expensive packaging—plastic versus ceramic—and the absence of a fan for cooling also limit total power consumption. We examine the issue of energy and power in more detail in Section 1.5. Applications on PMDs are often Web-based and media-oriented, like the Google Goggles example above. Energy and size requirements lead to use of Flash memory for storage (Chapter 2) instead of magnetic disks.

Responsiveness and predictability are key characteristics for media applications. A real-time performance requirement means a segment of the application has an absolute maximum execution time. For example, in playing a video on a PMD, the time to process each video frame is limited, since the processor must accept and process the next frame shortly. In some applications, a more nuanced requirement exists: the average time for a particular task is constrained as well as the number of instances when some maximum time is exceeded. Such approaches—sometimes called soft real-time—arise when it is possible to occasionally miss the time constraint on an event, as long as not too many are missed. Real-time performance tends to be highly application dependent.

Other key characteristics in many PMD applications are the need to minimize memory and the need to use energy efficiently. Energy efficiency is driven by both battery power and heat dissipation. The memory can be a substantial portion of the system cost, and it is important to optimize memory size in such cases. The importance of memory size translates to an emphasis on code size, since data size is dictated by the application.

Desktop Computing

The first, and probably still the largest market in dollar terms, is desktop computing. Desktop computing spans from low-end netbooks that sell for under $300 to high-end, heavily configured workstations that may sell for $2500. Since 2008, more than half of the desktop computers made each year have been battery operated laptop computers.

Throughout this range in price and capability, the desktop market tends to be driven to optimize price-performance. This combination of performance (measured primarily in terms of compute performance and graphics performance) and price of a system is what matters most to customers in this market, and hence to computer designers. As a result, the newest, highest-performance microprocessors and cost-reduced microprocessors often appear first in desktop systems (see Section 1.6 for a discussion of the issues affecting the cost of computers).

Desktop computing also tends to be reasonably well characterized in terms of applications and benchmarking, though the increasing use of Web-centric, interactive applications poses new challenges in performance evaluation.

Servers

As the shift to desktop computing occurred in the 1980s, the role of servers grew to provide larger-scale and more reliable file and computing services. Such servers have become the backbone of large-scale enterprise computing, replacing the traditional mainframe.

For servers, different characteristics are important. First, availability is critical. (We discuss availability in Section 1.7.) Consider the servers running ATM machines for banks or airline reservation systems. Failure of such server systems is far more catastrophic than failure of a single desktop, since these servers must operate seven days a week, 24 hours a day. Figure 1.3 estimates revenue costs of downtime for server applications.

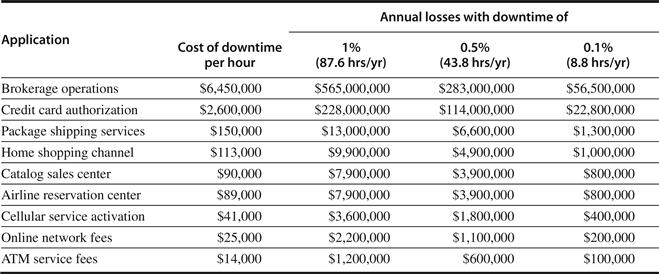
Figure 1.3 Costs rounded to nearest $100,000 of an unavailable system are shown by analyzing the cost of downtime (in terms of immediately lost revenue), assuming three different levels of availability and that downtime is distributed uniformly. These data are from Kembel [2000] and were collected and analyzed by Contingency Planning Research.

A second key feature of server systems is scalability. Server systems often grow in response to an increasing demand for the services they support or an increase in functional requirements. Thus, the ability to scale up the computing capacity, the memory, the storage, and the I/O bandwidth of a server is crucial.

Finally, servers are designed for efficient throughput. That is, the overall performance of the server—in terms of transactions per minute or Web pages served per second—is what is crucial. Responsiveness to an individual request remains important, but overall efficiency and cost-effectiveness, as determined by how many requests can be handled in a unit time, are the key metrics for most servers. We return to the issue of assessing performance for different types of computing environments in Section 1.8.

Clusters/Warehouse-Scale Computers

The growth of Software as a Service (SaaS) for applications like search, social networking, video sharing, multiplayer games, online shopping, and so on has led to the growth of a class of computers called clusters. Clusters are collections of desktop computers or servers connected by local area networks to act as a single larger computer. Each node runs its own operating system, and nodes communicate using a networking protocol. The largest of the clusters are called warehouse-scale computers (WSCs), in that they are designed so that tens of thousands of servers can act as one. Chapter 6 describes this class of the extremely large computers.

Price-performance and power are critical to WSCs since they are so large. As Chapter 6 explains, 80% of the cost of a $90M warehouse is associated with power and cooling of the computers inside. The computers themselves and networking gear cost another $70M and they must be replaced every few years. When you are buying that much computing, you need to buy wisely, as a 10% improvement in price-performance means a savings of $7M (10% of $70M).

WSCs are related to servers, in that availability is critical. For example, Amazon.com had $13 billion in sales in the fourth quarter of 2010. As there are about 2200 hours in a quarter, the average revenue per hour was almost $6M. During a peak hour for Christmas shopping, the potential loss would be many times higher. As Chapter 6 explains, the difference from servers is that WSCs use redundant inexpensive components as the building blocks, relying on a software layer to catch and isolate the many failures that will happen with computing at this scale. Note that scalability for a WSC is handled by the local area network connecting the computers and not by integrated computer hardware, as in the case of servers.

Supercomputers are related to WSCs in that they are equally expensive, costing hundreds of millions of dollars, but supercomputers differ by emphasizing floating-point performance and by running large, communication-intensive batch programs that can run for weeks at a time. This tight coupling leads to use of much faster internal networks. In contrast, WSCs emphasize interactive applications, large-scale storage, dependability, and high Internet bandwidth.

Embedded Computers

Embedded computers are found in everyday machines; microwaves, washing machines, most printers, most networking switches, and all cars contain simple embedded microprocessors.

The processors in a PMD are often considered embedded computers, but we are keeping them as a separate category because PMDs are platforms that can run externally developed software and they share many of the characteristics of desktop computers. Other embedded devices are more limited in hardware and software sophistication. We use the ability to run third-party software as the dividing line between non-embedded and embedded computers.

Embedded computers have the widest spread of processing power and cost. They include 8-bit and 16-bit processors that may cost less than a dime, 32-bit microprocessors that execute 100 million instructions per second and cost under $5, and high-end processors for network switches that cost $100 and can execute billions of instructions per second. Although the range of computing power in the embedded computing market is very large, price is a key factor in the design of computers for this space. Performance requirements do exist, of course, but the primary goal is often meeting the performance need at a minimum price, rather than achieving higher performance at a higher price.

Most of this book applies to the design, use, and performance of embedded processors, whether they are off-the-shelf microprocessors or microprocessor cores that will be assembled with other special-purpose hardware. Indeed, the third edition of this book included examples from embedded computing to illustrate the ideas in every chapter.

Alas, most readers found these examples unsatisfactory, as the data that drive the quantitative design and evaluation of other classes of computers have not yet been extended well to embedded computing (see the challenges with EEMBC, for example, in Section 1.8). Hence, we are left for now with qualitative descriptions, which do not fit well with the rest of the book. As a result, in this and the prior edition we consolidated the embedded material into Appendix E. We believe a separate appendix improves the flow of ideas in the text while allowing readers to see how the differing requirements affect embedded computing.

Classes of Parallelism and Parallel Architectures

Parallelism at multiple levels is now the driving force of computer design across all four classes of computers, with energy and cost being the primary constraints. There are basically two kinds of parallelism in applications:

1. Data-Level Parallelism (DLP) arises because there are many data items that can be operated on at the same time.

2. Task-Level Parallelism (TLP) arises because tasks of work are created that can operate independently and largely in parallel.

Computer hardware in turn can exploit these two kinds of application parallelism in four major ways:

1. Instruction-Level Parallelism exploits data-level parallelism at modest levels with compiler help using ideas like pipelining and at medium levels using ideas like speculative execution.

2. Vector Architectures and Graphic Processor Units (GPUs) exploit data-level parallelism by applying a single instruction to a collection of data in parallel.

3. Thread-Level Parallelism exploits either data-level parallelism or task-level parallelism in a tightly coupled hardware model that allows for interaction among parallel threads.

4. Request-Level Parallelism exploits parallelism among largely decoupled tasks specified by the programmer or the operating system.

These four ways for hardware to support the data-level parallelism and task-level parallelism go back 50 years. When Michael Flynn [1966] studied the parallel computing efforts in the 1960s, he found a simple classification whose abbreviations we still use today. He looked at the parallelism in the instruction and data streams called for by the instructions at the most constrained component of the multiprocessor, and placed all computers into one of four categories:

1. Single instruction stream, single data stream (SISD)—This category is the uniprocessor. The programmer thinks of it as the standard sequential computer, but it can exploit instruction-level parallelism. Chapter 3 covers SISD architectures that use ILP techniques such as superscalar and speculative execution.

2. Single instruction stream, multiple data streams (SIMD)—The same instruction is executed by multiple processors using different data streams. SIMD computers exploit data-level parallelism by applying the same operations to multiple items of data in parallel. Each processor has its own data memory (hence the MD of SIMD), but there is a single instruction memory and control processor, which fetches and dispatches instructions. Chapter 4 covers DLP and three different architectures that exploit it: vector architectures, multimedia extensions to standard instruction sets, and GPUs.

3. Multiple instruction streams, single data stream (MISD)—No commercial multiprocessor of this type has been built to date, but it rounds out this simple classification.

4. Multiple instruction streams, multiple data streams (MIMD)—Each processor fetches its own instructions and operates on its own data, and it targets task-level parallelism. In general, MIMD is more flexible than SIMD and thus more generally applicable, but it is inherently more expensive than SIMD. For example, MIMD computers can also exploit data-level parallelism, although the overhead is likely to be higher than would be seen in an SIMD computer. This overhead means that grain size must be sufficiently large to exploit the parallelism efficiently. Chapter 5 covers tightly coupled MIMD architectures, which exploit thread-level parallelism since multiple cooperating threads operate in parallel. Chapter 6 covers loosely coupled MIMD architectures—specifically, clusters and warehouse-scale computers—that exploit request-level parallelism, where many independent tasks can proceed in parallel naturally with little need for communication or synchronization.

This taxonomy is a coarse model, as many parallel processors are hybrids of the SISD, SIMD, and MIMD classes. Nonetheless, it is useful to put a framework on the design space for the computers we will see in this book.

1.3 Defining Computer Architecture

The task the computer designer faces is a complex one: Determine what attributes are important for a new computer, then design a computer to maximize performance and energy efficiency while staying within cost, power, and availability constraints. This task has many aspects, including instruction set design, functional organization, logic design, and implementation. The implementation may encompass integrated circuit design, packaging, power, and cooling. Optimizing the design requires familiarity with a very wide range of technologies, from compilers and operating systems to logic design and packaging.

Several years ago, the term computer architecture often referred only to instruction set design. Other aspects of computer design were called implementation, often insinuating that implementation is uninteresting or less challenging.

We believe this view is incorrect. The architect’s or designer’s job is much more than instruction set design, and the technical hurdles in the other aspects of the project are likely more challenging than those encountered in instruction set design. We’ll quickly review instruction set architecture before describing the larger challenges for the computer architect.

Instruction Set Architecture: The Myopic View of Computer Architecture

We use the term instruction set architecture (ISA) to refer to the actual programmer-visible instruction set in this book. The ISA serves as the boundary between the software and hardware. This quick review of ISA will use examples from 80x86, ARM, and MIPS to illustrate the seven dimensions of an ISA. Appendices A and K give more details on the three ISAs.

1. Class of ISA—Nearly all ISAs today are classified as general-purpose register architectures, where the operands are either registers or memory locations. The 80x86 has 16 general-purpose registers and 16 that can hold floating-point data, while MIPS has 32 general-purpose and 32 floating-point registers (see Figure 1.4). The two popular versions of this class are register-memory ISAs, such as the 80x86, which can access memory as part of many instructions, and load-store ISAs, such as ARM and MIPS, which can access memory only with load or store instructions. All recent ISAs are load-store.

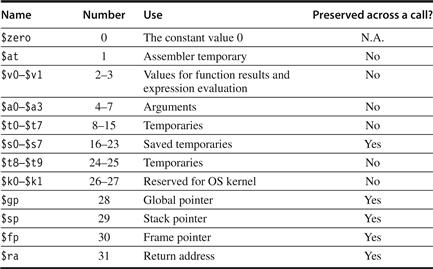
Figure 1.4 MIPS registers and usage conventions. In addition to the 32 general-purpose registers (R0–R31), MIPS has 32 floating-point registers (F0–F31) that can hold either a 32-bit single-precision number or a 64-bit double-precision number.

2. Memory addressing—Virtually all desktop and server computers, including the 80x86, ARM, and MIPS, use byte addressing to access memory operands. Some architectures, like ARM and MIPS, require that objects must be aligned. An access to an object of size s bytes at byte address A is aligned if A mod s = 0. (See Figure A.5 on page A-8.) The 80x86 does not require alignment, but accesses are generally faster if operands are aligned.

3. Addressing modes—In addition to specifying registers and constant operands, addressing modes specify the address of a memory object. MIPS addressing modes are Register, Immediate (for constants), and Displacement, where a constant offset is added to a register to form the memory address. The 80x86 supports those three plus three variations of displacement: no register (absolute), two registers (based indexed with displacement), and two registers where one register is multiplied by the size of the operand in bytes (based with scaled index and displacement). It has more like the last three, minus the displacement field, plus register indirect, indexed, and based with scaled index. ARM has the three MIPS addressing modes plus PC-relative addressing, the sum of two registers, and the sum of two registers where one register is multiplied by the size of the operand in bytes. It also has autoincrement and autodecrement addressing, where the calculated address replaces the contents of one of the registers used in forming the address.

4. Types and sizes of operands—Like most ISAs, 80x86, ARM, and MIPS support operand sizes of 8-bit (ASCII character), 16-bit (Unicode character or half word), 32-bit (integer or word), 64-bit (double word or long integer), and IEEE 754 floating point in 32-bit (single precision) and 64-bit (double precision). The 80x86 also supports 80-bit floating point (extended double precision).

5. Operations—The general categories of operations are data transfer, arithmetic logical, control (discussed next), and floating point. MIPS is a simple and easy-to-pipeline instruction set architecture, and it is representative of the RISC architectures being used in 2011. Figure 1.5 summarizes the MIPS ISA. The 80x86 has a much richer and larger set of operations (see Appendix K).

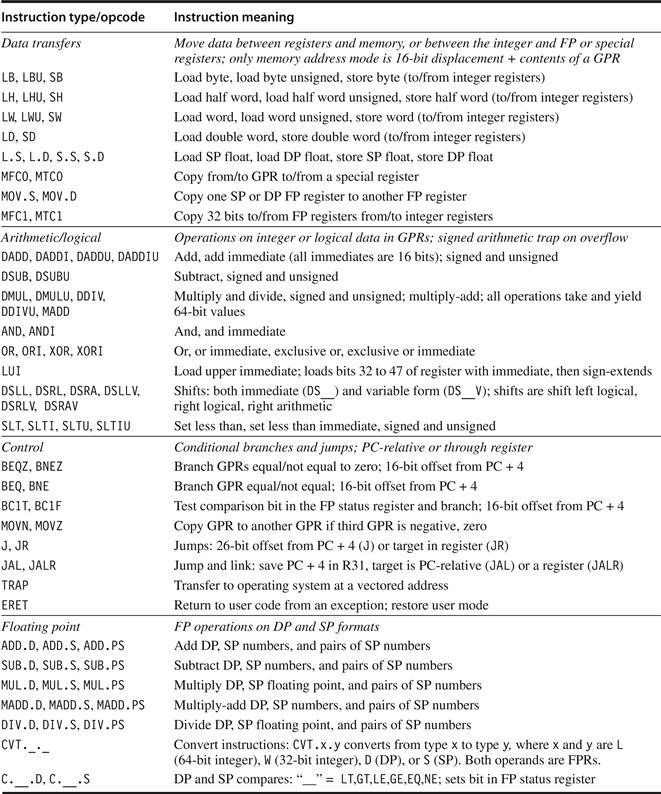
Figure 1.5 Subset of the instructions in MIPS64. SP = single precision; DP = double precision. Appendix A gives much more detail on MIPS64. For data, the most significant bit number is 0; least is 63.

6. Control flow instructions—Virtually all ISAs, including these three, support conditional branches, unconditional jumps, procedure calls, and returns. All three use PC-relative addressing, where the branch address is specified by an address field that is added to the PC. There are some small differences. MIPS conditional branches (BE, BNE, etc.) test the contents of registers, while the 80x86 and ARM branches test condition code bits set as side effects of arithmetic/logic operations. The ARM and MIPS procedure call places the return address in a register, while the 80x86 call (CALLF) places the return address on a stack in memory.

7. Encoding an ISA—There are two basic choices on encoding: fixed length and variable length. All ARM and MIPS instructions are 32 bits long, which simplifies instruction decoding. Figure 1.6 shows the MIPS instruction formats. The 80x86 encoding is variable length, ranging from 1 to 18 bytes. Variable-length instructions can take less space than fixed-length instructions, so a program compiled for the 80x86 is usually smaller than the same program compiled for MIPS. Note that choices mentioned above will affect how the instructions are encoded into a binary representation. For example, the number of registers and the number of addressing modes both have a significant impact on the size of instructions, as the register field and addressing mode field can appear many times in a single instruction. (Note that ARM and MIPS later offered extensions to offer 16-bit length instructions so as to reduce program size, called Thumb or Thumb-2 and MIPS16, respectively.)

Figure 1.6 MIPS64 instruction set architecture formats. All instructions are 32 bits long. The R format is for integer register-to-register operations, such as DADDU, DSUBU, and so on. The I format is for data transfers, branches, and immediate instructions, such as LD, SD, BEQZ, and DADDIs. The J format is for jumps, the FR format for floating-point operations, and the FI format for floating-point branches.

The other challenges facing the computer architect beyond ISA design are particularly acute at the present, when the differences among instruction sets are small and when there are distinct application areas. Therefore, starting with the last edition, the bulk of instruction set material beyond this quick review is found in the appendices (see Appendices A and K).

We use a subset of MIPS64 as the example ISA in this book because it is both the dominant ISA for networking and it is an elegant example of the RISC architectures mentioned earlier, of which ARM (Advanced RISC Machine) is the most popular example. ARM processors were in 6.1 billion chips shipped in 2010, or roughly 20 times as many chips that shipped with 80x86 processors.

Genuine Computer Architecture: Designing the Organization and Hardware to Meet Goals and Functional Requirements

The implementation of a computer has two components: organization and hardware. The term organization includes the high-level aspects of a computer’s design, such as the memory system, the memory interconnect, and the design of the internal processor or CPU (central processing unit—where arithmetic, logic, branching, and data transfer are implemented). The term microarchitecture is also used instead of organization. For example, two processors with the same instruction set architectures but different organizations are the AMD Opteron and the Intel Core i7. Both processors implement the x86 instruction set, but they have very different pipeline and cache organizations.

The switch to multiple processors per microprocessor led to the term core to also be used for processor. Instead of saying multiprocessor microprocessor, the term multicore has caught on. Given that virtually all chips have multiple processors, the term central processing unit, or CPU, is fading in popularity.

Hardware refers to the specifics of a computer, including the detailed logic design and the packaging technology of the computer. Often a line of computers contains computers with identical instruction set architectures and nearly identical organizations, but they differ in the detailed hardware implementation. For example, the Intel Core i7 (see Chapter 3) and the Intel Xeon 7560 (see Chapter 5) are nearly identical but offer different clock rates and different memory systems, making the Xeon 7560 more effective for server computers.

In this book, the word architecture covers all three aspects of computer design—instruction set architecture, organization or microarchitecture, and hardware.

Computer architects must design a computer to meet functional requirements as well as price, power, performance, and availability goals. Figure 1.7 summarizes requirements to consider in designing a new computer. Often, architects also must determine what the functional requirements are, which can be a major task. The requirements may be specific features inspired by the market. Application software often drives the choice of certain functional requirements by determining how the computer will be used. If a large body of software exists for a certain instruction set architecture, the architect may decide that a new computer should implement an existing instruction set. The presence of a large market for a particular class of applications might encourage the designers to incorporate requirements that would make the computer competitive in that market. Later chapters examine many of these requirements and features in depth.

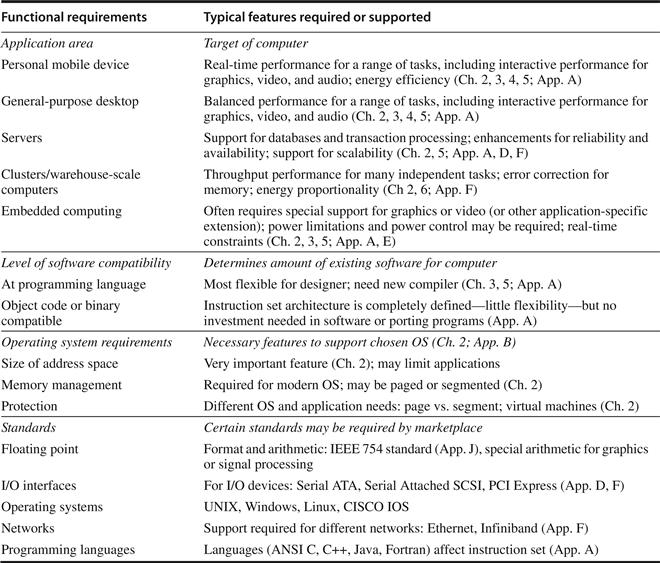
Figure 1.7 Summary of some of the most important functional requirements an architect faces. The left-hand column describes the class of requirement, while the right-hand column gives specific examples. The right-hand column also contains references to chapters and appendices that deal with the specific issues.

Architects must also be aware of important trends in both the technology and the use of computers, as such trends affect not only the future cost but also the longevity of an architecture.

1.4 Trends in Technology

If an instruction set architecture is to be successful, it must be designed to survive rapid changes in computer technology. After all, a successful new instruction set architecture may last decades—for example, the core of the IBM mainframe has been in use for nearly 50 years. An architect must plan for technology changes that can increase the lifetime of a successful computer.

To plan for the evolution of a computer, the designer must be aware of rapid changes in implementation technology. Five implementation technologies, which change at a dramatic pace, are critical to modern implementations:

■ Integrated circuit logic technology—Transistor density increases by about 35% per year, quadrupling somewhat over four years. Increases in die size are less predictable and slower, ranging from 10% to 20% per year. The combined effect is a growth rate in transistor count on a chip of about 40% to 55% per year, or doubling every 18 to 24 months. This trend is popularly known as Moore’s law. Device speed scales more slowly, as we discuss below.

■ Semiconductor DRAM (dynamic random-access memory)—Now that most DRAM chips are primarily shipped in DIMM modules, it is harder to track chip capacity, as DRAM manufacturers typically offer several capacity products at the same time to match DIMM capacity. Capacity per DRAM chip has increased by about 25% to 40% per year recently, doubling roughly every two to three years. This technology is the foundation of main memory, and we discuss it in Chapter 2. Note that the rate of improvement has continued to slow over the editions of this book, as Figure 1.8 shows. There is even concern as whether the growth rate will stop in the middle of this decade due to the increasing difficulty of efficiently manufacturing even smaller DRAM cells [Kim 2005]. Chapter 2 mentions several other technologies that may replace DRAM if it hits a capacity wall.

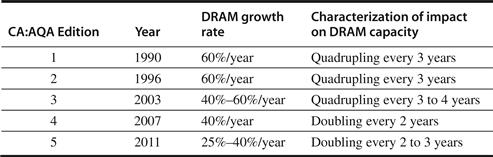
Figure 1.8 Change in rate of improvement in DRAM capacity over time. The first two editions even called this rate the DRAM Growth Rule of Thumb, since it had been so dependable since 1977 with the 16-kilobit DRAM through 1996 with the 64-megabit DRAM. Today, some question whether DRAM capacity can improve at all in 5 to 7 years, due to difficulties in manufacturing an increasingly three-dimensional DRAM cell [Kim 2005].

■ Semiconductor Flash (electrically erasable programmable read-only memory)—This nonvolatile semiconductor memory is the standard storage device in PMDs, and its rapidly increasing popularity has fueled its rapid growth rate in capacity. Capacity per Flash chip has increased by about 50% to 60% per year recently, doubling roughly every two years. In 2011, Flash memory is 15 to 20 times cheaper per bit than DRAM. Chapter 2 describes Flash memory.

■ Magnetic disk technology—Prior to 1990, density increased by about 30% per year, doubling in three years. It rose to 60% per year thereafter, and increased to 100% per year in 1996. Since 2004, it has dropped back to about 40% per year, or doubled every three years. Disks are 15 to 25 times cheaper per bit than Flash. Given the slowed growth rate of DRAM, disks are now 300 to 500 times cheaper per bit than DRAM. This technology is central to server and warehouse scale storage, and we discuss the trends in detail in Appendix D.

■ Network technology—Network performance depends both on the performance of switches and on the performance of the transmission system. We discuss the trends in networking in Appendix F.

These rapidly changing technologies shape the design of a computer that, with speed and technology enhancements, may have a lifetime of three to five years. Key technologies such as DRAM, Flash, and disk change sufficiently that the designer must plan for these changes. Indeed, designers often design for the next technology, knowing that when a product begins shipping in volume that the next technology may be the most cost-effective or may have performance advantages. Traditionally, cost has decreased at about the rate at which density increases.

Although technology improves continuously, the impact of these improvements can be in discrete leaps, as a threshold that allows a new capability is reached. For example, when MOS technology reached a point in the early 1980s where between 25,000 and 50,000 transistors could fit on a single chip, it became possible to build a single-chip, 32-bit microprocessor. By the late 1980s, first-level caches could go on a chip. By eliminating chip crossings within the processor and between the processor and the cache, a dramatic improvement in cost-performance and energy-performance was possible. This design was simply infeasible until the technology reached a certain point. With multicore microprocessors and increasing numbers of cores each generation, even server computers are increasingly headed toward a single chip for all processors. Such technology thresholds are not rare and have a significant impact on a wide variety of design decisions.

Performance Trends: Bandwidth over Latency

As we shall see in Section 1.8, bandwidth or throughput is the total amount of work done in a given time, such as megabytes per second for a disk transfer. In contrast, latency or response time is the time between the start and the completion of an event, such as milliseconds for a disk access. Figure 1.9 plots the relative improvement in bandwidth and latency for technology milestones for microprocessors, memory, networks, and disks. Figure 1.10 describes the examples and milestones in more detail.

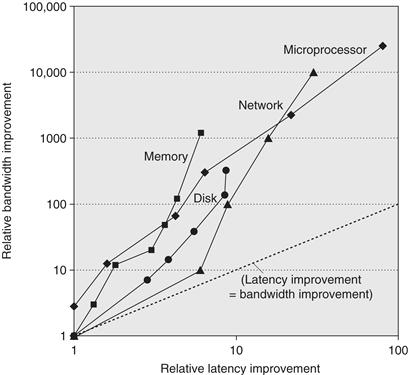
Figure 1.9 Log–log plot of bandwidth and latency milestones from Figure 1.10 relative to the first milestone. Note that latency improved 6X to 80X while bandwidth improved about 300X to 25,000X. Updated from Patterson [2004].

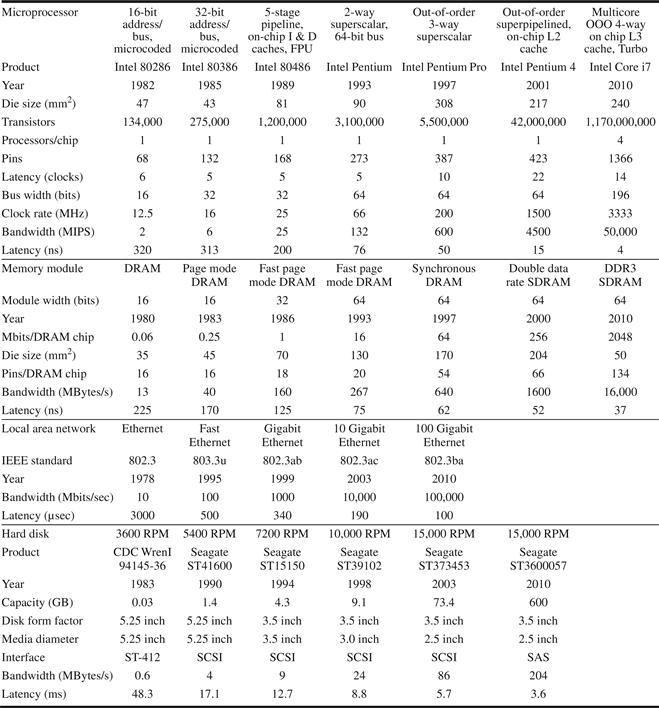
Figure 1.10 Performance milestones over 25 to 40 years for microprocessors, memory, networks, and disks. The microprocessor milestones are several generations of IA-32 processors, going from a 16-bit bus, microcoded 80286 to a 64-bit bus, multicore, out-of-order execution, superpipelined Core i7. Memory module milestones go from 16-bit-wide, plain DRAM to 64-bit-wide double data rate version 3 synchronous DRAM. Ethernet advanced from 10 Mbits/sec to 100 Gbits/sec. Disk milestones are based on rotation speed, improving from 3600 RPM to 15,000 RPM. Each case is best-case bandwidth, and latency is the time for a simple operation assuming no contention. Updated from Patterson [2004].

Performance is the primary differentiator for microprocessors and networks, so they have seen the greatest gains: 10,000–25,000X in bandwidth and 30–80X in latency. Capacity is generally more important than performance for memory and disks, so capacity has improved most, yet bandwidth advances of 300–1200X are still much greater than gains in latency of 6–8X.

Clearly, bandwidth has outpaced latency across these technologies and will likely continue to do so. A simple rule of thumb is that bandwidth grows by at least the square of the improvement in latency. Computer designers should plan accordingly.

Scaling of Transistor Performance and Wires

Integrated circuit processes are characterized by the feature size, which is the minimum size of a transistor or a wire in either the x or y dimension. Feature sizes have decreased from 10 microns in 1971 to 0.032 microns in 2011; in fact, we have switched units, so production in 2011 is referred to as “32 nanometers,” and 22 nanometer chips are under way. Since the transistor count per square millimeter of silicon is determined by the surface area of a transistor, the density of transistors increases quadratically with a linear decrease in feature size.

The increase in transistor performance, however, is more complex. As feature sizes shrink, devices shrink quadratically in the horizontal dimension and also shrink in the vertical dimension. The shrink in the vertical dimension requires a reduction in operating voltage to maintain correct operation and reliability of the transistors. This combination of scaling factors leads to a complex interrelationship between transistor performance and process feature size. To a first approximation, transistor performance improves linearly with decreasing feature size.

The fact that transistor count improves quadratically with a linear improvement in transistor performance is both the challenge and the opportunity for which computer architects were created! In the early days of microprocessors, the higher rate of improvement in density was used to move quickly from 4-bit, to 8-bit, to 16-bit, to 32-bit, to 64-bit microprocessors. More recently, density improvements have supported the introduction of multiple processors per chip, wider SIMD units, and many of the innovations in speculative execution and caches found in Chapters 2, 3, 4, and 5.

Although transistors generally improve in performance with decreased feature size, wires in an integrated circuit do not. In particular, the signal delay for a wire increases in proportion to the product of its resistance and capacitance. Of course, as feature size shrinks, wires get shorter, but the resistance and capacitance per unit length get worse. This relationship is complex, since both resistance and capacitance depend on detailed aspects of the process, the geometry of a wire, the loading on a wire, and even the adjacency to other structures. There are occasional process enhancements, such as the introduction of copper, which provide one-time improvements in wire delay.

In general, however, wire delay scales poorly compared to transistor performance, creating additional challenges for the designer. In the past few years, in addition to the power dissipation limit, wire delay has become a major design limitation for large integrated circuits and is often more critical than transistor switching delay. Larger and larger fractions of the clock cycle have been consumed by the propagation delay of signals on wires, but power now plays an even greater role than wire delay.

1.5 Trends in Power and Energy in Integrated Circuits

Today, power is the biggest challenge facing the computer designer for nearly every class of computer. First, power must be brought in and distributed around the chip, and modern microprocessors use hundreds of pins and multiple interconnect layers just for power and ground. Second, power is dissipated as heat and must be removed.

Power and Energy: A Systems Perspective

How should a system architect or a user think about performance, power, and energy? From the viewpoint of a system designer, there are three primary concerns.

First, what is the maximum power a processor ever requires? Meeting this demand can be important to ensuring correct operation. For example, if a processor attempts to draw more power than a power supply system can provide (by drawing more current than the system can supply), the result is typically a voltage drop, which can cause the device to malfunction. Modern processors can vary widely in power consumption with high peak currents; hence, they provide voltage indexing methods that allow the processor to slow down and regulate voltage within a wider margin. Obviously, doing so decreases performance.

Second, what is the sustained power consumption? This metric is widely called the thermal design power (TDP), since it determines the cooling requirement. TDP is neither peak power, which is often 1.5 times higher, nor is it the actual average power that will be consumed during a given computation, which is likely to be lower still. A typical power supply for a system is usually sized to exceed the TDP, and a cooling system is usually designed to match or exceed TDP. Failure to provide adequate cooling will allow the junction temperature in the processor to exceed its maximum value, resulting in device failure and possibly permanent damage. Modern processors provide two features to assist in managing heat, since the maximum power (and hence heat and temperature rise) can exceed the long-term average specified by the TDP. First, as the thermal temperature approaches the junction temperature limit, circuitry reduces the clock rate, thereby reducing power. Should this technique not be successful, a second thermal overload trip is activated to power down the chip.

The third factor that designers and users need to consider is energy and energy efficiency. Recall that power is simply energy per unit time: 1 watt = 1 joule per second. Which metric is the right one for comparing processors: energy or power? In general, energy is always a better metric because it is tied to a specific task and the time required for that task. In particular, the energy to execute a workload is equal to the average power times the execution time for the workload.

Thus, if we want to know which of two processors is more efficient for a given task, we should compare energy consumption (not power) for executing the task. For example, processor A may have a 20% higher average power consumption than processor B, but if A executes the task in only 70% of the time needed by B, its energy consumption will be 1.2 × 0.7 = 0.84, which is clearly better.

One might argue that in a large server or cloud, it is sufficient to consider average power, since the workload is often assumed to be infinite, but this is misleading. If our cloud were populated with processor Bs rather than As, then the cloud would do less work for the same amount of energy expended. Using energy to compare the alternatives avoids this pitfall. Whenever we have a fixed workload, whether for a warehouse-size cloud or a smartphone, comparing energy will be the right way to compare processor alternatives, as the electricity bill for the cloud and the battery lifetime for the smartphone are both determined by the energy consumed.

When is power consumption a useful measure? The primary legitimate use is as a constraint: for example, a chip might be limited to 100 watts. It can be used as a metric if the workload is fixed, but then it’s just a variation of the true metric of energy per task.

Energy and Power within a Microprocessor

For CMOS chips, the traditional primary energy consumption has been in switching transistors, also called dynamic energy. The energy required per transistor is proportional to the product of the capacitive load driven by the transistor and the square of the voltage:

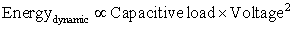
This equation is the energy of pulse of the logic transition of 0→1→0 or 1→0→1. The energy of a single transition (0→1 or 1→0) is then:

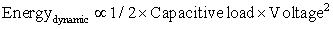
The power required per transistor is just the product of the energy of a transition multiplied by the frequency of transitions:

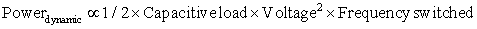
For a fixed task, slowing clock rate reduces power, but not energy.

Clearly, dynamic power and energy are greatly reduced by lowering the voltage, so voltages have dropped from 5V to just under 1V in 20 years. The capacitive load is a function of the number of transistors connected to an output and the technology, which determines the capacitance of the wires and the transistors.

Example

Some microprocessors today are designed to have adjustable voltage, so a 15% reduction in voltage may result in a 15% reduction in frequency. What would be the impact on dynamic energy and on dynamic power?

Answer

Since the capacitance is unchanged, the answer for energy is the ratio of the voltages since the capacitance is unchanged:

thereby reducing energy to about 72% of the original. For power, we add the ratio of the frequencies

shrinking power to about 61% of the original.

As we move from one process to the next, the increase in the number of transistors switching and the frequency with which they switch dominate the decrease in load capacitance and voltage, leading to an overall growth in power consumption and energy. The first microprocessors consumed less than a watt and the first 32-bit microprocessors (like the Intel 80386) used about 2 watts, while a 3.3 GHz Intel Core i7 consumes 130 watts. Given that this heat must be dissipated from a chip that is about 1.5 cm on a side, we have reached the limit of what can be cooled by air.

Given the equation above, you would expect clock frequency growth to slow down if we can’t reduce voltage or increase power per chip. Figure 1.11 shows that this has indeed been the case since 2003, even for the microprocessors in Figure 1.1 that were the highest performers each year. Note that this period of flat clock rates corresponds to the period of slow performance improvement range in Figure 1.1.

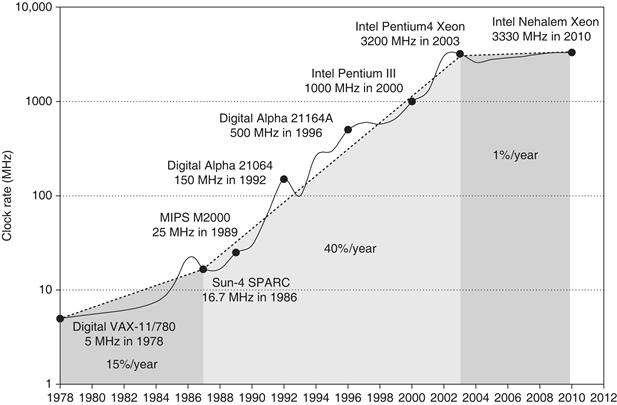
Figure 1.11 Growth in clock rate of microprocessors in Figure 1.1. Between 1978 and 1986, the clock rate improved less than 15% per year while performance improved by 25% per year. During the “renaissance period” of 52% performance improvement per year between 1986 and 2003, clock rates shot up almost 40% per year. Since then, the clock rate has been nearly flat, growing at less than 1% per year, while single processor performance improved at less than 22% per year.

Distributing the power, removing the heat, and preventing hot spots have become increasingly difficult challenges. Power is now the major constraint to using transistors; in the past, it was raw silicon area. Hence, modern microprocessors offer many techniques to try to improve energy efficiency despite flat clock rates and constant supply voltages:

1. Do nothing well. Most microprocessors today turn off the clock of inactive modules to save energy and dynamic power. For example, if no floating-point instructions are executing, the clock of the floating-point unit is disabled. If some cores are idle, their clocks are stopped.

2. Dynamic Voltage-Frequency Scaling (DVFS). The second technique comes directly from the formulas above. Personal mobile devices, laptops, and even servers have periods of low activity where there is no need to operate at the highest clock frequency and voltages. Modern microprocessors typically offer a few clock frequencies and voltages in which to operate that use lower power and energy. Figure 1.12 plots the potential power savings via DVFS for a server as the workload shrinks for three different clock rates: 2.4 GHz, 1.8 GHz, and 1 GHz. The overall server power savings is about 10% to 15% for each of the two steps.

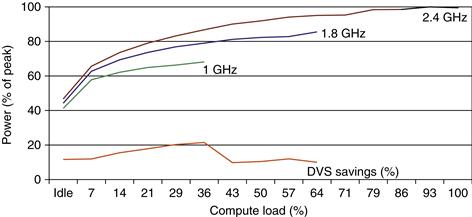
Figure 1.12 Energy savings for a server using an AMD Opteron microprocessor, 8 GB of DRAM, and one ATA disk. At 1.8 GHz, the server can only handle up to two-thirds of the workload without causing service level violations, and, at 1.0 GHz, it can only safely handle one-third of the workload. (Figure 5.11 in Barroso and Hölzle [2009].)

3. Design for typical case. Given that PMDs and laptops are often idle, memory and storage offer low power modes to save energy. For example, DRAMs have a series of increasingly lower power modes to extend battery life in PMDs and laptops, and there have been proposals for disks that have a mode that spins at lower rates when idle to save power. Alas, you cannot access DRAMs or disks in these modes, so you must return to fully active mode to read or write, no matter how low the access rate. As mentioned above, microprocessors for PCs have been designed instead for a more typical case of heavy use at high operating temperatures, relying on on-chip temperature sensors to detect when activity should be reduced automatically to avoid overheating. This “emergency slowdown” allows manufacturers to design for a more typical case and then rely on this safety mechanism if someone really does run programs that consume much more power than is typical.

4. Overclocking. Intel started offering Turbo mode in 2008, where the chip decides that it is safe to run at a higher clock rate for a short time possibly on just a few cores until temperature starts to rise. For example, the 3.3 GHz Core i7 can run in short bursts for 3.6 GHz. Indeed, the highest-performing microprocessors each year since 2008 in Figure 1.1 have all offered temporary overclocking of about 10% over the nominal clock rate. For single threaded code, these microprocessors can turn off all cores but one and run it at an even higher clock rate. Note that while the operating system can turn off Turbo mode there is no notification once it is enabled, so the programmers may be surprised to see their programs vary in performance due to room temperature!

Although dynamic power is traditionally thought of as the primary source of power dissipation in CMOS, static power is becoming an important issue because leakage current flows even when a transistor is off:

That is, static power is proportional to number of devices.

Thus, increasing the number of transistors increases power even if they are idle, and leakage current increases in processors with smaller transistor sizes. As a result, very low power systems are even turning off the power supply (power gating) to inactive modules to control loss due to leakage. In 2011, the goal for leakage is 25% of the total power consumption, with leakage in high-performance designs sometimes far exceeding that goal. Leakage can be as high as 50% for such chips, in part because of the large SRAM caches that need power to maintain the storage values. (The S in SRAM is for static.) The only hope to stop leakage is to turn off power to subsets of the chips.

Finally, because the processor is just a portion of the whole energy cost of a system, it can make sense to use a faster, less energy-efficient processor to allow the rest of the system to go into a sleep mode. This strategy is known as race-to-halt.

The importance of power and energy has increased the scrutiny on the efficiency of an innovation, so the primary evaluation now is tasks per joule or performance per watt as opposed to performance per mm² of silicon. This new metric affects approaches to parallelism, as we shall see in Chapters 4 and 5.

1.6 Trends in Cost

Although costs tend to be less important in some computer designs—specifically supercomputers—cost-sensitive designs are of growing significance. Indeed, in the past 30 years, the use of technology improvements to lower cost, as well as increase performance, has been a major theme in the computer industry.

Textbooks often ignore the cost half of cost-performance because costs change, thereby dating books, and because the issues are subtle and differ across industry segments. Yet, an understanding of cost and its factors is essential for computer architects to make intelligent decisions about whether or not a new feature should be included in designs where cost is an issue. (Imagine architects designing skyscrapers without any information on costs of steel beams and concrete!)

This section discusses the major factors that influence the cost of a computer and how these factors are changing over time.

The Impact of Time, Volume, and Commoditization

The cost of a manufactured computer component decreases over time even without major improvements in the basic implementation technology. The underlying principle that drives costs down is the learning curve—manufacturing costs decrease over time. The learning curve itself is best measured by change in yield—the percentage of manufactured devices that survives the testing procedure. Whether it is a chip, a board, or a system, designs that have twice the yield will have half the cost.

Understanding how the learning curve improves yield is critical to projecting costs over a product’s life. One example is that the price per megabyte of DRAM has dropped over the long term. Since DRAMs tend to be priced in close relationship to cost—with the exception of periods when there is a shortage or an oversupply—price and cost of DRAM track closely.

Microprocessor prices also drop over time, but, because they are less standardized than DRAMs, the relationship between price and cost is more complex. In a period of significant competition, price tends to track cost closely, although microprocessor vendors probably rarely sell at a loss.

Volume is a second key factor in determining cost. Increasing volumes affect cost in several ways. First, they decrease the time needed to get down the learning curve, which is partly proportional to the number of systems (or chips) manufactured. Second, volume decreases cost, since it increases purchasing and manufacturing efficiency. As a rule of thumb, some designers have estimated that cost decreases about 10% for each doubling of volume. Moreover, volume decreases the amount of development cost that must be amortized by each computer, thus allowing cost and selling price to be closer.

Commodities are products that are sold by multiple vendors in large volumes and are essentially identical. Virtually all the products sold on the shelves of grocery stores are commodities, as are standard DRAMs, Flash memory, disks, monitors, and keyboards. In the past 25 years, much of the personal computer industry has become a commodity business focused on building desktop and laptop computers running Microsoft Windows.

Because many vendors ship virtually identical products, the market is highly competitive. Of course, this competition decreases the gap between cost and selling price, but it also decreases cost. Reductions occur because a commodity market has both volume and a clear product definition, which allows multiple suppliers to compete in building components for the commodity product. As a result, the overall product cost is lower because of the competition among the suppliers of the components and the volume efficiencies the suppliers can achieve. This rivalry has led to the low end of the computer business being able to achieve better price-performance than other sectors and yielded greater growth at the low end, although with very limited profits (as is typical in any commodity business).

Cost of an Integrated Circuit

Why would a computer architecture book have a section on integrated circuit costs? In an increasingly competitive computer marketplace where standard parts—disks, Flash memory, DRAMs, and so on—are becoming a significant portion of any system’s cost, integrated circuit costs are becoming a greater portion of the cost that varies between computers, especially in the high-volume, cost-sensitive portion of the market. Indeed, with personal mobile devices’ increasing reliance of whole systems on a chip (SOC), the cost of the integrated circuits is much of the cost of the PMD. Thus, computer designers must understand the costs of chips to understand the costs of current computers.

Although the costs of integrated circuits have dropped exponentially, the basic process of silicon manufacture is unchanged: A wafer is still tested and chopped into dies that are packaged (see Figures 1.13, 1.14, and 1.15). Thus, the cost of a packaged integrated circuit is

In this section, we focus on the cost of dies, summarizing the key issues in testing and packaging at the end.

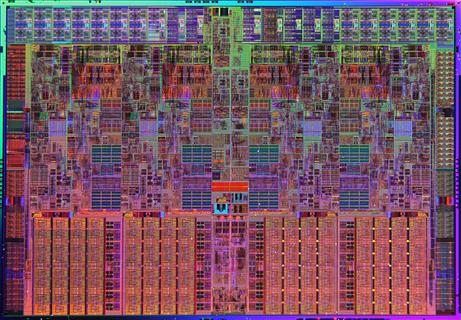
Figure 1.13 Photograph of an Intel Core i7 microprocessor die, which is evaluated in Chapters 2 through 5. The dimensions are 18.9 mm by 13.6 mm (257 mm2) in a 45 nm process. (Courtesy Intel.)

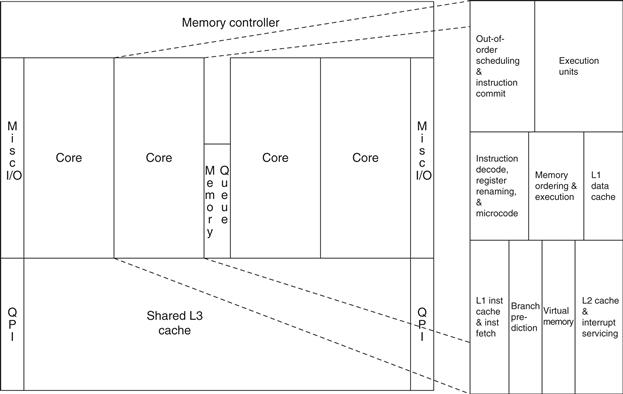
Figure 1.14 Floorplan of Core i7 die in Figure 1.13 on left with close-up of floorplan of second core on right.

Figure 1.15 This 300 mm wafer contains 280 full Sandy Bridge dies, each 20.7 by 10.5 mm in a 32 nm process. (Sandy Bridge is Intel’s successor to Nehalem used in the Core i7.) At 216 mm2, the formula for dies per wafer estimates 282. (Courtesy Intel.)

Learning how to predict the number of good chips per wafer requires first learning how many dies fit on a wafer and then learning how to predict the percentage of those that will work. From there it is simple to predict cost:

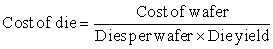
The most interesting feature of this first term of the chip cost equation is its sensitivity to die size, shown below.

The number of dies per wafer is approximately the area of the wafer divided by the area of the die. It can be more accurately estimated by

The first term is the ratio of wafer area (πr²) to die area. The second compensates for the “square peg in a round hole” problem—rectangular dies near the periphery of round wafers. Dividing the circumference (πd) by the diagonal of a square die is approximately the number of dies along the edge.

Example

Find the number of dies per 300 mm (30 cm) wafer for a die that is 1.5 cm on a side and for a die that is 1.0 cm on a side.

Answer

When die area is 2.25 cm²:

Since the area of the larger die is 2.25 times bigger, there are roughly 2.25 as many smaller dies per wafer:

However, this formula only gives the maximum number of dies per wafer. The critical question is: What is the fraction of good dies on a wafer, or the die yield? A simple model of integrated circuit yield, which assumes that defects are randomly distributed over the wafer and that yield is inversely proportional to the complexity of the fabrication process, leads to the following:

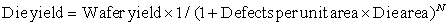
This Bose–Einstein formula is an empirical model developed by looking at the yield of many manufacturing lines [Sydow 2006]. Wafer yield accounts for wafers that are completely bad and so need not be tested. For simplicity, we’ll just assume the wafer yield is 100%. Defects per unit area is a measure of the random manufacturing defects that occur. In 2010, the value was typically 0.1 to 0.3 defects per square inch, or 0.016 to 0.057 defects per square centimeter, for a 40 nm process, as it depends on the maturity of the process (recall the learning curve, mentioned earlier). Finally, N is a parameter called the process-complexity factor, a measure of manufacturing difficulty. For 40 nm processes in 2010, N ranged from 11.5 to 15.5.

Example

Find the die yield for dies that are 1.5 cm on a side and 1.0 cm on a side, assuming a defect density of 0.031 per cm² and N is 13.5.

Answer

The total die areas are 2.25 cm² and 1.00 cm². For the larger die, the yield is

For the smaller die, the yield is

That is, less than half of all the large dies are good but two-thirds of the small dies are good.

The bottom line is the number of good dies per wafer, which comes from multiplying dies per wafer by die yield to incorporate the effects of defects. The examples above predict about 109 good 2.25 cm² dies from the 300 mm wafer and 424 good 1.00 cm² dies. Many microprocessors fall between these two sizes. Low-end embedded 32-bit processors are sometimes as small as 0.10 cm², and processors used for embedded control (in printers, microwaves, and so on) are often less than 0.04 cm².

Given the tremendous price pressures on commodity products such as DRAM and SRAM, designers have included redundancy as a way to raise yield. For a number of years, DRAMs have regularly included some redundant memory cells, so that a certain number of flaws can be accommodated. Designers have used similar techniques in both standard SRAMs and in large SRAM arrays used for caches within microprocessors. Obviously, the presence of redundant entries can be used to boost the yield significantly.

Processing of a 300 mm (12-inch) diameter wafer in a leading-edge technology cost between $5000 and $6000 in 2010. Assuming a processed wafer cost of $5500, the cost of the 1.00 cm² die would be around $13, but the cost per die of the 2.25 cm² die would be about $51, or almost four times the cost for a die that is a little over twice as large.

What should a computer designer remember about chip costs? The manufacturing process dictates the wafer cost, wafer yield, and defects per unit area, so the sole control of the designer is die area. In practice, because the number of defects per unit area is small, the number of good dies per wafer, and hence the cost per die, grows roughly as the square of the die area. The computer designer affects die size, and hence cost, both by what functions are included on or excluded from the die and by the number of I/O pins.

Before we have a part that is ready for use in a computer, the die must be tested (to separate the good dies from the bad), packaged, and tested again after packaging. These steps all add significant costs.

The above analysis has focused on the variable costs of producing a functional die, which is appropriate for high-volume integrated circuits. There is, however, one very important part of the fixed costs that can significantly affect the cost of an integrated circuit for low volumes (less than 1 million parts), namely, the cost of a mask set. Each step in the integrated circuit process requires a separate mask. Thus, for modern high-density fabrication processes with four to six metal layers, mask costs exceed $1M. Obviously, this large fixed cost affects the cost of prototyping and debugging runs and, for small-volume production, can be a significant part of the production cost. Since mask costs are likely to continue to increase, designers may incorporate reconfigurable logic to enhance the flexibility of a part or choose to use gate arrays (which have fewer custom mask levels) and thus reduce the cost implications of masks.

Cost versus Price

With the commoditization of computers, the margin between the cost to manufacture a product and the price the product sells for has been shrinking. Those margins pay for a company’s research and development (R&D), marketing, sales, manufacturing equipment maintenance, building rental, cost of financing, pretax profits, and taxes. Many engineers are surprised to find that most companies spend only 4% (in the commodity PC business) to 12% (in the high-end server business) of their income on R&D, which includes all engineering.

Cost of Manufacturing versus Cost of Operation

For the first four editions of this book, cost meant the cost to build a computer and price meant price to purchase a computer. With the advent of warehouse-scale computers, which contain tens of thousands of servers, the cost to operate the computers is significant in addition to the cost of purchase.

As Chapter 6 shows, the amortized purchase price of servers and networks is just over 60% of the monthly cost to operate a warehouse-scale computer, assuming a short lifetime of the IT equipment of 3 to 4 years. About 30% of the monthly operational costs are for power use and the amortized infrastructure to distribute power and to cool the IT equipment, despite this infrastructure being amortized over 10 years. Thus, to lower operational costs in a warehouse-scale computer, computer architects need to use energy efficiently.

1.7 Dependability

Historically, integrated circuits were one of the most reliable components of a computer. Although their pins may be vulnerable, and faults may occur over communication channels, the error rate inside the chip was very low. That conventional wisdom is changing as we head to feature sizes of 32 nm and smaller, as both transient faults and permanent faults will become more commonplace, so architects must design systems to cope with these challenges. This section gives a quick overview of the issues in dependability, leaving the official definition of the terms and approaches to Section D.3 in Appendix D.

Computers are designed and constructed at different layers of abstraction. We can descend recursively down through a computer seeing components enlarge themselves to full subsystems until we run into individual transistors. Although some faults are widespread, like the loss of power, many can be limited to a single component in a module. Thus, utter failure of a module at one level may be considered merely a component error in a higher-level module. This distinction is helpful in trying to find ways to build dependable computers.

One difficult question is deciding when a system is operating properly. This philosophical point became concrete with the popularity of Internet services. Infrastructure providers started offering service level agreements (SLAs) or service level objectives (SLOs) to guarantee that their networking or power service would be dependable. For example, they would pay the customer a penalty if they did not meet an agreement more than some hours per month. Thus, an SLA could be used to decide whether the system was up or down.

Systems alternate between two states of service with respect to an SLA:

1. Service accomplishment, where the service is delivered as specified

2. Service interruption, where the delivered service is different from the SLA

Transitions between these two states are caused by failures (from state 1 to state 2) or restorations (2 to 1). Quantifying these transitions leads to the two main measures of dependability:

■ Module reliability is a measure of the continuous service accomplishment (or, equivalently, of the time to failure) from a reference initial instant. Hence, the mean time to failure (MTTF) is a reliability measure. The reciprocal of MTTF is a rate of failures, generally reported as failures per billion hours of operation, or FIT (for failures in time). Thus, an MTTF of 1,000,000 hours equals 10⁹/10⁶ or 1000 FIT. Service interruption is measured as mean time to repair (MTTR). Mean time between failures (MTBF) is simply the sum of MTTF + MTTR. Although MTBF is widely used, MTTF is often the more appropriate term. If a collection of modules has exponentially distributed lifetimes—meaning that the age of a module is not important in probability of failure—the overall failure rate of the collection is the sum of the failure rates of the modules.

■ Module availability is a measure of the service accomplishment with respect to the alternation between the two states of accomplishment and interruption. For nonredundant systems with repair, module availability is

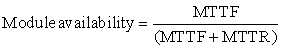
Note that reliability and availability are now quantifiable metrics, rather than synonyms for dependability. From these definitions, we can estimate reliability of a system quantitatively if we make some assumptions about the reliability of components and that failures are independent.

Example

Assume a disk subsystem with the following components and MTTF:

■ 10 disks, each rated at 1,000,000-hour MTTF

■ 1 ATA controller, 500,000-hour MTTF

■ 1 power supply, 200,000-hour MTTF

■ 1 fan, 200,000-hour MTTF

■ 1 ATA cable, 1,000,000-hour MTTF

Using the simplifying assumptions that the lifetimes are exponentially distributed and that failures are independent, compute the MTTF of the system as a whole.

Answer

The sum of the failure rates is

or 23,000 FIT. The MTTF for the system is just the inverse of the failure rate:

or just under 5 years.

The primary way to cope with failure is redundancy, either in time (repeat the operation to see if it still is erroneous) or in resources (have other components to take over from the one that failed). Once the component is replaced and the system fully repaired, the dependability of the system is assumed to be as good as new. Let’s quantify the benefits of redundancy with an example.

Example

Disk subsystems often have redundant power supplies to improve dependability. Using the components and MTTFs from above, calculate the reliability of redundant power supplies. Assume one power supply is sufficient to run the disk subsystem and that we are adding one redundant power supply.

Answer

We need a formula to show what to expect when we can tolerate a failure and still provide service. To simplify the calculations, we assume that the lifetimes of the components are exponentially distributed and that there is no dependency between the component failures. MTTF for our redundant power supplies is the mean time until one power supply fails divided by the chance that the other will fail before the first one is replaced. Thus, if the chance of a second failure before repair is small, then the MTTF of the pair is large.

Since we have two power supplies and independent failures, the mean time until one disk fails is MTTF_{power supply}/2. A good approximation of the probability of a second failure is MTTR over the mean time until the other power supply fails. Hence, a reasonable approximation for a redundant pair of power supplies is

Using the MTTF numbers above, if we assume it takes on average 24 hours for a human operator to notice that a power supply has failed and replace it, the reliability of the fault tolerant pair of power supplies is

making the pair about 4150 times more reliable than a single power supply.

Having quantified the cost, power, and dependability of computer technology, we are ready to quantify performance.

1.8 Measuring, Reporting, and Summarizing Performance

When we say one computer is faster than another is, what do we mean? The user of a desktop computer may say a computer is faster when a program runs in less time, while an Amazon.com administrator may say a computer is faster when it completes more transactions per hour. The computer user is interested in reducing response time—the time between the start and the completion of an event—also referred to as execution time. The operator of a warehouse-scale computer may be interested in increasing throughput—the total amount of work done in a given time.

In comparing design alternatives, we often want to relate the performance of two different computers, say, X and Y. The phrase “X is faster than Y” is used here to mean that the response time or execution time is lower on X than on Y for the given task. In particular, “X is n times faster than Y” will mean:

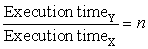
Since execution time is the reciprocal of performance, the following relationship holds:

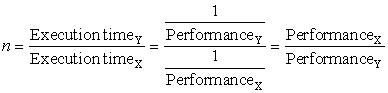
The phrase “the throughput of X is 1.3 times higher than Y” signifies here that the number of tasks completed per unit time on computer X is 1.3 times the number completed on Y.

Unfortunately, time is not always the metric quoted in comparing the performance of computers. Our position is that the only consistent and reliable measure of performance is the execution time of real programs, and that all proposed alternatives to time as the metric or to real programs as the items measured have eventually led to misleading claims or even mistakes in computer design.

Even execution time can be defined in different ways depending on what we count. The most straightforward definition of time is called wall-clock time, response time, or elapsed time, which is the latency to complete a task, including disk accesses, memory accesses, input/output activities, operating system overhead—everything. With multiprogramming, the processor works on another program while waiting for I/O and may not necessarily minimize the elapsed time of one program. Hence, we need a term to consider this activity. CPU time recognizes this distinction and means the time the processor is computing, not including the time waiting for I/O or running other programs. (Clearly, the response time seen by the user is the elapsed time of the program, not the CPU time.)

Computer users who routinely run the same programs would be the perfect candidates to evaluate a new computer. To evaluate a new system the users would simply compare the execution time of their workloads—the mixture of programs and operating system commands that users run on a computer. Few are in this happy situation, however. Most must rely on other methods to evaluate computers, and often other evaluators, hoping that these methods will predict performance for their usage of the new computer.

Benchmarks

The best choice of benchmarks to measure performance is real applications, such as Google Goggles from Section 1.1. Attempts at running programs that are much simpler than a real application have led to performance pitfalls. Examples include:

■ Kernels, which are small, key pieces of real applications

■ Toy programs, which are 100-line programs from beginning programming assignments, such as quicksort

■ Synthetic benchmarks, which are fake programs invented to try to match the profile and behavior of real applications, such as Dhrystone

All three are discredited today, usually because the compiler writer and architect can conspire to make the computer appear faster on these stand-in programs than on real applications. Depressingly for your authors—who dropped the fallacy about using synthetic programs to characterize performance in the fourth edition of this book since we thought computer architects agreed it was disreputable—the synthetic program Dhrystone is still the most widely quoted benchmark for embedded processors!

Another issue is the conditions under which the benchmarks are run. One way to improve the performance of a benchmark has been with benchmark-specific flags; these flags often caused transformations that would be illegal on many programs or would slow down performance on others. To restrict this process and increase the significance of the results, benchmark developers often require the vendor to use one compiler and one set of flags for all the programs in the same language (C++ or C). In addition to the question of compiler flags, another question is whether source code modifications are allowed. There are three different approaches to addressing this question:

1. No source code modifications are allowed.

2. Source code modifications are allowed but are essentially impossible. For example, database benchmarks rely on standard database programs that are tens of millions of lines of code. The database companies are highly unlikely to make changes to enhance the performance for one particular computer.

3. Source modifications are allowed, as long as the modified version produces the same output.

The key issue that benchmark designers face in deciding to allow modification of the source is whether such modifications will reflect real practice and provide useful insight to users, or whether such modifications simply reduce the accuracy of the benchmarks as predictors of real performance.

To overcome the danger of placing too many eggs in one basket, collections of benchmark applications, called benchmark suites, are a popular measure of performance of processors with a variety of applications. Of course, such suites are only as good as the constituent individual benchmarks. Nonetheless, a key advantage of such suites is that the weakness of any one benchmark is lessened by the presence of the other benchmarks. The goal of a benchmark suite is that it will characterize the relative performance of two computers, particularly for programs not in the suite that customers are likely to run.

A cautionary example is the Electronic Design News Embedded Microprocessor Benchmark Consortium (or EEMBC, pronounced “embassy”) benchmarks. It is a set of 41 kernels used to predict performance of different embedded applications: automotive/industrial, consumer, networking, office automation, and telecommunications. EEMBC reports unmodified performance and “full fury” performance, where almost anything goes. Because these benchmarks use kernels, and because of the reporting options, EEMBC does not have the reputation of being a good predictor of relative performance of different embedded computers in the field. This lack of success is why Dhrystone, which EEMBC was trying to replace, is still used.

One of the most successful attempts to create standardized benchmark application suites has been the SPEC (Standard Performance Evaluation Corporation), which had its roots in efforts in the late 1980s to deliver better benchmarks for workstations. Just as the computer industry has evolved over time, so has the need for different benchmark suites, and there are now SPEC benchmarks to cover many application classes. All the SPEC benchmark suites and their reported results are found at www.spec.org.

Although we focus our discussion on the SPEC benchmarks in many of the following sections, many benchmarks have also been developed for PCs running the Windows operating system.

Desktop Benchmarks

Desktop benchmarks divide into two broad classes: processor-intensive benchmarks and graphics-intensive benchmarks, although many graphics benchmarks include intensive processor activity. SPEC originally created a benchmark set focusing on processor performance (initially called SPEC89), which has evolved into its fifth generation: SPEC CPU2006, which follows SPEC2000, SPEC95 SPEC92, and SPEC89. SPEC CPU2006 consists of a set of 12 integer benchmarks (CINT2006) and 17 floating-point benchmarks (CFP2006). Figure 1.16 describes the current SPEC benchmarks and their ancestry.

Figure 1.16 SPEC2006 programs and the evolution of the SPEC benchmarks over time, with integer programs above the line and floating-point programs below the line. Of the 12 SPEC2006 integer programs, 9 are written in C, and the rest in C++. For the floating-point programs, the split is 6 in Fortran, 4 in C++, 3 in C, and 4 in mixed C and Fortran. The figure shows all 70 of the programs in the 1989, 1992, 1995, 2000, and 2006 releases. The benchmark descriptions on the left are for SPEC2006 only and do not apply to earlier versions. Programs in the same row from different generations of SPEC are generally not related; for example, fpppp is not a CFD code like bwaves. Gcc is the senior citizen of the group. Only 3 integer programs and 3 floating-point programs survived three or more generations. Note that all the floating-point programs are new for SPEC2006. Although a few are carried over from generation to generation, the version of the program changes and either the input or the size of the benchmark is often changed to increase its running time and to avoid perturbation in measurement or domination of the execution time by some factor other than CPU time.

SPEC benchmarks are real programs modified to be portable and to minimize the effect of I/O on performance. The integer benchmarks vary from part of a C compiler to a chess program to a quantum computer simulation. The floating-point benchmarks include structured grid codes for finite element modeling, particle method codes for molecular dynamics, and sparse linear algebra codes for fluid dynamics. The SPEC CPU suite is useful for processor benchmarking for both desktop systems and single-processor servers. We will see data on many of these programs throughout this text. However, note that these programs share little with programming languages and environments and the Google Goggles application that Section 1.1 describes. Seven use C++, eight use C, and nine use Fortran! They are even statically linked, and the applications themselves are dull. It’s not clear that SPECINT2006 and SPECFP2006 capture what is exciting about computing in the 21st century.

In Section 1.11, we describe pitfalls that have occurred in developing the SPEC benchmark suite, as well as the challenges in maintaining a useful and predictive benchmark suite.

SPEC CPU2006 is aimed at processor performance, but SPEC offers many other benchmarks.

Server Benchmarks

Just as servers have multiple functions, so are there multiple types of benchmarks. The simplest benchmark is perhaps a processor throughput-oriented benchmark. SPEC CPU2000 uses the SPEC CPU benchmarks to construct a simple throughput benchmark where the processing rate of a multiprocessor can be measured by running multiple copies (usually as many as there are processors) of each SPEC CPU benchmark and converting the CPU time into a rate. This leads to a measurement called the SPECrate, and it is a measure of request-level parallelism from Section 1.2. To measure thread-level parallelism, SPEC offers what they call high-performance computing benchmarks around OpenMP and MPI.

Other than SPECrate, most server applications and benchmarks have significant I/O activity arising from either disk or network traffic, including benchmarks for file server systems, for Web servers, and for database and transaction-processing systems. SPEC offers both a file server benchmark (SPECSFS) and a Web server benchmark (SPECWeb). SPECSFS is a benchmark for measuring NFS (Network File System) performance using a script of file server requests; it tests the performance of the I/O system (both disk and network I/O) as well as the processor. SPECSFS is a throughput-oriented benchmark but with important response time requirements. (Appendix D discusses some file and I/O system benchmarks in detail.) SPECWeb is a Web server benchmark that simulates multiple clients requesting both static and dynamic pages from a server, as well as clients posting data to the server. SPECjbb measures server performance for Web applications written in Java. The most recent SPEC benchmark is SPECvirt_Sc2010, which evaluates end-to-end performance of virtualized datacenter servers, including hardware, the virtual machine layer, and the virtualized guest operating system. Another recent SPEC benchmark measures power, which we examine in Section 1.10.

Transaction-processing (TP) benchmarks measure the ability of a system to handle transactions that consist of database accesses and updates. Airline reservation systems and bank ATM systems are typical simple examples of TP; more sophisticated TP systems involve complex databases and decision-making. In the mid-1980s, a group of concerned engineers formed the vendor-independent Transaction Processing Council (TPC) to try to create realistic and fair benchmarks for TP. The TPC benchmarks are described at www.tpc.org.

The first TPC benchmark, TPC-A, was published in 1985 and has since been replaced and enhanced by several different benchmarks. TPC-C, initially created in 1992, simulates a complex query environment. TPC-H models ad hoc decision support—the queries are unrelated and knowledge of past queries cannot be used to optimize future queries. TPC-E is a new On-Line Transaction Processing (OLTP) workload that simulates a brokerage firm’s customer accounts. The most recent effort is TPC Energy, which adds energy metrics to all the existing TPC benchmarks.

All the TPC benchmarks measure performance in transactions per second. In addition, they include a response time requirement, so that throughput performance is measured only when the response time limit is met. To model real-world systems, higher transaction rates are also associated with larger systems, in terms of both users and the database to which the transactions are applied. Finally, the system cost for a benchmark system must also be included, allowing accurate comparisons of cost-performance. TPC modified its pricing policy so that there is a single specification for all the TPC benchmarks and to allow verification of the prices that TPC publishes.

Reporting Performance Results

The guiding principle of reporting performance measurements should be reproducibility—list everything another experimenter would need to duplicate the results. A SPEC benchmark report requires an extensive description of the computer and the compiler flags, as well as the publication of both the baseline and optimized results. In addition to hardware, software, and baseline tuning parameter descriptions, a SPEC report contains the actual performance times, shown both in tabular form and as a graph. A TPC benchmark report is even more complete, since it must include results of a benchmarking audit and cost information. These reports are excellent sources for finding the real costs of computing systems, since manufacturers compete on high performance and cost-performance.

Summarizing Performance Results

In practical computer design, you must evaluate myriad design choices for their relative quantitative benefits across a suite of benchmarks believed to be relevant. Likewise, consumers trying to choose a computer will rely on performance measurements from benchmarks, which hopefully are similar to the user’s applications. In both cases, it is useful to have measurements for a suite of benchmarks so that the performance of important applications is similar to that of one or more benchmarks in the suite and that variability in performance can be understood. In the ideal case, the suite resembles a statistically valid sample of the application space, but such a sample requires more benchmarks than are typically found in most suites and requires a randomized sampling, which essentially no benchmark suite uses.

Once we have chosen to measure performance with a benchmark suite, we would like to be able to summarize the performance results of the suite in a single number. A straightforward approach to computing a summary result would be to compare the arithmetic means of the execution times of the programs in the suite. Alas, some SPEC programs take four times longer than others do, so those programs would be much more important if the arithmetic mean were the single number used to summarize performance. An alternative would be to add a weighting factor to each benchmark and use the weighted arithmetic mean as the single number to summarize performance. The problem would then be how to pick weights; since SPEC is a consortium of competing companies, each company might have their own favorite set of weights, which would make it hard to reach consensus. One approach is to use weights that make all programs execute an equal time on some reference computer, but this biases the results to the performance characteristics of the reference computer.

Rather than pick weights, we could normalize execution times to a reference computer by dividing the time on the reference computer by the time on the computer being rated, yielding a ratio proportional to performance. SPEC uses this approach, calling the ratio the SPECRatio. It has a particularly useful property that it matches the way we compare computer performance throughout this text—namely, comparing performance ratios. For example, suppose that the SPECRatio of computer A on a benchmark was 1.25 times higher than computer B; then we would know:

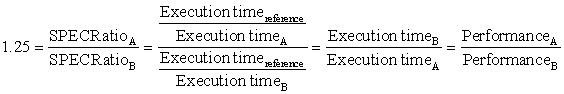
Notice that the execution times on the reference computer drop out and the choice of the reference computer is irrelevant when the comparisons are made as a ratio, which is the approach we consistently use. Figure 1.17 gives an example.

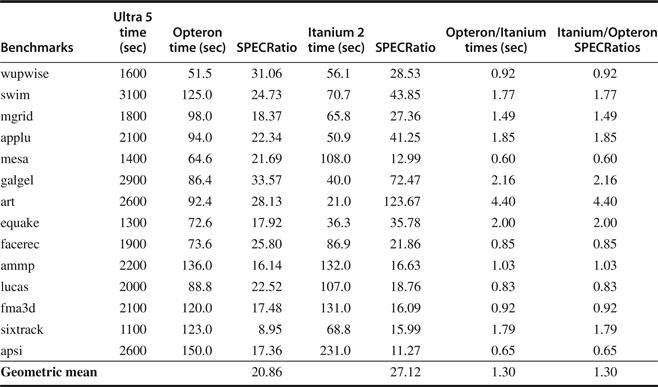
Figure 1.17 SPECfp2000 execution times (in seconds) for the Sun Ultra 5—the reference computer of SPEC2000—and execution times and SPECRatios for the AMD Opteron and Intel Itanium 2. (SPEC2000 multiplies the ratio of execution times by 100 to remove the decimal point from the result, so 20.86 is reported as 2086.) The final two columns show the ratios of execution times and SPECRatios. This figure demonstrates the irrelevance of the reference computer in relative performance. The ratio of the execution times is identical to the ratio of the SPECRatios, and the ratio of the geometric means (27.12/20.86 = 1.30) is identical to the geometric mean of the ratios (1.30).

Because a SPECRatio is a ratio rather than an absolute execution time, the mean must be computed using the geometric mean. (Since SPECRatios have no units, comparing SPECRatios arithmetically is meaningless.) The formula is

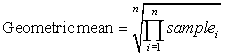
In the case of SPEC, sample_i is the SPECRatio for program i. Using the geometric mean ensures two important properties:

1. The geometric mean of the ratios is the same as the ratio of the geometric means.

2. The ratio of the geometric means is equal to the geometric mean of the performance ratios, which implies that the choice of the reference computer is irrelevant.

Hence, the motivations to use the geometric mean are substantial, especially when we use performance ratios to make comparisons.

Example

Show that the ratio of the geometric means is equal to the geometric mean of the performance ratios, and that the reference computer of SPECRatio matters not.

Answer

Assume two computers A and B and a set of SPECRatios for each.

That is, the ratio of the geometric means of the SPECRatios of A and B is the geometric mean of the performance ratios of A to B of all the benchmarks in the suite. Figure 1.17 demonstrates this validity using examples from SPEC.

1.9 Quantitative Principles of Computer Design

Now that we have seen how to define, measure, and summarize performance, cost, dependability, energy, and power, we can explore guidelines and principles that are useful in the design and analysis of computers. This section introduces important observations about design, as well as two equations to evaluate alternatives.

Take Advantage of Parallelism

Taking advantage of parallelism is one of the most important methods for improving performance. Every chapter in this book has an example of how performance is enhanced through the exploitation of parallelism. We give three brief examples here, which are expounded on in later chapters.

Our first example is the use of parallelism at the system level. To improve the throughput performance on a typical server benchmark, such as SPECWeb or TPC-C, multiple processors and multiple disks can be used. The workload of handling requests can then be spread among the processors and disks, resulting in improved throughput. Being able to expand memory and the number of processors and disks is called scalability, and it is a valuable asset for servers. Spreading of data across many disks for parallel reads and writes enables data-level parallelism. SPECWeb also relies on request-level parallelism to use many processors while TPC-C uses thread-level parallelism for faster processing of database queries.

At the level of an individual processor, taking advantage of parallelism among instructions is critical to achieving high performance. One of the simplest ways to do this is through pipelining. (It is explained in more detail in Appendix C and is a major focus of Chapter 3.) The basic idea behind pipelining is to overlap instruction execution to reduce the total time to complete an instruction sequence. A key insight that allows pipelining to work is that not every instruction depends on its immediate predecessor, so executing the instructions completely or partially in parallel may be possible. Pipelining is the best-known example of instruction-level parallelism.

Parallelism can also be exploited at the level of detailed digital design. For example, set-associative caches use multiple banks of memory that are typically searched in parallel to find a desired item. Modern ALUs (arithmetic-logical units) use carry-lookahead, which uses parallelism to speed the process of computing sums from linear to logarithmic in the number of bits per operand. These are more examples of data-level parallelism.

Principle of Locality

Important fundamental observations have come from properties of programs. The most important program property that we regularly exploit is the principle of locality: Programs tend to reuse data and instructions they have used recently. A widely held rule of thumb is that a program spends 90% of its execution time in only 10% of the code. An implication of locality is that we can predict with reasonable accuracy what instructions and data a program will use in the near future based on its accesses in the recent past. The principle of locality also applies to data accesses, though not as strongly as to code accesses.

Two different types of locality have been observed. Temporal locality states that recently accessed items are likely to be accessed in the near future. Spatial locality says that items whose addresses are near one another tend to be referenced close together in time. We will see these principles applied in Chapter 2.

Focus on the Common Case

Perhaps the most important and pervasive principle of computer design is to focus on the common case: In making a design trade-off, favor the frequent case over the infrequent case. This principle applies when determining how to spend resources, since the impact of the improvement is higher if the occurrence is frequent.

Focusing on the common case works for power as well as for resource allocation and performance. The instruction fetch and decode unit of a processor may be used much more frequently than a multiplier, so optimize it first. It works on dependability as well. If a database server has 50 disks for every processor, storage dependability will dominate system dependability.

In addition, the frequent case is often simpler and can be done faster than the infrequent case. For example, when adding two numbers in the processor, we can expect overflow to be a rare circumstance and can therefore improve performance by optimizing the more common case of no overflow. This emphasis may slow down the case when overflow occurs, but if that is rare then overall performance will be improved by optimizing for the normal case.

We will see many cases of this principle throughout this text. In applying this simple principle, we have to decide what the frequent case is and how much performance can be improved by making that case faster. A fundamental law, called Amdahl’s law, can be used to quantify this principle.

Amdahl’s Law

The performance gain that can be obtained by improving some portion of a computer can be calculated using Amdahl’s law. Amdahl’s law states that the performance improvement to be gained from using some faster mode of execution is limited by the fraction of the time the faster mode can be used.

Amdahl’s law defines the speedup that can be gained by using a particular feature. What is speedup? Suppose that we can make an enhancement to a computer that will improve performance when it is used. Speedup is the ratio:

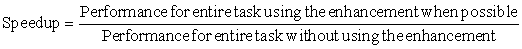
Alternatively,

Speedup tells us how much faster a task will run using the computer with the enhancement as opposed to the original computer.

Amdahl’s law gives us a quick way to find the speedup from some enhancement, which depends on two factors:

1. The fraction of the computation time in the original computer that can be converted to take advantage of the enhancement—For example, if 20 seconds of the execution time of a program that takes 60 seconds in total can use an enhancement, the fraction is 20/60. This value, which we will call Fraction_enhanced, is always less than or equal to 1.

2. The improvement gained by the enhanced execution mode, that is, how much faster the task would run if the enhanced mode were used for the entire program—This value is the time of the original mode over the time of the enhanced mode. If the enhanced mode takes, say, 2 seconds for a portion of the program, while it is 5 seconds in the original mode, the improvement is 5/2. We will call this value, which is always greater than 1, Speedup_enhanced.

The execution time using the original computer with the enhanced mode will be the time spent using the unenhanced portion of the computer plus the time spent using the enhancement:

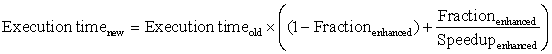
The overall speedup is the ratio of the execution times:

Example

Suppose that we want to enhance the processor used for Web serving. The new processor is 10 times faster on computation in the Web serving application than the original processor. Assuming that the original processor is busy with computation 40% of the time and is waiting for I/O 60% of the time, what is the overall speedup gained by incorporating the enhancement?

Answer

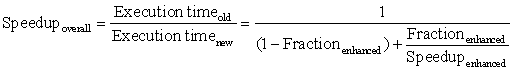
Amdahl’s law expresses the law of diminishing returns: The incremental improvement in speedup gained by an improvement of just a portion of the computation diminishes as improvements are added. An important corollary of Amdahl’s law is that if an enhancement is only usable for a fraction of a task then we can’t speed up the task by more than the reciprocal of 1 minus that fraction.

A common mistake in applying Amdahl’s law is to confuse “fraction of time converted to use an enhancement” and “fraction of time after enhancement is in use.” If, instead of measuring the time that we could use the enhancement in a computation, we measure the time after the enhancement is in use, the results will be incorrect!

Amdahl’s law can serve as a guide to how much an enhancement will improve performance and how to distribute resources to improve cost-performance. The goal, clearly, is to spend resources proportional to where time is spent. Amdahl’s law is particularly useful for comparing the overall system performance of two alternatives, but it can also be applied to compare two processor design alternatives, as the following example shows.

Example

A common transformation required in graphics processors is square root. Implementations of floating-point (FP) square root vary significantly in performance, especially among processors designed for graphics. Suppose FP square root (FPSQR) is responsible for 20% of the execution time of a critical graphics benchmark. One proposal is to enhance the FPSQR hardware and speed up this operation by a factor of 10. The other alternative is just to try to make all FP instructions in the graphics processor run faster by a factor of 1.6; FP instructions are responsible for half of the execution time for the application. The design team believes that they can make all FP instructions run 1.6 times faster with the same effort as required for the fast square root. Compare these two design alternatives.

Answer

We can compare these two alternatives by comparing the speedups:

Improving the performance of the FP operations overall is slightly better because of the higher frequency.

Amdahl’s law is applicable beyond performance. Let’s redo the reliability example from page 35 after improving the reliability of the power supply via redundancy from 200,000-hour to 830,000,000-hour MTTF, or 4150X better.

Example

The calculation of the failure rates of the disk subsystem was

Therefore, the fraction of the failure rate that could be improved is 5 per million hours out of 23 for the whole system, or 0.22.

Answer

The reliability improvement would be

Despite an impressive 4150X improvement in reliability of one module, from the system’s perspective, the change has a measurable but small benefit.

In the examples above, we needed the fraction consumed by the new and improved version; often it is difficult to measure these times directly. In the next section, we will see another way of doing such comparisons based on the use of an equation that decomposes the CPU execution time into three separate components. If we know how an alternative affects these three components, we can determine its overall performance. Furthermore, it is often possible to build simulators that measure these components before the hardware is actually designed.

The Processor Performance Equation

Essentially all computers are constructed using a clock running at a constant rate. These discrete time events are called ticks, clock ticks, clock periods, clocks, cycles, or clock cycles. Computer designers refer to the time of a clock period by its duration (e.g., 1 ns) or by its rate (e.g., 1 GHz). CPU time for a program can then be expressed two ways:

or

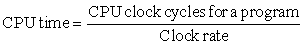
In addition to the number of clock cycles needed to execute a program, we can also count the number of instructions executed—the instruction path length or instruction count (IC). If we know the number of clock cycles and the instruction count, we can calculate the average number of clock cycles per instruction (CPI). Because it is easier to work with, and because we will deal with simple processors in this chapter, we use CPI. Designers sometimes also use instructions per clock (IPC), which is the inverse of CPI.

CPI is computed as

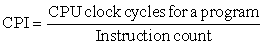
This processor figure of merit provides insight into different styles of instruction sets and implementations, and we will use it extensively in the next four chapters.

By transposing the instruction count in the above formula, clock cycles can be defined as IC × CPI. This allows us to use CPI in the execution time formula:

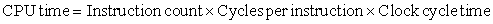
Expanding the first formula into the units of measurement shows how the pieces fit together:

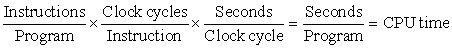
As this formula demonstrates, processor performance is dependent upon three characteristics: clock cycle (or rate), clock cycles per instruction, and instruction count. Furthermore, CPU time is equally dependent on these three characteristics; for example, a 10% improvement in any one of them leads to a 10% improvement in CPU time.

Unfortunately, it is difficult to change one parameter in complete isolation from others because the basic technologies involved in changing each characteristic are interdependent:

■ Clock cycle time—Hardware technology and organization

■ CPI—Organization and instruction set architecture

■ Instruction count—Instruction set architecture and compiler technology

Luckily, many potential performance improvement techniques primarily improve one component of processor performance with small or predictable impacts on the other two.

Sometimes it is useful in designing the processor to calculate the number of total processor clock cycles as

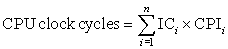
where IC_i represents the number of times instruction i is executed in a program and CPI_i represents the average number of clocks per instruction for instruction i. This form can be used to express CPU time as

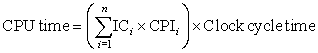
and overall CPI as

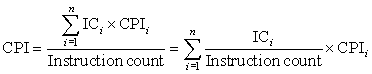
The latter form of the CPI calculation uses each individual CPI_i and the fraction of occurrences of that instruction in a program (i.e., IC_i ÷ Instruction count). CPI_i should be measured and not just calculated from a table in the back of a reference manual since it must include pipeline effects, cache misses, and any other memory system inefficiencies.

Consider our performance example on page 47, here modified to use measurements of the frequency of the instructions and of the instruction CPI values, which, in practice, are obtained by simulation or by hardware instrumentation.

Example

Suppose we have made the following measurements:

Frequency of FP operations = 25%

Average CPI of FP operations = 4.0

Average CPI of other instructions = 1.33

Frequency of FPSQR = 2%

CPI of FPSQR = 20

Assume that the two design alternatives are to decrease the CPI of FPSQR to 2 or to decrease the average CPI of all FP operations to 2.5. Compare these two design alternatives using the processor performance equation.

Answer

First, observe that only the CPI changes; the clock rate and instruction count remain identical. We start by finding the original CPI with neither enhancement:

We can compute the CPI for the enhanced FPSQR by subtracting the cycles saved from the original CPI:

We can compute the CPI for the enhancement of all FP instructions the same way or by summing the FP and non-FP CPIs. Using the latter gives us:

Since the CPI of the overall FP enhancement is slightly lower, its performance will be marginally better. Specifically, the speedup for the overall FP enhancement is

Happily, we obtained this same speedup using Amdahl’s law on page 46.

It is often possible to measure the constituent parts of the processor performance equation. This is a key advantage of using the processor performance equation versus Amdahl’s law in the previous example. In particular, it may be difficult to measure things such as the fraction of execution time for which a set of instructions is responsible. In practice, this would probably be computed by summing the product of the instruction count and the CPI for each of the instructions in the set. Since the starting point is often individual instruction count and CPI measurements, the processor performance equation is incredibly useful.

To use the processor performance equation as a design tool, we need to be able to measure the various factors. For an existing processor, it is easy to obtain the execution time by measurement, and we know the default clock speed. The challenge lies in discovering the instruction count or the CPI. Most new processors include counters for both instructions executed and for clock cycles. By periodically monitoring these counters, it is also possible to attach execution time and instruction count to segments of the code, which can be helpful to programmers trying to understand and tune the performance of an application. Often, a designer or programmer will want to understand performance at a more fine-grained level than what is available from the hardware counters. For example, they may want to know why the CPI is what it is. In such cases, simulation techniques used are like those for processors that are being designed.

Techniques that help with energy efficiency, such as dynamic voltage frequency scaling and overclocking (see Section 1.5), make this equation harder to use, since the clock speed may vary while we measure the program. A simple approach is to turn off those features to make the results reproducible. Fortunately, as performance and energy efficiency are often highly correlated—taking less time to run a program generally saves energy—it’s probably safe to consider performance without worrying about the impact of DVFS or overclocking on the results.

1.10 Putting It All Together: Performance, Price, and Power

In the “Putting It All Together” sections that appear near the end of every chapter, we provide real examples that use the principles in that chapter. In this section, we look at measures of performance and power-performance in small servers using the SPECpower benchmark.

Figure 1.18 shows the three multiprocessor servers we are evaluating along with their price. To keep the price comparison fair, all are Dell PowerEdge servers. The first is the PowerEdge R710, which is based on the Intel Xeon X5670 microprocessor with a clock rate of 2.93 GHz. Unlike the Intel Core i7 in Chapters 2 through 5, which has 4 cores and an 8 MB L3 cache, this Intel chip has 6 cores and a 12 MB L3 cache, although the cores themselves are identical. We selected a two-socket system with 12 GB of ECC-protected 1333 MHz DDR3 DRAM. The next server is the PowerEdge R815, which is based on the AMD Opteron 6174 microprocessor. A chip has 6 cores and a 6 MB L3 cache, and it runs at 2.20 GHz, but AMD puts two of these chips into a single socket. Thus, a socket has 12 cores and two 6 MB L3 caches. Our second server has two sockets with 24 cores and 16 GB of ECC-protected 1333 MHz DDR3 DRAM, and our third server (also a PowerEdge R815) has four sockets with 48 cores and 32 GB of DRAM. All are running the IBM J9 JVM and the Microsoft Windows 2008 Server Enterprise x64 Edition operating system.

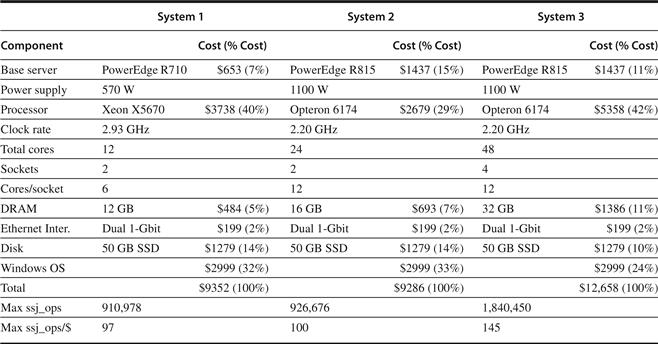
Figure 1.18 Three Dell PowerEdge servers being measured and their prices as of August 2010. We calculated the cost of the processors by subtracting the cost of a second processor. Similarly, we calculated the overall cost of memory by seeing what the cost of extra memory was. Hence, the base cost of the server is adjusted by removing the estimated cost of the default processor and memory. Chapter 5 describes how these multi-socket systems are connected together.

Note that due to the forces of benchmarking (see Section 1.11), these are unusually configured servers. The systems in Figure 1.18 have little memory relative to the amount of computation, and just a tiny 50 GB solid-state disk. It is inexpensive to add cores if you don’t need to add commensurate increases in memory and storage!

Rather than run statically linked C programs of SPEC CPU, SPECpower uses a more modern software stack written in Java. It is based on SPECjbb, and it represents the server side of business applications, with performance measured as the number transactions per second, called ssj_ops for server side Java operations per second. It exercises not only the processor of the server, as does SPEC CPU, but also the caches, memory system, and even the multiprocessor interconnection system. In addition, it exercises the Java Virtual Machine (JVM), including the JIT runtime compiler and garbage collector, as well as portions of the underlying operating system.

As the last two rows of Figure 1.18 show, the performance and price-performance winner is the PowerEdge R815 with four sockets and 48 cores. It hits 1.8M ssj_ops, and the ssj_ops per dollar is highest at 145. Amazingly, the computer with the largest number of cores is the most cost effective. In second place is the two-socket R815 with 24 cores, and the R710 with 12 cores is in last place.

While most benchmarks (and most computer architects) care only about performance of systems at peak load, computers rarely run at peak load. Indeed, Figure 6.2 in Chapter 6 shows the results of measuring the utilization of tens of thousands of servers over 6 months at Google, and less than 1% operate at an average utilization of 100%. The majority have an average utilization of between 10% and 50%. Thus, the SPECpower benchmark captures power as the target workload varies from its peak in 10% intervals all the way to 0%, which is called Active Idle.

Figure 1.19 plots the ssj_ops (SSJ operations/second) per watt and the average power as the target load varies from 100% to 0%. The Intel R710 always has the lowest power and the best ssj_ops per watt across each target workload level. One reason is the much larger power supply for the R815, at 1100 watts versus 570 in the R715. As Chapter 6 shows, power supply efficiency is very important in the overall power efficiency of a computer. Since watts = joules/second, this metric is proportional to SSJ operations per joule:

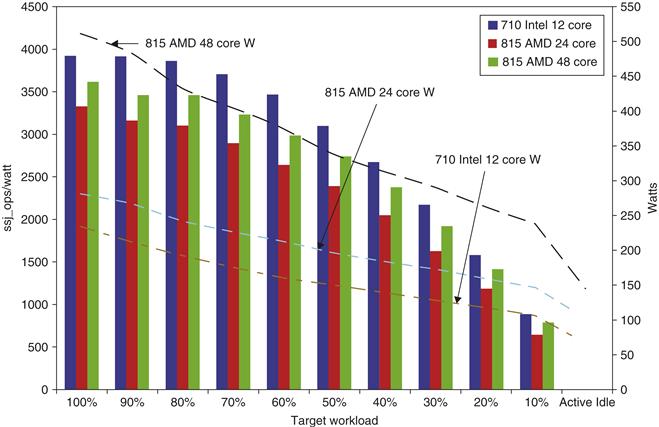
Figure 1.19 Power-performance of the three servers in Figure 1.18. Ssj_ops/watt values are on the left axis, with the three columns associated with it, and watts are on the right axis, with the three lines associated with it. The horizontal axis shows the target workload, as it varies from 100% to Active Idle. The Intel-based R715 has the best ssj_ops/watt at each workload level, and it also consumes the lowest power at each level.

To calculate a single number to use to compare the power efficiency of systems, SPECpower uses:

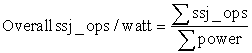
The overall ssj_ops/watt of the three servers is 3034 for the Intel R710, 2357 for the AMD dual-socket R815, and 2696 for the AMD quad-socket R815. Hence, the Intel R710 has the best power-performance. Dividing by the price of the servers, the ssj_ops/watt/$1000 is 324 for the Intel R710, 254 for the dual-socket AMD R815, and 213 for the quad-socket MD R815. Thus, adding power reverses the results of the price-performance competition, and the price-power-performance trophy goes to Intel R710; the 48-core R815 comes in last place.

1.11 Fallacies and Pitfalls

The purpose of this section, which will be found in every chapter, is to explain some commonly held misbeliefs or misconceptions that you should avoid. We call such misbeliefs fallacies. When discussing a fallacy, we try to give a counterexample. We also discuss pitfalls—easily made mistakes. Often pitfalls are generalizations of principles that are true in a limited context. The purpose of these sections is to help you avoid making these errors in computers that you design.

Fallacy Multiprocessors are a silver bullet

The switch to multiple processors per chip around 2005 did not come from some breakthrough that dramatically simplified parallel programming or made it easy to build multicore computers. The change occurred because there was no other option due to the ILP walls and power walls. Multiple processors per chip do not guarantee lower power; it’s certainly possible to design a multicore chip that uses more power. The potential is just that it’s possible to continue to improve performance by replacing a high-clock-rate, inefficient core with several lower-clock-rate, efficient cores. As technology improves to shrink transistors, this can shrink both capacitance and the supply voltage a bit so that we can get a modest increase in the number of cores per generation. For example, for the last few years Intel has been adding two cores per generation.

As we shall see in Chapters 4 and 5, performance is now a programmer’s burden. The La-Z-Boy programmer era of relying on hardware designers to make their programs go faster without lifting a finger is officially over. If programmers want their programs to go faster with each generation, they must make their programs more parallel.

The popular version of Moore’s law—increasing performance with each generation of technology—is now up to programmers.

Pitfall Falling prey to Amdahl’s heartbreaking law

Virtually every practicing computer architect knows Amdahl’s law. Despite this, we almost all occasionally expend tremendous effort optimizing some feature before we measure its usage. Only when the overall speedup is disappointing do we recall that we should have measured first before we spent so much effort enhancing it!

Pitfall A single point of failure

The calculations of reliability improvement using Amdahl’s law on page 48 show that dependability is no stronger than the weakest link in a chain. No matter how much more dependable we make the power supplies, as we did in our example, the single fan will limit the reliability of the disk subsystem. This Amdahl’s law observation led to a rule of thumb for fault-tolerant systems to make sure that every component was redundant so that no single component failure could bring down the whole system. Chapter 6 shows how a software layer avoids single points of failure inside warehouse-scale computers.

Fallacy Hardware enhancements that increase performance improve energy efficiency or are at worst energy neutral

Esmaeilzadeh et al. [2011] measured SPEC2006 on just one core of a 2.67 GHz Intel Core i7 using Turbo mode (Section 1.5). Performance increased by a factor of 1.07 when the clock rate increased to 2.94 GHz (or a factor of 1.10), but the i7 used a factor of 1.37 more joules and a factor of 1.47 more watt-hours!

Fallacy Benchmarks remain valid indefinitely

Several factors influence the usefulness of a benchmark as a predictor of real performance, and some change over time. A big factor influencing the usefulness of a benchmark is its ability to resist “benchmark engineering” or “benchmarketing.” Once a benchmark becomes standardized and popular, there is tremendous pressure to improve performance by targeted optimizations or by aggressive interpretation of the rules for running the benchmark. Small kernels or programs that spend their time in a small amount of code are particularly vulnerable.

For example, despite the best intentions, the initial SPEC89 benchmark suite included a small kernel, called matrix300, which consisted of eight different 300 × 300 matrix multiplications. In this kernel, 99% of the execution time was in a single line (see SPEC [1989]). When an IBM compiler optimized this inner loop (using an idea called blocking, discussed in Chapters 2 and 4), performance improved by a factor of 9 over a prior version of the compiler! This benchmark tested compiler tuning and was not, of course, a good indication of overall performance, nor of the typical value of this particular optimization.

Over a long period, these changes may make even a well-chosen benchmark obsolete; Gcc is the lone survivor from SPEC89. Figure 1.16 on page 39 lists the status of all 70 benchmarks from the various SPEC releases. Amazingly, almost 70% of all programs from SPEC2000 or earlier were dropped from the next release.

Fallacy The rated mean time to failure of disks is 1,200,000 hours or almost 140 years, so disks practically never fail

The current marketing practices of disk manufacturers can mislead users. How is such an MTTF calculated? Early in the process, manufacturers will put thousands of disks in a room, run them for a few months, and count the number that fail. They compute MTTF as the total number of hours that the disks worked cumulatively divided by the number that failed.

One problem is that this number far exceeds the lifetime of a disk, which is commonly assumed to be 5 years or 43,800 hours. For this large MTTF to make some sense, disk manufacturers argue that the model corresponds to a user who buys a disk and then keeps replacing the disk every 5 years—the planned lifetime of the disk. The claim is that if many customers (and their great-grandchildren) did this for the next century, on average they would replace a disk 27 times before a failure, or about 140 years.

A more useful measure would be percentage of disks that fail. Assume 1000 disks with a 1,000,000-hour MTTF and that the disks are used 24 hours a day. If you replaced failed disks with a new one having the same reliability characteristics, the number that would fail in a year (8760 hours) is

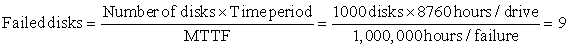
Stated alternatively, 0.9% would fail per year, or 4.4% over a 5-year lifetime.

Moreover, those high numbers are quoted assuming limited ranges of temperature and vibration; if they are exceeded, then all bets are off. A survey of disk drives in real environments [Gray and van Ingen 2005] found that 3% to 7% of drives failed per year, for an MTTF of about 125,000 to 300,000 hours. An even larger study found annual disk failure rates of 2% to 10% [Pinheiro, Weber, and Barroso 2007]. Hence, the real-world MTTF is about 2 to 10 times worse than the manufacturer’s MTTF.

Fallacy Peak performance tracks observed performance

The only universally true definition of peak performance is “the performance level a computer is guaranteed not to exceed.” Figure 1.20 shows the percentage of peak performance for four programs on four multiprocessors. It varies from 5% to 58%. Since the gap is so large and can vary significantly by benchmark, peak performance is not generally useful in predicting observed performance.

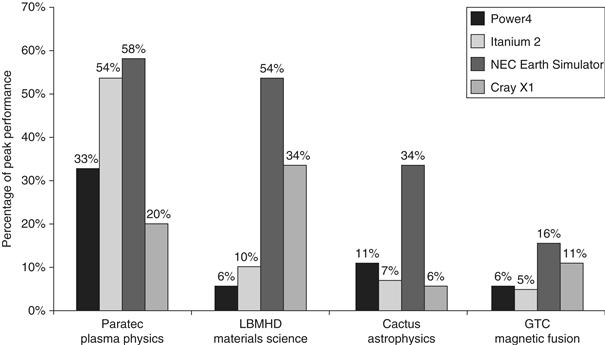
Figure 1.20 Percentage of peak performance for four programs on four multiprocessors scaled to 64 processors. The Earth Simulator and X1 are vector processors (see Chapter 4 and Appendix G). Not only did they deliver a higher fraction of peak performance, but they also had the highest peak performance and the lowest clock rates. Except for the Paratec program, the Power 4 and Itanium 2 systems delivered between 5% and 10% of their peak. From Oliker et al. [2004].

Pitfall Fault detection can lower availability

This apparently ironic pitfall is because computer hardware has a fair amount of state that may not always be critical to proper operation. For example, it is not fatal if an error occurs in a branch predictor, as only performance may suffer.

In processors that try to aggressively exploit instruction-level parallelism, not all the operations are needed for correct execution of the program. Mukherjee et al. [2003] found that less than 30% of the operations were potentially on the critical path for the SPEC2000 benchmarks running on an Itanium 2.

The same observation is true about programs. If a register is “dead” in a program—that is, the program will write it before it is read again—then errors do not matter. If you were to crash the program upon detection of a transient fault in a dead register, it would lower availability unnecessarily.

Sun Microsystems lived this pitfall in 2000 with an L2 cache that included parity, but not error correction, in its Sun E3000 to Sun E10000 systems. The SRAMs they used to build the caches had intermittent faults, which parity detected. If the data in the cache were not modified, the processor simply reread the data from the cache. Since the designers did not protect the cache with ECC (error-correcting code), the operating system had no choice but to report an error to dirty data and crash the program. Field engineers found no problems on inspection in more than 90% of the cases.

To reduce the frequency of such errors, Sun modified the Solaris operating system to “scrub” the cache by having a process that proactively writes dirty data to memory. Since the processor chips did not have enough pins to add ECC, the only hardware option for dirty data was to duplicate the external cache, using the copy without the parity error to correct the error.

The pitfall is in detecting faults without providing a mechanism to correct them. These engineers are unlikely to design another computer without ECC on external caches.

1.12 Concluding Remarks

This chapter has introduced a number of concepts and provided a quantitative framework that we will expand upon throughout the book. Starting with this edition, energy efficiency is the new companion to performance.

In Chapter 2, we start with the all-important area of memory system design. We will examine a wide range of techniques that conspire to make memory look infinitely large while still being as fast as possible. (Appendix B provides introductory material on caches for readers without much experience and background in them.) As in later chapters, we will see that hardware–software cooperation has become a key to high-performance memory systems, just as it has to high-performance pipelines. This chapter also covers virtual machines, an increasingly important technique for protection.

In Chapter 3, we look at instruction-level parallelism (ILP), of which pipelining is the simplest and most common form. Exploiting ILP is one of the most important techniques for building high-speed uniprocessors. Chapter 3 begins with an extensive discussion of basic concepts that will prepare you for the wide range of ideas examined in both chapters. Chapter 3 uses examples that span about 40 years, drawing from one of the first supercomputers (IBM 360/91) to the fastest processors in the market in 2011. It emphasizes what is called the dynamic or run time approach to exploiting ILP. It also talks about the limits to ILP ideas and introduces multithreading, which is further developed in both Chapters 4 and 5. Appendix C provides introductory material on pipelining for readers without much experience and background in pipelining. (We expect it to be a review for many readers, including those of our introductory text, Computer Organization and Design: The Hardware/Software Interface.)

Chapter 4 is new to this edition, and it explains three ways to exploit data-level parallelism. The classic and oldest approach is vector architecture, and we start there to lay down the principles of SIMD design. (Appendix G goes into greater depth on vector architectures.) We next explain the SIMD instruction set extensions found in most desktop microprocessors today. The third piece is an in-depth explanation of how modern graphics processing units (GPUs) work. Most GPU descriptions are written from the programmer’s perspective, which usually hides how the computer really works. This section explains GPUs from an insider’s perspective, including a mapping between GPU jargon and more traditional architecture terms.

Chapter 5 focuses on the issue of achieving higher performance using multiple processors, or multiprocessors. Instead of using parallelism to overlap individual instructions, multiprocessing uses parallelism to allow multiple instruction streams to be executed simultaneously on different processors. Our focus is on the dominant form of multiprocessors, shared-memory multiprocessors, though we introduce other types as well and discuss the broad issues that arise in any multiprocessor. Here again, we explore a variety of techniques, focusing on the important ideas first introduced in the 1980s and 1990s.

Chapter 6 is also new to this edition. We introduce clusters and then go into depth on warehouse-scale computers (WSCs), which computer architects help design. The designers of WSCs are the professional descendents of the pioneers of supercomputers such as Seymour Cray in that they are designing extreme computers. They contain tens of thousands of servers, and the equipment and building that holds them cost nearly $200 M. The concerns of price-performance and energy efficiency of the earlier chapters applies to WSCs, as does the quantitative approach to making decisions.

This book comes with an abundance of material online (see Preface for more details), both to reduce cost and to introduce readers to a variety of advanced topics. Figure 1.21 shows them all. Appendices A, B, and C, which appear in the book, will be review for many readers.

Figure 1.21 List of appendices.

In Appendix D, we move away from a processor-centric view and discuss issues in storage systems. We apply a similar quantitative approach, but one based on observations of system behavior and using an end-to-end approach to performance analysis. It addresses the important issue of how to efficiently store and retrieve data using primarily lower-cost magnetic storage technologies. Our focus is on examining the performance of disk storage systems for typical I/O-intensive workloads, like the OLTP benchmarks we saw in this chapter. We extensively explore advanced topics in RAID-based systems, which use redundant disks to achieve both high performance and high availability. Finally, the chapter introduces queuing theory, which gives a basis for trading off utilization and latency.

Appendix E applies an embedded computing perspective to the ideas of each of the chapters and early appendices.

Appendix F explores the topic of system interconnect broadly, including wide area and system area networks that allow computers to communicate.

Appendix H reviews VLIW hardware and software, which, in contrast, are less popular than when EPIC appeared on the scene just before the last edition.

Appendix I describes large-scale multiprocessors for use in high-performance computing.

Appendix J is the only appendix that remains from the first edition, and it covers computer arithmetic.

Appendix K provides a survey of instruction architectures, including the 80x86, the IBM 360, the VAX, and many RISC architectures, including ARM, MIPS, Power, and SPARC.

We describe Appendix L below.

1.13 Historical Perspectives and References

Appendix L (available online) includes historical perspectives on the key ideas presented in each of the chapters in this text. These historical perspective sections allow us to trace the development of an idea through a series of machines or describe significant projects. If you’re interested in examining the initial development of an idea or machine or interested in further reading, references are provided at the end of each history. For this chapter, see Section L.2, The Early Development of Computers, for a discussion on the early development of digital computers and performance measurement methodologies.

As you read the historical material, you’ll soon come to realize that one of the important benefits of the youth of computing, compared to many other engineering fields, is that many of the pioneers are still alive—we can learn the history by simply asking them!

Case Studies and Exercises by Diana Franklin

Case Study 1: Chip Fabrication Cost

Concepts illustrated by this case study

■ Fabrication Cost

■ Fabrication Yield

■ Defect Tolerance through Redundancy

There are many factors involved in the price of a computer chip. New, smaller technology gives a boost in performance and a drop in required chip area. In the smaller technology, one can either keep the small area or place more hardware on the chip in order to get more functionality. In this case study, we explore how different design decisions involving fabrication technology, area, and redundancy affect the cost of chips.

1.1 [10/10] <1.6> Figure 1.22 gives the relevant chip statistics that influence the cost of several current chips. In the next few exercises, you will be exploring the effect of different possible design decisions for the IBM Power5.

a. [10] <1.6> What is the yield for the IBM Power5?

b. [10] <1.6> Why does the IBM Power5 have a lower defect rate than the Niagara and Opteron?

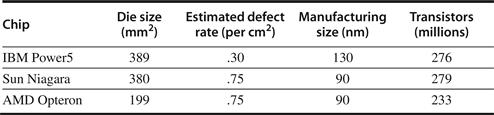
Figure 1.22 Manufacturing cost factors for several modern processors.

1.2 [20/20/20/20] <1.6> It costs $1 billion to build a new fabrication facility. You will be selling a range of chips from that factory, and you need to decide how much capacity to dedicate to each chip. Your Woods chip will be 150 mm2 and will make a profit of $20 per defect-free chip. Your Markon chip will be 250 mm2 and will make a profit of $25 per defect-free chip. Your fabrication facility will be identical to that for the Power5. Each wafer has a 300 mm diameter.

a. [20] <1.6> How much profit do you make on each wafer of Woods chip?

b. [20] <1.6> How much profit do you make on each wafer of Markon chip?

c. [20] <1.6> Which chip should you produce in this facility?

d. [20] <1.6> What is the profit on each new Power5 chip? If your demand is 50,000 Woods chips per month and 25,000 Markon chips per month, and your facility can fabricate 150 wafers a month, how many wafers should you make of each chip?

1.3 [20/20] <1.6> Your colleague at AMD suggests that, since the yield is so poor, you might make chips more cheaply if you placed an extra core on the die and only threw out chips on which both processors had failed. We will solve this exercise by viewing the yield as a probability of no defects occurring in a certain area given the defect rate. Calculate probabilities based on each Opteron core separately (this may not be entirely accurate, since the yield equation is based on empirical evidence rather than a mathematical calculation relating the probabilities of finding errors in different portions of the chip).

a. [20] <1.6> What is the probability that a defect will occur on no more than one of the two processor cores?

b. [20] <1.6> If the old chip cost $20 dollars per chip, what will the cost be of the new chip, taking into account the new area and yield?

Case Study 2: Power Consumption in Computer Systems

Concepts illustrated by this case study

■ Amdahl’s Law

■ Redundancy

■ MTTF

■ Power Consumption

Power consumption in modern systems is dependent on a variety of factors, including the chip clock frequency, efficiency, disk drive speed, disk drive utilization, and DRAM. The following exercises explore the impact on power that different design decisions and use scenarios have.

1.4 [20/10/20] <1.5> Figure 1.23 presents the power consumption of several computer system components. In this exercise, we will explore how the hard drive affects power consumption for the system.

a. [20] <1.5> Assuming the maximum load for each component, and a power supply efficiency of 80%, what wattage must the server’s power supply deliver to a system with an Intel Pentium 4 chip, 2 GB 240-pin Kingston DRAM, and one 7200 rpm hard drive?

b. [10] <1.5> How much power will the 7200 rpm disk drive consume if it is idle roughly 60% of the time?

c. [20] <1.5> Given that the time to read data off a 7200 rpm disk drive will be roughly 75% of a 5400 rpm disk, at what idle time of the 7200 rpm disk will the power consumption be equal, on average, for the two disks?

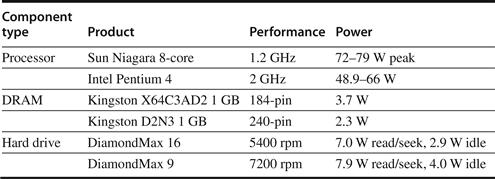
Figure 1.23 Power consumption of several computer components.

1.5 [10/10/20] <1.5> One critical factor in powering a server farm is cooling. If heat is not removed from the computer efficiently, the fans will blow hot air back onto the computer, not cold air. We will look at how different design decisions affect the necessary cooling, and thus the price, of a system. Use Figure 1.23 for your power calculations.

a. [10] <1.5> A cooling door for a rack costs $4000 and dissipates 14 KW (into the room; additional cost is required to get it out of the room). How many servers with an Intel Pentium 4 processor, 1 GB 240-pin DRAM, and a single 7200 rpm hard drive can you cool with one cooling door?

b. [10] <1.5> You are considering providing fault tolerance for your hard drive. RAID 1 doubles the number of disks (see Chapter 6). Now how many systems can you place on a single rack with a single cooler?

c. [20] <1.5> Typical server farms can dissipate a maximum of 200 W per square foot. Given that a server rack requires 11 square feet (including front and back clearance), how many servers from part (a) can be placed on a single rack, and how many cooling doors are required?

1.6 [Discussion] <1.8> Figure 1.24 gives a comparison of power and performance for several benchmarks comparing two servers: Sun Fire T2000 (which uses Niagara) and IBM x346 (using Intel Xeon processors). This information was reported on a Sun Web site. There are two pieces of information reported: power and speed on two benchmarks. For the results shown, the Sun Fire T2000 is clearly superior. What other factors might be important and thus cause someone to choose the IBM x346 if it were superior in those areas?

Figure 1.24 Sun power/performance comparison as selectively reported by Sun.

1.7 [20/20/20/20] <1.6, 1.9> Your company’s internal studies show that a single-core system is sufficient for the demand on your processing power; however, you are exploring whether you could save power by using two cores.

a. [20] <1.9> Assume your application is 80% parallelizable. By how much could you decrease the frequency and get the same performance?

b. [20] <1.6> Assume that the voltage may be decreased linearly with the frequency. Using the equation in Section 1.5, how much dynamic power would the dual-core system require as compared to the single-core system?

c. [20] <1.6, 1.9> Now assume the voltage may not decrease below 25% of the original voltage. This voltage is referred to as the voltage floor, and any voltage lower than that will lose the state. What percent of parallelization gives you a voltage at the voltage floor?

d. [20] <1.6, 1.9> Using the equation in Section 1.5, how much dynamic power would the dual-core system require as compared to the single-core system when taking into account the voltage floor?

qExercises

1.8 [10/15/15/10/10] <1.4, 1.5> One challenge for architects is that the design created today will require several years of implementation, verification, and testing before appearing on the market. This means that the architect must project what the technology will be like several years in advance. Sometimes, this is difficult to do.

a. [10] <1.4> According to the trend in device scaling observed by Moore’s law, the number of transistors on a chip in 2015 should be how many times the number in 2005?

b. [15] <1.5> The increase in clock rates once mirrored this trend. Had clock rates continued to climb at the same rate as in the 1990s, approximately how fast would clock rates be in 2015?

c. [15] <1.5> At the current rate of increase, what are the clock rates now projected to be in 2015?

d. [10] <1.4> What has limited the rate of growth of the clock rate, and what are architects doing with the extra transistors now to increase performance?

e. [10] <1.4> The rate of growth for DRAM capacity has also slowed down. For 20 years, DRAM capacity improved by 60% each year. That rate dropped to 40% each year and now improvement is 25 to 40% per year. If this trend continues, what will be the approximate rate of growth for DRAM capacity by 2020?

1.9 [10/10] <1.5> You are designing a system for a real-time application in which specific deadlines must be met. Finishing the computation faster gains nothing. You find that your system can execute the necessary code, in the worst case, twice as fast as necessary.

a. [10] <1.5> How much energy do you save if you execute at the current speed and turn off the system when the computation is complete?

b. [10] <1.5> How much energy do you save if you set the voltage and frequency to be half as much?

1.10 [10/10/20/20] <1.5> Server farms such as Google and Yahoo! provide enough compute capacity for the highest request rate of the day. Imagine that most of the time these servers operate at only 60% capacity. Assume further that the power does not scale linearly with the load; that is, when the servers are operating at 60% capacity, they consume 90% of maximum power. The servers could be turned off, but they would take too long to restart in response to more load. A new system has been proposed that allows for a quick restart but requires 20% of the maximum power while in this “barely alive” state.

a. [10] <1.5> How much power savings would be achieved by turning off 60% of the servers?

b. [10] <1.5> How much power savings would be achieved by placing 60% of the servers in the “barely alive” state?

c. [20] <1.5> How much power savings would be achieved by reducing the voltage by 20% and frequency by 40%?

d. [20] <1.5> How much power savings would be achieved by placing 30% of the servers in the “barely alive” state and 30% off?

1.11 [10/10/20] <1.7> Availability is the most important consideration for designing servers, followed closely by scalability and throughput.

a. [10] <1.7> We have a single processor with a failures in time (FIT) of 100. What is the mean time to failure (MTTF) for this system?

b. [10] <1.7> If it takes 1 day to get the system running again, what is the availability of the system?

c. [20] <1.7> Imagine that the government, to cut costs, is going to build a supercomputer out of inexpensive computers rather than expensive, reliable computers. What is the MTTF for a system with 1000 processors? Assume that if one fails, they all fail.

1.12 [20/20/20] <1.1, 1.2, 1.7> In a server farm such as that used by Amazon or eBay, a single failure does not cause the entire system to crash. Instead, it will reduce the number of requests that can be satisfied at any one time.

a. [20] <1.7> If a company has 10,000 computers, each with a MTTF of 35 days, and it experiences catastrophic failure only if 1/3 of the computers fail, what is the MTTF for the system?

b. [20] <1.1, 1.7> If it costs an extra $1000, per computer, to double the MTTF, would this be a good business decision? Show your work.

c. [20] <1.2> Figure 1.3 shows, on average, the cost of downtimes, assuming that the cost is equal at all times of the year. For retailers, however, the Christmas season is the most profitable (and therefore the most costly time to lose sales). If a catalog sales center has twice as much traffic in the fourth quarter as every other quarter, what is the average cost of downtime per hour during the fourth quarter and the rest of the year?

1.13 [10/20/20] <1.9> Your company is trying to choose between purchasing the Opteron or Itanium 2. You have analyzed your company’s applications, and 60% of the time it will be running applications similar to wupwise, 20% of the time applications similar to ammp, and 20% of the time applications similar to apsi.

a. [10] If you were choosing just based on overall SPEC performance, which would you choose and why?

b. [20] What is the weighted average of execution time ratios for this mix of applications for the Opteron and Itanium 2?

c. [20] What is the speedup of the Opteron over the Itanium 2?

1.14 [20/10/10/10/15] <1.9> In this exercise, assume that we are considering enhancing a machine by adding vector hardware to it. When a computation is run in vector mode on the vector hardware, it is 10 times faster than the normal mode of execution. We call the percentage of time that could be spent using vector mode the percentage of vectorization. Vectors are discussed in Chapter 4, but you don’t need to know anything about how they work to answer this question!

a. [20] <1.9> Draw a graph that plots the speedup as a percentage of the computation performed in vector mode. Label the y-axis “Net speedup” and label the x-axis “Percent vectorization.”

b. [10] <1.9> What percentage of vectorization is needed to achieve a speedup of 2?

c. [10] <1.9> What percentage of the computation run time is spent in vector mode if a speedup of 2 is achieved?

d. [10] <1.9> What percentage of vectorization is needed to achieve one-half the maximum speedup attainable from using vector mode?

e. [15] <1.9> Suppose you have measured the percentage of vectorization of the program to be 70%. The hardware design group estimates it can speed up the vector hardware even more with significant additional investment. You wonder whether the compiler crew could increase the percentage of vectorization, instead. What percentage of vectorization would the compiler team need to achieve in order to equal an addition 2× speedup in the vector unit (beyond the initial 10×)?

1.15 [15/10] <1.9> Assume that we make an enhancement to a computer that improves some mode of execution by a factor of 10. Enhanced mode is used 50% of the time, measured as a percentage of the execution time when the enhanced mode is in use. Recall that Amdahl’s law depends on the fraction of the original, unenhanced execution time that could make use of enhanced mode. Thus, we cannot directly use this 50% measurement to compute speedup with Amdahl’s law.

a. [15] <1.9> What is the speedup we have obtained from fast mode?

b. [10] <1.9> What percentage of the original execution time has been converted to fast mode?

1.16 [20/20/15] <1.9> When making changes to optimize part of a processor, it is often the case that speeding up one type of instruction comes at the cost of slowing down something else. For example, if we put in a complicated fast floating-point unit, that takes space, and something might have to be moved farther away from the middle to accommodate it, adding an extra cycle in delay to reach that unit. The basic Amdahl’s law equation does not take into account this trade-off.

a. [20] <1.9> If the new fast floating-point unit speeds up floating-point operations by, on average, 2×, and floating-point operations take 20% of the original program’s execution time, what is the overall speedup (ignoring the penalty to any other instructions)?

b. [20] <1.9> Now assume that speeding up the floating-point unit slowed down data cache accesses, resulting in a 1.5× slowdown (or 2/3 speedup). Data cache accesses consume 10% of the execution time. What is the overall speedup now?

c. [15] <1.9> After implementing the new floating-point operations, what percentage of execution time is spent on floating-point operations? What percentage is spent on data cache accesses?

1.17 [10/10/20/20] <1.10> Your company has just bought a new Intel Core i5 dual-core processor, and you have been tasked with optimizing your software for this processor. You will run two applications on this dual core, but the resource requirements are not equal. The first application requires 80% of the resources, and the other only 20% of the resources. Assume that when you parallelize a portion of the program, the speedup for that portion is 2.

a. [10] <1.10> Given that 40% of the first application is parallelizable, how much speedup would you achieve with that application if run in isolation?

b. [10] <1.10> Given that 99% of the second application is parallelizable, how much speedup would this application observe if run in isolation?

c. [20] <1.10> Given that 40% of the first application is parallelizable, how much overall system speedup would you observe if you parallelized it?

d. [20] <1.10> Given that 99% of the second application is parallelizable, how much overall system speedup would you observe if you parallelized it?

1.18 [10/20/20/20/25] <1.10> When parallelizing an application, the ideal speedup is speeding up by the number of processors. This is limited by two things: percentage of the application that can be parallelized and the cost of communication. Amdahl’s law takes into account the former but not the latter.

a. [10] <1.10> What is the speedup with N processors if 80% of the application is parallelizable, ignoring the cost of communication?

b. [20] <1.10> What is the speedup with 8 processors if, for every processor added, the communication overhead is 0.5% of the original execution time.

c. [20] <1.10> What is the speedup with 8 processors if, for every time the number of processors is doubled, the communication overhead is increased by 0.5% of the original execution time?

d. [20] <1.10> What is the speedup with N processors if, for every time the number of processors is doubled, the communication overhead is increased by 0.5% of the original execution time?

e. [25] <1.10> Write the general equation that solves this question: What is the number of processors with the highest speedup in an application in which P% of the original execution time is parallelizable, and, for every time the number of processors is doubled, the communication is increased by 0.5% of the original execution time?