Chapter 6

Algebra and the arithmetic of remainders

This chapter features a new type of algebra, the arithmetic of remainders, which is both an ancient topic and one that has found a major contemporary application in Internet cryptography. We first say a little more about abstract algebra, as it forms the backdrop to the particular example types that you will meet in the remainder of the book.

Groups, rings, and fields

The integers under the operation of addition, (ℤ, +), are a key example of what is known as a group. A group consists of an underlying set, which in the case of the integers is ℤ, coupled with an operation, addition (+) in this case, which allows two members of the set, a and b say, to interact and produce another member, a + b, of the same set. A group operation must be a binary operation, like addition, meaning that it involves two elements of the set. What is more, for a binary operation to be a group operation we insist further that the operation satisfies three particular conditions, all of which hold for integer addition: the operation, +, must be associative, i.e. a + (b + c) = (a + b) + c for any three members a, b, c of the set; there must be an identity element, denoted by 0, which has the property that a + 0 = 0 + a = a always holds; and, finally, each member a of the set must have an inverse element, denoted here by −a, that reverses the effect of adding a in the sense that a + (−a) = (−a) + a = 0, the identity element.

Integer addition also satisfies the commutative law in that a + b = b + a. Commutativity is not, however, part of the general definition of a group, but when the operation of a group G does respect the commutative law, we say that G is an abelian group, a term derived from the surname of Niels Abel (1802–29), who gave his name to the Ruffini-Abel Theorem mentioned in Chapter 5 in relation to the insolvability of fifth-degree polynomial equations.

From Chapter 7 onwards we will meet other examples of sets, in particular sets of matrices, which form groups with operations that are completely different from ordinary addition. However, because these new operations still satisfy the group axioms, any general results about groups will hold in these contexts as well, and this gives a pointer as to why groups and other abstract algebras are studied in full generality.

The payoff from this approach stems from the fact that whatever theorems and relationships come to light in the context of abstract algebra then apply to any particular algebraic object that obeys the rules in question. Mathematicians often seek out the widest setting in which key theorems hold, as that not only increases their scope but also gives a clearer understanding as to why they are true. For these reasons, you will find that textbooks on abstract algebra often refer to semigroups and groups, which are algebras with a single associative operation, while rings and fields, which are notions that we are about to introduce, are algebras with two operations linked via the distributive law. And there are more: lattices are algebras with an ordered structure, while vector spaces and modules are algebras where the members can be multiplied by scalar quantities from other fields or rings. Algebras themselves are also studied collectively. This holistic approach is known as universal algebra and its practitioners search for theorems that are valid for algebras of all kinds.

The integers under addition are an abelian group that we have been dealing with since childhood, which is why the group properties in this context are natural to all of us. However, right from the beginning, we work with two operations, addition and multiplication, when dealing with ℤ. For this reason we need to consider algebras like the integers and like the rational numbers, ℚ, which have a pair of binary operations, linked by the distributive law.

A commutative ring is a type of algebra, such as the integers ℤ, which possesses two operations, denoted by + and ⋅. Under the operation denoted by +, the set forms an abelian group. The multiplication operation too is associative and commutative but a ring is also required to satisfy the distributive law of addition, +, over multiplication, ⋅, namely that a ⋅(b + c) = a ⋅ b + a ⋅ c. A different kind of example of a commutative ring is the ring ℙ of all polynomials with, let us say, real coefficients, under the operations of polynomial addition and multiplication.

A field is a special type of commutative ring, an example being the rational numbers ℚ, where there is also a multiplicative identity, often denoted by 1 (an attribute that ℤ also possesses; for this reason ℤ is known as a unital ring), and every non-zero member a of a field has a multiplicative inverse, denoted by either a⁻¹ or 1/a, such that a⁻¹ ⋅ a = 1.

Our two extended number systems of the real numbers, ℝ, and the complex numbers, ℂ, both pass the test that earns them the title of a field. On the other hand, the collection ℙ of all polynomials with real coefficients form a commutative unital ring that is not a field.

In Chapter 2 we proved results such as a × 0 = 0 and that the additive inverse, −a, of a is unique. Although we were thinking of the letter a as an integer when conducting those arguments, the symbol a could have stood for any member of an arbitrary commutative ring, as the argument rests only on laws that apply in that context. It follows that these results apply in particular to the ring of polynomials, ℙ. Moreover, the Binomial Theorem holds in any commutative ring, so the symbols x and y in the binomial (x + y)ⁿ can stand for polynomials and the conclusion of the theorem is equally valid.

Although these are quite simple results, ℙ has more in common with ℤ, in that a form of the Euclidean Algorithm works for polynomials as well: for any polynomials p(x) and q(x), we may find a unique monic polynomial, g(x), which is a gcd of p(x) and q(x) in the sense that any other such common factor of p(x) and q(x) is itself a factor of g(x). This guarantees that the rings ℤ and ℙ share other more subtle algebraic properties concerning their internal make-up, known as their ideal structure, which will not be elaborated on further here but is central to their study.

We shall shortly be leaving these abstract considerations for the time being, but the idea to take forward is that various types of algebras have been defined where the collections under consideration need to satisfy a special set of algebraic rules. The reason why one particular arrangement of rules is the focus of attention is because certain important yet different collections of algebraic objects have been found to share these properties, and for that reason it is worthwhile studying particular types of algebra in full generality, groups, rings, and fields being three cases in point.

Before moving on, however, we make one more observation that particularly applies to the integers. Early in the piece we proved that any product involving zero is equal to zero: a × 0 = 0. Is the converse true? In other words, if a product of integers ab = 0, may we infer that at least one of the factors, a or b, must be 0?

In the case of the ring of integers, the answer is yes, and a commutative unital ring with this property is called an integral domain in recognition of this integer-like property. We can see this is true by observing that ℤ may be regarded as being embedded in its field of fractions, which is ℚ. If we have ab = 0 in ℤ then ab = 0 in ℚ as well, and then either a = 0 or, if not, we may multiply both sides of this equation by a⁻¹ to obtain

hence if ab = 0 then at least one of a and b is 0.

Although we cannot generally divide within an integral domain such as the integers, we can freely cancel because the characteristic property of an integral domain is just what is needed to guarantee this. Suppose we have ab = ac in an integral domain with a ≠ 0. Then ab − ac = a(b − c) = 0, and since a is not 0, it follows that b − c is zero, which is to say b = c, and so we may cancel the common factor a from both sides of ab = ac. Not every commutative ring enjoys this feature. As we shall see in the next section, there are commutative rings that are not integral domains (and so cannot be embedded into a field). Indeed, the members of these rings can be integers—the addition and multiplication operations, however, are a little different.

Modular arithmetic: rules of engagement

We now set out to establish the algebraic rules for the ring of integers modulo n. Modular arithmetic is often called clock arithmetic, as we imagine a clock face with n numbers, 0, 1, …, n − 1, and we do our arithmetic on that, meaning that whenever you go past n − 1 you return again to 0 in a fashion reminiscent of a clock, or of a turnstile, or of cycles of a calendar. That all sounds quite simple and inconsequential, but the opposite is true. Modern cryptography is based on clock arithmetic and if it were all simple, the codes that rely on it would be simple to crack, but they are anything but. The erratic and unpredictable way that remainders arise under division lies at the heart of it all. We begin by identifying where two integers are essentially the same from the point of view of our arithmetic clock.

We call two integers a and b equivalent or congruent modulo n if n|a − b, which is to say that a − b = kn for some integer k or, if you prefer, a = b + kn. Intuitively, a and b are equivalent if they represent the same time on the n-hour clock. We denote equivalence modulo n by the equation a ≡ b (mod n).

A third way of phrasing this notion, which is perhaps the most important, is that a ≡ b (mod n) if and only if a and b leave the same remainder when divided by n. For example, 22 ≡ 40 (mod 6) as both 22 and 40 leave the remainder 4 when divided by 6.

The congruence sign is meant to suggest something akin to equality, and this is borne out by the basic observations that a ≡ a (mod n), that if a ≡ b (mod n) then it is equally the case that b ≡ a (mod n), and, as with ordinary equality, that the congruence sign has the transitive property in that if a ≡ b (mod n) and b ≡ c (mod n) then a ≡ c (mod n), as all three numbers will necessarily leave the same remainder when divided by n. A consequence of these three properties is that congruence mod n partitions the integers into n equivalence classes, as they are called. For example, for n = 4 the four classes, are

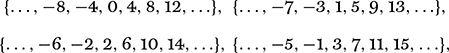
so that −3 ≡9 (mod 4), 24 ≡ 0 (mod 4), and so on. The n classes of equivalence modulo n are often written as [0], [1], [2], …,[n − 2], [n − 1] and the representatives of each of these classes, 0, 1, 2, …, n − 1, are called the least residues modulo n, which is to say they are the n possible remainders when an integer is divided by n. Every integer lies in one and only one of these n classes.

Modular arithmetic is all about manipulating these least-residue classes and, given that they represent infinite collections, that may sound daunting. However, you are well used to the idea that a fraction such as 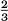is equal to, or more accurately is equivalent to, any of an infinite number of fractions of the form 2m/3m. As long as we are confident in the rules that govern fractions, this causes no trouble. The saving grace is that there is a unique representative of a fraction, that being the fraction cancelled to its lowest terms, which we tend to work with where possible. At times, however, fractions that are not fully cancelled down arise during calculations. In much the same way, the least residue is the smallest non-negative number in its equivalence class modulo n, and we shall normally work with these representatives while being aware that sometimes it may be convenient to use other representatives instead.

We will, however, need to know the algebraic rules that govern our new arithmetic, which is what we now go about establishing.

The notation a ≡ b (mod n) is highly suggestive of ordinary equality, tempting us to indulge in the same kinds of algebraic manipulations we have worked with since our schooldays. If this were not the case, the choice of notation would not be appropriate. We will find, however, that the laws of modular arithmetic, although similar, are not identical to those of ordinary addition and multiplication.

We do not record complete proofs of all the results listed in this section. However, the claims, which all follow from the definition of congruence and elementary properties of number division, can be found in any textbook on number theory.

We begin with a simple observation, (a + c) − (b + c) = a − b, from which it follows that a ≡ b (mod n) if and only if a + c ≡ b + c (mod n), so that we may freely add any integer to both sides of a congruence, as these equations are often called (and so also subtract any integer). This fact ensures that whenever a ≡ b (mod n) is true, we may replace a + c by b + c in any congruence equation modulo n.

Other nice properties of congruences now follow, which can be justified by arguments like the previous one. For instance, if a₁ ≡ a₂ (mod n) and b₁ ≡ b₂ (mod n), then a₁ + b₁ ≡ a₂ + b₂ (mod n). This in effect now gives us an addition operation on the congruence classes, for it says that when we add two numbers modulo n, the class of the answer does not depend on which numbers are used to represent those classes in the sum. For example

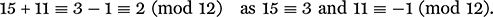
We call this addition of classes via their representatives addition modulo n and write (ℤ_n, +) to denote the set of least residues {0, 1, 2, …, n − 1} under the operation, +, of addition modulo n. The additive identity of this number system is 0, and the operation + is commutative and associative. We thus have a fully fledged abelian group, as each a ∈ ℤ_n has n − a as its inverse because a + (n − a) = n ≡ 0 (mod n).

For multiplication, it follows in a similar fashion to addition that a ≡ b (mod n) implies that ac ≡ bc (mod n), and from this we deduce that a₁ ≡ a₂ (mod n) and b₁ ≡ b₂ (mod n) imply that a₁b₁ ≡ a₂b₂ (mod n). Hence, as with addition, we may replace any number in an expression involving multiplication by any other from its congruence class modulo n and the result is congruent modulo n to the original. Moreover, congruence classes may be multiplied together through their representatives, and the outcome is independent of which representatives we adopt. What is more, commutativity, associativity, and distributivity of multiplication all hold in consequence of these laws being valid for the integers. In conclusion, we now have a commutative unital ring with a multiplicative identity 1, that ring being denoted by (ℤ_n, +, ×).

In the previous section, it was pointed out that the ring of integers is also an integral domain, giving multiplication in ℤ the cancellation property. Is that property also inherited by its ‘image’ ℤ_n? The answer is in general ‘no’ because if n is a composite number, n = ab say, then neither a nor b is congruent to 0 modulo n but ab = n ≡ 0 (mod n). As a consequence, we cannot cancel freely: for example, 15 × 6 ≡ 11 × 6 ≡ 18 (mod 24) but we cannot cancel the common factor of 6 to conclude that 15 ≡ 11 (mod 24), for that is clearly false.

An important class of exceptions is that of the rings ℤ_p, where p is a prime, as here Euclid’s Lemma comes to the rescue: if ab ≡ 0 (mod p) then p|ab, so that p|a or p|b, which is to say a ≡ 0 (mod p) or b ≡ 0 (mod p), which says exactly that ℤ_p is an integral domain. Indeed, that makes ℤ_p a field, for any finite integral domain F is a field. (This is because the cancellation law tells us that for any non-zero a ∈ F, the list of products of the form ab cannot have repeats and so, by finiteness, must exhaust the whole of F: in particular, one product ab must equal the multiplicative identity 1, and therefore a does indeed have an inverse, namely this number b.) Hence, for any prime p, the integral domain ℤ_p is a finite field with p elements. It turns out that there are other finite fields (indeed, there is exactly one finite field for every prime power p_n), but there are no others. This topic will be revisited in our final chapter.

Returning to the subject of the current chapter, the rings ℤ_n, there is nonetheless a form of cancellation that is valid across any congruence sign. Let d denote the gcd of c and n. Then ac ≡ bc (mod n) implies that a ≡ b (mod n/d). For example, from the equation 24a ≡ 60b (mod 93), we may wish to cancel the common factor of c = 12 in the congruence, while n = 93 = 3 × 31. Hence the gcd of c and n is d = 3, and we conclude that 2a ≡ 5b (mod 31). That is to say, you can be sure that 2a − 5b is a multiple of 31, but it is not necessarily a multiple of the larger, original modulus 93.

We close this section by drawing attention to one big advantage of arithmetic modulo n over the ordinary non-modular type, which is that since there are but n different possibilities to consider, important facts can often be verified simply by testing all the n numbers involved. For example, we now show that the sum of three squares, a² + b² + c², never has the form 8k + 7.

To see this, instead of using the least residues 0, 1, …, 7 to represent the eight congruence classes, let us use the alternative set −3, −2, −1, 0, 1, 2, 3, 4, as this collection is simpler to deal with when squaring. Any square a² equals modulo 8 one of 0, 1, 4; for example, if a ≡ −3 (mod 8) then a² ≡ (−3)² = 9 ≡1 (mod 8). It follows that the sum of three squares modulo 8 is equal to a sum of three of the numbers (with repeats allowed) from the list of possibilities of 0, 1, 4. We find that under these rules we can generate the numbers 0, 1, 2, 3,4 5, and 6 (for example, 6 = 1 + 1 + 4), but not 7. Therefore we conclude that for any three squares, a² + b² + c² ≢ 7 (mod 8). A famous theorem in number theory is that any non-negative integer is the sum of four squares. The preceding calculation shows, however, that there are infinitely many positive integers, namely 7, 15, 23, 31, …, that are not the sum of three.

Solving linear congruences

Having described the general algebraic structure of the ring ℤ_n, we will now show how to solve linear equations in this ring: equations of the form ax + c ≡ d (mod n). Of course, there is no difficulty in subtracting c from both sides of this equation, and so the real question is how do we solve congruences of the form ax ≡ b (mod n)?

To witness the range of behaviour offered by even the simplest congruences, consider the near-identical trio

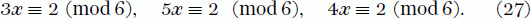
By testing each of the six possible values, we find that the first congruence has no solution at all, the second has a unique answer, 4, and the third equation has two solutions, namely 2 and 5.

The following theorem gives the number of solutions to ax ≡b (mod n). Let d stand for the gcd of a and n. There are no solutions to the congruence equation if d is not a factor of b, but if it is then there are d solutions.

This is consistent with what we have just observed about the three equations in (27). The first has no solution, as the gcd of the pair 3 and 6 is 3, which is not a factor of 2. In the second congruence, the gcd of 5 and 6 is 1, and of course 1 is a factor of 2 and our second equation indeed has exactly one solution. For the final equation, the relevant gcd is d = 2, the gcd of 4 and 6, and since 2|2 is certainly true, we expect and obtain two solutions here, all in accord with the general description provided by thetheorem.

To see that we must have d|b in order to have a solution, let us suppose that ax ≡ b (mod n), whence ax − b = kn, say, or, making b the subject, b = ax − kn. It follows that any common factor of a and n must divide b also, and in particular this is true of d, the gcd of a and n.

As was implicitly shown in Chapter 3, a linear equation ax = b in a field has a unique solution, x = a⁻¹b, so let’s begin with the case where n is a prime, for here we know from the previous section that ℤ_n is indeed a field.

The solution is formally given by x = a⁻¹b, but the question remains as to how to find a⁻¹. Let us take an example, 6x ≡ 14 (mod 31). Since 31 is prime and we are working in a field, we may indeed cancel and simplify to 3x ≡ 7 (mod 31). The simplest way to solve this is now to add multiples of the modulus to the RHS until we can cancel the remaining coefficient of 3, and so we consider the sequence 7, 7 + 31 = 38, 38 + 31 = 69, …. We now get the answer from 3x ≡ 69 (mod 31) and so x ≡ 23 (mod 31), which is to say that 23 is the unique least-residue solution to our original congruence.

In the case of a composite modulus, however, there may be more than one answer, as we saw with (27). However, the congruence can be solved by adding multiples of the modulus to the RHS until the coefficient of x has been cancelled down to 1. (The argument that justifies this claim is based on working the Euclidean Algorithm in reverse.) The full set of solutions then consists of the fundamental solution, x say, to which we may add multiples of n′ = n/d until we have the full suite of d solutions, as is illustrated in the next two examples.

For 4x ≡ 2 (mod 6), we have d = gcd(a, n) = gcd(4, 6) = 2. We may cancel the 2 to get 2x ≡ 1 (mod 3) ⇔ 2x ≡ 4 (mod 3) ⇔ x ≡ 2 (mod 3). The full set of least-residue solutions to the original congruence then consists of the fundamental solution, in this case x = 2, to which we may add d − 1 = 2 − 1 = 1 further solution, that being

A more challenging example is

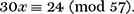
Here, a = 30, b = 24, n = 57, d = gcd(30, 57) = 3 and so

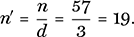
Since 3|24, we cancel accordingly and obtain 10x ≡ 8 (mod 19). We now have a prime modulus with a unique solution and we may freely cancel again to obtain 5x ≡ 4 (mod 19). We look through the sequence 4 + 19n to find a multiple of 5:

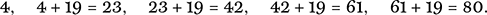
Hence 5x ≡ 80 (mod 19), whence x ≡ 16 (mod 19). Since d = 3, we have three solutions all told, and since n′ = 19 these are 16, 16 + 19 = 35, and 35 + 19 = 54.