Social Organization and Innovation

Why does social organization happen by itself? Why does it evolve as the movement of the members of the society increases? Why does the organization become more hierarchical, with greater nonuniformity in the distribution of movement over the inhabited territory when the size of the society increases?

The preceding chapters empowered us to address these questions from physics. Key is the idea that the phenomenon of social organization is rooted in the universal physics phenomenon of economies of scale, in the presence of freedom to change. It takes less power to move a unit mass in bulk, along with many units, than to move one unit alone. The freedom to change and to choose between competing changes is essential.

The physics aspect is crucial because many people believe that human life is too complicated to be predictable. That is true if one attempts to predict the single acts of a single individual. Brownian motion is also too complicated if one attempts to predict the behavior of one molecule. The whole society (the macro) has its own behavior, and that is predictable—the social, the Brownian, the river basin, and the spreading plague. The constructal law of physics covers them all.

Freedom enables the mover to opt for changes that enhance access and facilitate flow. Life is movement, and to live (to persist in time) every individual has the urge to move more easily by morphing its path and rhythm through its environment. Joining and organizing happen as a consequence. In transportation, the fuel spent per unit of freight is smaller on a large vehicle than on a small one. In animal locomotion, the food eaten per unit of animal mass moved is smaller for the elephant than for the antelope. This physics phenomenon is measurable and put on display in many studies of the evolution of animal design and power plants, which show that the efficiency increases with the size of the flow system (cf., Chap. 2).

In this chapter, we illustrate the natural phenomenon of joining (organization) with two highly dissimilar models [1]. One model is inanimate: river basins generated by several rules of construction (Fig. 9.2). The other model is also about water flow, but it is animate: the production and distribution of heated water over human settlements that grow on an area.

The question is whether the phenomenon of social organization can be placed on a physics foundation. This question is stimulating a growing domain in physics, with visible progress in crowd dynamics, economics, urban design, and cultural evolution. The physics literature reviewed in Ref. [1] and cited in the preceding chapters shows that a physics basis exists for phenomena and “intangibles” previously associated with the social realm, for example, economies of scale, diminishing returns, wealth distribution, hierarchy, the living space, and evolution as physics.

To get to the physics basis of social organization, it pays to review the core lessons of the preceding chapters: Nothing moves unless it is forced to move against an environment that resists. The forcing comes from power; the power comes from fuel and food consumed in “engines,” which are natural and human-made, and the movement evolves with freedom toward architectures that offer easier and greater access to what flows.

Furthermore, on a finite area or in a finite volume, the evolved flow architectures are tree-shaped, hierarchical, with few large and many small channels flowing together to bathe the whole flow system (river basins, lungs, snowflakes, city, and air traffic). In Chap. 4, we saw that the annual consumption of fuel in society is proportional to the annual measure of wealth. Because the movement on a territory is hierarchical, and because movement is the physical consequence of the consumed fuel, the consumption of fuel is also spread nonuniformly and hierarchically on the globe. Finally, because fuel consumed is proportional to wealth, the unavoidable conclusion from physics is that wealth must also be distributed hierarchically (“unequally”) in the live, flowing and freely morphing world.

The predictions that result from this physics theory are in accord with observations throughout the recorded history of civilization. Hierarchy and wealth inequality “happen,” while any effort to eliminate inequality completely is short lived, marginally successful at best, violent, and murderous at worst. The river basin has its physics basis, and because of the physics the architecture always emerges as hierarchical. Likewise, a flowing and thriving society is eminently hierarchical.

Caution: what I just wrote should not be misrepresented to mean that there is no point in trying to curtail inequality. Any society tries that naturally, because it is good for the peace, the life and the persistence of the whole. The message from physics is that to eliminate inequality is impossible. Every individual and society is better off knowing the difference between the possible and the impossible: the difference is explored further in Chap. 10. Everyone is better off knowing what to try and what not to try. This difference is the key to envisioning, designing, and implementing one’s future.

The clue to unearthing the physics basis of social organization is shown in Fig. 4.7, in which income inequality is indicated by the gap between the diagonal and each of the six curves. Intriguing is the impression that the society of South Africa is not making a strong effort to reduce inequality. The impression is wrong. Here is how to check the validity of this impression. Is every social group acting toward a more uniform distribution of wealth? If the answer is yes, then this is the physics basis of social organization with controlled inequality, which happens to be the defining feature of human society today.

The way to approach the question is to start from a reference design, where social organization is completely absent, as in river basins and other “vascular” architectures not made and maintained by humans, either bio or non-bio.

River basins are freely evolving flow architectures. As we saw already, river basins obey rules of construction that hold for all basin sizes, for example, four tributaries (M₁) to one mother channel (n = 4, on an average). This construction is sketched in Fig. 4.3, where each of the four tributaries comes from an elemental square area.

In the river basin, the movement is the water flow rate over the territory. Figure 5.1 shows the fraction of the total movement (ε) versus the fraction of the total population of river channels.

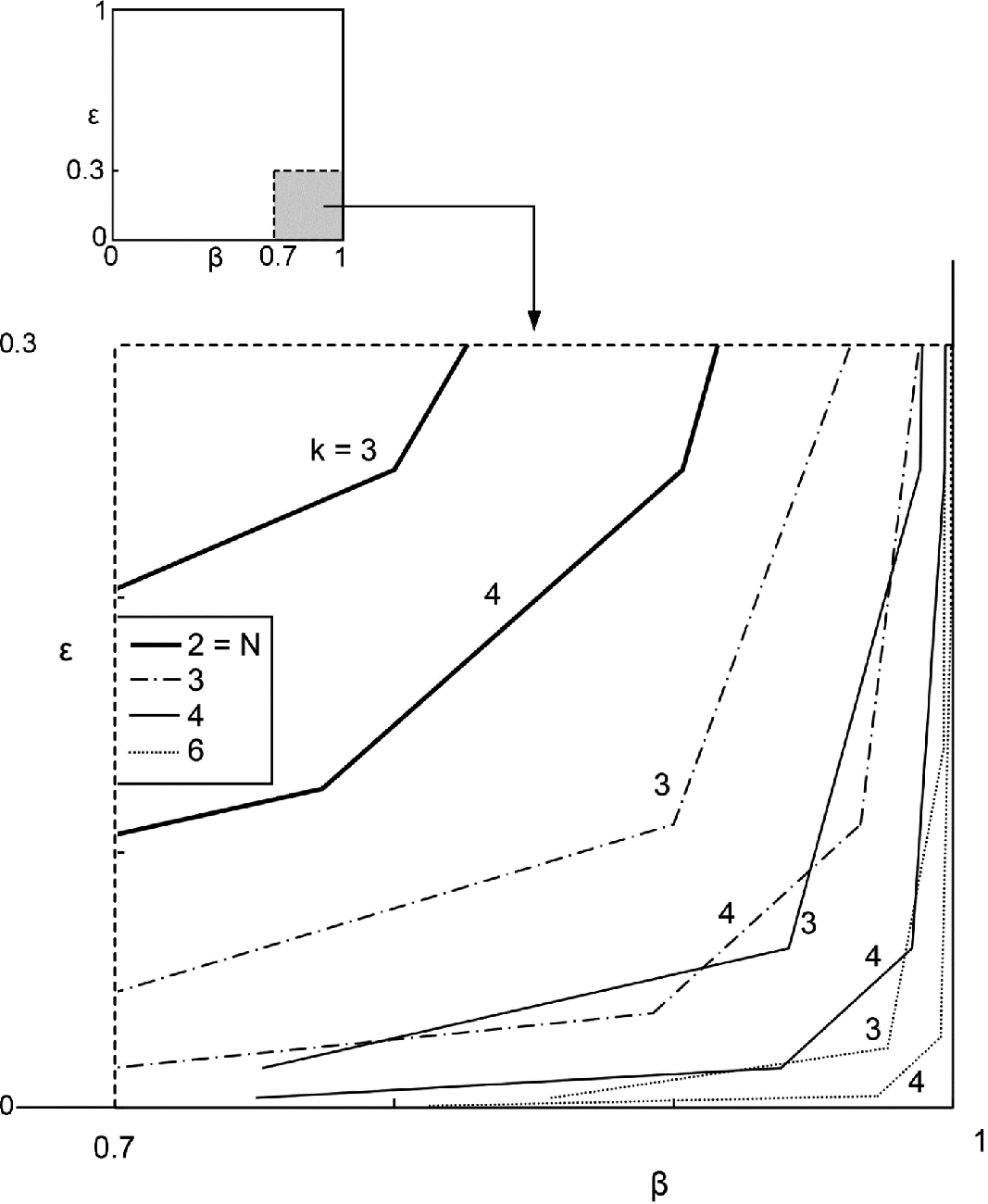
../images/482511_1_En_5_Chapter/482511_1_En_5_Fig1_HTML.png — Fig. 5.1
The hierarchical distribution of flow rate (ε) in the population of channels (β) in the river basin of Fig. 4.3. The figure shows that most of the population (large β), accounts for a small fraction of the total flow (small ε)

Compared with Fig. 4.7, the distribution of movement in river basins is severely nonuniform. In Fig. 5.1, the ε–β curves are crowded in the lower right corner. The hierarchy of this inanimate flow architecture is extreme. Perhaps in a thriving society things will be different.

Why does organization happen in a society in the first place? Throughout the history of social organization, the evolution away from the uniform distribution of flow over the population is a consequence of the trade-off between (a) the generation of the original flow, which is less wasteful when the original stream is larger (because of economies of scale), and (b) the route of transport from source to user, which is more wasteful when the length of the route is greater. Both losses, (a) and (b), are losses in the physics sense: they are measurable in terms of destruction of useful energy (exergy, joules), or waste of fuel and food (kilograms). Both losses increase with the size of the original stream that reaches every member of the population; however, (a) increases more slowly than (b).

The evolution from the “one size fits all” to hierarchy in the human realm can be predicted by considering the production and spreading of one material that enhances human movement (life), for example, a material that was made possible by the control and adoption of fire. Consider the use of hot water, which is essential for better food, more food (food preservation), shelter (warmth), hygiene, health, and every other essential feature of civilized living.

In the early days, water was heated in one vessel for the inhabitants of one settlement, as in the lower left design of Fig. 5.2. The round area element is the territory of one settlement. The point in the center is the settlement and its source of hot water. The amount of hot water used by one settlement per unit time is m₁. The use of hot water, like the burning of wood, was distributed equally over the population.

../images/482511_1_En_5_Chapter/482511_1_En_5_Fig2_HTML.png — Fig. 5.2
The loss of heat per user versus time $(\tilde{q} ,\;{\text{on}}\;{\text{the}}\;{\text{ordinate)}}$ versus the amount of water consumed by one individual ( $\tilde{m}$ , on the abscissa). From left to right (i.e., in time), the organization evolves from individual production and use of hot water (N = 1) to clusters of three and six users supplied radially by one central heater. Note the discrete changes in flow architecture on the ladder to better organization and performance over time

$$(\tilde{q} ,\;{\text{on}}\;{\text{the}}\;{\text{ordinate)}}$$ — Fig. 5.2
The loss of heat per user versus time $(\tilde{q} ,\;{\text{on}}\;{\text{the}}\;{\text{ordinate)}}$ versus the amount of water consumed by one individual ( $\tilde{m}$ , on the abscissa). From left to right (i.e., in time), the organization evolves from individual production and use of hot water (N = 1) to clusters of three and six users supplied radially by one central heater. Note the discrete changes in flow architecture on the ladder to better organization and performance over time

Over time, users formed a cluster around one central heater that delivered hot water to everyone, radially. Today, the modern distribution consists of increasingly more complex hierarchies with intermediate nodes of distribution between the one large center of production and the many small and equal peripheral users. Why should this have happened?

Complex hierarchies are understood more simply as tree-shaped flows, Fig. 5.3. Their complexity increases over time as the society becomes more advanced, the individual use of hot water (m₁, or $\tilde{m}$ ) increases, and the number of individuals who join the group increases. On the ordinates of Figs. 5.2 and 5.3, we see the loss of heating (or the wasteful consumption of fuel) during the production of the unit of hot water plotted on the abscissa. These losses occur during heating the water, and along the distribution lines. On the abscissa, the value of $\tilde{m}$ (dimensionless) is proportional to the amount of water needed by one individual per unit time, m₁. The analytical details behind these figures are available in Ref. [1].

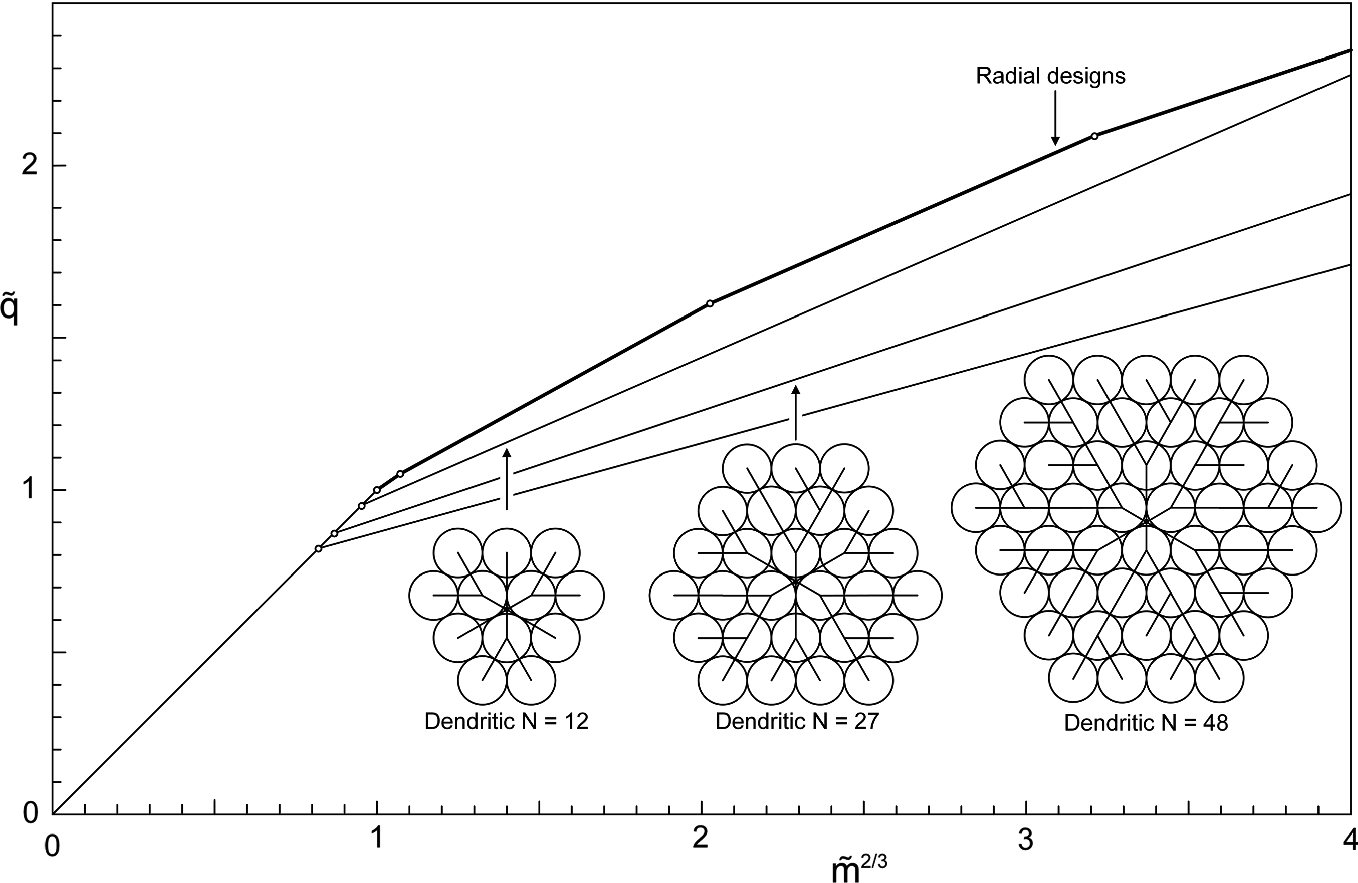
../images/482511_1_En_5_Chapter/482511_1_En_5_Fig3_HTML.png — Fig. 5.3
This figure is a continuation of the evolution sketched in Fig. 5.2. Note the beneficial effect of changing the design from radial (Fig. 5.2) to dendritic

As civilization develops, the amount of hot water used by one individual increases. The time axis points from left to right in Figs. 5.2 and 5.3. Over time, it becomes possible to produce and distribute hot water in central heaters that serve clusters of users. In the pursuit of less fuel waste $(\tilde{q})$ per unit of hot water delivered to the population, the arrangement of users and heaters must evolve stepwise, from uniformity (N = 1) to larger clusters (N = 3, 6, …) with longer distribution lines, as one can discern by reading Fig. 5.2 from left to right. The water production and distribution must evolve from uniformity to organization, that is, toward nonuniformity.

Radially fed clusters with 3, 6, 12, and 27 users are shown in Fig. 5.2. Tree-shaped distribution designs are shown in Fig. 5.3 for clusters with 12, 27, and 48 users. Clusters with 12 users are displayed in both figures, and they are different. In Fig. 5.2, the distribution lines are radial, and in Fig. 5.3 they are tree-shaped. The more economical design is the tree-shaped, the hierarchical.

The model used for the evolution of the use of hot water reveals two essential features of the natural occurrence of social organization. The first is the urge to unite, to coalesce around a more efficient producer that serves every member of the group. This is the incipient emergence of hierarchy, one large (the center) and many small but equal around the large one.

The second feature is the emergence of more complex hierarchies with intermediate nodes of distribution between the one large in the center and the many small and equal on the periphery. The more complex hierarchies are described graphically as tree-shaped flows. Their complexity increases over time as the society becomes more advanced, as $\tilde{m}$ increases in time (to the right on the abscissas of Figs. 5.2 and 5.3), and the number of individuals who join the organization increases.

We arrive in this way at Fig. 5.4, which illustrates the nonuniform distribution of the commodity (hot water) over the population. This figure is reminiscent of Fig. 4.7. The three curves are drawn for the three dendritic designs shown in Fig. 5.3. On the abscissa, from 0 to 1, is the population of flow channels of distribution. On the ordinate is the fraction (ε) of the total flow rate that corresponds to a fraction (β) of the population of channels. The piecewise linear curves are convex, just like in Fig. 5.1 for the river basins. The curves shift downward as the complexity of the organized flow system increases.

../images/482511_1_En_5_Chapter/482511_1_En_5_Fig4_HTML.png — Fig. 5.4
The hierarchical distribution of hot water flow over the population, and the effect of the increasing group size N. Note the similar features of this figure and Fig. 5.1

This trend agrees with the trend exhibited by river basins, except that the human-made designs have curves (Fig. 5.4) that are located well above the ε–β curves of the river basins (Fig. 5.1). Conclusion: Inequality is considerably less severe when social organization is present.

Inequality happens even when the natural hierarchical channels are destroyed and replaced with an artificial one-size design everywhere, as during communism. To see why, consider the flows presented in Fig. 5.5, because designs more egalitarian than these do not exist. The square territory is inhabited by identical elements, which are connected by identical one-size channels. The center of each element is indicated with a small circle. Each center receives the same flow input as its neighbors (from above, perpendicular to the plane of Fig. 5.5), and that flow is analogous to the uniform rain input M₀ falling on the river basin in Fig. 4.3. The individual inputs collected from all the elements are evacuated as one stream through one corner of the square territory.

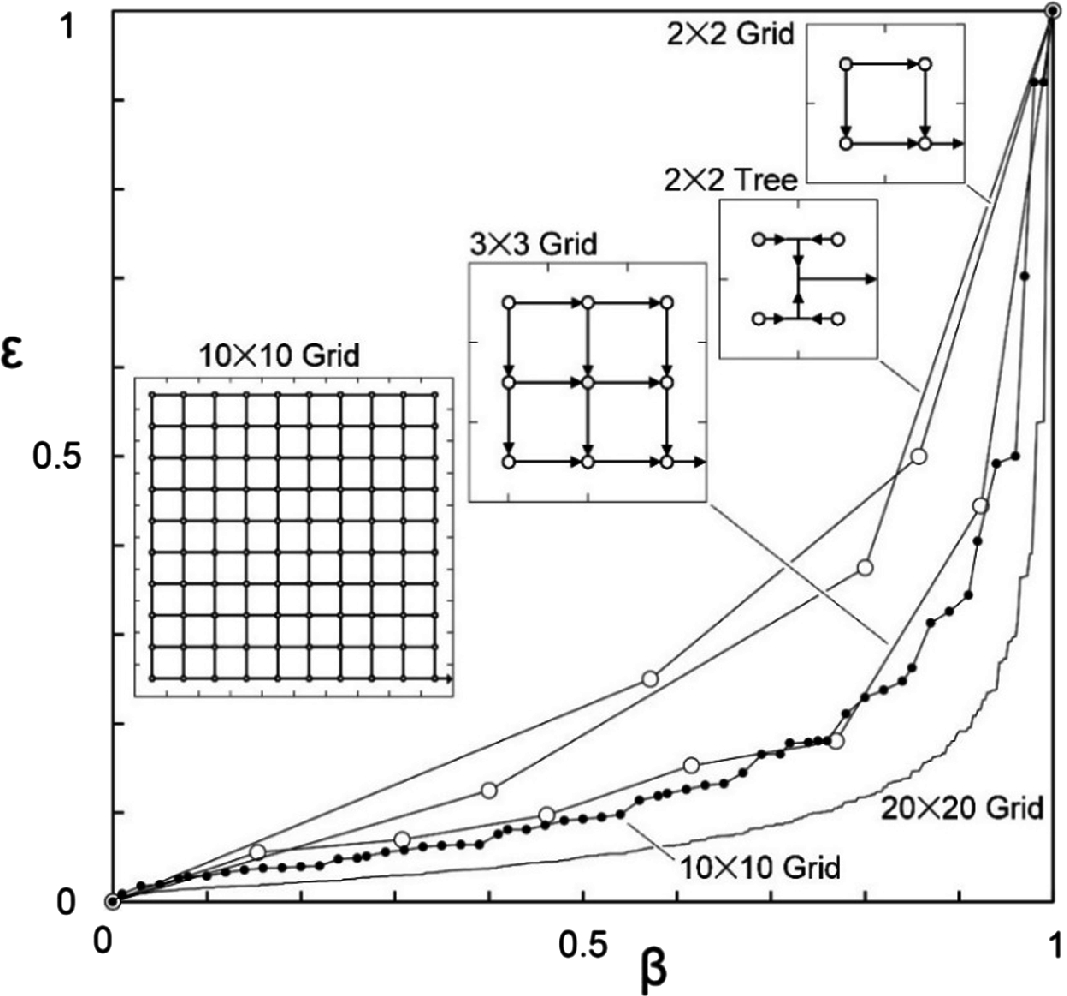
../images/482511_1_En_5_Chapter/482511_1_En_5_Fig5_HTML.png — Fig. 5.5
Equal inhabitants, equal inputs, and equal channels are not bathed by equal flow rates on a territory with area-point flow. The fraction of the total flow rate (ε) versus the fraction of the total population (β) on a territory connected by a square grid n × n. The inequality in the distribution of flow over the area becomes more accentuated as the population size increases

The concept of equality, however, is not to be confused with equal individuals and equal links between individuals. In Fig. 5.5, the one-size links form perfectly square grids of n × n individuals. Three territory sizes are shown for n = 2, 3, and 10. For calculating the node-to-node flow rates in cases n = 3, 10, and 20, it was assumed that the flow rate is proportional to the node-to-node difference that drives the flow (similar to pressure difference or altitude difference for fluid flow). In the limit $n\,\, \to \,\,\infty$ , the square territory is bathed by diffusion, with a diffusivity constant (a physical measure) that has the same value over the entire territory, and where the stream evacuated from the whole territory is generated uniformly at every point on the territory, like the rain falling on the plain.

After calculating the individual flow rates between adjacent nodes, we constructed [1] the ε–β curves shown in Fig. 5.5. The flow from the square territory to the outlet is distributed nonuniformly through the uniform grid. Most of the total flow rate (ε = 1) is concentrated in a small group of channels, near β = 1. Geographically, that group is composed of individuals who happen to be in the vicinity of the point of attraction, which serves as outlet for the big stream.

This is how we discover that inequality persists even when the “one-size” design is imposed artificially. Geography is the reason for inequality in this extreme design. The “equals” who are positioned close to the point source or sink are the huge beneficiaries. This is the physics basis of the birth of oligarchy in post-communism Russia.

The spreading of innovation events over the populated territory is a very subtle way to control inequality. Innovation happens when one individual seizes the opportunity to open the flow channel that he or she controls. This is analogous to opening a valve or flipping a switch for the first time. This local design change attracts more flow into the liberated channel: more flow means that the innovator becomes wealthier (Fig. 4.1). The subtle part is that the flow over the entire territory is also enhanced because of this singular act. The whole population becomes wealthier because of a single innovation. The distribution of wealth over the population becomes more equal than in the absence of innovation (Fig. 5.6).

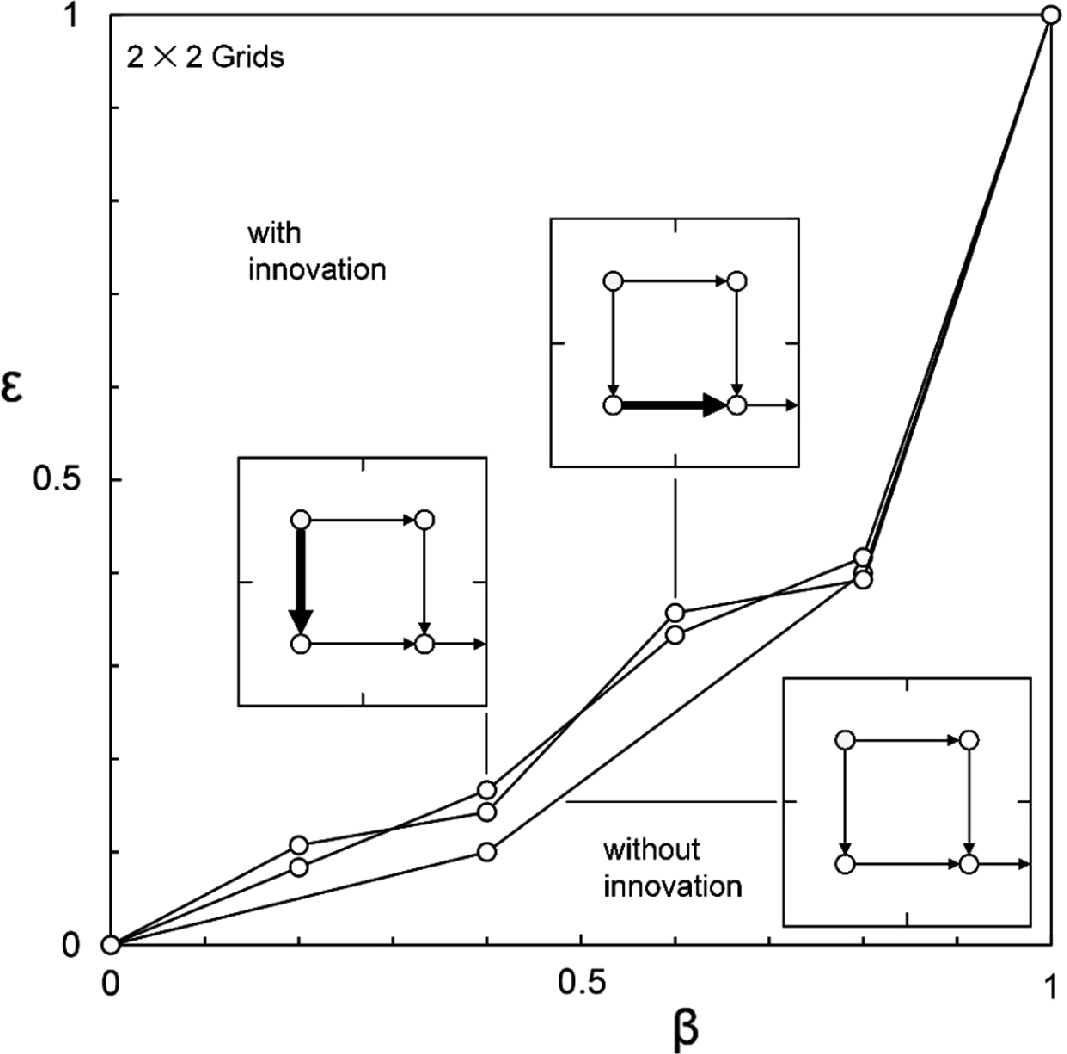
../images/482511_1_En_5_Chapter/482511_1_En_5_Fig6_HTML.png — Fig. 5.6
Compare this figure with Fig. 5.5. A single innovation is a local design change that eases the flow and attracts more flow (wealth) to the place of innovation. The result is a more equal distribution of flow over the area

To illustrate this change and its consequences, consider the flow distributed over the 2 × 2 grid shown at the top of Fig. 5.5 and also in the lower right corner of Fig. 5.6. This can be analyzed with pencil and paper. When the person-to-person channels are identical, the flows through the channels are distributed nonuniformly. Identical channels mean that the flow resistance is the same in every channel, where “resistance” is the name for the ratio between the node-to-node difference (pressure, voltage, altitude) and the current driven by that difference (fluid flow, electric current, river water).

What happens when one channel opens up? Assume that the resistance of one channel drops to half of the value that it had before this innovation. Figure 5.6 shows two possible locations where this change can happen. In both cases, the ε–β distribution of wealth becomes more equal, and closer to the diagonal of the frame. Why, because the innovation triggers an increase in the flow of channels in which the flow rates were not the greatest.

The effect of innovation on controlling inequality is an argument for spreading freedom, education, science, technology, know-how, and especially, the spirit to question and take risks. These add-ons to the design spread the flow to distant patches of the territory that are traditionally not flowing and not known for generating innovation.

In summary, social organization depends upon many factors, many of which are considered intangible. Inequality in movement (or in wealth) is intimately tied to geography, to the physical reality that everything that flows on an inhabited area flows from area to point, or from point to area. Even when the members of the population are equal and equally connected, those who happen to reside near the source or the sink are necessarily visited by a larger stream than the peripheral members. This is the physics basis of organization, and it is evident not only in human social organization but also in animal organization. Organization is born and evolves for the benefit of the whole.

In human society, it is not entirely a matter of happenstance who lives near the “source.” Inventions and creative thought tend to occur more in places where they have occurred many times before. This is how the advanced countries, societies, and territories rose above their neighboring areas. Examples from recent history are presented soon (page 63). The preceding paragraph holds true at the larger scale. The advanced area serves as “source” and attraction for those who are in it or near it. This, by the way, is the physics cause of human migration, and why human migration is unstoppable.

The only way to make the individuals equal and the flows between individuals equal is by distributing the evacuation port uniformly over the territory. In other words, every node on the map would receive or discharge the same flow as its neighbors. This would be a social organization without organization: every hut surviving on its own, not connected to its distant neighbors, as during the hunting and gathering era (Fig. 5.7). That will not happen again, because of the time arrow of evolution (view from left to right the abscissas in Figs. 5.2 and 5.3). Human power, movement, knowledge, and organization have evolved far and irreversibly from what they were even recently, at the dawn of steam power.

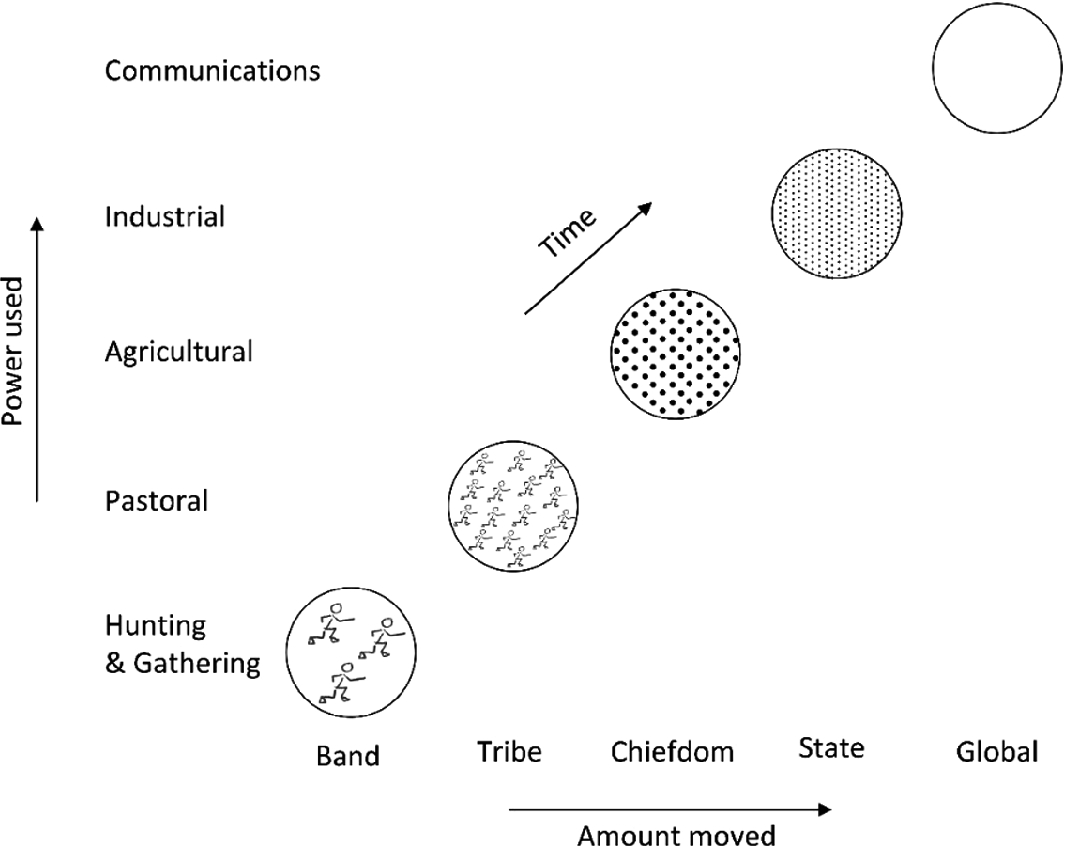
../images/482511_1_En_5_Chapter/482511_1_En_5_Fig7_HTML.png — Fig. 5.7
The evolving designs of human social organization are known by more familiar names. In time, the territory swept by organized members increases from the band, tribe, and chiefdom to the state and the globe today. This happened because at the same time the production and use of power increased along with other measures that characterize the sizes of the physical streams driven by the consumed power: subsistence, standard of living, rate of fuel consumption, hot water, traffic, gross domestic product, wealth, affluence, advancement

Even if sources and channels of a single size were distributed uniformly on the area, the hierarchy and inequality would persist. The efficiency of the whole complex flow architecture is increased over the whole territory when an individual design change (one innovation) is made to liberate the flow locally, in one spot on the flow territory. This is the physics basis for why innovation, which is individual, is of benefit to the whole society. It is addictive, valuable, and indispensable.

The world that we know today comes from individual, local innovations that have enriched inventor and society. The examples are innumerable—here are only a few:

The invention of steam power in Great Britain, which made Boulton and Watt rich and the whole British empire the richest and most powerful in the 1800s.
The invention of the distribution of electric power over huge areas (Tesla, Westinghouse), which had an even greater effect than the steam power that generated the electric power.
The awakening to economic activity in hot and humid tropical and equatorial areas, thanks to the invention of air conditioning by Willis Carrier in 1902.
The opening of the economy of communist China to the west, which allowed the vigorous and established economic flow architecture of the west to invade the economic wasteland that had been created by communism.
The never-ending inventions in communications (moving type, bookbinding, typewriter, computer, iPhone), which liberate the flows of society at the point of invention and on the whole territory.

To innovate is to have talent, and this is why innovation and talent have value in society. The physics of value was expressed from the beginnings of society in the word “talent,” from the Greek noun talanton (Latin talentum), which originally meant a scale or balance for weighing a valuable quantity measurable as a weight of gold or silver. In both Greek and Latin, the meaning of talent diversified to include a unit of money, a coin, and this meaning spread throughout the Roman empire and the western civilization that resulted from it.

Innovations, and how they liberate the human flow locally and then globally, offer an unexpected mental viewing of how a society flows and evolves, and where the future of a society resides. Innovations happen almost randomly in space and time, on the map. Each innovation is like a light that comes on and lights up the patch of territory around it. I said “almost randomly” because in every society there are concentrations of people and points of innovation, such as the communities of MIT and Duke on the U.S. map.

The country with more innovators is covered by more flickering lights, like a Christmas tree. The more innovative the society, the brighter its lighted territory, and the more enlightened its people. This is the physics basis of enlightenment [2], and it is the same as the origin of social organization. Innovations are the source of evolution in society. Innovators make history.

Brain design and its flows fit in the same mental image as a society covered and enlightened by flickering innovations that liberate flow. The cortex is covered by an immense number of neurons. Each neuron is connected to tens of thousands of neurons on the cortex. One connection at one point—a new concept, idea, or vision—illuminates the whole cortex, with lights that flash randomly, not synchronically. More numerous and more frequent lights make an enlightened mind. Ephrat Livni [2] summarized this way the unexpected consequence of the physics of social organization:

“When a single individual becomes ‘enlightened’ by knowledge or a realization, it creates new connections and fortifications in the brain’s synapses. A slew of previously unrealized connections may then follow so that the flow of thought is more evolved. The more ideas we encounter and are interested in, the more likely we are to be enlightened thinkers. To put it in physical terms, the metaphorical tree that blocks the river’s rush leads a persistent and creative person to an innovation or an insight. They push the tree out of the way somehow, with thought and application. This, in turn, causes more cortical connections and more ideas to flow. That has a good chance of improving not only their lives, but the world we all share.”

5. Social Organization and Innovation

Keywords