© Springer Nature Switzerland AG 2020
A. BejanFreedom and Evolutionhttps://doi.org/10.1007/978-3-030-34009-4_9

9. Evolution

Adrian Bejan1  
(1)
Duke University, Durham, NC, USA
 
 
Adrian Bejan
Email: abejan@duke.edu

Keywords

EvolutionPredictionFutureRetrospectLocomotionRiver basinsAircraftAquatic homoMacroscopicWhole

With freedom comes evolution, and with evolution come all these visible things, complexity, diversity, hierarchy, size, and seemingly free choices that speak of the universality of economies of scale. People often ask me to predict something that will happen. Can evolution be predicted?

Evolution can be predicted by invoking the law of physics that governs the evolution phenomenon. It is the same with other phenomena that are universal. For example, by invoking Newton’s second law of motion, we can predict movement in all its forms, past and future, from the movement of planets to the trajectories of projectiles of all sizes (bullets, water droplets) and the continuous flows of fluid everywhere. With the second law of thermodynamics (the law of irreversibility), we can predict that all movement (inanimate, animate, machine) will be dissipative (imperfect), and oriented one way if flowing by itself. By calculating the irreversibility (quantitatively, as the entropy generation rate), we can measure the difference between the real system with currents that flow one way, and the ideal system with currents that theoretically (in the limit) could flow unchanged and by themselves in both directions.

Even though it sounds like a contradiction, with a law of physics we can predict the past of a phenomenon. Why, because before the law was known there was no reason to investigate the past in order to test the law. The predictive power of the law has been demonstrated multiple times over the past two decades, which is why the law is now well established. The predicting goes this way:

First, by invoking the constructal law, the thinker’s mind “sees” an evolving (morphing) flow architecture—its physical characteristics and direction of changes over time—and anticipates the main features (for example, the scaling trends and even the formulas) of the architecture that “will be.” This first step is theory, or more precisely, the constructal theory of the particular evolutionary design that is being contemplated. One theory for one phenomenon.

The word “theory” must be used only when it is applicable. According to the dictionary, theory is a purely mental viewing, contemplation, or speculative idea of how something might be. Theory is the mental flash in the dark of the night. It is not a piece of mathematical analysis. Theory is not the practice of looking at nature, recording observations, and reporting measurements. That practice is empiricism, also known as monitoring, modeling, experimenting, tinkering, correlating, mimicking, and copying (as in biomimetics, p. 117). With theory, the human mind first sees the mental image—the new mental connection, the innovation (cf. Chap. 5)—and only later it checks the validity of the prediction by comparing it with observations of nature.

Theory is mental viewing first, and comparison with observations of nature later. The time arrow of empiricism is the opposite: observations first, which are followed in time by ideas about condensing, storing, and reporting observations. Theory must not be confused with empiricism. They are opposites. There is no such thing as “theoretical model.”

Second, after the theory other thinkers compare the predictions with the measurements that are available. If observations are not available, then new investigators will devise new experiments that will generate new data in order to check the validity of the predictions. After all, this is the purpose of experiment; it is to verify the correctness of an idea, a theory, a purely mental viewing. Experiment without an idea to define and justify the experiment is nonsense or, at best, a make-work project.

Many researchers have compared constructal theories with existing data, and with new data that came from their laboratories and library searches, after the theory. Not surprisingly, constructal theory papers begin with the predictions (the theory) and continue with the clouds of data that fall right on top of the theoretically predicted curves. This, by the way, is how to discover the correct curves that correlate the data, the allometric rules (cf. Chap. 7). This technique is general and useful. I proposed it in 1984, in the first edition of my book Convection Heat Transfer: if you want to discover the correct correlation and the correct dimensionless groups that summarize a phenomenon, first you must construct the theory that predicts the correlation and its proper dimensionless groups. This boils down to the need to understand the physics before you embark on measuring and correlating data.

Following the publication of the constructal law of 1996, the examples of its predictive power have been multiplying. Constructal law was used to predict many phenomena that seem unrelated: for a broad review with peer comments, see Refs. [1–10]. Here are just three examples taken from my publications, one animate, another inanimate, and the third from the human realm (technology evolution).

Animal locomotion. First, we predicted the formulas for the speeds, frequencies, and power requirements of all animal movers in all media (water, air, land). Later, by comparison with a very large volume of zoology data, the formulas became the physics-grounded correlations that underpin animal design. This theory was first proposed and validated (for fliers only) in my 2000 book [11], after which it was extended to swimmers and runners [12], Fig. 9.1.
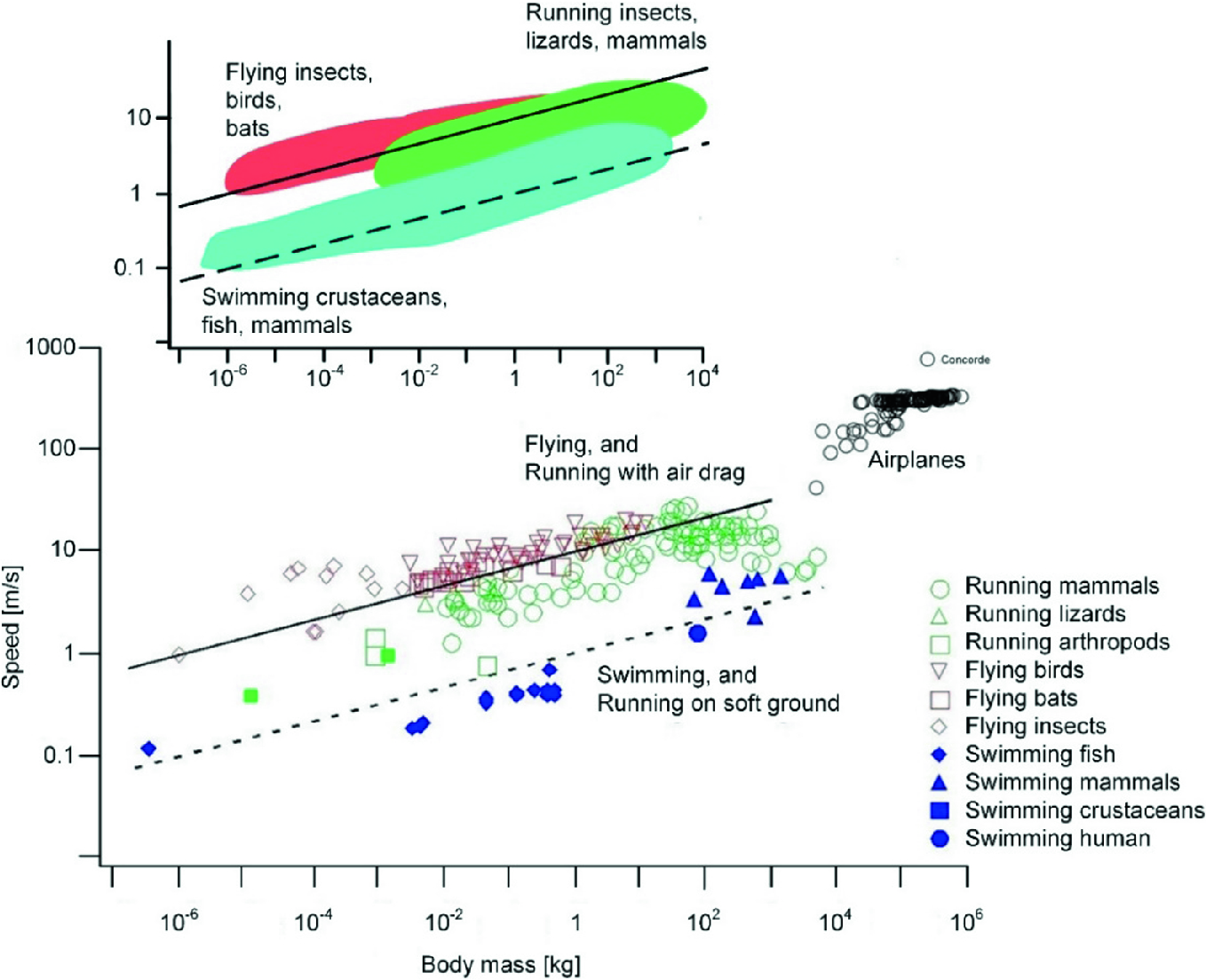
../images/482511_1_En_9_Chapter/482511_1_En_9_Fig1_HTML.png
Fig. 9.1

The characteristic speeds of all the bodies that fly, run, and swim. The upper frame offers a bird’s-eye view of the animal data put on display in the lower graph

In brief, easier access for the body that moves through its environment (water, land, air) means that at every time step a balance must be reached between the work spent on the vertical (to lift the weight that keeps falling under gravity) and the work spent on the horizontal (to get the environment out of the way). From this balance follow theoretically the most basic and best known facts about animal locomotion: bigger animals should be faster, should undulate their bodies less frequently, and should be stronger. This includes the swimmers, which must lift water in order to advance forward. The water displaced by the swimmer can only go up because the upper surface of the body of water is freely deformable while the bottom and the sides are rigid.

Evolving in accordance with the same principle is the locomotion of the human and machine species. The evolution of athletics [13–15] is one laboratory where the constructal law of animal locomotion has been tested successfully based on the recorded evolution of winning speeds in running and swimming, short distance and long distance, and men and women.

All locomotion is a rhythm, because all creatures on Earth locomote in the presence of gravity. The rhythm is the one–two that comes from balancing better and better the time spent on the vertical (to lift the body) and the time spent on the horizontal (to push the body forward). Freedom makes such choices possible.

To feel the need for such rhythm, imagine that you are crossing the Danube in a rowboat that is leaky. You must divide your time between pulling on the oars and scooping water from the bottom of the boat and dumping it overboard. If you don’t scoop, you sink and never reach the other shore. If you scoop all the time and don’t pull the oars, the boat stays dry but you never leave the shore.

River basins. First was the law-based prediction that any river basin on the globe should have on an average a modular structure with approximately four tributaries to a mother channel. Next, the prediction was compared with data correlated empirically by Horton and others since the 1930s [16–18], Table 9.1. The prediction and the validation were published together in 2006 [19], on the following theoretical basis:
Table 9.1

The theoretical architecture of constructal river basins

i

Ai/A0

$$L_{Ti} /A_{0}^{1 /2}$$

Ni

RLi

RBi

$$D_{\omega i} A_{0}^{1 /2}$$

FsiA0

$$F_{si} /D_{\omega i}^{2}$$

$$L_{Mi} /A_{i}^{1 /2}$$

0

1

$$\frac{1}{2}$$

1

–

–

$$\frac{1}{2}$$

1

4

$$\frac{1}{2}$$

1

4

$$\frac{7}{2}$$

5

3

4

$$\frac{7}{8}$$

$$\frac{5}{4}$$

1.63

$$\frac{3}{4}$$

2

42

$$\frac{35}{2}$$

21

2

4

$$\frac{35}{22}$$

$$\frac{21}{16}$$

1.10

$$\frac{3}{4}$$

3

43

76

85

2

4

$$\frac{76}{64}$$

$$\frac{85}{64}$$

0.94

$$\frac{3}{4}$$

4

44

316

341

2

4

$$\frac{316}{256}$$

$$\frac{341}{256}$$

0.87

$$\frac{3}{4}$$

River basins

   

1.5–3.5 Horton

3–5 Horton

  

0.7 Melton

~1.4 Hack

The constructal-law field began in June 1996 with imagining “the city” and formulating the fundamental “area-point access” problem in terms of people flowing through streets of various sizes [20–22]. Chief is the “modularity” of the construction of area-point flow architecture for access, which was demonstrated for heat conduction cooling, urban design (streets), and fluid flow through ducts and porous media.

The river basin construction is the constructal theory of the area-point design of a natural area-point flow system that everybody knows. The objective of this particular theory was to uncover the rule of construction that offers the entire basin access from area to point, regardless of its size (in Table 9.1 the size of the basin is indicated in the i column). Four rules of construction were evaluated sequentially, from left to right in Fig. 9.2:
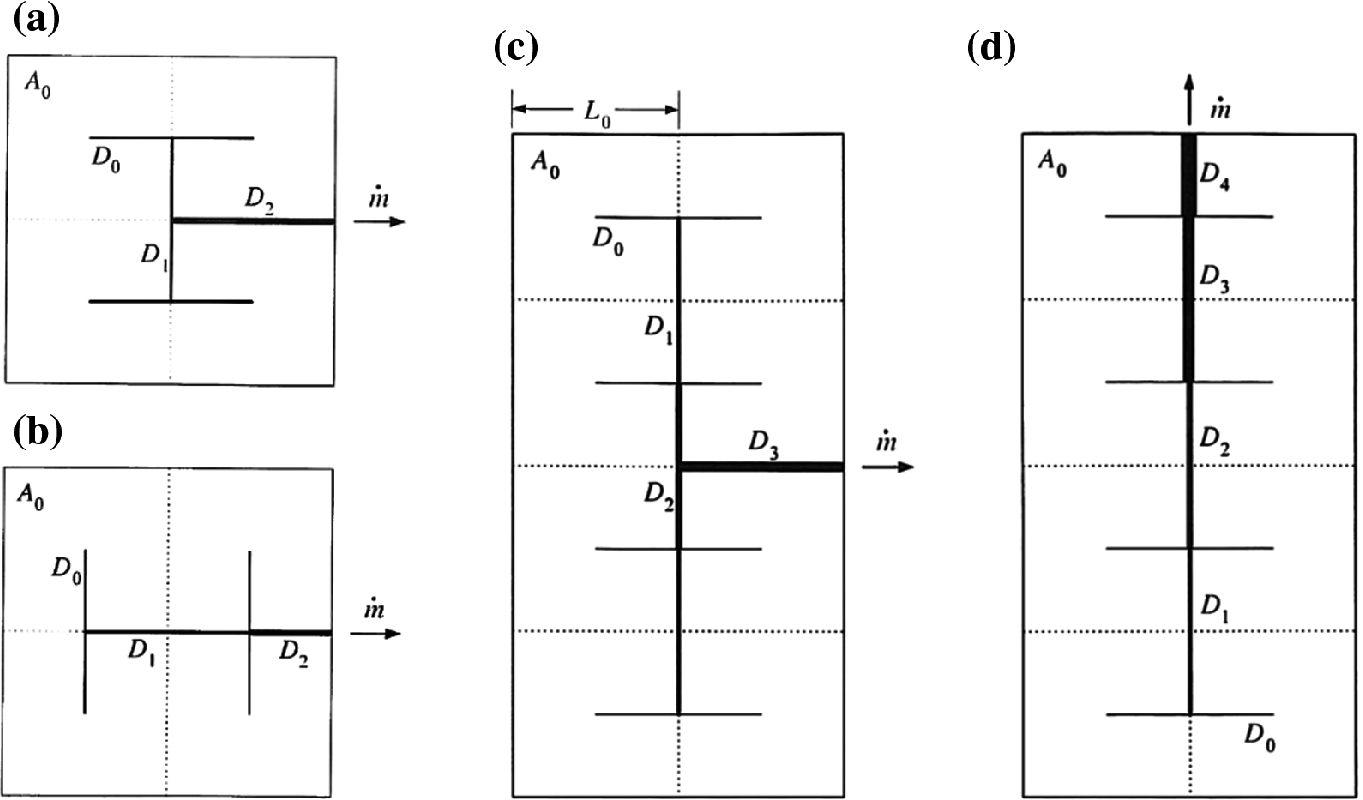
../images/482511_1_En_9_Chapter/482511_1_En_9_Fig2_HTML.png
Fig. 9.2

Four constructions of river basins consisting of area elements

  1. (a)

    River basin with four area elements A0. To build the area 4A0, one has to execute two steps of doubling, or two pairing events, from A0 to 2A0, and then from 2A0 to 4A0. In this construction, there is only one rule, doubling, or “the rule of 2.”

     
  2. (b)

    River basin with four area elements A0. To build the area 4A0, one has to assemble four A0 elements in a single step. This step is one of quadrupling, or “the rule of 4.”

     
  3. (c)

    Eight A0 elements are assembled in two steps: quadrupling, which gives birth to 4A0 constructs, and then doubling, which joins two 4A0 constructs into one 8A0 construct.

     
  4. (d)

    Eight A0 elements are built into one 8A0 construct in one step. This is “the rule of 8.”

     

By constructing and comparing (a)–(d), we found that the construction rule (b) offered the lower global pressure drop, which for rivers means a smaller altitude difference between inlets and outlet on the area, or easier flowing and greater access to what flows.

The construction uncovered in Fig. 9.2 is the origin of all vascular designs, inanimate and animate, in two and three dimensions [23]. The constructal-law phenomenon is why vascularization happens in so many flow systems, from river basins to the nervous system and the brain.

The example of river basins (Table 9.1, Fig. 9.2) teaches the most fundamental characteristic of any work that is theoretical. With a law of physics, one does not “explain.” One predicts by invoking the law, without looking at an actual object in nature. For example, in constructing Fig. 9.2, we invoked the constructal law in order to identify (b), and in this way we predicted that the counting of geometric features in all river basins in geophysics publishing history should turn out the way that our (b) construction recommends. This was validated by comparison with Refs. [16–18], as shown at the bottom of Table 9.1.

We do not know why the “whole” area has the natural tendency to evolve into a hierarchical flow construction that offers access greater than other constructions. All we know is that this natural tendency (along with other evolutionary designs, lungs, snowflakes, and city streets) is predictable if one invokes the law of physics of evolutionary design.

River erosion is akin to self-lubrication, as in the lava flowing through volcano shafts that acquire round cross sections [24], and in rolling stones that become rounder as they roll [25]. All these phenomena are manifestations of the constructal law and are predictable by invoking the law. In river basin evolution “erosion” underpins all the morphing that goes on:
  1. (i)

    In every channel, the river cross section channel becomes enlarged over time.

     
  2. (ii)

    Every channel cross section becomes lemon slice shaped, regardless of channel size, so that all river channels that are wide are also deep. The law commands that the ratio width/depth should be a universal proportionality for river channels of all sizes [11].

     
  3. (iii)

    The whole exhibits the natural tendency to organize and put its channels and area elements into seemingly modular constructions that are there for global flow access from area to point.

     

There is no “model” in the thinking that generated Fig. 9.2 and Table 9.1. We were not looking at a river map when we made the four drawings shown in the figure. The different channel thicknesses visible as thin and thick lines were derived from the constructal law, not from observations of nature. For the theorist, the page was initially blank, and on the page the theorist morphed the flow architecture while not knowing beforehand which architecture would be “naturally selected” by the constructal law.

By identifying the essential features of the flow architectures endowed with global access, we predict the direction of evolution over time. We do not predict an end design, because end design does not exist. With the law of physics of evolution, we predict the direction of evolutionary changes over time.

Aircraft. First, we predicted the formulas that express relations between dimension of organs and body size in small and large airplanes. After the theory, we compared the predictions with the voluminous body of data accumulated during the entire history of commercial aviation [26]. When plotted as recommended by the theory, the data aligned themselves. Every time, the agreement between the prediction and the alignment of its respective data was consistently excellent, a surprise for the reader maybe, but not for the theorist.

More recently, we extended this theory to predicting the evolutionary future of helicopters [27]. The same theory also allowed us to provide a physics basis for the surprising alignment of performance data from the early days of aviation [28], Fig. 9.3. Airplane technology is an example of how a newly formulated law of physics predicts the past of an evolutionary phenomenon by unifying the old volume of data with the new data.
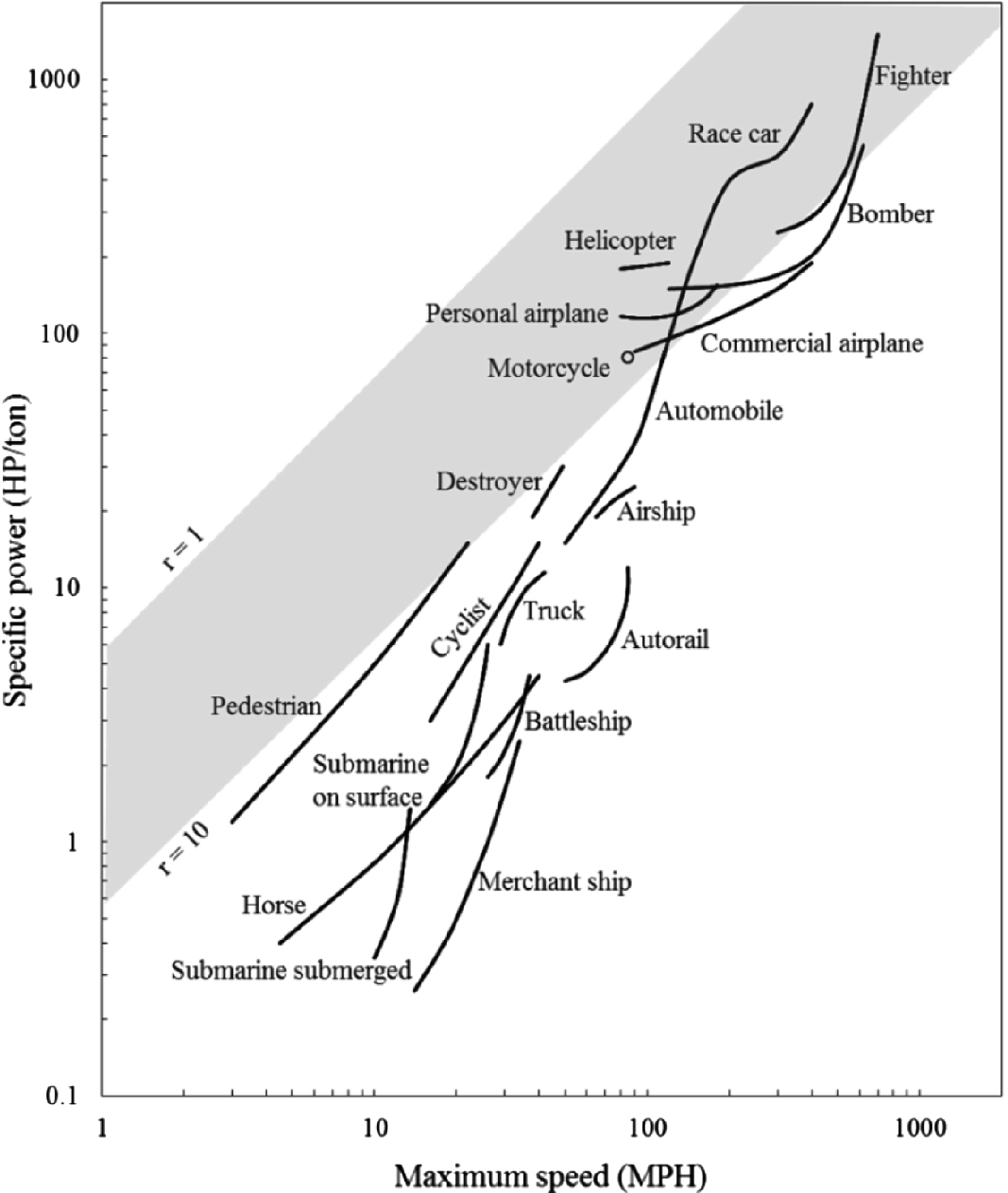
../images/482511_1_En_9_Chapter/482511_1_En_9_Fig3_HTML.png
Fig. 9.3

Specific power of single vehicle from before 1950. The dark band represents the domain predicted by the constructal theory of all locomotion, with r = 1 for air, r = 10 for water, and land in-between

In summary, there is one phenomenon (evolution), and one law of evolution. The theories that spring from the law are as many as the circumstances in which the thinker contemplates one phenomenon, which is just one natural manifestation of the law. There is one constructal law, and there are many constructal theories that cover the board, from biological to non-biological phenomena, and from the tiny pulmonary alveolus to big celestial bodies, lung structure, rhythm (respiration, heartbeat), animal locomotion, river basin structure, river channel cross sections, aircraft evolution, turbulent structure evolution, snowflake evolution, and many more. Theory is not Law.

While discussing the validation of the theory that celestial bodies should exhibit hierarchy—few large and many small bodies suspended together and attracting each other [29], instead of one size—we addressed Ellis and Silk’s test [30] that “the issue boils down to clarifying one question: What potential observational or experimental evidence is there that would persuade you that the theory is wrong and lead you to abandoning it? If there is none, it is not a scientific theory.” There are numerous tests of evolutionary design (in addition to the three discussed already, Figs. 9.1, 9.2 and 9.3) that validate the constructal law, in addition of the hierarchy of celestial bodies, for example:

  • A flat plume or jet should evolve into a round plume or jet, never the other way around [31].

  • Solid bodies that grow during rapid solidification (e.g., snowflakes, dust clusters) should be tree-like, not spherical [32, 33].

  • Bigger moving bodies (animals, rivers, vehicles) should live longer and travel farther, not live less and travel less [34].

  • The human lung should be tree-shaped with 23 levels of branching [35]. The number 23 emerges predictively from the trade-off between the time spent by air as it flows through hierarchical air tubes, and the time spent by the diffusion of O2 (and CO2) across the blood vascularized tissues that form the walls of the alveolar sacks. The trade-off is such that the sum of the two times (tube flow + diffusion) is minimal when the number of branching levels is 23. In an animal smaller than the human, the number of branching levels is predictably smaller.

  • All animal speeds (swimming, running, flying) should be proportional to the body size raised to the power 1/6, and, for a given body size, should increase from swimmers to runners and then flyers [12].

The examples go on, and every single one is evidence in answer to the question formulated by Ellis and Silk. There is more to this than meets the eye. Some readers may be tempted to argue that the evidence has long been available in the past, and that the theory cannot predict past observations. This argument is incorrect, in two ways:

First, predicting old observations that were not recognized and questioned previously is indeed theory. Examples are Galilei’s law of gravitational fall, and Clausius’ law of irreversibility (the second law). The fact that everything on earth has weight (gravitas in Latin, from which the word “gravity”) and the fact that everything flows by itself from high to low (one way, from which “irreversibility”) were old and familiar phenomena that were not brought into science before Galilei and Clausius questioned them and summarized them in the form of two succinct statements.

The obvious fact that animals of the same kingdom look different was not questioned before I predicted that in bigger terrestrial animals the legs (i.e., the lifting organs) should occupy a larger fraction of the body volume than in smaller terrestrials (cf. Fig. 5.2 in Ref. [36]). Now, in Fig. 9.4, I show that the same should be true in all animals, fliers, runners, and swimmers. The lifting organs of the flier are the wings, and the lifting organ of the swimmer is the undulating body. I drew all these animals so that on the page they have the same size, even though the animals in the right column are enormous in comparison with the animals in the left column.
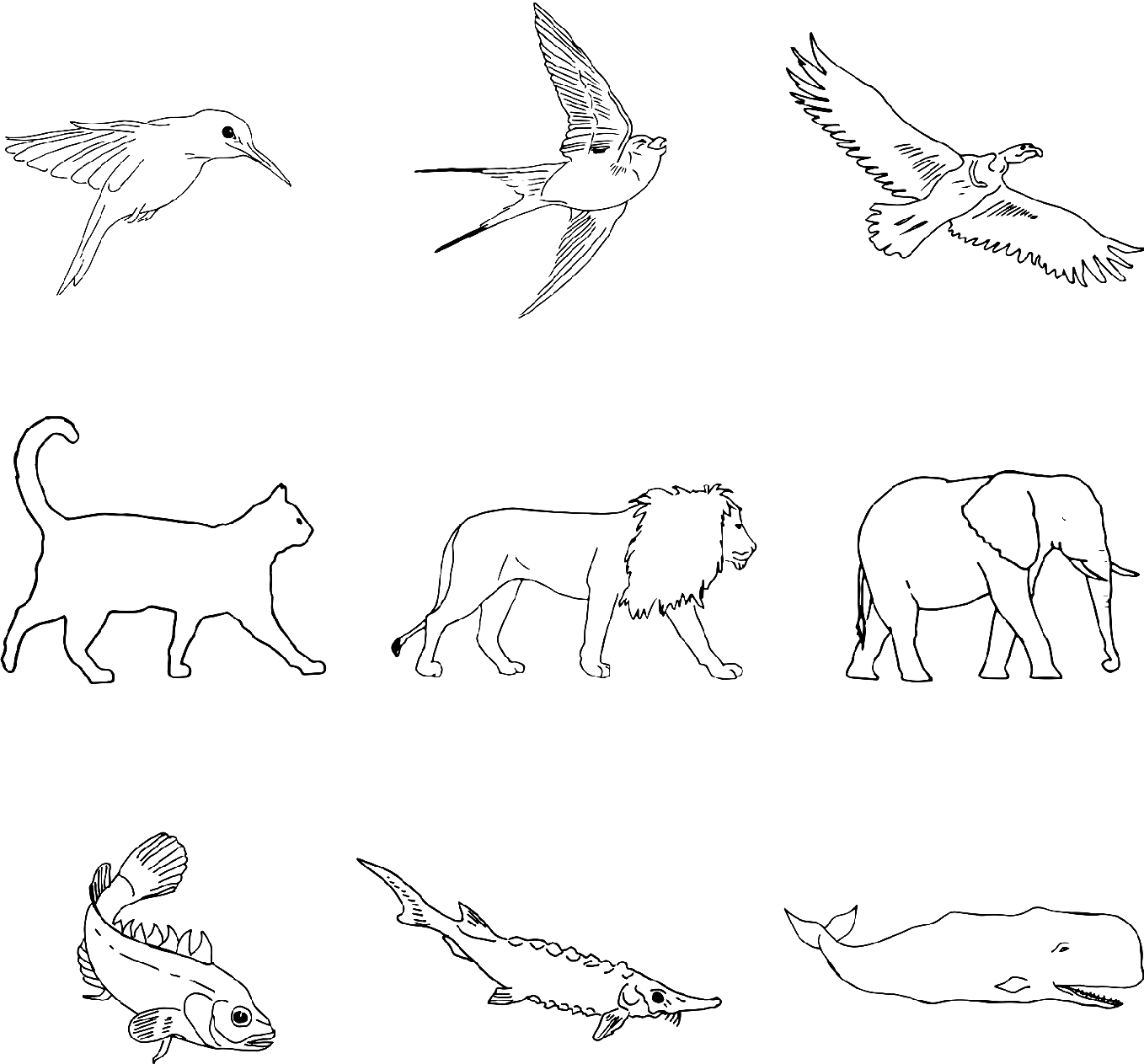
../images/482511_1_En_9_Chapter/482511_1_En_9_Fig4_HTML.png
Fig. 9.4

In bigger animals in all media a larger fraction of the body mass is occupied by the lifting organs, wings in the air, legs on land, and undulating body in water (Drawing by Adrian Bejan)

Every size has its own design. Said another way, design is another name for size. The diversity that is evident in Fig. 9.4 is a manifestation of the same physics principle as the human diversity detailed in Chap. 8. Accordingly, taller humans should distinguish themselves as having bodies in which the legs constitute a bigger fraction of the body.

Second, throughout the physics literature there are numerous predictions that refer to future observations, such as the examples given above for plumes [31], rolling stones [25], and snowflakes [32], and many more evolutionary designs that occur at short time scales that are comparable with the duration of one human life, for example, the evolution of technology [26–28] and athletics [13–15]. This should come as no surprise because all science is an artifact (an add-on to the mind, the brain design) that empowers humans to predict the future for human benefit.

Even more support for the predictive power of evolution as physics is available under different names. Biomimetics, or biomimicry, is portrayed as a new science the core idea of which is that the most efficient systems are found in life (bio) forms. First, “most efficient” cannot be true because the superlative “most” implies that life forms have stopped evolving. Second, “efficient” does not belong with imitating (mimicry). The concept of “efficient” requires an understanding, which happens in a mind endowed with knowledge, which is ideas, principles, and what to do with ideas and principles. Fashionable is also the claim that biomimetrics helps technology. Biomimetics does not, but the principle does. Biomimetics is successful only when the observer knows the principle that accounts for the observed natural object. Those who claim success with biomimetics are relying intuitively on the physics principle of evolution and design in nature. I was writing these observations while watching an elephant on the Lower Zambezi, as it was shaking the ana tree so that the dried pods would fall on the ground. The elephant discovered this knowledge on its own, not by mimicking the blowing wind that also shakes the tree. The elephant does not blow and does not mimic humans by throwing sticks at branches with fruit. Likewise, humans discovered that round pipes are good for water flow. They did not copy the cross sections of blood veins and pulmonary air tubes in order to make pipes.

The elephant does not rise on its hind legs to reach higher. The giraffe does not do that either. Getting up on two legs requires lots of work (and food, and muscle, and bone tissue mechanical strength) when one is a quadruped on land. But it takes no work if one is an aquatic quadruped, because the animal’s body density is nearly equal to the body density. This discovery adds physics in support of the view [37] that along its body-after-body parade of drawings of species from quadruped to biped (on the horizontal time line of Fig. 8.​4), the intelligent ape had an “aquatic” relative that made the discovery that lifting itself is much easier while submersed.

The support from physics for the aquatic phase is stronger, and it speaks of aquatic movement. Body hair disappeared almost entirely not only because it was useless as thermal insulation in water (hair insulates when its interstices are filled with air [38]), but also because it was shaved off by friction against water during movement. This is why hair persisted in body regions that were not exposed to fast water flow during forward movement (head, armpits, pubic area, and chest area between and under the pectoral muscles). Standing tall in water was necessary for breathing above water, which is also why the homo has a longer neck and nose in comparison with other apes. The swimming is why the aquatic homo developed limbs (hips, shoulders, collarbones) pointing to the sides, like in a crocodile, not ventral like in other land quadrupeds. It is also why the aquatic homo acquired feet that look like the flippers of seals, without opposing big toes, which are clearly not for arboreal life. An added advantage of being bipedal came when the aquatic ape ventured on land, where it looked taller than it really was among competitors, before returning to the water for even greater safety.

Evolution is a macroscopic phenomenon. It is the universal tendency of the whole to morph hand in glove with its environment to flow more easily, for greater access. The “whole” is your system (the object) and its surroundings, not the system alone. The macroscopic reality of the evolution phenomenon is why the words “finite size” appear in the 1996 statement of the constructal law (cf. Chap. 1, p. 5).

Object and finite size are old concepts in human thought, much older than the mirage of the infinitesimal size. I stressed this observation in the very last paragraph of my 2000 book [11]; this way: “Most of this work (i.e. constructal law) could have been done two centuries ago, before thermodynamics. It is a mystery that this was not done then. Instead, modern physics embarked on a course tailored to the principle of infinitesimal local effects. Constructal theory is a jolt the other way, a means to rationalize macroscopic features, objective, and behavior (i.e. evolutionary design).”

Evolution means a lot more than change over time. It is much more valuable to understand and to anticipate evolution than to discern the change after the change happens. It is valuable because most of us think in terms of what is important to us.

In evolution, there is no reset button, no return to past success. The design is constantly evolving. The future design must be different than the present design. The environment is dynamic, always changing and morphing. Accept it the way it is, and design with it. Do not force the environment to be steady (static) and peaceful, or you will be defeated.