© Springer Nature Switzerland AG 2020
A. BejanFreedom and Evolutionhttps://doi.org/10.1007/978-3-030-34009-4_6

6. Complexity

Adrian Bejan1  
(1)
Duke University, Durham, NC, USA
 
 
Adrian Bejan
Email: abejan@duke.edu

Keywords

ComplexityObjectDrawingIconFractal dimensionGolden-ratio shapesLawTheoryEmpiricismModels

Nature is lying naked on the table, and its description—called physics—is concise, simple, unambiguous, and constantly improving. Yet, confusion reigns especially with respect to complexity and other troublesome concepts such as the second law of thermodynamics. In this chapter, we step back and take a look at these notions—at their meaning and definition—on the background provided by nature.

What is discernible all around us is macroscopic, not infinitesimal, not statistics, particles, and subparticles. Those who took the reductionist path missed the macroscopic phenomenon, the form, the drawing, the photograph, the sculpture, and the movie. The preceding chapters showed that nature and the phenomena we know best are macroscopic, diverse, multi-scale, complex and morphing, and evolving.

What is complexity? Complexity is a lot like freedom: everybody knows, but very few can tell what it is. Complex is often confused with complicated and random. Here is how to see and tell the difference:

Complexity, organization, and evolution in nature are most powerful and useful when pursued as a discipline, not as jargon. A discipline has precise terms, rules, principles, and usefulness. Why is this important? Let’s review the central concepts and words that underpin the physics of evolutionary design today: information, knowledge, evolution, change, arrow of time, pattern, organization, drawings, complexity, fractal dimension, object, icon, model, empiricism, theory, disorder, and second law. Along this path, we will discover that information is not knowledge, fractal dimension is not a measure of complexity, and pattern is not a live flow architecture. Configurations, as physical means to facilitate the flow of knowledge, are subject to the natural tendency toward evolution over time.

During the twentieth century, statistical mechanics, quantum mechanics, information theory, and computer science have changed the scientific discourse on everything, from science itself to what life is. Instead of terms and images that do not require an advanced education, today it seems that legitimacy on this topic comes from speaking “scientific” language, not English. The scientific sounding language is about disorder, uncertainty, scale, emergence, chaos, entropies of innumerable types and, above all, “information” and information entropy. The fact that very few of us understand this kind of talk is going unnoticed, obviously, because the world does not speak jargon.

What a delightful thing is the conversation of specialists! One understands nothing and it’s charming. (Edgar Degas)

At age 17, I came home and told my father the veterinarian that the professor who was lecturing on analytical geometry was making me experience headaches because he was all about complicated “general” equations and no drawings. Imagine that, geometry with no drawings. My father said, “do not think about his abstract stuff, simply walk past what makes you unhappy.” His favorite metaphor was the rabid dog: “Act as if the rabid dog does not exist, walk past him, and he will not bite.”

This does not have to continue this way. Let’s not join the crowd, the marching column. Even better, let’s walk against the crowd (Fig. 11.​1). Start with the observation that information is not knowledge. The computer is not because it is nothing more than an extension of the human who uses it to move (to live) more easily. It is one artifact among very many. On the other hand, you are, you with that artifact. You are, you make decisions (purposeful choices and changes), and as a consequence you and your group move (live) more easily and with longer lasting power. You are a specimen of the evolving human and machine species. I am another specimen of that evolving species.

Those whose maternal language is not English have no choice but to learn English, and along the way they acquire the habit of checking the dictionary often. That is a huge advantage, and the more the dictionaries of other languages you check, the greater the advantage. Teach your children this: the treasure is in the dictionary, in the meaning of the words, and in their origin. Here is the meaning of some of the key words that do not require an advanced education:

Information is a universal term, like geometry, energy, and physics. It is expressed by the same word in many languages. Information comes from the Latin verb informo-informare, which means to give form and shape, to form, and to fashion. In English, it means something told, news, intelligence (as in spying), facts, data, text, and figures. These days, information also means data that can be stored in or retrieved from a computer. This is why ‘information’ sounds abstract, opaque, fancy and high level, as in information theory, information technology, information security, and information age. To see through the jargon, ask your computer what are all those 01 s and 10 s for?  They are instructions for how to make drawings, or signs: letters, numerals, text, lines, curves, shades, colors and sounds (musical notes).

In modern languages all over, information means a sign, a signal, such as seeing 24 June instead of 23 June on the headline of today’s newspaper. What you, the observer, decide to do with the sign is you. What I do with it is I. What we do are physical changes, design changes in your movement and mine, with time direction of change. The changes are dynamic, with power, in time. They are the action that knowledge is and are not to be confused with mere information.

There was a lot of the said information chiseled on obelisks in Egypt, and it meant absolutely nothing, no message, no imagination, no dream, no design, no change, no action, and no embodiment into anything. It stayed that way for millennia until a young nobody, Jean-François Champollion taught his contemporaries how to hear the sound of words from what was chiseled on obelisks. What you read and do today with Egyptian information is you, not somebody else.

Having knowledge but lacking the power to express it clearly is no better than never having any ideas at all (Pericles)

Change has a time direction, and its arrow of time is called evolution. The ability to affect design change is an integral part of the live system that morphs and evolves in order to move on earth more easily, farther, and longer in time. The “ability” of the moving thing comprises many physical features: freedom to change, power (watts) to move things and reshape flows, access to information, memory of past changes that facilitated movement, memory of changes that are detrimental, and so on, on the staircase to better flow organization over time. This is action, and it applies to everything, inanimate and animate. Knowledge is action based on information, not information alone [1].

Here is what information is and how we use it. When I make a drawing or a sequence of drawings (an evolving design) to describe what I see around me, I need to know where to put my lines, how long, how thick, what color, and straight or curved (cf., Chap. 7). To make a drawing I need freedom. The better painter gives himself more freedom.

When I was learning how to draw I was fascinated by how “messy” are the master’s pallet and the floor of his atelier. That is no mess, in fact, it is the best niche that the painter built around his working hand and mind so that the painting is his best, and his own pleasure reaches climax. That niche and what the painter puts on canvas are the “information,” and they come from imagination, observation, and also from the warehouse of information called education, culture, library, and parents.

In order to get from that warehouse to my drawing on paper, the information must travel, it must flow, and it must be communicated. Today, a lot of that is accomplished digitally, in three steps: from observed object to digital code, from digital code to me, and from my digital information to my drawing of the physical object. Before computers, the same three steps have been in place forever, as everyone can recognize by replacing the word “digital” with eye, brain, book, teacher, education, or training.

Design is a plan, a scheme, a project with purpose, and an intention (an aim) for an outcome. Design is the arrangement of parts, details, form, and color, so as to produce a complete whole that has purpose and performance.

Design is not “pattern.” The tree-shaped architecture of so many things that flow (river basin, lung, city traffic) is a changing design because it has purpose (direction in time), which is to facilitate flow between a point and an area, or between a point and a volume. On the contrary, pattern is a static, regular, and an unvarying arrangement of form, parts or elements. The tiles on the bathroom floor and the atoms locked in the crystal lattice have pattern but not design. They are in the “dead state,” according to thermodynamics. In them, there is no flow, no change, no morphing, no freedom, no time direction, and therefore no life and evolution.

Optimization means to make a choice, to opt, to select the configuration A as opposed to B, or the rhythm C instead of D. This action, to opt, comes from the Latin verb opto, optare, which means to choose, to elect, and to select. It is an expression of the human urge to change things for the better. The direction of the change comes naturally, most often from conscience in humans, and it is the choosing that paves the road to the better. The paved road is evolution.

Optimization is not mathematics. It is not the operation of finding an analytical function that is a simplified description (a facsimile of nature, called “model”) of a curved object in nature, then taking the first derivative of that function, setting the derivative equal to zero, and finally solving that equation. This operation is finding the extremum of the function, the hilltop or the valley bottom, and nothing more. It has nothing to do with choosing between two or three concrete options that are useful and available, with the objective of making your own life better.

Organization is a consolidated group of live flowing elements, as in an organ. Organization is a systemized whole (also called “system”), the organs connected and flowing together in the moving animal body, the river channels and wet interstices in the drainage basin, and the components moving together inside the vehicle on the highway. In society, organization is the live group assembled for a specific purpose (activity, movement), such as a club, union, political party, executive structure in business, sports team, university, or government. Design is living organization, not dead pattern.

A picture is worth a thousand words. This is why all these notions, from information (sign, form) to design and organization, occur as images in the mind before they are spoken as words. This is also why the most important keyword to understand is the image, which happens in the mind and later comes from the hand as a drawing.

Drawing is an image that can be discerned by the eye and understood by the mind. “Understood” means that the image is connected to other images in the brain in ways that make the storage of images more compact and their retrieval more rapid. The concept of drawing comes from disegno in Italian, and dessin in French, from which “design” in English. A drawing has three essential features, which are self-standing, independent of each other. The maker of a drawing can attest to the fact that one feature is chosen independently of the others [2]:

  1. (i)

    The drawing has size. Large or small, the size is represented by the length scale of its frame, sheet of paper, canvas, mural, or computer screen. The maker of the drawing selects the size of the image.

     
  2. (ii)

    The drawing has a meaning (a message) that is conveyed to the viewers. The message is “knowledge” when the recipients act and then make changes based on the received message. The message spreads naturally, from those who know to those who need to know. The meaning is represented by one or more features: shapes, structures, aspect ratios (proportions), and the organization of all these features on the viewed plane.

    Each feature is distinct. The round shape of the cross section of the blood capillary is not to be confused with the bifurcation of the blood vessel, or the pairing of smaller blood vessels into a larger vessel. All the features are organized in a particular way, and as a consequence they convey the message sharply, unequivocally. A simple line drawing of your face today displays the same organization as a drawing made 20 years ago, but a few features are different. The drawing morphs with your age, but the message remains: the portrait is yours.

     
  3. (iii)

    The drawing has svelteness, which is a measure of the relative thinness of the lines used to convey the message (ii). The svelteness is a dimensionless number defined as

    $$Sv\,\, = \,\,\frac{{{\text{the}}\,\,{\text{external}}\,\,{\text{length}}\,\,{\text{scale}}\,\,{\text{of}}\,\,{\text{the}}\,\,{\text{drawing}}}}{{{\text{the}}\,\,{\text{internal}}\,\,{\text{length}}\,\,{\text{scale}}\,\,{\text{of}}\,\,{\text{the}}\,\,{\text{drawing}}}}$$
    Scale means size in an order of magnitude sense, for example, a length comparable with one meter, not with one millimeter. The drawing made with relatively thin lines has a large Sv value (Fig. 6.1). It is svelte looking. The same drawing made with a thicker pen or brush, or copied on a poor copy machine has a smaller Sv value. It is heavy looking. A watercolor rendition of the original line drawing has an even smaller Sv. A good forgery has a different Sv than the original. The Sv value belongs to the artist, to one brush and one style of brush strokes, and distinguishes the original artist from the forgerer.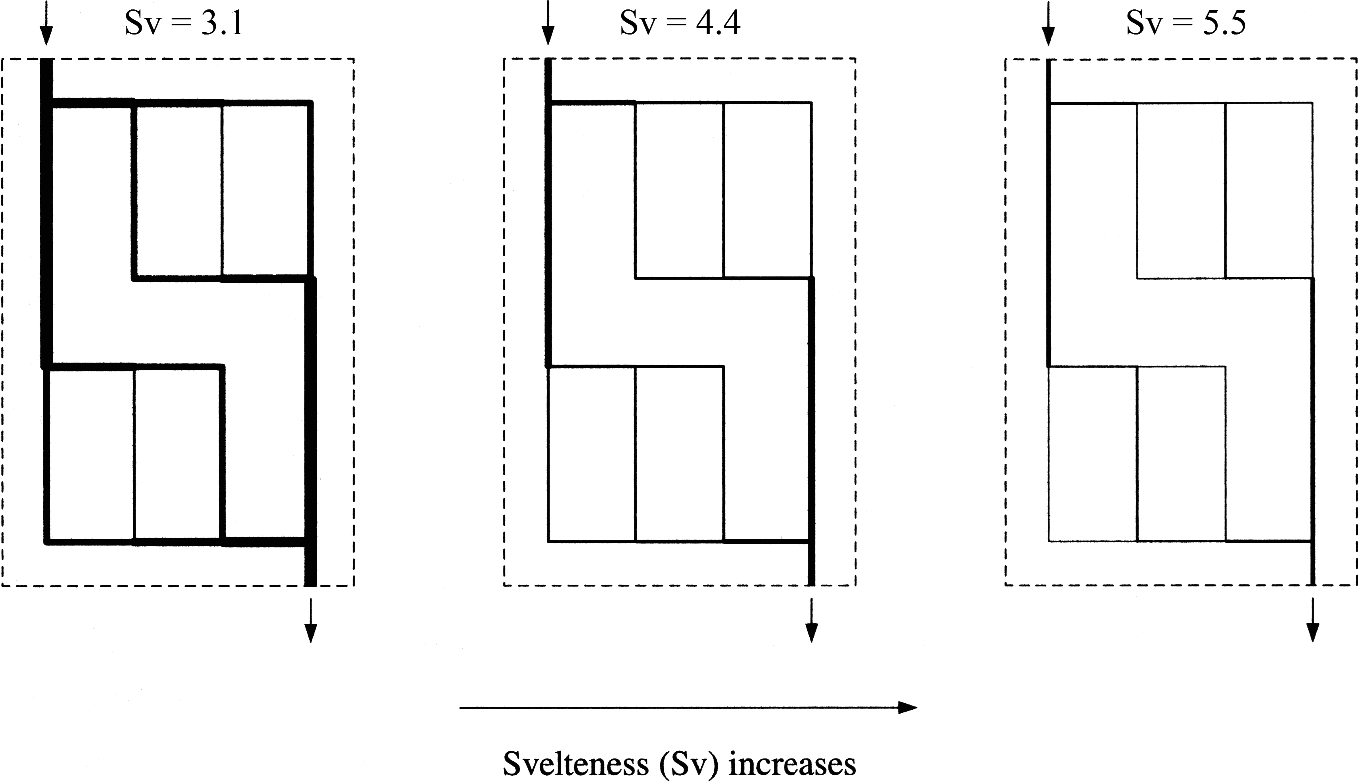
    ../images/482511_1_En_6_Chapter/482511_1_En_6_Fig1_HTML.png
    Fig. 6.1

    The three drawings are the same, but their lines are progressively thinner. The svelteness property Sv of a complex architecture accounts for the thinness of its lines: as svelteness increases, line thicknesses decrease, the drawing becomes sharper and lighter, and it breathes more. The message of the drawing does not change, but its “weight” changes. The svelteness of the flow architecture in this figure was calculated by taking the square root of the area of the dashed rectangle as external length scale, and the square root of the area covered by the channels (shown in black) as internal length scale

     

Amazing, even the discussion of a single drawing is complicated! Then again, what is complexity?

Complexity is a difficult concept, like chaos, or turbulence. In the beginning, when people knew a lot less than what we know today, complexity meant difficulty, fuzziness, headache, and why bother. Its Latin origin betrays this feeling of defeat: “complex” (cum + plex, i.e., twisted forms together) comes from the same Latin observation as “perplex” (through + twisted), which also speaks of defeat.

As science progressed, people began to see organization and message in the said complexity. As the thinking became sharper, higher, and deeper, the organization of complexity gave birth to theory, which is the mental viewing with which to predict the observed complexity. Once understood, complexity becomes easier, and we call it architecture, weave, tissue, design, organization, and many more names that are a lot less puzzling.

It happened this way with turbulence, which as a science evolved from fuzziness in the late 1800s (complications of fluid flow were effaced intentionally through a time-averaged description, thanks to Reynolds [3]), to the “large-scale structure” of turbulence in the 1970s, and to the evolution of the structure of turbulence, which is now predictable from the constructal law [4]. For example, a flat jet or plume always evolves into a stream with round cross section [5], Fig. 6.2. The reverse is not true: round jets and plumes do not evolve into streams with flat cross sections. This holds true for turbulent and laminar jets and plumes as well.
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig2_HTML.png
Fig. 6.2

Above a certain height, all turbulent plumes have round cross sections: flat plume rising from a row of smokestacks; round plume rising from a concentrated fire; and plume above a brush fire

It will happen the same way with complexity. The language of complexity will be replaced by geometrically precise notions such as size (i), organization (ii), svelteness (iii), and I am sure additional fundamental notions.

We often read that the fractal dimension (D) of an object (or drawing) is important because it increases with the complexity of the figure, and that it accounts quantitatively for complexity. Had this been true, we would have seen by now a fractal-dimension ranking of drawings according to their complexity, because newly calculated D values appear in the literature unabated. Whether the fractal dimension adds anything to the quantitative description of complexity is questionable.

Consider the drawing made in Fig. 6.3. An isosceles triangle is divided in half by the bisector of its 90° angle. The construction is repeated n times. The bisectors form a toothy line to which we add the left side (L) of the original triangle. The total length of the toothy line is $$L_{n} = L + rL + r^{ 2} L + \cdots + r^{n} L = L(1 - rG /L) /(1 - r)$$ where r = 2−1/2 = 0.707, and G is the smallest length segment in the drawing, G = rnL. In the limit $$n \to \infty$$, the total length approaches $$L_{\infty } = L /(1 - r)$$. The actual total length Ln can be expressed in dimensionless form as $$\tilde{L}_{n} = 1 - r\varepsilon$$, where $$\tilde{L}_{n} = L_{n} /L_{\infty }$$, and $$\varepsilon = G /L < 1$$.
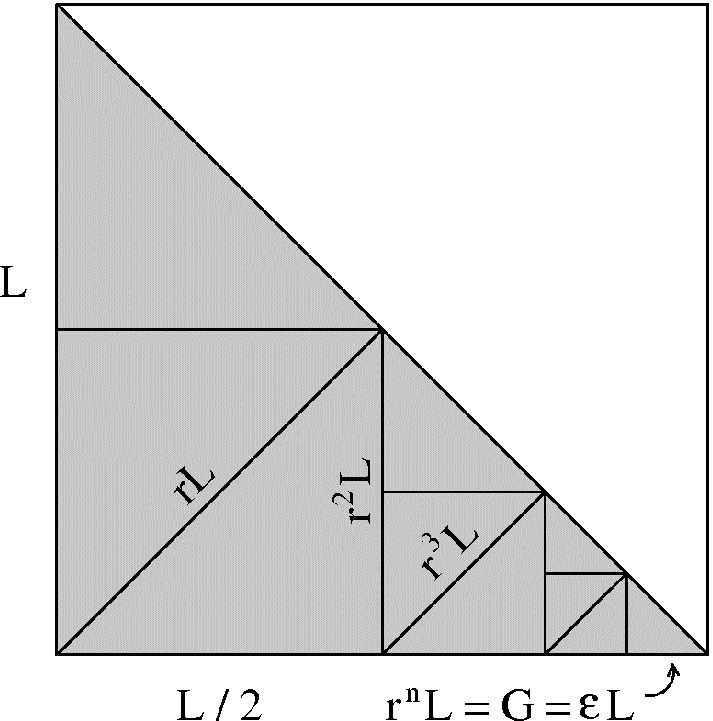
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig3_HTML.png
Fig. 6.3

The length of the toothy line increases as its smallest detail (G) becomes smaller

The fractal dimension (D) of the toothy line is defined as $$\tilde{L}_{n} = \varepsilon^{1 - D}$$, where D depends on ε and r. In the limit $$\varepsilon \,\, \to \,\,0$$, or $$n \to \infty$$, D approaches the irrational number $$D_{\infty } = 1 + r /\ln 10 = 1.3071$$. As ε decreases (or as n increases), the D value approaches $$D_{\infty }$$ from above. For example, when n = 2, ε is 0.5 and $$D \cong 1.379$$. When n = 4, the D value drops to 1.338, which is still above $$D_{\infty }$$.

What does all this mean? It means that the drawing of Fig. 6.3 is a “fractal object” strictly in the limit $$\varepsilon \,\, \to \,\,0$$ where the construction algorithm would have been repeated an infinite number of times, and the number of lines used in making the drawing would be infinite. To the artist who attempts to make the drawing, this would mean that the fractal object would have infinite complexity. This, by the way, is the physical reason why the fractal object is impossible to draw and see, and why the “fractal objects” that populate the literature are not fractal. None of them. They do not exist in nature. They are all Euclidean (this according to Mandelbrot himself [6], p. 39), because the algorithm assumed in making the drawing is intentionally and arbitrarily stopped (cut off) at a small length scale that is sufficiently macroscopic so that the drawing can be made, printed, viewed, discerned, remembered, and discussed.

Review now the fractal dimension calculated during the construction of Fig. 6.3. The drawing with infinite complexity has the fractal dimension $$D_{\infty } = 1.3071$$, which is finite, not infinite. Second, the Euclidean drawings with finite complexity (finite n and ε) have D values greater than $$D_{\infty }$$. All the drawings that the reader can see in Fig. 6.3 are decidedly less complex than the fractal drawing; yet, their calculated dimension D is greater than the fractal dimension $$D_{\infty }$$ of the drawing with infinite complexity. When D decreases, the complexity increases.

The fractal object that is talked about in the fractal geometry literature is not an object. The word “object” means a thing that can be seen or touched, or a person or thing to which action, thought, or feeling is directed. The original Latin word, objectus, means something thrown in front of you, a thing that appears in front of you (from the verb objicere, where ob means toward, for, before, and jacere means to throw, from which the word “jet” in all Latin based languages and English).

The fractal object is, at best, a thought “in the limit,” never achievable, never palpable, and never to be seen, like Sadi Carnot’s reversible heat engine. It is not part of nature. Yet, there is a big difference between the two thoughts in the limit: the reversible engine springs in the mind because of physics (the laws of thermodynamics), whereas the fractal object is as arbitrary as the algorithm chosen by the mathematics artist, or the paint and brush chosen by the painter.

A mathematician may say anything he pleases, but a physicist must be at least partially sane (Josiah Willard Gibbs)

Icon is a simple drawing that conveys the same message as numerous and much more complicated drawings. Making drawings is a means of communication that evolved under certain rules, which constitute the discipline of graphic design. The rules are much stricter when the icon is about human safety. For example, the design of the pedestrian “Walk” and “Don’t Walk” sign on street corners (Fig. 6.4) must meet traffic regulations. These signs evolved with the technology available for communicating messages visually.
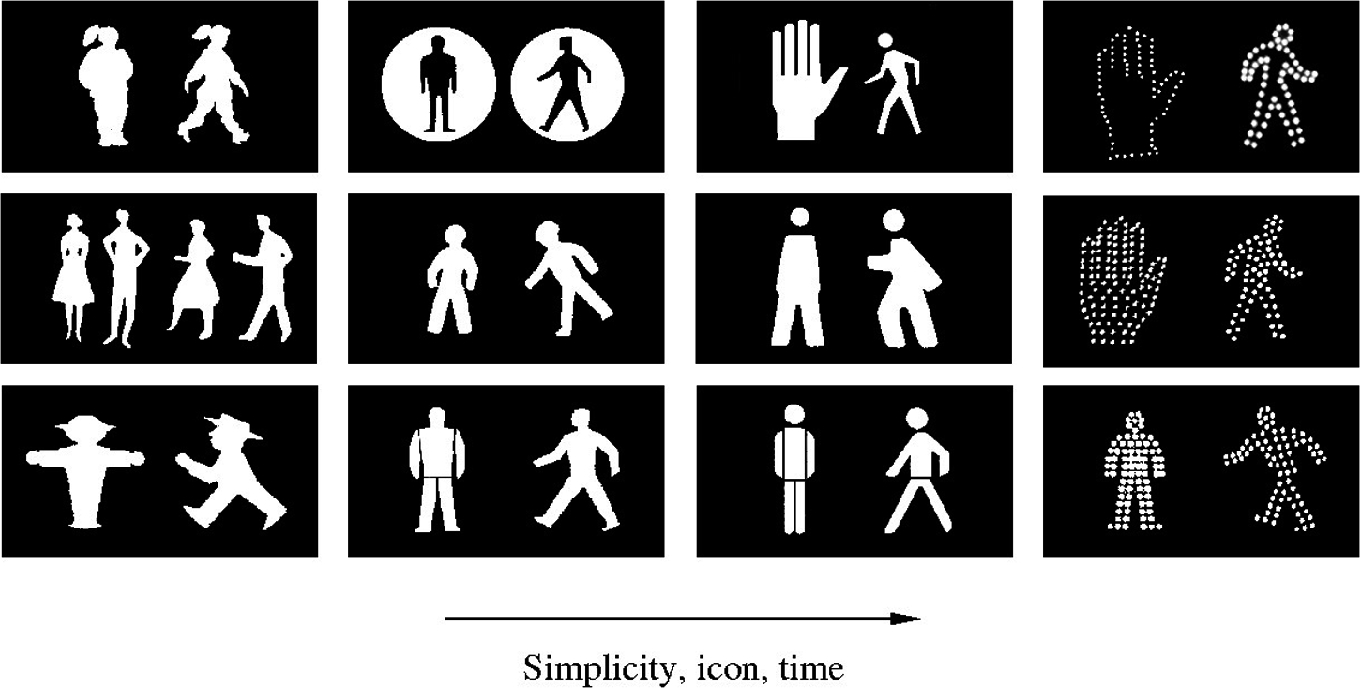
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig4_HTML.png
Fig. 6.4

Evolution from realism to simplicity in the icons that convey the messages “Walk” and “Don’t walk.” Note that each sign is a golden-ratio rectangle, that is, a rectangle the two sides of which form a ratio comparable to 3:2 and 2:1, or the golden ratio 1.618

Today, the world has adopted images of a walking person (pictogram) and a raised hand (ideogram) or standing person (pictogram), respectively, to indicate when to cross the street and when not to cross. The raised hand is an icon because it represents the hand gesture of a traffic policeman. These signs have a characteristic size: not too big, not too small. There is a size range that helps most pedestrians in most circumstances (Fig. 6.5). The larger size is easier to see, but it is more expensive to make. The smaller sign is cheaper but it is more difficult to see and understand.
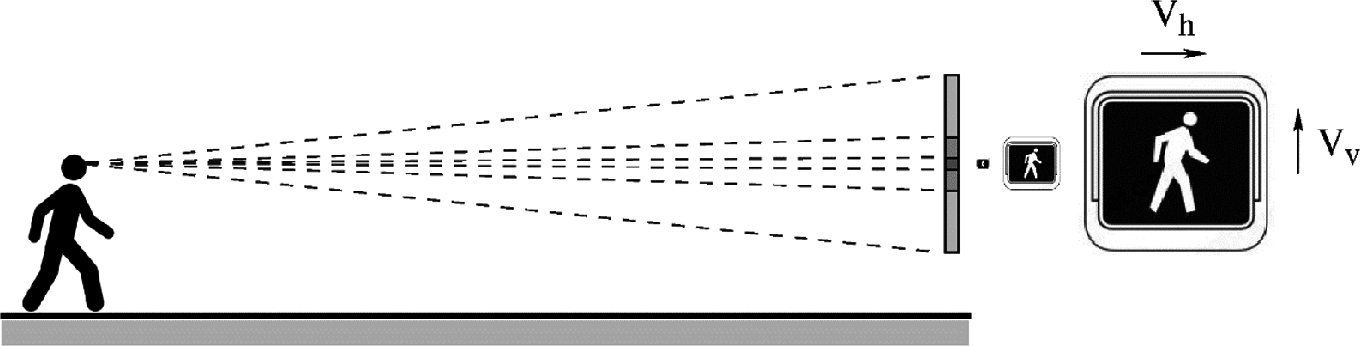
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig5_HTML.png
Fig. 6.5

Size possibilities of the “Walk” sign, and the scanning range of the viewer. The Vh and Vv are the speeds with which the two human eyes scan horizontally and vertically the rectangular image, and Vh > Vv

The golden-ratio shape of the sign plays an important role on the speed with which the message is scanned by the two human eyes [7]. The scanning is faster when the image is shaped as a golden-ratio rectangle, like the cinema screen, the computer screen, and the business card. Because the two eyes are aligned horizontally (like the observed world), the scanning of the image is faster by 50 percent horizontally than vertically.  For the same reason, the person who is blind in one eye perceives faster the image that is rounder, for example the square, not the 3:2 rectangle. This physics holds equally for all animals, two-eyed and one-eyed, because they hold for humans. If we can learn from experiments on animals about humans, we can learn on humans about the animals.

People express a preference for what comes easy. This is a physical psychological phenomenon, present and impossible to disregard. Niederhoffer [8] discovered it in the natural clustering of stock prices. Stock market decision-makers place their limit and stop orders at round numbers with which they are accustomed to deal. Niederhoffer called these numbers “constructal.” In them, we see the human preference for round numbers, because they are easier to discern, easier to remember, and faster to tell other people.

The icon represents an individual in the most general sense (male, female, tall, short, old, young). The drawing is an organization of simple elements that resemble the head, torso, legs, and arms (Fig. 6.6). By itself, each element is meaningless. The meaning is their organization. If the elements are organized in other ways, the pedestrian is puzzled, and the message does not flow from the sign to the mind of the viewer.
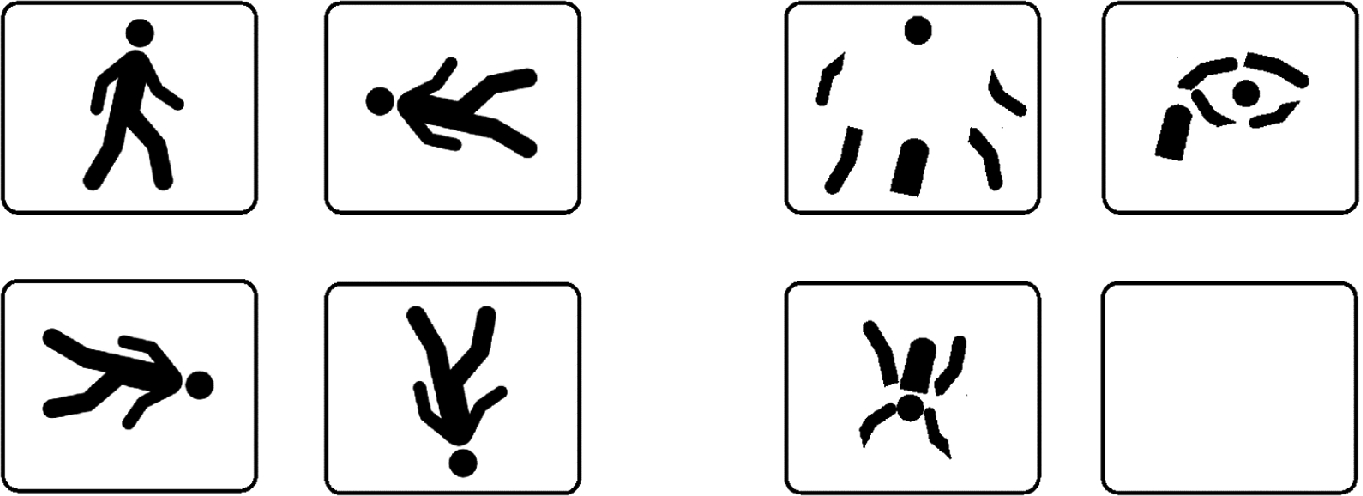
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig6_HTML.png
Fig. 6.6

Possible organizations of the shape elements that form the icon “Walk”

Svelteness is an essential property of all drawings, including the icon. In Fig. 6.7, the svelteness of each icon was calculated with the Sv definition (p. 69) by taking the effective outline as the internal length scale, and the square root of the lit area (white) as the external length scale. Icons with higher svelteness are newer designs. The icon with the highest svelteness appeals to the knowledge of the pedestrian, that is, it conveys information as a set of lit dots, and the mind of the pedestrian creates the image and then interprets it.
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig7_HTML.png
Fig. 6.7

Evolution of the svelteness of the “Walk” signs over time

A photograph or a moving picture of a person crossing the street would be more realistic than a line drawing, but would it be more effective? Key is the minimum detail that is sufficient to convey a quick, clear, and safe message. The few and simple lines, or the gestalt effect (the form) of aligned dots that are lit, are thick but not too thick to convey the message to the persons across the street.

Models share one characteristic with icons, their simplicity. Yet, models and icons are different. The icon is a simple drawing of a mental viewing, observed or imagined. The model is strictly about the observed: it is a manmade simplified facsimile of an object or phenomenon observed in nature. The duck from the woodshop is the model, and the duck on the lake is the observed natural object. The human action of modeling is empiricism, which means observation first and description later. Duck first, wood model later. Modeling is the opposite of theory (idea first, comparison with nature later). Modeling is not theory.

Evolution means changes that occur in a discernible direction in time. Evolution, the word, is defined unambiguously at its origin, the Latin verb evolvo, evolvěre, which means to roll out, to roll forth. Contrary to today’s discourse, evolution is a much older and more encompassing concept of physics (of everything) than Darwinian biology.

Why is simpler better? Drawings—their veracity and complexity—evolve along with the human ability and technology to describe the mental image. The evolution toward the simplest drawing that still captures the message was illustrated by Picasso in the sequence of lithographs called “The Bull”. In 11 plates, the artist captured the essence of the message that was ultimately expressed in a small set of organized lines with high svelteness (Fig. 6.8).
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig8_HTML.png
Fig. 6.8

Evolution from realism to simplicity in Picasso’s lithographs “The Bull”, showing the artist’s quest for the essential drawing of the bull

Evolution is also evident in the accuracy with which a drawing is made by computer, as technology evolves. Figure 6.9 illustrates this with two circles drawn with pens of two thicknesses. The circles are not perfect, but this is not why they are used as examples. They are used because their svelteness can be calculated as $$Sv = p /A_{b}^{1 /2}$$, where p is the inner perimeter of the black line, and Ab is the area occupied by the black line. To calculate p and Ab, the circle drawings were digitized with several resolution settings measured as PPI (points per inch), which in Fig. 6.9 are plotted on the abscissa. The scanned drawings were converted into binary (black and white) images in order to calculate their p and Ab values.
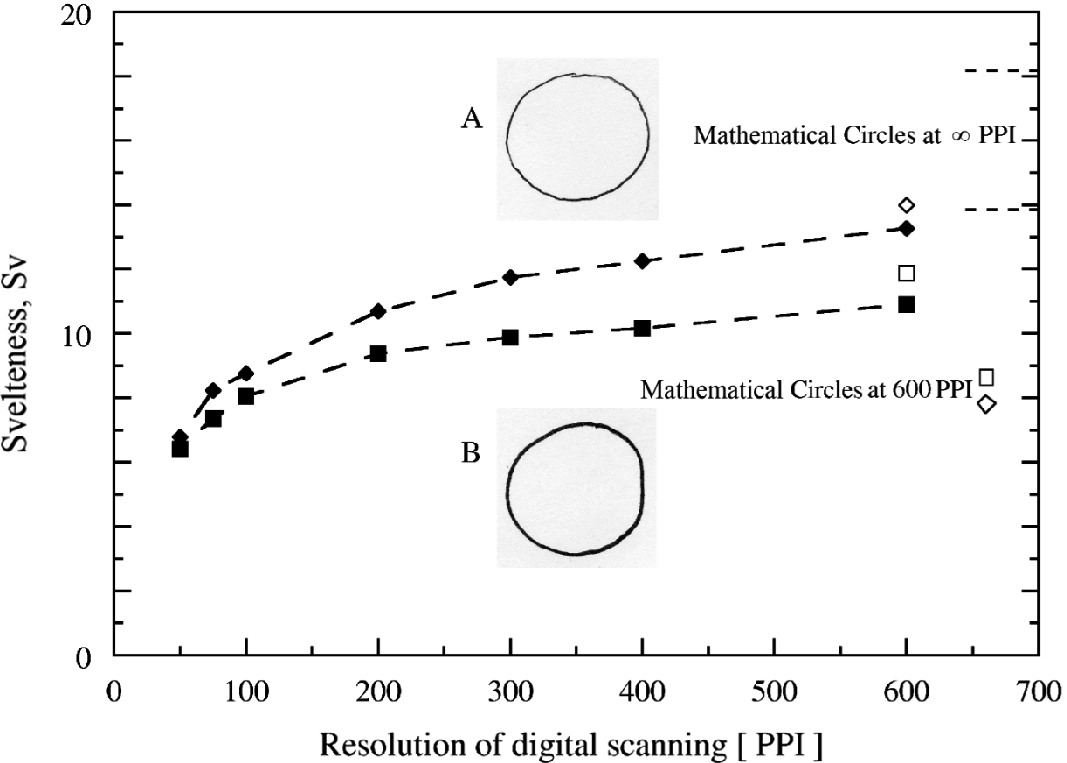
../images/482511_1_En_6_Chapter/482511_1_En_6_Fig9_HTML.png
Fig. 6.9

The evolution of the svelteness of two hand-drawn circles, as the scanning resolution (points per inch, PPI) increases

Figure 6.9 shows that Sv is not a constant, unlike the Sv of a mathematical circle with rim of constant thickness. The svelteness of the hand-drawn circle increases monotonically as the scanning and reproduction technology improves toward more PPI. The increasing trend is due to the rough and ill-defined edges between the black trace left by the pen and the white paper. The texture of the paper and the force on the pen on paper are features that belong to the particular hand that makes the drawing: they cannot be reproduced fully, not even in the limit of infinite machine power. Each curve (Sv versus PPI) is like the length of the coast of Britain, which was the calculation that served as starting point for fractal geometry [6].

Disorder is a concept that deserves particular questioning. Along with the claim that nature evolves toward increasing complexity, we often read that the natural tendency is toward greater disorder, and that this tendency is commanded by the second law of thermodynamics. This is wrong, as one can see by reading the statement of the second law [9–11] (also in Chap. 1, p. 8).

We often read that the second law states that “entropy must increase,” and that the “classical” laws of thermodynamics pertain to “equilibrium states.” Many even teach that thermodynamics should be called thermo “statics.” Such statements are not thermodynamics. I collected several false statements [9, 10], from which I quote one, from a physicist: “the second law applies to closed macroscopic systems consisting of an extremely large number of particles, such as liquids or gases.” This is not true. The second law statements hold for any system, open, closed, isolated, adiabatic, steady state, unsteady state, with configuration, without configuration, and evolving or not.

The second law says nothing about disorder. Many confuse the second law with the view that in a box filled with imaginary identical particles the assembly tends toward a larger number of possible energy states [12, 13]. This is the core idea of statistical mechanics, not thermodynamics, yet lost in the teaching of it are three important observations:

First, to assume a swarm of identical particles in a closed box is to throw away the “any system” power of thermodynamics. The “any system” is the most general system in physics. It is the system with unspecified organization and with infinite freedom. Compared with it, the box with bouncing particles is a very special case, with presumed internal components and rigid impermeable boundary.

Second, particles and disorder are not common observations. They are concepts, not phenomena. From such language, how can there be a “law of increasing disorder”? This has been a source of confusion in science because as we look around we are struck by the complete opposite phenomenon: design, change after change (evolution), self-organization, emergence, and order out of what some would describe as lack of order.

Third, decades before statistical mechanics, the second law and the first law were stated with reference to systems of unspecified size (e.g., heat engines), not infinitesimal. Engines are flow architectures that are macroscopic, organized, and evolutionary. Order, not disorder, is their chief characteristic and claim to fame. Engines are every day futuristic, not “classical.” They are full of life and motion, not in “equilibrium.” They are eminently dynamic, not “static.”

Phenomenon is the human observation that certain things happen innumerable times the same way. One phenomenon represents one natural tendency, which is distinct from other natural tendencies. To observe and describe a phenomenon is empiricism.

Law of physics is a compact statement (text, or formula) that summarizes one phenomenon.

Theory is to rely on the law to experience a purely mental viewing of how something should be.

The phenomenon covered by the first law of thermodynamics was known in mechanics as “what goes up must come down,” and also as vis viva (live force) and vis mortua (dead force). Today, we recognize this more generally as the conservation of energy, from kinetic to potential when a body is thrown upward, to the energy flow (from heat into work) through a closed system such as a heat engine operating in cycles.

The phenomenon covered by the second law is the one-way tendency of all flows, such as the flow of water under the bridge, and the flow of heat from hot to cold. Today, we recognize this natural tendency as irreversibility. Every flow, by itself, proceeds from high to low. Fluid flows through a duct from high pressure to low pressure. Heat through an insulation leaks from high temperature to low temperature. If you do not know beforehand which is the high and which is the low, then the direction of the flow will tell you. Why, because it is the law, and any system in nature obeys the law.

The phenomena observed as complexity, organization, design, and the other terms reviewed in this chapter are natural organization, evolution, and life [14, 15]. The occurrence and evolution of freely morphing configurations is present in everything that flows and moves more easily over time. This phenomenon is represented by the constructal law. Observations of this kind are everywhere: river basin evolution, lung architecture evolution, city traffic evolution, heat exchanger evolution, and aircraft evolution. These observations reveal the arrow of time [16] in nature, which points from existing flow configurations to new configurations through which the flowing is easier. Not the other way around. Why, because this is the law, and all systems in nature obey the law.

Words matter, especially in science. This is why it was essential to define unambiguously the terms of any discussion about complexity. When you hear somebody conflate disorder with the second law, ask that speaker to state the second law. You will then discover that the speaker does not know the subject even though before your question the speaker was convinced that he did. For you, the discovery is much more precious: you will suddenly see in front of you the empty suit and, if the speaker is well established, no suit at all, just the new clothes of the emperor.

The birth of the word “constructal” is a beautiful story of why words matter, and why it pays to be curious while still ignorant, unbiased, but creative. I had discovered the principle in September 1995, and I was using it to predict and draw flow architectures (heat flow, fluid flow, pedestrians). The principle had no name. One of my doctoral students at the time, Marcelo Errera from Brazil, came into my office and said that my drawings look like the drawings in a book called “The Fractal Geometry of Nature”. I was unaware of that book and fractal geometry. I asked him to get the book from the Duke library and show it to me. When I opened it, on one of the first pages, Mandelbrot (born and raised as a child in Poland) explained that he invented the word “fractal” from the Latin verb frangere (accent on the “ah”), which means to break something into two smaller pieces. I immediately realized that he was wrong about the Latin: the word “frangere” is preserved 100% in Romanian, in spelling and pronunciation, and obviously nature does not “snap” sticks and bones into smaller bits all the way to dust. The time arrow of design evolution in nature is the complete opposite of that.

I told Marcelo that Mandelbrot should have used the opposite of frangere, which is the verb construěre (construire in Romanian, construer in Portuguese), and we laughed that “the geometry of nature is constructal, not fractal.”

By chance, at the time I was revising two manuscripts right before publication, and I inserted the word “constructal” and its Latin meaning in those articles [17, 18], both published in 1996. To my surprise, the readers decided that constructal was a useful word. Perhaps you also had this experience: something that you create for pure fun is later taken as serious, heavy, and profound by scientists steeped in deep contemplation.

In this story, helpful was the fact that Marcelo and I had been constantly comparing Portuguese with Romanian, Italian, Spanish, French, and Latin. We had fun with stories about the origin of languages, people, migrations, ideas, and words. I still collaborate with Marcelo, who is now a professor in Brazil.

Fractal algorithms are descriptive, not predictive. Fractal geometry is no theory. One guesses an algorithm that would lead to a drawing that resembles a natural image. The fractal mathematician is no fool: he or she does not reveal to you the multitude of algorithms that led to drawings that looked like nothing. The masters were no fools either: they did not show anybody the discarded paintings strewn all over the floor.

The constructal law is predictive. It teaches how to discover the drawing (and the “fractal algorithm,” if you wish) and how to predict the evolution—the morphing—of the natural configuration over time. Description is empiricism, and it is very common, banal, diverse, and abundant. Prediction requires a law and a theory based on that law. Prediction is extremely rare because it unifies the abundant phenomena.

Science needs both: the many small and the few large, the diversity and the unifying view, the many descriptions and the extremely few predictions, the abundant empiricism and the rare theory.