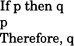
Reasoning and decision making are topics of central importance in the study of human intelligence. Reasoning is the process by which we can apply our vast stores of knowledge to the problem at hand, deducing specific consequences from our general beliefs. Reasoning also takes place when we infer the general from the specific, by formulating and then testing new ideas and hypotheses. Rules for correct reasoning have been laid down by great thinkers in normative systems (principally logic and probability theory) and it is tempting to define, and evaluate, human rationality by referring only to these rules. However, we shall argue in this book that this approach is mistaken. The starting point for any understanding of human rationality should be behavioural: we must ask how decisions taken and actions performed serve the goals of the individual. Formulating and making use of logical and other rules has always had to rest on a more fundamental human ability to achieve behavioural goals.
The psychology of thinking has a long history, but the past 25 years or so have witnessed an explosion of research effort in the areas of decision making, judgement and reasoning, with many hundreds of experiments reported in the psychological literature. These studies are reviewed in detail in several recent textbooks (e.g. Baron, 1988; Evans, Newstead, & Byrne, 1993a; Garnham & Oakhill, 1994) and we will make no attempt to repeat the exercise here. In this book our purposes are theoretical and integrative: we seek to make sense of research in these vast literatures and to resolve some central theoretical issues of importance concerning rationality and the nature of human thinking. Hence our discussion of the published studies will be highly selective, although we believe focused on findings that are both important and representative of the area as a whole.
The aims of this book are three-fold. First, we address and attempt to resolve an apparent paradox of rationality that pervades in these fields. The issue of rationality is central to the first two chapters and underpins much of our later discussion. Next, we seek to achieve integration between the study of reasoning and decision making. Despite some recent efforts to bridge the gap, research in these two areas has proceeded largely in isolation. It seems to us that the mental processes of reasoning and decision making are essentially similar, although we shall see how an emphasis on rule-following as the basis of rationality has rendered this resemblance less than self-evident. Finally, we shall present a dual process theory of thinking which advances understanding of the phenomena we discuss and the psychological mechanisms underlying the kinds of rationality that people display in their reasoning and decision making.
The human species is far and away the most intelligent on earth. Human beings are unique in their cognitive faculties—for example, their possession of an enormously powerful linguistic system for representing and communicating information. They have learned not only to adapt to the environment but to adapt the environment to suit themselves; and they have organised vastly complex economic, industrial, and political systems. They have also developed a capacity for abstract thinking that has enabled them, among other things, to create logic and other normative systems for how they ought to reason.
What happens when representatives of this highly intelligent species are taken into the psychological laboratory to have their processes of thinking, reasoning, and decision making studied by psychologists? The surprising answer is that people seem to make mistakes of all kinds, as judged by the normative rules that human beings have themselves laid down. Many of these rule violations are systematic and arise in cases where a bias is said to exist. Some psychologists use this term as a necessarily pejorative one, but for us it will be descriptive, meaning only a departure from an apparently appropriate normative system. We are not talking here about minor aspects of human performance: systematic deviations from normative principles have been identified and reported in many hundreds of published studies within the past twenty years alone. Although we discuss the issues in general terms in this chapter, a number of specific examples of reasoning and decision biases will be discussed throughout this book. Lest this chapter be too abstract, however, we present a single example of the kind of thing we are talking about.
In syllogistic reasoning tasks, subjects are presented with two premises and a conclusion. They are instructed to say whether the conclusion follows logically from the premises. They are told that a valid conclusion is one that must be true if the premises are true and that nothing other than the premises is relevant to this judgement. Suppose they are given the following problem:
No addictive things inexpensive |
|
Some cigarettes are inexpensive |
|
Therefore, some addictive things are not cigarettes |
On the basis of the information given, this syllogism is invalid. In other words, the conclusion does not necessarily follow from the premises. The class of cigarettes might include all addictive things, thus contradicting the conclusion. Of course, those cigarettes that were inexpensive would not be the ones that were addictive, but this is quite consistent with the premises. However, the majority of subjects given problems like 1.1 state erroneously that the conclusion does follow logically from the premises (71% in the study of Evans, Barston, & Pollard, 1983). Now suppose the problem is stated as follows:
No cigarettes are inexpensive |
|
Some addictive things are inexpensive |
|
Therefore, some cigarettes are not addictive things |
The logical structure of 1.2 is the same as 1.1; all we have done is to interchange two of the terms. However, with problems of type 1.2 very few subjects say that the conclusion follows (only 10% in the study of Evans et al., 1983). What is the critical difference between the two? In the case of 1.1 the conclusion is believable and in the case of 1.2 it is not believable. This very powerful effect is known as “belief bias” and is discussed in detail in Chapter 5. It is clearly a bias, from the viewpoint of logic, because a feature of the task that is irrelevant given the instructions has a massive influence on judgements about two logically equivalent problems.
There seems to be a paradox. On the basis of their successful behaviour, human beings are evidently highly intelligent. The psychological study of deduction, on the other hand, appears to suggest that they are illogical. Although some authors in research on biases have been careful to qualify their claims about human behaviour, others have made fairly strong claims that their work shows people to be irrational (see Lopes, 1991, which discusses a number of examples). It is perhaps not surprising that research on biases in reasoning and judgement has come under close scrutiny from philosophers and psychologists who simply cannot accept these findings at face value and who take exception to the inferences of irrationality that are often drawn from the studies concerned. These criticisms mostly come from authors who take human rationality to be obvious, for the reasons outlined above, and who therefore conclude that there is something wrong with the research or its interpretation.
Evans (1993a) has discussed the nature of this criticism of bias research in some depth and classified the arguments into the following three broad groupings:
the normative system problem;
the interpretation problem; and
the external validity problem.
The first major critique of bias research by a philosopher was that of Cohen (1981) whose paper includes examples of all three types of argument. The normative system problem, as Cohen discusses it, is that the subject may be reasoning by some system other than that applied in judgement by the experimenter. For example, psychologists studying deductive reasoning tend to assume a standard logic—such as extensional propositional logic—as their normative framework, whereas many other logics are discussed by logicians in the philosophical literature. Cohen (1982) suggested further that people might be using an old Baconian system of probability based on different principles from modem probability theory. We find this suggestion implausible—substituting, as it does, one normative system for another. However, the idea that rationality is personal and relative to the individual is important in our own framework as we shall see shortly.
A different slant on the normative system problem is the argument that conventional normative theories cannot be used to assess rationality because they impose impossible processing demands upon the subject. We would not, for example, describe someone as irrational because they were unable to read the text of a book placed beyond their limit of visual acuity, or because they could not recall one of several hundred customer addresses, or were unable to compute the square root of a large number in their heads. For this reason, Baron (1985) distinguishes normative theories from prescriptive theories. The latter, unlike the former, prescribe heuristics and strategies for reasoning that could be applied by people within their cognitive processing capabilities. For example, people cannot be expected to internalise probability theory as an axiomatic system and to derive its theorems, but they can learn in general to take account of the way in which the size and variability of samples affects their evidential value.
In the case of deductive reasoning, this type of argument has been proposed in several recent papers by Oaksford and Chater (e.g. 1993, 1995). They point out that problems with more than a trivial number of premises are computationally intractable by methods based on formal logic. For example, is is known that to establish the logical consistency of n statements in propositional logic requires a search that increases exponentially with n. Oaksford and Chater go on to argue that the major theories of deductive reasoning based on mental logic and mental models (discussed later) therefore face problems of computational intractability when applied to non-trivial problems of the sort encountered in real life, where many premises based on prior beliefs and knowledge are relevant to the reasoning we do. In this respect the argument of Oaksford and Chater bears also upon the external validity problem, also discussed later.
The interpretation problem refers to the interpretation of the problem by the subject, rather than the interpretation of the behaviour by the psychologist. The latter is a problem too, but one which belongs under the third heading, discussed below. The interpretation argument has featured prominently in some criticism of experimental research on deductive reasoning. For example, in a very influential paper, Henle (1962) asserted that people reason in accordance with formal logic, despite all the experimental evidence to the contrary. Her argument is that people’s conclusions follow logically from their personalised representation of the problem information. When the conclusion is wrong, it is because the subject is not reasoning from the information given: they may, for example, ignore a premise or redefine it to mean something else. They might also add premises, retrieved from memory. Henle illustrates her argument by selective discussion of verbal protocols associated with syllogistic reasoning. There are some cases, however, in which her subjects appear to evaluate the conclusion directly without any process of reasoning. These she classifies as instances of “failure to accept the logical task”.
Another version of the interpretation problem that has received less attention than it deserves is the argument of Smedslund of a “circular relation between logic and understanding” (see Smedslund, 1970, for the original argument and 1990 for a recent application of it). Smedslund argues that we can only decide if someone is reasoning logically if we presume that they have represented the premises as intended. Conversely, we can only judge their understanding of the problem information if we assume that they have reasoned logically Smedslund’s surprising conclusion from his discussion of this circularity is that “the only possible coherent strategy is always to presuppose logicality and regard understanding as a variable”. This argument was scrutinised in detail by Evans (1993a) who refuted it by discussion of the specific example of conditional inference. He showed that subjects’ reasoning in such cases is not logically consistent with any interpretation that can be placed upon the conditional sentence and nor is there logical consistency between reasoning on one problem and another.
Perhaps the most potentially damaging critique of bias research is that based on the external validity problem. In its least sympathetic form, as in Cohen’s (1981) paper, the argument can aim to undermine the value of the research fields concerned on the basis that they study artificial and unrepresentative laboratory problems. Consider, for example, the Wason selection task (Wason, 1966), which we discuss in some detail later in this book. Devised as a test of hypothesis testing and understanding of conditional logic, this problem is solved— according to its conventional normative analysis—by less than 10% of intelligent adult subjects, and has become the single most studied problem in the entire reasoning literature (see Evans et al., 1993a, Chapter 4, for a detailed review). Cohen attempted to dismiss the phenomenon as a “cognitive illusion”, analogous to the Muller-Lyer illusion of visual perception. If he is right, then many researchers have chosen to spend their time studying a problem that is wholly unrepresentative of normal thinking and reasoning and that presents an untypically illogical impression of human thought. We disagree with Cohen, but we will nevertheless consider in some detail how performance on this particular task should be interpreted. Where we will agree with him is in rejecting the notion that the selection task provides evidence of irrationality. However, unlike Cohen we believe that study of this task has provided much valuable evidence about the nature of human thought.
Other aggressive forms of the external validity argument include suggestions that bias accounts are proposed to accord with fashion and advance the careers of the psychologists concerned and that researchers create an unbalanced picture by citing disproportionately the results of studies that report poor reasoning (see Berkeley & Humphreys, 1982; Christensen-Szalanski & Beach, 1984). A milder version of the argument has been presented by such authors as Funder (1987) and Lopes (1991) who, like us, are sympathetic to the research fields but concerned by interpretations of general irrationality that are placed upon them. Experiments that are designed to induce errors in subjects’ performance are valuable in advancing our theoretical understanding of thought processes. It is a mistake, however, to draw general inferences of irrationality from these experimental errors. As an analogy, consider that much memory research involves overloading the system to the point where errors of recall will occur. This provides useful experimental data so that we can see, for example, that some kinds of material are easier to recall than others, with consequent implications for the underlying process. Such research is not, however, generally used to imply that people have bad and inadequate systems of memory. So why should explorations of cognitive constraints in reasoning be taken as evidence of poor intelligence and irrationality?
Our own theoretical arguments stem from an attempt to resolve the problems outlined in this section and to address some of the specific issues identified. In doing this we rely heavily upon our interpretation of a distinction between two forms of rationality, first presented by Evans (1993a) and by Evans, Over, and Manktelow (1993b).
Human rationality can be assessed in two different ways: one could be called the personal and the other the impersonal. The personal approach asks what our individual goals are, and whether we are reasoning or acting in a way that is usually reliable for achieving these. The impersonal approach, in contrast, asks whether we are following the principles of logic and other normative theories in our reasoning or decision making. Flanagan (1984, p. 206) gives a good statement of an impersonal view of rationality:
Often rationality is taken as equivalent to logicality. That is, you are rational just in case you systematically instantiate the rules and principles of inductive logic, statistics, and probability theory on the one hand, and deductive logic and all the mathematical sciences, on the other.
Taking this approach, we would say that people are rational if they have reasons for what they believe or do that are good ones according to logic or some other impersonal normative system. But this way of looking at rationality should be combined with a personal view, which sees an individual’s mental states or processes as rational if they tend to be of reliable help in achieving that individual’s goals. Nozick (1993, p.64) comments that neither the personal nor impersonal view taken on its own “… exhausts our notion of rationality.”
As a simple example of the need for both views, consider a man who tries to dismiss a woman’s ideas about economics by arguing that women are incapable of understanding the subject. We could rightly, from the impersonal point of view, call this irrational and charge that the man does not have a good reason for dismissing these ideas. Invoking normative principles to justify ourselves, we would point out that he is committing an ad hominem fallacy. This should not, however, be the end of the story. It is probably not even in the woman’s interest to stop thinking about this man. For what is his underlying goal, and is he likely to achieve it? To ask this question is to take the personal view, which can be of great practical importance. Perhaps the man is a politician who is trying to advance his own position at the expense of the woman’s. He may succeed in this by appealing to the prejudices of a section of the electorate if the woman takes no steps to stop him. It is foolish in itself to assume that someone who violates some normative principle does not know what he is doing nor how to achieve the goal he has in mind. The man in our example could be rational from the personal point of view. We should keep this in mind if we do not want to underestimate him, but do want to predict what he will try to do, so that we can stop him from doing it. Of course, one way to stop him may be to go back to the impersonal view and point out in public that he is violating normative principles. This would be, in effect, to show that his private, personal goal is not at all that of discovering the best economic theory.
To avoid confusion, we shall introduce a terminological difference between these two ways of looking at rationality, and try to make the distinction between them more precise. We shall use “rationality!” for our view of personal rationality, and “rationality2” for our view of impersonal rationality. Until recently, most research on deductive reasoning has presupposed a version of impersonal rationality and almost totally ignored personal rationality. Our object is to explain how we think this distinction should be made, and to bring out its importance for future work on reasoning. As a first step, we adopt the following rough introductory definitions:
Rationality1: Thinking, speaking, reasoning, making a decision, or acting in a way that is generally reliable and efficient for achieving one’s goals.
Rationality2: Thinking, speaking, reasoning, making a decision, or acting when one has a reason for what one does sanctioned by a normative theory.
Returning to our example, we can now describe it as one in which someone is not rational2 but may be rational1. The male politician tries to achieve a selfish personal goal by using an invalid argument, and yet he could still be rational1 if his attempt to appeal to prejudice has a good chance of success. Of course, the principles of valid inference from logic are properly used for a specific purpose—that of inferring what must follow from premises assumed to be true. Logicians sometimes have this purpose as an end in itself, but most of us use valid inferences to help us achieve some further end—say, that of advancing scientific knowledge about economics or psychology. In our example, the politician did not have this goal; his only goal was his personal political advantage. Fortunately, he could not openly acknowledge this in our society and still hope to attain it. The use of logic could also have some utility in a political debate with him, as people do have some deductive competence without special training (Chapter 6). As we shall see later in this chapter, however, the usefulness of logic has its limits even in science.
An important contrast in the aforementioned definitions is between the use of “generally reliable” in the first and “when one has a reason” in the second. Both phrases are there to indicate that one cannot properly be said to be rational or indeed irrational, in either sense, by accident or merely as a result of good or bad luck. To possess rationality2, people need to have good reasons for what they are doing, which must be part of an explanation of their action. They have to follow rules sanctioned by a normative theory: this is what makes the reasons “good” ones. In this book, we are only concerned with normative theories (mainly logic and decision theory, including probability theory) for manipulating propositional representations. For example, people would have a good reason for concluding that it will rain by following an inference rule, modus ponens, which permits them to infer that conclusion from the propositions that the barometer is falling and that it will rain if this is so. If people are being rational2, we expect the existence of such reasons to be indicated in their protocols, where they are asked to give a verbal report of their thinking or reasoning while they do it.
The rational1 perspective is a different one. What makes people more or less rational in this sense is the extent of their ability to achieve their goals. People will usually be aware of a goal they have and may have some awareness of some of the steps required to attain it. But they will usually be unaware and unable to describe the processes that do much to help them achieve their ordinary goals. Still less will they have good reasons for the way these processes work. People may know, for example, that they are going out to buy a newspaper at a shop, but will know next to nothing about how their visual system works to enable them to get there. The working of this system is beyond their knowledge or control, and so they can hardly be said to have good reasons for making it produce representations of the world in one way rather than another.
We believe that human cognition depends on two systems. What we shall call the tacit or implicit system is primarily responsible for rationality1, while what we shall call the explicit system mainly affects the extent of people’s rationality2 The latter system is employed in sequential verbal reasoning, which people consciously engage in and can give some report about.1 On the other hand, tacit systems operate in parallel, are computationally extremely powerful, and present only their end-products to consciousness. Such systems may have an innate basis—as many psychologists and linguists now believe to be the case with linguistic learning and understanding—but are always extensively shaped by interactions with the environment. In the case of reasoning and decision making, tacit processes are largely responsible for the selective representation of information—what we term relevance processes—and hence the focus of attention of the reasoner. We will see evidence in Chapters 2 and 3 that many basic decisions are largely determined by such implicit processes, with conscious thought contributing little more than some overall justification for the actions. The nature of these dual thought processes—the implicit/tacit one and the explicit one—will be discussed in more detail in the final chapter of this book, though the distinction really calls for a book in itself. For the time being we note that some philosophers have argued for such a duality (Harman, 1986, pp. 13–14), and that strong evidence for it may be found in the literature on implicit learning (see Reber, 1993, and Berry & Dienes, 1993). Sloman (1996) also argues for a similar distinction between what he calls associative- and rule-based reasoning.
Contemporary reasoning theories are addressed to several different objectives which Evans (1991) has analysed as the explanation of (a) deductive competence, (b) errors and biases observed in experiments and (c) the dependence of reasoning upon content and context. In the course of this book we shall be examining all of these issues and the associated theories, but for the moment we confine our attention to deductive competence which links directly to rationality2. The major theories that have addressed the issue of deductive competence are those of mental logic (or inference rules) and mental models.
Mental logic and mental models
Rationality2 is most obviously presupposed by the theory that people reason by use of an abstract internalised logic. The notion that the laws of logic are none other than the laws of thought enjoys a long philosophical tradition and was popularised in psychology by the Piagetian theory of formal operational thinking (Inhelder & Piaget, 1958) and by the paper of Henle (1962) already mentioned. These authors did not propose computational models of the kind expected by today’s cognitive scientists, however, so contemporary advocates of mental logic have attempted to provide better specified accounts of precisely how people reason (see for example, Braine & O’Brien, 1991; Rips, 1983, 1994).
Formal logic provides a normative standard for deductive inference. Valid deductions are inferences that add no new semantic information, but derive conclusions latent in premises assumed to be true. Deductive systems (such as expert consultant systems programmed on computers) are powerful in that they can store knowledge in the form of general principles that can be applied to specific cases. However, such systems must have effective procedures for making deductions. Furthermore, if the system in question is a person rather than a computer, we require a psychologically plausible and tractable account of this reasoning process.
Propositional logic, as the basic formal logic, deals with propositions constructed from the connectives not, if, and and or, and provides several alternative and equivalent procedures for inferences containing these propositions. Premises consist of such propositions: for example, the premise “if p then q” connects two propositions, p and q, by the conditional connective. One way of establishing the validity of an argument is by a method known as truth table analysis. In this approach, all possible combinations of truth values of the premises are considered in turn. If no situation can be found where the premises are all true and the conclusion false then the argument is declared valid. This exhaustive algorithm neatly demonstrates the exponential growth of logical proof spaces as one must consider “2 to the power of n” situations, where n is the number of propositions.
In fact, no one seriously suggests that human reasoning resembles a truth table analysis. Mental logic theories are built instead upon the other main proof procedure provided by logic—abstract inference rules, known in philosophical tradition as “natural” deduction. An example of such a rule is modus ponens, which takes the general form:
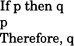
A rule of this kind is abstract and therefore general purpose. The idea is that particular verbal reasoning problems are encoded in an abstract manner and then rules like this are followed. So on encountering the propositions “If the switch is down the light is on” and “the switch is down” one would encode “the switch is down” as p, and so on, and follow the rule. This leads to a conclusion q, which is translated back into the context as “the light is on”. There are a number of mental logic theories differing in detail about the number and nature of the inferences and rules and the procedures for applying them. One of the best known—and best specified—is the ANDS model of Rips (1983, renamed PSYCOP by Rips, 1994), which is a working computer program.
The theory of mental logic is self-evidently committed to the idea that people often display rationality2: they have the best of reasons—logical ones—for the inferences they perform. The hypothetical mental system has its limitations, of course, but there are supposed to be many valid inference rules, like modus ponens, that people systematically use in their reasoning: this is the force of saying that they have a mental logic. Notice how this theory implies that people explicitly follow logical rules, in a step-by-step or sequential pattern of manipulating propositional representations. People are supposed to follow modus ponens because their mental or verbal representations of a conditional and its antecedent match the conditions for the application of the rule, with the result that they perform the inference. People do not merely come to the same conclusion that logic would sanction but in some other way: they are held to do more than just passively comply with or conform to logic.2 Indeed, people’s grasp of the meaning of if and the other connectives supposedly consists in their ability to follow logical rules. Moreover, the supporters of mental logic hold that people can give some report, in verbal protocols, of the inferences they are drawing from conditionals and other logical forms.
The other contemporary theory to address the issue of deductive competence is the highly influential view which holds that people reason by constructing mental models—i.e. mental structures that are similar to the situations they represent (Johnson-Laird & Byrne, 1991). People are supposed here to have some understanding of validity, some grasp that an inference cannot be valid if its premises are true and its conclusion false in some model, and that the inference is valid if there is no model of this kind. However, it is not proposed that people go through an exhaustive truth table analysis, examining all logical possibilities. Rather they are held to set up models in which the premises are true, and aim to discover what else must be true in those models. The effort at deduction is achieved by focusing on a putative conclusion and making some attempt to find a counter-example to the claim that its supporting argument is valid—i.e. a model in which the premises all hold but the conclusion does not. People draw as deductions those conclusions that hold in all the models constructed, and their understanding of the connectives consists in their ability to construct and manipulate mental models in the right way. Fallacious inferences will typically result when there are too many possible models for them all to be considered. Hence this theory incorporates its own specific notions of cognitive constraint—especially due to limited working memory capacity.
As an example, the equivalent of modus ponens is achieved by model construction. On receiving a proposition of the form “if p then q”, the reasoners set up a model that looks like this:
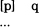
Each line represents a possible situation in which the propositions are true, and the square brackets mean that a proposition is exhausted in that model. Hence the first line means there may be a situation in which a p is linked with a q and this will be true of every p. The second line, the “…”, means that there may be other situations as well—ones where by implication of the exhausted representation of p in the explicit model, p does not hold. On receipt of the second premise of the modus ponens argument, i.e. the assertion that p is true, the first, explicit line of the model allows the immediate inference of q. Were the second premise to be of the form not-q, however, the reasoning would be more difficult as the other line of the model would need to be made explicit.
The theory of mental models may itself be viewed as a form of mental logic, albeit based upon a semantic rather than inference rule approach to logic (see Lowe, 1993; Rips, 1994). It requires some understanding of the meanings of the connectives and of validity. It also requires some general and abstract rules for processing propositional representations that may be used to describe the mental models themselves. The relevant normative theory would be a formal logical system known as semantic tableaux (Jeffrey, 1981)—people would follow all the rules formalised in this theory if they searched in the logical way for counter-examples to arguments. Actually, Johnson-Laird and Byrne do not hold that a mental tableaux system exists in this very strong form (see Chapter 6). But in their proposal, people’s reasons for accepting or rejecting an inference as valid would depend on whether they had found a counter-example in their mental models. We shall take the theories of mental logic and of mental models to be our prime examples of what it would be to follow rules sanctioned by a normative theory in one’s inferences—i.e. to have good reasons for these inferences.
In our terminology, the theories of mental logic and of mental models both imply that people ought to and often do display rationality2. That this is so follows from the fact that these theories have some deep similarity to each other. They both take a normative theory—a formal natural deduction system in one case, and a formal semantic tableaux system in the other—and modify it for the limited processing powers and memory of human beings. They then postulate that the result is the means by which people understand the logical connectives and perform their deductive inferences. We shall have more to say about these theories throughout this book, but especially in Chapter 6 where we focus on the issue of deductive competence.
Theoretical and practical reasoning
We can begin to see the strengths and weaknesses of the theories of mental logic and mental models by noting that they cover only a part of what philosophers would call theoretical reasoning. This does not just refer to reasoning about theoretical entities, like electrons and quarks, but more generally to reasoning that has the object of inferring true beliefs, which we do when we hope to describe the world accurately. It is contrasted in philosophy with practical reasoning, which has the object of helping us decide which actions to perform to try to achieve some goal. We do this when we want to bring about some change in the world to our advantage. For example, we would use theoretical reasoning to try to infer what the weather will be like in the next month, and practical reasoning to decide, in the light of what we think we have discovered about the weather and other matters, where we should go on holiday during that time. (Audi, 1989, has more on this distinction and is an introduction to the philosophical study of practical reasoning.)
This distinction rests on the psychological fact that beliefs are not actions, and acquiring a belief, such as that it will rain tomorrow, is a different process than performing an action, such as picking up an umbrella. Good theoretical and practical reasoning, however, do depend on each other. We have little chance of achieving most of our goals if we cannot describe the world at least fairly accurately. On the other hand, to describe the world accurately we need to perform actions, such as opening our eyes to begin with, looking at objects, and manipulating them, and also identifying, interacting with, and communicating with other people. Note that, if people were not rational in basic activities like these, there would be no grounds for holding that they had any beliefs at all, accurate or inaccurate.
To engage in good practical reasoning is to have rationality1, which—as we have already indicated—involves much implicit or tacit processing of information. In practical reasoning we need, not only to have identified a goal, but to have adopted a reliable way of attaining it, which for the most part is accomplished almost immediately with little awareness on our part of how it is done. Our eyes identify, say, an apple we want to pick up or a person we want to talk to. If we are not experts in perception, we have little idea how this is done. We then choose some way to get to the apple or person, avoiding any obstacles that may be in the way, and we are largely unaware of how we do this. Finally, we pick up the apple with ease, or with almost equal ease speak to the person and understand what the individual says in reply. Such simple acts of communication require significant computations, many of which are tacit. These commonplace abilities are really remarkable, as we realise if we have any knowledge of how difficult it has been to program computers to display them in crude and simple forms.
When most psychologists talk about “reasoning”, they mean an explicit, sequential thought process of some kind, consisting of propositional representations. As our examples reveal, however, we do not think that what has traditionally been called practical reasoning in philosophy always requires much “reasoning” in this sense. The psychologists’ use of the term—which is linked with their endorsement of rationality2—is much closer to what a philosopher would call theoretical reasoning. Certainly much of practical thought, as it would be better to call it, does not depend on conscious step-by-step inferences from general premises we believe or know to be true. It requires more than performing inferences that we have good reasons for, and the rationality1 displayed in good practical thought cannot in some way be reduced to rationality2.
Anderson (1990) has made a distinction similar to ours between rationality as “logically correct reasoning”, and rationality as behaviour that is “optimal in terms of achieving human goals”. This is clearly a distinction between an impersonal idea of rationality and a personal one. He holds that the latter sense should be the basic one in cognitive science, which should be guided by what he calls the General Principle of Rationality: “The cognitive system operates at all times to optimise the adaptation of the behaviour of the organism” (p. 28).
For example, Anderson argues that our ability to categorise objects, such as when we recognise an apple tree, is rational in his personal sense. This adaptive sense of rationality is obviously close in some respects to what we mean by rationality1, and we have been influenced by much of what he says. However, we are unhappy with talk of human beings “optimising” or “maximising” anything in their behaviour; we shall say more about this in the following chapter on decision making (Chapter 2). Note that Anderson is himself somewhat uncomfortable with this idea, and that there is considerable doubt that natural selection can be said to optimise adaptations in a very strong sense.
It is easy to see why this should be so. Our hands, for example, can still be used effectively for climbing trees, though there would be better designs for this. They are also fairly effective at using computer keyboards, though they could have a better design for this as well. Perhaps they have the “optimal” design, given what evolution initially had to work on, for the kind of life style that they were originally evolved to serve in one of our hominid ancestors. That was a long time ago, and it is hard to say for sure. However, our hands are quite well designed for many practical purposes, as are the mental processes we use in our practical thought to guide our hands to do their work. Our hands and most of these mental processes have been shaped by evolution from the time even of our pre-human ancestors. Our more conscious and explicit cognitive processes, of the type we use in our most theoretical reasoning, can be less effective, as we shall see in this book. These processes are of more recent origin, and yet are sometimes called on to try to solve problems in the contemporary world for which evolution did not prepare them.
The Limitations of Logical Reasoning
Our ability to reason, whether theoretically or practically, did not evolve for its own sake. We do not naturally reason in order to be logical, but are generally logical (to the extent that we are) in order to achieve our goals. Of course, very sophisticated thinkers, beginning with Aristotle, have reflected on our ordinary deductive reasoning and identified the rudiments of a formal system that can be abstracted from it. Such thinkers can have the abstract goal of using this system as an end in itself to prove theorems, or as the foundation of mathematics and science, which themselves can be pursued for the goal of acquiring knowledge that is seen as an intrinsic good. But even logicians, mathematicians, and scientists have practical goals in mind as well when they use logic in their academic work, such as finding cures for serious diseases and making money from consultancy work.
Formal logic, whether axiomatised as a natural deduction or a semantic tableaux system, begins with assumptions. It does not specify where these assumptions come from, and it takes no interest in their truth in the actual world. To say that they are assumptions is, in effect, to treat them for the moment as if they were certainly true. Logic as an axiomatic system was set up by mathematicians, who could think of their premises as certain because these embodied abstract mathematical truths. But in ordinary reasoning we are mainly interested in performing inferences from our beliefs, few of which we hold to be certain, or from what we are told—in little of which we have absolute confidence. Arbitrary assumptions that are obviously false, or highly uncertain, have no utility for us when we are trying to infer a conclusion that will help us to achieve a practical goal. What we need for such a purpose is an inference from our relevant beliefs in which we have reasonable confidence, or at least an inference from suppositions that we can make true ourselves, as when we try to infer whether we shall have good weather supposing that we go to France for a holiday.
We have already illustrated the form of inference known as modus ponens. Consider, now a second and more interesting (i.e. less apparently trivial) inference associated with conditionals, known as modus tollens:
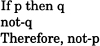
In each case, we have an inference form with two premises, the major premise being conditional and the minor one categorical. Except where these premises depend on earlier assumptions, they are to be assumed true, at least until some further inference form discharges them. Both modus ponens and modus tollens are valid: their conclusions must be true given that their premises are true.
In experiments on conditional reasoning, however, people have a substantially greater tendency to perform or endorse modus ponens than modus tollens (Evans et al., 1993a, Chapter 2). To supporters of mental logic and mental models, with their eyes fixed only on rationality2, the failure to make modus tollens is seen as an error, though one to be excused by the limited processing powers of human beings. Hence believers in mental logic simply hold that people do not have modus tollens as an underived inference rule in their mental natural deduction systems. Thus this inference can only be drawn by “indirect reasoning” which is prone to error (see Braine & O’Brien, 1991). Believers in mental models claim that people tend not to construct an initial model in which the consequent of a conditional is false (see above) and hence that “fleshing-out” is required for this inference. Neither theory has an explanation of why people have these limitations considering that very little processing power would be needed to overcome them.
We can start to see the difference between these two inference forms in a new light by using an example about ordinary reasoning from our beliefs. Suppose we see what looks very much like an apple tree in the distance. It looks so much like other apple trees that we have looked at before that we are highly confident that we have identified it correctly. We cannot tell from this distance whether it has apples on it hidden among its branches, but it is the autumn and we are confident enough to assert:
If that is an apple tree then it has apples on it.
But now someone we trust coming from the tree replies:
That does not have apples on it.
In this case, we would be most unlikely to apply modus tollens, and we would hardly display rationality1 by doing so. If we did assume that the above two statements were true, we could apply modus tollens as a valid inference form, inferring “That is not an apple tree”. But in actual reasoning we would be concerned to perform an inference from our relevant and sufficiently confident beliefs, with the object of extending those beliefs in a way that would help us to achieve our goals. To acquire the belief that we are not seeing an apple tree would be to reject the evidence of our eyes, and this could force us to try to modify our recognition ability for apple trees. That might not be easy, and if we succeeded in doing it, we might be less able to recognise apple trees in the future, to our disadvantage when we wanted an apple. To use Anderson’s terms, we should be cautious in rejecting the output of an adaptive system that, if not optimal, has at least served us well in the past.
What we would probably do in a real case like this would be to reject the conditional above, at least if we continued to trust our eyes and the person who made the second assertion. More precisely, we would lose our moderate confidence in what was conveyed by the conditional, and would perhaps become confident that it was a bad year for apples on that tree. In general, we would tend not to apply modus tollens to a conditional, after learning of the falsity of its consequent, if we were then more confident of its antecedent than of the conditional itself. Instead of performing this inference, we might well give up holding the conditional. In contrast, the cases in which we would decline to perform modus ponens are much rarer. One such exception would be when we had asserted a conditional like, “If what you say is true, then I’m a monkey’s uncle”, which has the pragmatic point of indicating that we think the antecedent is false. (Stevenson & Over, 1995, has more on these points, and a study of inferences when the premises are made uncertain.)
It often seems to be forgotten in experiments on deductive reasoning that logic itself allows us to perform an infinite number of inferences from any premises. In more technical terms, any one of an infinite number of conclusions validly follows from any premises, and, as a normative theory, logic should be thought of as telling us what we may infer from assumptions, rather than what we have to infer from them. As an analogy consider the distinction between the rules of chess and the strategy of chess. Someone who merely knows the rules, does not know how to play, except in the sense of producing a legal game. Choosing from among the large number of legal moves those likely to advance the goal of winning the game, requires a strategy based upon both a relevant goal hierarchy and sound understanding of the semantics of chess positions. In the same way, the use of logic itself in ordinary reasoning requires good practical judgement to select a conclusion that is relevant to a goal we hope to attain. Logic no more provides a strategy for reasoning than do the laws of chess tell you how to be a good chess player.
Even more practical judgement is necessary to have the right degree of confidence in our beliefs to help us to attain our goals, and to know when to extend our beliefs with an inference, and when to give up one of them instead. Of course, logic can give us some help with this through the use of the reductio ad absurdum inference, which allows us to reject, or technically discharge, one of our assumptions when an inconsistency follows from them. People sometimes use this form of argument to attack positions they disagree with, and then they will do what is rare in ordinary reasoning and use premises they have no inclination to believe. But logic is of limited help even here. It does not tell us which assumption to give up when we derive an inconsistency; we must make a judgement on this ourselves, in the light of what we think will best serve our goals. Again, reductio ad absurdum as a logical inference applies to assumptions and inconsistent conclusions, and not to the general case, in which we are trying to extend or modify beliefs, and to make good judgements about the degree of confidence we should have in our conclusions.
Sometimes we can express our confidence in, or in other words our subjective probability judgement about, a proposition precisely enough for probability theory to apply. Using this in conjunction with logic, one can prove that our degree of uncertainty in the conclusion of a valid inference should not exceed the sum of the uncertainties of the premises (Adams, 1975; Edgington, 1991). Here the uncertainty of a proposition is one minus its subjective probability, and so a proposition that has high, or low, probability for us has low, or high, uncertainty. To be rational2 we should follow this principle about uncertainty and others that can be derived from probability theory, which can be of more help than logic alone in our practical thought. Still, this help also has its limits. These principles generally allow us an unlimited number of ways of adjusting our degrees of confidence in the premises and the conclusion of a valid argument. Going beyond them, we have rationality1 when we raise our confidence in certain propositions, and lower it in others, in a way that helps us to achieve our goals.
Johnson-Laird (1994a, b) has recently started to attempt a combined account of deductive and inductive reasoning in terms of mental models, but the standard theory of mental logic is very limited indeed by the fact that it takes no account of subjective probability judgements. The limitations of both theories are well illustrated by what they say about modus tollens. For them, people make a mistake, and reveal a limitation that they have, when they do not perform this inference in experiments on reasoning. Mental logic and mental model theorists have yet to take account of the fact that almost all ordinary reasoning is from relevant beliefs, and not from arbitrary assumptions. They could claim that this is beside the point in their experiments, in which the subjects are supposed to say what follows from the given assumptions alone. But the main object of study should be subjects’ ordinary way of reasoning, which may anyway interfere with any instructions they are given. In the interpretations of psychological experiments that we provide throughout this book, we shall argue repeatedly that habitual methods of reasoning are based largely on tacit processes, beyond conscious control. Hence, they will not easily be modified by presentation of verbal instructions for the sake of an experiment.
We shall argue generally in this book that psychologists of reasoning should move beyond their narrow concentration on deductive logic, and investigate the relevance of probability judgement and decision making to their subject. Much research on deductive reasoning has uncritically applied a simple Popperian view of rationality, which is a type of rationality2 defined only in terms of deductive logic. According to this, there is no rational way of confirming hypotheses—i.e. making them more probable. Deductive logic alone should be used to derive empirical conclusions from a theory, and if these conclusions turn out to be false, then the theory is falsified and should be rejected. Hypotheses and theories can never be confirmed in any legitimate sense, from this point of view. Ordinary people do apparently try to make their beliefs more probable, and consequently they have been said to have an irrational confirmation bias by psychologists influenced by Popper (see Popper, 1959, 1962; and Evans, 1989, Chapter 3 for a discussion of the psychological literature on confirmation bias).
Popperian philosophy of science, however, has been heavily criticised in recent years, in part just because it allows no place for confirmation. Background assumptions, e.g. about the reliability of our eyes or of experimental equipment, are needed to derive testable predictions from scientific theories. Our eyes sometimes do deceive us, and the best equipment can fail to be accurate, and so we can rarely be certain about what we derive from a theory plus some background assumptions. If a prediction turns out to be false, this means that we may be uncertain that the theory itself, or even some part of it, is at fault and should be declared falsified. For this and other reasons, there are good grounds for preferring a non-Popperian framework that allows hypotheses to be confirmed (Howson & Urbach, 1993). In this book, we shall discuss the probability of hypotheses to support our case that human thought and reasoning should not be condemned because it departs from the limited confines of deductive logic. We develop these points in Chapter 2.
Form and Objectives of this Book
We have laid out in this chapter the fundamentals of our theory of rationality and begun to explore the implications that it has for the study of human reasoning, and for reasoning theory. In the next chapter, we develop further our distinction between rationality1 and rationality2 and begin our discussion of the other major topic of interest—the psychology of decision making and judgement. Throughout this book, we shall argue that a rational1 analysis is the crucial starting point and one which provides a perspective from which we can understand much apparently puzzling behaviour in the literature on reasoning and decision making. People should be rational1—though not necessarily rational2—within broad cognitive constraints provided by such limitations as finite memory capacity and limited ability to process information.
It is most important, however, to appreciate that this kind of rational analysis is not in itself a descriptive psychological theory. What it provides is rather an important constraint upon a psychological theory of reasoning: any mechanisms proposed must have the property of achieving outcomes that are broadly rational1 in nature. The reason that we need to start with a rational1 analysis is to be able to identify the cognitive constraints upon reasoning and hence to develop our theory of the underlying processes. It is by probing the limits or bounds upon rationality1 that we begin to develop our understanding of the psychological mechanisms of inference and decision making.
Our descriptive psychological theory is developed from Chapter 3 onwards and is focused on the nature of the cognitive processes underlying reasoning and decision making. Our theory rests critically on the distinction between implicit and explicit cognitive systems. In particular we shall argue for a relevance theory account in which attention to selective features of problem information, together with retrieval of information from memory, is determined by rapid, preconscious processes of a connectionist nature. Such tacit processes are often primarily responsible for judgements and actions. In general, our personal rationality depends more on tacit or implicit processes than on our conscious ability to form explicit mental representations and apply rules to them. Even our ability to manipulate propositional representations, in a way justified by impersonal normative rules, requires the selection of relevant premises, which is mainly the result of implicit processes.
Much of this book is taken up with providing rational1 accounts of behaviour normally classified as constituting error or bias and hence, by definition, irrational2. Rationality2 requires compliance with experimental instructions: for example, if subjects are told to reason deductively, draw only necessary conclusions and disregard prior beliefs, then they are irrational2 if they fail to achieve these goals. However, because we believe that rationality1 resides in the tacit cognitive system we regard it as reflecting habitual, normally adaptive processes that may not always generalise effectively to an arbitrary experimental task. We consider in some detail the Wason selection task (see Chapters 3 and 4) on which behaviour is highly irrational2 from a logicist perspective. We will show that when viewed as a decision task strongly influenced by preconscious judgemental processes, the extensive research on this problem reveals surprising evidence of adaptive thought. In Chapter 5 we look at the influence of prior belief in reasoning and decision making, and critically examine the various claims that people are irrational by taking either insufficient or too much account of prior knowledge.
Nozick (1993, p.76) speculates that what we have called tacit processing may be a better way for human beings to think than the conscious application of rules. He even suggests that philosophers could become “technologically obsolescent” if this is so. We do not support such a sad prediction, nor the extreme conclusion of Harman (1986, p. 11) that “… logic is not of any special relevance to reasoning”, which could make logicians redundant. Explicit logical thinking—conscious, verbal and sequential—affects some of our decisions and actions and is of some value. In Chapter 6 we review the evidence for deductive competence, concluding that people do possess an abstract deductive competence—albeit of a fragile nature—and that the processes responsible for this are explicit. In that chapter we also return to the debate about whether mental logic or mental model theorists have the more plausible explanation of how such competence occurs. Finally, in Chapter 7 we explicate our dual process theory of thinking in detail and consider the general nature and function of both the tacit and explicit systems of thought.
1. |
The extent to which conscious verbal processes can be reported is a subject of great theoretical and methodological debate. The relevant issues are discussed in Chapter 7. |
2. |
See Smith, Langston, and Nisbett (1992), Sloman (1996), and Chapter 7 on the distinction between following rules and complying with or conforming to them. |