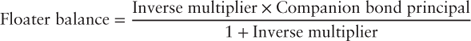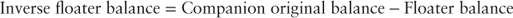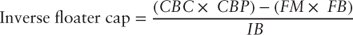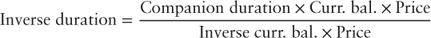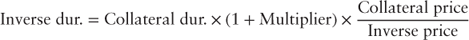Chapter 18
PAC-Floater-Inverse Floater REMIC
A fixed-rate bond may be divided into both a floating- and an inverse floating-rate bond. This chapter finalizes the PAC-companion structure presented in Chapter 16, creating par execution across the capital structure by restructuring the companion bond into a floating and inverse floating rate bond, another example of the division of interest.
Singularly, the PAC-companion structure is an example of the division of principal. The PAC-floater-inverse floater structure is an example of both the division of principal (PAC-companion) and interest (floater-inverse floater). Chapter 16 outlined the division of principal required to create the companion bond whose cash flow is the input for the division of interest, which creates the floater-inverse floater structure. The “trick” is to create a structure including a floating and inverse floating rate bond from one that accrues at a fixed rate in such a manner that the PAC and floating rate bonds are priced at par and the REMIC arbitrage is profitable.
18.1 Structuring the Floater and Inverse Floater
In the case of the PAC-floater-inverse floater structure it follows from Chapter 16 that the first structuring step is the creation of the PAC bond payment and sinking fund schedule. In turn, the PAC bond's original balance determines the companion bond's original balance and the size of its cash flows. Both the PAC balance and its coupon define the companion cash flows that will be split intothe floater and inverse floater. Extending the PAC-companion structure presented in Chapter 16 to create a floater-inverse floater companion bond is as follows:
- Establish the PAC bond.
- The PAC bands are set at 75 and 250 PSA and the resulting original balance is $148.7 million.
- The PAC coupon is set at 4.00%.
- Establish the companion bond's original balance and its cash flows.
- The companion bond's original balance is $51.3 million.
- The companion coupon is set at 4.00%.
At first blush, setting the fixed-rate coupons of the PAC and companion bonds may seem counterintuitive. However, once the technique of splitting the companion bond into a floating and inverse floating rate bond is shown the reason for the initial fixed coupon strikes will become evident. After establishing the companion bond's principal balance and fixed-rate coupon it may be split into a floating and inverse floating rate bond as follows:
- Determine both the floating rate bond's structure and inverse floater coupon multiplier.
- Compute the floater and inverse floater principal split.
- Establish the floater-inverse floater coupon structure.
18.1.1 Floater Structure
The floater cap is struck subject to the floater-inverse structuring rule set forth in 18.1. The floater margin used in rule 18.1 is set based on market pricing. In the forthcoming example the floater margin is struck at 0.30%:
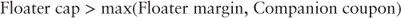
while the inverse floater multiplier is determined by equation 18.2.
Equation 18.2 reveals the need for the structuring rule 18.1. If the floater cap is struck at a rate equal to or below that given by 18.1 then the denominator of equation 18.2 is zero or negative, respectively. Consequently, the inverse floater multiplier is either infinity or a negative value and as a result the inverse floater multiplier as an input to equation 18.3—the floater balance—produces a non-sensical result (infinity or a negative balance) and one is unable to split the companion bond into the floater and inverse floater combination. Thus far, structuring rule 18.1 and equation 18.2 illustrate the companion floater-inverse floater structure is dependent on the companion coupon and original balance, both of which are a function of the PAC bond's structuring bands.
Given a multiplier and floating rate bond margin one can solve for the floater cap. Assuming a 1.5 inverse floater multiplier the floater cap is.
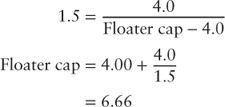
Notice, as the PAC coupon is struck to lower levels the companion coupon increases. In turn, the floater cap also increases for a given multiplier. In this case, a par execution PAC bond coupon of 2.25% results in a companion coupon in excess of 9.00%, which implies a floater cap of 15.00%—too high for a reasonable execution in a low interest rate environment.
18.1.2 The Floater-Inverse Principal Split
The floater-inverse floater principal split begins with the determination of the floater balance given by equation 18.3.
The floater balance is derived from equation 18.3. An inverse multiplier 1.5
results in a floater balance is $30.7 million.
Once the floater balance is established, calculating the inverse floater balance is simple and given by equation 18.4.
In our example the inverse floater balance is $20.5 million.
18.1.3 The Floater-Inverse Coupon Structure
The inverse floater coupon is calculated as shown in equation 18.5.
| where: CBC | = | Companion bond coupon |
| CBP | = | Companion bond principal |
| FM | = | Floater margin |
| FB | = | Floater orig. balance |
| IB | = | Inverse floater orig. balance |
Deconstructing 18.5 provides additional insight with respect to the inverse floater.
- Companion bond coupon
Companion bond principal. The first term in the numerator represents, absent principal amortization, the maximum annual interest available. - Floater margin
Floater principal. The second term assumes the floating rate benchmark is zero and represents, absent principal amortization, the minimum interest paid to the floating rate bond.
Differencing the quantities in the numerator yields the maximum annual interest available to the inverse floater. Division by the inverse floater's original balance, the denominator, yields the maximum annual interest rate at which the inverse floating rate may accrue—its cap.
In our example, the inverse floater cap is:
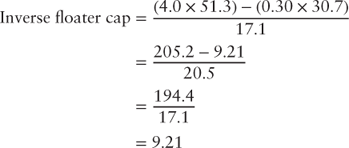
With the above structuring completed, both the floating and inverse floating bonds' coupon formulas can be written. The formula for each is:
- Floating rate bond, min(6.66, max
, 0.30)) - Inverse floating rate bond, min(9.21, max((
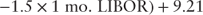, 0))
Table 18.1 REMIC PAC-PAC IO-Floater-Inverse Floater
| MBS 4.00% | Tranche A (PAC) | Tranche B (PAC-IO) | Tranche C (Floater) | Tranche D (Inverse) | |
| Net Coupon | 4.00% | 2.25% | 1.75% | 0.55% | 8.83% |
| Note Rate | 4.75% | 4.75% | 4.75% | 4.75% | 4.75% |
| Term | 360 mos. | 360 mos. | 360 mos. | 360 mos. | 360 mos. |
| Loan Age | 0 mos. | 0 mos. | 0 mos. | 0 mos. | 0 mos. |
| Orig. Bal. | $148.7mm | $148.7mm | $30.7mm | $20.5mm | |
| Price | $105.75 | $100.00 | $15.3125 | $100.00 | $102.00 |
| Index (1 mo. LIBOR) | 0.25% | 0.25% | |||
| Cap | 6.66% | 9.21% | |||
| Floor | 0.30% | 0.00% |
The one-month LIBOR rate used to set the floater and inverse floater coupons, assuming the Jan. 10, 2013, swap rate curve as the transaction's pricing curve, is 0.25%. Based on the one-month LIBOR rate the floater's initial coupon is 0.55% and the inverse floater's initial coupon is 8.83%. At this point, presumably both the floater and inverse floater should be priced at or near par, leaving a premium PAC bond with a 4.00% coupon. Therefore, assuming a par PAC bond coupon of 2.25%, the dealer must take a 1.75% IO strip from the PAC bond to achieve a par execution and thus complete the transaction. Figure 18.1 details the PAC-floater-inverse floater deal structure.
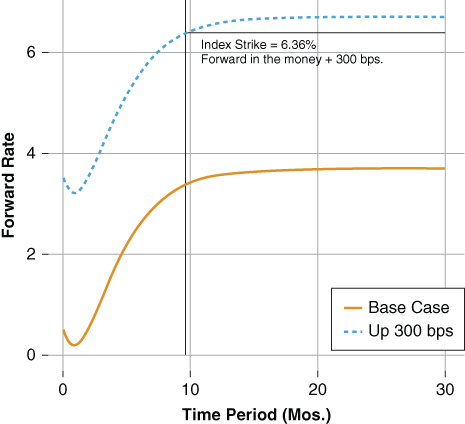
Figure 18.1 Interest Rate Cap Forward Curve Analysis
Because the collateral used in structuring the transaction is priced above par, the interest only derivative execution once again takes center stage in a successful arbitrage. By now, it should be readily apparent that derivative execution is often key to a profitable REMIC execution. The waterfall cash allocation rules are as follows:
- { Pay 100% of available interest to each class pro-rata, based on each class's respective accrued interest}
- { Pay 100% of the available principal in the following order:}
- Pay principal to Tranche A the minimum of:
- The amount required to bring its period outstanding balance equal to the period target balance.
- Tranche A's bond beginning balance.
- Pay the remaining principal received in each period pro-rata to Tranche C and Tranche D until each tranche's principal balance is reduced to zero.
- Once Tranches C's and D's outstanding balances are reduced to zero, pay to Tranche A the minimum of:
- Tranche A period beginning balance.
- Tranche A beginning balance less the principal paid in (1) above,
until tranche A's balance is reduced to zero.
- Pay principal to Tranche A the minimum of:
18.2 A Framework for Floating Rate Securities
A pure floating rate security, that is one absent a margin, cap, or floor, is generally considered to be a zero or near-zero duration security. For example, consider a 10-year floating rate note indexed to one-month LIBOR which pays its coupon monthly. Recall from Chapter 2, the equivalent investment is a one-month LIBOR deposit and the investor reinvests each subsequent maturity in the same. This strategy replicates the 10-year floating rate note. Hence, it stands to reason the 10-year note's duration is equivalent to that of a one-month LIBOR deposit.
18.2.1 Deconstructing a Floating Rate Bond
- Margin: The introduction of a floater margin (spread), is added to the value of the index to determine the floating rate coupon. The margin gives rise to duration. That is, one may consider the floating bond's margin a fixed coupon based on the notional amount of a LIBOR deposit. Consider a floating rate Bond A issued at time
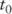with a margin of LIBOR + 0.25% and priced at par. Floating rate Bond B is issued at time 
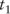with a margin of LIBOR + 0.35%. Thus, Bond A must price to an effective discount margin of 0.35%, which will cause its price to fall—the effect of spread duration. The investor often calculates spread duration to measure a floating rate bond's price sensitivity to changes in the spread (discount margin), holding the index constant. - Interest Rate Cap and Floor: In practice, most floating rate securities are not “pure.” Often they are structured with a floor—the minimum coupon the floater may pay, and/or a cap—the maximum coupon the floater may pay. The cap and floor are interest rate options. The floating rate investor is said to be “short the cap” and “long the floor.” Once a floating rate note's coupon reaches its cap the floater's price will behave like that of fixed-rate bond. Thus, the presence of interest rate options also introduces duration. For example, as a floating rate note's coupon approaches the value of the cap its duration will increase.
- Margin as Interest Only Strip: Finally, in the case of a floating rate note collateralized by mortgages, one may think of the floater margin as an interest-only strip that is based on the notional amount of the floater. Recall from the previous chapters, interest-only strips exhibit a negative effective duration. Thus, it stands to reason that a floating rate bond collateralized by mortgages may also exhibit a modest amount of negative effective duration, the degree to which is dependent on the floating rate bond's embedded options (cap and floor) being sufficiently out of the money.
-
Inverse Floater Duration: Given that both the floating rate and inverse floating rate bonds are created from a fixed-rate bond, in this case a companion bond, it follows that the combined dollar duration of the floating rate and inverse floating rate bonds should equal that of their parent bond.
where: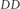 
= Duration 
Curr. bal. 
PriceDropping the float term (the zero duration term) and rearranging 18.6 yields the inverse floating rate bond's duration:
Rearranging equation 18.7, the inverse floater's duration can expressed as follows:
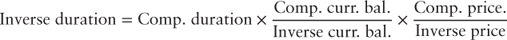
- The ratio of the companion current balance to the inverse current balance is the leverage of the inverse floater and can be restated as
, equation 18.2. - In this example, the companion bond is the collateral from which the inverse floater is derived. Furthermore, the companion bond can be generalized to its underlying collateral.
With the above in mind and further assuming the duration of the floater is zero, which is often not the case, the equation for the effective duration of the inverse floater can be written as follows:
- The ratio of the companion current balance to the inverse current balance is the leverage of the inverse floater and can be restated as
Revising our example and substituting the known values into equation 18.8 yields an inverse floater effective duration:
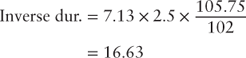
18.3 Option-Adjusted Spread Analysis
Table 18.2 illustrates the full execution of the PAC-PAC IO-floater-inverse floater transaction. The floating and inverse floating rate bonds' yield to maturity and spread to the curve are calculated using the forward LIBOR curve. Notice the floating rate bond reports a modestly negative effective duration while the inverse floater's effective duration is close to that estimated by equation 18.8.
Table 18.2 REMIC PAC-PAC IO-Floater-Inverse Floater OAS Analysis
| MBS 4.00% | Tranche A (PAC) | Tranche B (IO) | Tranche C (Floater) | Tranche D (Inverse) | |
| Net Coupon | 4.00% | 2.25% | 1.75% | 0.55% | 8.91% |
| Note Rate | 4.75% | 4.75% | 4.75% | 4.75% | 4.75% |
| Term | 360 mos. | 360 mos. | 360 mos. | 360 mos. | 360 mos. |
| Loan Age | 0 mos. | 0 mos. | 0 mos. | 0 mos. | 0 mos. |
| Orig. Bal. | $148.7mm | $148.7mm | $30.7mm | $20.5mm | |
| Price | $105.75 | $100.00 | $15.3125 | $100.00 | $102.00 |
| Yield to Maturity | 3.26% | 2.25% | 2.91% | 2.91% | 5.42% |
| OAS | 0.51% | 0.31% | −0.16% | 0.16% | 2.91% |
| ZV-Spread | 1.33% | 0.28% | −0.32 | 0.13% | 3.56% |
| Spread | 1.46% | 0.45% | −0.49 | 1.06% | 1.83% |
| Effective Duration | 7.13 | 7.11 | 10.7 | −1.58 | 18.5 |
| Effective Convexity | −15065 | 183 | 1917 | 510514 | −539075 |
Naturally, the average life profiles of the floating and inverse floating rate bonds will mirror that of the companion bond from which they are derived. The companion bond analysis was covered in Chapter 16 and will not be repeated. Rather, the remainder of the chapter will focus on key rate duration analysis to explore the sources of duration for both the floating and inverse floating rate bonds. Table 18.2 provides the OAS analysis used to explore the value of the cap and floor options embedded therein.
18.4 Key Rate Duration Analysis
The index strike of a floating rate security is given by:
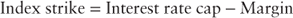
Consider Tranche C, its cap is 6.66%, and its margin is 0.30%. Its one-month LIBOR strike is 6.36%. Under the base case curve, Figure 18.1 shows the cap is forward out-of-the-money but given a +300 bps interest shift the cap is forward in-the-money. When investing in floating rate REMICs the investor should consider the following:
- Forward index strike: a lower forward strike reduces the value of the floating rate tranche relative to one with a higher forward strike.
- Slower prepayments: A longer average life (due to slower prepayments) increases the time value of the investor's short interest rate cap position thereby reducing the floating rate bond's value.
- If the floating rate bond's cap is in-the-money then the floating-rate bond's price will behave like that of a comparable fixed-rate bond in a rising interest rate environment.
18.4.1 Floating Rate Bond
Figure 18.2 is an analysis of the key rate duration of Tranche C, the floating rate tranche. The effective duration of Trance C is −1.58. To most, a negative duration floating rate security seems counterintuitive. However, recall effective duration is the sum of each key rate duration. Thus, a negative effective duration implies a set of negative key rates, the degree to which is sufficient to shift the floating rate bond's effective duration from modestly positive to negative.
- The shorter key rate tenors are positive to seven years.
- The sum of the short and intermediate key rates—seven years or less—is 3.81, suggesting the floating rate bond's price declines as short and intermediate term interest rates go up. The intuition is as follows:
- Higher short-term rates, all other tenors held constant, imply a flatter yield curve, lower forward rates, and a lower forward floating coupon, which is negative for the floater.
- A wider spread between short and intermediate rates result in higher forward rates, which, although positive for the implied forward coupon is somewhat mitigated by the fact that the short cap position is now nearer to the money increasing its value and reducing the value of the floating rate bond.
The extent to which these points influence the price of a floating rate bond is dependent on the index strike relative to the short-term rate.
- Both the 10- and 15-year key rate durations are negative. In fact, the floater exhibits a 10-year key rate duration rivaling that of an interest only class (Figure 14.2) and reflecting the companion bond's key rate durations from which it is derived.
- A higher 10-year rate results in a slower prepayment expectation and a higher forward coupon. The higher forward coupon rate is positive for a floating rate REMIC. However, the longer average life increases the value of the short cap position, which could be a negative for the floating rate bond. In the case presented, a net higher 10-year is positive for the floater.
- A lower 10-year rate results in a flatter yield curve and lower forward rates, which implies a faster prepayment expectation and lower forward coupon—negative for a floating rate REMIC.
- The longer key rate duration tenors (20-, 25-, and 30-year) are positive. Generally, these key rate tenors reflect the value of the short cap position. Specifically, as long-term rates rise and mortgage prepayments slow, the time value of the short option position increases while the floating rate coupon approaches its cap strike.
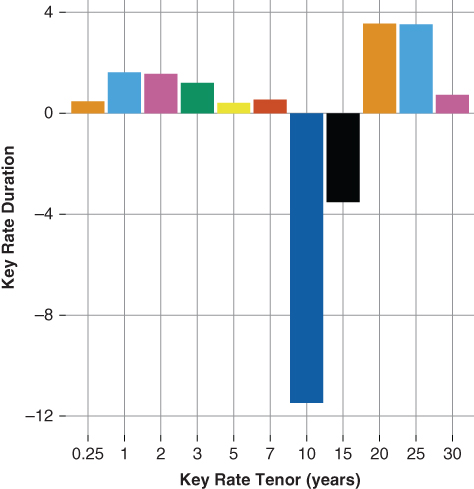
Figure 18.2 Key Rate Duration—Floating Rate Bond
Key rate duration analysis highlights an important point when investing in floating rate bonds collateralized by mortgage-backed securities. Namely, the REMIC floater's value is tied to both the level and slope of the yield curve in unique ways apart from those of a plain vanilla floating rate bond that pays its principal at maturity. The unique nature of a REMIC floating rate bond principally arises from the interaction between expected prepayments and the value of the embedded cap and floor options. Indeed, in the case of a bullet maturity floater the time value of the short interest rate cap declines linearly with the maturity of the bond. However, in the case of a floating rate REMIC the time value of the short interest rate cap changes as the overall prepayment environment changes, complicating relative value analysis beyond that of simply considering the discount margin.
Indeed, recall from Chapter 16, a lower PAC-Companion ratio increases the stability of the companion bond. Thus, not only do the underlying collateral, margin, cap, and floor strikes influence the value of a floating rate REMIC, but so do the structural choices made. For example, all else equal, a floating rate REMIC structured to a lower PAC-Companion ratio should trade to a narrower discount margin or option-adjusted spread than one structured to a higher PAC-Companion ratio, due to the greater certainty of its average life and hence the value of its embedded short cap position.
Clearly, a REMIC floating rate bond is more complicated than it first appears. Option-adjusted spread analysis may help the investor untangle the myriad of embedded options in the REMIC floating rate bond. The LIBOR OAS of a floating rate bond, like its fixed-rate cousin, reflects the asset swap spread, or the spread the investor would expect to earn over LIBOR after hedging costs. In the case of a floating rate bond, the option cost is:
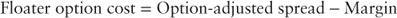
In our example presented, the floating rate bond's (Tranche C) option cost is 14 bps (
). That is, after hedging both the cap and prepayment risk, the investor expects to earn LIBOR + 16 bps (the OAS) yielding an option cost of 14 bps.
18.4.2 Inverse Floating Rate Bond
Figure 18.3 presents the key rate duration analysis of tranche D—the inverse floating rate tranche. The effective duration of the inverse floating rate tranche is 18.5. The high effective duration is largely a product of the inverse floater's leverage relative to the underlying collateral (equation 18.8).
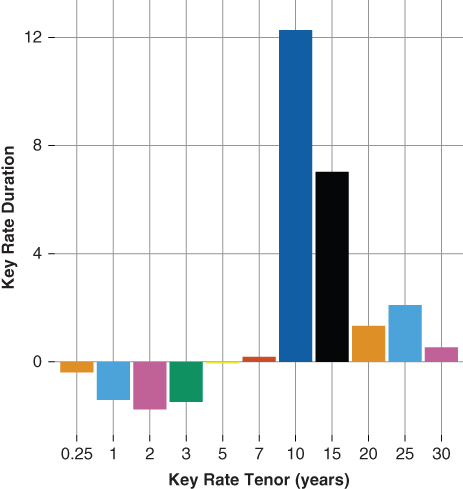
Figure 18.3 Key Rate Duration—Inverse Floating Rate Bond
Notice the following:
- The shorter tenor key rate durations are negative up to the three-year tenor while the intermediate key rate durations are positive.
- The sum of the short and intermediate key rates −4.96, suggesting the inverse floating rate bond's price increases as the short- and intermediate-tenor rates go up. The intuition is as follows:
- Higher short-term rates resulting in a flatter yield curve, which implies lower forward rates and a higher forward coupon for the inverse floating rate bond.
- Higher intermediate rates result in a steeper forward curve and higher forward rates. The higher forward rates imply a lower coupon for the inverse floating rate bond.
- Unlike the floating rate bond, the inverse floater's 10- and 15-year key rate durations are positive. A higher 10-year rate results in a higher forward curve and slower prepayment expectation. For the inverse floater, this means a lower coupon on a forward rate basis and a longer average life.
- Like the floating rate bond, the inverse floater's longer key rate duration tenors are positive. The positive duration of the longer tenors implies that as the long tenor rates rise, each tranche approaches its respective cap (floater) or floor (inverse floater) at which point their interest rate sensitivity (duration) converges to that of the fixed-rate companion bond from which they are derived.
The key rate duration analysis provides greater intuition with respect to the influence of changes in both the level and slope of the term structure on the value of an inverse floating rate bond collateralize by MBS. Namely, the companion inverse floating rate bond is leveraged against both the short-term rate via its floating coupon formula, and prepayment rates via its exposure to the 10-year tenor and by extension the mortgage rate. For example, as the PAC:Companion bond ratio increases the inverse floating rate bond from which it is created will exhibit greater leverage relative to the ten-year note. Conversely, a lower PAC:Companion ratio will reduce the inverse floating rate bond's leverage relative to the 10-year note.
The PAC-PAC IO-floater-inverse floater structure is an example of the division of principal used to create a prepayment protected class—the PAC bond—as well as the division of interest. The inclusion of the PAC IO, which was created to facilitate the par execution of the PAC bond, completes the REMIC arbitrage. IO classes were evaluated earlier, and consequently, the PAC IO presented herein was not reviewed. However, the reader is encouraged to analyze the PAC IO using Bond Lab. The PAC IO, floater, and inverse floater allow the investor to express her view with respect to the evolution of the forward rate curve. For example, the PAC IO and floating rate bond allow her to follow the forward rate curve, while the inverse floater allows her to fade the forward rate curve.