5 William Garnett (?–1932) was a pupil at the City of London School from 1864 until 1869, and he was present on the day of Abbott’s arrival as headmaster in 1865. He was “captain” (top of the school) in mathematics in the same year that H. H. Asquith was captain in classics. Garnett went to Trinity College, Cambridge, where he became chief assistant to the great Scottish physicist James Clerk Maxwell. In the same year that Flatland was published, he coauthored with Lewis Campbell a biography of Maxwell (The Life of James Clerk Maxwell, Macmillan 1884). The book refers to Maxwell’s interest in four-dimensional space:
- My soul is an entangled knot
Upon a liquid vortex wrought
The secret of its Untying
In four-dimensional space is lying.
(Knots can be untied in four dimensions; see Flat-terland, chapter 4, “A Hundred and One Dimensions.”) Garnett became principal of Durham College of Science and educational adviser to the London County Council. His brother Edward, an author and critic, was instrumental in promoting the works of Joseph Conrad (1857–1924) and D(avid) H(erbert) Lawrence (1885–1930). After leaving the school, Garnett maintained contact with Abbott, and upon retirement he moved to Hampstead, where Abbott lived. He signed Abbott’s eightieth-birthday message and attended his funeral in 1926. He was therefore the obvious choice to write a preface for the 1926 Blackwell reissue of Flatland.
6 Said by Titus in Shakespeare’s Titus Andronicus, act 3, scene 2, line 31, in a passage concerning the loss of his and Lavinia’s hands. The word square had innumerable meanings in Shakespeare’s day, including “to regulate,” “to make appropriate,” “to adapt,” “to differ,” and (the exact opposite) “to agree.” From the context, it seems that Titus is embarrassed because he has unconsciously been adapting his words to reflect the circumstances and has just realized that this is completely unnecessary because nobody is going to forget that they’ve just lost their hands. The quotation is not especially appropriate, and its main relevance to Flatland is that the narrator is A. Square: The Square talks, rather than the talk being squared.
To
The Inhabitants of SPACE IN GENERAL
and H.C. IN PARTICULAR7
This Work is Dedicated
By a Humble Native of Flatland
In the Hope that
Even as he was Initiated into the Mysteries
Of THREE Dimensions
Having been previously conversant
With ONLY TWO
So the Citizens of that Celestial Region
May aspire yet higher and higher
To the Secrets of FOUR FIVE OR EVEN SIX Dimensions
Thereby contributing
To the Enlargement of the IMAGINATION
And the possible Development
Of that most rare and excellent Gift of MODESTY8
Among the Superior Races
OF SOLID HUMANITY
Introduction
IN AN ADDRESS to the Committee of the Cayley9 Portrait Fund in 187410 Clerk Maxwell,11 after referring in humorous terms to the work of Arthur Cayley in higher algebra and algebraical geometry, concluded his eulogium12 with the lines—
- March on, symbolic host! with step sublime, Up to the flaming bounds of Space and Time! There pause, until by Dickenson depicted,13 In two dimensions, we the form may trace Of him whose soul, too large for vulgar space In n dimensions flourished unrestricted.14
In those days any conception of “dimensions” beyond length breadth and height was confined to advanced mathematicians; and even among them, with very few exceptions, the fourth and higher dimensions afforded only a field for the practice of algebraical analysis with four or more variables instead of the three which sufficiently describe the space to which our footrules are applicable. Any geometrical conclusions reached were regarded only as analogies to the corresponding results in geometry of three dimensions and not as having any bearing on the system of Nature. As an illustration, reference may be made to the “more divine offspring of the divine Cube in the Land of Four Dimensions” mentioned on p. 171 infra which has for its faces eight three-dimensional cubes and possesses sixteen four dimensional angular points or corners.
During the present century the work of Einstein, 15 Lorentz,16 Larmor,17 Whitehead18and others has shewn that at least four dimensions of space-time 19 are necessary to account for the observed phenomena of nature, and there are some suggestions of the necessity for more than four. It is only when dealing with very high velocities,20 such as are comparable with the velocity of light, that the unity of time with space thrusts itself upon the notice of physicists, for even with such a velocity as that of the planet Mercury in its orbit21 it is only after the lapse of centuries that any divergence from the motion strictly calculated on the basis of Euclidean Geometry22 and Newton’s23 laws of gravitation and of motion has become apparent. The observed behaviour of electrons, moving in high vacua with velocities comparable with the velocity of light, has confirmed some of Einstein’s conclusions and necessitated a revision of our fundamental notions of kinematics and the laws of motion when these high velocities are concerned. But the whole subject of Relativity has strongly appealed to popular interest through the brilliant confirmation of Einstein’s theory of gravitation by the bending of light24 in passing close to the sun’s surface and the consequent apparent displacement of stars which are very close to the sun from their true relative position when photographed during a solar eclipse. The best popular exposition of the whole subject of relativity and gravitation is to be found in Professor Edding-ton’s25 Space, Time, and Gravitation.
But when a great truth comes to light it is generally found that there have already been prophets crying in the wilderness and preparing the way for the reception of the Revelation when the full time has come. In an anonymous letter published in Nature 26 on February 12th, 1920, entitled “Euclid, Newton, and Einstein,” attention was called to such a prophet in the following words:—
“Some thirty or more years ago, a little jeu d’esprit was written by Dr. Edwin Abbott, entitled ‘Flatland.’ At the time of its publication it did not attract as much attention as it deserved. Dr. Abbott pictures intelligent beings whose whole experience is confined to a plane, or other space of two dimensions, who have no faculties by which they can become conscious of anything outside that space and no means of moving off the surface on which they live. He then asks the reader, who has the consciousness of the third dimension, to imagine a sphere descending upon the plane of Flatland and passing through it. How will the inhabitants regard this phenomenon? They will not see the approaching sphere and will have no conception of its solidity. They will only be conscious of the circle in which it cuts their plane. This circle, at first a point, will gradually increase in diameter, driving the inhabitants of Flatland outwards from its circumference, and this will go on until half the sphere has passed through the plane, when the circle will gradually contract to a point and then vanish, leaving the Flatlanders in undisturbed possession of their country. . . . Their experience will be that of a circular obstacle gradually expanding or growing, and then contracting, and they will attribute to growth in time what the external observer in three dimensions assigns to motion in the third dimension. Transfer this analogy to a movement of the fourth dimension through three-dimensional space. Assume the past and future of the universe to be all depicted in four-dimensional space and visible to any being who has consciousness of the fourth dimension. If there is motion of our three-dimensional space relative to the fourth dimension, all the changes we experience and assign to the flow of time will be due simply to this movement, the whole of the future as well as the past always existing in the fourth dimension.”
It will be noticed that in the presentation of the Sphere to the Flatlander the third dimension involves time through the motion of the Sphere. In the Space-Time Continuum of the Theory of Relativity the fourth dimension is a time function, and the simplest element is an “event.” One set of parallel sections of the four-dimensional continuum present the universe as it exists in three-dimensional space at the instants corresponding to the sections. Sections in all other directions involve the time element and represent the universe as it appears to an observer in motion.
There are some mathematical minds which are completely satisfied by the results expressed in al-gebraical symbols of the analysis of a continuum of four dimensions; but there are others which crave for the visualization of these results27 which, in their symbolic forms, they do not question. To many, perhaps to the great majority, of these, Dr. Abbott’s sphere penetrating Flatland points the way to the clearest imagery of the fourth dimension to which they are likely to attain.
WM. GARNETT.
7 H. C. is Howard Candler (?–1916), Abbott’s best and lifelong friend. Candler was mathematics master at Uppingham School, where for some years Charles Hinton was science master. In the introduction to his theological book The Fourfold Gospel, written just after Candler died, Abbott explicitly states that Candler was “H. C.” The first edition of Flatland in the library of Trinity College, Dublin, donated by one of Candler’s grandsons, is inscribed with the handwritten message “To H.C., in particular.”
8 In The Spirit on the Waters (1897), Abbott relates the climax of Flatland, in which A. Square experiences a visitation from the third dimension— the Sphere, perceived as a series of ever-changing Circles. Would A. Square be right in worshipping the Sphere because of its God-like powers? No, Abbott tells his readers. It is wrong to attribute spiritual or moral superiority to a being merely because of its physical or mental abilities. And he enlarges on this section of Flatland’s Dedication:
This illustration from four dimensions . . . may serve a double purpose in our present investigation. On the one hand it may lead us to vaster views of possible circumstances and existence; on the other hand it may teach us that the conception of such possibilities cannot, by any direct path, bring us closer to God. Mathematics may help us to measure and weigh the planets, to discover the materials of which they are composed, to extract light and warmth from the motion of water and to dominate the material universe; but even if by these means we could mount up to Mars, or hold converse with the inhabitants of Jupiter or Saturn, we should be no nearer to the divine throne, except so far as these new experiences might develop our modesty, respect for facts, a deeper reverence for order and harmony, and a mind more open to new observations and to fresh inferences from old truths.
9 Arthur Cayley (1821–1895), English mathematician, educated at Cambridge University, becoming a fellow of Trinity College in 1845 but leaving after three years because he did not wish to take holy orders. He then spent fifteen years as a lawyer before being appointed the first Sadleirian Professor of Mathematics at Cambridge in 1863. Apart from half a year spent at Johns Hopkins University in the United States (1881–1882), he remained at Cambridge until his death. Cayley is best known for his work with James Joseph Sylvester (1814–1897) on invariants, algebraic expressions that remain unchanged when their variables are transformed. The theory of invariants, generalized to differentials of the variables, formed the mathematical basis of Albert Einstein’s General Theory of Relativity—the idea that gravity is a manifestation of the curvature of a four-dimensional space-time. Cayley was also responsible for matrix algebra, which is now widely used in all branches of pure and applied mathematics: A matrix is a rectangular table of numbers and represents a transformation of variables. Most significantly for this book, Cayley was one of the creators of higher-dimensional geometry, beginning with a paper of 1845 on spaces of n dimensions. The main founder of this theory was the German mathematician Hermann Grassman (1809–1877), in his Ausdehnungslehre (Theory of Extension) of 1844, but Cayley’s early work was done independently.
10 The portrait concerned, which was painted by Lowes Cato Dickinson (1819–1908) in 1874, is in the possession of Trinity College, Cambridge. It is shown in the frontispiece to volume VI of The Collected Mathematical Papers of Arthur Cayley Sc.D., F.R.S., Cambridge University Press 1893 (13 volumes and an index). The “portrait fund” was set up by a group of private individuals and was not an official activity of Trinity College; however, the group presented the portrait to the college and probably included several fellows of Trinity. The membership of the group seems not to be known, but the college archives state that the portrait was “given by the subscribers through Mr Walton Chairman of the Cayley Portrait Committee, Apr, 1874.” It measures 43 inches by 331/2 inches, and is described as follows:
Life size seated figure—to knee. Head three quarters to rt [right], features [are] elderly. Long wavy brown hair at sides—head nearly bald on crown. Figure three quarters to rt, seated at a sloping desk, right hand holding quill pen to sheet of paper lying on the desk. Left hand resting on right wrist. Inkstand on desk. Drawer at end of desk partly open showing papers & sealing wax. Wears black coat, M.A. [Master of Arts] gown, soft white collar & dark necktie.
On canvas: LCD [monogram of Lowes Cato Dickinson] 1873.
On frame: Arthur Cayley Sc.D. F.R.S. Painted by Lowes Dickinson 1874. Presented to Trinity College by the Subscribers.
F.R.S. stands for Fellow of the Royal Society, Britain’s most prestigious scientific organization (then and now). The disagreement in dates suggests that the painting was done in 1873 but not presented until 1874.
11 James Clerk Maxwell (1831–1879), Scottish mathematical physicist who revolutionized technology with Maxwell’s Equations for electricity and magnetism, which he devised in 1864 to provide a mathematical basis for the discoveries of Michael Faraday (1791–1867). The existence of electromagnetic waves (and hence radio, television, and radar) is a direct consequence of Maxwell’s Equations, and such waves were discovered as a result of this mathematical prediction. Maxwell published his first scientific paper at the age of 14 and obtained a degree in mathematics from Trinity College, Cambridge, in 1854. In 1856 he became professor of natural philosophy at Marischal College, Aberdeen; in 1860 he moved to King’s College, London; in 1871 he became the first Cavendish Professor of Physics at Cambridge University. Maxwell’s interests were broad, as was typical of the “Scottish Enlightenment” period. He worked on color vision (his theories influenced several Scottish painters, and he produced one of the earliest color photographs), Saturn’s rings, mechanics, and the kinetic theory of gases (which explains such phenomena as temperature and pressure in terms of the chaotic motion of gas molecules). His main relevance to Garnett’s introduction to Flatland is his contribution to the development of multidimensional geometry.
12 The arts and sciences in the nineteenth century were more closely related than they are today, and it was not uncommon for a scientific paper or address to include verse. One of the great exponents of such scientific poetry was Cayley’s collaborator Sylvester, who wrote a pamphlet called The Laws of Verse in 1870. Sylvester provides an important link between Flatland and H. G. Wells’s famous story The Time Machine of 1895 (discussed later), and he was generally an oddball character. He applied for the Gresham Professorship of Geometry (see the preface to this book) but failed to secure the post. After some difficulty he obtained the position of professor of mathematics at the Royal Military Academy, Woolwich, until he was forcibly retired in 1870 at the age of fifty-six because he was superannuated —the official term for someone who was too old to be of further use. Such retirement might have made sense for soldiers, but it made none for Sylvester, who was approaching the pinnacle of his intellectual powers. In 1876 he moved to the United States to take a founding professorship at the new Johns Hopkins University. There he remained until 1883, when he was persuaded to accept the newly vacant Savilian Chair of Geometry at Oxford University. During his inaugural lecture, he broke into verse in order to emphasize the strange absence of a particular term in an algebraic expression:
Lone and discarded one! divorced by fate, From thy wished-for fellows—whither art flown? Where lingerest thou in thy bereaved estate, Like some lost star or buried meteor stone? Thou mindst me much of the presumptuous one Who loth, ought less than greatest, to be great from Heaven’s immensity fell headlong down to live forlorn, self-centred, desolate: Or who, new Heraklid, hard exile bore, Now buoyed by hope, now stretched on rack of fear, Till throned Astraea, wafting to his ear Words of dim portent through the Atlantic roar, Bade him “the sanctuary of the Muse revere And strew with flame the dust of Isis’ shore.”
He then resumed his mathematical discussion.
13 The spelling is wrong: The portrait of Cayley was painted by Lowes Cato Dickinson. Dickinson painted many Victorian intellectuals and celebrities, among them Charles Kingsley (1819–1875, portrait 1862), a clergyman who accepted Darwin’s theory of evolution and was thereby inspired to write The Water-Babies in 1863; the novelist Mary Ann Evans (George Eliot, portrait 1872); Sir Charles Lyell (1797–1875, portrait—a replica—1883), the geologist who discovered “deep time”; and the whole of Gladstone’s cabinet (painted 1869–1874).
14 The logical basis of the mathematics of n-dimensional space is straightforward and does not depend on the properties of actual physical space. The psychological ramifications are more convoluted. Cay-ley formulated the main ideas clearly in 1845 (recall that Grassmann had done so independently the year before), although their prehistory goes back much further. The geometry of n dimensions is defined by analogy with two and three dimensions but then takes on a life of its own. In Cartesian coordinate geometry, the plane is represented as the set of all points with coordinates (x, y), where x and y are positive or negative numbers.
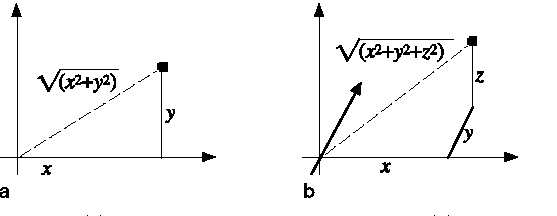
Figure 2 (a) Distances in two-dimensional space. (b) Distances in three-dimensional space.
The distance between two points (x, y) and (u, v) can be deduced from the Pythagorean theorem and is given by the formula
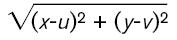
See Figure 2a. Similarly, three-dimensional space is represented as the set of all points with coordinates (x, y, z), and the distance between two points (x, y, z) and (u, v, w) is given by the formula
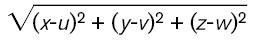
See Figure 2b. The algebraic generalization to n dimensions is natural and, to modern tastes, inevitable: A point in n-dimensional “space” is considered to be represented by an n-tuple of numbers (x1, ..., xn), and the distance between that point and another one (w1, ..., wn) is defined to be
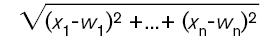
All the main features of Euclidean geometry can be expressed purely in terms of distances, so these features can be extended to n-dimensional space by applying the above formula. The generalization is purely formal, so the “space” that it defines has no specific physical interpretation—but its mathematics can readily be worked out. Only later did it become clear that this kind of multidimensional “geometry” is widely applicable—for example in mechanics, statistics, and economics. By the 1960s, mathematicians had become so used to the concept that working in n-dimensional space was a natural reflex.
See “The Fourth Dimension in Mathematics” in this book for a history of the mathematics of multidimensional spaces.
15 Albert Einstein (1879–1955), German physicist famous for his Special and General Theories of Relativity, which overthrew the physical theories of Sir Isaac Newton. Einstein was born in Ulm and educated in Zürich. In one year, 1905, he published four groundbreaking papers in widely differing areas of physics. In 1919 his prediction that a gravitational field can bend light was verified by observations of stars made during a solar eclipse by a team headed by Sir Arthur Stanley Eddington. Einstein was awarded the Nobel Prize in 1921. Fleeing Nazi Germany, he moved to the Institute for Advanced Study in Princeton in 1933 and became a U.S. citizen in 1940.
According to the Special Theory of Relativity, no material particle can travel faster than light (186,000 miles, or 300,000 kilometers, per second). Special relativity includes Einstein’s celebrated formula E = mc2, which expresses the conversion of matter m into energy E. Here c is the speed of light, which (as we have just seen) is very large, and its square c2 is even larger, implying that a small amount of matter “contains” a huge amount of energy. This equation is fundamental to nuclear power and the atomic bomb, although Einstein himself was a pacifist. According to the General Theory of Relativity, gravity is a result of the curvature of space-time. One spectacular consequence of general relativity is the existence of black holes—regions of space-time from which nothing, not even light, can escape. It is now believed that most galaxies have giant “supermassive” black holes at their cores.
The mathematics of relativity, both special and general, rests on considering space and time to form a single, four-dimensional “space-time continuum.” Until the mid-twentieth century, this was the principal—and without doubt the best-known— application of multidimensional geometry. See Flat-terland chapter 12 (“The Paradox Twins”) and the first part of chapter 13 (“Domain of the Hawk King”) for a treatment of special relativity. See the rest of chapter 13 and chapter 14 (“Down the Wormhole”) for general relativity.
16 Hendrik Antoon Lorentz (1853–1928), Dutch physicist who won the Nobel Prize in 1902 for his theory of electromagnetism, which gave rise to Einstein’s Special Theory of Relativity. Lorentz was born in Arnhem and became professor of mathematical physics at Leiden in 1878. The central aim of his work was to devise a unified theory of electricity, magnetism, and light, improving on that of Maxwell. He predicted that a strong magnetic field should affect the wavelength of light emitted from atoms, and in 1896 his pupil Pieter Zeeman (1865– 1943) verified the prediction experimentally, in what is now called the Zeeman effect. The Nobel Prize was awarded to Lorentz and Zeeman for this work. However, Lorentz’s theory failed to explain the experiments of the American physicist Albert Abraham Michelson (1852–1931) and the American chemist Edward Williams Morley (1838–1923), who in 1887, while testing the theory that electromagnetic radiation was conveyed by the “luminiferous ether,” showed that the motion of the Earth relative to the alleged ether was negligible. Lorentz was led to suggest that local time depends on the velocity of the observer. In conjunction with a similar suggestion by the Irish physicist George Francis FitzGerald (1851–1901), in which the length of a body is held to contract as its speed increases, Lorentz formulated his “Lorentz transformations,” upon which Einstein based the Special Theory of Relativity. See Flatterland chapter 12.
17 Sir Joseph Larmor (1857–1942), Irish physicist born in Magheragall, County Antrim. Larmor calculated the rate at which an accelerated electron radiates energy and offered the first successful explanation for the splitting of spectral lines by a magnetic field. His work was based on the (now discredited) idea that matter is composed entirely of electrical particles moving through the ether. He taught at Queen’s College, Galway, from 1880 to 1885 and at Cambridge from 1885 to 1932. He was knighted in 1909 and served as a member of parliament (for Cambridge University) from 1911 to 1922.
18 Alfred North Whitehead (1861–1947), English mathematical logician and philosopher. Born in Ramsgate, Whitehead is best known for his collaboration with the English mathematician and philosopher Bertrand Russell (1872–1970) on Principia Mathematica, an impressively technical three-volume work on the logical foundations of mathematics that was published between 1910 and 1913. Whitehead became a fellow of Trinity College, Cambridge, in 1884, moved to London in 1910, and secured a position at University College London in 1911. In 1914 he was made professor of applied mathematics at Imperial College of Science and Technology, London. In 1924 he moved to the United States, becoming professor of philosophy at Harvard University. His relevance to Garnett’s introduction to Flatland stems from his interest in the philosophy of science: For the first half of the 1920s, he devoted much effort to constructing philosophical foundations for physics, seeking to understand the perceptual aspects of relativity. His books Enquiry Concerning the Principles of Natural Knowledge and the more popular The Concept of Nature date from this period. In 1925 he emphasized the distinction between a mathematical description of nature in terms of matter, energy, and motion, and the actual concrete reality described by the mathematics. These ideas were published as Science and the Modern World, and he returned to the theme in his Adventures of Ideas in 1933.
19 The geometrical basis of relativity is the idea that the traditional three dimensions of space should be augmented by a fourth: time. In Newtonian physics, space is considered to be the standard three-dimensional space of Euclid, in which the position of a point can be defined by three coordinates (x, y, z) relative to three specified axes (east-west, north-south, up-down). Time t can be thought of as a fourth coordinate, leading to a four-dimensional structure with coordinates (x, y, z, t ). This idea goes back at least to Jean le Rond D’Alembert (1717– 1783), who suggested thinking of time as a fourth dimension in his article on “dimension” in the Ency-lopédie ou Dictionnaire Raisonné des Sciences, Arts, et des Métiers (Reasoned Encyclopedia or Dictionary of Sciences, Arts, and Crafts), published 1751–1780. Joseph-Louis Lagrange (1736–1813) used time as a fourth dimension in his Mécanique Analytique (Analytical Mechanics) of 1788 and again in his Théorie des Fonctions Analytiques (Theory of Analytic Functions) of 1797, in which he says, “Thus we may regard mechanics as a geometry of four dimensions.” However, Einstein’s innovation goes deeper. In Newtonian physics, the time coordinate is physically very different from the space coordinates. In relativity, spatial and temporal coordinates can be transformed into each other when the laws of physics are expressed relative to a moving coordinate system—a moving observer. The basic geometry of special relativity was introduced by the Russian-born German mathematician Hermann Minkowski (1864–1909) in a paper of 1908, wherein the terms world line and light cone first appear (see Flatterland chapter 13). Minkowski reformulated Maxwell’s Equations in tensor form, a step that Einstein at the time denounced as “superfluous learnedness.” By 1912 Einstein had changed his mind and was employing tensor methods himself; in 1916 he stated that Minkowski’s first steps in that direction had greatly eased the transition from special to general relativity.
In Stella, and more extensively in An Unfinished Communication, C. H. Hinton develops the remarkable idea of two-dimensional time. Represent a being’s life as a fixed world line in conventional four-dimensional space-time. But now imagine that the world line can vary along a fifth dimension. In such a setting, the future of an event is not uniquely determined, so this idea can be seen as an early anticipation of the “parallel worlds” or “alternat(iv)e universes” trope of science fiction, which was introduced into mainstream physics by Hugh Everett in his “many worlds” interpretation of quantum reality. See John Gribbin, In Search of Schrödinger’s Cat.
20 The difference between Newtonian physics and relativity becomes apparent only for bodies (or observers) that are moving with a velocity that is an appreciable percentage of the speed of light. This is why we do not notice relativistic effects in everyday life. It is also why Newtonian physics was good enough for nearly all scientific purposes until the twentieth century—and is still good enough for most of them in the twenty-first.
21 The first observational evidence for the General Theory of Relativity antedated that theory by many years. According to Johannes Kepler (1571–1630) and Isaac Newton, planetary orbits are (to an excellent approximation) ellipses. This and two other “laws” of planetary motion discovered by Kepler led Newton to formulate his Inverse-Square Law of Gravitation: Every particle in the universe attracts every other particle with a force that is proportional to their masses and inversely proportional to the square of the distance between them. This law is still used for most astronomical purposes. Observations show that the perihelion of Mercury’s orbit —its point of closest approach to the Sun—pre-cesses. That is, its position in space (relative to the sun) slowly rotates. In the framework of Newtonian physics, calculations show that most of the precession is caused by perturbations from other planets in the solar system (especially Jupiter and Saturn, the most massive ones), but even when these perturbations are taken into account, a discrepancy remains. The first person to notice this and to offer an explanation was the French astronomer Urbain Jean Joseph Le Verrier (1811–1877), who in 1859 published the text of a letter to Hervé Faye (1814–1902) in which he stated that the perihelion of Mercury advances by 38 seconds of arc per century. How could this be explained? It would make sense if the mass of Venus were increased by at least 10 percent, but that had to be ruled out on other grounds. A new planet inside Mercury’s orbit could also do the trick, but that was unlikely. Le Verrier postulated a swarm of asteroids inside Mercury’s orbit.
In 1882 the American astronomer Simon New-comb (1835–1909) improved Le Verrier’s measurement and found an advance of 43 seconds of arc per century, a figure that has not changed significantly since. This advance of Mercury’s perihelion is exceedingly tiny, but celestial mechanics is a very precise area. Possible explanations included a planetary ring inside Mercury’s orbit and an unnoticed moon of Mercury. Newcomb himself came “to prefer provisionally the hypothesis that the Sun’s gravitation is not exactly as the inverse square.” In 1916 Einstein calculated the rate of precession on the basis of the General Theory of Relativity—in which Newcomb’s hypothesis is correct—and exactly accounted for the discrepancy. Because Mercury is very close to the sun, it experiences a much stronger gravitational field than any other planet in the solar system; the amount of perihelion precession for the remaining planets is so small that it is swamped by other variations in the orbit, which are caused by perturbations by other planets.
In 1967 the American physicist Robert H(enry) Dicke (1916– ) suggested that part of the 43 seconds could be explained in Newtonian physics by the flattening of the sun’s poles, opening up the possibility that relativity might need to be modified because Einstein’s calculations now explained too much. However, Einstein’s original version was supported by work of the American astronomer Ronald W. Hellings on the motion of the solar system and by that of the American astronomer Joseph H. Taylor on the binary pulsar system PSR 1913+16.
22 Eucleides, anglicized as Euclid (365?–275? B.C.), Greek geometer, author of the Elements, a treatise on geometry in thirteen volumes. Euclid deduced a large part of Greek geometry (of the plane and space) from a small number of definitions (“point,” “line,” and so on) and five axioms—statements whose validity would be assumed at the outset, such as “all right angles are equal” and “any two points can be joined by a line.”
Later generations of mathematicians found flaws in Euclid’s presentation (additional unstated assumptions, such as “if a line passes through one side of a triangle, then it will meet another side if sufficiently extended”). In his Grundlagen der Geometrie (Foundations of Geometry) of 1899, the German mathematician David Hilbert (1862–1943) wrote down a system of axioms (this system was repeatedly revised—there were twenty axioms in the seventh edition of 1930) and derived Euclid’s geometry from them in full logical rigor. Nonetheless, Euclid did an amazingly good job for 300 B.C. In particular, he saw the need for his infamous Parallel Axiom (axiom 5): “If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side where the angles are less than two right angles.” (See Figure 3.) Euclid’s Parallel Axiom is logically equivalent to the following one, which is simpler-looking, though still complicated: “Given a line, and any point not on that line, there exists one and only one line parallel to the given line and passing through the given point.” This reformulation is generally known as Playfair’s Axiom, after the English mathematician John Playfair (1748–1819), who stated it in 1795, but in fact it was known to Proclus (410–485), a Greek commentator on Euclid. For most of the next 2,000 years, many people thought that the Parallel Axiom was superfluous and tried to deduce it from the other four. Only around 1830 did the invention of non-Euclidean geometry prove that no such deduction is possible and that Euclid had done the right thing after all. Non-Euclidean geometry has a long and complex history and prehistory, but the definitive breakthrough stemmed from the work of three mathematicians:
- The German Carl Friedrich Gauss (1777–1855) between 1792 and 1816
- The Hungarian János Bolyai (1802–1860), who worked his ideas out around 1825 and published them in 1832
- The Russian Nikolai Ivanovich Lobachevskii (1793–1856), who submitted his work to his home university in 1826 and published it in 1829
No original manuscripts by Euclid survive (although his book became one of the most widely copied, and most influential, texts ever), and little is known for certain about his life. We do know that he founded and taught at a school in Alexandria, Egypt, during the reign of Ptolemy I Soter (323–285/283 B.C.). About 800 years later, the Greek philosopher Proclus related one anecdote about Euclid: He is alleged to have told Ptolemy that “there is no royal road to geometry”—no shortcut to save the king effort or time. Supposedly also, when asked what was the point of learning geometry, he told his slave to offer a student money, on the grounds that “he must needs make gains by what he learns.” Until the twentieth century, “geometry” in English schools meant a simplified version of the early parts of Euclid’s Elements. It is this material that provided such fertile ground for Abbott’s imagination. Every schoolboy— though not every schoolgirl—would be only too familiar with the Euclidean world of a flat plane inhabited by Triangles, Circles, and Squares.
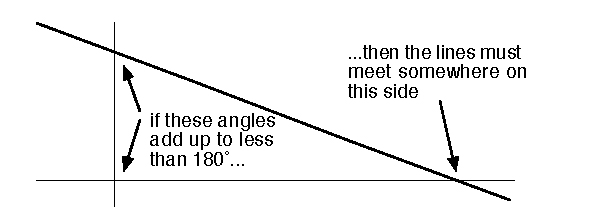
Figure 3 Euclid’s Parallel Axiom.
23 Sir Isaac Newton (1642–1727), English mathematician, physicist, alchemist, and—according to the economist John Maynard Keynes—last of the Magi. He was born the same year Galileo died, in the manor house of Woolsthorpe, near the village of Colsterworth, a few miles from Grantham in Lincolnshire. Newton became one of the three greatest mathematicians of all time, the others being Archimedes (287–212 B.C.) and Gauss. His most influential work is the Philosophiae Naturalis Principia Mathe-matica (Mathematical Principles of Natural Philosophy) of 1687, revised in 1713 and again in 1726, which set out “the system of the world.” Building on the work of predecessors such as Kepler and Galileo Galilei (1564–1642), Newton developed a new approach to nature in terms of underlying mathematical laws based on rates of change—now called differential equations. His most important discoveries were his three Laws of Motion and his Law of Gravity. He is also famous for co-inventing calculus, along with the German mathematician and philosopher Gottfried Wilhelm Leibniz (1646–1716), and for the heated controversy over priority that ensued. Newton also discovered many fundamental principles in optics, dabbled in alchemy, tried to date the events in the Bible, and served as master of the Royal Mint.
24 One of the predictions of the General Theory of Relativity is that gravity bends light by twice the amount that Newton’s laws imply. In 1919 this prediction was confirmed when Eddington (see next note) led an expedition to Príncipe Island in West Africa, where a total eclipse of the sun was due to occur. A second expedition to Sobral, in Brazil, was led by Andrew Crommelin (1865–1939) of Greenwich Observatory. The expeditions observed stars near the edge of the sun during the period of totality (only during an eclipse would these stars not be swamped by the light of the sun). The observers found slight displacements in the stars’ apparent positions—a result consistent with the relativistic predictions. Einstein sent his mother a postcard to relay the news: “Dear Mother, joyous news today. H.A. Lorentz telegraphed that the English expeditions have actually demonstrated the deflection of light from the Sun.” The amount of bending predicted by a Newtonian theory of gravity was 0.87", whereas Einstein’s prediction was double that: 1.74". (Here the symbol " means “seconds of arc,” 1/3600 of a degree.) The Sobral expedition measured 1.98" ± 0.30" and the Príncipe expedition 1.61" ± 0.30". The Times of 7 November 1919 ran the following headline: “REVOLUTION IN SCIENCE. NEW THEORY OF THE UNIVERSE. NEWTONIAN IDEAS OVERTHROWN.” Halfway down the second column is the subheading “SPACE ‘WARPED’.” Einstein became a celebrity overnight.
25 Sir Arthur Stanley Eddington (1882–1944), English astronomer, physicist, and mathematician. Born in Kendal, Eddington was both a scientist and a popularizer of science. His greatest work was in astrophysics—the structure and evolution of stars. In 1913 he became Plumian Professor of Astronomy at Cambridge University and in 1914 was appointed Director of its observatory. From 1906 to 1913 he was also chief assistant at the Royal Greenwich Observatory in London. His 1923 book The Mathematical Theory of Relativity was considered by Einstein to be the best exposition of the subject in any language. From the late 1920s onward, Eddington also published expository books on science for the general public. Space, Time, and Gravitation was published in 1920.
26 Garnett fails to mention that this letter to Nature, referring to Abbott as a prophet of space-time, was signed “W. G.” By a strange coincidence, these are Garnett’s own initials. Banchoff points out that, if we really need any further confirmation, the relatively unusual phrase jeu d’esprit in the letter’s opening sentence appears twice in Garnett and Campbell’s biography of Maxwell.
27 The technique of visualization—representing concepts by intuitively accessible geometric images —is widely used in mathematics. In 1637 René Descartes (1596–1650), in an appendix to his Discours de la Méthode (Discourse on Method), described the technique of Cartesian coordinates: representing points in the plane by pairs (x, y) of numbers defined by two mutually perpendicular axes (Figure 4a). Similarly, points in three-dimensional space can be represented by triples (x, y, z) defined by three mutually perpendicular axes (Figure 4b). (In fact, Descartes also considered systems of oblique axes, which need not meet at right angles.) Cartesian coordinates allow algebraic concepts (in the variables x, y, z) to be interpreted as geometric forms. For example, the equation
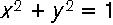
corresponds to a circle of unit radius, centered at the origin (0,0). The link is the Pythagorean theorem about right triangles: “The square on the hypotenuse of a right triangle is equal to the sum of the squares on the two adjacent sides” (Elements [1,47], the Proposition immediately following the construction of a square). This theorem implies that every point (x, y) on the unit circle satisfies the above equation and, conversely, any point that satisfies the equation lies on the circle (see Figure 5).
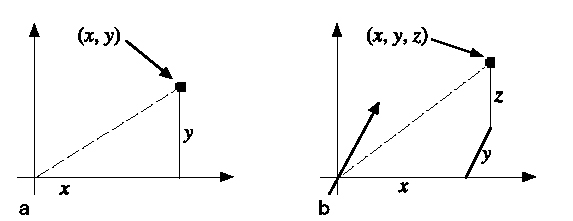
Figure 4 (a) Cartesian coordinate system on the plane. (b) Coordinate system in three-dimensional space.

Figure 5 How to turn a circle into an algebraic equation.
The technique has developed beyond all recognition since then. In Banchoff’s words,
What Abbott and other 19th-century writers envisioned has become a reality in our present day. Encounters with phenomena from the fourth and higher dimensions were the fabric of fantasy and occultism. People (other than the spiritualists) did not expect to see manifestations of four-dimensional forms any more than they expected to encounter Lilliputians or Mad Hatters. Today, however, we do have the opportunity not only to observe phenomena in four and higher dimensions, but we can also interact with them. The medium for such interaction is computer graphics. . . . Unlike its human operator, a computer has few preconceptions about what dimension it is in. Just as easily as it keeps track of three coordinates for each point, it can, when properly programmed, keep track of four or more coordinates. Often a fourth coordinate can indicate some property of the point on the screen, like color or brightness. At other times it can represent a fourth spatial coordinate, interchangeable with the other three, just as the length, width, and height of a box can be manipulated in three-space. . . . Thus we use all of our experience with interpreting two-dimensional images of three-dimensional objects to help us move up one further step to interpret the three-dimensional representations of objects which require a fourth coordinate for their effective description.
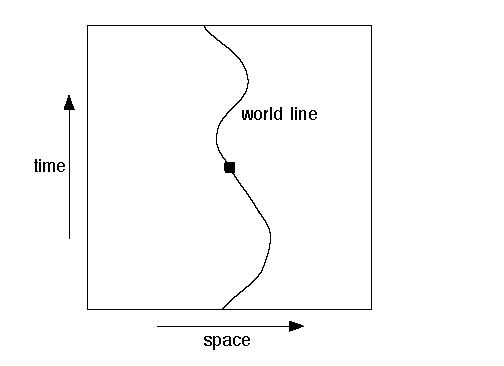
Figure 6 Minkowski’s geometry of relativistic space-time. Here space is schematically represented as being one-dimensional.
In 1908 Minkowksi applied Descartes’s idea to physics, introducing a geometric image for space-time in which time t is explicitly represented as an extra coordinate axis. For example, in cases where only one dimension x of space is relevant, space-time can be depicted as a plane (Figure 6) with one spatial axis and one temporal axis. In this interpretation, the path of a moving body in space is visualized as a single, unchanging path in space-time. For example, suppose that a point particle moves through space, occupying position x (t) at time t. The corresponding set of points (x (t ), t) forms a curve in space-time, the world line of the particle. This geometric image of space-time is extremely useful in relativity (see “The Fourth Dimension in Mathematics” in this book).
Philosophically, the “world line” image raises an interesting question about free will. In the mathematical formulation of relativity, a particle’s world line is a single, unchanging, complete object. Now, a human being is composed of innumerable particles (atoms or subatomic particles), each of which has its own world line. If humans have free will, then their particles’ world lines must “unfold” as time passes: At any instant, they exist in the past but not (yet) in the future. Therefore, if the world line has the properties assumed in the mathematical formulation of relativity, humans do not possess free will but only the illusion of free will. However, the interpretational link between mathematical descriptions of reality and reality itself is subtle, and not every concept employed in the mathematical formulation need have a direct real-world meaning, so this argument is open to many objections. The issue is central to the “process philosophy” introduced by Henri (–Louis) Bergson (1859–1941), who wrote to William James that “I saw, to my astonishment, that scientific time does not endure.” This led him to see reality as a system of ongoing processes, not fixed things. His 1899 Time and Free Will summarizes his views, which were taken up by Whitehead.