§ 2.—Of the Climate and Houses in Flatland.
AS WITH YOU, so also with us, there are four points of the compass1—North, South, East, and West.
There being no sun nor other heavenly bodies, it is impossible for us to determine the North in the usual way; but we have a method of our own. By a Law of Nature with us, there is a constant attraction to the South; and, although in temperate climates this is very slight—so that even a Woman in reasonable health can journey several furlongs northward without much difficulty—yet the hampering effect of the southward attraction is quite sufficient to serve as a compass in most parts of our earth. Moreover, the rain (which falls at stated intervals) coming always from the North, is an additional assistance; and in the towns we have the guidance of the houses, which of course have their side-walls running for the most part North and South, so that the roofs may keep off the rain from the North. In the country, where there are no houses, the trunks of the trees serve as some sort of guide. Altogether, we have not so much difficulty as might be expected in determining our bearings.
Yet in our more temperate regions,2 in which the southward attraction is hardly felt, walking sometimes in a perfectly desolate plain where there have been no houses nor trees to guide me, I have been occasionally compelled to remain stationary for hours together, waiting till the rain came before continuing my journey. On the weak and aged, and especially on delicate Females, the force of attraction tells much more heavily than on the robust of the Male Sex, so that it is a point of breeding, if you meet a Lady in the street, always to give her the North side of the way—by no means an easy thing to do always at short notice when you are in rude health and in a climate where it is difficult to tell your North from your South.
Windows there are none in our houses: for the light comes to us alike in our homes3 and out of them, by day and by night, equally at all times and in all places, whence we know not. It was in old days, with our learned men, an interesting and oft-investigated question, “What is the origin of light?” and the solution of it has been repeatedly attempted, with no other result than to crowd our lunatic asylums with the would-be solvers. Hence, after fruitless attempts to suppress such investigations indirectly by making them liable to a heavy tax, the Legislature, in comparatively recent times, absolutely prohibited them. I—alas, I alone in Flatland—know now only too well the true solution of this mysterious problem; but my knowledge cannot be made intelligible to a single one of my countrymen; and I am mocked at—I, the sole possessor of the truths of Space and of the theory of the introduction of Light from the world of three Dimensions—as if I were the maddest of the mad! But a truce to these painful digressions: let me return to our houses.
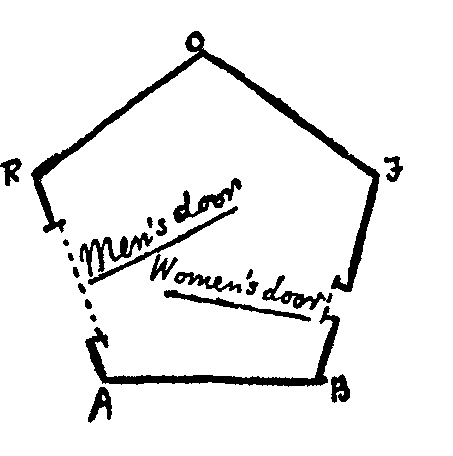
The most common form for the construction of a house is five-sided or pentagonal, as in the annexed figure. The two Northern sides RO, OF, 4 constitute the roof, and for the most part have no doors; on the East is a small door for the Women; on the West a much larger one for the Men; the South side or floor is usually doorless.
Square and triangular houses are not allowed, and for this reason. The angles of a Square5 (and still more those of an equilateral Triangle,) being
much more pointed than those of a Pentagon, and the lines of inanimate objects (such as houses) being dimmer than the lines of Men and Women, it follows that there is no little danger lest the points of
little danger lest the points of a square or triangular house residence might do serious injury to an inconsiderate or perhaps absentminded traveller suddenly running against them: and therefore, as early as the eleventh century of our era, triangular houses were universally forbidden by Law, the only exceptions being fortifications,6 powder-magazines, barracks, and other state buildings, which it is not desirable that the general public should approach without circumspection.
At this period, square houses were still everywhere permitted, though discouraged by a special tax. But, about three centuries afterwards, the Law decided that in all towns containing a population above ten thousand, the angle of a Pentagon was the smallest house-angle that could be allowed consistently with the public safety. The good sense of the community has seconded the efforts of the Legislature; and now, even in the country, the pentagonal construction has superseded every other. It is only now and then in some very remote and backward agricultural district that an antiquarian may still discover a square house.
1 The basis of (rectilinear) Cartesian coordinates in the plane is the choice of two lines meeting at right angles, the axes of coordinates. Straight lines parallel to these form a “coordinate grid” of horizontal and vertical lines, which cross at right angles where they meet. On the surface of the Earth, there is a similar (but different) coordinate system: lines of latitude and longitude. The difference is that lines of latitude and longitude are circles, not straight lines, as becomes especially apparent near the poles. However, small regions of the Earth’s surface are nearly flat, and this permits mapmakers to represent the local geography on a flat sheet of paper with a rectilinear coordinate grid. Conventionally, one coordinate axis runs from west to east and one from north to south. Thus Abbott is equipping Flatland with a Cartesian coordinate system analogous to what would be seen on a reasonably small map, such as one of the British Isles. His readers would be especially familiar with such maps because they were routinely produced by the Ordnance Survey, which was initiated in 1791 and published its first map (of the county of Kent) in 1801 on a scale of one inch to the mile. In 1858 this scale was approved by a royal commission for mapping the whole of Britain. In Flatland, however, the grid goes on forever: The territory is an infinite plane, not a sphere.
2 By making the north-south direction distinguishable from the east-west direction, Abbott is making the physics of Flatland anisotropic—that is, direction- dependent. However, he tells us that in the more temperate regions, this distinction becomes negligible and all directions appear essentially identical: Now the physics is isotropic—independent of direction. In modern mathematics these ideas are related to the symmetries of the plane—the “rigid motions” that preserve distance. There are three types of rigid motion: translation (in which the plane slides in some direction), rotation (in which it turns about some fixed center), and reflection (in which it flips over as though reflected in some mirror). See Figure 13. The anisotropic plane of Flatland is symmetric (appears not to change) under any translation and reflection in any mirror that runs north-south. In the temperate regions, it also becomes symmetric under any rotation and any reflection. This difference affects the physics of Flatland because (as Einstein emphasized in our own universe) the laws of physics reflect the symmetries of the space(-time) in which they hold.
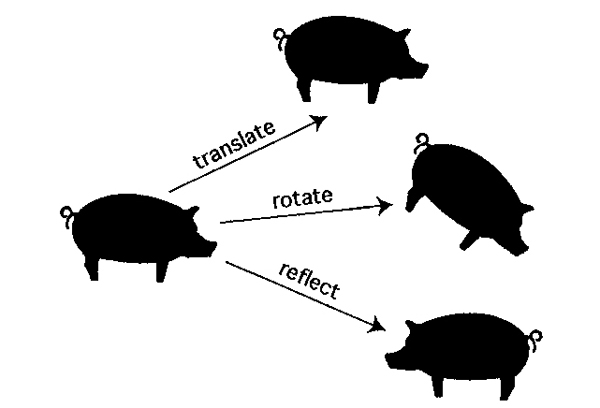
Figure 13 Three types of rigid motion in the plane.
3 Flatland’s light is like that of the schoolboy’s lamp on his page from Euclid: It is generated by a source outside the plane. Strictly speaking, this assumption contains unnecessary traces of three-dimensional thinking; the light of a truly two-dimensional universe would not require an external source. A sufficiently perceptive Flatlander might deduce the existence of the third dimension from the properties of Flatland light as Abbott describes them—contrary to his central analogy, because light in our universe does not require an external source. However, Abbott is forced to make this assumption for plot reasons. If light in Flatland came from internal sources, every inhabitant would leave a long shadow (infinitely long for a point light source; see Figure 14). Flatland vision, and the entire narrative, would be unduly complicated by shadows. For example, the method for ascertaining the rank of an individual by visual means (page 66) would depend on where the light was coming from.
This is an elegant literary solution to a narrative problem, but to some extent the problem is occasioned by Abbott’s decision to allow the Flatlanders to roam at will throughout their Euclidean plane. Humans (at least if we ignore the invention of flight) inhabit a thin region on the surface of an approximate sphere, a two-dimensional surface. Our light source comes from outside that surface: above during the day, tangential at dawn and dusk, and below (hence blocked by the Earth) at night. During the main part of the day, shadows do not block our visual perceptions, and we are in the same position as a Flat-lander with an external light source. At night, we would see only a shadow (that of the Earth) were it not for starlight, moonlight, or artificial lighting. If Abbott had pursued his analogy more relentlessly, as did Hinton and Dewdney, he would have placed his creatures on the surface of a circular disk, with a distant external sun (also a disk), and light would have come from above during the day and would have been blocked by the disk-planet at night. Of course, such an arrangement leads to other narrative problems, such as how two creatures pass each other when they meet.
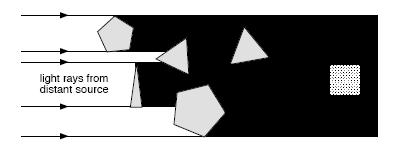
Figure 14 If there were shadows in Flatland, what would A. Square see?
A modern disk-shaped world, the aforementioned Discworld of Terry Pratchett, handles light in quite a different manner. There, the disk is supported by four giant elephants standing on the back of a huge turtle, and the sun is a small, hot body about sixty miles away that orbits half-above, half-below the plane of the disk. (One of the elephants has to keep lifting a foot to let the sun pass.) On Discworld there are two main kinds of light: light you see things by and light by which you see the dark. See The Science of Discworld for a discussion of how this is related to “privatives”: concepts defined as the absence of something else.
4 Observe the visual pun in which the letters R, O, and F, designating three vertices of the pentagonal house, spell out roof when the two adjacent sides are specified—using Euclid’s convention that the line joining a point P to a point Q should be named PQ. This is the only such visual pun in Flatland, and indeed it seems to be the only pun. Abbott had a sense of humor but reserved it for appropriate occasions. He instituted regular “Declamations” at his school, in which each boy composed and presented a speech on a topic of his own choice. The school has a legend that Robert Chalmers (1858–1938, later a high-ranking civil servant and first Baron Chalmers of Northiam) chose the topic of cremation and began by stating that it was “a grave subject and a burning question.” Abbott immediately cut the performance short with a thunderous “Sit down, Chalmers, sit down!”
5 Here and elsewhere, Abbott alludes to features of Euclidean geometry that would be taught in most school texts. Ever the educator, he can’t resist a gentle reminder to his readers. The internal angles of a regular n-sided polygon (or n-gon) are equal to 180–360/n degrees (Figure 15). For polygons with 3, 4, 5, 6 sides these angles are 60°, 90°, 108°, 120°—the angle becomes larger as the number of sides increases. Small angles make sharp points; larger angles make blunter ones. As the number of sides becomes very large (as in the so-called Circles, the Flatland priesthood), the internal angle becomes very close to 180°, a straight line. This is as “blunt” as an angle can get.
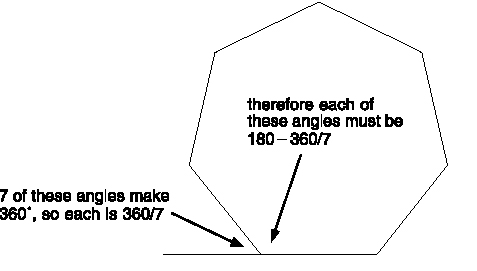
Figure 15 Internal angles of a regular n-sided polygon: here we take n=7.
6 Abbott is mostly having some fun here with the idea that sharp corners are good for keeping people away, but he was probably aware that in the seventeenth century, fortifications developed increasingly elaborate angular perimeters, often star-shaped (Figure 16). The reason, though, was not to achieve sharp edges. It was so that the bases of the walls of the fortification could be fired upon from inside the fortification itself. This was a good defense against tunnels or other methods for destroying the walls.
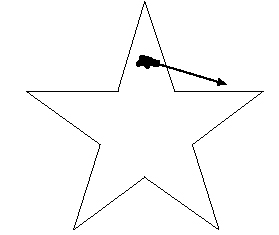
Figure 16 Star-shaped fortifications make it possible to defend the outside of the castle walls from inside the castle.