Why do the forces have such disparate strengths and ranges?We all agree that your theory is crazy. But is it crazy enough?
Niels Bohr
Before we proceed, I should warn you that everything included here is completely speculative. We’ve left the comforting confines of what we know and have leapt into the unknown. At the frontier of knowledge, there is never certainty. Indeed, what we find in our experiments at the LHC may be similar to what we discuss below, or it may be something entirely different. Keep this in mind as you read. But this chapter does give you a good idea of what physicists wonder about as the LHC goes into operation and some of the things we think that we might find.
Although we know a lot about our universe, no one would argue that we know it all. Let’s very briefly recap what we do know and see what sorts of questions are raised.
The observed universe is composed of two types of particles: quarks and leptons. Quarks are affected by all of the four forces: strong, electromagnetism, weak, and gravity. Leptons are not affected by the strong force, and a subclass of electrically neutral leptons, the neutrinos, is not affected by the electromagnetic force. We also know that there appear to be three identical generations of particles, with each generation containing heavier copies of similar quarks and leptons.
We also know about the four forces and that they have very different strengths, with gravity being ten thousand, trillion, trillion, trillion (about 1040) times smaller than the strong force. Some forces are attractive, while others are both attractive and repulsive. Each of the forces (except gravity) has been shown to be caused by the transfer of subatomic particles, called photons, gluons, and the W and Z bosons. These particles can be electrically charged or neutral and can have either zero mass or considerable mass.
Another interesting piece of the story of forces is historical. In the past, our understanding of the nature of the world was less advanced than it is now. People saw that things fell when you dropped them. They also saw that the sun rose and set, the moon had phases, and the seasons came and went. These phenomena seemed to be unrelated, until a young genius by the name of Isaac Newton showed that the cause of all of them was gravity. We could say that Newton “unified” the behavior of falling things and the motions of the heavens with a single principle that explained both phenomena.
Similarly, although people have been aware of static charge, lightning, magnetism, and light for millennia, it was only in the 1800s that they were shown to be a single thing, now called electromagnetism. More recently, in the 1960s, physicists were able to show that electromagnetism and the force governing some kinds of radioactive decay (the weak force) were actually the same thing. Particle physicists now speak of the “electroweak” force.
This historical interlude leads us to the following question. While we speak of four forces (strong, electromagnetism, weak, and gravity), or three if we use the term electroweak, is it possible that further study will reveal that these seemingly unrelated phenomena are really all the same thing?
With these thoughts in mind, let’s ask some questions:
Why do the forces have such disparate strengths and ranges?
Do the known forces end up being different ways to observe a single principle? If so, at what energy and why?
Why quarks and leptons? Why do some particles have mass and others don’t? Ditto electric charge? Why are quarks the only particles that feel the strong force? Why are there three generations? Could there be other generations?
We live in a universe with three spatial dimensions and one time dimension. Why? Could there be more? What would they look like and, if they exist, why haven’t we seen them?
Why is the universe made only of matter, when we make matter and anti-matter in equal quantities in our experiments? Where did the antimatter go?
There are other questions on which the LHC is expected to be silent or to comment on only indirectly. We’ll sketch some of them in chapter 5. But the LHC is designed to explore the questions listed above (and many, many more), as well as to accurately measure familiar phenomena at the higher energies that only the powerful collisions of the LHC can provide.
A book like this cannot possibly address all these questions. Thus we will restrict the discussion to a few major topics, outlined below.
What is the origin of mass and why do some particles have mass, while others don’t?
Will all the forces be shown to actually be the same thing, and why is it that current experiments hint that the energy at which this unification of forces might occur is so high?
Why are there generations, and do they signal that there is something smaller inside quarks and leptons?
Finally, there are two additional questions that will be discussed here but will be given less attention. The reduced attention doesn’t mean that they are of lower importance (after all, I’ve skipped some very important questions) but rather indicates that the LHC is not the only facility addressing these particular questions. But as the two more specialized of the LHC’s detectors relate to them, these two questions will be raised here. One effort is the intensive study of particles that include bottom quarks, which scientists hope will shed light on why we don’t see antimatter in the universe. The second is the study of what happens when nuclei of atoms of the element lead are slammed together at high energy. These studies will investigate what happens when matter is heated enough to allow quarks to freely escape their proton and neutron cocoons. We hope it will explore what conditions might have been during a period of the early universe about which we are currently largely ignorant.
It’s completely wrong- minded to say that “the LHC was built to discover X.” That would mean that “X” is understood well enough to know that it’s there and therefore to find it isn’t really a discovery. No, the purpose of the LHC is to study the nature of matter under conditions that are seven times hotter and more energetic than ever before observed. We will see what we see. Interesting, fascinating, or disappointing, the universe will reveal some of her secrets, and the world will become slightly less mysterious.
Scientists could not have persuaded the world’s funding agencies to support a multibillion- dollar endeavor if they didn’t have a very good reason to expect that there would be valuable discoveries. Probably the most likely and anticipated discovery for the LHC’s experiments is the explanation of why subatomic particles have mass. Rather counterintuitively, this is related to understanding how the electromagnetic and weak forces are one and the same.
The story of our understanding of the origins of mass has a complex history. It begins in the 1960s, when a bunch of young physicists were working to see if the electromagnetic and weak forces might be two sides of the same coin. When you get right down to it, this wasn’t such an obvious thing to do. After all, the weak force’s strength is about a thousand times smaller than the electromagnetic force’s and, further, the two forces have very different characteristics. For instance, the electromagnetic force has an infinite range, while the weak force’s range is very short and only felt over distances about a thousand times smaller than a proton. Also, for a particle to feel electromagnetism, the particle must have electric charge. Particles that feel the weak force can be electrically neutral (e.g., the neutrino).
Early in the 1960s, the weak force was not known to be governed by the exchange of particles in the same way that the electromagnetic force was governed by the exchange of a photon. However, by knowing the range over which the weak force is felt, physicists could calculate the mass of the weak force particle if it existed. The result was that the weak force particle had to have something like a hundred times the mass of a proton (which is considered huge in the particle realm even now and was almost unthinkable at the time). Given that the electromagnetic- carrying photon was known to be massless, this goal of unifying the weak and electromagnetic forces could well have been impossible.
So the physicists of the day did what physicists do. They made a simplifying assumption. Suppose that the mass of the weak- force carrying particle was zero like the photon. What then? Well, through an intellectual tour de force, it was accomplished; the electromagnetic force and an “almost correct” version of the weak force were shown to be governed by a single equation. This equation predicted four massless particles involved with the newly understood electro-weak force.
The actual history of this triumph is beyond the scope of this book, but it can be found in the suggested reading. The story, like most big scientific discoveries, had many heroes, although too few villains to make a topnotch movie. These physicists made false starts and made brilliant insights, both successes and failures, and by 1970, the basic understanding was in place. Physicists then predicted the heavy particles (the W and Z bosons discussed in chapter 1) that are the source of the weak force. In 1983, these particles were observed for the first time, validating the theory. Everybody was happy.
However, you might ask, “How do you get from the four massless particles discussed two paragraphs ago to the four observed electroweak particles: photon, Z boson, and the positively and negatively charged W bosons, only one of which is massless?” Understanding this link is one of the primary goals of the LHC.
In 1964, Peter Higgs, a Scottish physicist, followed a suggestion from Phillip Anderson and proposed that perhaps the universe was filled with a new kind of field. This field has come to be called the Higgs field. To get a feel for an energy field, think about the gravity here on Earth. Gravity is everywhere. It passes through everything. So too it is with the Higgs field. Then the question arises, “So what?” What does the Higgs field do, and why is it interesting? Further, how does the Higgs field solve the problem of the origin of particle mass?
To get an idea about how the Higgs field comes into play requires two crucial ideas. The first is the idea of an add- on or modifier. The idea is pretty simple. The world is a complex place, and physicists like simplicity. For instance, physicists always say that all objects fall at the same rate. Drop a marble and a bowling ball from the same height, and they’ll hit the ground at the same time. This is an experiment you can do and, after a little practice in simultaneously releasing the two objects, you can see that it is true.
Yet my students don’t really like the assertion that “all objects fall at the same rate.” They correctly point out that if one drops a hammer and a feather, they fall at quite different rates. This observation makes them unreceptive to further learning. I even show them the video of an Apollo astronaut dropping a feather and a hammer on the moon, where the two objects do indeed fall at the same rate, to no avail. And yet this video illustrates the idea of the add- on. There is no air on the moon and there is on Earth. It is air friction that invalidates this simple statement about gravity.
Yet the statement isn’t wrong. Gravity does cause all objects to fall at the same rate, as evidenced by the lunar video. It’s just that gravity isn’t the entire story. You need to include the effect of air friction to get a more accurate prediction of reality. Similarly, in the particle world, the equations that involve massless particles are also correct to a point. But it takes the Higgs field to account for the observed particle masses.
The second crucial idea is the idea of symmetry and how to break it. Symmetry is a mathematical term, describing equations. However, the idea is simpler and more universal than that, and we can understand it without using any math at all. Symmetry is when something looks unchanged after a change is made.
Figure 2.1 shows a circle and a square. The circle is the most symmetrical two- dimensional object; rotate it any way you want and it looks the same. The square is symmetrical, too, just less so. If you rotate the square by anything other than a multiple of 90°, you can see that it has been disturbed. However rotate the square by 90° (or 180° or 270° or, well, you get the picture), and you’re back to a situation that is indistinguishable from where you started.
In the math sense, the equations are said to be symmetrical if you can swap the symbols around and end up with the same equation. So in the case of the electroweak equation, if you swapped the symbols denoting the various force- carrying particles, it doesn’t matter, the equation is unchanged.
Figure 2.1. A circle can be rotated by any amount without looking different, while a square has very specific rotations after which the change is not evident.
To break symmetry is to do something that makes it obvious that a change has occurred. Suppose that you have a table with two chairs and two people sit in them, facing one another, as shown in Figure 2.2. As far as the two people are concerned, it doesn’t matter who sits in what seat; the two people are always facing one another. But now put three seats at the table and use three people. Now if two people swap seats, everyone can tell. This is because the people involved can tell that the others have moved from their left- hand to their right- hand side. The addition of the chair has broken the symmetry. In the particle case, we say that the addition of the Higgs field has made it possible to identify which symbols denote the massless photon and which the massive Z0 boson.
So let’s get back to the Higgs field. The Higgs field is an add- on to the simpler theory, just like air friction is an add- on to gravity when describing how things fall. The basic idea is that different particles will interact differently with the Higgs field. Massive particles interact more with the Higgs field, while the massless photon is not affected by the Higgs field at all. In fact, particles are massive because they interact with the Higgs field. It is this interaction that gives them their mass. Please note that in the context of physics, the word “massive” connotes something completely different from its usual meaning. It indicates that we are looking at a particle with mass, as opposed to a massless particle such as a photon.
Think of our air friction analogy. A falcon can cut through the air with the greatest of ease, plunging swiftly from great heights to catch its prey. The air has little effect on the falcon’s descent. Compare the falcon with a guy with a parachute. The parachute interacts a lot with the air. The air friction that stands in for our Higgs field gives the parachutist great mass and gives almost none to the falcon.
So thus far we’ve described what the Higgs idea means. The next and most important question is, “Why should we believe it is true?” And that’s a good question, as the Higgs idea is unproven. Even Higgs’ original 1964 paper submission was rejected, since it predicted nothing new. It was only after he added a sentence to the end of the paper that it was accepted. This sentence noted that if his hypothetical field were true, then one experimental consequence followed. He predicted a new particle.
Figure 2.2. In the case of two diners (left,shown by different circles), if they swap seats, there is no apparent change, as they still see each other as sitting across the table. However, in the event of three diners (right), a seating swap is obvious as people now can tell that their companions have moved from their left to right. The symmetry is broken.
The correspondence between a particle and a field is not an obvious one, so although we mentioned this topic in chapter 1, let’s take a brief detour to explore the idea again. Everyone is familiar with air; it is everywhere. It is gaseous and fluidic and permeates everything. You can’t take a coffee cup and scoop out some air and leave a hole behind. You can think of air as a continuous field in which we live.
And yet, it’s not. You also know that air is composed of molecules: there are “smallest bits of air.” We can say without too much sloppiness that there are air particles. If we simultaneously hold in our head the idea of a pervasive fluidic air and air molecules, then it is easy to hold in our head the idea of a field and an associated particle. A more scientific, but relatively familiar, example is an electric field. If you rub a latex balloon on your shirt and run the balloon just over your arm, you’ll feel your arm hairs affected by the electric field. This field fills the space between your arm and the balloon.
Even though the electric field is somewhat familiar, you need to remember that the electric field is composed of countless photons, just like air is made of individual air molecules. Similarly, if there is a Higgs field, there is a Higgs particle. This particle, if it exists, is called the Higgs boson.
The Higgs boson is predicted to have rather specific properties. It is electrically neutral. It has no size and no structure and yet it has mass. No structure means that we do not believe that there are any smaller particles within it. Earlier in the book I referred to such particles as fundamental. It is a scalar particle, which means it doesn’t spin. My scientific colleagues will cringe a bit at that, since “spin” in the quantum realm is subtly different from the ordinary meaning of the word. But, for our purposes, we can forgo the distinction and simply say “Higgs bosons don’t spin,” which is in contrast to every other known subatomic particle. We would then say that the Higgs boson is an electrically neutral, massive, fundamental scalar.
If such a particle did exist, how would you see it? Like all short- lived particles, you would not see it directly but rather its longer- lived decay products. We are in a tricky situation in attempting to describe the Higgs boson. As stated earlier, it has not yet been observed. However, we can predict many things about it and its properties. For example, we can predict that when the Higgs boson decays, it will generally decay into two particles with opposite electric charges. Further, because the Higgs idea is integrally related to mass, the Higgs boson will generally decay into the heaviest pair of particles it can.
So, if we look at Table 1.1, we can find the list of known particles and identify those that have the most mass. They are—in descending order of mass, measured in billions of electron volts (GeV) in which each GeV is about the mass of a proton—top quarks (175 GeV), Z bosons (91 GeV), W bosons (80 GeV), and bottom quarks (4.5 GeV). Because you can’t get something for nothing, the Higgs boson’s mass must be at least twice the mass of the objects into which it decays. For instance, to make two 175 GeV top quarks, you need a minimum of 350 GeV to start.
The reader may wonder why the unit “electron volts” are used to measure the quantity of mass, instead of the more familiar pounds or kilograms. An electron volt is a unit of energy gained by an electron when it is accelerated by a one-volt electric field. Since Einstein showed that matter and energy are the same, we can freely interchange their units and use the term electron volt to describe mass. This is an incredibly convenient choice for particle physicists and allows us to easily understand the linkage between the strength of our accelerator and the mass of the particles that we can make using it.
Because scientists believe the Higgs boson prefers to interact with heavy particles, we believe it will decay into the heaviest particles that it can. For instance, if the mass of the Higgs boson is more than 350 GeV, it can decay into a top antimatter/top-quark pair. If its mass is above 182 GeV, it can decay into pairs of Z0 bosons. Above 160 GeV, the daughter particles (or particles created as a result of decay of a given “mother” particle) will be a W+ W– pair, while between 9 and 160 GeV, the way to look for Higgs bosons is to try to find bottom-antimatter/bottom- quark pairs.
When one looks very carefully at the theoretical predictions, one sees that the situation is slightly more complex, as illustrated in Figure 2.3. The Higgs bosons definitely can decay in the ways described in the previous paragraph. But subtle physics effects also come into play that give an edge to W and Z bosons in the competition as to how the Higgs boson will likely decay. The net effect is that below a possible mass of the Higgs boson of 135 GeV, it will decay predominantly to bottom/antibottom quark pairs, while above that the preferred decay mode is into W boson pairs. However, the other decay modes we’ve listed will be possible, in addition to ones not mentioned here. LHC physicists will be looking for all of these possible types of pairs.
Figure 2.3. Predicted decay percentages of the Higgs boson. If the Higgs boson mass is below 135 GeV (billion electron volts), it preferentially decays into bottom- antibottom quarks. Above that threshold, pairs of W bosons are preferred. Above 190 GeV Higgs bosons are predicted to decay into pairs of Z bosons about 30% of the time. If the mass of the Higgs boson is larger than 350 GeV, it can also decay into a pair of top quarks.
Given that bottom quarks, W and Z bosons, and top quarks are the most likely particles into which the Higgs boson will decay, let’s explore a little bit about how these decay particles will themselves be observed in a detector. After all, we will never see the Higgs boson itself but only infer its existence from its daughter particles. The problem is that all of these daughter particles decay as well. Top quarks decay 100% of the time into bottom quarks and W bosons. So this gets us to the final point. Any LHC detector that wants to look for the Higgs boson predicted by current theory had better be able to measure W and Z bosons and bottom quarks well. So let’s briefly examine how Z bosons, W bosons, and bottom quarks decay.
Because of the nature of the strong force, quarks don’t like to be alone. If a quark is pulled away from other quarks, the strong force acts a bit like a glob of water thrown from a glass. First there is a slug of water, but surface tension pulls it apart into individual water droplets. Figure 2.4 illustrates this analogy.
Thus a single quark will turn into many particles, all traveling in the same direction. This stream of particles is called a “jet” and resembles the blast of pellets that come out of a shotgun. Just as a single shotgun cartridge turns into many pellets, all going in generally the same direction after they leave the barrel, a single quark turns into many particles all traveling in the same direction after they leave the vicinity of other quarks. Obviously, the physical mechanisms governing the two phenomena are very different, but the mental picture is very valuable.
Figure 2.4. Just as a slug of water will turn into water droplets, a single quark will turn into many particles. The physical mechanism is quite different, but the essentials of the process are quite similar. Water drawings courtesy Dan Claes.
All quarks turn into jets after a particle collision except for top quarks, which turn into bottom quarks and W bosons before there is time for a jet to form. But the daughter bottom quarks that result from the collision do form a jet.
The Z and W bosons can also decay into quarks. But these bosons have an option not available to quarks. The bosons can also decay into pairs of leptons, of which the electron is the most familiar. Figure 2.5 shows the various ways that the Z and W bosons can decay. From an experimenter’s point of view, the most interesting decays are those involving electrons, muons, and neutrinos. These are interesting because they are very distinct and generally indicate that a W or Z boson was created in the collision.
So let’s combine our information. Suppose the Higgs boson is very light, say 115 GeV (or about 115 times greater than a proton). We see in Figure 2.3 that the Higgs boson will most frequently decay into a bottom quark and an antimatter/bottom quark pair. Thus to see a light Higgs boson, you need a detector that can measure two jets very well, both coming from bottom quarks.
If the Higgs boson is much heavier than a proton, say 160 GeV, then the Higgs boson most likely decays into a W+ W– pair. Since jets can come from quarks from W boson decay as well as more ordinary quarks just getting knocked out of the proton (and jets from ordinary quarks are much, much more common), experimenters are more interested in the decays involving the leptons. Say one W boson decays into an electron and neutrino, and the other decays into a muon and neutrino. Since both the Higgs and W bosons decay rapidly, what we as experimenters would see is an electron, a muon, and two neutrinos. Since neutrinos don’t interact very much with matter, they escape undetected. So we would see an electron, a muon, and missing energy.
Figure 2.5.Top, representative decay. The tables (bottom) show the frequency by which the W and Z bosons can decay. The missing 1% in the table at the right is a rounding- off error.
Missing energy makes things a little tricky. Even though it is thought that Higgs bosons decay into W boson pairs about twice as often as they do into Z boson pairs, that Z bosons decay into pairs of charged leptons make that particle a very attractive way to look for Higgs bosons. For instance, if a Higgs boson decays into two Z bosons, and both Z bosons decay into electron/antimatter-electron pairs, the experimental signature of a Higgs boson would be two electrons and two antimatter electrons (positrons) in your detector. If one of the Z bosons decayed into a muon/antimatter- muon pair instead, then you’d see a pair of electrons and a pair of muons. The most important point is that when a Z boson decays, you see both decay particles, which you wouldn’t for the W boson.
Obviously the experimenters at the LHC will look at all possible ways in which the Higgs boson can decay, keeping in mind the various ways in which its daughter particles may themselves decay. Studying all these possibilities will keep a small army of physicists busy for quite some time. There is a way the Higgs boson can decay that is attractive to physicists. Higgs bosons decay into a quark and antimatter quark pair. These two particles can touch each other, annihilate, and emit two photons. Sifting through events in which two photons are produced may well be the way in which the Higgs boson is discovered.
While I’ve told you how people intend to search for the Higgs boson, I’ve not told you where we’re going to find it. That’s because we don’t know. As of the summer of 2008, the direct evidence for the Higgs boson is zero. That’s right . . . zero.
So why do we believe the Higgs boson or something like it exists? Because the circumstantial evidence is high. The electroweak theory—recall this is a theory that describes the behavior of photons and the W and Z bosons—has been tested to exquisite precision. The Higgs boson is an integral part of the theory, even though it is only an add- on. Given the precision with which the theory has been tested, we have reason to believe the theory, including the Higgs boson. Of course, “reason to believe” is not good enough. You need proof. Taking a legal analogy, it’s the difference in the level of proof needed to charge someone with a crime compared with the burden of proof needed to convict that person. All we really know is that the symmetry between the weak and electromagnetic force is broken. One (and the most popular) candidate is Peter Higgs’ original idea. However, there are others, one of which I will mention briefly in a moment.
Even without ironclad certainty that Higgs’ idea is right, we can still ask sensible questions. The following question may sound weird to someone who has taken high school or even college science classes, because in those classes uncertainty is not encouraged; science (and the teacher) knows all the answers. However, at the research frontier, uncertainty is rampant. In fact, much of a scientist’s postcollege education is dedicated to learning how to handle uncertainty in a rigorous way. So the question that researchers ask of the Higgs idea is the following: “Suppose that the Higgs idea is correct. If so, what do existing measurements tell us about the Higgs boson’s properties?”
We know that any possible Higgs boson mass that goes against the current electroweak theory can be ruled out. That means we can guess a Higgs boson mass, put it in our equations, and calculate something involving W or Z bosons. If that prediction turns out to disagree with our measurements, we know that was a bad guess. By using this kind of indirect logic, we know that the Higgs boson, if it exists at all, has a mass between about 50 and 175 GeV. That’s a big range, but it’s something. At least we can rule out zero, 500, and 1,000 GeV as possible masses for the Higgs boson.
However, we’ve not exhausted all ways in which we can limit the possible masses that the Higgs boson could have. Not only have we tried the “guess a Higgs boson mass and see its effects on other things” approach, but we have also looked directly for the Higgs boson. We have determined that if its mass is below 135 GeV or so, we just need to look for decaying events with two bottom quark jets.
Before the LHC was constructed, another particle accelerator inhabited the same tunnel. This accelerator was called LEP (for Large Electron Positron), and it supplied electron and positron beams to four superb detectors. Together, they looked for Higgs bosons and failed to find any. However, even though these detectors didn’t find any Higgs bosons, they had the ability to recognize the bo-sons if their mass were below the precise number of 114.4 GeV.
So, as of the summer of 2008, we know that if the Higgs boson exists that it will have a mass in the range of 114 to 175 GeV. The most likely spot is about 125 GeV or so. And, we know if it exists at all, the LHC will find it.
But “if” is the operative word. The LHC is a discovery machine. There are no guarantees. Just like Columbus could not predict that he would find the New World—indeed he predicted he would find something else entirely—neither can scientists working with the LHC say with certainty what they will find.
In fact, the Higgs idea is not the only one that could explain electroweak symmetry breaking. A theory called technicolor explains electroweak symmetry breaking in an entirely different way, involving fermions (particles with a half- integer spin such as electrons and protons) instead of Higgs bosons. Recall that Higgs bosons are believed to be scalar, or having no spin. We’ll come back to the concept of spin later in the chapter.
There are also theories that predict a Higgs- boson- like particle, except in these theories, the Higgs boson is itself composed of particles within this purported particle. One idea is that the Higgs boson consists of top quarks in a manner similar to how the proton contains up and down quarks. Until we make measurements that tell us how the universe actually acts, we cannot definitively rule out any of these ideas yet.
Another theory that can explain electroweak symmetry breaking is one involving a principle called supersymmetry. A search for supersymmetry is another big focus for the LHC, and one we will discuss extensively soon. Theories involving supersymmetry can predict electroweak symmetry breaking in ways that don’t have that clumsy “add- on” flavor of the Higgs idea. Of course, super-symmetry predicts a whole slew of particles not yet observed, including more than one Higgs boson. This theory further suggests that these other Higgs bo-sons have an electric charge.
The bottom line is that electroweak symmetry breaking is not understood and, while the Higgs boson idea is the most popular of the ideas put forward to explain it, it is by no means a foregone conclusion that Professor Higgs’ boson is the answer. Only through experiments can we know. Assuming that there are no unforeseen difficulties, this question should be resolved within five years of the startup of the LHC and, we hope, even more quickly.
Mathematical principles govern the universe and are embodied in the equations that physicists use to make their predictions. The most critical of these principles are called symmetries. There are many kinds of symmetries, some well established and with which the reader is very familiar, and some rather nonintuitive and about which it is hoped that the LHC will say something profound. Before we can understand this particular LHC goal, we need to spend time defining some basic ideas.
Figure 2.6. Circles are the most symmetrical two- dimensional object. Do nearly anything to them, and you can’t tell that something happened.
The first idea is that of symmetry itself, a concept that we touched on earlier. Symmetry is both a mathematical and a visual or artistic concept. Basically in both math and art, a symmetry is something you can change and nobody will know.
A circle is the most symmetrical two- dimensional object. (We pick two- dimensional because this page is two- dimensional. We could as easily use three- dimensional, but then the symmetrical shape would be a sphere.) In Figure 2.6, we see that when we start with a circle, we can flip, rotate, move, or look at it again tomorrow and not tell the difference. Technically, we say that the circle is “symmetrical” under all these possible changes. For the more mathematically inclined, we’d say that the shortest distance between the center and a point on the perimeter is unchanged under these operations. See the discussion surrounding Figure 2.1 for a figure that isn’t quite as symmetrical, the square.
In physics, symmetry has a similar meaning, but it also has an added physical significance. Imagine a bug at the bottom of a bowl. To crawl out, he’ll have to do a lot of work. If he crawls out by going to the right, he’ll have to do a certain amount of work. If he tries to crawl out to the left, he has to do the same amount. Here’s the important thing: If you switch the words “right” and “left” in the last two sentences, nothing would change. Similarly, if you moved the bowl across the room or moved it from the table to the floor or vice versa, the bug’s predicament would be identical. And, assuming that he brought a snack and a little bug sleeping bag, so he’d be well fed and rested, his effort needed to get out would be the same tomorrow as well.
Getting beyond examples of bugs and bowls, physicists can write equations describing the standard model, which you recall is the theory that embodies our current understanding of the universe. In fact, the standard model equation includes all possible symmetries save one. This additional symmetry deals with how particles spin at the quantum level. Before we finish introducing this interesting new symmetry, we need to go over a couple of things about spin and quantum mechanics.
We are accustomed to thinking about certain aspects of the world as being “quantized,” or coming in discrete units. Electrons come with only one mass. It is impossible to have an electron with half the mass of the others. Similarly, electrons only have one charge. However, electrons have another feature that is not as quite as familiar. Every electron in the universe is spinning identically. This is counterintuitive, since we are used to objects being able to spin faster or slower and not having a single amount of spin that is allowed. In contrast, we’re also accustomed to being able to change mass at will. A wheelbarrow of sand can have more or less weight, depending on whether we toss in that final shovelful. And yet each electron has an identical mass. So the disparity between the standard concept of spin and the quantum concept maybe isn’t so hard to accept.
The numerical amount of spin isn’t so important. (For the technically minded, the spin of the electron is 1?2 h¯, where h¯ stands for the Planck constant and is a tiny number.) We can ignore its numeric value and just recall that all spins are expressed in units of h¯ and therefore simply drop the “h¯”, calling the spin of the electron 1?2. Not only is it true that all electrons have a spin of 1?2 but the same is also true of quarks. In contrast, the force- carrying particles—the W and Z bosons, the gluons, and the photons—all have a spin of 1, or twice that of the quark and electron. The Higgs boson, if it exists, has a spin of 0.
Further study has revealed that there are two fundamental classes of particles: the fermions, with half- integer spin (e.g., 1?2, 3?2, 5?2, and so on), and bosons, with integer spin (e.g., 0, 1, 2, 3, and so on). You’d think that a little thing like a half unit of spin wouldn’t make all that much difference, but it does. Fermions, which include quarks and electrons, are the rugged individualists of the particle world. No two fermions can be in the same space at the same time and with the same energy. This has huge consequences for chemistry, which, after all, is the study of the fermion electrons around atoms. For those who have taken chemistry, this is the source of the Pauli exclusion principle and explains a great deal about the structure of the periodic table.
Bosons, on the other hand, are gregarious. “The more the merrier” is their motto. Two bosons can be in the same place at the same time and with the same energy. No problem.
Getting back to symmetries, there remains a possible symmetry not yet observed. It is called supersymmetry, often denoted by the letters SUSY, and is predicated on the idea that you could exchange fermions and bosons everywhere in the equations (and in the universe) and nobody would notice the difference.
Well, this symmetry has not been officially added to quantum mechanics for the simple reason that it’s absurd. If we replaced the observed fermionic electrons with a boson equivalent, all of chemistry would be radically different.
Nonetheless, mathematically at least, one can think of constructing a physics theory that includes supersymmetry and in which you can swap all fermions for bosons and vice versa. It is important to note that supersymmetry is not a theory. It is a principle. It’s like “conservation of energy” for the scientifically minded or “greatest good for the greatest number” for the philosophers. There are many ways one might try to apply this guiding philosophical principle, with some adopting a “Mother Teresa” behavior to help the poor and others adopting a “Bill Gates” behavior and setting up a philanthropic foundation. The principle is “greatest good,” while a theory would be the Mother Teresa or the Bill Gates individual implementation of the principle.
Similarly, in physics, many specific theoretical models incorporate the principle of supersymmetry. But these theoretical models are not supersymmetry, per se. Supersymmetry is much bigger than that.
In 1981 someone took the conventional standard model and added super-symmetric principles to it. This new model is called the minimal supersymmetric standard model, or MSSM. As its name suggests, MSSM is the usual standard model, with the absolute minimum number of changes necessary to incorporate supersymmetry. It would be easy to overcomplicate what was done but in essence scientists added terms to the standard model equation. The standard model has terms for the matter fermions (e.g., the quarks and leptons) and for the force- carrying bosons (e.g., gluons, photons, and W and Z bosons). The MSSM had these terms, plus two more, or equivalent to the quarks and leptons, except as bosons, and the other equivalent to the force carriers, except as fermions.
With the addition of these terms, a most unsettling thing occurred. Just like the existence of the first two types of particles—fermions and bosons—in the standard model meant that of necessity quarks, leptons, and the force- carrying bosons had to exist, adding the second two terms in the MSSM predicts that still more particles must exist. Quite logically the number of particles predicted by the MSSM is precisely double those we currently know about. That we’ve never seen these extra particles has led some skeptical physicists to note (with not a little sarcasm) that at least we’ve discovered half of the particles predicted by the MSSM theory. The MSSM also requires that we have not one, but four, different Higgs bosons. Thus, if the LHC experiments find more than one Higgs boson, this will be evidence that the idea of supersymmetry has some merit.
Simple naming rules apply to these newly predicted particles. The bosonic equivalents to our familiar matter particles would have the same name, except with an “s” before them. Thus quark would become squark; lepton would become slepton, and so on. The fermionic equivalent of the familiar force- carrying particle would get an “- ino” added to the end, with occasionally a little phonetic surgery to make the word easier to say. So the W boson would become a wino (pronounced “ween- o”), photon would become photino, and so on. In all cases, we can denote a supersymmetric particle by putting a tilde (~) over the symbol, thus a photino is Ÿ, a stop squark t. Figure 2.7 gives the entire list.
Figure 2.7. The supersymmetric, or SUSY, particles have an identical organization to that of normal particles. They are indicated by adding a tilde over the abbreviation of the particle. Courtesy of Deutsches Elektronen-Synchrotron.
In a moment, we’ll get to how we might find supersymmetry in the LHC’s detectors. But in the meantime, let’s discuss why you might want to add terms to your equations that would double the number of particles you predict, with zero physical evidence that they actually exist. As I mentioned at the beginning of this chapter, there are mysteries in the universe. And, no, I’m not talking about “What do women really want?” or “Why can’t men keep the toilet seat down?” I’m talking about questions of physical phenomena. One of the interesting questions is that of force unification. Just like Newton showed that the phenomenon that keeps my cat firmly placed on my keyboard as I write is the same thing that governs the planets, current physicists hope to show that the four forces of which we are aware are really one and the same. It is not true that this idea is taken as an article of faith, nor do all physicists believe that it is inevitable. But it sure would be elegant if it were true.
In the 1960s, physicists were able to show that the weak and electromagnetic forces were one and the same (and should properly be called the “electroweak force”). Now the questions are, “Can we show that the strong force and the electroweak force are just different ways of looking at the same thing? And can we show that they are both the same as gravity?” The answer to these questions is currently no, but there are reasons to think that these questions are within the realm of the possible and that the answers may eventually become yes.
For instance, we can measure just how strong the three quantum forces (strong, electromagnetic, and weak) are. If we measure the strength at different energies (that is to say in collisions of different violence), we see that their strengths aren’t constant and actually change with energy. If we project the trend of the three forces, we see that they all become the same at the rather high energy of 1014 to 1015 GeV, or a hundred thousand billion times the mass of a proton. We call this the grand unification theory of energy. Contrast this to the energy at which the symmetry between electromagnetism and the weak force is broken, which is about 1,000 GeV. The fact that the three forces “just happen” to have the same strength at some energy is suggestive (but not proof) that they are all one and the same thing. The fact that they all merge at one particular energy is very interesting.
On closer examination, we see that the three forces do not project to exactly the same spot in the standard model theory, as shown in Figure 2.8. However, and this is a suggestive beauty of the MSSM, it is pretty easy to use super-symmetry to make the three forces merge at exactly the same energy. This is not proof that supersymmetry is right, but it gives us a warm and fuzzy feeling nonetheless.
Even without the perfect unification of supersymmetry, there is a nagging question. Why does electroweak symmetry breaking occur at so much lower an energy than the grand unification energy? That’s just weird and unnatural. It’s kind of like the finances of a billionaire. Every month, she has earnings and expenditures. Large amounts of money slosh into and out of her bank account. If at the end of every month her account had under a dollar in it that would be weird. It’s hard to imagine these large million- dollar deposits and withdrawals could balance so perfectly without some principle making it so.
If it turned out that this was her “charity account” and it was set up so that the deposits were carefully designed to cover planned donations that were automatically transferred to the charity, then the bank balance would make sense. But without the “charity principle,” it would remain very mysterious that the account would be balanced so well.
Similarly in physics, it’s rather odd to have the grand unification theory scale to be a hundred billion times greater than the electroweak symmetry breaking scale. By all rights, they should both be more similar (and nearer the high end). Thus the Higgs boson mass (recall this plays a critical role in electroweak symmetry breaking) should be much, much higher than suggested by the data we’ve collected to date. So perhaps there is a principle that explains this disparity in the unification energies, and supersymmetry seems to fit the bill quite well. If supersymmetry turns out to be true, it’s relatively easy to explain the low Higgs boson mass.
Figure 2.8. While all forces seem to approach the same strength at high energy even under the standard model (shown as No SUSY, left), it is possible using supersymmetric principles to make the three forces unify at a single energy (shown with supersymmetry, or SUSY, right). GeV = one billion electron volts; EM = electromagnetic force.
Even though we have yet to prove the concept of supersymmetry, we can make predictions about it. One prediction is that there should be twice the number of particles compared with what we currently know. So what do we know of these hypothetical particles?
The answer is very little. We know that we haven’t found them, which means that they have to have a large mass, if they exist at all. This brings us to another point. Recall what we’re talking about: supersymmetry, where the operative word is symmetry. If the symmetry of supersymmetry was, in fact, symmetrical, then the masses of the new particles would be the same as regular particles. We would see that the mass of the selectron was the same as the electron. But we don’t. That means that just as the Higgs idea (or something equivalent) breaks the symmetry between electromagnetism and the weak force, something breaks the supersymmetric symmetry as well. That’s another conundrum, about which we have some ideas. But until we start finding some new particles, this is a concern we can table for the time being.
Given that we haven’t discovered these new supersymmetric particles, we can conclude that if they exist, they must have a mass no lower than about a hundred times heavier than a proton or more. (If their mass were lower, we would have found them already.) But what would we expect to see if they’re real? The LHC is a proton collider and therefore mostly collides quarks and gluons, as they are natural constituents of protons. In a collision making supersymmetric particles, we would expect squarks and gluinos to be made most frequently as these particles also are predicted to feel the strong force.
Many different types of interactions are possible involving supersymmetric particles, but supersymmetry makes one useful and pervasive prediction. If a super symmetric particle is made, then it always has to have a supersymmetric particle in its decay. That means that supersymmetric particles will decay until the daughter particle is the lightest supersymmetric particle, or LSP. Because super symmetric particles must have a supersymmetric particle as a daughter in the decay and the LSP (by definition) is the lightest supersymmetric particle, there is no lighter possible supersymmetric daughter. Therefore, the LSP is stable.
Further, if the universe once made gazillions of supersymmetric particles, it should contain a similar number of LSPs from all the decays. Since we haven’t detected them, we know the LSPs must be electrically neutral. Consequently, they can’t interact via the electromagnetic force. The strong force is out, too, although the weak force is in according to the theory. So if supersymmetry is real, the universe should be full of LSPs, essentially a bath of heavy, neutrino- like particles. This idea has consequences for cosmology, which we return to in chapter 5.
Let’s go back to the LHC and consider an event in which we make two squarks, like the one shown in Figure 2.9. The squarks must be heavy and decay into quarks and LSPs. The quarks make jets as usual, and the LSPs escape undetected as they don’t feel the strong or electromagnetic force. So in this particular case, you’d expect to see two jets and you’d notice that energy is missing. Thus your detector would need to be able to measure jets and also to measure energy accurately enough to know some is missing. This is a crucial capability, as the one common prediction of essentially all supersymmetry- incorporating theories is the existence of an LSP that can escape the detector and thus that energy will be missing.
There are many types of collisions possible in the supersymmetry theory, more than we can discuss here. Even worse, we recall that supersymmetry is a principle and not a theory in its own right, so this means that there are many theories that include supersymmetry. Most of these theories are much more complex than the relatively simple MSSM. So killing the idea of supersymmetry will be hard. The best we can do is to disprove individual models that incorporate supersymmetry. However, we do know one thing. If (and I stress the if ) super symmetry is the explanation for why the Higgs boson mass is so low, then we must be able to find supersymmetric particles at the LHC. If we don’t, then we may not have entirely killed the principle of supersymmetry, but we will have ruled it out as an explanation for the light Higgs boson mass.
Just to make things a bit more interesting, some models that incorporate supersymmetry make predictions about the Higgs boson itself. Some of the models actually predict that there is more than one Higgs boson and even that the Higgs bosons carry an electric charge. This is clearly a very different prediction than standard Higgs theory and is therefore useful in helping us to sort out what is right.
Figure 2.9. Representative decay of supersymmetric particles. Supersymmetric particles decay until they end with the lightest supersymmetric particle (LSP) daughter. The quarks turn into jets, which are sprays of particles in the detector. The solid circles denote a spot at which an interaction occurred.
The LHC and its detectors were designed with all these questions in mind. It should be able to resolve some of this theoretical controversy. Those first few years after start- up will be unbelievably exciting, something that happens only three or four times per century.
The Victorian- era mathematician Augustus de Morgan wrote:
Great fleas have little fleas upon their backs to bite ’em,
And little fleas have lesser fleas, and so ad infinitum.
And the great fleas themselves, in turn, have greater fleas to go on,
While these again have greater still, and greater still, and so on.
This oft- quoted passage is a parody of Jonathan Swift’s 1733’s On Poetry: A Rhapsody. Although this was written about poetry, scientists have taken those lines as a metaphor for the natural world. As one learns about the microworld, one is quickly faced with the observation that all matter is made of molecules. Molecules are in turn made of atoms, which are themselves made of electrons and atomic nuclei. The nuclei are made of protons and neutrons, and these are composed of quarks. This progression to ever- tinier structures is illustrated in Figure 1.4.
However, as far as we know, quarks and electrons are it. That’s the end of the line as far as structure goes. Unlike the atom or the proton, both of which have a rich structure with complex interactions between their components, quarks and electrons are currently believed to have no internal structure at all. Both theoretically and physically, they are considered to be mathematical points.
Of course anyone with an ounce of imagination can’t help saying, “Now just hold on a minute. Why couldn’t the quarks and leptons themselves have structure?” Well there’s only one possible answer and it is, “They could.” The quarks and electrons (and, by extension, all leptons) could be made of even smaller objects. Or they (rather improbably) may indeed be fundamental (i.e., structureless). In the following pages we consider the evidence for structure as well as how we might winnow out the answer to that question.
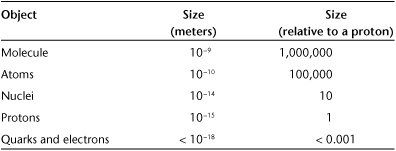
Before we proceed farther, let’s consider the sizes involved. For convenience, they are tabulated in Table 2.1. Everything in the microworld is small. A single molecule is so small that you could lay a million of them side by side in a single millimeter. They are so small that you can’t use ordinary light to see them. And yet, such smaller objects are enormously large; they are a billion times larger than the sizes explored at the research frontier.
Molecules are composed of atoms, which are about a tenth their size. This factor of ten is not very precise, as there are many kinds of molecules, from hydrogen, consisting of just two hydrogen atoms (H2), through simple sugar, with 24 atoms (C6H12O6), to large organic molecules, consisting of hundreds of atoms. However, we can roughly say that a millimeter is ten million times larger than an atom.
The mental picture of an atom as a little solar system, with a nuclear sun and planetary electrons, is flawed and yet not without merit. It highlights the fact that an atom consists of mostly empty space, with the electrons swirling frenziedly far from a small, dense nucleus. Figure 1.2 (and the relevant discussion in text near the figure) gives an idea of the relative sizes involved. Most important for our purposes, this figure shows just what a tiny fraction of the atom the nucleus takes up. The radius of the nucleus is about ten thousand times smaller than the atom, and the nucleus takes up but a trillionth of the volume.
The nucleus of the atom consists of protons and neutrons, packed tightly together. My mental picture of the nucleus is a mass of frog eggs, or marbles after being handled by a toddler with very sticky fingers. Each proton or neutron is about 10–15 meters wide and you would need a trillion laid end- to- end to span a single millimeter. That’s small.
Protons and neutrons contain within them quarks and gluons. The simplest way to think of a proton is that there are two up quarks and one down quark stuck in a force field of gluons. Think of three Ping- Pong balls in one of those air- blown lottery machines and you get the basic idea.
Table 2.1 The enormous range in size of the supersmall
The mental picture of quarks as Ping- Pong balls has one major drawback. Ping- Pong balls are large compared with a lottery machine. Quarks are small. So maybe a better mental picture of the proton is three little flecks of Styrofoam in the same machine.
So what do we know of the size of quarks? Earlier I said that they have no size, and that’s certainly how the current theory treats them. However, as an experimenter, I’m more concerned with measurements. You the reader must be curious as to what measurements have revealed the size of a quark to be. And now the answer . . . a drum roll, please . . . they haven’t. This doesn’t mean we know nothing. We’ve studied this question rather thoroughly and we know very precisely how good our equipment is. If quarks (and electrons) were larger than about a thousand times smaller than a proton, we’d have seen that they have a size. In all of our experiments, we’ve never seen even the slightest believable hint of a size. We therefore conclude that while we can’t say what the size of a quark or electron actually is, we can safely say that if quarks have size at all, they are smaller than a thousand times smaller than a proton.
If this idea is hard to understand, let’s consider how small an object you can see with your eyes. You can easily see a grain of sand. With very considerable effort, you might be able to see the smallest bit of flour in your cupboard. But that’s about it. With your bare eye, you can’t see anything smaller. Thus when you decide to look at a germ with your eye, you could conclude that they have no size, but the strictly correct conclusion you should draw is that germs are smaller than a tiny fleck of flour.
With better equipment, say a powerful microscope, one can see that germs actually do have a measurable size. So once you’ve hit the limitation of your equipment, you simply need to get a more powerful microscope. The microscope that is the LHC and its two primary detectors will observe the size of quarks if they are no less than one ten thousandth of the size of a proton; in other words, they will set a limit that is about ten times smaller than is currently thought.
So, observations, intuition, and de Morgan’s ditty may be enough to reveal a casual suspicion that there may be other levels of matter that occur at ever- smaller sizes—a whole new layer or set of layers in the cosmic onion. But there are more scientific reasons as well. For instance, consider the periodic table shown in Figure 1.1. While Mendeleev intended it to be an organizational scheme, with the formulation of the theory of the nuclear atom and quantum mechanics in the first few decades of the twentieth century, it became clear that the periodic table was actually the first indication of atomic structure, half a century before this structure was truly understood.
To make this point more clearly, let’s focus on the columns at both ends of the periodic table. The leftmost column includes chemically active elements. Hydrogen, lithium, sodium, and all the rest are chemically similar and have the same valences (for those of you who recall your introductory chemistry classes). Yet each of these elements in turn is heavier than the one above them in the column. With our understanding of chemical structure, we came to understand the increasing mass as being caused by ever more protons and neutrons in the nucleus, while the chemical similarity turned out to be explained by a repeating pattern in the arrangement of atomic electrons, with each of these elements having a single electron available to interact with other atoms. These atoms have differing numbers of electrons, but all but one of them are safely packed away, unable to interact with other atoms.
The story in the right- hand column is essentially identical. Helium, neon, and argon are all chemically similar elements with increasing mass. They are all inert because of the arrangements of atomic electrons. These elements all have their electrons tidily packed away around the atom, with no stray electrons available to interact with other atoms.
The story told by the periodic table clearly hinted at atomic structure. Similiarly, the story of nuclear radiation suggests a nuclear structure. For instance, cesium (13755Cs, with 55 protons and 82 neutrons) emits an electron and becomes barium (13756Ba, with 56 protons and 81 neutrons). This decay emits a neutrino, too, although that fact was not definitively established until the 1950s. This decay could be understood as having a neutron in the cesium spit out an electron and thereby became a proton. But even before protons, neutrons, and neutrinos were understood, the idea that the nucleus of one element could change into the nucleus of another element was seen as a hint of nuclear structure.
So let’s take these historical examples and apply the reasoning to the modern world. We realize that historical lessons do not always apply. But sometimes they do.
Figure 2.10. Decay of particles that transform from one quark or lepton type to another.
Our current periodic table is shown in Figure 1.6. Its organization is different from the chemical periodic table. In the figure, there are six types of quarks. The up, charm, and top quarks all have +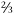
charge (in a system where the charge of a proton is +1), and the mass of the charm quark exceeds that of the up quark, which in turn is surpassed by the top quark. Similarly, the down, strange, and bottom quarks all have electric charge –
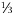, with the mass increasing as one goes toward the right.
In the case of the leptons, the electron, muon, and tau all have an electric charge of –1, with the usual mass pattern. The three neutrinos are all electrically neutral and their mass is not known, although the fact that they have nonzero (and different) mass is not in dispute.
In the modern periodic table, the chemically similar units are the rows, in contrast to the columns of Mendeleev’s table. We see that there are three generations, or carbon copies, of the same quark and lepton pattern. This is highly reminiscent of the hints that the chemical periodic table was giving us in the second half of the nineteenth century.
There is another historical similarity to consider. Just like the various atomic nuclei could decay into other nuclei, so too can the quarks and leptons. A top quark can decay into a bottom quark and a W boson. Likewise, the muon can decay into an electron and two neutrinos. These processes are sketched in Figure 2.10. Other types of quark and lepton decay are also possible. In fact, all particles in generations II and III eventually decay into the particles of generation I. One crucial clue is that the only force that can change one quark or lepton into another (we say “change the quark or lepton’s ‘flavor’”) is the weak force. Further, only the electrically charged W boson can do the job.
So while there is no hard evidence that the presence of quark and lepton generations indicates that quarks and leptons are themselves composed of smaller (and thus far undiscovered) particles, the historical analogy is powerfully suggestive and certainly warrants closer attention. That, by emitting a W boson, one can change the quark or lepton flavor is an extremely valuable clue that is screaming something important at physicists.
I just wish that I had the wits to understand what it was saying.
Even without the crucial insight that cracks the conundrum wide open, however, we can speculate intelligently on the subject and (much more important) sift through our mounds of data, looking for additional clues. As with all searches for new physical phenomena, you have to make an educated guess about what to look for and then look for it. So what are the likely experimental signatures of quark or lepton structure? Since the LHC will be colliding protons (which are essentially bags of quarks), we focus on the search for quark structure.
Before we get into specifics of quark structure, let’s consider how a hypothetical being the size of a galaxy would prove that the Earth had a size and isn’t a single point of matter. Recall that Newton’s law of gravity treats all objects, even planets, stars, and galaxies, as pointlike particles. As long as you are outside a star, you can replace an entire star with the same amount of mass concentrated at a microscopic point and not be able to tell the difference at least as far as gravity is concerned. Once you got inside the star, then the rules would change and the two cases (the star’s having a size and there being a pointlike mass) would not be equivalent.
Let’s go back to our method of deciding whether the Earth has a size or not and consider Figure 2.11. The way a galactic- sized being might figure this out would be to take comets and fling them toward Earth. As long as the comets don’t pass closer than 6,400 km (4,000 miles) from the center of the Earth (note that the radius of the Earth is the same measurement), he can’t distinguish between the real Earth and the pointlike Earth. All comets’ paths would be bent identical amounts by gravity.
When the comets are made to pass within 6,400 kilometers (4,000 miles) of the Earth’s center, well, then the two models would give different results. For the pointlike Earth equivalent, Newton’s laws would still apply, and you could use them to calculate how the comet would be affected by gravity. The real Earth would act differently. The comet would plow into the Earth’s surface, and different physical principles would apply. The electromagnetic force that governs the behavior of the atoms in the comet and the Earth would determine how big the “splat” will be. So at a particular size the relevant laws of physics change, with gravity no longer being the only relevant force and electricity (i.e., atomic forces) taking over.
There is an analogy that illustrates how the beam energy—in other words, the beams used to collide protons in the LHC or any other particle accelerator— matters a lot in the ability to see the supersmall. To illustrate this idea, we need to recall a couple of things. The first is the famous quantum mechanical postulate that objects can act both like particles and waves. It is the wave nature of our particles that is relevant here. For purposes of our discussion, we need to consider two principles: wavelength and diffraction.
Figure 2.11. As long as a comet’s path takes it outside the planet’s surface, a planet (left) and a point-like mass (right) are indistinguishable from the comet’s point of view. However, once the comet’s path brings it to a radius smaller than the Earth’s surface, you can tell the difference.
Wavelength is the distance between peaks in a wave. The wavelength of a particle is related to the energy of the particle. The higher the energy, the shorter the wavelength, as illustrated in Figure 2.12. So why is the wavelength relevant? This is where diffraction comes in. Suppose you’re looking at a lake in which there are waves moving past a stick stuck in the water to measure water level. If the waves are very long, they move past the stick without any notice, unaffected by its presence. However, if the waves are short, as shown in Figure 2.13, there is a “shadow” of the stick after the waves pass by.
The important points here are the following: (1) to see something small requires wavelengths even smaller than the object being observed, and (2) particles with high energy have short wavelengths. In fact, the wavelength of a particle with the full energy of the LHC is 2 × 10–19 meters, or about ten thousand times smaller than a proton. This means that if the quarks and leptons have a size slightly greater than this number, then the high energy beam of the LHC will be able to distinguish between a pointlike particle and one with a size. In the next chapters we will look much more closely at how the LHC, and particle accelerators in general, works.
With all these preliminaries out of the way, you might ask, “OK, but what will physicists at the LHC be looking for that could signal quark structure?” Several techniques will be used. As with all frontier research, we don’t know what the answers will be and therefore we will look in a lot of places. One of them may (and, as usual, I stress the may) be the right place to look.
Historically, one of the best places to look has been the most violent collisions. You smash two objects together and see how many collisions there are at each level of violence. Specifically, you look at the amount of “sideward violence.” Technically we call this “transverse momentum,” which means perpendicular to the beam. There are technical reasons for this choice, but mostly it is because you have to hit something hard for it to go sideward from its original direction.
Figure 2.12. The effective wavelength is related to the energy of a particle, with lower energy particles having longer wavelengths. Seeing small objects requires short wavelengths and therefore large energies.
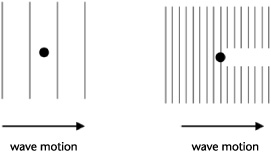
Figure 2.13. An illustration of how waves interact with a stick in the water. If the wavelength is larger than the object, the waves pass by unscathed. If the wavelength is smaller than the stick, the waves will be disturbed as they pass by it.
Let’s examine at what an experimental signature of quark structure might look like. We recall from our earlier discussion of the Higgs boson that if you smash a quark out of a proton, it forms a jet. We can simply add up all the energy of the particles in the jet and that does a pretty good job of looking a lot like the original quark. So we’ll just talk about quarks here, although experimentally we measure jets.
In Figure 2.14, we see a plot of how often a collision of a particular level of violence occurs. First, we see that low- violence collisions are more likely. Looking at the region of energy labeled “proton- proton regime,” that’s where the protons are collided with such little energy that the protons act as little billiard balls, and there is no hint of the existence of quarks. The dashed continuation of the line shows what the theory predicted would happen if the protons had no structure and always acted pointlike. However, at a particular level of violence, the decreasing trend changes. This is because at that level of energy, the collision became violent enough to see individual quarks, rather than the proton as a whole.
Figure 2.14. The correspondence between the violence (or energy) of the collision and how likely it is. At low energy, protons collide with such little violence that they don’t break up. However, when these collisions become more energetic, the protons begin to fall apart and the quarks contained within them start to be seen. The onset of seeing quarks comes with a change in the slope in the graph. The dashed line indicates the behavior we expected to see if protons had no quarks within them. As protons are collided more violently, we hope to see objects inside quarks using the same techniques. Another change in slope will hail the onset of seeing quark substructure.
Harking back to our earlier analogies, you can think of the protons as finally running into one another or the energy finally being high enough to make short wavelengths. (Indeed, the technical answer includes both ideas.) In any event, the signature that demonstrated the existence of quarks was that at a particular level of violence, there started to be more of that particular energy collision than you would expect from the lower- energy trend. In Figure 2.14, we predicted we would see the number of collisions indicated by the dashed line, but what we actually saw was the solid one. Quarks were discovered using this and other techniques in the 1970s and early 1980s.
We expect the case to be similar in the event that quark structure is observed at the LHC. Because the energy in the LHC’s beams of protons is unprecedented, perhaps we will finally make collisions with sufficient violence to start seeing more than the long- observed trend in the scattering of quarks.
Scientists have many ideas as to what might be found inside quarks (including the idea that quarks are indeed pointlike). While the “up- like” quarks have a charge of +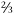, “down- like” –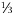, and leptons –1, the objects within quarks could have charges that are a multiple of , 
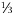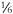, or other possibilities. Unlike the case of electroweak symmetry breaking and the Higgs boson, no favorite has emerged from the various contenders. Indeed, with precisely zero direct evidence for the existence of quark and lepton structure, most physicists have taken a “wait and see” attitude, preferring to see what hints the universe will give us. Even so, names have been proposed for these objects smaller than quarks, with the most popular being “preon” (for pre- quark). However, each theoretical physicist who has devised a theory has invented his or her own name, with subquarks, maons, alphons, quinks, rishons, tweedles, helons, haplons, and Y- particles all having been suggested. I kind of like the names quinks or tweedles myself.
One additional question on the topic of quark structure is the following: Just like the atomic model of the atom has led us to find more and more elements, would it not be true that we would expect additional generations of quarks and leptons? Why are there only three, and how do we know there aren’t four or more?
The short answer is, of course, there could be more generations. Experiments have tried to find the so- called b- prime quark, which is a yet unnamed fourth generation “bottom- like” quark. As of the summer of 2008, no evidence for its existence has been observed.
Probably the strongest evidence for there being only three generations comes from the LEP experiments that once inhabited the underground tunnel that now houses the LHC. The LEP accelerator collided electrons and positrons in the heart of four superb detectors. Much of the time, the detectors tuned their beam energy to make millions of Z bosons. With such a large sample of Z bo-sons, experimenters could study them in great detail, and the precision of these measurements is extraordinary. The LEP experimenters were able to measure the fraction of time a Z boson decayed into quarks, electrons, muons, and so on.
For purposes of our discussion, the interesting decay was when the Z boson decayed into a pair of neutrinos. In Figure 2.5, we noted that the Z boson decayed into neutrinos about 20% of the time. Since neutrinos don’t interact with matter, these kinds of decays are never observed. However, they do make their presence felt. One can calculate how often you expect the LEP beams to make a Z boson depending on how many neutrino generations there are. The LEP experiments concluded that the data were consistent with there being between 2.95 and 3.05 generations. Because the only possible answers for the number of generations are integers (1, 2, 3, 4, . . . ), that’s just a fancy way to say that LEP concluded that there were precisely three neutrino generations with considerable certainty.
So that’s pretty strong evidence that, for whatever reason, the universe allows only three generations. However, there is one little bit of wiggle room. Technically, the LEP experiments showed that there were three generations of nearly massless neutrinos. If there is a fourth generation and the neutrino of this generation is massive, then the LEP data can’t rule that out. While there is no reason to expect a generation IV neutrino to be massive, that the top quark is so much more massive than the other quarks tells us that the idea of a hypothetical heavy neutrino isn’t ludicrous. After all, there are ample examples of particles in higher generations being more massive than their lower- generation counterparts, so the idea remains viable. Like anything at the research frontier, only through experiments will the question of quark and lepton structure be resolved.
“Space. The final frontier” is the opening of a wonderful television show from the 1960s called Star Trek. A youthful Don would look forward to watching it in syndication, peering at a fuzzy picture on a UHF station. (You youngsters ask your parents what UHF was. If you know, don’t admit it, because that means you’re getting old.) In this show, a mighty starship called the U.S.S. Enterprise, captained by the legendary James T. Kirk, would scoot around the galaxy encountering situations that frequently had moral relevance to the social problems of the day.
For our purposes, the show itself isn’t so important as the ship’s engines. They were powered by antimatter. It could be true that, like many of the high- tech doodads in the show, antimatter was merely a fictional device, on par with dilithium crystals, a convenient futuristic plot device to make plausible their speedy journeys.
However, unlike many things that appear in science fiction, antimatter is entirely real. (Further, antimatter could be used, as it is the highest energy power source ever discovered, making not so silly its presence in a starship’s engines.) Antimatter is the opposite of matter and, when combined with matter, will completely annihilate into pure energy.
Antimatter is perhaps most simply understood at a particle level. For every particle discovered, there is a corresponding antiparticle. There are antimatter electrons (with the special name of positron) and antiquarks, which have no special name. Some particles, like the photon, are their own antiparticle. From antiquarks, you can make antiprotons and antineutrons. Toss in antielectrons and you can make antiatoms. With antiatoms, you could in principle make anti- anything: anti- you, anti- me, antipasto (or should that be anti- antipasto?), and on and on.
Antimatter can be created in physics laboratories by converting a prodigious amount of energy into matter and antimatter. In fact, it would take the entire energy of a Hiroshima- type nuclear explosion, converted with 100% efficiency, to make enough antimatter to make an anti- paper clip.
Figure 2.15. Examples of how energy can be turned into antimatter but only with a corresponding matter particle.
The operative words here are “into matter and antimatter.” The way antimatter is made is to convert energy into identical pairs of matter and antimatter. Figure 2.15 illustrates the general idea. Yet this leads us to one nagging problem. If we combine two observations, namely (1) matter and antimatter are made in equal pairs, and (2) we only see matter in the universe, we’re led to the obvious question “Where the heck is all the antimatter that should be here?” This remains one of the unsolved mysteries of science.
We do know some things about how the universe treats matter and antimatter. To the best of our knowledge, the strong and electromagnetic forces treat matter and antimatter identically. However, the weak force doesn’t treat them the same, as was shown in a series of experiments beginning in 1956.
Before I describe the outcome of these experiments, let’s backtrack a little and introduce a few more particles. First, this book is about the “Large Hadron Collider,” so what is a hadron? It is a subatomic particle, such as a proton or a neutron, that is composed of quarks. There are two types of hadrons: baryons and mesons. Baryons are made up of three quarks, and mesons are made up of a quark and an antiquark. Mesons are further divided into different types, including pions (made up of a quark and an antiquark of the up or down variety and is shown with the Greek letter π), neutral K mesons (which contain either a strange quark and a down antiquark or a down quark and a strange antiquark), and neutral B mesons (containing a bottom quark and a down antiquark or vice versa).
In 1964, a paradigm- shifting experiment revealed a slight asymmetry in the decay of neutral K mesons (or kaons) and gave the first indication that matter and antimatter might act slightly differently. Later, in 1999, additional measurements involving kaons revealed more about the matter- antimatter asymmetry. Knowing that some physical processes favored matter over antimatter was a huge step in understanding why we live in a matter- dominated universe, but the slight preference for matter observed in neutral kaon decays wasn’t enough. There had to be more. Even several decades ago, physicists calculated that they expected a greater asymmetry in mesons involving bottom quarks. The story of the study of neutral kaons should not be treated this cursorily, because the story involves brilliant scientific detective work. But to limit the scope of this book and to focus on the LHC, the study of neutral kaons is only sketched here. The full story is given in the suggested reading.
Figure 2.16. The 
(4S) particle, containing a bottom quark (b) and antiquark (b¯) can decay into pairs of neutral bosons called mesons containing bottom quarks. These bosons are the B¯0, containing both bottom and antimatter down quarks (d¯), and the B0, in which the quark and antiquark are reversed. This is an especially interesting process for studying the matter- antimatter asymmetry.
In 1999, two detectors, Belle in Japan and BaBar in California, were turned on with the sole purpose of making bottom- quark- containing mesons in prodigious quantities, with neutral B mesons being of particular interest. Because the study of hadrons containing bottom quarks is an important goal for the LHC, we will sketch the Belle and BaBar experiments here. While scientists working with Belle and BaBar had intermediate successes, in 2004 they announced an enormous asymmetry that preferred matter over antimatter in the decay of neutral B mesons. This preference for matter is one hundred thousand times greater than that seen in the decay of neutral kaons discussed above.
Both Belle and BaBar were detectors designed to study collisions of electrons and positrons. And not just any old collisions would do; the beam energies were carefully selected to produce the so-called (4S) meson (that’s “upsilon four S”), which consists of a bottom and antibottom quark. The (4S) can decay into two neutral B mesons. These daughter mesons are called B¯0, consisting of a down antiquark and a bottom quark, and B0, consisting of a bottom antiquark and a down quark. You’ll note that this is similar to the neutral kaon case, with the bottom quark taking the place of the strange quark. Figure 2.16 shows how the (4S) can decay, highlighting that matter bottom quarks (denoted b) and antimatter bottom quarks (denoted b¯) occur in equal quantities.
To study the decays of neutral mesons containing bottom quarks, a particular decay mode was used. This decay was into a charged K meson and a charged π meson. Because the B meson was electrically neutral, the K and π mesons had to have opposite electric charges to balance out. These mesons consisted of the following quarks: K+ (up and anti- strange), K– (strange and anti- up), π+ (up and anti- down), and π– (down and anti- up). The need for this level of detail will become apparent in a moment.
Figure 2.17. An illustration of how neutral B mesons can tranform into chargedπand K mesons. Most readers can ignore the details of the transformation and should focus only on the fact that the sign of the charged K meson identifies the parent neutral B meson.
Figure 2.17 shows how B0 and B¯0 mesons decay. Most readers can ignore everything between the circles on the ends. The most important thing to note is that if you see a K+π– decay, you know it came from a B0. A K–π+ decay comes from B¯0.
So here’s the big point. Because B0 and B¯0 mesons are made in equal quantities, you’d expect to see the K+π– and K–π+ decay modes occurring with equal frequency. But both Belle and BaBar didn’t. Both saw that there was about 80% of the K+ compared with K–. That means the number of antimatter bottom quarks seen was about 80% that of bottom quarks: less antimatter than matter.
This measurement firmly established that the study of bottom quarks could easily be crucial for shedding light on the preponderance of matter in the universe. In both Belle and BaBar, these measurements took about 200 million (4S) and ended up with about a thousand charged K and ? decays. A thousand samples of the desired decay isn’t all that many, highlighting the need for more data. In addition, the decay mode described here is only one of many being investigated. Thus many more examples of bottom- quark- containing hadrons can only help the situation.
The LHC is, in many ways, a superior source of bottom quarks compared with Belle and BaBar’s electron- positron collider. Belle and BaBar’s strength was the fact that they had an exquisitely pure sample of specific bottom- quark-containing hadrons. Unfortunately, this fact is also their weakness. They can make what they make and that’s it. In contrast, different types of quarks will abound in the LHC. Many different hadrons containing bottom quarks are possible, allowing for a much richer set of studies. These studies are a crucial point of the LHC’s design and research goal.
Most of the LHC’s experimental program will focus on colliding protons together at the highest energy; however, this is not everything the LHC will do. About one month each year, the LHC will accelerate the nuclei of atoms of the element lead and collide them together. The physics questions being explored in lead- lead collisions are vastly different than those in proton- proton ones. In proton collisions, the idea is to focus as much energy in as tiny a spot as possible, like the pressure at the point of a pin. In the case of lead collisions, the idea is to spread a lot of energy over a large volume. Energy across a large volume can reveal phenomena that a focused energy collision would miss.
Like all experimental programs, one can ask countless different questions and make countless different measurements while colliding lead nuclei. However, there is one phenomenon that stands out in the study of lead and indeed all heavy nuclei collisions. This is observing and characterizing an entirely different type of matter.
People are familiar with the three most common states of matter: solid, liquid, and gas. When you think about it, the insight that the same materials can have such vastly different properties and yet still be the same thing is pretty amazing. Air and a frozen clod of dirt (i.e., a gas and a cold solid) are entirely different things and yet steam and ice (also a gas and a cold solid) actually are the same thing.
We call these various states of matter “phases.” What most people don’t know is that there are other phases, both observed and merely hypothesized. Typically one can change matter from one form to another by heating or cooling it (or equivalently adding or subtracting energy). Let’s think about what happens to water when you add energy to it. Start with a familiar ice cube. If you heat it, first the ice cube warms up. When it reaches 0°C (32°F), the ice melts. Water changes from its solid to its liquid form, that is to say it changes phase. Heating the water changes it to steam, water’s gaseous form. In its gaseous form, individual water molecules can fly around, interacting very little with one another. In contrast, water in its liquid form exhibits very different behavior. Molecules of liquid water “know about” each other. That’s why liquid water can experience such behaviors as viscosity and surface tension. The fact that the same matter can act so differently under different energy and temperature conditions is one of the reasons we study matter. We want to see all the rich behaviors that it can exhibit.
Since gaseous water consists of individual molecules, we need to know about them. Water molecules consist of three atoms, two of hydrogen and one of oxygen. (Hence, water’s molecular formula: H2O.) In its gaseous form just above the temperature at which water boils (100°C, or 212°F), each molecule acts individually.
However, as the temperature of the steam is increased, the water molecules bounce around with more and more energy. Eventually they start bouncing into one another hard enough that the molecules are broken apart, with hydrogen and oxygen atoms individually wandering around willy- nilly.
The electrons are strongly bound to their respective nuclei, but as the temperature is raised, the nuclei are no longer able to hold onto their electrons, which are then stripped away. Oxygen and hydrogen nuclei are intermixed with free electrons. The whole mix is electrically neutral. This is actually considered a new stage of matter called a plasma. You can see an example of an electrically produced plasma in a fluorescent light bulb.
Further heating this mixture eventually will cause nuclei to break apart, leaving electrons, protons, and neutrons flying around. Temperatures as hot and energies as high as this have been achievable for decades.
We recall that protons and neutrons are made of quarks. Each proton could be thought of as roughly a bag with three quarks locked firmly within it. Technically, as was discussed in chapter 1, we say that the quarks are “confined” in the proton or neutron. The question to be asked is whether at high enough temperatures can the quarks be freed from their protective nucleonic cocoons?
Figure 2.18 illustrates the basic idea. Above a certain temperature, the quarks are unconfined and allowed to mix freely. In some ways, the situation is analogous to a tumbler full of ice cubes (the protons and neutrons in the analogy), which melt when heat (i.e., energy) is added to form liquid water (the intermixed quarks). This state of matter has historically been called “quark- gluon plasma” in analogy with the electrical plasma of fluorescent lights.
The ice cube analogy is more apt than you might think. For a long time, it was thought that a quark- gluon plasma would behave like a superhot gas, with the quarks bouncing around, ignoring one another. However in 2005, experiments at the Relativistic Heavy Ion Collider, or RHIC, on Long Island, showed that when nuclei of gold collide, the resultant is a new form of matter that acts more like a liquid. In fact, when nuclei are heated to the point where the protons and neutrons melt in place, the freed quarks and gluons act like a liquid with zero viscosity.
Viscosity is a property of liquids that basically relates to how thick they are and how much they slosh. Take out a spoon, stir your coffee, and remove the spoon. The coffee will continue to swirl around in the cup. Repeat these actions in a bowl full of warm honey and the swirling will die down quickly. We say that honey is more viscous than water. Rather surprisingly, when quarks were freed from the proton and neutrons, the resultant state of matter acted like a fluid that swirled forever. It had zero viscosity.
Figure 2.18. In ordinary matter (left), quarks are held inside protons and neutrons, three at a time. In a quark-gluon plasma (right), the quarks are no longer held inside the nucleons and are allowed to intermix freely.
So just how does one free the quarks? By heating up a nucleus, of course. Specifically, one aims beams of atomic nuclei at one another. These nuclei generally miss one another or occasionally experience a grazing impact. However, once in a great while, the two nuclei hit head- on. Just like hitting two bullets together at high speed can cause them to melt, doing so causes the nuclei to melt. (If you have trouble believing that an impact can make something warm, try banging a hammer many times on a solid rock and then feel the head of the hammer. It will be hot.)
Figure 2.19 shows an example of such a collision. In Figure 2.19a, the two nuclei are coming together at high energy. While nuclei are basically spherical, in a particle accelerator, they look more like two pancakes hitting face on. This is because of Einstein’s theory of special relativity, which says that fast- moving objects will contract in their direction of motion. Thus the sideward dimensions are not shrunken and remain circular. The result is this pancake.
In Figure 2.19b, the “pancakes” pass through one another, with some of the energy being deposited in the nuclei, heating them up. If the conditions (i.e., energy levels) are right, the nuclear matter will be heated enough to free the quarks and a quark- gluon plasma will be formed as seen in Figure 2.19c. Finally, the ensuing fireball will continue to expand and cool off, with the quarks recoalescing into protons, neutrons, and other hadrons, as shown in panel 2.19d. The collision is over.
A fair question one might ask is this: “How would you know a quark- gluon plasma if you saw one?” Like every question asked at the LHC (or any modern experiment for that matter), there will be many different ways to answer. However, we can discuss one way that will illustrate the important points. This is a technique called jet quenching.
Figure 2.19. The stages of formation of a quark-gluon plasma: a, two nuclei approach one another, flattened into a pancake shape by relativistic effects; b, the actual collision; c, the formation of the quark-gluon plasma as the shock wave heats the nuclear matter; and d, eventual expansion and cooling of the fireball. Courtesy Jeffery T. Mitchell, Brookhaven National Laboratory; simulation by the UrQMD Collaboration.
Jet quenching is a pretty cool and intuitive idea. Earlier in our discussion of the experimental signatures of the Higgs boson, we mentioned that if you knock a quark out of a proton or neutron, a jet will form. Jets, we recall, are “shotgun blasts” of particles that are the characteristic signature of a quark escaping a proton.
In a collision between any heavy nuclei (e.g., lead or gold), two quarks will sometimes hit one another just like when beams consisting only of protons collide. In the case of a collision that is violent enough to dislodge quarks from a nucleon, but not violent enough to form a quark- gluon plasma, the scattered quark can escape the fireball mostly unscathed. The quark passes by the protons, neutrons, and other hadrons in the fireball. Because these hadrons have no net color (the strong force discussed in chapter 1), effectively the quark simply doesn’t “see” them. This behavior is illustrated in Figure 2.20.
However, if the fireball is hot enough to melt the protons and neutrons into a quark- gluon plasma, then the violently scattered quarks will pass by free quarks, each with its own color. These high energy quarks will then bounce into the quark- gluon plasma quarks and sometimes never make it out of the fireball. So you’d expect to see that, as the collision becomes hotter and hotter, you’d see fewer and fewer high- energy scattered quarks (and therefore fewer jets). Thus we say that jets will be “quenched.” This is one of the many signatures for which physicists will look.
So why is this kind of study interesting? It’s because scientists believe that collisions like these re- create the conditions of the universe just instants after its creation. This is not a book on cosmology, but briefly we believe that the universe was once much smaller and hotter. This is what is known as the big bang theory. Much of the details of the very early universe are unknown, and only through intelligent speculation can we guess what might have occurred.
Figure 2.20. Jet quenching. In ordinary nuclear matter (left), a quark will scatter and leave the volume, making a jet. In a quark- gluon plasma (right), the quarks will bounce around, hitting the free quarks. Thus the quark does not leave the volume as often, with fewer jets being produced as a result.
We believe that the universe once had a temperature that was high enough that the weak force and the electromagnetic force acted the same. Above this temperature, we say that the electric and weak forces were symmetric, and the study of the breaking of this symmetry—the concept of electroweak symmetry breaking discussed earlier in the chapter—is one of the important goals of the LHC. No matter the mechanism that breaks this symmetry, be it the Higgs idea, or something else, it is thought that the universe cooled enough that the electric and weak forces became two distinct phenomena by about a trillionth of a second after the big bang.
For the period of about one trillionth of a second until a millionth (10–12– 10–6) of a second, the quark- gluon plasma is thought to have reigned supreme. The entire universe was so hot that quarks could (at least in principle) swim from one side of the universe to the other, unfettered by such considerations as protons and neutrons. It is this period in the history of the universe, called the “quark epoch,” that the study of heavy ions is intended to illuminate.
At the end of the first millionth of a second in the history of the universe, it is thought that matter had cooled enough that quarks and gluons could not move around at will. Just like water freezes at 0°C (32°F), the quark- gluon plasma froze, leaving the quarks firmly ensconced in the resultant protons and neutrons. The universe would eventually cool further, allowing protons and neutrons to combine to make helium nuclei (consisting of two protons and two neutrons). Further cooling would let electrons attach to nuclei to make hydrogen and helium, which in turn would slowly coalesce into stars and galaxies.
But all the physical phenomena that govern that later cooling are relatively well known. It is the phase transition between quarks trapped in protons and neutrons and the free- ranging, low viscosity liquid quark- gluon plasma that heavy ion collisions at the LHC will explore. Perhaps the LHC will attain temperatures that could reach another phase transition from the low viscosity quark-gluon plasma to something more akin to a gas. Only time (and experiments) will tell.
The kinds of topics discussed thus far all tend to cluster near the frontier of knowledge and, for all of them, the LHC may reveal phenomena never before observed. However, in addition to frontier- blazing experiments, there are questions that scientists ask that are more evolutionary, that is to say the answers to these questions will improve and extend our understanding of phenomena about which we already know a great deal. In fact, all of the four large detectors at the LHC (ALICE, ATLAS, CMS, and LHCb, all described in chapter 4) will spend a great deal of their time on just these kinds of measurements.
However, there are two phenomena that will be studied at the LHC by small, dedicated experiments, called Totem and LHCf (for LHC forward). While the thrust of this book is the new horizons, the uncharted vistas that we hope the LHC will let us discover, these more progressive measurements are also interesting, and I mention them briefly here. These two phenomena are called proton diffraction and cosmic rays. I sketch both of them below.
Proton diffraction takes its name from an optical analogy. In optics, diffraction is the phenomenon whereby light waves can bend around corners. In fact, diffraction is a phenomenon exhibited by all waves, as shown in Figure 2.14 in our discussion of quark structure searches. Recall that all particles have a wave equivalent, and the protons in the LHC are no exception. Thus it is expected that protons will exhibit diffractive behavior when they pass by one another.
Indeed, this kind of interaction between protons has been observed and studied for decades, most recently in detectors at Fermilab’s Tevatron, in which protons and antiprotons are accelerated to an appreciable fraction (14%) of the LHC’s energy. So studying this phenomenon at the LHC is expected to extend our current understanding, rather than open up an entirely new realm to study. Of course, there can always be surprises. This is the research frontier, after all.
The experimental signature for these kinds of studies is quite distinct. When the two protons collide, one or both of them survive the collision intact. One can contrast these kinds of collisions with the ones that are to be most frequently studied at the LHC, ones in which both protons are torn completely apart. Figure 2.21 illustrates the differences. While the destructive collisions are to be the most studied at the LHC, as they are the most violent and are most likely to reveal new physical phenomena, they are quite rare. Collisions in which at least one proton survives intact form the vast majority of proton- proton collisions. The Totem experiment is designed to explore this well- studied phenomenon at the higher energy the LHC will provide.
Figure 2.21. When protons collide, one, both, or neither protons might break up.
Cosmic rays are a generic term for particles that rain down on the Earth from outer space. They were discovered well over a century ago, when physicists used the Eiffel Tower and the new- fangled hot air balloon to show that air was more conductive at great altitudes than it was on the ground.
Our understanding of cosmic rays has improved dramatically over the past hundred years. We now know that highly energetic particles from space, typically protons, hit the Earth’s atmosphere and slam into an air molecule high above the Earth’s surface, as illustrated in Figure 2.22. The most interesting cosmic rays are highly energetic, indeed much, much higher than any particle beam we can make on Earth. To give some perspective, the highest energy cosmic rays have about a hundred million times more energy than the beams at the LHC.
To study cosmic rays is actually rather tricky. Unlike in an experiment at a particle collider, you have very little information. You can’t measure the energy or identity of the particle from space prior to the collision. You can’t put instruments around the spot in the atmosphere where it collided with the air molecule. You can’t observe exactly how the debris from outer space travels through the atmosphere. The only thing you can do is construct a detector that sits more or less at sea level 20 to 30 km (10 to 20 miles) from the collision itself. From this meager information, we try to figure out the energy of the particle from space and even the direction from which the particle came.
Figure 2.22. Protons from space hit air molecules, and the result is a shower of particles (shown by the letters e andN and Greek letters) that pass through the atmosphere and hit the Earth’s surface. Courtesy CERN.
Figure 2.23. Three identical cosmic rays at different heights and angles of incidence. The relative darkness of the gray at the ellipse represents how much of the shower will be observed at ground level. This illustrates the need to know very well the height, angle, and general details of the cosmic ray shower’s evolution.
Figure 2.23 shows what the cosmic ray experimenter is up against. Three identical cosmic rays interact in the atmosphere at different altitudes and with different incoming angles. The density of particles in the cosmic ray shower is most dense near the collision point and dies off as the particles are slowed and stopped in the atmosphere. In the figure, this loss of particles is illustrated by the lightening of the shower in the cone. The only measurement occurs in the ellipse at ground level. The figure clearly shows that these three identical cosmic ray showers will have very different signatures in the ground- based detectors.
To use the single measurement to determine the energy of the highest energy cosmic rays obviously requires a couple of things. First, you need a large detector, as a large shower can cover a vast area at ground level. Note that the Auger detector covers about 2,500 square km (1,000 square miles) of the Argentinean desert, or an area about the size of Rhode Island. The second is some method for determining both the direction and height of the start of the shower. This is usually done with timing techniques, but other methods are also used.
The third requirement and one most relevant to the LHC is a good understanding of just what happens when a very high energy proton hits another one. Without a good model of this process, the study is all guesswork. The problem is that there has never been a way to test our predictions of how such high energy protons interact with matter. The LHC will be able to provide tests never before possible. While not strictly speaking part of the LHC’s main mission, the LHCf experiment will make measurements that will help out a lot.
In this chapter, we have only mentioned the tiniest fraction of questions that will be explored by the various detectors arrayed around the LHC. The Higgs boson, supersymmetry, and quark structure are some of the main topics that will be studied, but with about 5,000 experimental physicists involved, you can expect a veritable torrent of scientific results to come from these efforts.
What will be the next big discovery? I have no idea. It may well be one of the topics mentioned here. Or, even more exciting, it may be something utterly unexpected; something that just hits us out of the blue. As they say, time will tell.
While all these fascinating physics ideas are interesting to consider, it is only through experiment that we will know which idea is right. In the next two chapters, we will learn about the equipment, both the accelerator and the detectors, that will teach of this exciting and glorious frontier.
